A Multilevel Bayesian Approach to Improve Effect Size Estimation in Regression Modeling of Metabolomics Data Utilizing Imputation with Uncertainty
Abstract
1. Introduction
2. Results
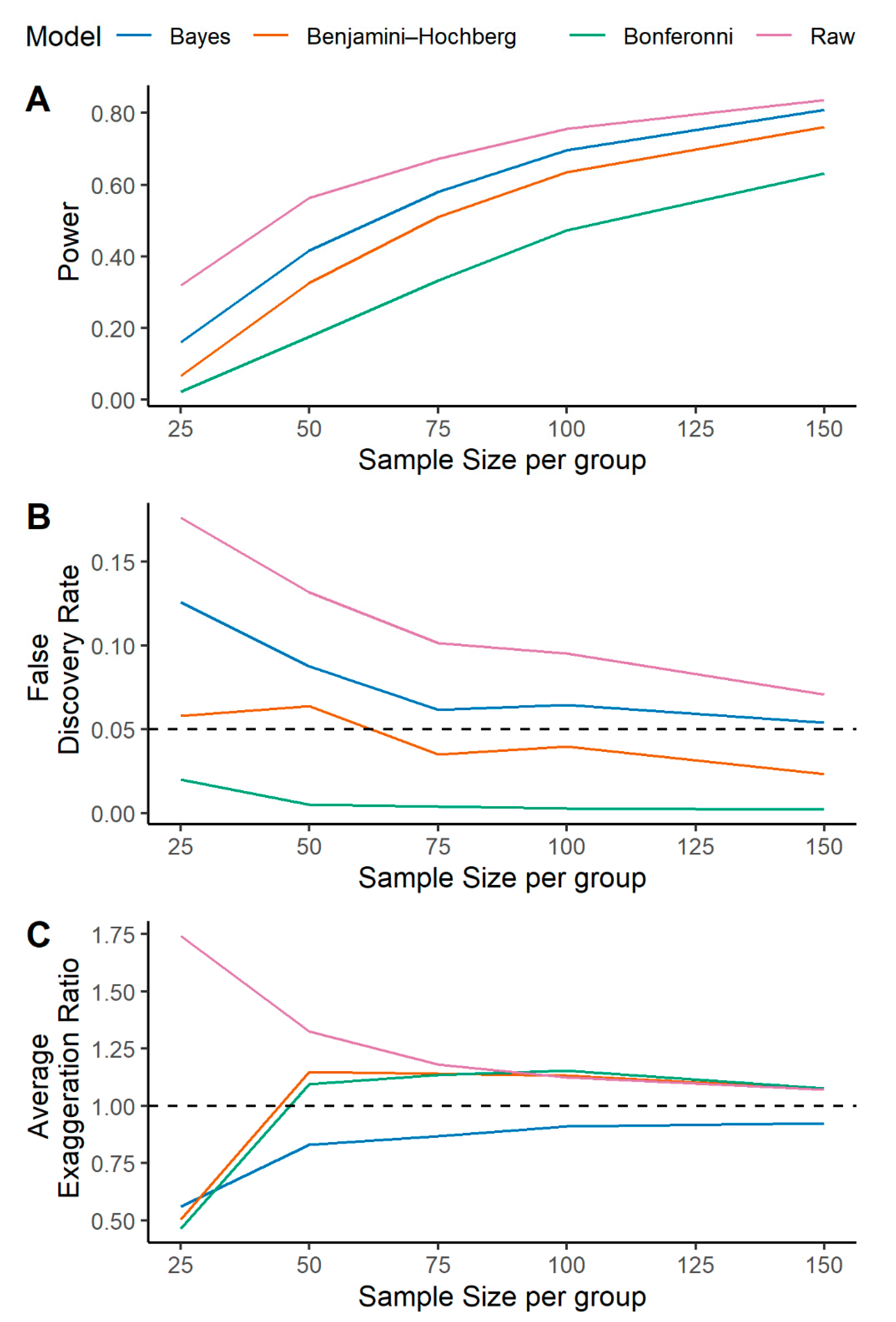
2.1. A Multilevel Bayesian Approach Has Higher Power, Controls for False Discovery, and More Reliably Estimates Metabolite Effect Size across a Variety of Simulated Scenarios
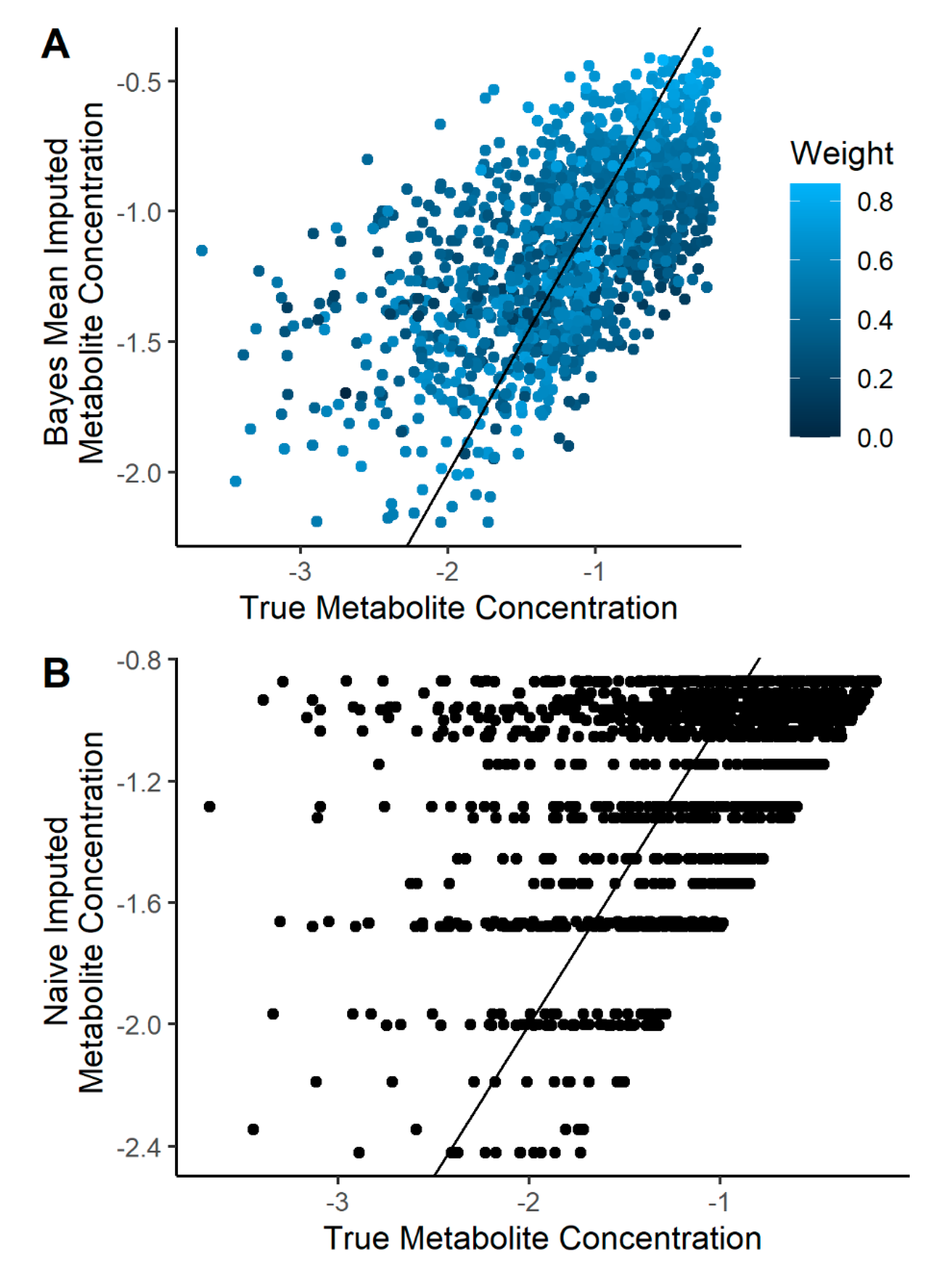
2.2. Imputation Incorporating Uncertainty Improves Predicted Metabolite Concentration
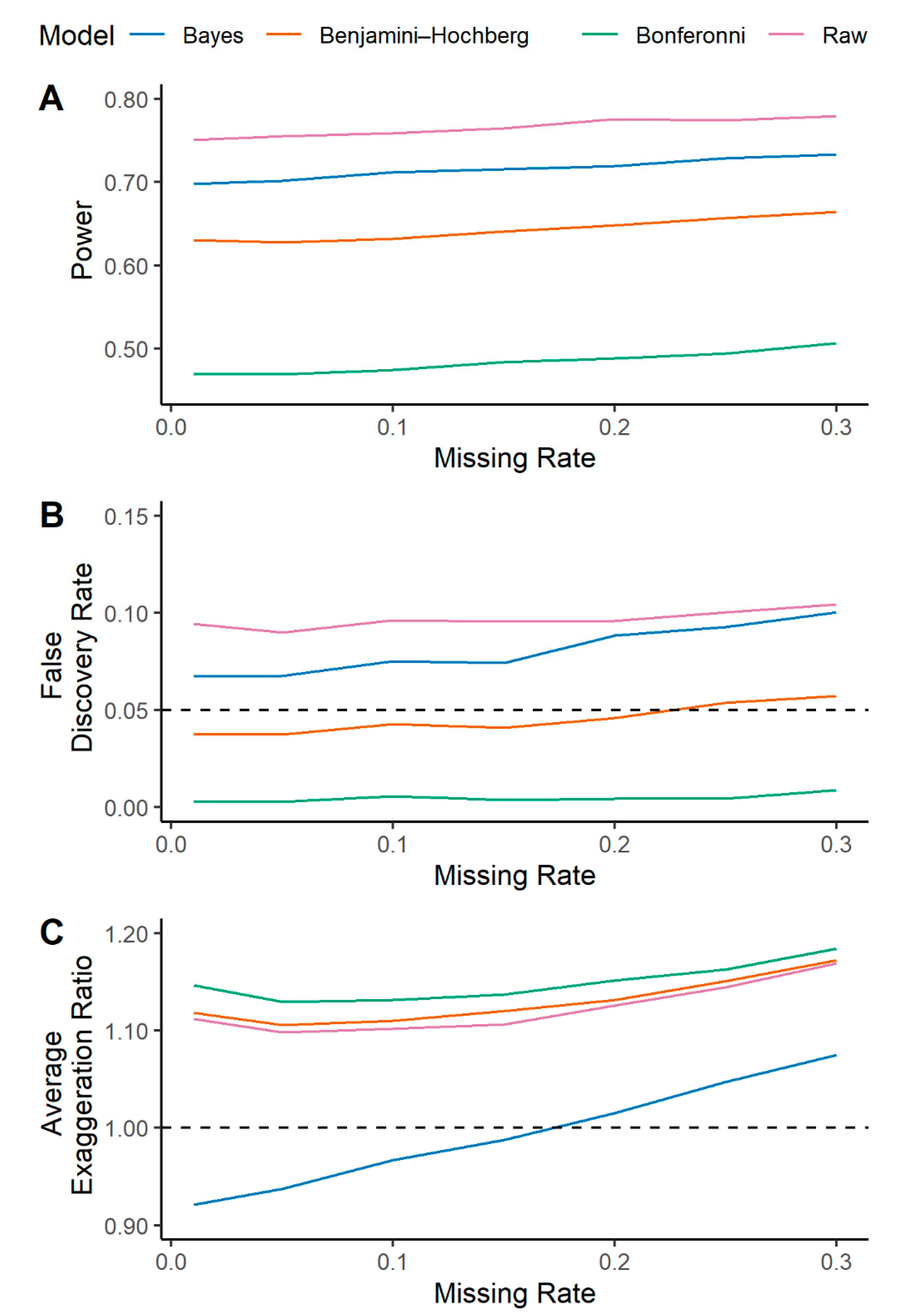
2.3. Multilevel Bayesian Models Incorporating Uncertainty into Imputation Leads to Improving Effect Size Estimation in the Presence of Missing Data
2.4. Application of Bayesian Models to Metabolomics Data
2.5. Prior Probability Distribution Sensitivity Analysis
3. Discussion
4. Materials and Methods
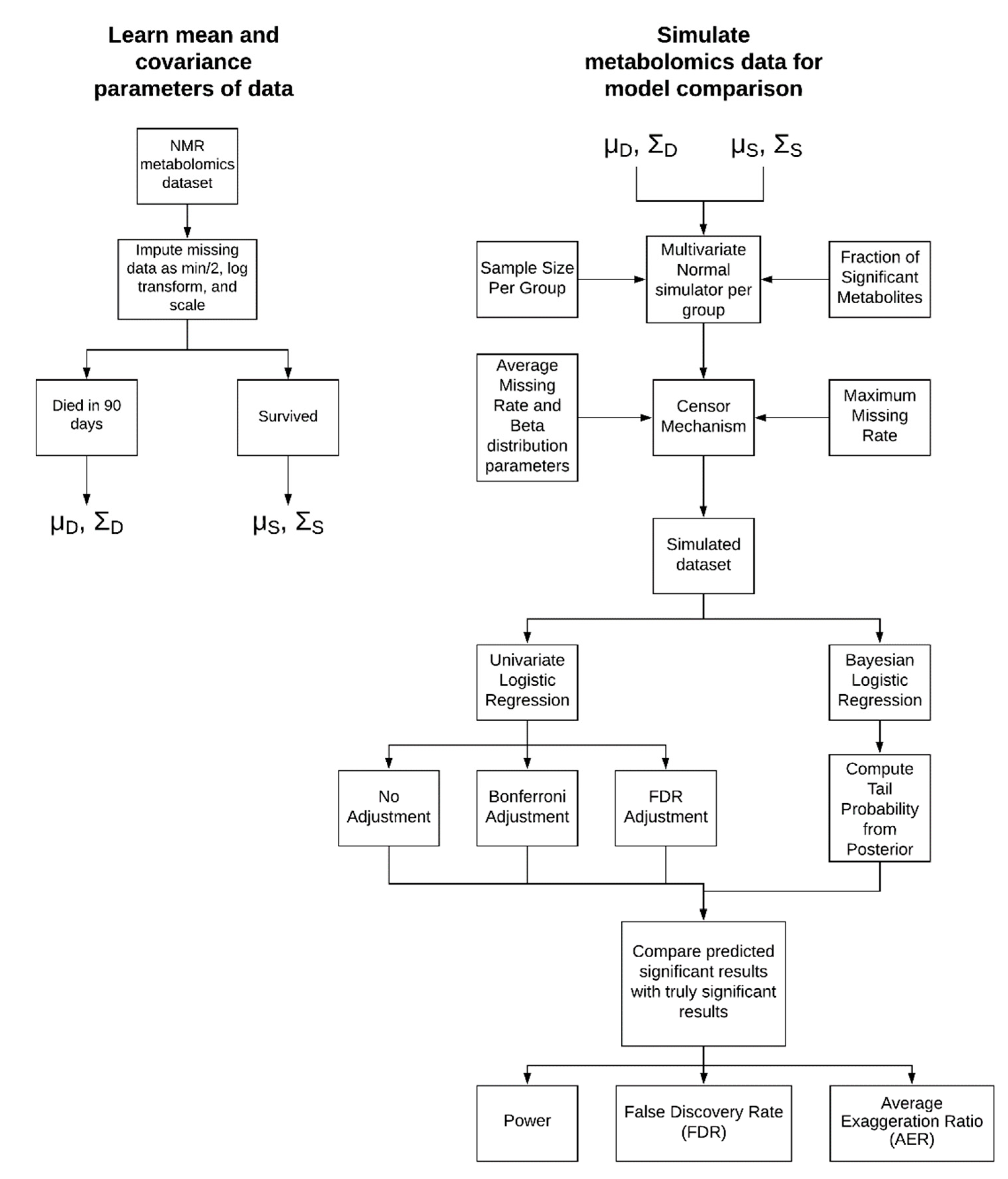
4.1. Simulation Approach
4.1.1. Parameter Learning from Experimental Data
4.1.2. Simulation Parameters
4.2. Multilevel Bayesian Logistic Regression Model
4.3. Two-Stage Imputation Model
4.3.1. Imputation Model
4.3.2. Logistic Regression with Uncertainty
4.3.3. Method Comparison
4.4. Imputation Quality Evaluation
4.5. Real Data Comparison
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Data and Code Availability
References
- Baker, M. 1500 scientists lift the lid on reproducibility. Nature 2016, 533, 452–454. [Google Scholar] [CrossRef]
- Head, M.L.; Holman, L.; Lanfear, R.; Kahn, A.T.; Jennions, M.D. The extent and consequences of p-hacking in science. PLOS Biol. 2015, 13, e1002106. [Google Scholar] [CrossRef] [PubMed]
- Amrhein, V.; Greenland, S.; McShane, B. Scientists rise up against statistical significance. Nature 2019, 567, 305–307. [Google Scholar] [CrossRef] [PubMed]
- Xiao, R.; Boehnke, M. Quantifying and correcting for the winner’s curse in genetic association studies. Genet. Epidemiol. 2009, 33, 453–462. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A.; Carlin, J. Beyond power calculations: Assessing Type S (Sign) and Type M (Magnitude) errors. Perspect. Psychol. Sci. A J. Assoc. Psychol. Sci. 2014, 9, 641–651. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A.; Tuerlinckx, F. Type S error rates for classical and Bayesian single and multiple comparison procedures. Comput. Stat. 2000, 15, 373–390. [Google Scholar] [CrossRef]
- Calin-Jageman, R.J.; Cumming, G. The new statistics for better science: Ask how much, how uncertain, and what else is known. Am. Stat. 2019, 73, 271–280. [Google Scholar] [CrossRef]
- Cumming, G. The new statistics: Why and how. Psychol. Sci. 2013, 25, 7–29. [Google Scholar] [CrossRef]
- Siskos, A.P.; Jain, P.; Römisch-Margl, W.; Bennett, M.; Achaintre, D.; Asad, Y.; Marney, L.; Richardson, L.; Koulman, A.; Griffin, J.L.; et al. Interlaboratory reproducibility of a targeted metabolomics platform for analysis of human serum and plasma. Anal. Chem. 2017, 89, 656–665. [Google Scholar] [CrossRef]
- Li-Gao, R.; Hughes, D.A.; le Cessie, S.; de Mutsert, R.; den Heijer, M.; Rosendaal, F.R.; Willems van Dijk, K.; Timpson, N.J.; Mook-Kanamori, D.O. Assessment of reproducibility and biological variability of fasting and postprandial plasma metabolite concentrations using 1H NMR spectroscopy. PLoS ONE 2019, 14, e0218549. [Google Scholar] [CrossRef]
- Chong, J.; Wishart, D.S.; Xia, J. Using MetaboAnalyst 4.0 for comprehensive and integrative metabolomics data analysis. Curr. Protoc. Bioinform. 2019, 68, e86. [Google Scholar] [CrossRef] [PubMed]
- Gross, T.; Mapstone, M.; Miramontes, R.; Padilla, R.; Cheema, A.K.; Macciardi, F.; Federoff, H.J.; Fiandaca, M.S. Toward reproducible results from targeted metabolomic studies: Perspectives for data pre-processing and a basis for analytic pipeline development. Curr. Top. Med. Chem. 2018, 18, 883–895. [Google Scholar] [CrossRef] [PubMed]
- Antonelli, J.; Claggett, B.L.; Henglin, M.; Kim, A.; Ovsak, G.; Kim, N.; Deng, K.; Rao, K.; Tyagi, O.; Watrous, J.D.; et al. Statistical workflow for feature selection in human metabolomics data. Metabolites 2019, 9, 143. [Google Scholar] [CrossRef] [PubMed]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Kruschke, J.K.; Liddell, T.M. The Bayesian New Statistics: Hypothesis testing, estimation, meta-analysis, and power analysis from a Bayesian perspective. Psychon. Bull. Rev. 2018, 25, 178–206. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A.; Hill, J.; Yajima, M. Why we (usually) don’t have to worry about multiple comparisons. J. Res. Educ. Eff. 2012, 5, 189–211. [Google Scholar] [CrossRef]
- Shah, J.; Brock, G.N.; Gaskins, J. BayesMetab: Treatment of missing values in metabolomic studies using a Bayesian modeling approach. BMC Bioinform. 2019, 20, 673. [Google Scholar] [CrossRef]
- Wei, R.; Wang, J.; Jia, E.; Chen, T.; Ni, Y.; Jia, W. GSimp: A Gibbs sampler based left-censored missing value imputation approach for metabolomics studies. PLOS Comput. Biol. 2018, 14, e1005973. [Google Scholar] [CrossRef]
- Puskarich, M.; Evans, C.; Karnovsky, A.; Gillies, C.; Jennaro, T.; Jones, A.; Stringer, K.A. Pretreatment Acetyl-Carnitine Levels Predict Mortality Benefit from L-Carnitine Treatment in Sepsis: A Pharmacometabolomics Based Clinical Trial Enrichment Strategy. In A103. SEPSIS: TRANSLATIONAL STUDIES; American Thoracic Society: New York, NY, USA, 2020; p. A2604. [Google Scholar] [CrossRef]
- McHugh, C.E.; Flott, T.L.; Schooff, C.R.; Smiley, Z.; Puskarich, M.A.; Myers, D.D.; Younger, J.G.; Jones, A.E.; Stringer, K.A. Rapid, reproducible, quantifiable NMR metabolomics: Methanol and methanol: Chloroform precipitation for removal of macromolecules in serum and whole blood. Metabolites 2018, 8, 93. [Google Scholar] [CrossRef]
- Jones, A.E.; Puskarich, M.A.; Shapiro, N.I.; Guirgis, F.W.; Runyon, M.; Adams, J.Y.; Sherwin, R.; Arnold, R.; Roberts, B.W.; Kurz, M.C.; et al. Effect of levocarnitine vs placebo as an adjunctive treatment for septic shock: The Rapid Administration of Carnitine in Sepsis (RACE) randomized clinical TrialEffect of levocarnitine vs placebo as an adjunctive treatment for septic ShockEffect of levocarnitine vs placebo as an adjunctive treatment for septic shock. JAMA Netw. Open 2018, 1, e186076. [Google Scholar] [CrossRef]
- Zhou, M.; Sharma, R.; Zhu, H.; Li, Z.; Li, J.; Wang, S.; Bisco, E.; Massey, J.; Pennington, A.; Sjoding, M.; et al. Rapid breath analysis for acute respiratory distress syndrome diagnostics using a portable two-dimensional gas chromatography device. Anal. Bioanal. Chem. 2019, 411, 6435–6447. [Google Scholar] [CrossRef] [PubMed]
- Lemoine, N.P. Moving beyond noninformative priors: Why and how to choose weakly informative priors in Bayesian analyses. Oikos 2019, 128, 912–928. [Google Scholar] [CrossRef]
- Armitage, E.G.; Godzien, J.; Alonso-Herranz, V.; López-Gonzálvez, Á.; Barbas, C. Missing value imputation strategies for metabolomics data. Electrophoresis 2015, 36, 3050–3060. [Google Scholar] [CrossRef] [PubMed]
- Karpievitch, Y.V.; Dabney, A.R.; Smith, R.D. Normalization and missing value imputation for label-free LC-MS analysis. BMC Bioinform. 2012, 13 (Suppl. 16), S5. [Google Scholar] [CrossRef]
- Lee, M.; Rahbar, M.H.; Brown, M.; Gensler, L.; Weisman, M.; Diekman, L.; Reveille, J.D. A multiple imputation method based on weighted quantile regression models for longitudinal censored biomarker data with missing values at early visits. BMC Med. Res. Methodol. 2018, 18, 8. [Google Scholar] [CrossRef]
- Wei, R.; Wang, J.; Su, M.; Jia, E.; Chen, S.; Chen, T.; Ni, Y. Missing value imputation approach for mass spectrometry-based metabolomics data. Sci. Rep. 2018, 8, 663. [Google Scholar] [CrossRef]
- Patti, G.J.; Yanes, O.; Siuzdak, G. Metabolomics: The apogee of the omics trilogy. Nat. Rev. Mol. Cell Biol. 2012, 13, 263–269. [Google Scholar] [CrossRef]
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.; Guo, J.; Li, P.; Riddell, A. Stan: A probabilistic programming language. J. Stat. Softw. 2017, 76, 32. [Google Scholar] [CrossRef]
- Gelman, A. Prior Choice Recommendations. Available online: https://github.com/stan-dev/stan/wiki/Prior-Choice-Recommendations (accessed on 22 April 2020).
- Goodrich, B.; Gabry, J.; Ali, I.; Brilleman, S. Rstanarm: Bayesian Applied Regression Modeling via Stan, R package version 2.19.3. 2020. Available online: https://mc-stan.org/rstanarm.

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gillies, C.E.; Jennaro, T.S.; Puskarich, M.A.; Sharma, R.; Ward, K.R.; Fan, X.; Jones, A.E.; Stringer, K.A. A Multilevel Bayesian Approach to Improve Effect Size Estimation in Regression Modeling of Metabolomics Data Utilizing Imputation with Uncertainty. Metabolites 2020, 10, 319. https://doi.org/10.3390/metabo10080319
Gillies CE, Jennaro TS, Puskarich MA, Sharma R, Ward KR, Fan X, Jones AE, Stringer KA. A Multilevel Bayesian Approach to Improve Effect Size Estimation in Regression Modeling of Metabolomics Data Utilizing Imputation with Uncertainty. Metabolites. 2020; 10(8):319. https://doi.org/10.3390/metabo10080319
Chicago/Turabian StyleGillies, Christopher E., Theodore S. Jennaro, Michael A. Puskarich, Ruchi Sharma, Kevin R. Ward, Xudong Fan, Alan E. Jones, and Kathleen A. Stringer. 2020. "A Multilevel Bayesian Approach to Improve Effect Size Estimation in Regression Modeling of Metabolomics Data Utilizing Imputation with Uncertainty" Metabolites 10, no. 8: 319. https://doi.org/10.3390/metabo10080319
APA StyleGillies, C. E., Jennaro, T. S., Puskarich, M. A., Sharma, R., Ward, K. R., Fan, X., Jones, A. E., & Stringer, K. A. (2020). A Multilevel Bayesian Approach to Improve Effect Size Estimation in Regression Modeling of Metabolomics Data Utilizing Imputation with Uncertainty. Metabolites, 10(8), 319. https://doi.org/10.3390/metabo10080319




