On the Use of Correlation and MI as a Measure of Metabolite—Metabolite Association for Network Differential Connectivity Analysis
Abstract
1. Introduction
2. Results
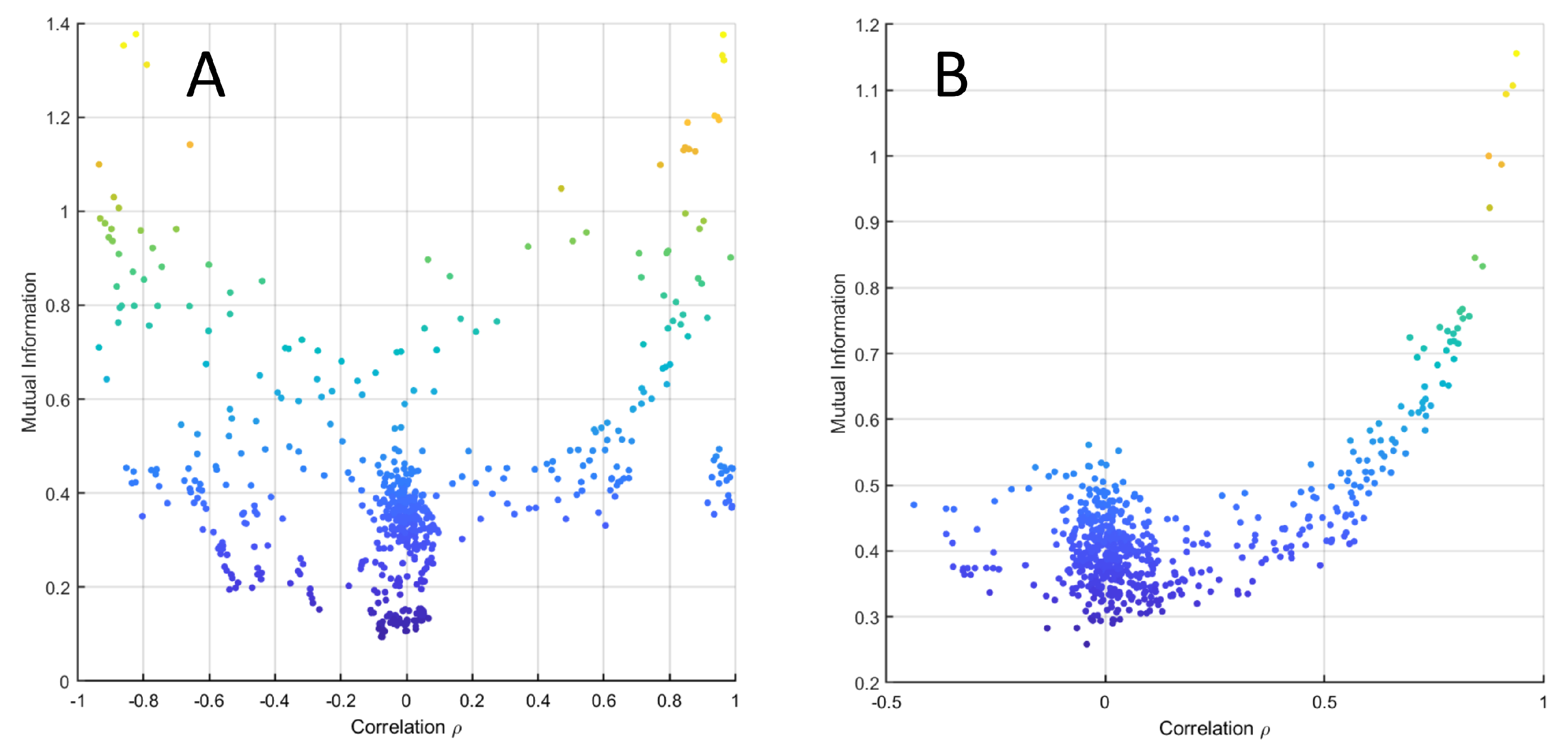
2.1. Differential Connectivity Analysis on Experimental Data
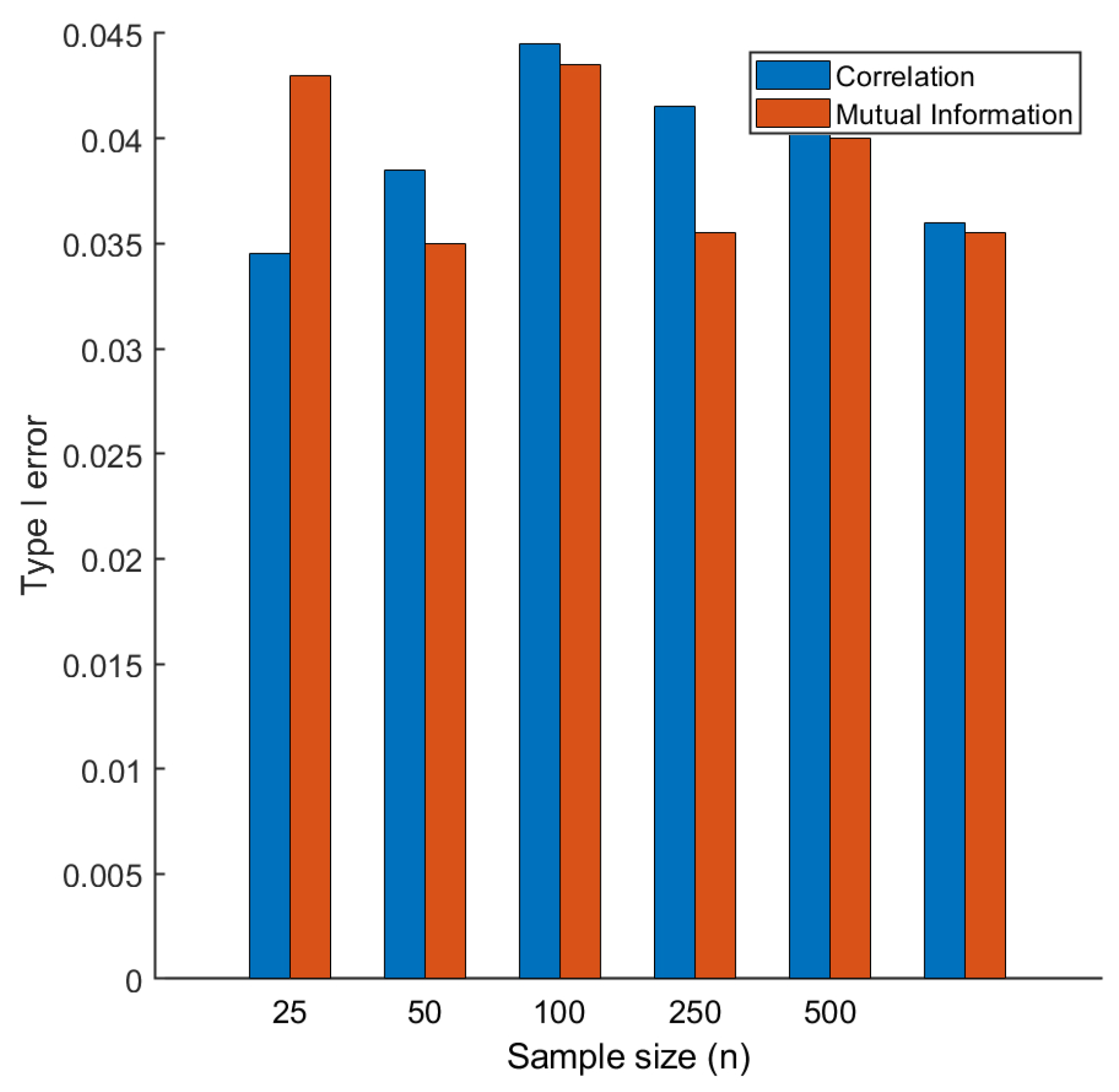
2.2. Type I Error
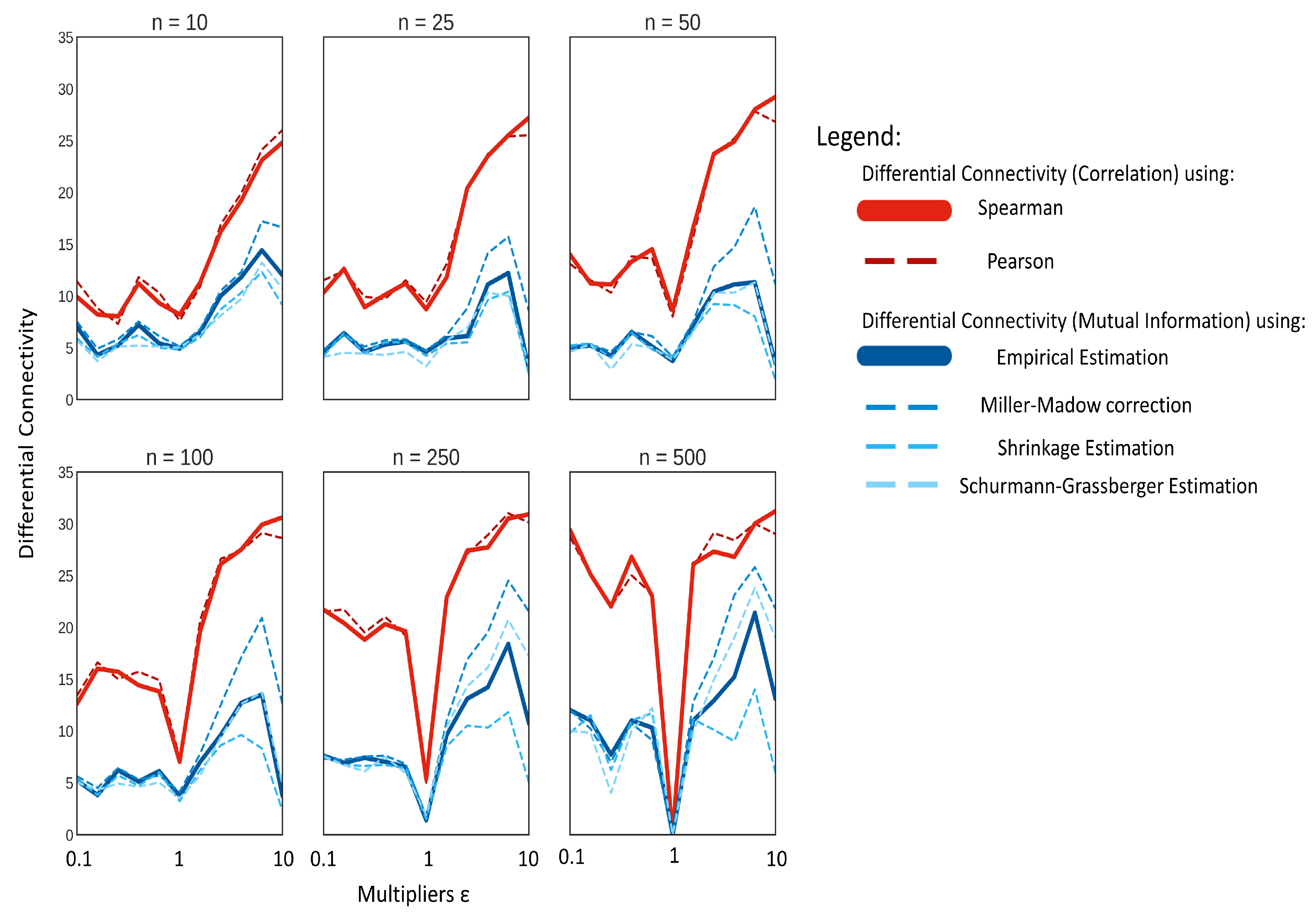
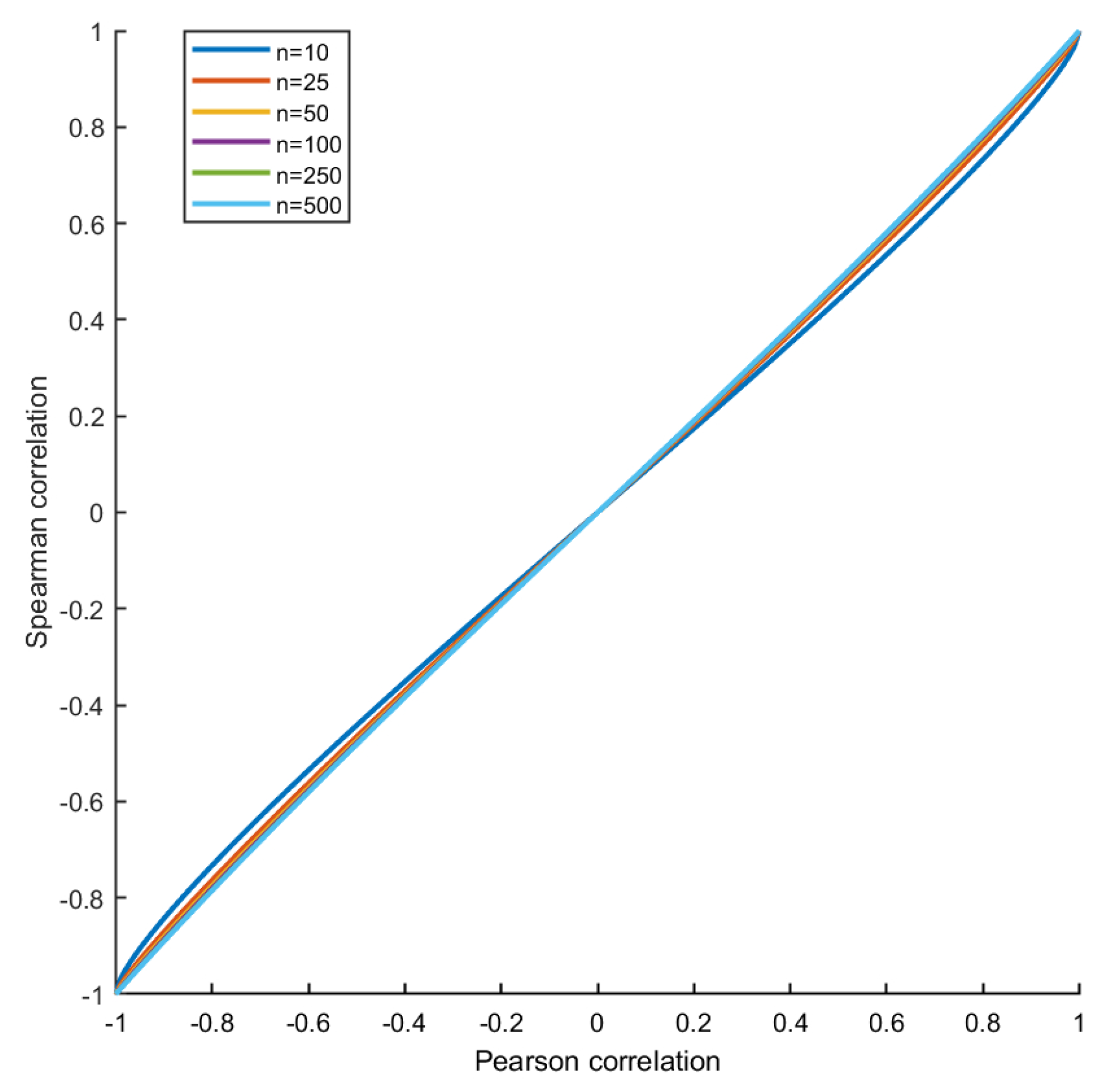
2.3. Comparison of Correlation and MI on Simulated Data with Known Correlation Structure
2.4. Comparison of Correlation and MI on Simulated Data from a Dynamic Model
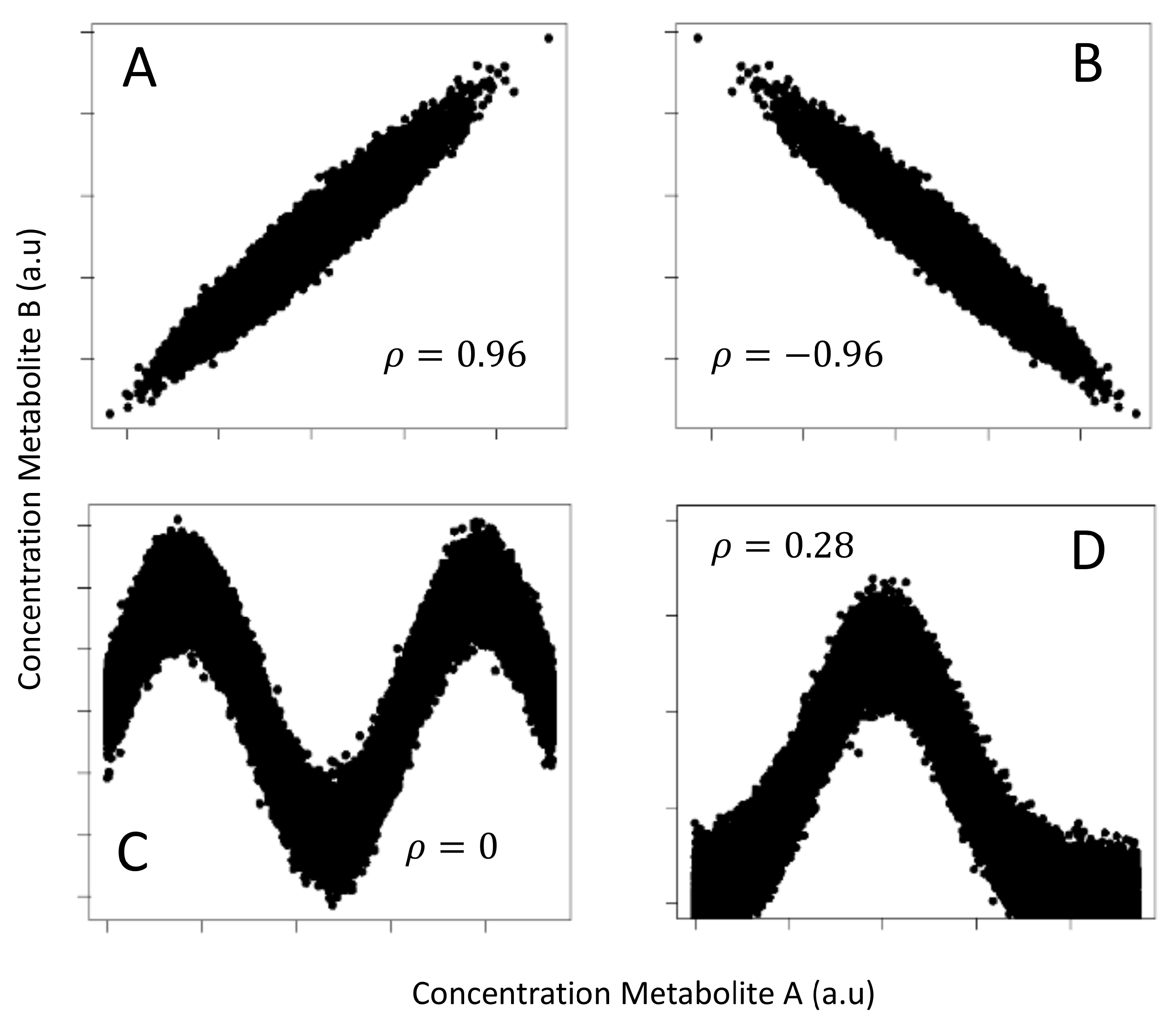
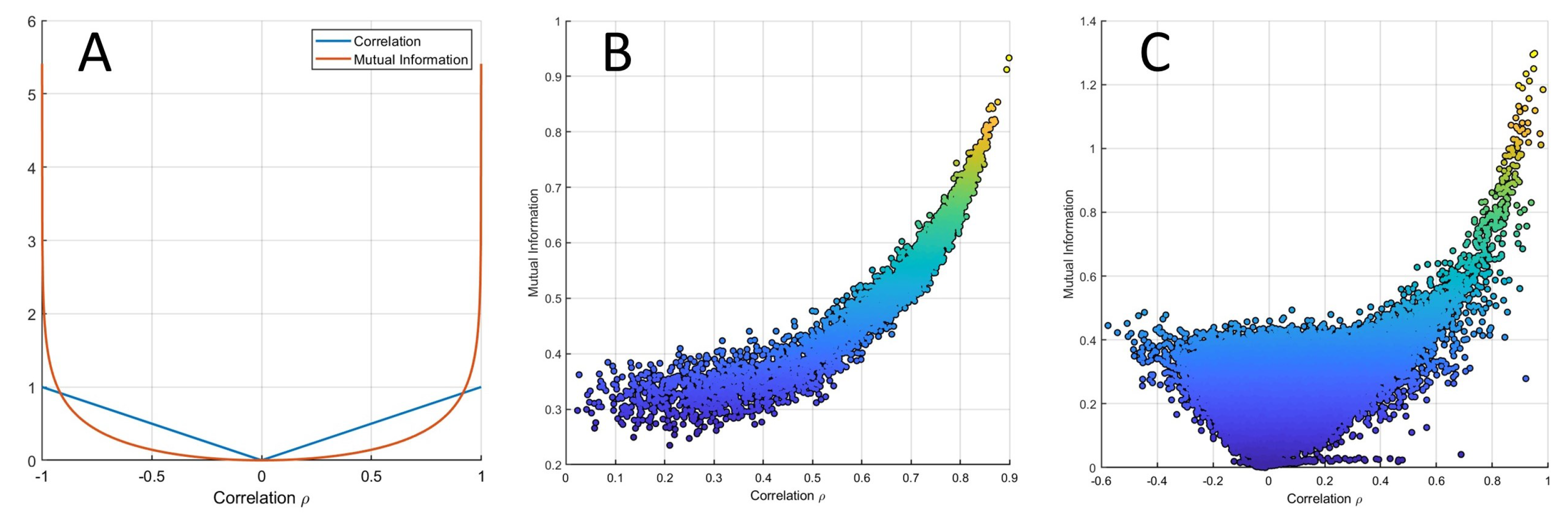
2.5. Relationship between Correlation and MI
3. Materials and Methods
3.1. Association Measures
Correlation Indices
3.2. MI
3.2.1. Entropy of Empirical Probability Distribution
3.2.2. Miller-Madow Asymptotic Bias Corrected Empirical Estimator
3.2.3. Shrinkage Estimate of the Entropy of a Dirichlet Probability Distribution
3.2.4. Schurmann-Grassberger Estimation
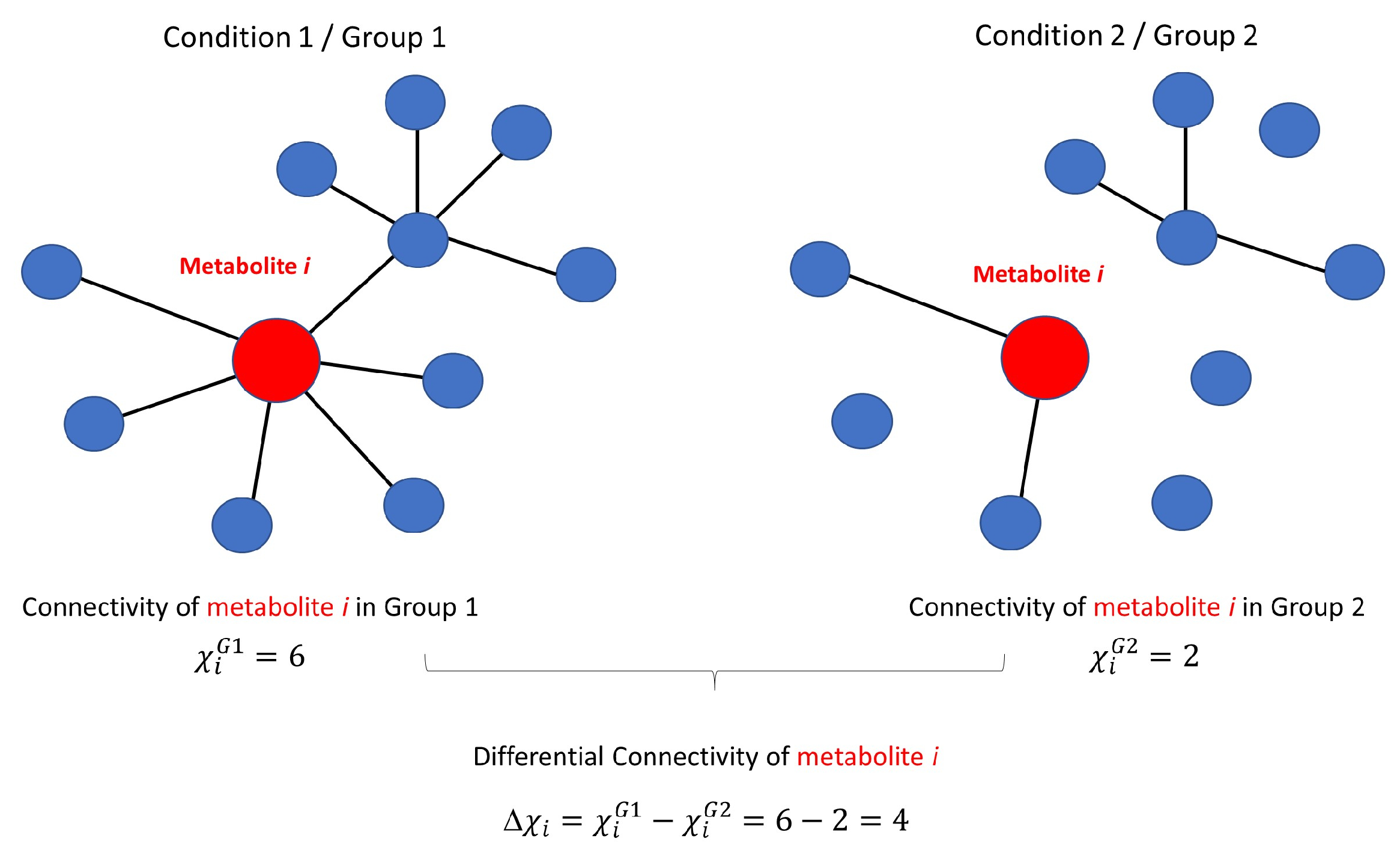
3.3. Network Concepts
3.3.1. Differential Network Analysis
3.3.2. Permutation Tests to Assess Statistical Significance of Differential Connectivity
3.4. Data Simulations
3.4.1. Toeplitz Correlation Structure
3.4.2. Hub Correlation Structure
3.4.3. Average
3.5. Data Generation Using a Dynamic Metabolic Model
Simulation of Individual Metabolite Concentration Profiles
3.6. Experimental Data
3.7. Software
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NF-κB | Nuclear Factor kappa-light-chain-enhancer of activated B cells |
| NMR | Nuclear magnetic resonance |
| MI | MI |
| MS | Mass spectrometry |
References
- Tavassoly, I.; Goldfarb, J.; Iyengar, R. Systems biology primer: The basic methods and approaches. Essays Biochem. 2018. [Google Scholar] [CrossRef]
- Vignoli, A.; Ghini, V.; Meoni, G.; Licari, C.; Takis, P.G.; Tenori, L.; Turano, P.; Luchinat, C. High-throughput metabolomics by 1D NMR. Angew. Chem. Int. Ed. 2019, 58, 968–994. [Google Scholar] [CrossRef] [PubMed]
- Emwas, A.H.; Roy, R.; McKay, R.T.; Tenori, L.; Saccenti, E.; Gowda, G.; Raftery, D.; Alahmari, F.; Jaremko, L.; Jaremko, M.; et al. NMR spectroscopy for metabolomics research. Metabolites 2019, 9, 123. [Google Scholar] [CrossRef] [PubMed]
- Ma’ayan, A. Introduction to network analysis in systems biology. Sci. Signal. 2011, 4, tr5. [Google Scholar] [CrossRef]
- Trudeau, R.J. Introduction to Graph Theory; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Rosato, A.; Tenori, L.; Cascante, M.; De Atauri Carulla, P.R.; Martins dos Santos, V.A.; Saccenti, E. From correlation to causation: Analysis of metabolomics data using systems biology approaches. Metabolomics 2018. [Google Scholar] [CrossRef]
- Saccenti, E.; Suarez-Diez, M.; Luchinat, C.; Santucci, C.; Tenori, L. Probabilistic networks of blood metabolites in healthy subjects as indicators of latent cardiovascular risk. J. Proteome Res. 2015, 14, 1101–1111. [Google Scholar] [CrossRef]
- Jahagirdar, S.; Suarez-Diez, M.; Saccenti, E. Simulation and Reconstruction of metabolite-metabolite Association Networks Using a Metabolic Dynamic Model and Correlation Based Algorithms. J. Proteome Res. 2019, 18, 1099–1113. [Google Scholar] [CrossRef]
- Vignoli, A.; Tenori, L.; Luchinat, C.; Saccenti, E. Age and sex effects on plasma metabolite association networks in healthy subjects. J. Proteome Res. 2017, 17, 97–107. [Google Scholar] [CrossRef]
- Vignoli, A.; Tenori, L.; Giusti, B.; Valente, S.; Carrabba, N.; Balzi, D.; Barchielli, A.; Marchionni, N.; Gensini, G.F.; Marcucci, R.; et al. Differential network analysis reveals metabolic determinants associated with mortality in acute myocardial infarction patients and suggest potential mechanisms underlying different clinical scores used to predict death. J. Proteome Res. 2020, 19, 949–961. [Google Scholar] [CrossRef]
- Afzal, M.; Saccenti, E.; Madsen, M.; Hansen, M.B.; Hyldegaard, O.; Skrede, S.; Martins dos santos, V.; Norrby Teglund, A.; Svensson, M. Integrated univariate, multivariate and correlation-based network analyses reveal metabolite-specific effects on bacterial growth and biofilm formation in necrotizing soft tissue infections. J. Proteome Res. 2019. [Google Scholar] [CrossRef]
- Rist, M.J.; Roth, A.; Frommherz, L.; Weinert, C.H.; Krüger, R.; Merz, B.; Bunzel, D.; Mack, C.; Egert, B.; Bub, A.; et al. Metabolite patterns predicting sex and age in participants of the Karlsruhe Metabolomics and Nutrition (KarMeN) study. PLoS ONE 2017, 12, e0183228. [Google Scholar] [CrossRef] [PubMed]
- Smith, R. A MI approach to calculating nonlinearity. Stat 2015, 4, 291–303. [Google Scholar] [CrossRef]
- Haug, K.; Cochrane, K.; Nainala, V.C.; Williams, M.; Chang, J.; Jayaseelan, K.V.; O’Donovan, C. MetaboLights: A resource evolving in response to the needs of its scientific community. Nucleic Acids Res. 2019. [Google Scholar] [CrossRef]
- Sud, M.; Fahy, E.; Cotter, D.; Azam, K.; Vadivelu, I.; Burant, C.; Edison, A.; Fiehn, O.; Higashi, R.; Nair, K.S.; et al. Metabolomics Workbench: An international repository for metabolomics data and metadata, metabolite standards, protocols, tutorials and training, and analysis tools. Nucleic Acids Res. 2015, 44, D463–D470. [Google Scholar] [CrossRef]
- Meyer, F.; Paarmann, D.; D’Souza, M.; Olson, R.; Glass, E.M.; Kubal, M.; Paczian, T.; Rodriguez, A.; Stevens, R.; Wilke, A.; et al. The metagenomics RAST server–a public resource for the automatic phylogenetic and functional analysis of metagenomes. BMC Bioinform. 2008, 9, 386. [Google Scholar] [CrossRef]
- Wehrens, R.; Franceschi, P. Meta-Statistics for Variable Selection: The R Package BioMark. J. Stat. Softw. Artic. 2012, 51, 1–18. [Google Scholar] [CrossRef][Green Version]
- Cacciatore, S.; Tenori, L.; Luchinat, C.; Bennett, P.R.; MacIntyre, D.A. KODAMA: An R package for knowledge discovery and data mining. Bioinformatics 2017, 33, 621–623. [Google Scholar] [CrossRef]
- Rohart, F.; Gautier, B.; Singh, A.; Lê Cao, K.A. mixOmics: An R package for ‘omics feature selection and multiple data integration. PLoS Comput. Biol. 2017, 13, e1005752. [Google Scholar] [CrossRef]
- Mcnicholas, P.D.; Murphy, T.B. Parsimonious Gaussian mixture models. Stat. Comput. 2008, 18, 285–296. [Google Scholar] [CrossRef]
- Ganna, A.; Salihovic, S.; Sundström, J.; Broeckling, C.D.; Hedman, Å.K.; Magnusson, P.K.; Pedersen, N.L.; Larsson, A.; Siegbahn, A.; Zilmer, M.; et al. Large-scale metabolomic profiling identifies novel biomarkers for incident coronary heart disease. PLoS Genet. 2014, 10, e1004801. [Google Scholar] [CrossRef] [PubMed]
- Hilvo, M.; Gade, S.; Hyötyläinen, T.; Nekljudova, V.; Seppänen-Laakso, T.; Sysi-Aho, M.; Untch, M.; Huober, J.; von Minckwitz, G.; Denkert, C.; et al. Monounsaturated fatty acids in serum triacylglycerols are associated with response to neoadjuvant chemotherapy in breast cancer patients. Int. J. Cancer 2014, 134, 1725–1733. [Google Scholar] [CrossRef] [PubMed]
- Stevens, V.L.; Wang, Y.; Carter, B.D.; Gaudet, M.M.; Gapstur, S.M. Serum metabolomic profiles associated with postmenopausal hormone use. Metabolomics 2018, 14, 97. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, C.W.; McGregor, N.R.; Lewis, D.P.; Butt, H.L.; Gooley, P.R. Metabolic profiling reveals anomalous energy metabolism and oxidative stress pathways in chronic fatigue syndrome patients. Metabolomics 2015, 11, 1626–1639. [Google Scholar] [CrossRef]
- Thévenot, E.A.; Roux, A.; Xu, Y.; Ezan, E.; Junot, C. Analysis of the human adult urinary metabolome variations with age, body mass index, and gender by implementing a comprehensive workflow for univariate and OPLS statistical analyses. J. Proteome Res. 2015, 14, 3322–3335. [Google Scholar] [CrossRef]
- Zheng, X.; Huang, F.; Zhao, A.; Lei, S.; Zhang, Y.; Xie, G.; Chen, T.; Qu, C.; Rajani, C.; Dong, B.; et al. Bile acid is a significant host factor shaping the gut microbiome of diet-induced obese mice. BMC Biol. 2017, 15, 120. [Google Scholar] [CrossRef] [PubMed]
- Fahrmann, J.F.; Kim, K.; DeFelice, B.C.; Taylor, S.L.; Gandara, D.R.; Yoneda, K.Y.; Cooke, D.T.; Fiehn, O.; Kelly, K.; Miyamoto, S. Investigation of metabolomic blood biomarkers for detection of adenocarcinoma lung cancer. Cancer Epidemiol. Prev. Biomark. 2015, 24, 1716–1723. [Google Scholar] [CrossRef] [PubMed]
- Sakanaka, A.; Kuboniwa, M.; Hashino, E.; Bamba, T.; Fukusaki, E.; Amano, A. Distinct signatures of dental plaque metabolic byproducts dictated by periodontal inflammatory status. Sci. Rep. 2017, 7, 42818. [Google Scholar] [CrossRef]
- Franzosa, E.A.; Sirota-Madi, A.; Avila-Pacheco, J.; Fornelos, N.; Haiser, H.J.; Reinker, S.; Vatanen, T.; Hall, A.B.; Mallick, H.; McIver, L.J.; et al. Gut microbiome structure and metabolic activity in inflammatory bowel disease. Nat. Microbiol. 2019, 4, 293. [Google Scholar] [CrossRef]
- Chan, A.W.; Mercier, P.; Schiller, D.; Bailey, R.; Robbins, S.; Eurich, D.T.; Sawyer, M.B.; Broadhurst, D. 1 H-NMR urinary metabolomic profiling for diagnosis of gastric cancer. Br. J. Cancer 2016, 114, 59. [Google Scholar] [CrossRef]
- Eisner, R.; Stretch, C.; Eastman, T.; Xia, J.; Hau, D.; Damaraju, S.; Greiner, R.; Wishart, D.S.; Baracos, V.E. Learning to predict cancer-associated skeletal muscle wasting from 1 H-NMR profiles of urinary metabolites. Metabolomics 2011, 7, 25–34. [Google Scholar] [CrossRef]
- Lusczek, E.R.; Lexcen, D.R.; Witowski, N.E.; Mulier, K.E.; Beilman, G. Urinary metabolic network analysis in trauma, hemorrhagic shock, and resuscitation. Metabolomics 2013, 9, 223–235. [Google Scholar] [CrossRef]
- Powers, R.K.; Sullivan, K.D.; Culp-Hill, R.; Ludwig, M.P.; Smith, K.P.; Waugh, K.A.; Minter, R.; Tuttle, K.D.; Lewis, H.C.; Rachubinski, A.L.; et al. Trisomy 21 activates the kynurenine pathway via increased dosage of interferon receptors. Nature Commun. 2019, 10, 4766. [Google Scholar] [CrossRef] [PubMed]
- Bernini, P.; Bertini, I.; Luchinat, C.; Nepi, S.; Saccenti, E.; Schäfer, H.; Schütz, B.; Spraul, M.; Tenori, L. Individual human phenotypes in metabolic space and time. J. Proteome Res. 2009, 8, 4264–4271. [Google Scholar] [CrossRef] [PubMed]
- Caldana, C.; Degenkolbe, T.; Cuadros-Inostroza, A.; Klie, S.; Sulpice, R.; Leisse, A.; Steinhauser, D.; Fernie, A.R.; Willmitzer, L.; Hannah, M.A. High-density kinetic analysis of the metabolomic and transcriptomic response of Arabidopsis to eight environmental conditions. Plant J. 2011, 67, 869–884. [Google Scholar] [CrossRef] [PubMed]
- Khan, J.; Wei, J.S.; Ringner, M.; Saal, L.H.; Ladanyi, M.; Westermann, F.; Berthold, F.; Schwab, M.; Antonescu, C.R.; Peterson, C.; et al. Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nat. Med. 2001, 7, 673. [Google Scholar] [CrossRef]
- Bushel, P.R.; Wolfinger, R.D.; Gibson, G. Simultaneous clustering of gene expression data with clinical chemistry and pathological evaluations reveals phenotypic prototypes. BMC Syst. Biol. 2007, 1, 15. [Google Scholar] [CrossRef]
- Stanley, D.; Geier, M.S.; Hughes, R.J.; Denman, S.E.; Moore, R.J. Highly variable microbiota development in the chicken gastrointestinal tract. PLoS ONE 2013, 8, e84290. [Google Scholar] [CrossRef]
- Forina, M.; Armanino, C.; Lanteri, S.; Tiscornia, E. Classification of olive oils from their fatty acid composition. Food research and data analysis. In Proceedings of the IUFoST Symposium, Oslo, Norway, 20–23 September 1982; Martens, H., Russwurm, H., Jr., Eds.; Applied Science Publishers: London, UK, 1983. [Google Scholar]
- Streuli, H. Der heutige stand der kaffeechemie. In Proceedings of the ASSIC, 6e, Colloque, Bogota, Colombia, 4–5 October 1973; Volume 61. [Google Scholar]
- Forina, M.; Armanino, C.; Castino, M.; Ubigli, M. Multivariate data analysis as a discriminating method of the origin of wines. Vitis 1986, 25, 189–201. [Google Scholar]
- Nemenman, I.; Bialek, W.; Van Steveninck, R.D.R. Entropy and information in neural spike trains: Progress on the sampling problem. Phys. Rev. E 2004, 69, 056111. [Google Scholar] [CrossRef]
- Gelfand, I.M.; Yaglom, A.M. Calculation of amount of information about a random function contained in another such function. Am. Math. Soc. Transl. 1957, 2, 199–246. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1948. [Google Scholar]
- Zimmerman, D.W.; Zumbo, B.D.; Williams, R.H. Bias in estimation and hypothesis testing of correlation. Psicológica 2003, 24, 133–158. [Google Scholar]
- Pearson, K. VII. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar]
- Spearman, C. Measurement of association, Part II. Correction of ‘systematic deviations’. Am. J. Psychol. 1904, 15, 88–101. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Meyer, P.E. Information-Theoretic Variable Selection and Network Inference from Microarray Data; Universite Libre de Bruxelles: Brussels, Belgium, 2008. [Google Scholar]
- Paninski, L. Estimation of entropy and MI. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Schäfer, J.; Strimmer, K. An empirical Bayes approach to inferring large-scale gene association networks. Bioinformatics 2005, 21, 754–764. [Google Scholar] [CrossRef]
- Schäfer, J.; Strimmer, K. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Stat. Appl. Genet. Mol. Biol. 2005, 4. [Google Scholar] [CrossRef]
- Schürmann, T.; Grassberger, P. Entropy estimation of symbol sequences. Chaos: Interdiscip. J. Nonlinear Sci. 1996, 6, 414–427. [Google Scholar] [CrossRef]
- Wu, L.; Neskovic, P.; Reyes, E.; Festa, E.; William, H. Classifying n-back EEG data using entropy and MI features. In Proceedings of the ESANN, Bruges, Belgium, 26–28 April 2017; pp. 61–66. [Google Scholar]
- Guo, Y.; Hastie, T.; Tibshirani, R. Regularized linear discriminant analysis and its application in microarrays. Biostatistics 2006, 8, 86–100. [Google Scholar] [CrossRef]
- Hardin, J.; Garcia, S.R.; Golan, D. A method for generating realistic correlation matrices. Ann. Appl. Stat. 2013, 7, 1733–1762. [Google Scholar] [CrossRef]
- Ghosh, S.; Henderson, S.G. Behavior of the NORTA method for correlated random vector generation as the dimension increases. ACM Trans. Model. Comput. Simul. (TOMACS) 2003, 13, 276–294. [Google Scholar] [CrossRef]
- Lewandowski, D.; Kurowicka, D.; Joe, H. Generating random correlation matrices based on vines and extended onion method. J. Multivar. Anal. 2009, 100, 1989–2001. [Google Scholar] [CrossRef]
- Malik-Sheriff, R.S.; Glont, M.; Nguyen, T.V.N.; Tiwari, K.; Roberts, M.G.; Xavier, A.; Vu, M.T.; Men, J.; Maire, M.; Kananathan, S.; et al. BioModels—15 years of sharing computational models in life science. Nucleic Acids Res. 2019. [Google Scholar] [CrossRef] [PubMed]
- Sharp, G.C.; Ma, H.; Saunders, P.T.; Norman, J.E. A computational model of lipopolysaccharide-induced nuclear factor kappa B activation: A key signalling pathway in infection-induced preterm labour. PLoS ONE 2013, 8, e70180. [Google Scholar] [CrossRef] [PubMed]
- Mendez, K.M.; Reinke, S.N.; Broadhurst, D.I. A comparative evaluation of the generalised predictive ability of eight machine learning algorithms across ten clinical metabolomics data sets for binary classification. Metabolomics 2019, 15, 150. [Google Scholar] [CrossRef]
- Stekhoven, D.J.; Bühlmann, P. MissForest—Non-parametric missing value imputation for mixed-type data. Bioinformatics 2011, 28, 112–118. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- MATLAB. Version 9.5.0 (R2018b); The MathWorks Inc.: Natick, MA, USA, 2018. [Google Scholar]
- RPython Core Team. Python: A Dynamic, Open Source Programming Language; Python Software Foundation: Wilmington, DE, USA, 2015. [Google Scholar]
- Zhao, J.; Zhou, Y.; Zhang, X.; Chen, L. Part MI for quantifying direct associations in networks. Proc. Natl. Acad. Sci. USA 2016, 113, 5130–5135. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Steuer, R.; Kurths, J.; Daub, C.O.; Weise, J.; Selbig, J. The MI: Detecting and evaluating dependencies between variables. Bioinformatics 2002, 18, S231–S240. [Google Scholar] [CrossRef]
- Lindlöf, A.; Lubovac, Z. Simulations of simple artificial genetic networks reveal features in the use of Relevance Networks. Silico Biol. 2005, 5, 239–249. [Google Scholar]
- Song, L.; Langfelder, P.; Horvath, S. Comparison of co-expression measures: MI, correlation, and model based indices. BMC Bioinform. 2012, 13, 328. [Google Scholar] [CrossRef]
- Numata, J.; Ebenhöh, O.; Knapp, E.W. Measuring correlations in metabolomic networks with mutual information. In Genome Informatics 2008: Genome Informatics Series Vol. 20; World Scientific: Singapore, 2008; pp. 112–122. [Google Scholar]
- You, Y.; Liang, D.; Wei, R.; Li, M.; Li, Y.; Wang, J.; Wang, X.; Zheng, X.; Jia, W.; Chen, T. Evaluation of metabolite-microbe correlation detection methods. Anal. Biochem. 2019, 567, 106–111. [Google Scholar] [CrossRef] [PubMed]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating MI. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, H. Physical nature of higher-order MI: Intrinsic correlations and frustration. Phys. Rev. E 2000, 62, 3096. [Google Scholar] [CrossRef] [PubMed]
- Camacho, D.; De La Fuente, A.; Mendes, P. The origin of correlations in metabolomics data. Metabolomics 2005, 1, 53–63. [Google Scholar] [CrossRef]
- Saccenti, E.; Hendriks, M.H.; Smilde, A.K. Corruption of the Pearson correlation coefficient by measurement error and its estimation, bias, and correction under different error models. Sci. Rep. (Nat. Publ. Group) 2020, 10, 1–9. [Google Scholar] [CrossRef]
- Saccenti, E. Correlation patterns in experimental data are affected by normalization procedures: Consequences for data analysis and network inference. J. Proteome Res. 2017, 16, 619–634. [Google Scholar] [CrossRef]
- Mason, M.J.; Fan, G.; Plath, K.; Zhou, Q.; Horvath, S. Signed weighted gene co-expression network analysis of transcriptional regulation in murine embryonic stem cells. BMC Genom. 2009, 10, 327. [Google Scholar] [CrossRef]
- Doquire, G.; Verleysen, M. A Comparison of Multivariate MI Estimators for Feature Selection. In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, Vilamoura, Portugal, 6–8 February 2012; pp. 176–185. [Google Scholar]



| No. Differentially Connected Features | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Study ID | Ref. | Platform | Type | No. Observations | No. Features | Design | Correlatio | MI | Only in Corr | Only in MI | Overlap |
| 1 | MTBLS90 | [21] | LC–MS | Plasma | 968 (485/483) | 189 | Sex (M/F) | 132 | 101 | 68 | 37 | 64 |
| 2 | MTBLS92 | [22] | LC–MS | Plasma | 253 (142/111) | 138 | Chemotherapy (before/after) | 138 | 12 | 126 | 0 | 12 |
| 3 | MTBLS136 | [23] | LC–MS | Serum | 668 (337/331) | 371 | Homone (E/E+P) | 255 | 125 | 167 | 37 | 88 |
| 4 | MTBLS161 | [24] | NMR | Serum | 59 (34/25) | 30 | CFS (case/control) | 14 | 12 | 6 | 4 | 8 |
| 5 | MTBLS404 | [25] | LC–MS | Urine | 184 (101/83) | 120 | Sex (M/F) | 105 | 58 | 51 | 4 | 54 |
| 6 | MTBLS547 | [26] | LC–MS | Caecal | 97 (46/51) | 35 | High fat diet (case/control) | 35 | 4 | 31 | 0 | 4 |
| 7 | ST000369 | [27] | GC–MS | Serum | 80 (49/31) | 181 | Adenocarcinoma/Healthy | 181 | 69 | 112 | 0 | 69 |
| 8 | ST000496 | [28] | GC–MS | Saliva | 100 (50/50) | 69 | Debridement (pre/post) | 59 | 31 | 32 | 4 | 27 |
| 9 | ST001000 | [29] | LC–MS | Stool | 121 (68/53) | 124 | IBD (CD/UC) | 96 | 79 | 33 | 16 | 63 |
| 10 | ST001047 | [30] | NMR | Urine | 83 (43/40) | 149 | Gastric cancer/healthy | 109 | 85 | 42 | 18 | 67 |
| 11 | ST000061 | GC-MS | Tissue | 118 (59/59) | 157 | subcutaeus/visceral fat | 156 | 83 | 73 | 0 | 83 | |
| 12 | [31] | NMR | Urine | 50 (25/25) | 200 | cachexia (case/control) | 163 | 57 | 115 | 9 | 48 | |
| 13 | [31] | NMR | Urine | 77 (47/30) | 63 | cachexia (case/control) | 63 | 33 | 30 | 0 | 33 | |
| 14 | [31] | NMR | Urine | 60 (30/30) | 63 | cachexia (case/control) | 55 | 43 | 15 | 3 | 40 | |
| 15 | [12] | GC-MS | Plasma | 291(172/119) | 128 | Sex (M/F) | 128 | 23 | 105 | 0 | 23 | |
| 16 | [12] | GC-MS | Plasma | 200 (100/100) | 128 | Sex (M/F) | 103 | 51 | 56 | 4 | 47 | |
| 17 | [12] | GC-MS | Urine | 301 (129/172) | 324 | Sex (M/F) | 256 | 143 | 136 | 23 | 120 | |
| 18 | MTBLS123 | [32] | NMR | Urine | 151 (79/72) | 63 | Shock (pre/post) | 63 | 9 | 54 | 0 | 9 |
| 19 | ST001243 | [33] | GC-MS | Plasma | 98 (48/50) | 69 | Trisomy 21 (yes/no) | 69 | 28 | 41 | 0 | 28 |
| 20 | MTBLS147 | [9] | NMR | Plasma | 370 (185/185) | 417 | Sex (M/F) | 417 | 414 | 3 | 0 | 414 |
| 21 | KODAMA | [34] | NMR | Urine | 80(40/40) | 490 | Subject (A/B) | 459 | 293 | 187 | 21 | 272 |
| 22 | [35] | GC-MS | Plant | 70 (35/35) | 67 | Light/Dark | 37 | 19 | 22 | 4 | 15 | |
| 23 | BioMark | [17] | LC–MS | Apple | 20 (10/10) | 198 | Treated/Untreated | 124 | 58 | 83 | 17 | 41 |
| 24 | MixOmics | [36] | MA | Cell | 43 (23/20)− | 250 | Sarcoma (RMS/ES) | 250 | 18 | 232 | 0 | 18 |
| 25 | MixOmics | [36] | MA | Cell | 43 (23/20)+ | 250 | Sarcoma (RMS/ES) | 250 | 8 | 242 | 0 | 8 |
| 26 | MixOmics | [37] | MA | Cell | 32 (16/16)r | 500 | High/Low dose | 405 | 279 | 170 | 44 | 235 |
| 27 | 4537568.3-776.3 | [38] | 16S seq | Faeces | 145 (71/74) | 243 | Flock (A/B) | 241 | 150 | 91 | 0 | 150 |
| 28 | pgmm | [39] | Chemical assay | Oil | 50 (25/25) | 7 | Region (A/B) | 4 | 0 | 4 | 0 | 0 |
| 29 | pgmm | [40] | Chemical assay | Coffee | 43 (36/7) | 12 | Variety (Arabica/Robusta) | 4 | 11 | 0 | 7 | 4 |
| 30 | pgmm | [41] | Chemical assay | Wine | 130 (59/71) | 27 | Type (Barolo/Grignolino) | 8 | 10 | 5 | 7 | 3 |
| Pathway Enrichment Based On | ||||
| Data Set 12 | Correlation | MI | ||
| Pathway | Raw P | FDR | Raw p | FDR |
| Aminoacyl-tRNA biosynthesis | 3 × 10−12 | 3 × 10−12 | 0.0006 | 0.05 |
| Valine, leucine and isoleucine biosynthesis | 3 × 10−5 | 0.001 | ||
| Alanine, aspartate and glutamate metabolism | 3 × 10−5 | 0.002 | ||
| Arginine biosynthesis | 0.0004 | 0.008 | 0.006 | 0.18 |
| Glyoxylate and dicarboxylate metabolism | 0.001 | 0.020 | 0.25 | 1.00 |
| Glycine, serine and threonine metabolism | 0.002 | 0.020 | 0.03 | 0.72 |
| Citrate cycle (TCA cycle) | 0.002 | 0.020 | ||
| Phenylalanine metabolism | 0.002 | 0.020 | 0.09 | 0.91 |
| Phenylalanine, tyrosine and tryptophan biosynthesis | 0.004 | 0.040 | ||
| Pathway Enrichment Based On | ||||
| Data Set 25 | Correlation | MI | ||
| Pathway | Raw P | FDR | Raw p | FDR |
| Citrate cycle (TCA cycle) | 3 × 10−5 | 0.004 | ||
| Alanine, aspartate and glutamate metabolism | 0.0004 | 0.016 | 0.15 | 1 |
| Glyoxylate and dicarboxylate metabolism | 0.001 | 0.020 | 0.17 | 1 |
| Glycine, serine and threonine metabolism | 0.001 | 0.020 | 0.18 | 1 |
| Histidine metabolism | 0.002 | 0.036 | 0.09 | 1 |
| Tyrosine metabolism | 0.004 | 0.050 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jahagirdar, S.; Saccenti, E. On the Use of Correlation and MI as a Measure of Metabolite—Metabolite Association for Network Differential Connectivity Analysis. Metabolites 2020, 10, 171. https://doi.org/10.3390/metabo10040171
Jahagirdar S, Saccenti E. On the Use of Correlation and MI as a Measure of Metabolite—Metabolite Association for Network Differential Connectivity Analysis. Metabolites. 2020; 10(4):171. https://doi.org/10.3390/metabo10040171
Chicago/Turabian StyleJahagirdar, Sanjeevan, and Edoardo Saccenti. 2020. "On the Use of Correlation and MI as a Measure of Metabolite—Metabolite Association for Network Differential Connectivity Analysis" Metabolites 10, no. 4: 171. https://doi.org/10.3390/metabo10040171
APA StyleJahagirdar, S., & Saccenti, E. (2020). On the Use of Correlation and MI as a Measure of Metabolite—Metabolite Association for Network Differential Connectivity Analysis. Metabolites, 10(4), 171. https://doi.org/10.3390/metabo10040171






