Knowledge Spillovers: An Evidence from The European Regions
Abstract
1. Introduction
- What is the role of R&D and human capital in the knowledge production processes in the EU regions?
- What specific types of knowledge spillovers occur in the knowledge production processes?
2. Literature Review
2.1. Mechanism of Knowledge Spillovers and Externalities
2.2. Knowledge Spillovers and The Regional Knowledge Production Function
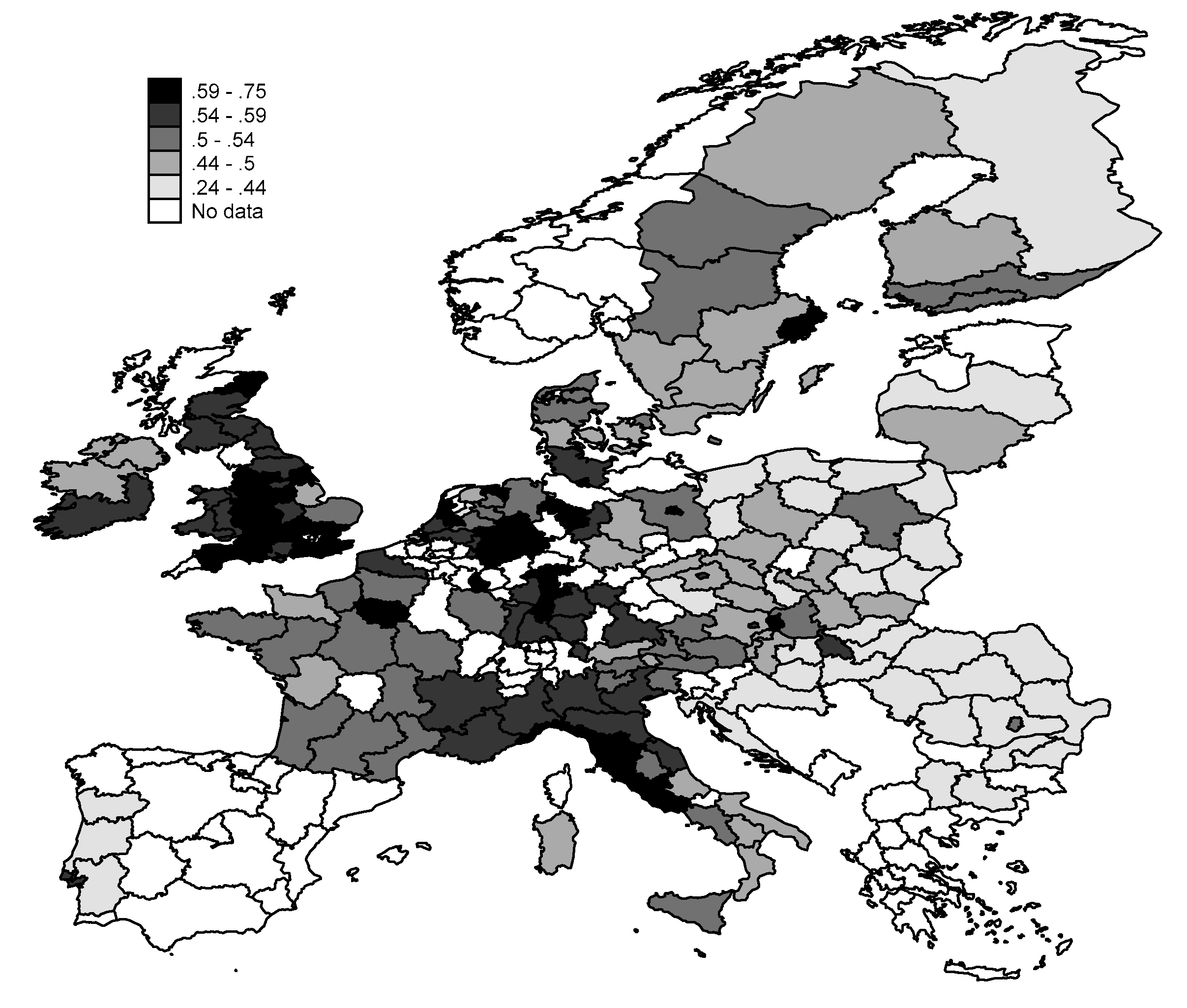
3. Data and Methods
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jaffe, A.B. Real effects of academic research. Am. Econ. Rev. 1989, 79, 957–970. [Google Scholar]
- Boschma, R.A. Proximity and innovation: A critical assessment. Reg. Stud. 2005, 39, 61–74. [Google Scholar] [CrossRef]
- Mattes, J. Dimensions of Proximity and Knowledge Bases: Innovation between Spatial and Non-spatial Factors. Reg. Stud. 2011, 46, 1085–1099. [Google Scholar] [CrossRef]
- Corrado, L.; Fingleton, B. Where is the economics in spatial econometrics? J. Reg. Sci. 2012, 52, 210–239. [Google Scholar] [CrossRef]
- Meade, J.E. External Economies and Diseconomies in a Competitive Situation. Econ. J. 1952, 62, 54–67. [Google Scholar] [CrossRef]
- Antonelli, C.; Ferraris, G. The creative response and the endogenous dynamics of pecuniary knowledge externalities: An agent based simulation model. J. Econ. Interact. Coord. 2018, 13, 561–599. [Google Scholar] [CrossRef]
- Nelson, R.R. The Economics of Invention: A Survey of the Literature. J. Bus. 1959, 32, 101–127. [Google Scholar] [CrossRef]
- Arrow, K. Economic Welfare and the Allocation of Resources for Invention. In The Rate and Direction of Inventive Activity: Economic and Social Factors; National Bureau of Economic Research, Ed.; Princeton University Press: Princeton, NJ, USA, 1962; pp. 609–626. [Google Scholar]
- Klenow, P.J.; Rodriguez-Clare, A. Externalities and Growth. In Handbook of Economic Growth, 1st ed.; Aghion, P., Durlauf, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 1, pp. 817–861. [Google Scholar]
- Grossman, G.M.; Helpman, E. Protection for Sale. Am. Econ. Rev. 1994, 84, 833–850. [Google Scholar]
- Jones, C.I. Population and Ideas: A Theory of Endogenous Growth; Mimeo, Department of Economics, Stanford University: Stanford, CA, USA, 1998. [Google Scholar]
- Lucas, R.E. On the Mechanics of Economic Development. J. Monet. Econ. 1988, 22, 3–42. [Google Scholar] [CrossRef]
- Nordhaus, W.D. Invention, Growth, and Welfare: A Theoretical Treatment of Technological Change, 18th ed.; MIT Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Cohen, W.M.; Levinthal, D.A. Innovation and Learning: The Two Faces of R & D. Econ. J. 1989, 99, 569–596. [Google Scholar]
- Litan, R.E. Handbook on Law, Innovation and Growth; Edward Elgar Publishing: Cheltenham, UK, 2011. [Google Scholar]
- Mansfield, E.; Schwartz, M.; Wagner, S. Imitation Costs and Patents: An Empirical Study. Econ. J. 1981, 91, 907–918. [Google Scholar] [CrossRef]
- Foray, D. Economics of Knowledge; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Zaby, A. The Decision to Patent; Springer: Berlin, Germany, 2010. [Google Scholar]
- Denicolὀ, V.; Franzoni, L.A. Patents, secrets, and the first-inventor defense. J. Econ. Manag. Strategy 2004, 13, 517–538. [Google Scholar] [CrossRef]
- Nonaka, I. A Dynamic Theory of Organizational Knowledge Creation. Organ. Sci. 1994, 5, 14–37. [Google Scholar] [CrossRef]
- Desrochers, P. Geographical Proximity and the Transmission of Tacit Knowledge. Rev. Austrian Econ. 2001, 14, 25–46. [Google Scholar] [CrossRef]
- Howells, J. Tacit knowledge, innovation and economic geography. Urban Stud. 2002, 39, 871–884. [Google Scholar] [CrossRef]
- Caragliu, A.; Nijkamp, P. Space and knowledge spillovers in European regions: The impact of different forms of proximity on spatial knowledge diffusion. J. Econ. Geogr. 2015, 16, 749–774. [Google Scholar] [CrossRef]
- Santos, F.; Crocco, M.; Frederico, G.J. Knowledge externalities and growth in peripheral regions: Introductory notes. In Textos Para Discussão Cedeplar-UFMG td278; Cedeplar, Ed.; Universidade Federal de Minas Gerais: Belo Horizonte, Brazil, 2005. [Google Scholar]
- Cooke, P.; Asheim, B.; Boschma, R.; Martin, R.; Schwartz, D.; Tödtling, F. Handbook of Regional Innovation and Growth; Edward Elgar Publishing: Cheltenham, UK, 2011. [Google Scholar]
- Von Hippel, E. “Sticky Information” and the Locus of Problem Solving: Implications for Innovation. Manag. Sci. 1994, 40, 429–439. [Google Scholar] [CrossRef]
- Murray, A.; Hanlon, P. An Investigation into the Stickiness of Tacit Knowledge Transfer. In Proceedings of the 13th Annual conference of the Irish Academy of Management, Cork Institute of Technology, Cork, UK, 1–3 September 2010. [Google Scholar]
- Szulanski, G. Exploring internal Stickiness: Impediments to the transfer of best practice within the firm. Strateg. Manag. J. 1996, 17, 27–43. [Google Scholar] [CrossRef]
- Aldieri, L. Technological and geographical proximity effects on knowledge spillovers: Evidence from the US patent citations. Econ. Innov. New Technol. 2011, 20, 597–607. [Google Scholar] [CrossRef]
- Autant-Bernard, C.; LeSage, J. Quantifying knowledge spillovers using spatial econometric models. J. Reg. Sci. 2011, 51, 471–496. [Google Scholar] [CrossRef]
- Jacobs, J. The Economies of Cities; Random House: New York, NY, USA, 1969. [Google Scholar]
- Beaudry, C.; Schiffauerova, A. Who’s right, Marshall or Jacobs? The localization versus urbanization debate. Res. Policy 2009, 38, 318–337. [Google Scholar] [CrossRef]
- Mokyr, J. The Rise and Fall of the Factory System: Technology, firms, and households since the Industrial Revolution. In Carnegie-Rochester Conference Series on Public Policy; Meltzer, A.H., Ed.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 55, pp. 1–45. [Google Scholar]
- Jaffe, A.; Trajtenberg, M.; Henderson, R. Geographic localization of knowledge spillovers as evidenced by patent citations. Q. J. Econ. 1993, 108, 577–598. [Google Scholar] [CrossRef]
- Anselin, L.; Acs, Z.J.; Varga, A. Local geographic spillovers between university research and high technology innovations. J. Urban Econ. 1997, 42, 422–448. [Google Scholar] [CrossRef]
- Vermeulen, B.; Paier, M. Innovation Networks for Regional Development. Economic Complexity and Evolution; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Griliches, Z. Issues in Assessing the Contribution of Research and Development to Productivity Growth. Bell J. Econ. 1979, 10, 92–116. [Google Scholar] [CrossRef]
- Antonelli, C.; Colombelli, A. Knowledge cumulability and complementarity in the knowledge generation function. Department of Economics and Statistics Cognetti de Martiis; Working Papers 201305; University of Turin: Turin, Italy, 2013. [Google Scholar]
- Howells, J.; Bessant, J. Introduction: Innovation and economic geography: A review and analysis. J. Econ. Geogr. 2012, 12, 929–942. [Google Scholar] [CrossRef]
- Storper, M.; Venables, A.J. Buzz: Face-to-face contact and the urban economy. J. Econ. Geogr. 2004, 4, 351–370. [Google Scholar] [CrossRef]
- Bottazzi, L.; Peri, G. Innovation and spillovers in regions: Evidence from European patent data. Eur. Econ. Rev. 2003, 47, 687–710. [Google Scholar] [CrossRef]
- Moreno, R.; Paci, R.; Usai, S. Spatial spillovers and innovation activity in European regions. Environ. Plan. A 2005, 37, 1793–1812. [Google Scholar] [CrossRef]
- Parent, O.; LeSage, J. Using the variance structure of the conditional autoregressive specification to model knowledge spillovers. J. Appl. Econ. 2008, 23, 235–256. [Google Scholar] [CrossRef]
- Paci, R.; Marrocu, E.; Usai, S. The complementary effects of proximity dimensions on knowledge spillovers. Spat. Econ. Anal. 2014, 9, 9–30. [Google Scholar] [CrossRef]
- Charlot, S.; Crescenzi, R.; Musolesi, A. Econometric modelling of the regional knowledge production function in Europe. J. Econ. Geogr. 2015, 15, 1227–1259. [Google Scholar] [CrossRef]
- Gertler, M.S. Tacit knowledge and the economic geography of context, or the undefinable tacitness of being (there). J. Econ. Geogr. 2003, 3, 75–99. [Google Scholar] [CrossRef]
- Cooke, P. Introduction: Regional innovation systems—An evolutionary approach. In Regional Innovation Systems: The Role of Governances in a Globalized World, 2nd ed.; Cooke, P., Heidenreich, M., Braczyk, H.J., Eds.; UCL Press: London, UK, 2004; pp. 1–18. [Google Scholar]
- Gilly, J.P.; Torre, A. Proximity Relations. Elements for an Analytical Framework. In Industrial Networks and Proximity; Green, M.B., Mac Naughton, R.B., Eds.; Ashgate: Aldershot, UK, 2000; pp. 1–16. [Google Scholar]
- Romer, P.M. Endogenous Technological Change. J. Political Econ. 1990, 98, 71–102. [Google Scholar] [CrossRef]
- Jones, C.I. R&D-Based Models of Economic Growth. J. Political Econ. 1995, 103, 759–784. [Google Scholar]
- Redding, S. Low-skill, low-quality trap: Strategic complementarities between human capital and R&D. Econ. J. 1996, 106, 458–470. [Google Scholar]
- Scicchitano, S. Complementarity between heterogeneous human capital and R&D: Can job-training avoid low development traps? Empirica 2010, 37, 361–380. [Google Scholar]
- Sanso-Navarro, M.; Vera-Cabello, M.; Ximénez-De-Embún, D.P. Human capital spillovers and regional development. J. Appl. Econ. 2017, 32, 923–930. [Google Scholar] [CrossRef]
- Saxenian, A. From Brain Drain to Brain Circulation: Transnational Communities and Regional Upgrading in India and China. Stud. Comp. Int. Dev. 2005, 40, 35–61. [Google Scholar] [CrossRef]
- Arbia, G. A Primer for Spatial Econometrics: With Applications in R; Palgrave Macmillan: New York, NY, USA, 2014. [Google Scholar]
- O’Donnell, C.J. DPIN Version 3.0: A Program for Decomposing Productivity Index Numbers; University of Queensland: Brisbane, Australia, 2011. [Google Scholar]
- Hoekman, J.; Frenken, K.; Van Oort, F. The geography of collaborative knowledge production in Europe. Ann. Reg. Sci. 2009, 43, 721–738. [Google Scholar] [CrossRef]
- Evangelista, R.; Meliciani, V.; Vezzani, A. The Specialisation of EU Regions in Fast Growing and Key Enabling Technologies; JRC Technical Report; Joint Research Centre: Brussels, Belgium, 2015. [Google Scholar]
- Afshartous, D.; Presto, R.A. Key Results of Interaction Models with Centering. J. Stat. Educ. 2011, 19, 1–24. [Google Scholar] [CrossRef]
- Diebolt, C.; Hippe, R. The long-run impact of human capital on innovation and economic development in the regions of Europe. Appl. Econ. 2019, 51, 542–563. [Google Scholar] [CrossRef]
- Carree, M.; Lokshin, B.; Belderbos, R. A note on testing for complementarity and substitutability in the case of multiple practices. J. Prod. Anal. 2011, 35, 263–269. [Google Scholar] [CrossRef]
- LeSage, J.; Pace, R.K. Introduction to Spatial Econometrics; Chapman & Hall: Boca Raton, FL, USA, 2009. [Google Scholar]
- Maurseth, P.B.; Verspagen, B. Knowledge spillovers in Europe: A patent citations analysis. Scand. J. Econ. 2002, 104, 531–545. [Google Scholar] [CrossRef]
- Harmon, R.R.; Castro-Leon, E.G. Service Innovation in the Cloud: Implications for Strategy Development. In Proceedings of the 2018 Portland International Conference on Management of Engineering and Technology (PICMET), Honolulu, HI, USA, 19–23 August 2018; pp. 1–15. [Google Scholar]
- Russo-Spena, T.; Tregua, M.; Bifulco, F. Searching through the jungle of innovation conceptualisations: System, network and ecosystem perspectives. J. Serv. Theory Pract. 2017, 27, 977–1005. [Google Scholar] [CrossRef]
- Metcalfe, J.S. Technology systems and technology policy in an evolutionary framework. Camb. J. Econ. 1995, 19, 25–46. [Google Scholar]
- Roper, S.; Love, J.H. Innovation and regional absorptive capacity: The labor market dimension. Ann. Reg. Sci. 2006, 40, 437–447. [Google Scholar] [CrossRef]
- Giannetti, M. Skill Complementarities and Migration Decisions. Labour 2001, 15, 1–31. [Google Scholar] [CrossRef]
- Cavallini, S.; Soldi, R.; Di Matteo, L.; Utma, M.A.; Errico, B. Addressing Brain Drain: The Local and Regional Dimension; The European Committee of the Regions, European Union: Brussels, Belgium, 2018. [Google Scholar]
- Bana, L. Brain Circulation, the Phenomenon and Challenges. Eur. J. Interdiscipl. Stud. 2016, 4, 158–165. [Google Scholar] [CrossRef][Green Version]
| Author | Sample | Main Findings | |
|---|---|---|---|
| Number of Regions | NUTS Level | ||
| Bottazzi and Peri [41] | 86 European regions | 1, 2 | There are small positive externalities accrue to regions within 300 km from the region that employs the R&D resources. |
| Moreno, Paci, and Usai [42] | 175 regions of 17 countries in Europe | 0, 1, 2 | Spillovers are mostly constrained by national borders within less than 250 km. |
| Parent and LeSage [43] | 323 regions in 9 European countries | 1, 2 | The largest spillovers are for the most part taking place between a limited set of highly developed regions in Europe. |
| Autant-Bernard and LeSage [30] | 94 metropolitan French “d´epartements” | - | The spatial spillover effects from cross-industry private research are larger than spatial spillover effects from other types of R&D activity. |
| Paci, Marrocu, Usai [44] | 276 regions in 29 countries (EU27 plus Norway, Switzerland) | 2 | Geography is not the only dimension which may help knowledge diffusion. Technological proximity is the most important one. |
| Charlot, Crescenzi, Musolesi [45] | 169 EU regions | 1, 2 | Geographical links matter for knowledge spillovers. R&D expenditure of neighboring regions have a positive impact on a region’s invention performance for the central part of R&D distribution. |
| Variable | Description | Method of Measurement |
|---|---|---|
| European Patent Office (EPO) | Patent applications to the EPO | Number of patent applications per million inhabitants |
| RD | Total intramural R&D expenditure in all sectors | Expenditure on R&D as % of GDP |
| HR | Human resources in science and technology | Scientists and engineers as a share of the active population in the age group 15–74 |
| Variables/Spatial Matrices | (1) | (2) | (3) | (4) |
| RD | 30.87 *** | 29.19 *** | 26.31 *** | 24.39 *** |
| HR | 9.162 *** | 9.716 *** | 8.501 *** | 9.016 *** |
| RD·HR | x | x | 2.721 ** | 2.677 ** |
| CONST | 66.35 *** | 41.30 *** | 52.05 *** | 16.83 |
| W1 | ||||
| EPO | −0.083 | 0.151 | −0.035 | 0.309 *** |
| RD | x | −20.31 * | x | −29.01 *** |
| HR | x | 0.598 | x | 1.772 |
| W2 | ||||
| EPO | 0.381 *** | 0.404 *** | 0.439 *** | 0.458 *** |
| RD | 33.81 *** | 32.78 *** | 29.91 *** | 28.29 *** |
| HR | −13.44 *** | −13.36 *** | −12.59 *** | −12.57 *** |
| Pseudo R2 | 0.539 | 0.533 | 0.538 | 0.518 |
| Wald test of spatial terms (p-value) | 278.65 (0.000) | 272.17 (0.000) | 286.82 (0.000) | 329.34 (0.000) |
| Effects of Explanatory Variables | (1) | (2) | (3) | (4) |
| direct | ||||
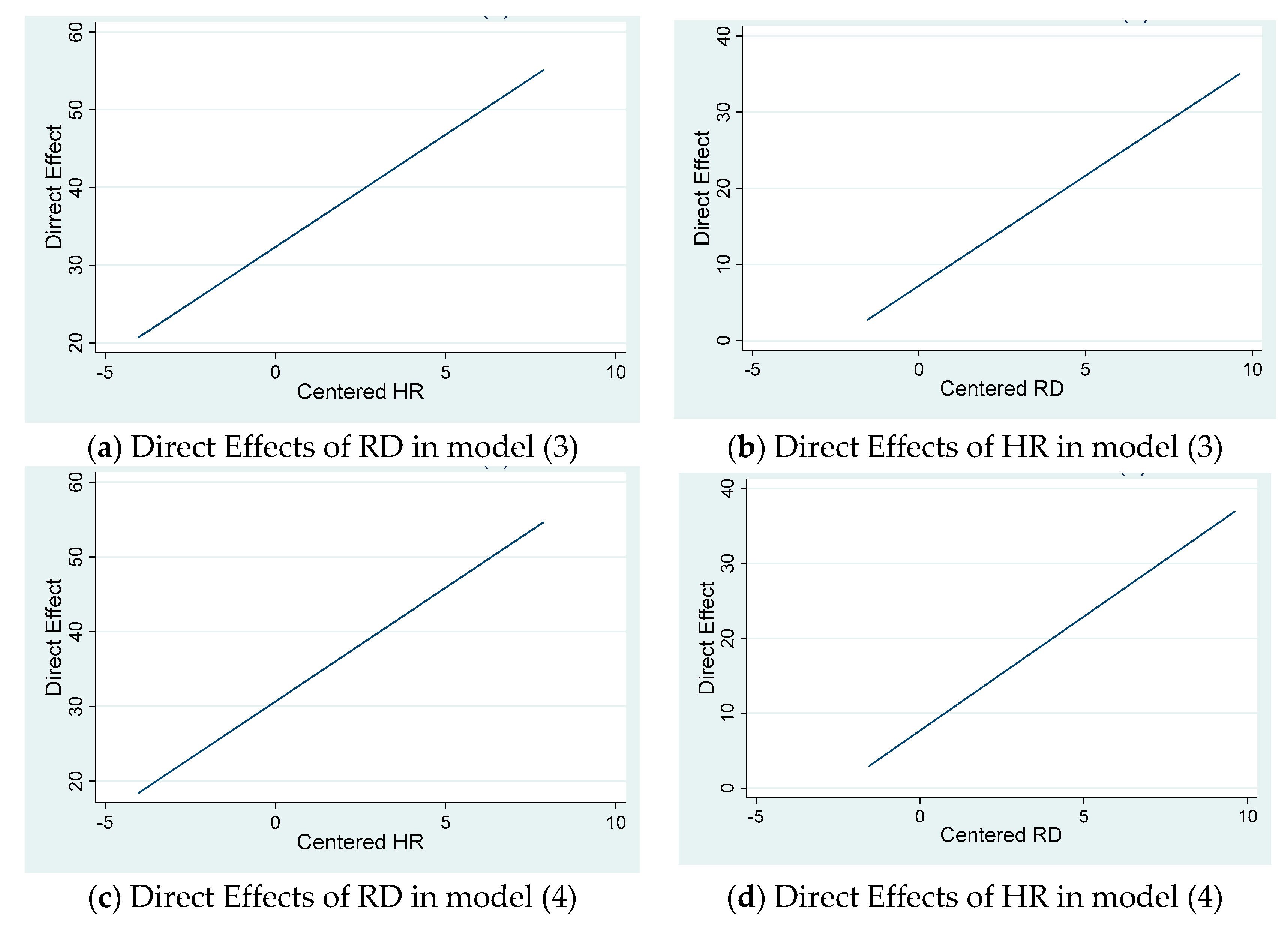
| RD | 36.09 *** | 35.04 *** | 32.27 *** | 30.58 *** |
| HR | 8.003 *** | 8.402 *** | 7.195 *** | 7.665 *** |
| indirect | ||||
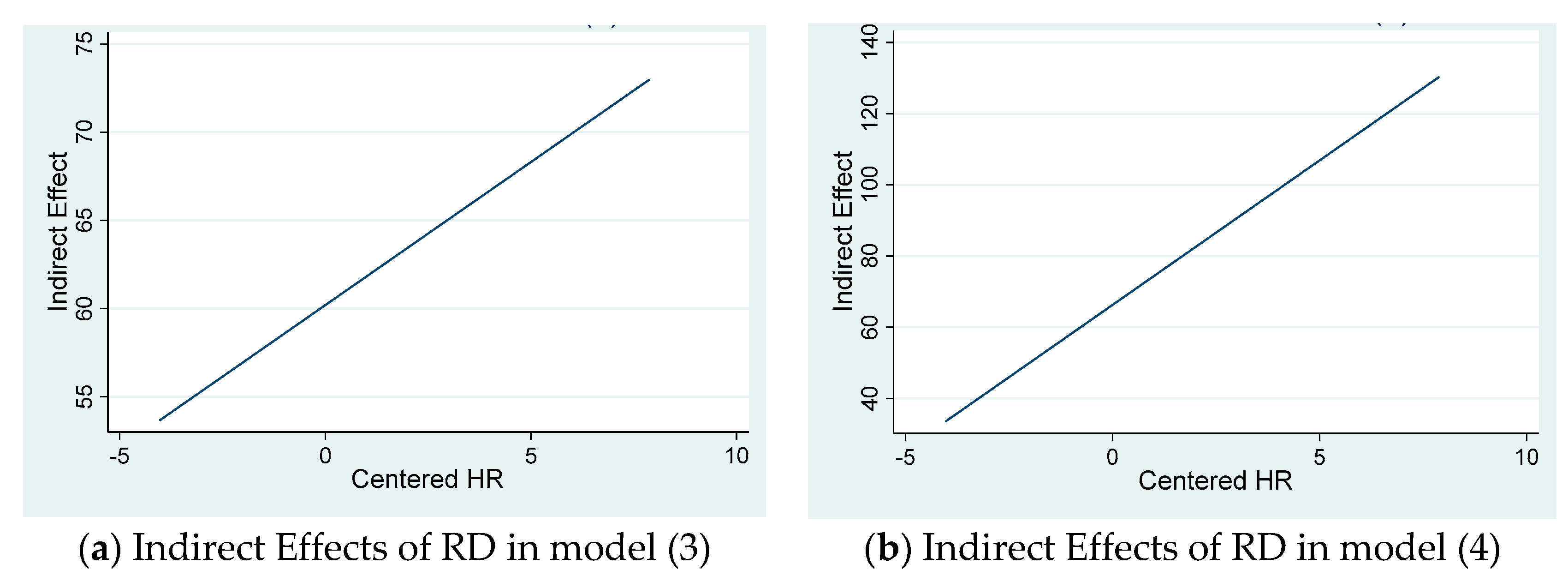
| RD | 54.38 *** | 56.137 *** | 56.00 *** | 65.60 *** |
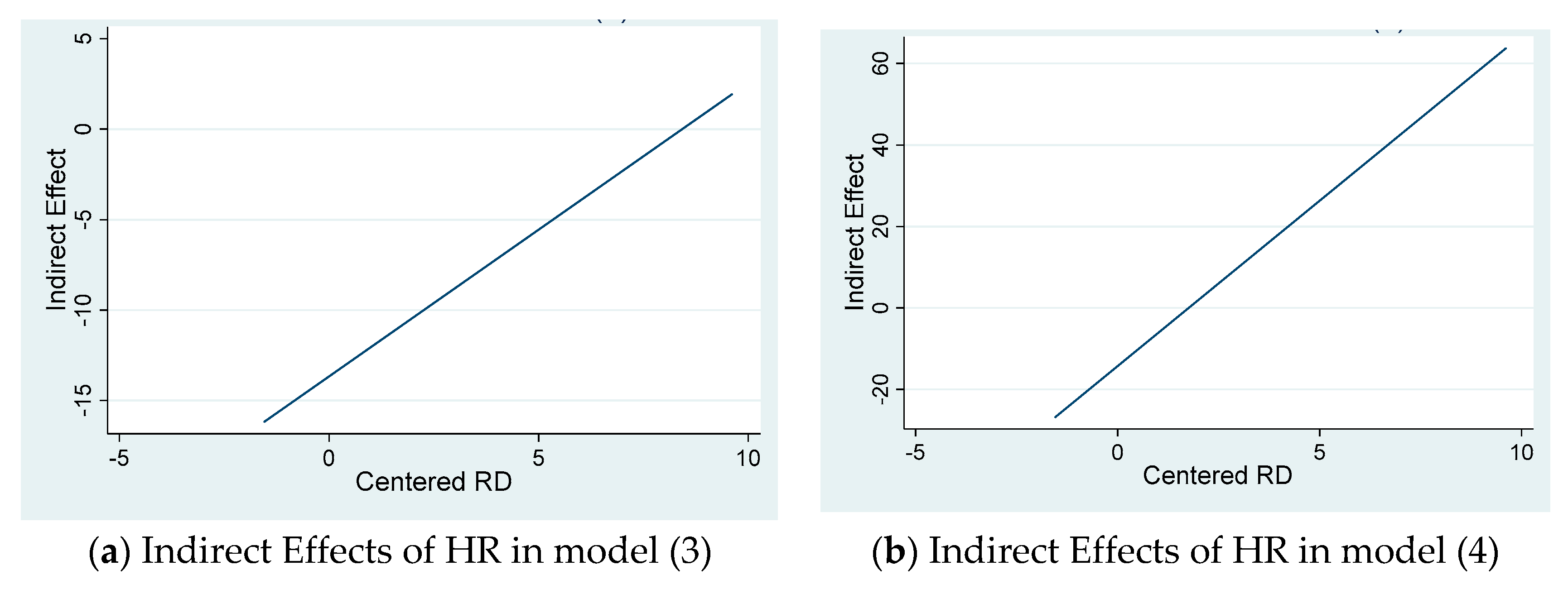
| HR | −13.72 *** | −14.67 *** | −13.62 *** | −13.72 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kijek, A.; Kijek, T. Knowledge Spillovers: An Evidence from The European Regions. J. Open Innov. Technol. Mark. Complex. 2019, 5, 68. https://doi.org/10.3390/joitmc5030068
Kijek A, Kijek T. Knowledge Spillovers: An Evidence from The European Regions. Journal of Open Innovation: Technology, Market, and Complexity. 2019; 5(3):68. https://doi.org/10.3390/joitmc5030068
Chicago/Turabian StyleKijek, Arkadiusz, and Tomasz Kijek. 2019. "Knowledge Spillovers: An Evidence from The European Regions" Journal of Open Innovation: Technology, Market, and Complexity 5, no. 3: 68. https://doi.org/10.3390/joitmc5030068
APA StyleKijek, A., & Kijek, T. (2019). Knowledge Spillovers: An Evidence from The European Regions. Journal of Open Innovation: Technology, Market, and Complexity, 5(3), 68. https://doi.org/10.3390/joitmc5030068






