Open-Circuit Fault Tolerance Method for Three-Level Hybrid Active Neutral Point Clamped Converters

Abstract

Three-level converters are the most important technologies used in high power applications. Among these technologies, active neutral point clamped (ANPC) converters are mainly used for industrial applications. Meanwhile, recent developments have reduced losses and increased efficiency by using a hybrid combination of Si-IGBT and SiC-MOSFET switches to achieve hybrid ANPC (HANPC) converters. Open-circuit failure is regarded as a common and serious problem that affects the operational performance. In this paper, an effective fault-tolerant method is proposed for HANPC converters to safely re-utilize normal operation and increase the reliability of the system under fault conditions. Sequentially, regarding different topologies with reference to earlier fault tolerance methods which could not be applied to the HANPC, the proposed strategy enables continuous operation under faulty conditions effectively without using any additional devices by creating new voltage references, voltage offset, and switching sequences under the faulty conditions. Consequently, no additional costs or changes are associated with the inverter. A detailed analysis of the proposed strategy is presented highlighting the effects on the voltage, currents, and the corresponding total harmonic distortion (THD). The simulation and experimental results demonstrate the capability and effectiveness of the proposed method to maintain normal operation and eliminate the output distortion.

1. Introduction

Most of the efforts on DC/AC converters including the recent developments have been focused on improving renewable energy technologies such as photovoltaic (PV) systems. These technologies require robust and reliable power electronics topology to be associated with to get an efficient output [1]. Many topologies have been developed for achieving higher reliability and efficient performance. Neutral point clamped (NPC) converters have received considerable attention because of their very high efficiency and low leakage current. This topology was initially proposed in Baker’s patent in the 1970s and was published by Nabae et al. in 1981 [2]. Additionally, NPC topology does not produce common-mode (CM) current, thus it is more suitable for PV generation systems [3,4] and can support longer device lifetime with a lower instantaneous rate of voltage change (dv/dt) [5]. However, NPC topology suffers from unequal heat distribution among the semiconductor devices owing to uneven power loss distribution, as reported in [6,7,8,9]. To overcome this problem, the active clamped diodes were replaced by active switches, achieving and an active neutral point clamped (ANPC) topology [9]. Although two more switches are used, it provides an additional switching state to facilitate loss distribution balancing for the whole system [10,11,12,13,14]. Among the many studies undertaken on new modulation schemes for controlling the ANPC converter, the authors of [15] proposed a new modulation scheme to perform a new commutation loop that offers better switching performance with lower stress on each switch. They discussed the proposed method based on quantitative analysis and comparison with different switching schemes. It is reported that the conventional virtual space vector modulation (VSVM) depends on selecting the nearest three vectors to form a linear combination of real vectors. This can control the neutral point (NP) at any modulation index (MI), but it cannot reduce the switching losses or suppress the CM voltage. Therefore, an improved VSVM to reduce the efficiency and switching losses by selecting two pairs of small vectors based on the NP charge and the pulse sequence was developed [16]. The results of the improved VSVM method confirm the flexibility in balancing the NP voltage with different MI. Similar works can be found in [17,18,19,20].

Among the various control switching strategies, better combinations for the same topology used in industrial applications can be achieved by a higher switching frequency by using a wide band gap (WBG). In this regard, a creative method was presented to improve the reliability of wind turbine generation (WTG), by proposing an open-circuit fault detection method using back-to-back converters using the NPC topology as shown in [21] and similarly in [22], while a new hybrid combination including two different types of switches to perform hybrid ANPC (HANPC) converters has been recently considered by many researchers. Although Si-IGBTs are the commonly used technology in power converters, they have some limitations in terms of switching frequency. Therefore, the trends are to move toward using SiC-MOSFETs as they can work under higher switching frequency with lower switching losses, as shown in [23]. However, the usage of full SiC-MOSFET topology is regarded as uneconomical because the cost of SiC-MOSFETs is up to a factor of 8 higher than that of Si-IGBTs and almost a factor of 2 higher than that of Si-MOSFETs [24]. Conventional NPC, ANPC, and HANPC converters are opposed to fault during operation. Meanwhile, in some systems, reliable and continuous operation is highly important because of the sensitivity, cost, and critical application of these systems. Therefore, the need for fault tolerance and the capability of re-operating the power system adequately and safely has drawn considerable interest during the past decade [25]. In general, most studies have focused on tolerating faults by adding new parts to the main topology [26]. The authors of [27] maintained a fault tolerance strategy for full-SiC devices in an ANPC inverter by adding an additional leg to the inverter. The main objective was to obtain the output waveforms for safe operation. Similarly, another study added two additional switches and six diodes to the middle switches of all phases in T-type converters [28]. The main purpose was to maintain additional paths for the current in the case of device failure. Similarly, in [29] and [30], the fault-tolerant capability for different topologies converters was investigated; where the proposed fault-tolerant method in [29] focused on the equivalent substitution of voltage space vector for cascaded H-bridge multilevel inverter. While, in [30], the proposed method applied for NPC/H-bridge (CNHB) inverters. It mainly works on maintaining the three-phase equilibrium and minimizing the imbalance between the stacks. Nevertheless, in some of the fault scenarios, the inverter has to be controlled with decreased MI. Furthermore, some studies consider the diagnosis and fault tolerance for different T-type and NPC inverters as shown in [31,32,33,34,35,36]. In these studies, the diagnosis was performed for the open-circuit fault within the proposed topology concerning the turn-on time for fault control.

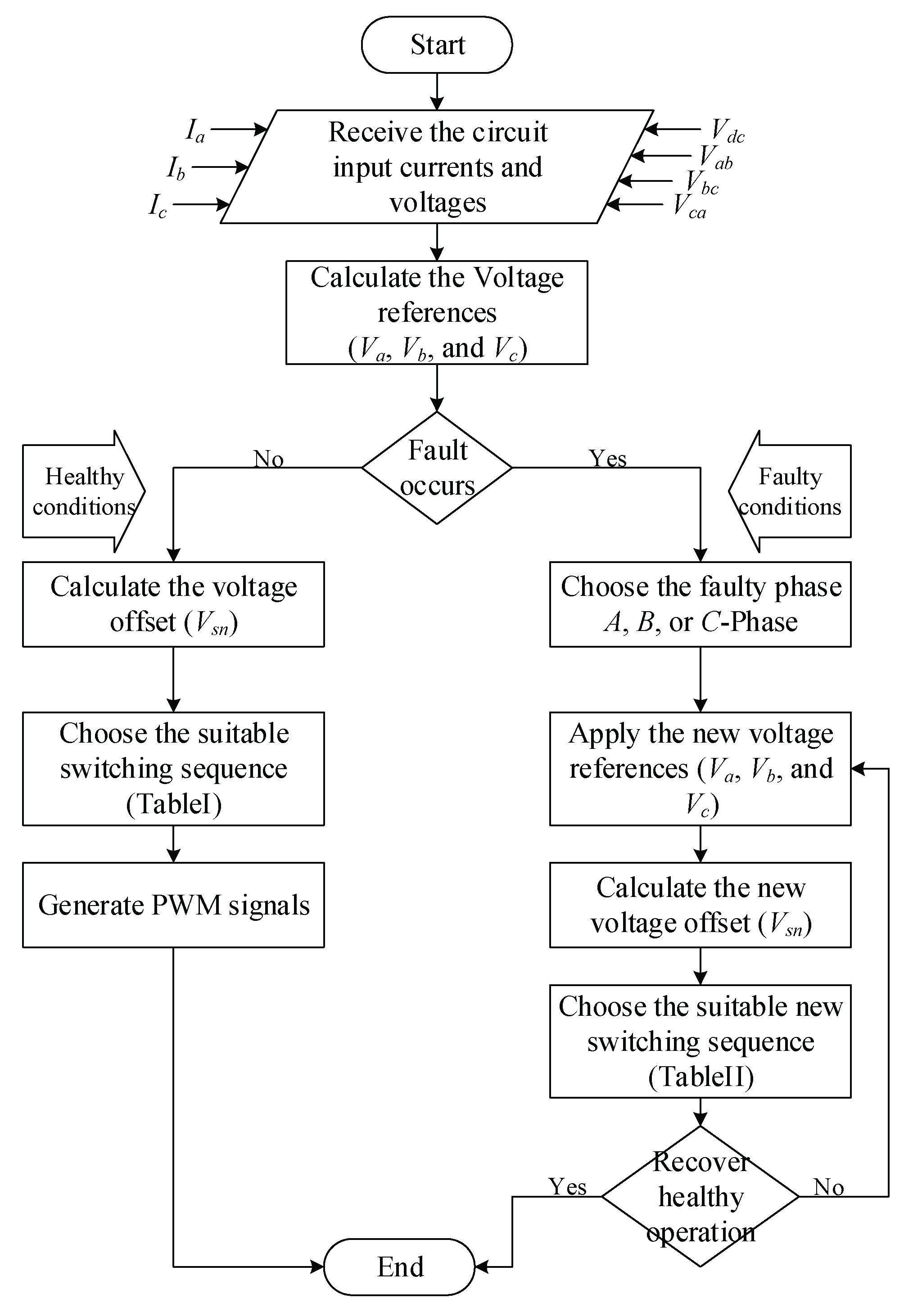
Generally, most of the previous methods require additional devices such as fuses, switches, or entire legs to be added to the standard inverter topology for tolerating device failure. Moreover, the systems exhibited low response, higher ripple output, or lower output waveforms (from three to two levels), which would increase the cost and could even reduce the reliability of the inverters and drive systems. In these regards, this paper proposed an effective method that can be applied for HANPC to recover the healthy operation and eliminate the fault effects on the system without the need for adding any extra devices. Therefore, it results in recovering the healthy operation, improving the reliability of the converter’s applications, eliminating the output distortion that clearly appears in the total harmonic distortion (THD), and works on balancing the DC link voltages.

2. Physical Model of HANPC Inverters

The proposed algorithm in this paper focuses on HANPC topology, where this topology built and operated mainly for high-efficiency and high-power appliance. Besides, it has unique switching sequences and circuit combination as it includes a hybrid combination of Si-IGBT and SiC-MOSFET devices, which is built and developed with reference to other topologies such as the standard NPC and the conventional ANPC topologies. NPC topology is a common three-level topology, and it is widely used in medium and high-power photovoltaic inverters. The voltage stress on each power device of the NPC is only half of the bus voltage thus smaller rating devices are used. Moreover, its output voltage harmonic content is lower compared with the two-level inverters. In these regards, the NPC converters seem to be one of the most promising and used topologies in different industrial applications. While multilevel converters are regarded as an industry-standard solution to realize AC–DC or DC–AC power conversion in high power applications. They have been applied to a medium voltage drive system, wind energy generation system, photovoltaic generation system, battery charging system for electric vehicles, and power supplies for modern data centers, etc. It is worth mentioning that three-level converters are the most popular choices in the family of multilevel converters and the most available in different industrial applications. Compared with other multi-level topologies, three-level converters have low switching losses, smaller AC side filter size, and less complexity, as well as the lowest associated costs [36]. Among all the existing three-level topologies, the NPC converters are the most popular topologies [24,37].

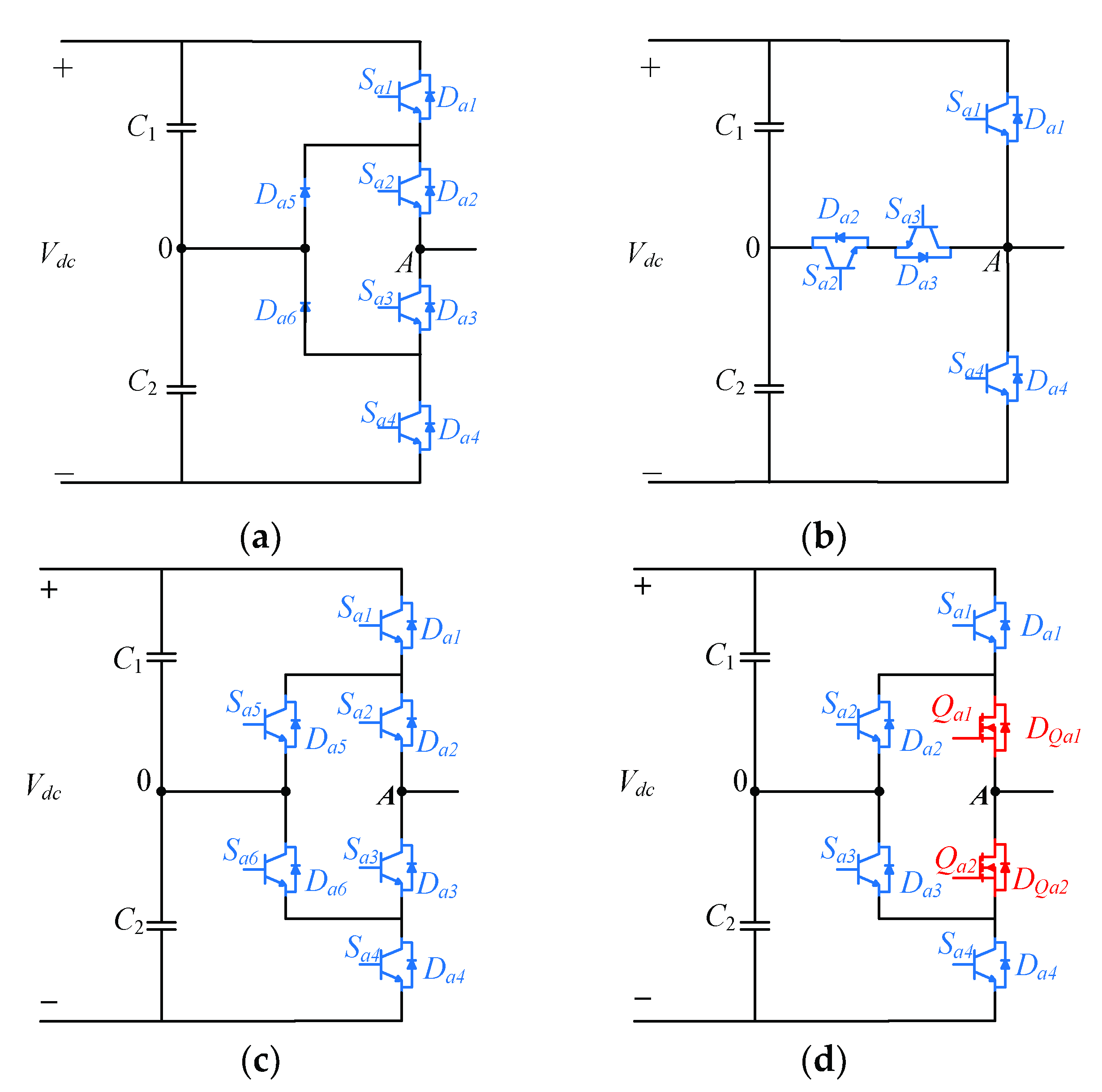
The basic idea of the HANPC circuit has been developed from the conventional NPC and T-type topologies as shown in Figure 1. Figure 1a,b present the optimal single leg configuration of the conventional three-level NPC and T-Type converters, respectively. The NPC converter consists of 4-IGBT switches (S_x1/D_x1 to S_x4/D_x4) with the associated diodes in addition to 2-active diodes (D_x5 to D_x6) in each phase. Similarly, the T-type converter is combined of 4-IGBTs (S_x1/D_x1 to S_x4/D_x4) two of them work as half-bridge and two as neutral point IGBTs. Where x represents A-, B-, or C-phases. For the NPC topology, there are two loops for commutation paths. The first path includes the inner loop which starts when the current flows through the clamping diode (D_a6) with the outer switch (S_a4). While the second loop starts when the inner switch (S_a2) with either the inner diode (D_a3) or the outer diode (D_a4) being based on the modulation scheme where due to the symmetrical structure of the top and bottom these loops, it can reflect the remaining commutation loops. In the same manner, in the T-type two main loops are performed; the first when the current pass through the upper switch (S_a1) and the inner switch (S_a2) while the other loop goes through the lower switch (S_a4) and the inner switch (S_a3) depending on the modulation scheme. Meanwhile, the NPC inverter uses two switches connected in series to block the full DC link voltages compared to one switch in T-type inverters. Consequently, the basic configuration of the conventional ANPC is shown in Figure 1c. It consists of six Si-IGBT (S_x1/D_x1 to S_x4/D_x6) in each phase leg, where the main advantage of the ANPC is balancing the switching losses that appear in the NPC topology, as explained in the literature. Meanwhile, the HANPC topology is shown in Figure 1d. it consists of four Si-IGBT (S_x1/D_x1 to S_x4/D_x4) and two SiC-MOSFET (Q_x1/D_Qx1 and Q_x2/D_Qx2) switches alongside with the associated diodes in each phase leg. A total of 12 Si-IGBT and 6 SiC-MOSFET switches. It is worth mentioning that the total number of the switches in HANPC is the same when compared to the conventional ANPC but the HANPC is considered as a new topology that can reduce the switching losses and enhancing the system performance by reducing the total harmonic distortion (THD) and work on higher switching frequencies with its unique switching sequences [30]. It also replaces the inner two IGBTs (S_a1/D_a1 – S_a4/D_a4) with two MOSFETs (Q_a1/D_Qa1 and Q_a2/D_Qa2) switches.

The new and conventional switching sequence of all topologies is shown in Figure 2. Figure 2a shows the conventional switching sequences of the NPC, T-type, and ANPC topologies. While Figure 2b shows the new switching sequences for HANPC topology. These changes have the advantage of using the IGBT switches on the lowest possible frequencies (fundamental frequency 50 Hz) and the MOSFET switches on high frequency (30 kHz) due to the fact that the switching losses are lower than the conduction losses for the MOSFETs while having the potential to operate at a higher junction temperature than regular Si-IGBT switches. On the other hand, the opposite is correct for the IGBTs [24].

Therefore, balancing the losses distribution is unnecessary between the different switching devices. Besides, by using the hybrid combination of these switches offers an affordable price with almost the same efficiency as the full SiC-MOSFET converters. In this work, we consider the A-phase for offering the necessary explanation.

The detailed switching sequences of the HANPC are shown in

Table 1. Switching conditions of HANPC under healthy conditions

Switching States	Sa1	Sa2	Sa3	Sa4	Qa1	Qa2
P	1	0	1	0	1	0
O+	1	0	1	0	0	1
O−	0	1	0	1	1	0
N	0	1	0	1	0	1

. The proposed modulation scheme depends on working based on four different switching states (P, O+, O–, and N) as shown in Table 1. In this table, the three-voltage states O, P, and N represent the zero, positive, and negative voltage levels, respectively.

Additionally, the On-Off switching states for all Si-IGBT and SiC-MOSFET switches under healthy conditions (i.e., with no-fault occurring). During the healthy operation, the IGBT switches are working in pairs with complementary behavior (S_a1/D_a1 and S_a3/D_a3) and (S_a2/D_a2 and S_a4/D_a4). While the SiC-MOSFET switches have the same complementary procedure between Q_a1/D_Qa1 and Q_a2/D_Qa2. Subsequently, in the positive half cycle, S_a1/D_a1 and S_a3/D_a3 are in the On-state 1, and S_a2/D_a2 and S_a4/D_a4 are in the off-state 0, at the same rate of the fundamental frequency. While a complementary operation at 30 kHz is applied by Q_a1/D_Qa1 and Q_a2/D_Qa2. The opposite occurs during the negative half cycle.

Accordingly, numerous fault tolerance methods were proposed in the literature for conventional topologies. Some researchers have focused on tolerating the faults by inserting additional hardware parts to the basic topology, which results in increasing the system cost which could be regarded as a huge drawback and adding complexity to the control and the hardware design [27,28,29,30]. Accordingly, the usage of the available vectors instead of the impossible vectors are applied for T-type inverter as shown in [31]. However, such control scheme relatively eliminates the current distortion when an open-circuit fault occurs. Besides, it still limited to the proposed topology and inapplicable for other topologies such as HANPC, due to the differences in the topology configuration and working principle as shown in previous sections. Consecutively, in the case of the fault, the conventional methods are inapplicable for HANPC topology. Therefore, the need of finding a new method that can be applied to the HANPC is highly needed.

3. Proposed Fault Tolerance Method for Open-Circuit Faults

3.1. Operation of HANPC Inverters under Failure Condition

In industrial applications, there are many factors that can affect the normal operation of the inverters. These effects can result in serious faults which result in disturbing the normal operation. The conventional control scheme of the HANPC inverters is shown in Table 1. This switching sequence is proposed to maintain the desired output voltages and current of the A-, B-, and C-phases under healthy conditions as explained in Section 2. However, if any of the switches fails to operate in the proposed sequence, the inverter would be partially or unable to provide the desired output voltage and current. The fault commonly occurs at the switch or the associated diodes as explained in the literature. Therefore, it is necessary to study the operational behavior under different conditions.

In this manner, based on the symmetrical structure of the HANPC inverter, faults for S_a1/D_a1, S_a2/D_a2, and Q_a1/D_Qa1 will be analyzed where this is valid for the remaining IGBT and MOSFET switches. Due to the symmetrical performance of the HANPC converters, A-phase is considered to carry out all necessary explanations and justifications, where the analysis is also valid for the remaining B- and C-phases. Figure 3 shows the effects of different open-circuit fault on the system performance and the affected paths of the current for diverse cases of the fault’s location at S_a1/D_a1, S_a2/D_a2, and Q_a1/D_Qa1 as shown in Figure 3. The analysis can be applied to the other switches of the faulty phase because of the symmetrical merits of the HANPC topology (i.e., S_a1/D_a1, S_a2/D_a2, and Q_a1/D_Qa1).

The effects on the current paths during the fault at different output voltage are shown in this figure. Many factors should be considered before analyzing the effects of the faults of the systems. Mainly, in real systems, the faults can either locate at the switch or the associated diodes with respect to the positive and negative cycles [25,26]. Therefore, the analysis of each case of the fault at the switches and diodes is considered in this paper. The current movements in the positive and negative direction have different effects concerning the fault location. Figure 3a,b show the effects in positive and negative directions of the current, respectively. It is clear in Figure 3a,b, when an open-circuit failure occurred at S_a1/D_a1, it is impossible to get the P state when the load current I_a > 0 in A-phase, where the output is connected to the NP of the DC link bus. However, other states such as O+ and O– are still applicable. Meanwhile, Figure 3c,d show open-circuit failure occurred at S_a2/D_a2. In this case, instead of connecting the output to the NP it is connected to the DC; however, in this case, although the current I_a < 0, O– is not applicable.

Moreover, Figure 3e,f show the influence on the output voltage when an open-circuit fault is occurring at the MOSFET switch Q_a1/D_Qa1. In this case, instead of connecting the output to the NP, the output is connected to the N while the current is in the positive direction (I_a > 0). As a result, because of the incorrect output voltage level, an unsymmetrical output and an unbalanced waveform are found. For example, when an open-circuit fault occurs when the combined diode with the MOSFET switch Q_a1/D_Qa1 is open as a result of the open-circuit failure as shown in Figure 3f when I_a < 0, the current became discontinuous as a result of cutting off the current path. In this case, due to the inductive nature of the load, an overvoltage would occur at the load inductor, destroying the inverter devices. Similarly, other failure scenarios could be analyzed in the same way.

To understand these operations in more detail, the performance based on the vector diagram is further analyzed. The first case shows the healthy conditions is shown in Figure 4a. as it is clear in this figure all three cases of voltage level—i.e., P, N, and O—all are applicable, thus all voltage vectors are available. At healthy conditions shown in Figure 4a, all ranges of the voltage vectors are available which includes the large, medium, and small vectors. In contrast, after the fault, some status became inapplicable such as P, N, O+, or O−. Considering an open-circuit fault at S_a1/D_a1, the all large and medium vectors which include (+) at the right side of Figure 4a are lost, thus it is impossible to get the P. Similarly, considering an open-circuit fault at S_a4/D_a4, all large and medium vectors which include (–) at the left side of Figure 4a are lost, thus it is impossible to get the N. Nevertheless, Figure 4b shows the available vectors for different cases of the fault where the available vectors include the small voltage vectors which the system could use.

Subsequently, in the case of a fault in the upper switch for S_a1/D_a1 and Q_a1/D_Qa1, then the available vectors are shown in Figure 4b. in this case, only six vectors can be reached which are located on the perimeter of the inner hexagon—small vectors only (highlighted in black color). Therefore, the maximum MI which can be applied is reduced to 0.577 of the original MI. For instance, tow vectors seem to be applicable [(0+–) and (0–+)], but it should be highlighted that these vectors are considered as medium vectors while under the faulty conditions, only the small vectors are applicable. Otherwise, the system would suffer from unbalancing DC link voltages and would result in undesirable output waveforms. Therefore, these vectors are not considered in the proposed fault tolerance strategy. On the other hand, in the case of open-circuit failure of S_a2/D_a2, by applying the proposed fault tolerant, the HANPC converter can be operated as a conventional NPC inverter thus the inverter can still be operated at maximum MI with all available vectors.

3.2. Proposed Fault-Tolerant Strategy

The main process of the proposed method is illustrated in the flowchart shown in Figure 5. The proposed fault-tolerance strategy aims to create a safe operation of the inverter after the fault occurred. It will also result in improving the reliability after the fault is detected for the whole system. It is worth mentioning that fault detection is not a part of this work: the fault is presumed to be detected and then the proposed fault-tolerance strategy is applied. To realize the proposed control operation, some points should be clarified in advance. Firstly, after the fault occurs in the DC link capacitor—i.e., the upper and lower capacitors—one of the charges and the other discharges continuously depending on the fault position, which unbalances the DC link voltage. Therefore, the proposed fault-tolerance strategy must balance the system.

Secondly, the line-to-line and pole voltages and current get disturbed not only in the faulty leg but also in the other phases because of NP unbalancing, which is an important issue that needs to be solved. Finally, the loss balancing capability of the HANPC converter should be satisfied to some extent concerning the location of the fault. Moreover, in the HANPC converter, because of the use of two different types of switching devices, the hybrid switching of the SiC-MOSFET switches should be kept during the fault as much as possible to reduce the stress on the Si-IGBT switches and enhance the performance of the HANPC inverter compared with that of the conventional ANPC. While, in the proposed fault tolerance topology, the hybrid switching topology is kept even in the faulty phase with respect to the fault location (i.e., at S_a1/D_a1, S_a2/D_a2, and Q_a1/D_Qa1.).

Under the faulty conditions, some current paths became inapplicable due to the loss of the control capability of the switching devices. The fault affects the devices’ performance, where the conventional switching strategy that is shown in Table 1 is limited to the healthy operating conditions. therefore, under the faulty conditions, new switching sequences which allow the system to handle the new working conditions under the faulty conditions. For example, when an open fault occurred at S_a2/D_a2 or Q_a1/D_Qa1, it is impossible to control the aforementioned devices. as a consequence, it is necessary to find a suitable replacement for the current paths so the system would recover the healthy operation. In these regards,

Table 2. Proposed switching sequence at open-circuit fault conditions

Fault-Device	Switch Status
	Sa1/Da1	Sa4/Da4	Sa2/Da2	Sa3/Da3	Qa1/DQa1	Qa2/DQa2
Sa1/Da1	Fault	0	1	0	1/0	0/1
	Fault	0	0	1	0/1	1/0
Sa2/Da2	0	1	Fault	0	0/1	1/0
	1	0	Fault	1	1/0	0/1
Qa1/DQa1	0	0	1	0	Fault	1/0
	0	0	0	1	Fault	0/1

shows the proposed switching sequence using the proposed fault tolerance strategy. Which indicates the switching sequences at different states under the faulty condition. The switching is kept within the fundamental frequency for the IGBT switches and at high switching frequency for the SiC-MOSFET switches. In this case, the inverter is still able to work under low switching losses for the IGBT and SiC-MOSFET devices without being opposed to higher conduction losses. After the fault occurs, the operational behavior of the circuit changes and results in undesirable waveforms and switching status as well. Therefore, to solve these issues and enhance the performance of the system, the main point in the proposed approach is to clamp the faulty phase into the NP to eliminate the fault effects on the output waveforms (i.e., the associated disturbance in the current, voltage, and unbalance DC link voltage). We also assign new switching sequences to tolerate the fault and re-operate the system safely and adequately. The details of the proposed switching sequences are presented in Table 2.

The switching sequence for open-circuit fault switching is applied only for the faulty leg (and symmetrical behavior of the converter means that the same procedure can be applied to the other switches S_a4/D_a4, S_a3/D_a3, and Q_a2/D_Qa2). One of the main advantages of this method is that each switch needs to withstand only half the DC link voltage. Therefore, there is no risk of breaking down from overvoltage. The new references are shown in Equation (1)

$$\begin{array}{cc}\begin{array}{l}{V}_a=MI·\sin (\omega t)\\ V_b=MI·\sin (\omega t-\frac{2\pi }{3})\\ V_c=MI·\sin (\omega t+\frac{2\pi }{3})\end{array}& \begin{array}{l}\to V_a=0,\\ \to V_b=-\frac{MI}{\sqrt{3}}·\sin (\omega t+\frac{2\pi }{3}),\\ \to V_c=\frac{MI}{\sqrt{3}}·\sin (\omega t-\frac{2\pi }{3}).\end{array}\end{array}$$

(1)

The fault is assumed to be on A- phase, where, V_a, V_b, and V_c are the three phases voltage references for A-, B-, and C-phases, respectively. While t is the time and ω is the fundamental frequency. However, due to the changes in the switching sequence, the MI should be changed to avoid overmodulation and set to be (0.577 × MI) compared to the original MI at healthy conditions. The new voltage references shown in (1), include a reduction in the MI down to one-third of its original value (i.e., $\frac{1}{\sqrt{3}}=0.577$) which is the maximum value of the modulation index under the faulty conditions, due to the loss of P and N status in the case of open-circuit faults at S_a1/D_a1 and Q_a1/D_Qa1. In these regards, Figure 4 Shows the possible voltage vectors under healthy and faulty conditions before and after the faults occurred. where under the faulty conditions the medium and large vectors became unachievable while only small vectors are applicable. However, in the case of an open fault in S_a2/D_a2 the inverter is still able to achieve the full MI due to operating the HANPC converter as a conventional NPC converter. However, the original and new voltage references still need to be added to the offset voltage reference (V_sn) as shown in Equation (2)

$$V_{xn}=V_x+V_{sn}.$$

(2)

where x represents the three phases A-, B-, and C-phases, respectively. As a consequence, at normal conditions, the voltage reference will be added to the original V_sn, but after the fault occurred the calculation would include the new the V_sn as illustrated in Figure 5. Meanwhile, Figure 6 shows the calculation process of V_sn.

In Figure 6, the calculating of the V_sn is started by calculating the new voltage references, then comparing these references to find the maximum, minimum, and medium values. Finally, based on the obtained values the new V_sn can be calculated. Meanwhile, this process should be calculated at each switching cycle. Where V_max, V_min, and V_mid are the maximum, minimum, and medium reference voltages, respectively. Accordingly, after the fault happens, the new V_sn should be regenerated with reference to the new voltage references in all phases as shown in Figure 7.

In order to use the proposed method for controlling the inverter under the faulty conditions, it is necessary to modify the V_sn to obtain the required performance. Before applying the proposed algorithm, the frequency of old V_sn frequency is three times faster than the fundamental frequency, while it is necessary to be reduced to the same value of the fundamental frequency. When calculating the V_sn as described earlier in Figure 7 then, it will be summed with the new voltage references, it is necessary to consider all voltage references including the faulty phase. Meanwhile, it should be highlighted that under the healthy conditions, if one of the phases is clamped to ‘O’ status, then the active control of the neutral point would be lost and would result in unbalancing the DC link voltages (i.e., under the healthy conditions switching sequence showed in Table 1).

However, the proposed fault tolerance control method depends on changing the voltage references by clamping one phase into ‘O’ status while modifying the voltage references of the other phases as shown in Equation (1). Also, the proposed method depends on changing the switching sequence (i.e., under the faulty conditions switching sequence showed in Table 2) in order to effectively control the inverter under the different fault conditions. Moreover, the calculation of the new voltage offset (V_sn) is carried out with different approach to include the new voltage references all in the calculation, and changing the V_sn frequency form being three times the fundamental frequency (3 × F_fundamental) down to the same value of the fundamental frequency as shown in Figure 7. As a result, the proposed control scheme can effectively control the Neutral potential and balancing the neutral point voltage (DC link) under all cases of the faults. Furthermore, it is worth mentioning that the proposed fault tolerance strategy can be applied to the basic ANPC converters with respect to the difference in the maximum switching frequency of the IGBT switching devices and the differences between the basic ANPC and the HANPC topologies as illustrated in Section 2.

4. Simulation Verification and Performance Analysis

To clarify the effects of an open-circuit fault on any switch, an analyzed simulation using PSIM and Visual Studio software is carried-out.

Table 3. Main simulation and experimental parameters

Parameter	Value
Inductance	1 mH
Resistance	10 Ω
Fundamental frequency	50 Hz
IGBT switching frequency	50 Hz
MOSFET switching frequency	30 kHz

shows the simulation parameters. In Figure 8, shows the line-to-line voltage (V_ab), pole voltage (V_an), three-phase load currents, and the DC link voltages (V_C1 and V_C2) of A-phase before and after a fault in S_a1/D_a1. Meanwhile, the fault is assumed to happen and detected at t = 0.05 s. Regarding the results shown in Figure 8a, shows the effects of open-circuit fault in S_a1/D_a1 before applying the proposed algorithm, the influence on the pole voltage and load current is clear as described in Section 3.1.

As clarified in Table 2, the proposed fault tolerant strategy should be able to keep hybrid switching frequency to avoid any further conduction losses or additional load on any IGBT or SiC-MOSFET devices for each case of the fault at S_a1/D_a1, S_a2/D_a2, and Q_a1/D_Qa1. The other switching sequences can be obtained by following the proposed switching sequences which are shown in Table 2.

The results in Figure 8b show the resuming of the normal operation and the effects on the THD as it improved from 52.47% at fault to 2.75% using the proposed method compared with 1.17% in the healthy condition. Figure 8c shows the distribution of the THD after applying the proposed control strategy. However, the maximum MI is reduced to 0.577 of the original value at healthy conditions due to the fault and changing the reference voltages as described in Section 3.1. Meanwhile, hybrid switching should be kept as mentioned earlier, by considering inverting the switching sequence for the MOSFET switches (Q_a1/D_Qa1 and Q_a2/D_Qa2), as illustrated in Table 2.

Additionally, the loss balancing capability of the HANPC converter should be satisfied to some extent with respect to the location of the fault. Moreover, the loss balancing capability of the HANPC converter should be satisfied to some extent with respect to the location of the fault. Figure 9 presents the result of simulating the fault in S_a2/D_a2.

It shows a slight difference in the output signal after applying the proposed algorithm since in this case, the inverter is applicable to re-operate with the full MI as is it in the healthy conditions. This is due to operating the faulty leg (A-phase) as a conventional leg NPC, as clarified in Figure 4 for the vectors’ selection. While the other leg still worked according to the HANPC strategy. Therefore, the inverter is still capable of balancing the losses distribution. In this case, S_a2/D_a2 is open due to the open-circuit fault, and in the tolerance control strategy. S_a3/D_a3 is forced to be open and then changing the switching sequence to operate similarly to the conventional NPC inverter. However, due to the physical limitation of the IGBT switches, the switching frequency of the MOSFET and IGBT switches is set to 10 kHz only, while the results are shown in Figure 9b the resuming of the normal operation and the effects on the THD as it improved from 8.58% at fault to 1.19% using the proposed method compared with 1.17% at the healthy condition.

Figure 9c shows the distribution of the FFT after applying the proposed control strategy. The simulation result is shown in Figure 10a. For Q_a1/D_Qa1 open-circuit fault, the tolerance general operational performance is similar to S_a1/D_a1 in terms of reducing the MI as described in Section 3.1 by following the switching sequence that is described in Table 2. Additionally, the loss balancing capability of the HANPC converter should be satisfied to some extent with respect to the location of the fault. Meanwhile, Figure 10b shows the simulation result under Q_a1/D_Qa1 open-circuit with the effects on the THD of 52.44% to 2.74% using the proposed method before and after using the proposed method. While Figure 10c shows the distribution of the THD after applying the proposed control strategy. Accordingly, the proposed switching sequences under an open-circuit fault are shown in Figure 11.

The description of Figure 11 can be clarified with respect to Figure 3. Under the device failure condition, due to the symmetrical structure of HANPC topology, the failure of S_a1/D_a1 and S_a4/D_a4 has similar effects on the inverter, and this is also valid for the other pairs: S_a2/D_a2 and S_a3/D_a3, Q_a1/D_Qa1, and Q_a2/D_Qa2. Therefore, only one from each pair of devices in A-phase is analyzed. Figure 3 shows the examples of the current flow path at different output voltage levels under the open failure of S_a1/D_a1, S_a2/D_a2, and Q_a1/D_Qa1, respectively. The positive current direction is defined as flowing out of the phase. As seen, when S_a1 open failure occurs at “P” state, if I_a > 0, as shown in Figure 3a, then the phase output is connected to the neutral point (NP) of DC link instead of the positive DC bus. In Figure 3e, Q_a1 open failure occurs at ‘O−’ state when I_a > 0, then the phase output is connected to the negative DC bus terminal rather than NP of DC link. Figure 3d shows that S_a2 open failure occurs at ‘O−’ state when I_a < 0, then the phase output is connected to the positive DC bus instead of NP of dc-link. Due to the incorrect output voltage, the output current will become unsymmetrical and the NP of the DC link will be unbalanced. Moreover, when D_a1 open fault occurs at ‘P’ state and I_a < 0, as shown in Figure 3b, the condition is even worse since the phase current I_a becomes discontinuous due to the cutoff of the conduction path, then the induced voltage on the load inductor and loop inductor may cause overvoltage on the inverter and cause damage. For other device failure cases, the circuit can be analyzed in a similar way.

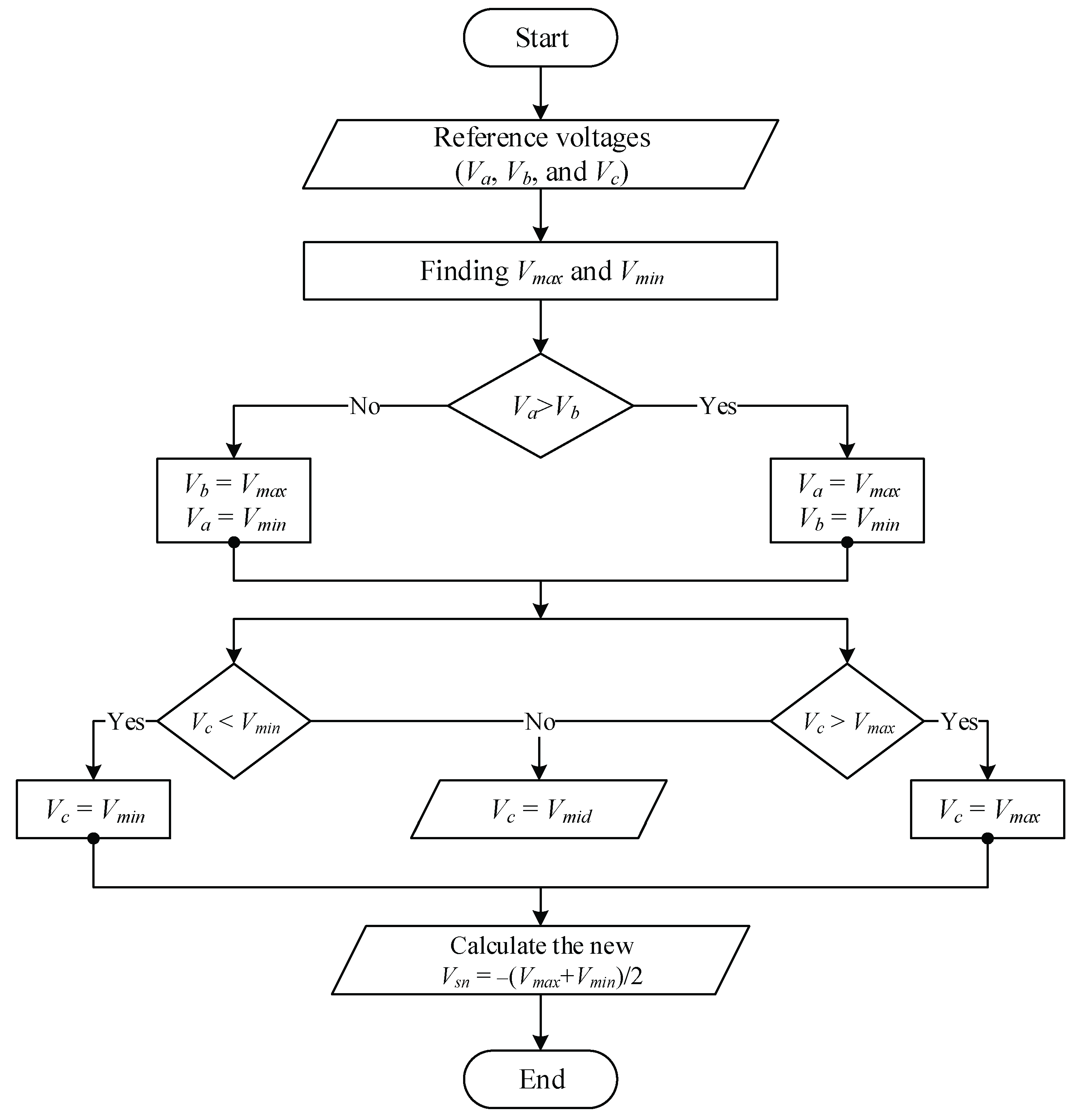
In these regards, the modified switching sequences for the fault-tolerant operation under open failure are given in Table 2. After device open failure, the inverter is no longer operates under the normal conditions and it changes to operate under fault tolerant operation (faulty conditions). A new switching sequence is selected to generate each switching state in a specific order with respect to the fault. In this case, when an open circuit fault occurred at S_a1/D_a1 as shown in Figure 11a, the HANPC inverter is derived into an unnormal operation which leads to disturbing the output terminal of the faulty phase and results in unbalanced output. Therefore, the faulty phase needs to be connected to the NP of the DC link. While the modulation signals also need to be modified in order to maintain the balanced three-phase line-to-line voltages. When the faulty phase can only output ‘0’ voltage level, instead of using the balanced phase voltages as the reference signals, it must modify the reference signals to ensure that the line-to-line voltages are balanced in HANPC inverters while the pole voltage is clamped to the NP. Therefore, the proposed switching sequences are shown in Figure 11a, the new switching sequences aim always to clamp the faulty phase to the NP as explained earlier. For example, when the switches Q_a1/D_Qa1, and Q_a2/D_Qa2 are switching in a complementary order at 30 kHz while S_a2/D_a2 and S_a3/D_a3 operate at the fundamental frequency 50 Hz. The complementary working principle is still necessary to keep the value of the maximum DC link voltage to half (0.5) of its maximum value, so every switch is still needed to block half of the DC link value without being proposed to the overvoltage. Besides, I_a is connected to NP of the DC link, instead of the positive DC bus terminal, which causes an unbalance of NP voltage and thus unbalanced output current. Therefore, the output current would be always clamped to the NP which is the main point of the proposed strategy.

Figure 11b, shows the proposed switching sequence after an open circuit happened at S_a2/D_a2. The main principle of the proposed method when an open circuit fault occurred at S_a2/D_a2 is to operate at a switching frequency of 10 kHz for all IGBTs (the allowable frequency for the Si-IGBTs [38]), and reduce the switching frequency of the SiC-MOSFET switches from 30 kHz to 10 kHz. Besides, when S_a2/D_a2 fails to open, the HANPC inverter is derived into a similar configuration as the conventional NPC inverter. The faulty phase is still able to output three voltage levels, and the maximum modulation index and the output voltage waveform almost the same as normal operation. Moreover, the device power loss balancing function can still be implemented to some extent during fault-tolerant operation as explained earlier. For more clarifications, if only D_a2 fails, while S_a2 is healthy, then besides the ‘O+’ switching states, the faulty phase can still generate ‘O−’ switch in states when the phase current is negative, which can be used for power loss balancing as well. However, in only S_a2 fails, while D_a2 is healthy, then the ‘O+’ and ‘O−’ switching states could be generated at the positive cycle of the current.

Figure 11c shows the proposed switching sequence after an open circuit happened at Q_a1/D_Qa1. In the proposed method, after an open circuit fault occurred at Q_a1/D_Qa1, its necessary to clamp the faulty phase to the NP. This is carried out by changing the switching states of the faulty phase by cutting the current paths to the (+) and (−) terminals; in this way, the ‘P’ and ‘N’ status are terminated. Consequently, the upper switches and lower switches (i.e., S_a1/D_a1 and S_a4/D_a4) state are set to ‘0’. In these regards, and to clamp the faulty phase to the NP when Q_a1 has an open circuit, the switching of the Q_a2 should be kept switching, therefore it works on providing a path of the current to the NP. Following the switching sequence that is clarified in Table 2. In addition, it still necessary to provide a new set of voltage references as shown in Equations (1) and (2). As seen, to avoid over modulation, the maximum modulation index is limited to 0.577 during fault-tolerant operation, which is 1/√3 of that in normal operation.

5. Experimental Verification

To verify the proposed fault tolerant method a 15 kW HANPC inverter Prototype is used. Figure 12, shows the experimental setup in this paper. The power devices used are Si IGBTs (SK75GBB066T, Semikron, Nuremberg, Germany) and SiC MOSFETs (C2M0040120D, Cree, NC, USA), modules, using TMS320F28335 digital signal processor (DSP) control board from Texas Instruments (TI, TX, USA). Owing to hardware limitations, the DC-link voltage is reduced to 200 V.

The fault effects on the circuit after an open-circuit fault occurred at S_a1/D_a1 is shown in Figure 13a. The effects of the fault are clear on the three-level line-to-line voltage, pole voltage, and three-phase currents. On the other hand, applying the proposed figure results in recovering the healthy operation of the inverter as Figure 13b. However, the proposed method restored the normal operation, but the MI is reduced to 0.577 of it is the original value at the normal operation. This is due to the loss of large and medium voltage vector due to cutting the current path as explained in Section 3.1 and Section 3.2. Figure 13c, shows the effectiveness of the proposed method in balancing the DC link voltages. The left part of Figure 13c shows the result of an open-circuit fault at S_a1/D_a1 on unbalancing DC link voltages before applying the proposed control strategy. On the other hand, the right part of Figure 13c confirmed the capability of balancing the system after applying the proposed strategy, where the reduction in the MI and the usage of the small vectors unaffected the system performance in balancing the DC link voltages and marinating healthy operation of the HANPC inverter.

Figure 14 shows the experimental results for open fault at S_a2/D_a2 before and after applying the proposed algorithm. In this case of the fault, the inverter is still capable to operate at its full MI without any reduction in it. This is due to following the proposed switching sequences to re-operate the HANPC inverter is derived into a similar configuration as the conventional NPC inverter. The faulty phase is still able to output three voltage levels, and the output voltage waveform quality is the same as normal operation. in Figure 14a, the fault effects on the output voltage and current waveforms are presented. While Figure 14b confirms the capability of the proposed method in obtaining the full MI and recovering the healthy operation under the fault case. By comparing the result of this figure and the healthy operation which is shown in Figure 13b, the output showed the three-level line-to-line voltage, pole voltage, and three-phase currents. Moreover, Figure 14c shows the effects of the fault on the DC link voltage. The left part of the figure shows the unbalance DC link voltages, while the right part of the figure shows the result of applying the proposed fault tolerance strategy in balancing the DC link voltages.

Furthermore, it is noticed that in the case of an open fault in this switch, the inverter is still capable of working on the full MI in a similar way to the healthy operation despite the increased level of the THD as shown in Section 4. For the open-circuit fault at Q_a1/D_Qa1, the results are shown in Figure 15a. It is clear that the operational behavior of the healthy conditions is operated with reduced MI unlike the case of S_a2/D_a2 open-circuit failure where the MI can be totally recovered to be the same as in the healthy conditions. By applying the proposed fault tolerance strategy, the MI is reduced to 0.577 of it is the original value. Figure 15b shows obtaining a healthy operation after applying the proposed algorithm on the line-to-line voltage, pole voltage, and three-phase currents. Also, the proposed method results in balancing the DC link voltages as shown in Figure 15c. The unbalanced DC link voltages is shown in the left part of the figure, while the right part confirms the capability of the proposed method in balancing the DC link voltages.

Based on the experimental result for the various cases of the fault at S_a1/D_a1, S_a2/D_a2, and Q_a1/D_Qa1, it could be concluded that the experimental results confirmed the effectiveness of the proposed control strategy under the faulty conditions. By maintaining the same operation as the simulation results accurately for each case. Therefore, the experimental results guarantee that the proposed method performs the fault tolerance of open-circuit faults for the three-level HANPC inverters.

6. Conclusions

This paper proposed a creative fault tolerant method for controlling hybrid active neutral point clamped converters under open-circuit fault in different switch failures. The simulation and experimental results prove the capability of the proposed method in maintaining safe and reliable performance. Also, deep investigation and comprehensive operational performance analysis were carried-out to illustrate and explain the fault effects and influence on the inverter operation. The results showed an improvement in the circuit performance, whereas the switching sequence that includes hybrid switching is kept as much as possible in order to keep running close to the healthy conditions. Moreover, the results demonstrate the high capability of the proposed method in recovering the healthy operation under the faulty conditions of a single open-circuit faults, as well as the ability to balance the DC-link voltages. Besides, the effects of the faults on the THD levels have been shown and discussed. The proposed method results in enhancing the THD for an acceptable level (THD < 3%). The analysis signifies that the developed strategy demonstrates a considerable tolerant improvement and higher reliably performance. With reference to the findings of this work, its recommended to extend this work to include multiple open and short circuit faults.