Predictive Torque Control Based on Discrete Space Vector Modulation of PMSM without Flux Error-Sign and Voltage-Vector Lookup Table
Abstract
:1. Introduction
2. Conventional FS-PTC of PMSM
2.1. PMSM Model
2.2. Conventional FS-PTC
- , , ,
3. Proposed PTC-DSVM Strategy
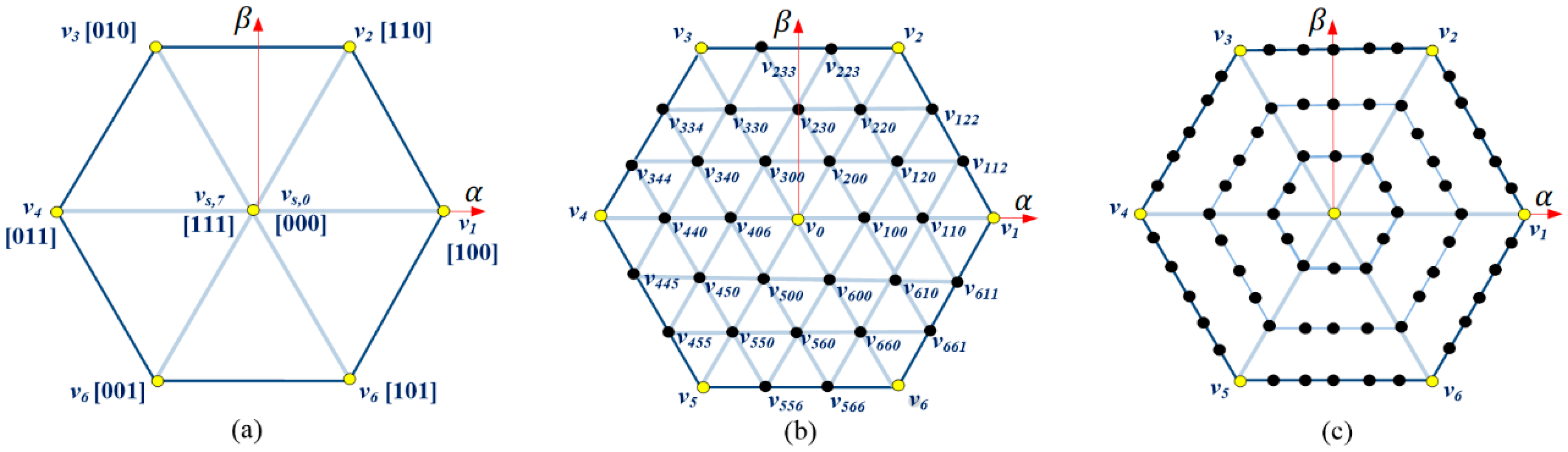
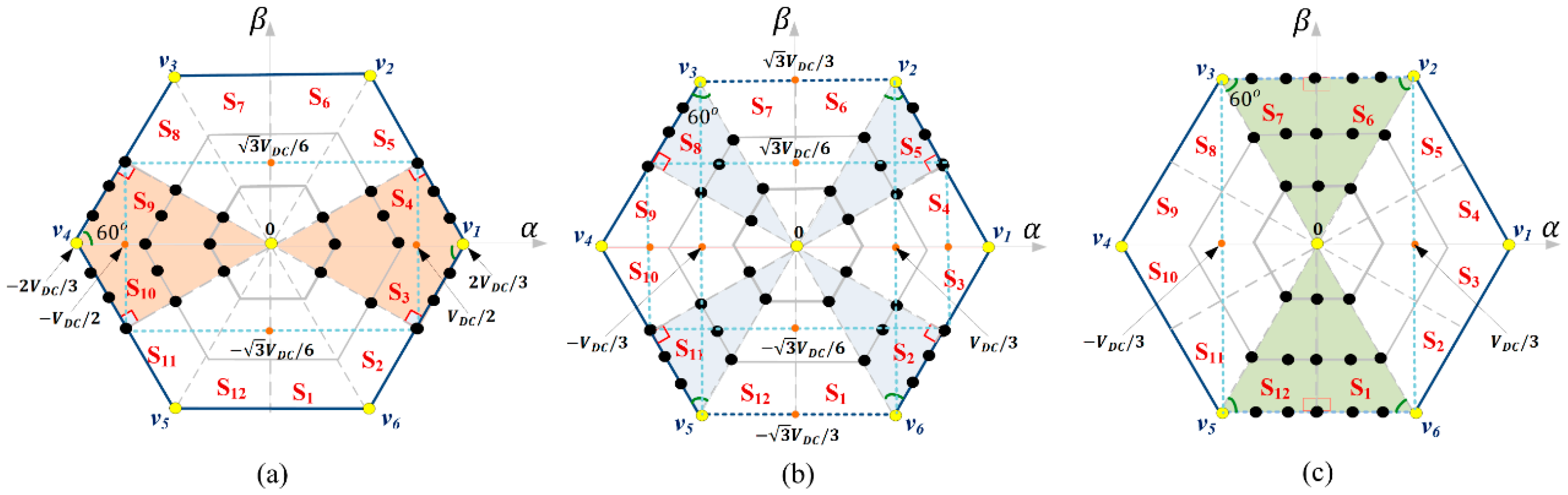
3.1. Synthesis of Virtual VVs
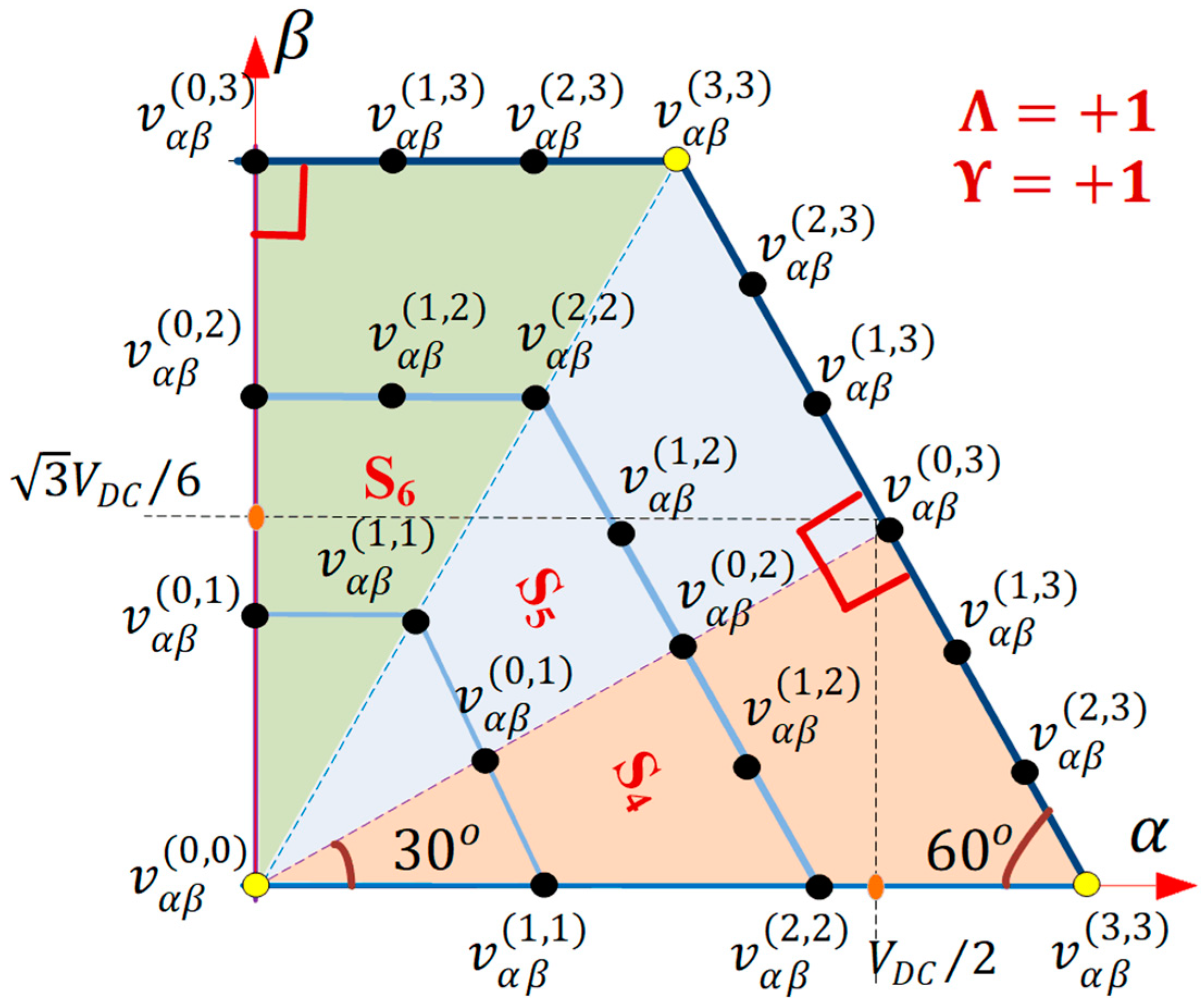
3.2. Predicted Online-Generated VVs
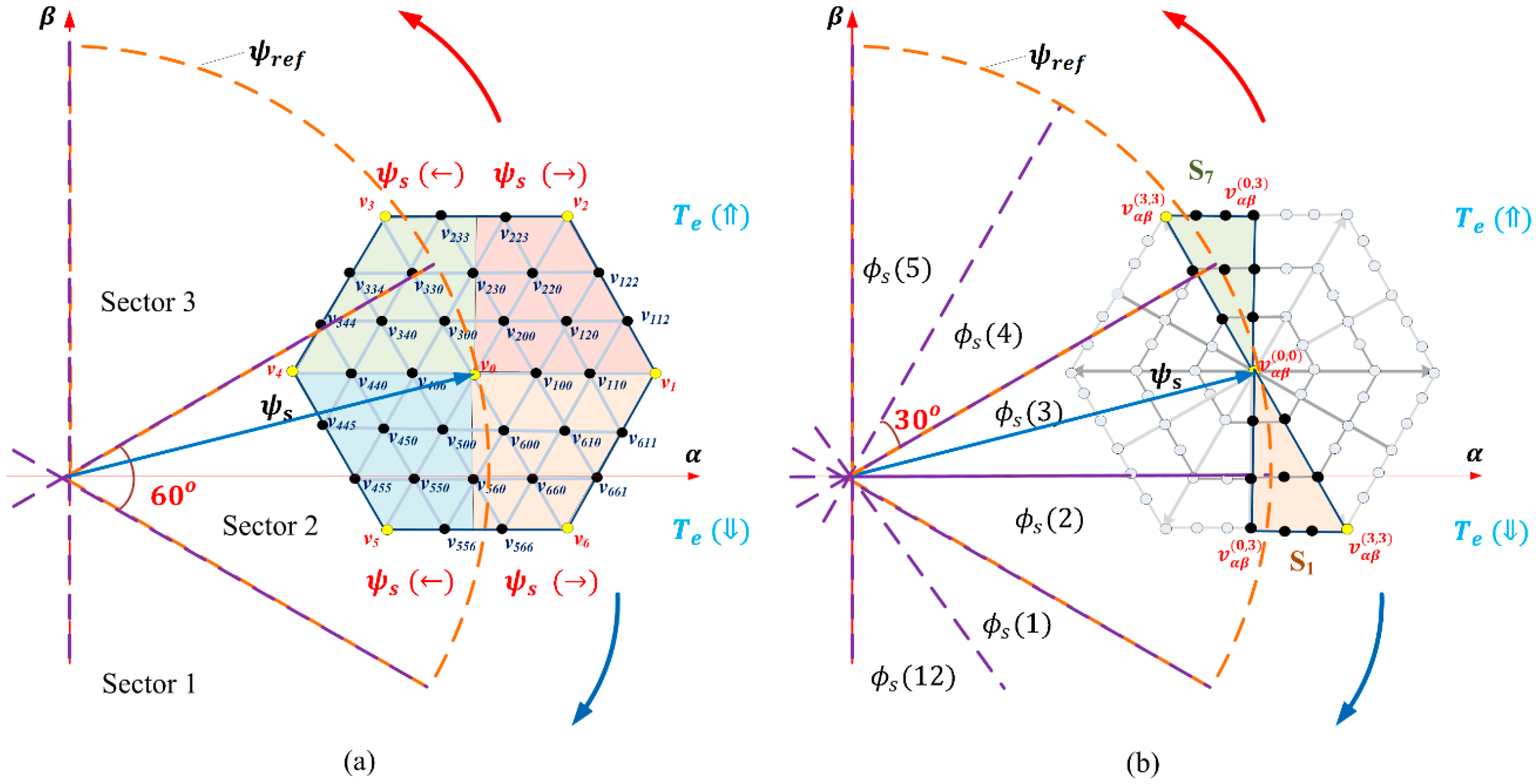
3.3. Delay Compensation and Cost Function Minimization
3.4. Overall Control Procedure of the Proposed PTC-DSVM
- Estimate the stator flux, , and torque, .
- Predict the stator current, , stator flux, and torque, by applying the optimal VV, .
- Obtain the optimal SVD zone based on the torque requirement at the specified flux position according to Table 2.
- Generate the voltages in the selected SVD zone with respect to the corresponding equations (i.e., (14) to (16)), and then select coefficients and in Table 1.
- Predict the stator flux, stator current, for each reduced VV in the SVD zone.
- Select the optimal VV, vopt, that minimizes the cost function (18), and apply it at the next sampling time using a space vector PWM.
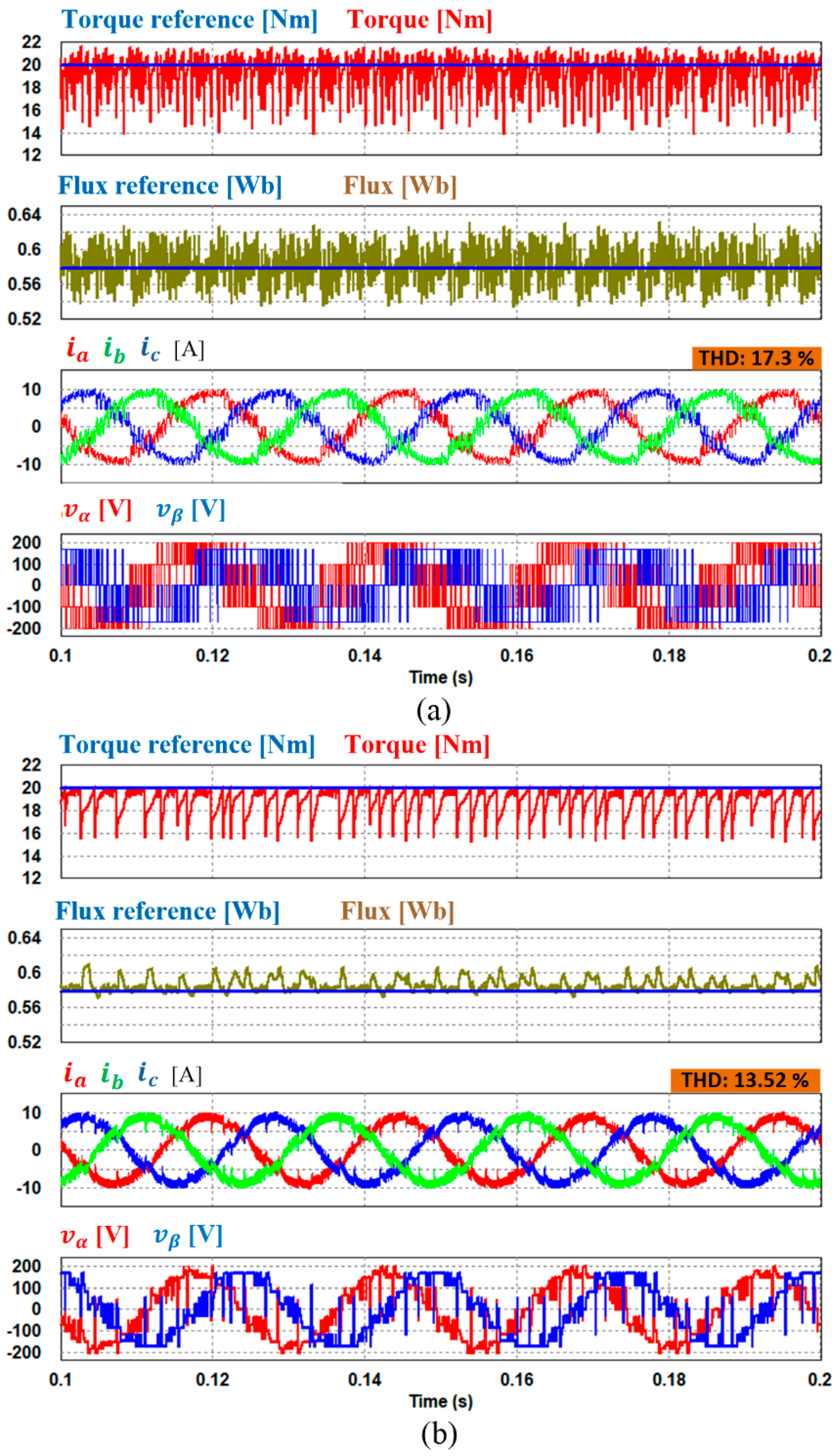
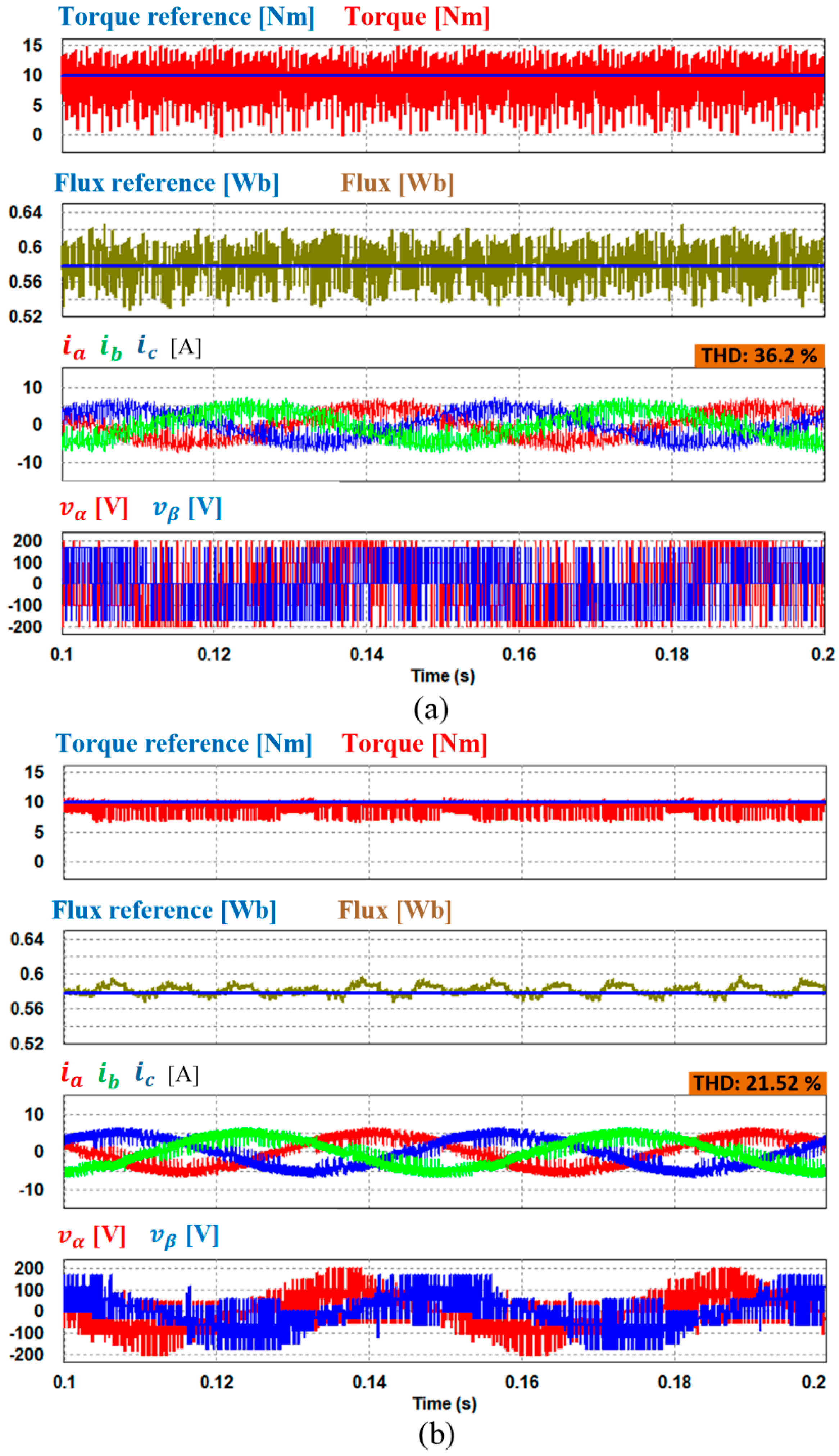
4. Simulation Results
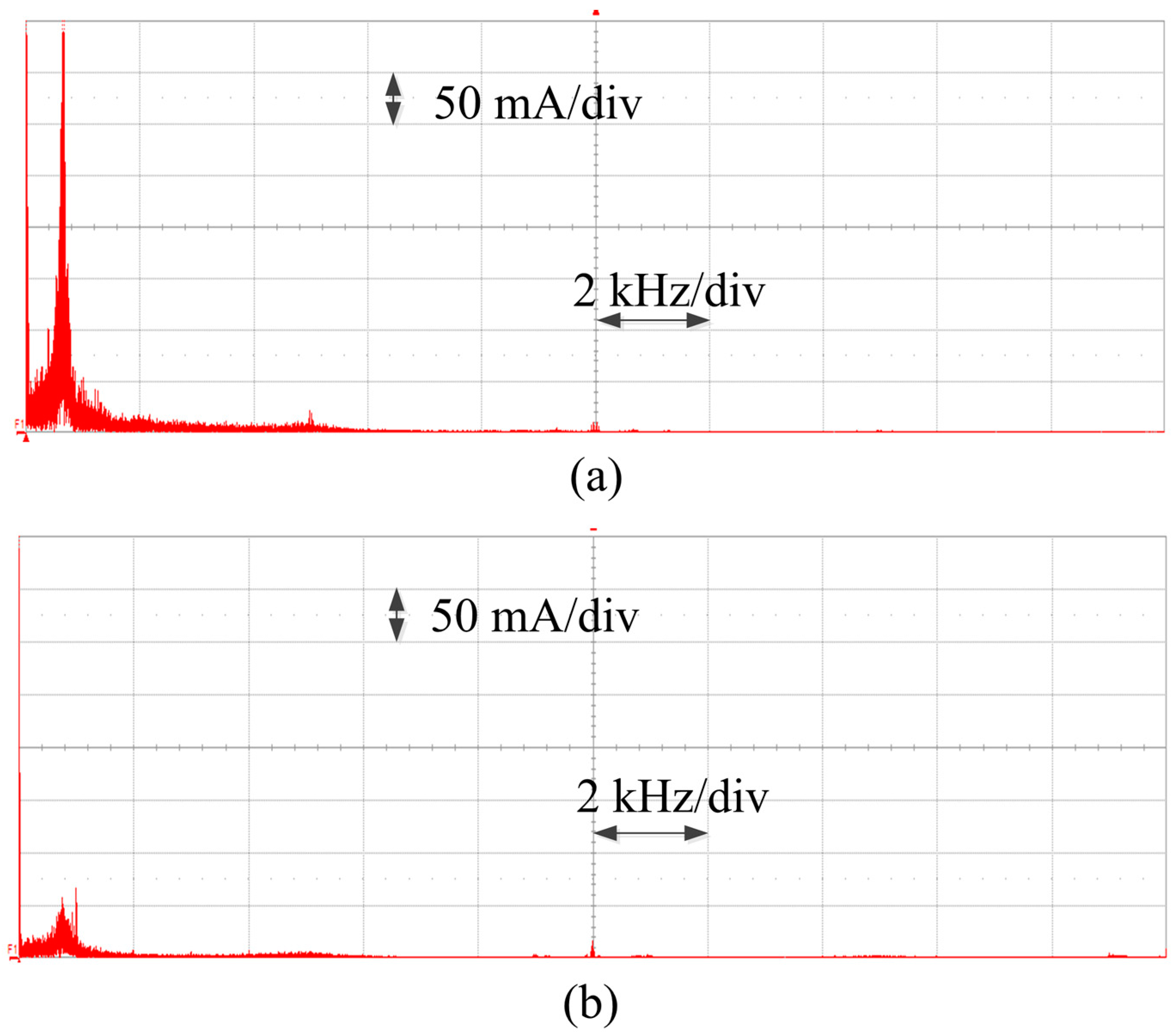
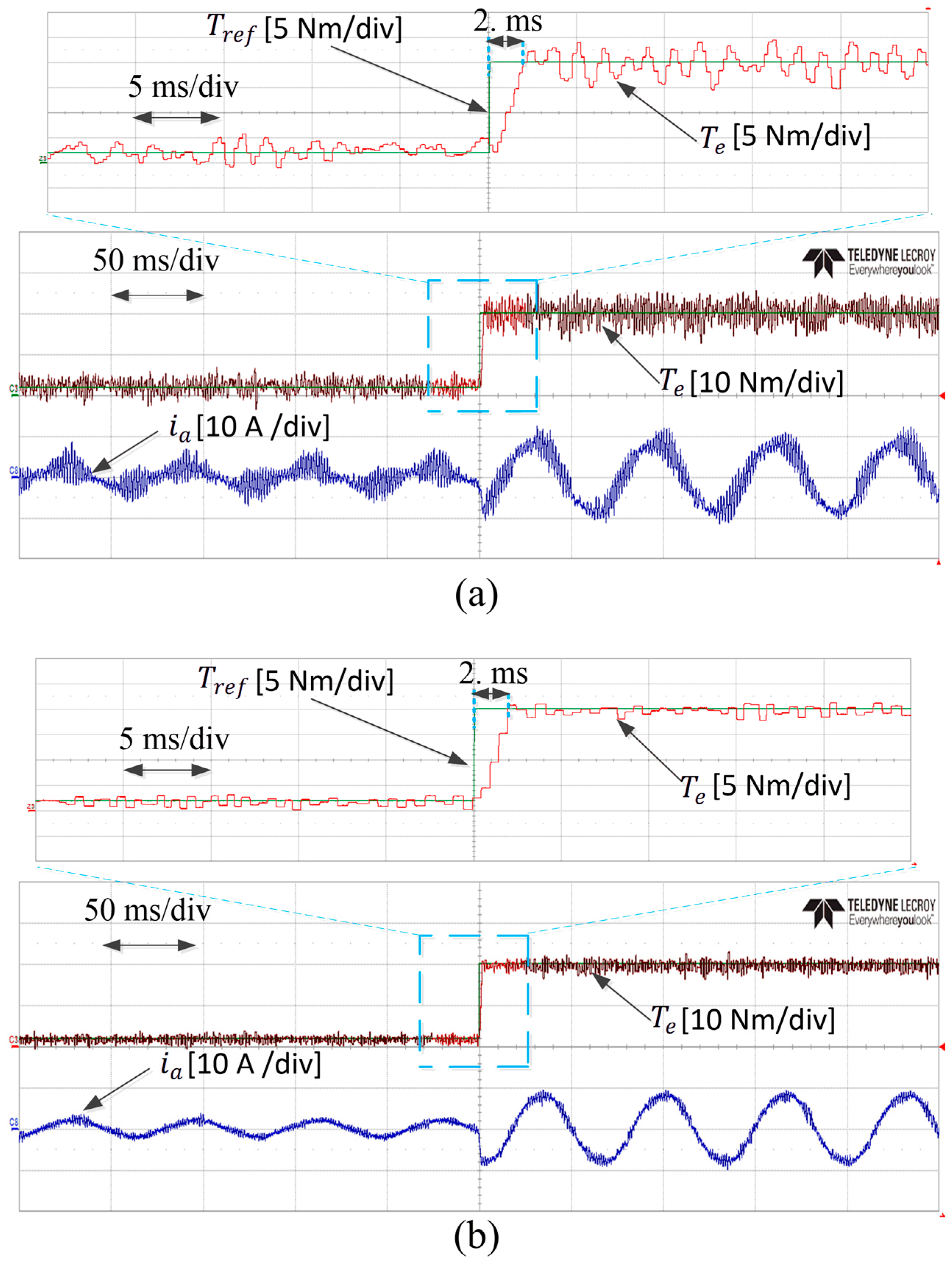
5. Experimental Results
5.1. Implementation
5.2. Steady-State Operation
5.3. Transient Torque Operation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Choi, Y.S.; Choi, H.H.; Jung, J.W. Feedback linearization direct torque control with reduced torque and flux ripples for IPMSM drives. IEEE Trans. Power Electron. 2016, 31, 3728–3737. [Google Scholar] [CrossRef]
- Mwasilu, F.; Jung, J.W. Enhanced fault-tolerant control of interior PMSMs based on an adaptive EKF for EV traction application. IEEE Trans. Power Electron 2016, 31, 5746–5758. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Kim, K.Y.; Lee, S.S.; Lee, K.B. A Modified Flux Regulation Method to Minimize Switching Frequency and Improve DTC-Hysteresis-Based Induction Machines in Low-Speed Regions. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2346–2355. [Google Scholar] [CrossRef]
- Hakami, S.S.; Mohd Alsofyani, I.; Lee, K.-B. Low-Speed Performance Improvement of Direct Torque Control for Induction Motor Drives Fed by Three-Level NPC Inverter. Electronics 2020, 9, 77. [Google Scholar] [CrossRef] [Green Version]
- Alsofyani, I.M.; Bak, Y.; Lee, K.B. Fast Torque Control and Minimized Sector-Flux Droop for Constant Frequency Torque Controller Based DTC of Induction Machines. IEEE Trans. Power Electron. 2019, 34, 12141–12153. [Google Scholar] [CrossRef]
- Habibullah, M.; Lu, D.D.; Xiao, D.; Osman, I.; Rahman, M.F. Selected Prediction Vectors Based FS-PTC for 3L-NPC Inverter Fed Motor Drives. IEEE Trans. Ind. Appl. 2017, 53, 3588–3597. [Google Scholar] [CrossRef]
- Adase, L.A.; Alsofyani, I.M.; Lee, K. Predictive Torque Control With Simple Duty-Ratio Regulator of PMSM for Minimizing Torque and Flux Ripples. IEEE Access 2020, 8, 2373–2381. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, G. Predictive DTC strategy with fault-tolerant function for six-phase and three-phase PMSM series-connected drive system. IEEE Trans. Ind. Electron. 2018, 65, 9101–9112. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Lee, K. Improved Transient-Based Overmodulation Method for Increased Torque Capability of Direct Torque Control With Constant Torque-Switching Regulator of Induction Machines. IEEE Trans. Power Electron. 2020, 35, 3928–3938. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Lee, K.B. Finite-Set Predictive Torque Control Based on Sub-divided Voltage Vectors of PMSM with Deadbeat Control and Discrete Space Vector Modulation. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1853–1857. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Wang, X.; Zhu, W. Adaptive Digital Predictive Peak Current Control Algorithm for Buck Converters. J. Power Electron. 2019, 19, 613–624. [Google Scholar]
- Zhang, X.; Hou, B. Double vectors model predictive torque control without weighting factor based on voltage tracking error. IEEE Trans. Ind. Electron. 2018, 33, 2368–2380. [Google Scholar] [CrossRef]
- Li, C.; Wang, G.; Li, F.; Li, H.; Xia, Z.; Liu, Z. Fault-Tolerant Control for 5L-HNPC Inverter-Fed Induction Motor Drives with Finite Control Set Model Predictive Control Based on Hierarchical Optimization. J. Power Electron. 2019, 19, 989–999. [Google Scholar]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model predictive control for power converters and drives: Advances and trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Yang, H. Model Predictive Torque Control of Induction Motor Drives with Optimal Duty Cycle Control. IEEE Trans. Power Electron. 2014, 29, 6593–6603. [Google Scholar] [CrossRef]
- Yan, L.; Dou, M.; Hua, Z.; Zhang, H.; Yang, J. Optimal Duty Cycle Model Predictive Current Control of High-Altitude Ventilator Induction Motor with Extended Minimum Stator Current Operation. IEEE Trans. Power Electron. 2018, 33, 7240–7251. [Google Scholar] [CrossRef]
- Zhao, B.; Li, H.; Mao, J. Double-Objective Finite Control Set Model-Free Predictive Control with DSVM for PMSM Drives. J. Power Electron. 2019, 19, 168–178. [Google Scholar]
- Casadei, D.; Serra, G.; Tani, A. Implementation of a direct control algorithm for induction motors based on discrete space vector modulation. IEEE Trans. Power Electron. 2000, 15, 769–777. [Google Scholar] [CrossRef]
- Wei, X.; Chen, D.; Zhao, C. Minimization of torque ripple of direct torque controlled induction machines by improved discrete space vector modulation. Elect. Power Syst. Res. 2004, 72, 103–112. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Carrasco, J.M.; Martinez, O.; Rodriguez, J.; Cortes, P.; Kouro, S. Model predictive control with constant switching frequency using a discrete space vector modulation with virtual state vectors. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Gippsland, VIC, Australia, 10–13 February 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–6. [Google Scholar]
- Villegas, J.; Vazquez, S.; Carrasco, J.M.; Gil, I. Model predictive control of a switched reluctance machine using discrete space vector modulation. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics, Bari, Italy, 4–7 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 3139–3144. [Google Scholar]
- Wang, Y.; Wang, X.; Xie, W.; Wang, F.; Dou, M.; Kennel, R.M.; Lorenz, R.D.; Gerling, D. Deadbeat Model-Predictive Torque Control with Discrete Space-Vector Modulation for PMSM Drives. IEEE Trans. Ind. Electron. 2017, 64, 3537–3547. [Google Scholar] [CrossRef]
- Moon, H.; Lee, J.; Lee, K. A Robust Deadbeat Finite Set Model Predictive Current Control Based on Discrete Space Vector Modulation for a Grid-Connected Voltage Source Inverter. IEEE Trans. Energy Convers. 2018, 33, 1719–1728. [Google Scholar] [CrossRef]
- Amiri, M.; Milimonfared, J.; Khaburi, D.A. Predictive Torque Control Implementation for Induction Motors Based on Discrete Space Vector Modulation. IEEE Trans. Ind. Electron. 2018, 65, 6881–6889. [Google Scholar] [CrossRef]
- Osman, I.; Xiao, D.; Alam, K.S.; Akter, M.P.; Shakib, S.M.S.I.; Rahman, M.F. Discrete Space Vector Modulation Based Model Predictive Torque Control with No Sub-Optimization. IEEE Trans. Ind. Electron. 2020, 67, 8164–8174. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, Z.Q.; Liu, J. Direct Torque Control of Permanent-Magnet Synchronous Machine Drives with a Simple Duty Ratio Regulator. IEEE Trans. Ind. Electron. 2014, 61, 5249–5258. [Google Scholar] [CrossRef]



| SVD Zones | ||||
|---|---|---|---|---|
| Coefficient Values | S1–S3 | S4–S6 | S7–S9 | S10–S12 |
| +1 | +1 | –1 | –1 | |
| –1 | +1 | +1 | –1 | |
| S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 | S1 | S2 | S3 | S4 | |
| S11 | S12 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 |
| Parameter | Value |
|---|---|
| Rated power | 11 [kW] |
| Rated current | 19.9 [A] |
| Rated speed | 1750 [r/min] |
| Rated torque | 60 [Nm] |
| Number of poles | 6 |
| Stator resistance | 0.349 [Ω] |
| Stator inductance | 15.6 [mH] |
| Permanent magnet flux | 0.554 [Wb] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohd Alsofyani, I.; Lee, K.-B. Predictive Torque Control Based on Discrete Space Vector Modulation of PMSM without Flux Error-Sign and Voltage-Vector Lookup Table. Electronics 2020, 9, 1542. https://doi.org/10.3390/electronics9091542
Mohd Alsofyani I, Lee K-B. Predictive Torque Control Based on Discrete Space Vector Modulation of PMSM without Flux Error-Sign and Voltage-Vector Lookup Table. Electronics. 2020; 9(9):1542. https://doi.org/10.3390/electronics9091542
Chicago/Turabian StyleMohd Alsofyani, Ibrahim, and Kyo-Beum Lee. 2020. "Predictive Torque Control Based on Discrete Space Vector Modulation of PMSM without Flux Error-Sign and Voltage-Vector Lookup Table" Electronics 9, no. 9: 1542. https://doi.org/10.3390/electronics9091542
APA StyleMohd Alsofyani, I., & Lee, K.-B. (2020). Predictive Torque Control Based on Discrete Space Vector Modulation of PMSM without Flux Error-Sign and Voltage-Vector Lookup Table. Electronics, 9(9), 1542. https://doi.org/10.3390/electronics9091542






