Random Nyström Approach to Clutter Subspace Estimation for Polarimetric Space-Time Adaptive Processing
Abstract
:1. Introduction
- (1)
- Enabling fast principal subspace identification within the Nyström framework while making full use of the CNCM information.
- (2)
- The computational burden in pSTAP can be reduced with high clutter suppression performance compared with the existing methods.
2. Data Model
3. Clutter Subspace Based pSTAP
4. The Random Nyström Method
4.1. Revisit of Standard Nyström
4.2. The Random Nyström Method
- (a)
- determine the selection matrix by (26), (31) and (32)
- (b)
- obtain the low-dimensional matrix by (33)
- (c)
- estimate the matrix representation of the clutter subspace by (34)
4.3. Application of R-Nyström to pSTAP
5. Computational Complexity Analysis
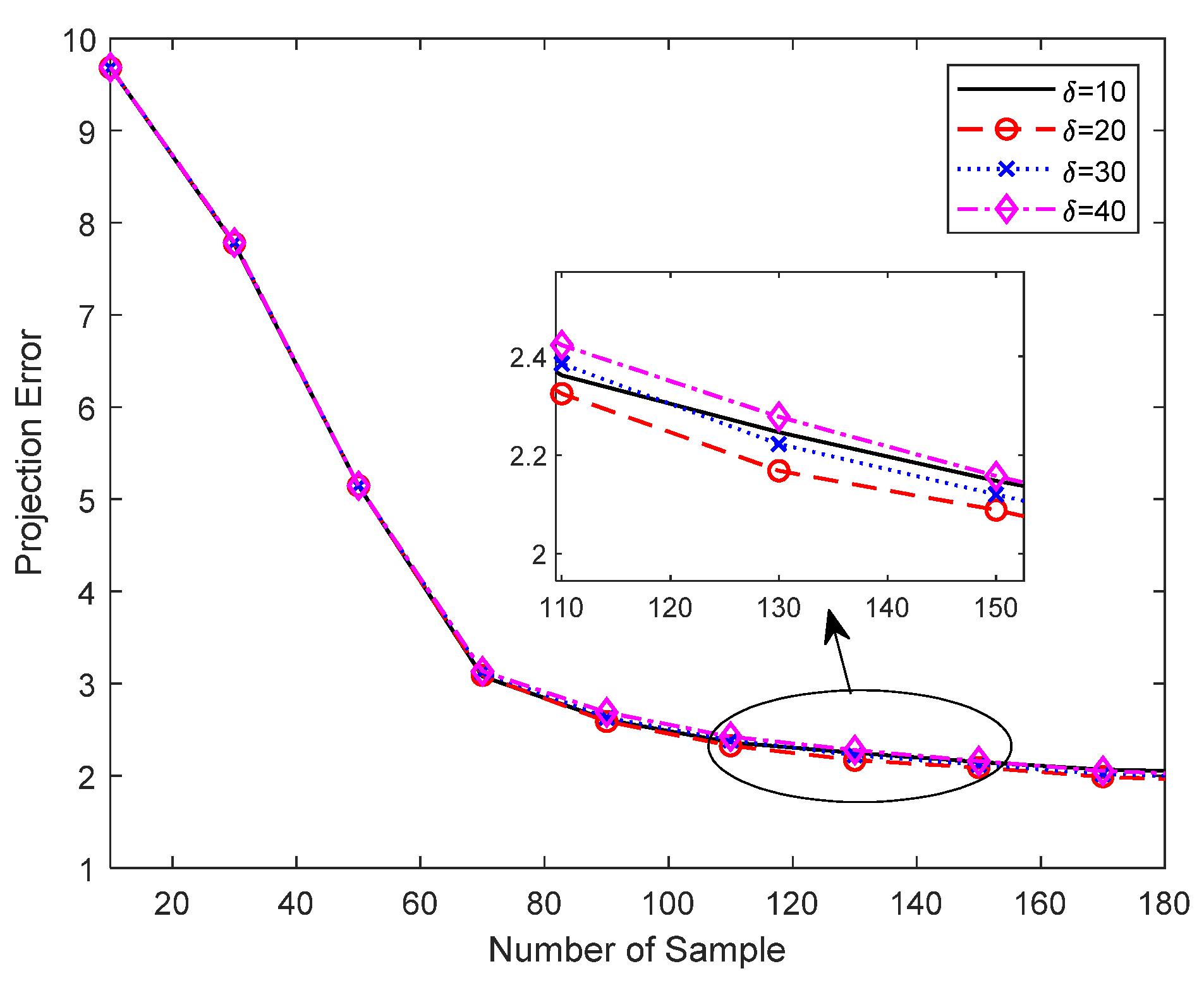
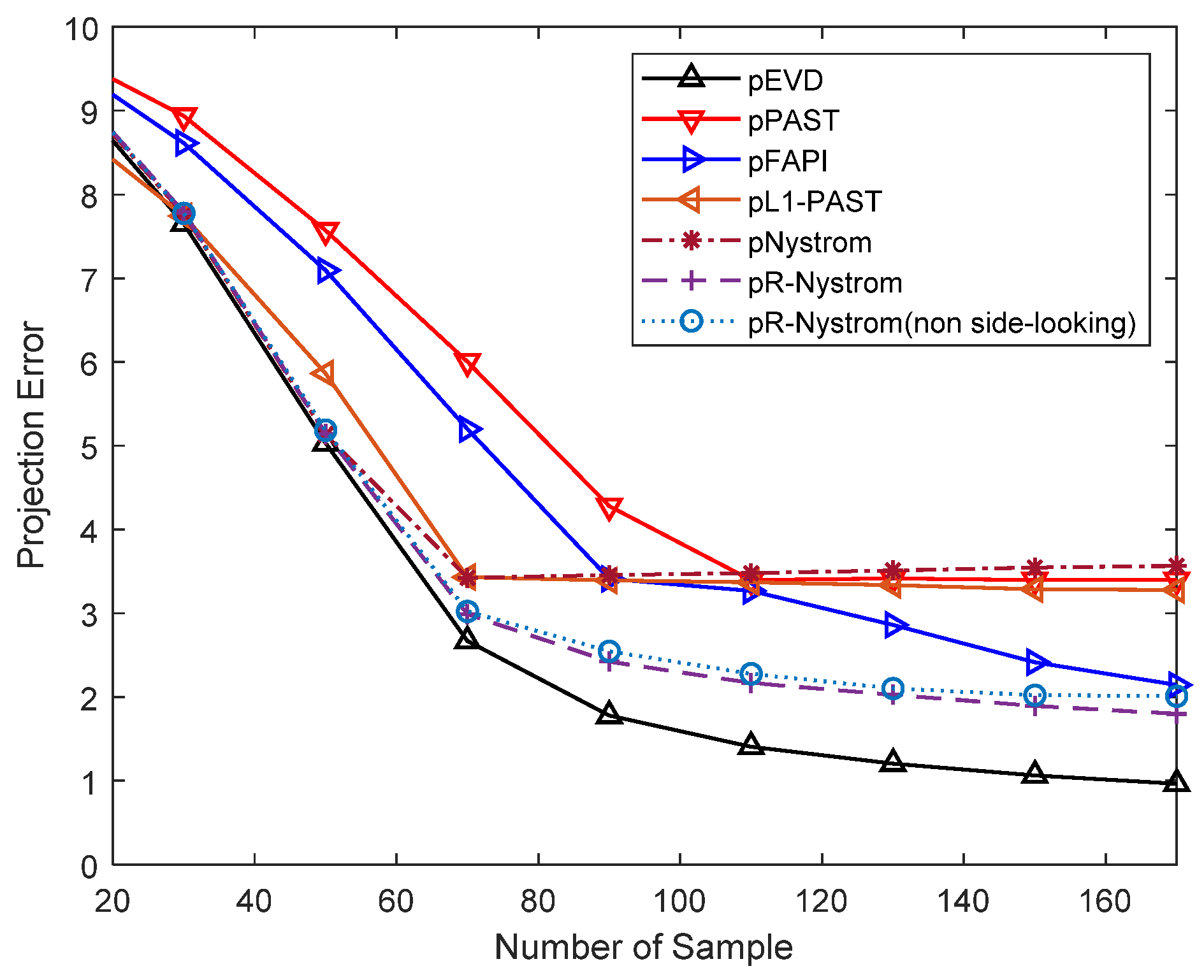
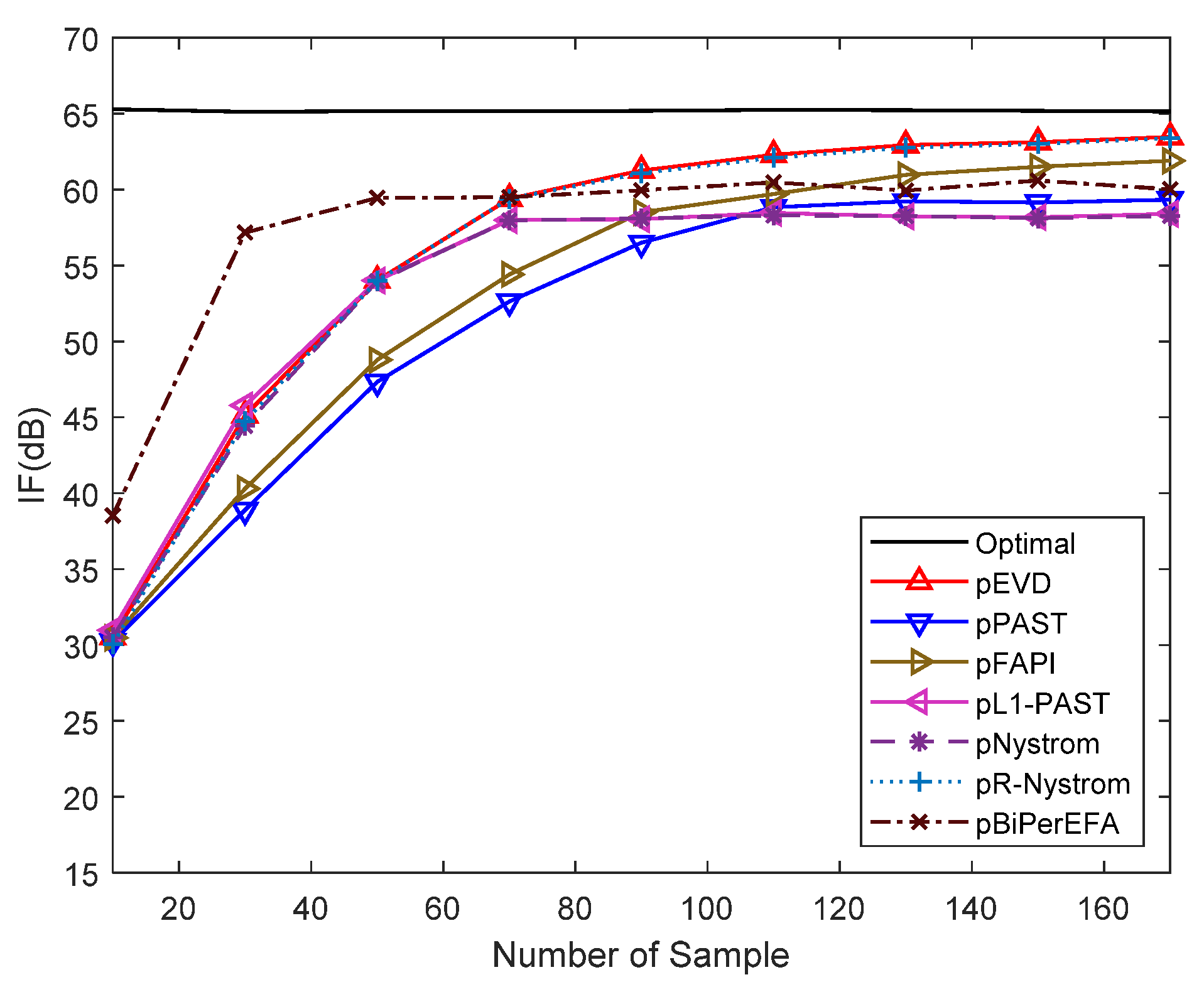
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Park, H.R.; Wang, H.; Li, J. An adaptive polarization-space-time processor for radar system. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Ann Arbor, MI, USA, 28 June–2 July 1993; pp. 698–701. [Google Scholar]
- Wu, D.; Xu, Z.; Zhang, L.; Xiong, Z.; Xiao, S. Performance analysis of polarization-space-time three-domain joint processing for clutter suppression in air-borne radar. Prog. Electromagn. Res. 2012, 129, 579–601. [Google Scholar] [CrossRef] [Green Version]
- Wu, D.; Xu, Z.; Xiong, Z.; Zhang, L.; Xiao, S. Polarization-space-time joint domain processing for clutter suppression in subspace leakage environments. In Proceedings of the 2011 IEEE CIE International Conference on Radar, Chengdu, China, 24–27 October 2011; pp. 692–695. [Google Scholar]
- Du, W.; Liao, G.; Yang, Z. Clutter space-time covariance matrix estimate based on multi-polarised data. IET Radar Sonar Navig. 2014, 8, 1109–1115. [Google Scholar] [CrossRef]
- Ward, J. Space-Time Adaptive Processing for Airborne Radar; IET: London, UK, 1998. [Google Scholar]
- Melvin, W.L. Space-time adaptive radar performance in heterogeneous clutter. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 621–633. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Duan, K.; Xie, W. Subspace-augmented clutter suppression technique for STAP radar. IEEE Geosci. Remote Sens. Lett. 2016, 13, 462–466. [Google Scholar] [CrossRef]
- Yang, B. Projection approximation subspace tracking. IEEE Trans. Signal Process. 1995, 43, 95–107. [Google Scholar] [CrossRef]
- Badeau, R.; David, B.; Richard, G. Fast approximated power iteration subspace tracking. IEEE Trans. Signal Process. 2005, 53, 2931–2941. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Sun, Y.; Zeng, T.; Long, T.; Sarkar, T.K. Fast STAP method based on PAST with sparse constraint for airborne phased array radar. IEEE Trans. Signal Process. 2016, 64, 4550–4561. [Google Scholar] [CrossRef]
- Zhang, K.; Kwok, J.T. Clustered Nyström method for large scale manifold learning and dimension reduction. IEEE Trans. Neural Netw. 2010, 21, 1576–1587. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, S.; Mohri, M.; Talwalkar, A. Sampling methods for the Nyström method. J. Mach. Learn. Res. 2012, 13, 981–1006. [Google Scholar]
- Wang, S.; Zhang, Z. Improving CUR matrix decomposition and the Nyström approximation via adaptive sampling. J. Mach. Learn. Res. 2013, 14, 2729–2769. [Google Scholar]
- Qian, C.; Huang, L.; So, H.C. Computationally efficient ESPRIT algorithm for direction-of-arrival estimation based on Nyström method. Signal Process. 2014, 94, 74–80. [Google Scholar] [CrossRef]
- Baker, C.T.H. The Numerical Treatment of Integral Equations; Oxford University Press: Oxford, UK, 1978. [Google Scholar]
- Williams, C.K.I.; Seeger, M. Using the Nyström method to speed up kernel machines. In Proceedings of the 13th International Conference on Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Fowlkes, C.; Belongie, S.; Chung, F.; Malik, J. Spectral grouping using the Nyström method. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 214–225. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Drineas, P.; Magdon-Ismail, M.; Mahoney, M.W.; Woodruff, D.P. Fast approximation of matrix coherence and statistical leverage. J. Mach. Learn. Res. 2012, 13, 3475–3506. [Google Scholar]
- Cohen, M.B.; Musco, C.; Musco, C. Ridge leverage scores for low-rank approximation. arXiv 2015, arXiv:1511.07263. [Google Scholar]
- Calandriello, D.; Lazaric, A.; Valko, M. Analysis of Nyström method with sequential ridge leverage score sampling. In Proceedings of the 2016 Thirty-Second Conference on Uncertainty in Artificial Intelligence, New York, NY, USA, 25–29 June 2016. [Google Scholar]
- Musco, C.; Musco, C. Recursive sampling for the Nyström method. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Wang, W.; Chen, Z.; Li, X.; Wang, B. Space time adaptive processing algorithm for multiple-input-multiple-output radar based on Nyström method. IET Radar Sonar Navig. 2016, 10, 459–467. [Google Scholar] [CrossRef]
- Reed, I.S.; Mallet, J.D.; Brennan, L.E. Rapid convergence rate in adaptive arrays. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 853–863. [Google Scholar] [CrossRef]
- Smith, M.S.; Tan, T.G. Sidelobe reduction using random methods for antenna arrays. Electron. Lett. 1983, 19, 931–933. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, X.; Li, Y.; Li, Y.; Wang, L.; Jiang, B.; Fang, D. A fast STAP method using persymmetry covariance matrix estimation for clutter suppression in airborne MIMO radar. EURASIP J. Adv. Signal Process. 2019, 2019, 13. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| antenna array | side-looking array |
| the number of antennas | 16 |
| pulse number in one CPI | 16 |
| CNR | 40 dB |
| PRF | 1200 |
| velocity | 200 m/s |
| airborne height | 9 km |
| looking direction | 0° |
| target auxiliary polarization angle | 30° |
| target polarization phase difference | 60° |
| clutter degree of polarization | 0.99 |
| the power ratio between two channels | 1 |
| clutter statistical average phase difference | 90° |
| Method | Complexity | Time/ms |
|---|---|---|
| mLSM | 15.0 | |
| pEVD | 59.5 | |
| pPAST | 47.8 | |
| pFAPI | 50.1 | |
| pL1-PAST | 126.9 | |
| pNyström | 21.5 | |
| pR-Nyström | 36.4 | |
| pBiPerEFA | 29.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, K.; Liu, Z.; Shi, S.; Huang, Y.; Xu, Y. Random Nyström Approach to Clutter Subspace Estimation for Polarimetric Space-Time Adaptive Processing. Electronics 2020, 9, 1488. https://doi.org/10.3390/electronics9091488
Zhao K, Liu Z, Shi S, Huang Y, Xu Y. Random Nyström Approach to Clutter Subspace Estimation for Polarimetric Space-Time Adaptive Processing. Electronics. 2020; 9(9):1488. https://doi.org/10.3390/electronics9091488
Chicago/Turabian StyleZhao, Kang, Zhiwen Liu, Shuli Shi, Yulin Huang, and Yougen Xu. 2020. "Random Nyström Approach to Clutter Subspace Estimation for Polarimetric Space-Time Adaptive Processing" Electronics 9, no. 9: 1488. https://doi.org/10.3390/electronics9091488
APA StyleZhao, K., Liu, Z., Shi, S., Huang, Y., & Xu, Y. (2020). Random Nyström Approach to Clutter Subspace Estimation for Polarimetric Space-Time Adaptive Processing. Electronics, 9(9), 1488. https://doi.org/10.3390/electronics9091488





