Sliding Mode Observer-Based Fault-Tolerant Secondary Control of Microgrids

Abstract

This paper proposes two sliding mode observer (SMO)-based fault-tolerant secondary control schemes for microgrids. The first scheme consists of a central SMO-based fault tolerant controller that uses outputs from the microgrid and estimates all states in the microgrid as well as the fault. The estimated fault is then used to reject the effect of faults on the microgrid. The second scheme is decentralised, where each distributed generator (DG) has its own SMO-based fault tolerant controller which would estimate faults affecting that DG alone, and compensate for faults in only that DG. By rejecting the effect of faults in each DG, the effect of faults on the entire microgrid can be negated. Finally, we simulate an example using both schemes, and its results verify the efficacy of the schemes for fault-tolerant secondary control of microgrids.

1. Introduction

A microgrid is defined as a group of loads and distributed energy resources (which include distributed generators (DGs)) operating in a controlled, coordinated manner while connected to the main grid, or while islanded [1]. The main grid would perceive the microgrid as a single element that responds accordingly when fed the appropriate control signal [2]. The structure of a microgrid gives rise to many possible configurations depending on its size and function, and the ability to operate in an islanded manner increases its resilience towards emergencies and blackouts [3]. A pertinent challenge in the control of microgrids however arises from the geographical dispersion of DGs from each other [4], as well as variations in the performance of each element, which are especially common in renewable energy-based microgrids [5,6,7]. The control of many separate elements to function as a single entity responding to input control signals is difficult, and requires innovative methods to guarantee the stability and performance of the microgrid [3,8,9].

Hierarchical control is a popular approach in the control of microgrids [10,11,12]. First formalised in the context of microgrids in [13], hierarchical control treats microgrid control as three separate control loops: primary, secondary, and tertiary control. The primary control loop adjusts the frequency and amplitude of the voltage in each DG, while secondary control compensates for the deviations in voltage amplitude and frequency, and finally tertiary control coordinates the overall power flow in and out of the microgrid [11]. Consensus-based methods were used to implement the various control loops in microgrids [7,14,15,16,17], where each DG is treated as a node in a network, and only relies on information from its neighbouring nodes, unlike in schemes requiring full state knowledge [5,18] or the centralised schemes in [3,19]. A consensus-based scheme for current sharing and voltage regulation was proposed in [7]; the reference voltage into each DG is however assumed to be constant, which may not be realistic given that he microgrid may be subject to fluctuations in demand, and that each DG generally operates under its own varying conditions [4,6]. Another consensus-based scheme for multi-area systems was proposed in [20], which focusses on the tertiary control loop and performs sensor fault-tolerant control (FTC) using knowledge of local and neighbouring subsystem states. The scheme however relies on the secondary control loop not being affected by faults. In particular, Park et al. [14] introduced a consensus protocol-based method for secondary control in microgrids. Using the states of its neighbouring DGs, the consensus protocol ensures that the voltage amplitude and frequency of each DG follow the prescribed reference.

The control scheme in [14], however, assumes that the control signal is relayed to each DG without any corruption (any unwanted deviation in the control signal will henceforth be referred to as a fault). Recall that DGs in a microgrid can be spread far apart and also are subject to varying operational conditions [6]. These circumstances can lead to faults arising in the control of each DG [7,18,19], which can cause erroneous behaviour that can cascade into other DGs due to the consensus protocol. Hence it is important to negate the influence of these faults on the microgrid to prevent potentially damaging behaviour.

Sliding mode observers (SMOs) are a special type of observer with a discontinuous switching term that forces the estimation error for outputs to zero in finite time [21]. Furthermore, the switching term is found to contain information on the fault, which could be used to estimate the fault [22]. Then by using information of the estimated fault (such as its location, magnitude, and shape), we can overcome the effects of the fault [23,24]. SMO-based FTC was employed to reject the influence of faults on the operation of various practical systems, such as in wind turbine pitch control [25], multi-area power systems [20], and motor control for electric vehicles [26] and induction motors [27].

Motivated by the above, we propose two SMO-based fault-tolerant secondary control schemes for microgrids based on the method in [14]. The first scheme is centralised, consisting of a central SMO-based fault-tolerant controller. Outputs from the DGs (which are a subset of all states in the microgrid) are transmitted to a central SMO, which estimates all states and faults in the microgrid. The SMO-based controller then uses the estimated fault to negate the effects of all faults in the entire microgrid. The second scheme is decentralised, where each DG has its own SMO-based fault-tolerant controller. Each SMO would receive the states of its respective DG and its connected neighbours to estimate faults affecting that DG alone. Based on the estimated fault, the SMO-based fault-tolerant controller would reject faults affecting its respective DG. By rejecting the faults acting on each DG, the effect of faults on the entire microgrid is negated. The main contributions of the presented work are hence summarised as follows:

• Two observer-based fault-tolerant secondary control schemes for a faulty microgrid are presented. Both schemes use a SMO to estimate faults affecting the microgrid (which were not considered in [4,6,10,11,12,13,14,15,16,17]), and negate the effect of the faults on the microgrid.
• The first scheme uses a single, central SMO. Based on a subset of all states in the microgrid, the SMO estimates the remaining states and estimates all faults in the microgrid. The fault compensator then uses the estimated faults to negate the faults affecting the microgrid.
• The second scheme uses a SMO for each DG. Based on states available to its DG, each SMO estimates the faults affecting their respective DG. The fault compensator for that DG uses the estimated fault to reject faults affecting that DG alone. By rejecting the influence of faults in each DG, the effects of faults on the microgrid are negated.

The paper is organised as follows: Section 2 first introduces the background theory, and formulates the problem. Section 3 then details the central SMO-based fault-tolerant secondary control scheme, while Section 4 describes the distributed SMO-based scheme for fault-tolerant secondary control. Section 5 presents a simulated example verifying the efficacy of the scheme, and Section 6 draws some conclusions. The following notation is used: the norm of a vector $z\in {\mathbb{R}}^a$ is given by $∥z∥=\sqrt{{\sum }_{i=1}^a{z}_i^2}$, the spectrum of a matrix Z is denoted as $\lambda \left(Z\right),r\left(·\right)$ is the unit ramp function, and $I_b$ denotes a $b\times b$ identity matrix.

2. Preliminaries

Some necessary background for graph theory [28] is first presented. The communication network between the DGs is modelled as a directed graph $\mathcal{G}=\left(\mathcal{V},\mathcal{E}\right)$, where $\mathcal{V}=\{1,2,\dots N\}$ is the vertex set and $\mathcal{E}\subset \mathcal{V}\times \mathcal{V}$ is the edge set. The adjacency matrix of $\mathcal{G}$ is defined as $\mathcal{A}=\left[a_{ij}\right]\in {\mathbb{R}}^{N\times N}$, where $a_{ii}=0$, and $a_{ij}=1\iff \left(i,j\right)\in \mathcal{E}$ (i.e., if there is an edge from DG i to DG j), and $a_{ij}=0$ otherwise. The Laplacian matrix of $\mathcal{G}$ is defined as $\mathcal{L}=\left[l_{ij}\right]\in {\mathbb{R}}^{N\times N}$, where $l_{ii}={\sum }_{j=1,j\ne i}^N{a}_{ij}$, and $l_{ij}=-a_{ij}$ if $i\ne j$.

The hierarchical control structure of microgrids consists of three levels of control: primary, secondary, and tertiary control [2]. In the primary control level, the droop method is used to adjust the frequency and amplitude of the voltage reference provided to the inner control loops in the DG [11]. The droop method (applied onto DG i) is described by the following voltage and frequency droop characteristics:

$$\begin{array}{cc}\hfill v_i^d& =v_{n,i}-n_{Q,i}{Q}_i,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill v_i^q& =0,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill w_i& =w_{n,i}-m_{P,i}{P}_i,\hfill \end{array}$$

(3)

where $v_i^d$ and $v_i^q$ are the voltage amplitudes along the direct axis and quadrature axis in the frame of the primary control of DG i respectively, $P_i$ and $Q_i$ are the active and reactive powers measured from the terminal of DG i respectively, $v_{n,i}$ and $w_{n,i}$ are the references for the primary control of the voltage and frequency of DG i respectively, and $n_{Q,i}$ and $m_{P,i}$ are the voltage-reactive power and frequency-active power droop coefficients of DG i respectively.

The secondary control loop is then applied to compensate for deviations in the voltage amplitude and frequency [13]. The consensus protocol structure for secondary control is derived according to the method outlined in [14] as follows. Differentiating (1) and (3) yields

$$\begin{array}{cc}\hfill {\dot{v}}_i^d& ={\dot{v}}_{n,i}-n_{Q,i}{\dot{Q}}_i,\hfill \\ \hfill {\dot{w}}_i& ={\dot{w}}_{n,i}-m_{P,i}{\dot{P}}_i.\hfill \end{array}$$

(4)

Define ${\dot{v}}_{n,i}-n_{Q,i}{\dot{Q}}_i$ and ${\dot{w}}_{n,i}-m_{P,i}{\dot{P}}_i$ as the consensus protocol structure, and then the secondary control for the microgrid can be designed for DG $i=1,2,\dots N$ as ${\dot{v}}_i^d=u_{v,i},{\dot{w}}_i=u_{w,i}$, and the references are given by ${\dot{v}}_r^d=u_{v,r},{\dot{w}}_r=u_{w,r}$. The control laws are set to satisfy

$$\underset{t\to \infty }{lim}{v}_i^d-v_r^d=0,\underset{t\to \infty }{lim}{w}_i-w_r=0,$$

(5)

that is, the reference voltage $v_{n,i}$ and frequency $w_{n,i}$ are the secondary control parameters to ensure the DG voltage and frequencies track the given reference values.

Next, consider a microgrid consisting of N DGs and one reference, where the consensus protocol in [14] is used to regulate the dynamics of each DG (and therefore, the microgrid). The nominal dynamics of the i-th DG in the microgrid is then given as follows:

$$u_i^n=\sum _{j=1,j\ne i}^N{a}_{ij}\left[\begin{array}{c}{v}_j^d-v_i^d\\ w_j-w_i\end{array}\right]-b_i\left[\begin{array}{c}{v}_i^d-v_r^d\\ w_i-w_r\end{array}\right],$$

(6)

where $i=1,2,\dots N$, and $a_{ij}$ and $b_i$ are connection weights which are defined as follows: $a_{ij}=1$ if DG i is connected to and sends information to DG j, and $a_{ij}=0$ otherwise (note that $a_{ii}=0$); likewise, $b_i=1$ if DG i is connected to the reference, and $b_i=0$ otherwise. The consensus protocol resulting in the dynamics in (6) however does not consider faults that may occur in each DG, which could cause inaccurate readings to be transmitted to other DGs and result in faulty behaviour of the microgrid.

To account for faulty behaviour in the microgrid, suppose that the voltage and frequency of the i-th DG is affected by the fault $f_{v,i}$ and $f_{w,i}$, respectively. We then define the compensation $u_{cv,i}$ and $u_{cw,i}$ to reject the effects of faults on the voltage and frequency of the i-th DG, respectively. The dynamics in (6) becomes

$$\begin{array}{cc}\hfill \underset{u_i}{\underbrace{\left[\begin{array}{c}{u}_{v,i}\\ u_{w,i}\end{array}\right]}}& =u_i^n+\left[\begin{array}{cc}{m}_{v,i}& 0\\ 0& m_{w,i}\end{array}\right]\left[\begin{array}{c}{f}_{v,i}\\ f_{w,i}\end{array}\right]+\left[\begin{array}{c}{u}_{cv,i}\\ u_{cw,i}\end{array}\right]\hfill \\ \hfill & =\sum _{j=1,j\ne i}^N{a}_{ij}\left[\begin{array}{c}{v}_j^d-v_i^d\\ w_j-w_i\end{array}\right]-b_i\left[\begin{array}{c}{v}_i^d-v_r^d\\ w_i-w_r\end{array}\right]+\left[\begin{array}{cc}{m}_{v,i}& 0\\ 0& m_{w,i}\end{array}\right]\left[\begin{array}{c}{f}_{v,i}\\ f_{w,i}\end{array}\right]+\left[\begin{array}{c}{u}_{cv,i}\\ u_{cw,i}\end{array}\right],\hfill \end{array}$$

(7)

where $m_{v,i}$ and $m_{w,i}$ are fault distribution weights defined as follows: if $u_{v,i}$ ($u_{w,i}$) is faulty (i.e., $f_{v,i}\left(f_{w,i}\right)$ is non-zero for some time $t\ge 0$), then $m_{v,i}\left(m_{w,i}\right)=1$; otherwise if $u_{v,i}\left(u_{w,i}\right)$ is not faulty (i.e., $f_{v,i}\left(f_{w,i}\right)=0\forall t\ge 0$), $m_{v,i}\left(m_{w,i}\right)=0$.

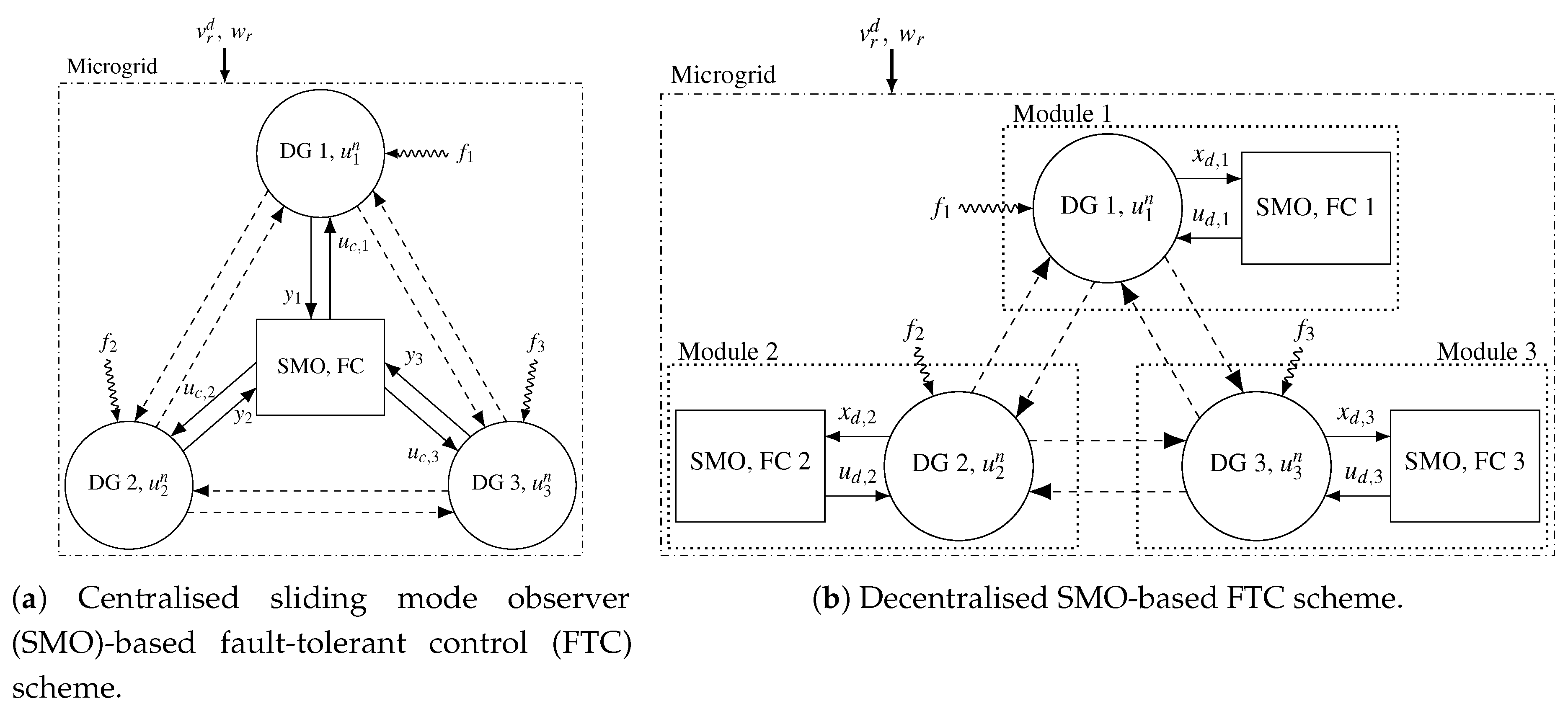
Assumption A1.

The magnitude of the faults affecting the microgrid are bounded, i.e.,

$$∥{\left[\begin{array}{ccccc}{f}_{v,1}^T& f_{w,1}^T& \cdots & f_{v,N}^T& f_{w,N}^T\end{array}\right]}^T∥<{\theta }_f,$$

(8)

where ${\theta }_f\in {\mathbb{R}}^{+}$ is known.

Remark 1.

Assumption 1 is a general assumption; microgrids generally operate within certain bounds, and the faults affecting them in practical situations would also be bounded [7,20].

We propose two schemes for SMO-based fault-tolerant secondary control in microgrids. The first scheme is the centralised scheme, where a central SMO is designed to estimate all faults affecting the microgrid based on the outputs from the microgrid (which are a subset of its states). The estimated faults are used by the fault compensator (FC) to reject the influence of all faults on the microgrid. The second scheme is the decentralised scheme, where each DG has its own SMO-based fault-tolerant controller. Each DG only supplies its states to its SMO (as well as other connected DGs), which will estimate faults affecting only that DG. The estimate is then used by the FC to negate the effect of faults on that DG, which by extension, would negate the effects of faults on the entire microgrid. Figure 1 illustrates the structure of the two proposed schemes.

We will first detail the design of the centralised scheme in Section 3, and then present the design for the decentralised scheme in Section 4 afterwards.

3. The Centralised Fault-Tolerant Control Scheme

We first define the following for brevity of notation:

$$\begin{array}{cc}\hfill \mathcal{B}& =\left[\begin{array}{ccc}{b}_1& & \\ & \ddots & \\ & & b_N\end{array}\right],{\overline{\mathcal{M}}}_v=\left[\begin{array}{ccc}{m}_{v,1}& & \\ & \ddots & \\ & & m_{v,N}\end{array}\right],{\overline{\mathcal{M}}}_w=\left[\begin{array}{ccc}{m}_{w,1}& & \\ & \ddots & \\ & & m_{w,N}\end{array}\right],x_s=\left[\begin{array}{c}{x}_v\\ x_w\end{array}\right],\hfill \\ \hfill x_v& =\left[\begin{array}{c}{v}_1^d-v_r^d\\ ⋮\\ v_N^d-v_r^d\end{array}\right],x_w=\left[\begin{array}{c}{w}_1-w_r\\ ⋮\\ w_N-w_r\end{array}\right],{\overline{f}}_v=\left[\begin{array}{c}{f}_{v,1}\\ ⋮\\ f_{v,N}\end{array}\right],{\overline{f}}_w=\left[\begin{array}{c}{f}_{w,1}\\ ⋮\\ f_{w,N}\end{array}\right],u_{cv}=\left[\begin{array}{c}{u}_{cv,1}\\ ⋮\\ u_{cv,N}\end{array}\right],u_{cw}=\left[\begin{array}{c}{u}_{cw,1}\\ ⋮\\ u_{cw,N}\end{array}\right].\hfill \end{array}$$

(9)

Define $rank\left({\overline{\mathcal{M}}}_v\right)=g$ and $rank\left({\overline{\mathcal{M}}}_w\right)=h$. This implies that there are $N-g$ and $N-h$ zero columns within ${\overline{\mathcal{M}}}_v$ and ${\overline{\mathcal{M}}}_w$, respectively. Hence define ${\mathcal{M}}_v\in {\mathbb{R}}^{n\times g}$ and ${\mathcal{M}}_w\in {\mathbb{R}}^{n\times h}$ as matrices containing the g and h non-zero columns of ${\overline{\mathcal{M}}}_v$ and ${\overline{\mathcal{M}}}_w$, respectively. Next, define $f_v\in {\mathbb{R}}^g$ and $f_w\in {\mathbb{R}}^h$ to be vectors containing the elements of ${\overline{f}}_v$ and ${\overline{f}}_w$ corresponding to the non-zero columns of ${\overline{\mathcal{M}}}_v$ and ${\overline{\mathcal{M}}}_w$, respectively. Then recall the definitions of $m_{v,i}$ and $m_{w,i}$ after (7), where $m_{v,i}\left(m_{w,i}\right)=1$ if $f_{v,i}\left(f_{w,i}\right)$ is non-zero for some time $t\ge 0$, and $m_{v,i}\left(m_{w,i}\right)=0$ otherwise (i.e., if $f_{v,i}\left(f_{w,i}\right)=0\forall t\ge 0$). It can be then seen that ${\overline{\mathcal{M}}}_v{\overline{f}}_v={\mathcal{M}}_v{f}_v$ and ${\overline{\mathcal{M}}}_w{\overline{f}}_w={\mathcal{M}}_w{f}_w$. Then suppose that only a subset of $x_s$ (given by $y_c=C_s{x}_s$, where $y_c\in {\mathbb{R}}^p$) is transmitted back to the central control centre. Using (9), the dynamics of the microgrid in (7) becomes

$$\begin{array}{cc}\hfill {\dot{x}}_s& =\underset{A_s}{\underbrace{\left[\begin{array}{cc}-\left(\mathcal{B}+\mathcal{L}\right)& 0\\ 0& -\left(\mathcal{B}+\mathcal{L}\right)\end{array}\right]}}{x}_s+\underset{M_s}{\underbrace{\left[\begin{array}{cc}{\mathcal{M}}_v& 0\\ 0& {\mathcal{M}}_w\end{array}\right]}}\underset{f_c}{\underbrace{\left[\begin{array}{c}{f}_v\\ f_w\end{array}\right]}}+\underset{K_s}{\underbrace{\left[\begin{array}{cc}{I}_N& 0\\ 0& I_N\end{array}\right]}}\underset{u_{cc}}{\underbrace{\left[\begin{array}{c}{u}_{cv}\\ u_{cw}\end{array}\right]}},\hfill \\ \hfill y_c& =C_s{x}_s,\hfill \end{array}$$

(10)

where $\mathcal{L}$ is the Laplacian matrix associated with the graph describing the structure of the microgrid, and $f_c\in {\mathbb{R}}^{g+h}$. We then make the following assumptions on system (10) to facilitate further re-expression.

Assumption 2.

$rank\left(C_s{M}_s\right)=rank\left(M_s\right)=g+h$.

Assumption 3.

$rank\left[\begin{array}{cc}s{I}_{2N}-A_s& M_s\\ C_s& 0\end{array}\right]=2N+g+h\forall s\in {\mathbb{C}}^{+}.$

Remark 2.

Assumptions 2 and 3 are standard and were assumed in various observer-related works [22,29,30]. Assumption 2 is the matching condition, which merely implies that faults only affect states that are measurable outputs, while Assumption 3 is required for the stability of the SMO, which will be designed in the next subsection.

Define a matrix $N_C\in {\mathbb{R}}^{\left(2N-p\right)\times 2N}$ satisfying $C_s{N}_C=0$. Hence there exists a non-singular matrix $T_a=\left[\begin{array}{c}{N}_C^T\\ C_s\end{array}\right]$ where $C_s{T}_a^{-1}=\left[\begin{array}{cc}0& I_p\end{array}\right]$. Apply the transformation $x_s\mapsto T_a{x}_s=x_a$, and re-express (10) as

$$\begin{array}{cc}\hfill {\dot{x}}_a=& \underset{A_a}{\underbrace{\left[\begin{array}{cc}{A}_{a1}& A_{a2}\\ A_{a3}& A_{a4}\end{array}\right]}}{x}_a+\underset{M_a}{\underbrace{\left[\begin{array}{c}{M}_{a1}\\ M_{a2}\end{array}\right]}}{f}_c+\underset{K_a}{\underbrace{\left[\begin{array}{c}{K}_{a1}\\ K_{a2}\end{array}\right]}}{u}_{cc},\hfill \\ \hfill y_c=& \underset{C_a}{\underbrace{\left[\begin{array}{cc}0& I_p\end{array}\right]}}{x}_a.\hfill \end{array}$$

(11)

We now introduce the following proposition to further re-express system (11) for later analysis.

Proposition 1.

Suppose that Assumption 2 is satisfied. Then there exists a set of transformations such that system (11) can be re-expressed as:

$$\begin{array}{cc}\hfill {\dot{x}}_{c1}=& \left(A_{c1}+L{A}_{c3}\right)x_{c1}+\left(A_{c2}+L{A}_{c4}-\left(A_{c1}+L{A}_{c3}\right)L\right)x_{c2}+\left(K_{c1}+L{K}_{c2}\right)u_{cc},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\dot{x}}_{c2}=& A_{c3}{x}_{c1}+\left(A_{c4}-A_{c3}L\right)x_{c2}+M_{c2}{f}_c+K_{c2}{u}_{cc},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill y_c=& C_{c2}{x}_{c2},\hfill \end{array}$$

(14)

where $L\in {\mathbb{R}}^{\left(2N-p\right)\times p}=\left[\begin{array}{cc}0& L_0\end{array}\right],L_0\in {\mathbb{R}}^{\left(2N-p\right)\times \left(p-g-h\right)}$, and $A_{c1},A_{c2},A_{c3},A_{c4},K_{c1},K_{c2},M_{c2}$, $C_{c2},x_{c1}$, and $x_{c2}$ are defined in the proof. Suppose that Assumption 3 is also satisfied; then $L_0$ can be chosen such that $A_{c1}+L{A}_{c3}$ has stable eigenvalues, i.e., $\lambda \left(A_{c1}+L{A}_{c3}\right)<0$.

Proof. 

Assumption 2 implies $rank\left(M_{a2}\right)=g+h$, and therefore there exist a matrix $T_{b1}\in {\mathbb{R}}^{\left(2N-p\right)\times p}$ and a non-singular matrix $T_{b2}\in {\mathbb{R}}^{p\times p}$ such that $T_{b1}{M}_{a2}=-M_{a1}$ and $T_{b2}{M}_{a2}=\left[\begin{array}{c}{I}_{g+h}\\ 0\end{array}\right]$. Hence define a non-singular matrix $T_b=\left[\begin{array}{cc}{I}_{2N-p}& T_{b1}\\ 0& T_{b2}\end{array}\right]$ and by applying the transformation $x_a\mapsto T_b{x}_a=x_b$, the matrices $\left(A_a,M_a,K_a,C_a\right)$ would be transformed to have the structures $C_a\mapsto C_a{T}_b^{-1}=\left[\begin{array}{cc}0& C_{c2}\end{array}\right]$ and

$$\begin{array}{cc}\hfill \left(A_a,M_a,K_a\right)\mapsto \left(T_b{A}_a{T}_b^{-1},T_b{M}_a,T_b{K}_a\right)=& \left[\begin{array}{cccc}{A}_{c1}& A_{c2}& 0& K_{c1}\\ A_{c3}& A_{c4}& M_{c2}& K_{c2}\end{array}\right],\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \left[\begin{array}{ccc}{A}_{c3}& M_{c2}& K_{c2}\end{array}\right]=& \left[\begin{array}{ccc}{A}_{c31}& I_{g+h}& K_{c21}\\ A_{c32}& 0& K_{c22}\end{array}\right],\hfill \end{array}$$

(16)

where $C_{c2}=T_{b2}^{-1},A_{c4}\in {\mathbb{R}}^{p\times p}$, and $A_{c32}\in {\mathbb{R}}^{\left(p-g-h\right)\times \left(2N-p\right)}$. Then define a non-singular matrix $T_L=\left[\begin{array}{cc}{I}_{2N-p}& L\\ 0& I_p\end{array}\right]$ and apply the transformation $x_b\mapsto T_L{x}_b=\left[\begin{array}{c}{x}_{c1}\\ x_{c2}\end{array}\right]$, where $x_{c2}\in {\mathbb{R}}^p$ to obtain the system in the coordinates of (12)–(14).

Next, since $T_L{T}_b{T}_a$ and $C_{c2}$ are non-singular, it can be seen from the structures in (12)–(16) that

$$\begin{array}{cc}\hfill rank\left[\begin{array}{cc}s{I}_{2N}-A_s& M_s\\ C_s& 0\end{array}\right]=& rank\left[\begin{array}{cc}{T}_L{T}_b{T}_a& 0\\ 0& I_p\end{array}\right]\left[\begin{array}{cc}s{I}_{2N}-A_s& M_s\\ C_s& 0\end{array}\right]\left[\begin{array}{cc}{\left(T_L{T}_b{T}_a\right)}^{-1}& 0\\ 0& I_{g+h}\end{array}\right]\hfill \\ \hfill =& rank\left[\begin{array}{ccc}s{I}_{n-p}-\left(A_{c1}+L{A}_{c3}\right)& -\left(A_{c2}+L{A}_{c4}-\left(A_{c1}+L{A}_{c3}\right)L\right)& 0\\ -A_{c3}& s{I}_p-\left(A_{c4}-A_{c3}L\right)& M_{c2}\\ 0& C_{c2}& 0\end{array}\right]\hfill \\ \hfill =& rank\left[\begin{array}{cc}{I}_{2N-p}& -L_0\\ 0& -I_{p-g-h}\end{array}\right]\left[\begin{array}{c}s{I}_{2N-p}-A_{c1}\\ A_{c32}\end{array}\right]+p+g+h\hfill \\ \hfill rank\left[\begin{array}{cc}s{I}_{2N}-A_s& M_s\\ C_s& 0\end{array}\right]=& rank\underset{R\left(s\right)}{\underbrace{\left[\begin{array}{c}s{I}_{2N-p}-A_{c1}\\ A_{c32}\end{array}\right]}}+p+g+h.\hfill \end{array}$$

(17)

Assumption 3 then implies $rank\left(R\left(s\right)\right)=2N-p\forall s\in {\mathbb{C}}^{+}$. This in turn implies from the Popov-Hautus-Rosenbrock (PHR) rank test [31] that the unobservable modes of $\left(A_{c1},A_{c32}\right)$ (i.e., the values of s that make $R\left(s\right)$ lose rank) are stable, i.e., $\left(A_{c1},A_{c32}\right)$ is detectable. Thus, $L_0$ can always be chosen such that $\lambda \left(A_{c1}+L_0{A}_{c32}\right)=\lambda \left(A_{c1}+L{A}_{c3}\right)<0$, completing the proof.□

The dynamics in (7) are re-expressed as the state-space system (12)–(14), which is compatible with the Edwards-Spurgeon SMO [22].

3.1. The Observer for Fault Estimation

The Edwards-Spurgeon SMO [22] for system (12)–(14) has the structure:

$$\begin{array}{cc}\hfill {\dot{\widehat{x}}}_{c1}=& \left(A_{c1}+L{A}_{c3}\right){\widehat{x}}_{c1}+\left(A_{c2}+L{A}_{c4}-\left(A_{c1}+L{A}_{c3}\right)L\right)C_{c2}^{-1}{y}_c+\left(K_{c1}+L{K}_{c2}\right)u_{cc},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\dot{\widehat{x}}}_{c2}=& A_{c3}{\widehat{x}}_{c1}+\left(A_{c4}-A_{c3}L\right){\widehat{x}}_{c2}+\left(C_{c2}^{-1}{A}_{c0}-\left(A_{c4}-A_{c3}L\right)C_{c2}^{-1}\right)\left(C_{c2}{\widehat{x}}_{c2}-y_c\right)+K_{c2}{u}_{cc}+{\nu }_c,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\widehat{y}}_c=& C_{c2}{\widehat{x}}_{c2},{\nu }_c=-{\rho }_c{C}_{c2}^{-1}\frac{{\widehat{y}}_c-y_c}{∥{\widehat{y}}_c-y_c∥},\hfill \end{array}$$

(20)

where $A_{c0}\in {\mathbb{R}}^{p\times p}$ and ${\rho }_c\in \mathbb{R}$ are designed in the succeeding analysis.

Remark 3.

The purpose of ${\widehat{x}}_{c2}$ is not to estimate $x_{c2}$ (which can already be calculated from (14)). Rather, ${\widehat{x}}_{c2}$ is used together with (19) and (20) to compute ${\nu }_c$, which will later be used to estimate $f_c$.

Define the errors $e_{c1}={\widehat{x}}_{c1}-x_{c1}$ and $e_{cy}={\widehat{y}}_c-y_c$. Then from (12)–(14) and (18)–(20), the following error system (which characterises the performance of the SMO) is obtained:

$$\begin{array}{cc}\hfill {\dot{e}}_{c1}=& \left(A_{c1}+L{A}_{c3}\right)e_{c1},\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\dot{e}}_{cy}=& C_{c2}{A}_{c3}{e}_{c1}+A_{c0}{e}_{cy}-C_{c2}{M}_{c2}{f}_c+C_{c2}{\nu }_c.\hfill \end{array}$$

(22)

The following proposition is then used to show how sliding motion is achieved in SMO (18)–(20).

Proposition 2.

Suppose that for a given positive scalar ${\eta }_c$, there exist a symmetric positive definite matrix $P_c\in {\mathbb{R}}^{\left(2N-p\right)\times \left(2N-p\right)}$ and any matrix $Q_c\in {\mathbb{R}}^{\left(2N-p\right)\times \left(p-g-h\right)}$ satisfying the following linear matrix inequality (LMI):

$$P_c{A}_{c1}+Q_c{A}_{c32}+{\left(P_c{A}_{c1}+Q_c{A}_{c32}\right)}^T+{\eta }_c{P}_c<0.$$

(23)

Suppose also that SMO (18)–(20) is designed using $L_0=P_c^{-1}{Q}_c$, and

$$\begin{array}{cc}\hfill A_{c0}<& 0,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\rho }_c>& ∥C_{c2}{A}_{c3}∥{\zeta }_c+∥C_{c2}{M}_{c2}∥{\theta }_c,\hfill \end{array}$$

(25)

where ${\zeta }_c\ge ∥e_{c1}\left(0\right)∥\sqrt{\frac{{\lambda }_{max}\left(P_c\right)}{{\lambda }_{min}\left(P_c\right)}}$ and ${\theta }_c>{∥f_c∥}_{max}$. Then an ideal sliding motion for error system (21) and (22) takes place on surface ${\mathcal{S}}_c=\{e_{c1},e_{cy}:e_{cy}=0\}$ in finite time.

Proof. 

There are two parts to the proof: the first portion would show how $e_{c1}$ is bounded by ${\zeta }_c$. Define a Lyapunov candidate function $V_{c1}=e_{c1}^T{P}_c{e}_{c1}$, and differentiating it with respect to time yields

$${\dot{V}}_{c1}=e_{c1}^T\left(P_c\left(A_{c1}+L{A}_{c3}\right)+{\left(A_{c1}+L{A}_{c3}\right)}^T{P}_c\right)e_{c1}.$$

(26)

Substituting for $P_c$ and $Q_c$ into LMI (23) gives

$$P_c\left(A_{c1}+L{A}_{c3}\right)+{\left(A_{c1}+L{A}_{c3}\right)}^T{P}_c+{\eta }_c{P}_c<0.$$

(27)

Hence satisfying LMI (23) implies ${\dot{V}}_{c1}<-{\eta }_c{e}_{c1}^T{P}_c{e}_{c1}=-{\eta }_c{V}_{c1}$, which then implies $∥e_{c1}\left(t\right)∥\le ∥e_{c1}\left(0\right)∥e^{-\frac{{\eta }_{c}t}{2}}\sqrt{\frac{{\lambda }_{max}\left(P_c\right)}{{\lambda }_{min}\left(P_c\right)}}\le {\zeta }_c$ [32]. Thus, the first part of the proof is complete.

In the next and final part of the proof, it will be shown that setting $A_{c0}$ and ${\rho }_c$ to satisfy (24), (25) will result in sliding motion on ${\mathcal{S}}_c$ taking place in finite time. Define another Lyapunov candidate function $V_{cy}=e_{cy}^T{e}_{cy}$, and differentiating it with respect to time results in

$${\dot{V}}_{cy}=e_{cy}^T\left(A_{c0}+A_{c0}^T\right)e_{cy}+2e_{cy}^T\left(C_{c2}{A}_{c3}{e}_{c1}-C_{c2}{M}_{c2}{f}_c+C_{c2}{\nu }_c\right).$$

(28)

Recall $∥e_{c1}∥\le {\zeta }_c$ and ${∥f_c∥}_{max}<{\theta }_c$. Hence, substituting for ${\nu }_c$ from (20) into (28) and setting $A_{c0}<0$ (satisfying Equation (24)) yields

$${\dot{V}}_{cy}<-2∥e_{cy}∥\left({\rho }_c-∥C_{c2}{A}_{c3}∥{\zeta }_c-∥C_{c2}{M}_{c2}∥{\theta }_c\right).$$

(29)

It can therefore be seen that setting ${\rho }_c$ to satisfy (25) results in ${\dot{V}}_{cy}<-2{\delta }_c∥e_{cy}∥<-2{\delta }_c\sqrt{V_{cy}}$ (where ${\delta }_c$ is an arbitrary positive constant). This is the reachability condition [33], which results in $e_{cy}=0$ in finite time. Thus, a sliding motion on ${\mathcal{S}}_c$ is induced in finite time, completing the proof. □

Remark 4.

For convenience, define ${\breve{\nu }}_c=\frac{{\widehat{y}}_c-y_c}{∥{\widehat{y}}_c-y_c∥}$. After sliding motion occurs, ${\breve{\nu }}_c$ rapidly switches between $+1$ and $-1$ to maintain the sliding motion on ${\mathcal{S}}_c$, which could result in chattering [34]. To alleviate the chattering, ${\rho }_c$ should be set to be as small as possible while still satisfying (25). An additional measure is to implement a modified switching term ${\overline{\nu }}_c=-{\rho }_c{C}_{c2}^{-1}\frac{{\widehat{y}}_c-y_c}{∥{\widehat{y}}_c-y_c∥+{\kappa }_c}$, where ${\kappa }_c$ is a small positive constant. The use of ${\overline{\nu }}_c$ would however result in ideal sliding motion on ${\mathcal{S}}_c$ no longer taking place - instead, $e_{cy}$ would be constrained within a small boundary region around zero, and the size of the boundary region is proportional to ${\kappa }_c$ [34].

The following theorem then shows how $x_{c1}$ (and therefore $x_s$) and $f_c$ are estimated using the system structure in (12)–(14) and SMO (18)–(20).

Theorem 1.

SMO (18)–(20) can estimate $x_{c1}$ and $f_c$ if and only if Propositions 1 and 2 are satisfied.

Proof. 

The satisfaction of Proposition 1 allows system (10) to be re-expressed as (12)–(14), upon which SMO (18)–(20) is designed. Then satisfying Proposition 2 results in sliding motion on ${\mathcal{S}}_c$ being induced in finite time. After sliding motion occurs, $e_{cy},{\dot{e}}_{cy}=0$, and error system (21)–(22) becomes

$$\begin{array}{cc}\hfill {\dot{e}}_{c1}=& \left(A_{c1}+L_0{A}_{c32}\right)e_{c1},\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill 0=& C_{c2}{A}_{c3}{e}_{c1}-C_{c2}{M}_{c2}{f}_c+C_{c2}{\nu }_{c,eq},\hfill \end{array}$$

(31)

where ${\nu }_{c,eq}$ is the equivalent output error injection required to maintain an ideal sliding motion on surface ${\mathcal{S}}_c$. Pre-multiply (31) with $C_{c2}^{-1}$, substitute for $A_{c3}$ and $M_{c2}$ from (16), and rearrange to obtain

$${\nu }_{c,eq}=\left[\begin{array}{c}-A_{31}\\ -A_{32}\end{array}\right]e_{c1}+\left[\begin{array}{c}{I}_{g+h}\\ 0\end{array}\right]f_c.$$

(32)

Then define the estimated fault ${\widehat{f}}_c$ and fault estimation error $e_{cf}$ as

$${\widehat{f}}_c=\left[\begin{array}{cc}{I}_{g+h}& 0\end{array}\right]{\nu }_{c,eq},e_{cf}={\widehat{f}}_c-f_c,$$

(33)

respectively. Substituting for $e_{cf}$ into (32) yields

$$e_{cf}=-A_{c31}{e}_{c1}.$$

(34)

Next, recall from Proposition 2 that as $t\to \infty ,e_{c1}\to 0$; this implies that the observer estimates $x_{c1}$ asymptotically. Additionally, from (34), as $t\to \infty ,e_{cf}\to 0$. Hence the observer can simultaneously estimate $x_{c1}$ as well as $f_c$, i.e., as $t\to \infty ,{\widehat{x}}_{c1}\to x_{c1}$ and ${\widehat{f}}_c\to f_c$, thus completing the proof.□

Thus, the analysis of the SMO to estimate the states and faults in system (12)–(14) (and therefore, (10)) was completed.

3.2. Design of the Compensation

In this subsection, the estimated fault ${\widehat{f}}_c$ will be used to design the compensation $u_{cc}$ to reject the influence of $f_c$ on system (10). Partition the matrices ${\mathcal{M}}_v$ and ${\mathcal{M}}_w$ from (10) as

$$\begin{array}{c}\hfill {\mathcal{M}}_v=\left[\begin{array}{c}{\mathcal{M}}_{v,1}\\ ⋮\\ {\mathcal{M}}_{v,N}\end{array}\right],{\mathcal{M}}_w=\left[\begin{array}{c}{\mathcal{M}}_{w,1}\\ ⋮\\ {\mathcal{M}}_{w,N}\end{array}\right].\end{array}$$

(35)

The compensation for the i-th DG, $u_{c,i}$, is given by

$$\left[\begin{array}{c}{u}_{cv,i}\\ u_{cw,i}\end{array}\right]=\left[\begin{array}{cc}-{\mathcal{M}}_{v,i}& 0\\ 0& -{\mathcal{M}}_{w,i}\end{array}\right]{\widehat{f}}_c.$$

(36)

Then by using (9), (10) and (36), it can be seen that $K_s{u}_{cc}=-M_s{\widehat{f}}_c$. Therefore, substituting for $u_{cc}$ from (36), and the definition of $e_{cf}$ from (33) into (10) yields

$${\dot{x}}_s=A_s{x}_s+M_s\left(f_c-{\widehat{f}}_c\right)=A_s{x}_s-M_s{e}_{cf}.$$

(37)

Recall from Theorem 1 that as $t\to \infty ,e_{cf}\to 0$. Hence the effects of $f_c$ on the dynamics of the microgrid in (10) are rejected by $u_{cc}$. Thus, the design of the centralised fault-tolerant scheme is complete.

3.3. Design Procedure

A summarised design procedure for the centralised fault-tolerant scheme is given as follows:

• Formulate the system in the form of (10) using (7)–(9).
• Check that Assumptions 1–3 hold. If not, do not continue as the scheme is not applicable.
• Calculate $T_a$ from before (11) and $T_b$ from Proposition 1. Apply the transformation $x_s\mapsto T_b{T}_a{x}_s$ to obtain the structures in (15)–(16).
• Pick a value for LMI parameter ${\eta }_c$, and use a LMI solver to determine $P_c$ and $Q_c$ from LMI (23). Then calculate $L_0$ using $L_0=P_c^{-1}{Q}_c$.
• Choose $A_{c0}<0$ to satisfy (24), and set ${\rho }_c$ in (20) to satisfy (25).
• If necessary, set ${\kappa }_c$ and implement ${\overline{\nu }}_c$ in Remark 4.
• Estimate $x_{c1}$ (and therefore $x_s$) from (18), and $f_c$ from (33).
• Implement the compensation $u_{cc}$ using (36).

4. The Decentralised Fault-Tolerant Control Scheme

In this next section, we denote the collective i-th DG-observer-FC structure as module i (in accordance with Figure 1b). In this scheme, a SMO is used to estimate $f_i$ for each module. Then the compensation $u_{d,i}$ is designed based on the estimated fault affecting each module to compensate for the effects of $f_i$ on the module itself. Since each module estimates and compensates for faults affecting themselves, the effects of faulty behaviour on the entire microgrid are negated. The consensus protocol would then work as intended (i.e., without the effects of faulty behaviour), and drive the dynamics of the microgrid towards its intended trajectory. The following are defined for convenience:

$$\begin{array}{c}\hfill {\overline{a}}_i=\sum _{j=1,j\ne i}^N{a}_{ij},{\overline{b}}_{vi}=\sum _{j=1,j\ne i}^N{a}_{ij}\left(v_j^d-v_r^d\right),{\overline{b}}_{wi}=\sum _{j=1,j\ne i}^N{a}_{ij}\left(w_j-w_r\right),x_{n,i}=\left[\begin{array}{c}{\overline{b}}_{vi}\\ {\overline{b}}_{wi}\end{array}\right],\\ \hfill A_{d,i}=\left[\begin{array}{cc}-\left({\overline{a}}_i+b_i\right)& 0\\ 0& -\left({\overline{a}}_i+b_i\right)\end{array}\right],x_{d,i}=\left[\begin{array}{c}{v}_i^d-v_r^d\\ w_i-w_r\end{array}\right],f_{d,i}=\left[\begin{array}{c}{f}_{v,i}\\ f_{w,i}\end{array}\right],u_{d,i}=\left[\begin{array}{c}{u}_{cv,i}\\ u_{cw,i}\end{array}\right],\end{array}$$

(38)

where $i=1,2,\dots N$. We now make the following assumption to ease analysis.

Assumption 4.

Measurements of $x_{d,i}$ are assumed to be available to the SMO of the i-th module.

Remark 5.

Assumption 4 implies that the sensor readings for the i-th DG, and the reference voltage and frequencies are known by the SMO for the same module, which is a reasonable assumption.

Without loss of generality, it is assumed that $m_{v,i}=m_{w,i}=1\forall i=1,2,\dots N$ (i.e., $u_{v,i}$ and $u_{w,i}$ are faulty for all modules). Then from (38) and Assumption 4, the dynamics of each module in (7) can be re-expressed as

$${\dot{x}}_{d,i}=A_{d,i}{x}_{d,i}+x_{n,i}+f_{d,i}+u_{d,i}.$$

(39)

System (39) has fully measurable states (similar to the system in ([35], Section 3.2)), known inputs $x_{n,i}$ and $u_{d,i}$, and the unknown input $f_i$. Hence the observer used to estimate $f_i$ is a specific case of the Edwards-Spurgeon SMO with the same number of states and outputs [22].

4.1. The Distributed Observer for Estimating $f_i$

The observer for system (39) has the structure [22]:

$$\begin{array}{cc}\hfill {\dot{\widehat{x}}}_{d,i}=& A_{d0,i}{\widehat{x}}_{d,i}+\left(A_{d,i}-A_{d0,i}\right)x_{d,i}+x_{n,i}+u_{d,i}+{\nu }_{d,i},\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill {\nu }_{d,i}=& -{\rho }_{d,i}\frac{{\widehat{x}}_{d,i}-x_{d,i}}{∥{\widehat{x}}_{d,i}-x_{d,i}∥},\hfill \end{array}$$

(41)

where $A_{d0,i}\in {\mathbb{R}}^{2\times 2}$ and ${\rho }_{d,i}\in \mathbb{R}$ are designed in the succeeding analysis.

Remark 6.

Please note that the purpose of ${\widehat{x}}_{d,i}$ is not to estimate $x_{d,i}$ (which can already be obtained from sensor measurements). Instead, ${\widehat{x}}_{d,i}$ is used to compute ${\nu }_{d,i}$ in (41), which will later be used to estimate $f_{d,i}$.

Define the error $e_{d,i}={\widehat{x}}_{d,i}-x_{d,i}$. Then from (39)–(40), the following error system (which characterises the performance of the SMO) is obtained:

$$\begin{array}{cc}\hfill {\dot{e}}_{d,i}=& A_{d0,i}{e}_{d,i}-f_{d,i}+{\nu }_{d,i}.\hfill \end{array}$$

(42)

The following theorem is used to design SMO (40) and (41) to estimate $f_{d,i}$.

Theorem 2.

Suppose that SMO (40)–(41) is designed using

$$\begin{array}{cc}\hfill A_{d0,i}<& 0,\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill {\rho }_{d,i}>& {\theta }_{d,i},\hfill \end{array}$$

(44)

where ${\theta }_{d,i}>{∥f_{d,i}∥}_{max}$. Then $f_{d,i}$ can be estimated by SMO (40) and (41) in finite time.

Proof. 

There are two parts to the proof: the first portion will show how sliding motion on surface ${\mathcal{S}}_{d,i}=\{e_{d,i}:e_{d,i}=0\}$ is achieved. Define a Lyapunov candidate function $V_{d,i}=e_{d,i}^T{e}_{d,i}$, and differentiating it with respect to time results in

$${\dot{V}}_{d,i}=e_{d,i}^T\left(A_{d0,i}+A_{d0,i}^T\right)e_{d,i}+2e_{d,i}^T\left(-f_{d,i}+{\nu }_{d,i}\right).$$

(45)

Substituting for ${\nu }_{d,i}$ from (41) into (45) and satisfying (43) yields

$${\dot{V}}_{d,i}<-2∥e_{d,i}∥\left({\rho }_{d,i}-{\theta }_{d,i}\right).$$

(46)

It can therefore be seen that setting ${\rho }_{d,i}$ to satisfy (44) results in ${\dot{V}}_{d,i}<-2{\delta }_{d,i}∥e_{d,i}∥<-2{\delta }_{d,i}\sqrt{V_{d,i}}$ (where ${\delta }_{d,i}$ is an arbitrary positive constant). This is the reachability condition [33], which results in $e_{d,i}=0$ in finite time. Thus, a sliding motion on ${\mathcal{S}}_{d,i}$ is induced in finite time, completing the first part of the proof.

The next and final part of the proof will show how $f_{d,i}$ is estimated. After sliding motion occurs, $e_{d,i},{\dot{e}}_{d,i}=0$, and error system (42) becomes

$$0=-f_{d,i}+{\nu }_{dq,i},$$

(47)

where ${\nu }_{dq,i}$ is the equivalent output error injection required to maintain an ideal sliding motion on surface ${\mathcal{S}}_{d,i}$. Define the fault estimation ${\widehat{f}}_{d,i}$ and fault estimation error $e_{df,i}$ as

$${\widehat{f}}_{d,i}={\nu }_{dq,i},e_{df,i}={\widehat{f}}_{d,i}-f_{d,i},$$

(48)

respectively. Substituting for $e_{df,i}$ into (47) yields $e_{df,i}=0$. Since sliding motion (and therefore (47)) is obtained in finite time, then $e_{df,i}=0$ (and hence ${\widehat{f}}_{d,i}=f_{d,i}$) is achieved in finite time as well. Hence the observer estimates $f_{d,i}$ in finite time, thus completing the proof.□

Remark 7.

Define ${\breve{\nu }}_{d,i}=\frac{{\widehat{x}}_{d,i}-x_{d,i}}{∥{\widehat{x}}_{d,i}-x_{d,i}∥}$. After sliding motion occurs, ${\breve{\nu }}_{d,i}$ switches rapidly between $+1$ and $-1$ to maintain the sliding motion on ${\mathcal{S}}_{d,i}$, giving rise to chattering. Similar to Remark 4, measures to reduce the effects of chattering include setting ${\rho }_{d,i}$ to be as small as possible while still satisfying (44), and using a modified switching term ${\overline{\nu }}_{d,i}=-{\rho }_{d,i}\frac{{\widehat{x}}_{d,i}-x_{d,i}}{∥{\widehat{x}}_{d,i}-x_{d,i}∥+{\kappa }_{d,i}}$, where ${\kappa }_{d,i}$ is a small positive constant.

The SMO for module i was designed. Thus, by designing SMOs for each module, the faults affecting each module, and by extension the microgrid, can be estimated.

4.2. Design of the Compensation $u_{d,i}$

In this subsection, the estimated fault ${\widehat{f}}_{d,i}$ will be used to design $u_{d,i}$ to reject the influence of $f_{d,i}$ on system (39). Partition ${\widehat{f}}_{d,i}$ as follows:

$${\widehat{f}}_{d,i}=\left[\begin{array}{c}{\widehat{f}}_{v,i}\\ {\widehat{f}}_{w,i}\end{array}\right],$$

(49)

where ${\widehat{f}}_{v,i}\in {\mathbb{R}}^1$ and ${\widehat{f}}_{w,i}\in {\mathbb{R}}^1$ are estimations of the faults $f_{d,i}$ and $f_{w,i}$, respectively. Then let the compensation for the i-th module, $u_{d,i}$, be given by

$$u_{cv,i}=-{\widehat{f}}_{v,i},u_{cw,i}=-{\widehat{f}}_{w,i}.$$

(50)

From (38) and (48), it can be seen that $u_{d,i}=-{\widehat{f}}_{d,i}$. Therefore, substituting for $f_{d,i}$ and $u_{d,i}$ from (38) and (50), and using the definition of $e_{df,i}$ from (48) on (38) yields

$${\dot{x}}_{d,i}=A_{d,i}{x}_{d,i}+\left(f_{d,i}-{\widehat{f}}_{d,i}\right)=A_{d,i}{x}_{d,i}-e_{df,i}.$$

(51)

Recall from Theorem 2 that $e_{df,i}=0$ after sliding motion is achieved. Hence the effects of $f_{d,i}$ on (39) (i.e., module i) are rejected by $u_{d,i}$. Then by designing the compensation (50) for each module, the effects of faults on the microgrid can also be negated. Thus, the design of the decentralised fault-tolerant protocol is complete.

4.3. Design Procedure

A summarised design procedure for the presented scheme is given as follows. For each DG i,

• Formulate the system in the form of (39) using (7) and (38).
• Check that Assumption 1 and 4 hold. If not, do not continue as the scheme is not applicable.
• Choose $A_{d0,i}<0$ and set ${\rho }_{d,i}$ in (41) to satisfy (43)–(44).
• Reconstruct $f_i$ from (48).
• If necessary, set ${\kappa }_{d,i}$ and implement ${\overline{\nu }}_{d,i}$ in Remark 7.
• Implement the compensation $u_{d,i}$ in (50).

Remark 8.

Two observer-based FTC schemes are presented: a centralised one in Section 3, and a decentralised one in Section 4. The centralised scheme can only estimate (and therefore, reject the influence of) faults affecting states that are measured by the central SMO. The decentralised scheme can however estimate (and therefore, negate the effects of) faults entering any state in the microgrid since each SMO has access to both states in its module. On the other hand, the centralised scheme is less computationally intensive, since only a single SMO is required for the entire microgrid. In the decentralised scheme however, each module has its own SMO, which can translate to greater hardware and implementation costs. Designers should thus consider this cost-reliability trade-off when deciding on which scheme to use for their system.

5. Simulation Example

To demonstrate the effectiveness of our proposed scheme, consider a modified version of the 3-DG microgrid in [14], which is illustrated in Figure 2. To showcase the performance of the scheme, suppose that the voltage of the third DG, and the frequencies of the first and third DG is affected by the faults $f_{v,3},f_{w,1}$, and $f_{w,3}$, respectively. While both states of each DGs can be locally measured by the DG itself, only the voltages and frequencies of the first and third DGs can be reliably broadcast back to the control centre. Control inputs can however be fed into all DGs. The consensus protocol between each DG in (7) is therefore given by

$$\begin{array}{cc}\hfill u_1=& \left[\begin{array}{c}{v}_2^d-v_1^d\\ w_2-w_1\end{array}\right]-\left[\begin{array}{c}{v}_1^d-v_r^d\\ w_1-w_r\end{array}\right]+\left[\begin{array}{c}0\\ f_{w,1}\end{array}\right]+\left[\begin{array}{c}{u}_{cv,1}\\ u_{cw,1}\end{array}\right],\hfill \\ \hfill u_2=& \left[\begin{array}{c}{v}_3^d-v_2^d\\ w_3-w_2\end{array}\right]+\left[\begin{array}{c}{u}_{cv,2}\\ u_{cw,2}\end{array}\right],\hfill \\ \hfill u_3=& \left[\begin{array}{c}{v}_1^d-v_3^d\\ w_1-w_3\end{array}\right]+\left[\begin{array}{c}{v}_2^d-v_3^d\\ w_2-w_3\end{array}\right]+\left[\begin{array}{c}{f}_{v,3}\\ f_{w,3}\end{array}\right]+\left[\begin{array}{c}{u}_{cv,3}\\ u_{cw,3}\end{array}\right].\hfill \end{array}$$

(52)

The centralised fault-tolerant scheme in Section 3 will first be designed according to the steps in Section 3.3. Next, the decentralised fault-tolerant scheme in Section 4 will be designed using the procedure in Section 4.3.

5.1. Design of the Centralised Scheme

• Step 1. The microgrid in (52) can be rewritten in the form of (10) as

  $$\begin{array}{cc}\hfill \underset{{\dot{x}}_s}{\underbrace{\left[\begin{array}{c}{\dot{v}}_1^d-{\dot{v}}_r^d\\ {\dot{v}}_2^d-{\dot{v}}_r^d\\ {\dot{v}}_3^d-{\dot{v}}_r^d\\ {\dot{w}}_1-{\dot{w}}_r\\ {\dot{w}}_2-{\dot{w}}_r\\ {\dot{w}}_3-{\dot{w}}_r\end{array}\right]}}=& \underset{A_s}{\underbrace{\left[\begin{array}{cccccc}-2& 1& 0& 0& 0& 0\\ 0& -1& 1& 0& 0& 0\\ 1& 1& -2& 0& 0& 0\\ 0& 0& 0& -2& 1& 0\\ 0& 0& 0& 0& -1& 1\\ 0& 0& 0& 1& 1& -2\end{array}\right]}}\underset{x_s}{\underbrace{\left[\begin{array}{c}{v}_1^d-v_r^d\\ v_2^d-v_r^d\\ v_3^d-v_r^d\\ w_1-w_r\\ w_2-w_r\\ w_3-w_r\end{array}\right]}}+\underset{M_s}{\underbrace{\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right]}}\underset{f_c}{\underbrace{\left[\begin{array}{c}{f}_{v,3}\\ f_{w,1}\\ f_{w,3}\end{array}\right]}}+\underset{K_s}{\underbrace{I_6}}\underset{u_{cc}}{\underbrace{\left[\begin{array}{c}{u}_{cv,1}\\ u_{cv,2}\\ u_{cv,3}\\ u_{cw,1}\\ u_{cw,2}\\ u_{cw,3}\end{array}\right]}},\hfill \\ \hfill \underset{y_c}{\underbrace{\left[\begin{array}{c}{v}_{c,1}^d\\ v_{c,3}^d\\ w_{c,1}\\ w_{c,3}\end{array}\right]}}=& \underset{C_s}{\underbrace{\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right]}}{x}_s.\hfill \end{array}$$

  (53)
• Step 2. The following is obtained from (53):

  $$N=3,p=4,g=1,h=2,rank\left(C_s{M}_s\right)=3,rank\left(M_s\right)=3,rank\left[\begin{array}{cc}s{I}_6-A_s& M_s\\ C_s& 0\end{array}\right]=9\forall s\in {\mathbb{C}}^{+}.$$

  (54)

  It can be verified that Assumptions 2 and 3 are satisfied.
• Step 3. The non-singular matrices $T_a$ and $T_b$ are calculated to be

  $$T_a=\left[\begin{array}{ccccc}0& 0& 0& 1& 0\\ 0& -1& 0& 0& 0\\ 1& 0& 0& 0& 0\\ 0& 0& I_2& 0& 0\\ 0& 0& 0& 0& 1\end{array}\right],T_b=\left[\begin{array}{ccc}{I}_2& 0& 0\\ 0& 0& I_3\\ 0& 1& 0\end{array}\right].$$

  (55)

  The structures in (15)–(16) are then found to be $C_{c2}=\left[\begin{array}{cc}0& 1\\ I_3& 0\end{array}\right]$ and

  $$\left[\begin{array}{cc}{A}_{c1}& A_{c2}\\ A_{c3}& A_{c4}\end{array}\right]=\left[\begin{array}{cccccc}-1& 0& 0& 0& 1& 0\\ 0& -1& -1& 0& 0& 0\\ 0& -1& -2& 0& 0& 1\\ 1& 0& 0& -2& 0& 0\\ 1& 0& 0& 1& -2& 0\\ 0& -1& 0& 0& 0& -2\end{array}\right],\left[\begin{array}{c}{K}_{c1}\\ K_{c2}\end{array}\right]=\left[\begin{array}{ccccc}0& 0& 0& 1& 0\\ 0& -1& 0& 0& 0\\ 0& 0& I_2& 0& 0\\ 0& 0& 0& 0& 1\\ 1& 0& 0& 0& 0\end{array}\right],M_{c2}=\left[\begin{array}{c}{I}_3\\ 0_{1\times 3}\end{array}\right].$$

  (56)
• Step 4. The SeDuMi solver for YALMIP in MATLAB is used on LMI (23) with ${\eta }_c=1$, yielding $P_c=\left[\begin{array}{cc}2.046& -0.2907\\ -0.2907& 1.265\end{array}\right]$ and $Q_c=\left[\begin{array}{c}1.237\\ 0.9980\end{array}\right]$. Therefore, $L_0=P_c^{-1}{Q}_c=\left[\begin{array}{c}0.7409\\ 0.9585\end{array}\right]$.
• Steps 5–7. The parameters $A_{c0},{\rho }_c$, and ${\kappa }_c$ are chosen as $A_{c0}=-10I_4,{\rho }_c=100$, and ${\kappa }_c={10}^{-5}$. Then $f_c$ is estimated by ${\widehat{f}}_c=\left[\begin{array}{cc}{I}_3& 0_{3\times 1}\end{array}\right]{\nu }_{c,eq}$, and $x_{c1}$ is estimated using

  $${\dot{\widehat{x}}}_{c1}=\left[\begin{array}{cc}-1& -0.7409\\ 0& -1.958\end{array}\right]{\widehat{x}}_{c1}+\left[\begin{array}{cccc}-0.0307& 0& 0& 1\\ -0.0398& -1& 0& 0\end{array}\right]y_c+\left[\begin{array}{cccccc}0.7409& 0& 0& 0& 1& 0\\ 0.9585& -1& 0& 0& 0& 0\end{array}\right]u_{cc}.$$

  (57)
• Step 8. Partition ${\widehat{f}}_c$ as ${\widehat{f}}_c=\left[\begin{array}{c}{\widehat{f}}_{c,1}\\ {\widehat{f}}_{c,2}\\ {\widehat{f}}_{c,3}\end{array}\right]$, where ${\widehat{f}}_{c,1},{\widehat{f}}_{c,2}$, and ${\widehat{f}}_{c,3}$ are the estimations of $f_{v,3},f_{w,1}$, and $f_{w,3}$, respectively. From (53), the compensation $u_{cc}$ is designed as

  $$u_{cv,1},u_{cv,2},u_{w,2}=0,u_{cv,3}=-{\widehat{f}}_{c,1},u_{cw,1}=-{\widehat{f}}_{c,2},u_{cw,3}=-{\widehat{f}}_{c,3}.$$

  (58)

The design of the centralised fault-tolerant scheme is complete. We now proceed to the design of the decentralised fault-tolerant scheme.

5.2. Design of the Decentralised Scheme

Steps 1 and 2. The dynamics of each DG in (52) can be rewritten in the form of (39) using (7) and (38) as

$$\begin{array}{cc}\hfill \underset{{\dot{x}}_{o,1}}{\underbrace{u_1}}& =\underset{A_{d,1}}{\underbrace{\left[\begin{array}{cc}-2& 0\\ 0& -2\end{array}\right]}}\underset{x_{d,1}}{\underbrace{\left[\begin{array}{c}{v}_1^d-v_r^d\\ w_1-w_r\end{array}\right]}}+\underset{x_{n,1}}{\underbrace{\left[\begin{array}{c}{v}_2^d-v_r^d\\ w_2-w_r\end{array}\right]}}+\underset{f_{d,1}}{\underbrace{\left[\begin{array}{c}0\\ f_{w,1}\end{array}\right]}}+\underset{u_{d,1}}{\underbrace{\left[\begin{array}{c}{u}_{cv,1}\\ u_{cw,1}\end{array}\right]}},\hfill \\ \hfill \underset{{\dot{x}}_{d,2}}{\underbrace{u_2}}& =\underset{A_{d,2}}{\underbrace{\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]}}\underset{x_{d,2}}{\underbrace{\left[\begin{array}{c}{v}_2^d-v_r^d\\ w_2-w_r\end{array}\right]}}+\underset{x_{n,2}}{\underbrace{\left[\begin{array}{c}{v}_3^d-v_r^d\\ w_3-w_r\end{array}\right]}}+\underset{f_{d,2}}{\underbrace{\left[\begin{array}{c}0\\ 0\end{array}\right]}}+\underset{u_{d,2}}{\underbrace{\left[\begin{array}{c}{u}_{cv,2}\\ u_{cw,2}\end{array}\right]}},\hfill \\ \hfill \underset{{\dot{x}}_{d,3}}{\underbrace{u_3}}& =\underset{A_{d,3}}{\underbrace{\left[\begin{array}{cc}-2& 0\\ 0& -2\end{array}\right]}}\underset{x_{d,3}}{\underbrace{\left[\begin{array}{c}{v}_3^d-v_r^d\\ w_3-w_r\end{array}\right]}}+\underset{x_{n,3}}{\underbrace{\left[\begin{array}{c}\left(v_1^d-v_r^d\right)+\left(v_2^d-v_r^d\right)\\ \left(w_1-w_r\right)+\left(w_2-w_r\right)\end{array}\right]}}+\underset{f_{d,3}}{\underbrace{\left[\begin{array}{c}{f}_{v,3}\\ f_{w,3}\end{array}\right]}}+\underset{u_{d,3}}{\underbrace{\left[\begin{array}{c}{u}_{cv,3}\\ u_{cw,3}\end{array}\right]}},\hfill \end{array}$$

(59)

Since each DG can locally measure both of its own states, Assumption 4 is satisfied.

Steps 3–6. The parameters for each SMO are chosen as follows:

$$\begin{array}{cc}\hfill A_{d0,1}=-3I_2,A& {}_{d0,2}=-2.5I_2,A_{d0,3}=-2I_2,{\rho }_{d,1}=40,{\rho }_{d,2}=50,{\rho }_{d,3}=30,\hfill \\ \hfill & {\kappa }_{d,1}={\kappa }_{d,2}={10}^{-5},{\kappa }_{d,3}=3\times {10}^{-5}.\hfill \end{array}$$

(60)

The faults affecting each module are then estimated from

$${\widehat{f}}_{d,1}={\nu }_{dq,1},{\widehat{f}}_{d,2}={\nu }_{dq,2},{\widehat{f}}_{d,3}={\nu }_{dq,3}.$$

(61)

Partition ${\widehat{f}}_{d1}$ and ${\widehat{f}}_{d3}$ as ${\widehat{f}}_1=\left[\begin{array}{c}{\widehat{f}}_{dv,1}\\ {\widehat{f}}_{dw,1}\end{array}\right]$ and ${\widehat{f}}_3=\left[\begin{array}{c}{\widehat{f}}_{dv,3}\\ {\widehat{f}}_{dw,3}\end{array}\right]$, respectively. It can then be seen that ${\widehat{f}}_{dv,3},{\widehat{f}}_{dw,1}$, and ${\widehat{f}}_{dw,3}$ are the estimations for $f_{v,3},f_{w,1}$, and $f_{w,3}$, respectively. The compensation for each module are then designed using (50) and (61) as

$$\underset{u_{d,1}}{\underbrace{\left[\begin{array}{c}{u}_{cv,1}\\ u_{cw,1}\end{array}\right]}}=-{\widehat{f}}_{d,1},\underset{u_{d,2}}{\underbrace{\left[\begin{array}{c}{u}_{cv,2}\\ u_{cw,2}\end{array}\right]}}=-{\widehat{f}}_{d,2},\underset{u_{d,3}}{\underbrace{\left[\begin{array}{c}{u}_{cv,3}\\ u_{cw,3}\end{array}\right]}}=-{\widehat{f}}_{d,3}.$$

(62)

5.3. Performance of the Schemes

The design of both fault-tolerant schemes is complete. To demonstrate the effectiveness of the observers at estimating the fault, we first simulate a case where the compensation for both schemes are set to be zero, i.e., $u_{cc},u_{d,i}=0$, for $i=1,2,3$. Then to show the efficacy of the fault compensation, we simulate a second case where the compensation for the centralised scheme is set to be as designed in (58), and the compensation for the decentralised scheme is set to be as designed in (62). In both cases, the initial condition of the microgrid is set as $\left[\begin{array}{cccccc}{v}_1^d\left(0\right)& v_2^d\left(0\right)& v_3^d\left(0\right)& w_1\left(0\right)& w_2\left(0\right)& w_3\left(0\right)\end{array}\right]=\left[\begin{array}{cccccc}300& 310& 290& 324& 319& 304\end{array}\right]$, while the observer is set to have zero initial conditions. The reference inputs are set to be

$$\begin{array}{cc}\hfill v_r^d=& 300+15r\left(t-39\right)-15r\left(t-40\right)-20r\left(t-74\right)+20r\left(t-75\right),\hfill \\ \hfill w_r=& 314+63r\left(t-39\right)-63r\left(t-40\right)-31r\left(t-74\right)+31r\left(t-75\right).\hfill \end{array}$$

(63)

The fault signals are then set as

$$\begin{array}{ll}{f}_{v,3}=& 3.5sin\left(1.2t-\pi /4\right)-4+r\left(t-10\right)-r\left(t-20\right)-2r\left(t-50\right)+2r\left(t-60\right),\\ f_{w,1}=& 1.1sin\left(1.5t-8\pi /5\right)+6-r\left(t-30\right)+r\left(t-55\right)+0.5r\left(t-60\right)-0.5r\left(t-83\right),\\ f_{w,3}=& 2.6sin\left(1.4t-3\pi /2\right)+1+0.5r\left(t-20\right)-0.5r\left(t-40\right)-0.75r\left(t-45\right)+0.75r\left(t-85\right).\end{array}$$

(64)

For ease of notation, define the state and fault estimation errors respectively as

$$e_x=\left[\begin{array}{c}{e}_{x,1}\\ e_{x,2}\\ e_{x,3}\\ e_{x,4}\\ e_{x,5}\\ e_{x,6}\end{array}\right]=\left[\begin{array}{c}{\widehat{v}}_{c,1}^d-v_{c,1}^d\\ {\widehat{v}}_{c,2}^d-v_{c,2}^d\\ {\widehat{v}}_{c,3}^d-v_{c,3}^d\\ {\widehat{w}}_{c,1}-w_{c,1}\\ {\widehat{w}}_{c,2}-w_{c,2}\\ {\widehat{w}}_{c,3}-w_{c,3}\end{array}\right],e_f=\left[\begin{array}{c}{e}_{f,1}\\ e_{f,2}\\ e_{f,3}\end{array}\right]=\left[\begin{array}{c}{\widehat{f}}_{v,3}-f_{v,3}\\ {\widehat{f}}_{w,1}-f_{w,1}\\ {\widehat{f}}_{w,3}-f_{w,3}\end{array}\right].$$

(65)

5.3.1. The Centralised Scheme

Figure 3, Figure 4, Figure 5 and Figure 6 show the performance of the centralised scheme for the case where the compensation is set to be zero (i.e., $u_{cc}=0$). Figure 3 shows the states of system (53), their estimates, and the reference, while Figure 4 shows the state estimation errors. It can be seen that the states are severely affected by the faults, and track the references very poorly. The observer is however able to estimate the states despite the presence of the fault, and after about $t=4$ s, the state estimation errors converge to zero. Figure 5 then shows the faults affecting system (53) and their estimates, while Figure 6 shows the fault estimation errors. The observer is able to estimate the fault faithfully after about $t=4$ s, thus proving the effectiveness of the proposed centralised scheme at state and fault estimation.

Figure 7 and Figure 8 then show the performance of the scheme when the compensation is set as it was designed in (58). Figure 7 shows the states of system (53), their estimates, and the reference, while Figure 8 shows the compensation into each state. It can now be seen that the states now track the references (after an initial transient period due to the differences in initial conditions of the system and the observer). Thus, the effectiveness of the proposed centralised scheme was demonstrated.

5.3.2. The Decentralised Scheme

Figure 9, Figure 10, Figure 11 and Figure 12 show the performance of the decentralised scheme for the case where the compensation is set to be zero (i.e., $u_{d,i}=0$ for $i=1,2,3$). Figure 9 shows the states of system (53), their estimates, and the reference, while Figure 10 shows the state estimation errors. As was with the centralised case, the system states are severely affected by the faults, and poorly track the references. The observers are still however able to estimate the states even in the presence of faults, and after about $t=0.3$ s, the state estimation errors converge to zero. Figure 11 then shows the faults affecting system (53) and their estimates, while Figure 12 shows the fault estimation errors. The observers are able to faithfully estimate the fault after about $t=0.5$ s, thus proving the effectiveness of the proposed decentralised scheme at state estimation and fault estimation.

Figure 13 and Figure 14 on the other hand show the performance of the decentralised scheme when the compensation is set as it was designed in (62). Figure 13 shows the states of system (53), their estimates, and the reference, while Figure 14 shows the compensation into each state. The states track the references (after an initial transient period due to the differences in the initial conditions of the system and the observer). Thus, the efficacy of the proposed decentralised scheme has also been shown.

6. Conclusions

Two schemes for fault-tolerant secondary control in microgrids were presented. The dynamics of the microgrid considered in the paper includes faults in the secondary control, as well as compensation to negate the effects of these faults. The first scheme consists of a centralised SMO-based fault-tolerant controller. The system is first re-expressed using transformations to ease analysis and design of the fault-tolerant scheme. Outputs from the microgrid (which are a subset of its states) are measured by the central SMO to estimate the faults affecting the microgrid. The estimated faults are used to negate the effects of the faults on the microgrid. The second scheme uses a SMO-based fault-tolerant controller for each DG, which would estimate faults affecting only that DG, and compensate for only those faults. Simulations were carried out, and the results demonstrate the effectiveness of both presented schemes. The presented work however has only considered the secondary control of the microgrid. Hierarchical control consists of two more controls: primary and tertiary. Furthermore, the sensitivity of the microgrid performance with respect to parameter variation and measurement noise are important considerations. We thus aim to take these into account in our future investigations.