Optimum State-of-Charge Operating Range for Frequency Regulation of Energy Storage Systems Using a Master–Slave Parallel Genetic Algorithm
Abstract
1. Introduction
2. Energy Storage System for Primary Frequency Regulation
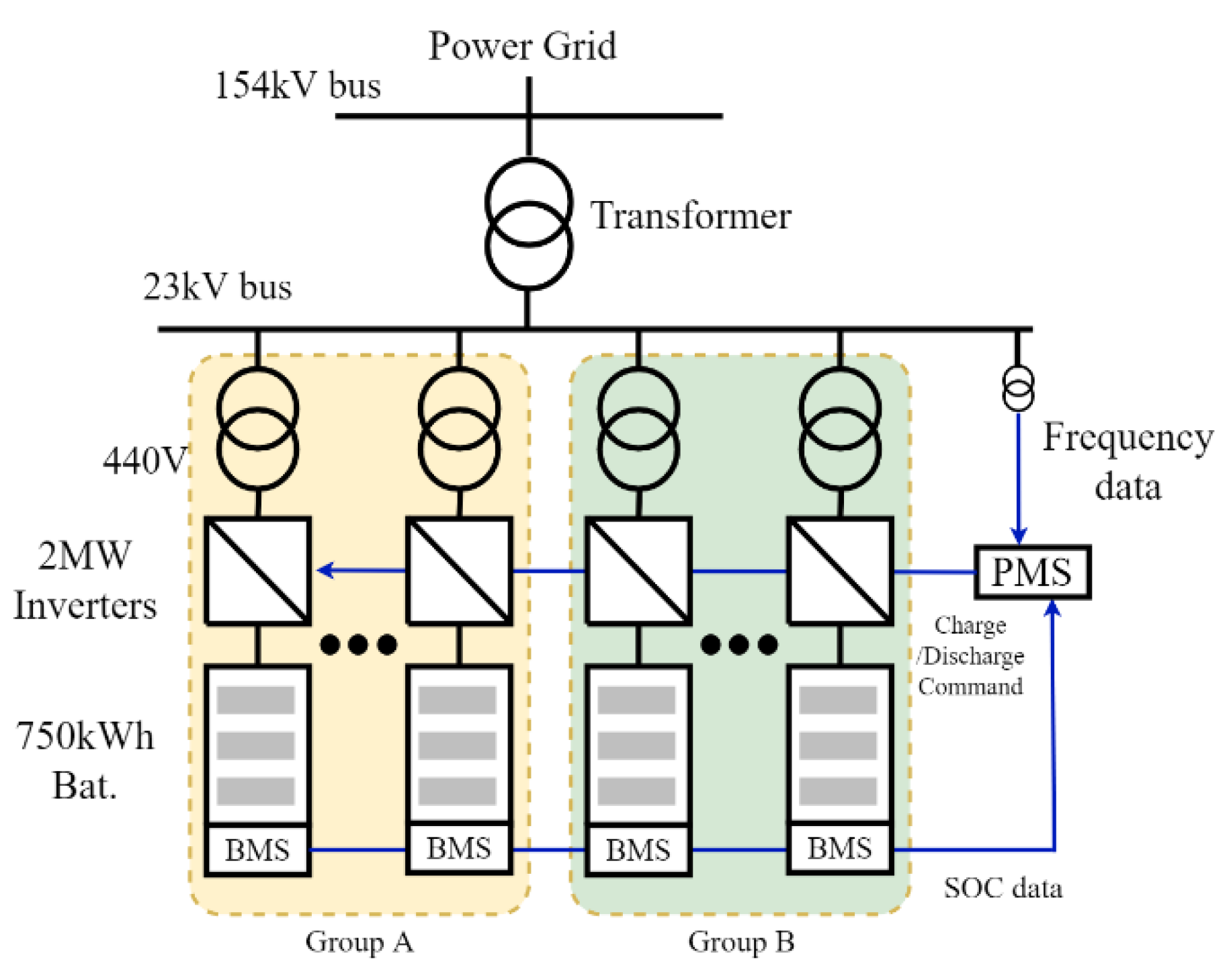
2.1. System Configuration
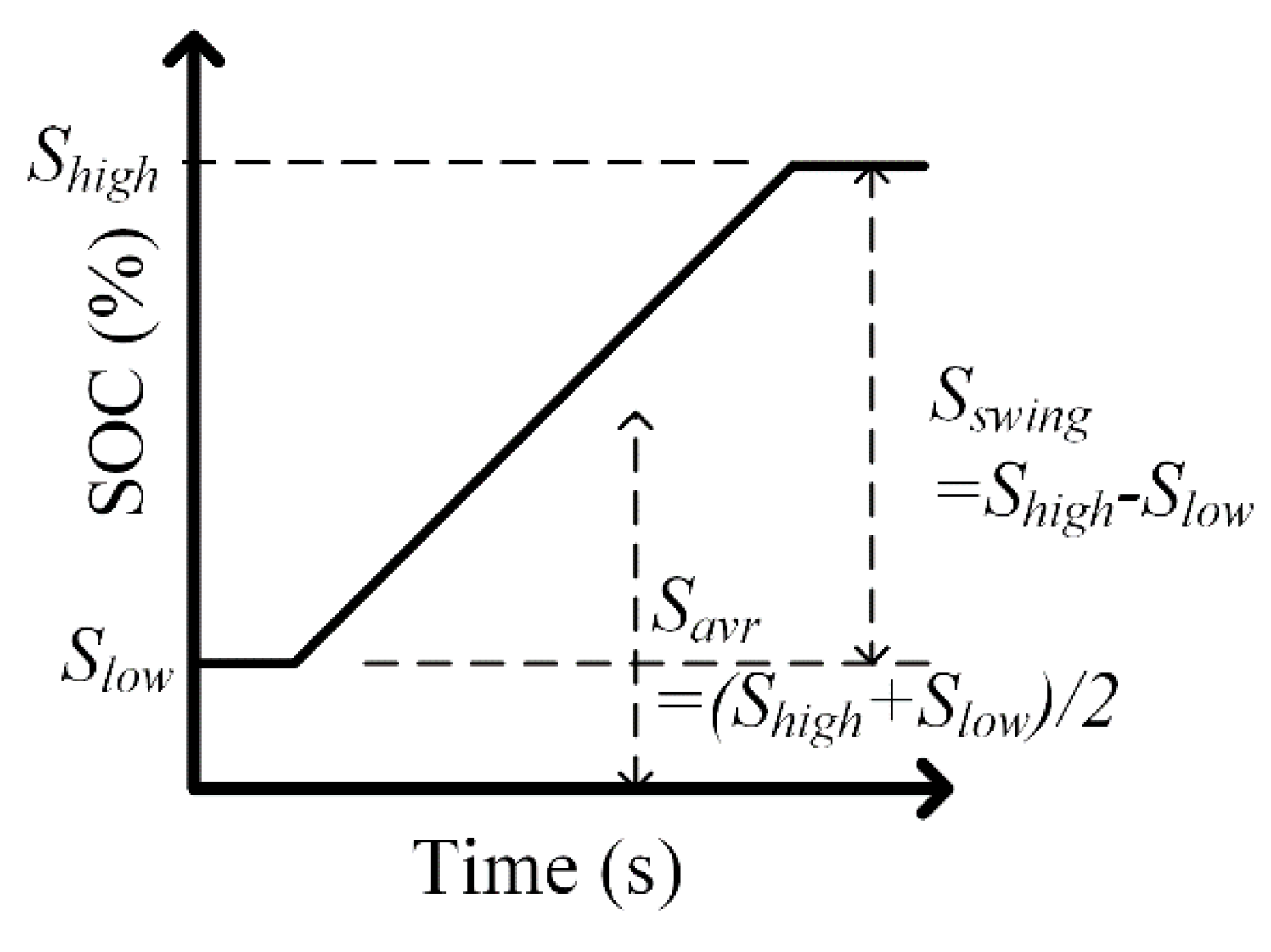
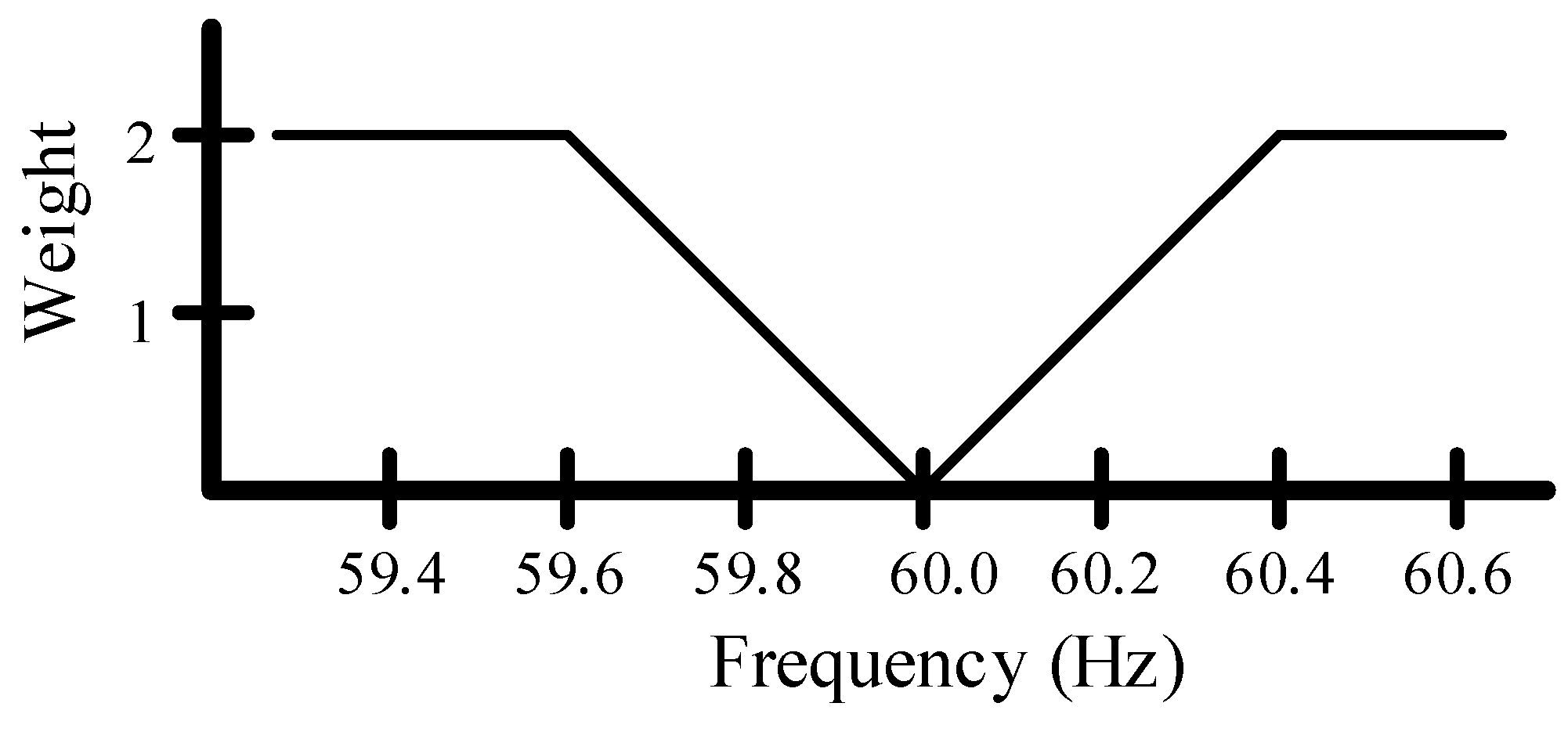
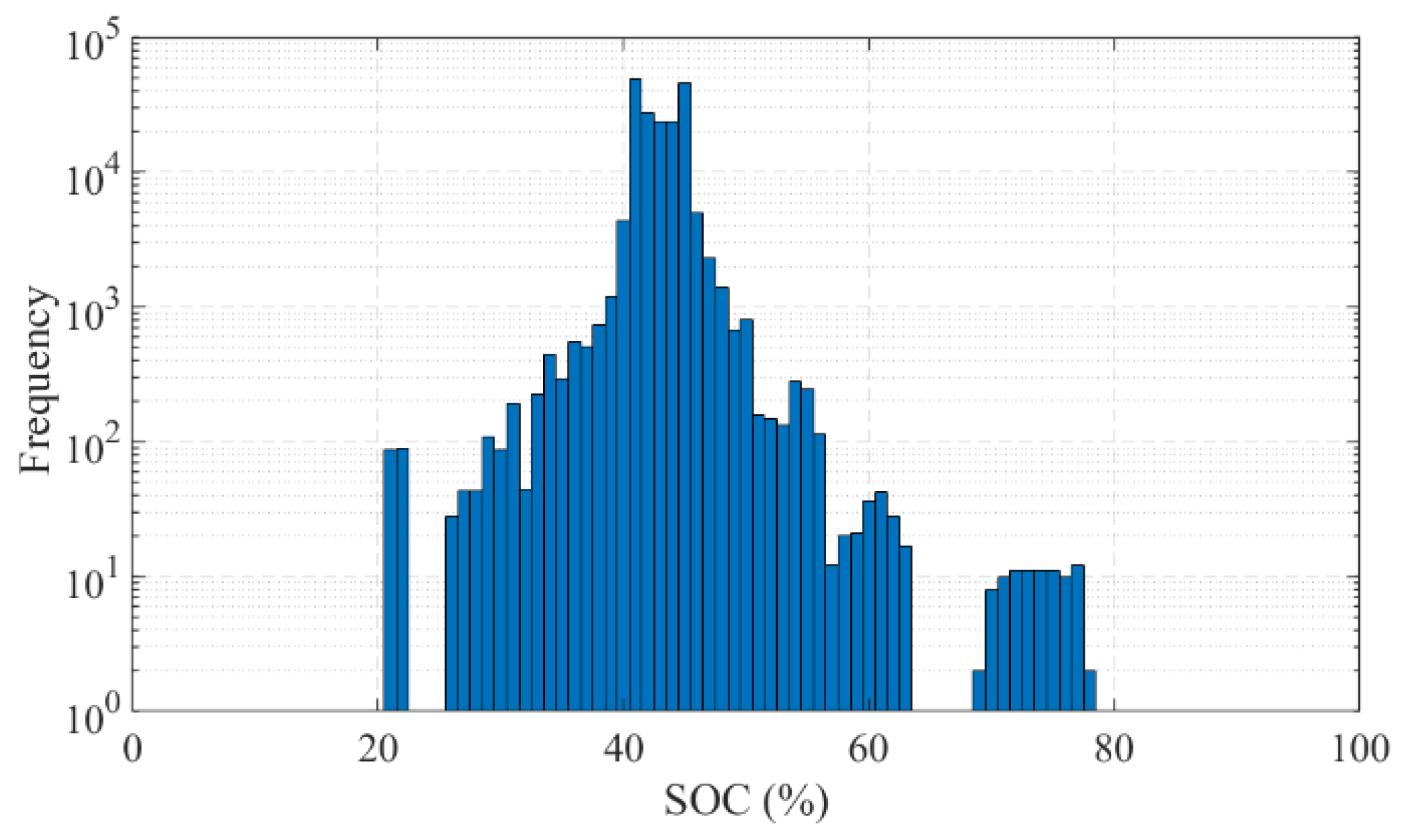
2.2. Primary Frequency Control
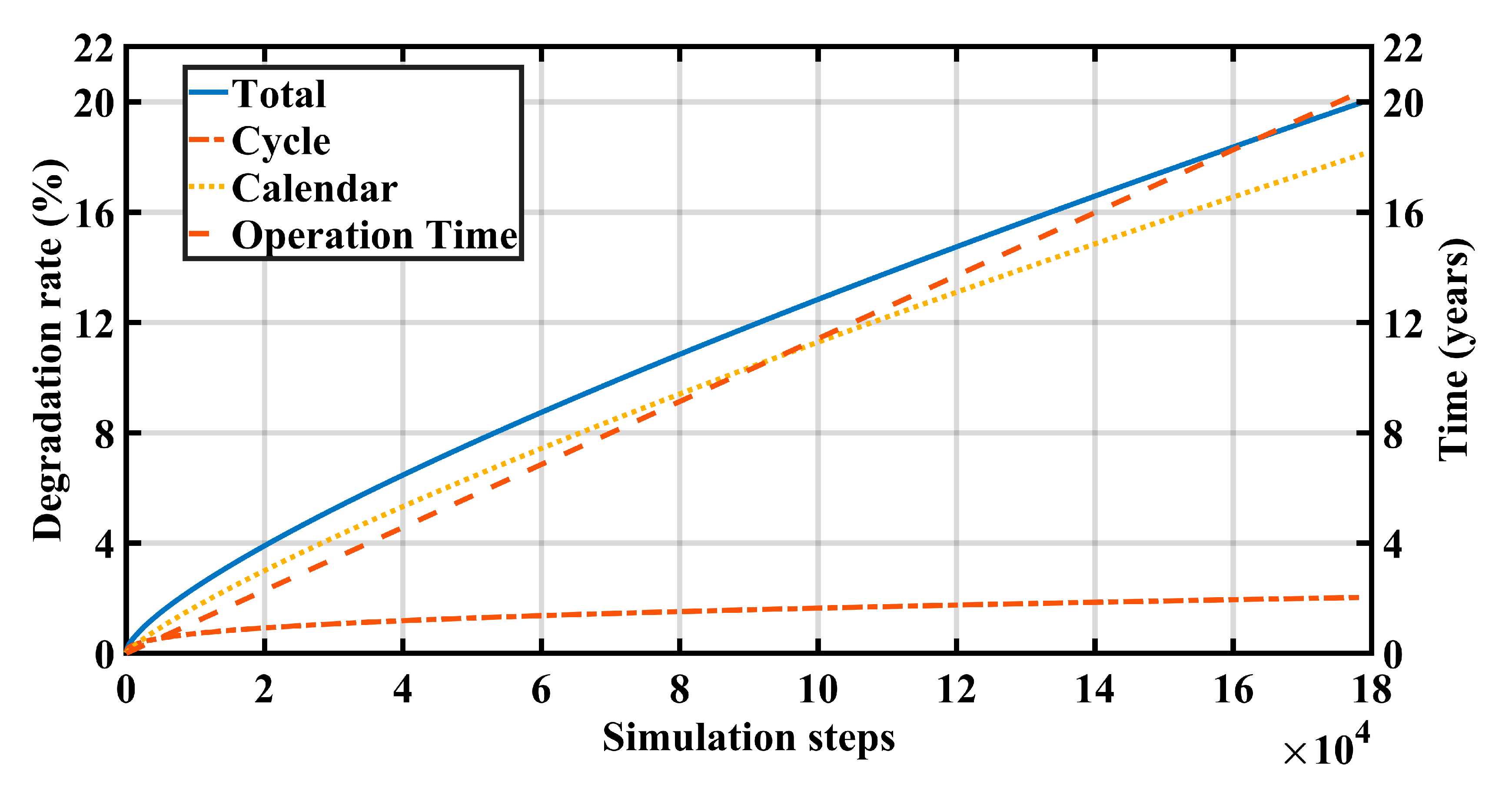
2.3. Battery-Based Energy Storage Systems Degradation
3. Optimizing SOC Operating Range Using a Parallel Genetic Algorithm
3.1. Objective Function
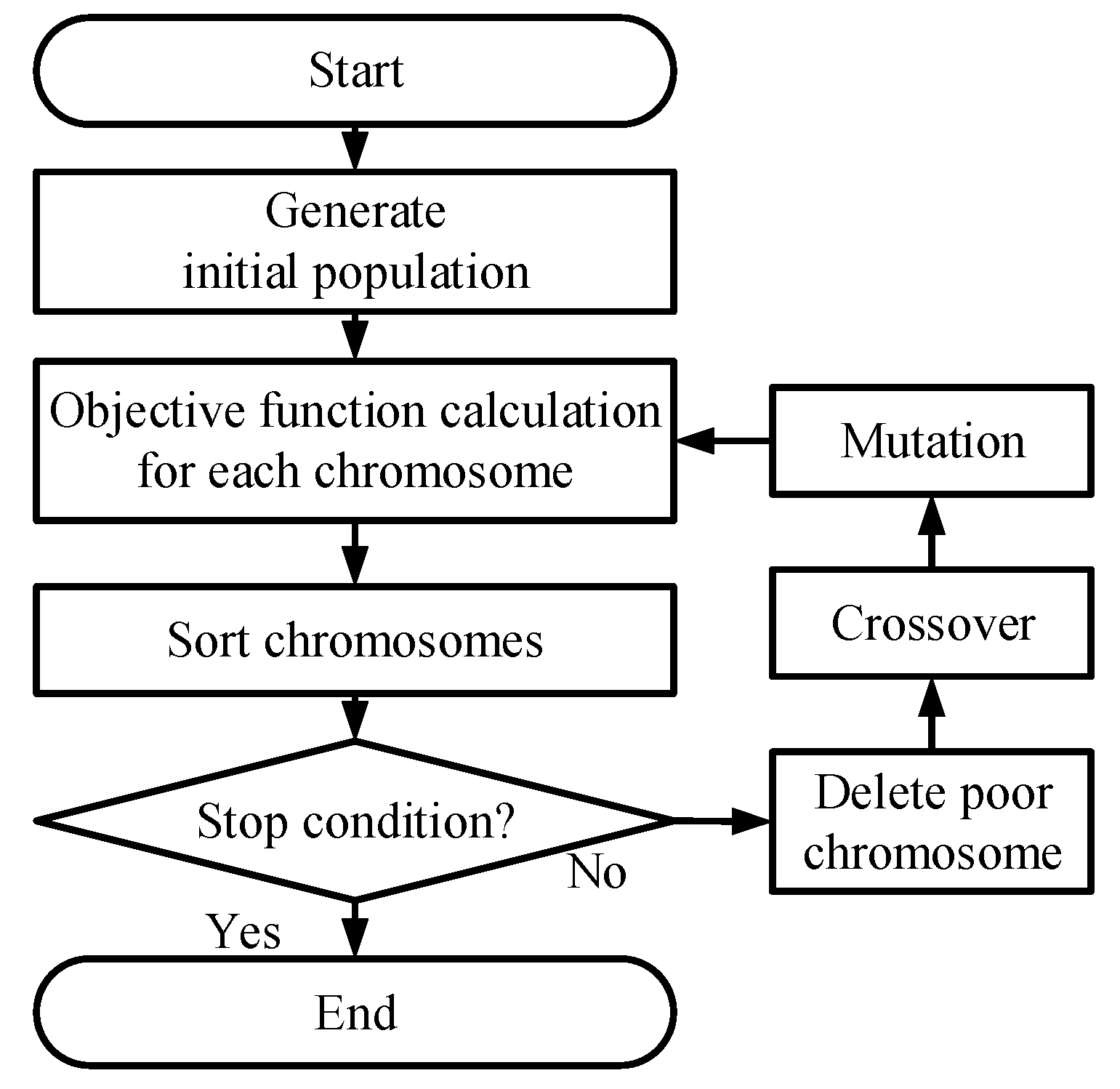
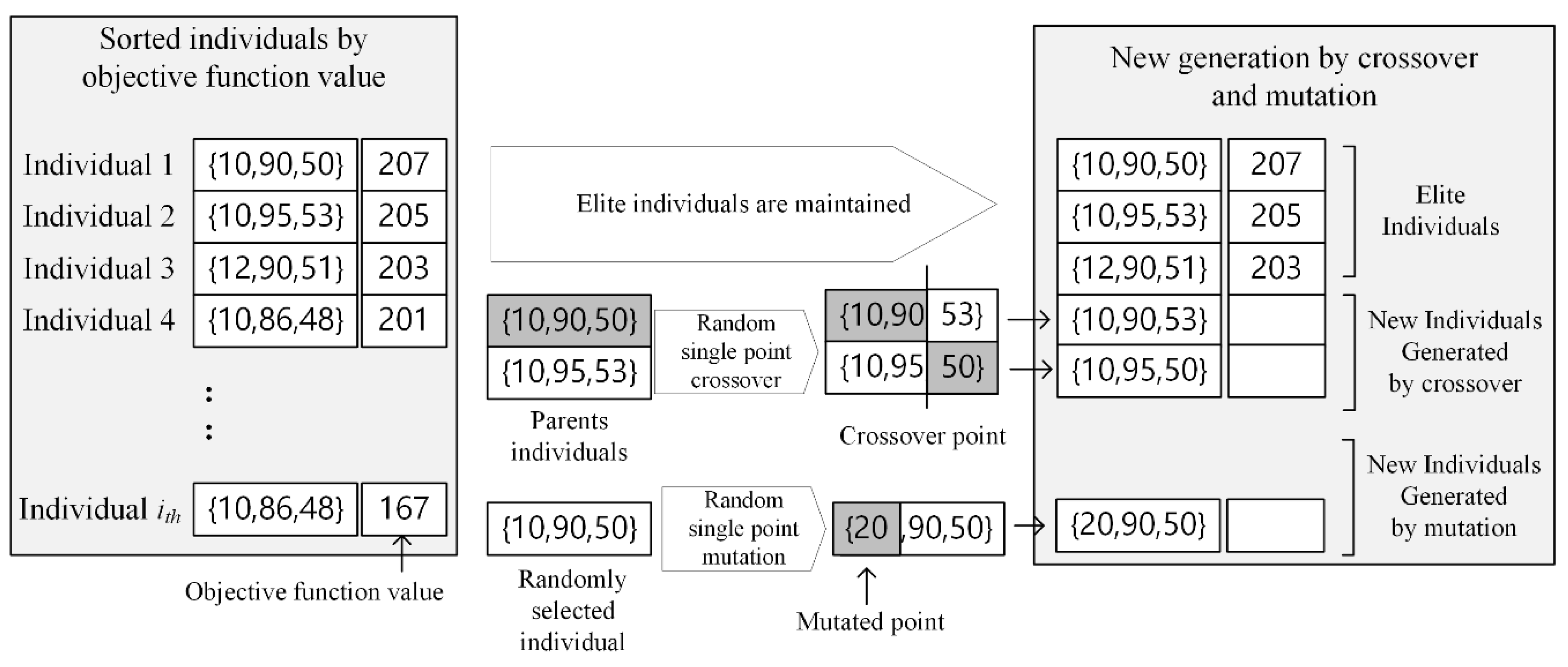
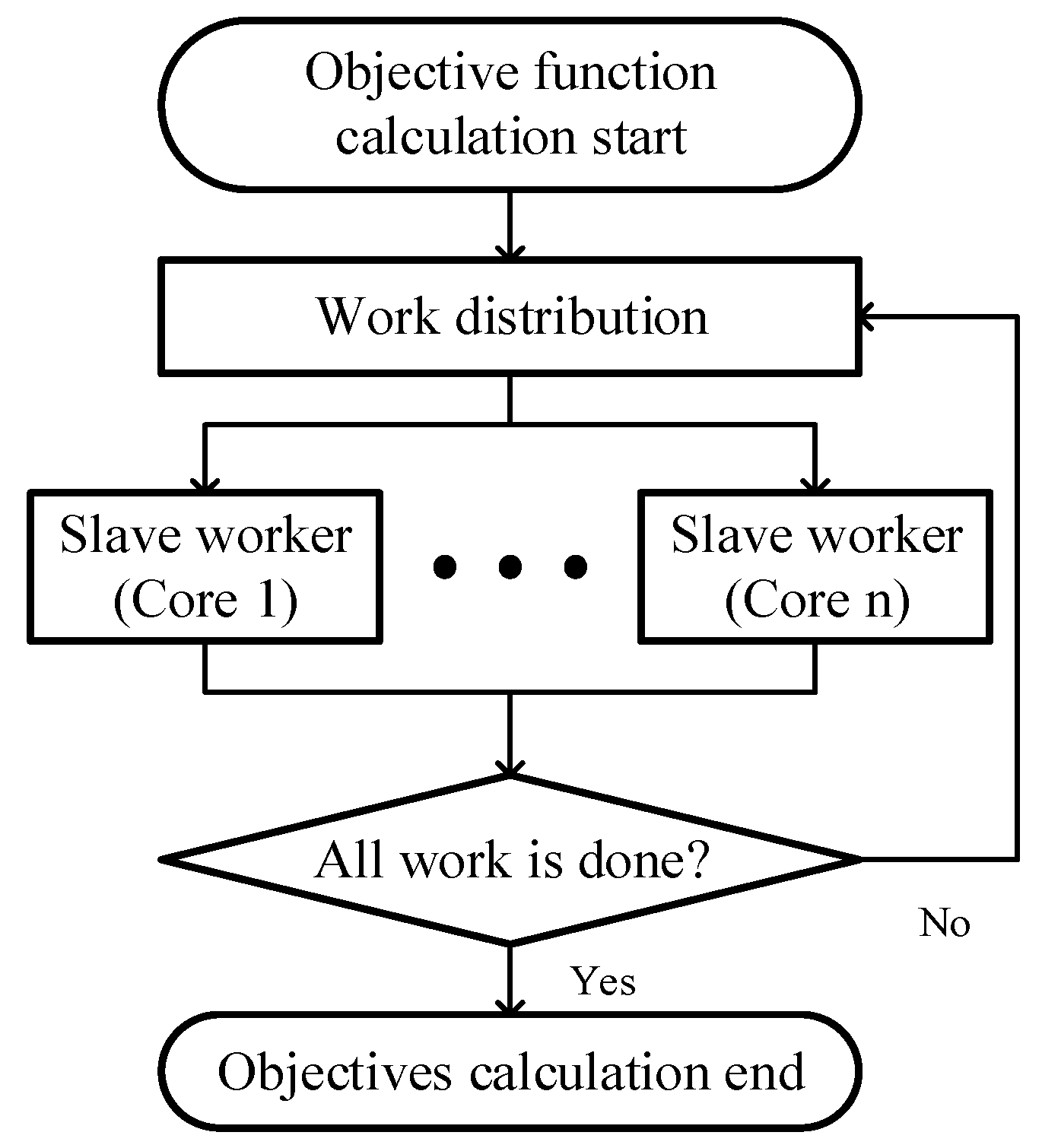
3.2. Parallel Genetic Algorithm
4. Case Studies
4.1. Genetic Algorithm Parameter Calibration Experiment
4.2. Effect of Simulation Duration on Objectives
4.3. Computation Time Comparison
4.4. Convergence Verification
4.5. Usability of SOC Range Optimization Considering Degradation Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kundur, P.S. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; ISBN 9780070359581. [Google Scholar]
- Greenwood, D.M.; Lim, K.Y.; Patsios, C.; Lyons, P.F.; Lim, Y.S.; Taylor, P.C. Frequency response services designed for energy storage. Appl. Energy 2017, 203, 115–127. [Google Scholar] [CrossRef]
- Li, X.; Yao, L.; Hui, D. Optimal control and management of a large-scale battery energy storage system to mitigate fluctuation and intermittence of renewable generations. J. Mod. Power Syst. Clean Energy 2016, 4, 593–603. [Google Scholar] [CrossRef]
- Knap, V.; Chaudhary, S.K.; Stroe, D.I.; Swierczynski, M.; Craciun, B.I.; Teodorescu, R. Sizing of an energy storage system for grid inertial response and primary frequency reserve. IEEE Trans. Power Syst. 2015, 31, 3447–3456. [Google Scholar] [CrossRef]
- Cho, S.-M.; Yun, S.-Y. Optimal Power Assignment of Energy Storage Systems to Improve the Energy Storage Efficiency for Frequency Regulation. Energies 2017, 10, 2092. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, Y.J.A. Optimal coordinated control of multiple battery energy storage systems for primary frequency regulation. IEEE Trans. Power Syst. 2019, 34, 555–565. [Google Scholar] [CrossRef]
- Miao, Y.; Hynan, P.; von Jouanne, A.; Yokochi, A. Current Li-ion battery technologies in electric vehicles and opportunities for advancements. Energies 2019, 12, 1074. [Google Scholar] [CrossRef]
- Divya, K.C.; Østergaard, J. Battery energy storage technology for power systems—An overview. Electr. Power Syst. Res. 2009, 79, 511–520. [Google Scholar] [CrossRef]
- Oudalov, A.; Buehler, T.; Chartouni, D. Utility Scale Applications of Energy Storage. In Proceedings of the IEEE Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008. [Google Scholar]
- Kwon, S.-J.; Lee, S.-E.; Lim, J.-H.; Choi, J.; Kim, J. Performance and Life Degradation Characteristics Analysis of NCM LIB for BESS. Electronics 2018, 7, 406. [Google Scholar] [CrossRef]
- Sarasketa-Zabala, E.; Gandiaga, I.; Martinez-Laserna, E.; Rodriguez-Martinez, L.M.; Villarreal, I. Cycle ageing analysis of a LiFePO4/graphite cell with dynamic model validations: Towards realistic lifetime predictions. J. Power Sources 2015, 275, 573–587. [Google Scholar] [CrossRef]
- Ecker, M.; Nieto, N.; Käbitz, S.; Schmalstieg, J.; Blanke, H.; Warnecke, A.; Sauer, D.U. Calendar and cycle life study of Li(NiMnCo)O2-based 18650 lithium-ion batteries. J. Power Sources 2014, 248, 839–851. [Google Scholar] [CrossRef]
- de Hoog, J.; Timmermans, J.M.; Ioan-Stroe, D.; Swierczynski, M.; Jaguemont, J.; Goutam, S.; Omar, N.; Van Mierlo, J.; Van Den Bossche, P. Combined cycling and calendar capacity fade modeling of a Nickel-Manganese-Cobalt Oxide Cell with real-life profile validation. Appl. Energy 2017, 200, 47–61. [Google Scholar] [CrossRef]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of Lithium-Ion Battery Degradation for Cell Life Assessment. IEEE Trans. Smart Grid 2018, 9, 1131–1140. [Google Scholar] [CrossRef]
- Mureddu, M.; Facchini, A.; Damiano, A. A Statistical Approach for Modeling the Aging Effects in Li-Ion Energy Storage Systems. IEEE Access 2018, 6, 42196–42206. [Google Scholar] [CrossRef]
- Shen, D.; Xu, T.; Wu, L.; Guan, Y. Research on Degradation Modeling and Life Prediction Method of Lithium-Ion Battery in Dynamic Environment. IEEE Access 2019, 7, 130638–130649. [Google Scholar] [CrossRef]
- Stroe, D.I.; Swierczynski, M.; Stan, A.I.; Teodorescu, R.; Andreasen, S.J. Accelerated lifetime testing methodology for lifetime estimation of lithium-ion batteries used in augmented wind power plants. IEEE Trans. Ind. Appl. 2014, 50, 4006–4017. [Google Scholar] [CrossRef]
- Stroe, D.I.; Swierczynski, M.; Stroe, A.I.; Laerke, R.; Kjaer, P.C.; Teodorescu, R. Degradation Behavior of Lithium-Ion Batteries Based on Lifetime Models and Field Measured Frequency Regulation Mission Profile. IEEE Trans. Ind. Appl. 2016, 52, 5009–5018. [Google Scholar] [CrossRef]
- Gatta, F.M.; Geri, A.; Lamedica, R.; Lauria, S.; Maccioni, M.; Palone, F.; Rebolini, M.; Ruvio, A. Application of a LiFePO4 Battery Energy Storage System to Primary Frequency Control: Simulations and Experimental Results. Energies 2016, 9, 887. [Google Scholar] [CrossRef]
- Stroe, D.I.; Knap, V.; Swierczynski, M.; Stroe, A.I.; Teodorescu, R. Operation of a grid-connected lithium-ion battery energy storage system for primary frequency regulation: A battery lifetime perspective. IEEE Trans. Ind. Appl. 2017, 53, 430–438. [Google Scholar] [CrossRef]
- Lian, B.; Sims, A.; Yu, D.; Wang, C.; Dunn, R.W. Optimizing LiFePO4 Battery Energy Storage Systems for Frequency Response in the UK System. IEEE Trans. Sustain. Energy 2017, 8, 385–394. [Google Scholar] [CrossRef]
- Cho, S.M.; Kim, J.S.; Kim, J.C. Optimal operation parameter estimation of energy storage for frequency regulation. Energies 2019, 12, 1782. [Google Scholar] [CrossRef]
- Lim, G.; Park, C.; Labios, R.; Yoon, Y. Development of the Control System for Fast-Responding Frequency Regulation in Power Systems using Large-Scale Energy Storage Systems. KEPCO J. Electr. Power Energy 2015, 1, 9–13. [Google Scholar] [CrossRef]
- Lim, G.-P.; Han, H.-G.; Chang, B.-H.; Yang, S.-K.; Yoon, Y.-B. Demonstration to Operate and Control Frequency Regulation of Power System by 4MW Energy Storage System. Trans. Korean Inst. Electr. Eng. 2014, 63, 169–177. [Google Scholar] [CrossRef]
- Omar, N.; Monem, M.A.; Firouz, Y.; Salminen, J.; Smekens, J.; Hegazy, O.; Gaulous, H.; Mulder, G.; Van den Bossche, P.; Coosemans, T.; et al. Lithium iron phosphate based battery—Assessment of the aging parameters and development of cycle life model. Appl. Energy 2014, 113, 1575–1585. [Google Scholar] [CrossRef]
- Weise, T. Global Optimization Algorithms–Theory and Application, Abrufdatum 2009. Available online: http://www.it-weise.de/projects/book.pdf (accessed on 1 December 2019).
- Lienig, J. A parallel genetic algorithm for performance-driven VLSI routing. IEEE Trans. Evol. Comput. 1997, 1, 29–39. [Google Scholar] [CrossRef]
- Alba, E.; Troya, J.M. A survey of parallel distributed genetic algorithms. Complexity 1999, 4, 31–52. [Google Scholar] [CrossRef]
- Srinivas, C.; Reddy, B.R.; Ramji, K.; Naveen, R. Sensitivity Analysis to Determine the Parameters of Genetic Algorithm for Machine Layout. Procedia Mater. Sci. 2014, 6, 866–876. [Google Scholar] [CrossRef]


| frated | Sn | Smax | Smin | r | K | Pr | Erated | η |
|---|---|---|---|---|---|---|---|---|
| 60 Hz | 65 | 90 | 10 | 0.10 | 0.33 | 12 MW | 4.5 MWh | 0.97 |
| Model | α | β | α2 | β2 | γ |
|---|---|---|---|---|---|
| 1 | 3.4262 × 10−8 | 0.0092 | 2.205 × 10−4 | −0.0389 | 1.420 |
| 2 | 4.1115 × 10−8 | 0.0092 | 2.205 × 10−4 | −0.0389 | 1.420 |
| 3 | 3.4262 × 10−8 | 0.0092 | 2.205 × 10−4 | −0.0389 | 1.492 |
| Procedure of MSPGA | Processor | |
|---|---|---|
| 1 | Begin | |
| 2 | Initialize population of individuals {like (16)} randomly | Master |
| 3 | Initialize MATLAB parallel pool {parpool} | Master |
| 4 | While (Ending criterion flag is not true) | Master |
| 5 | For i = 1: number of individuals | Master |
| 6 | Master core assigns the workload to slave core | Slaves |
| 7 | Each slave core calculates fitness | Slaves |
| 8 | { F(i) = parfeval(@fitness_fn, individual) } | |
| 9 | After completing the current calculation, the slave requests for the next workload | Slaves |
| 10 | End | |
| 11 | Sort individual by fitness value | Master |
| 12 | Check Ending criterion | Master |
| 13 | Nelite individuals are maintained for elitism | Master |
| 14 | Nco individuals newly generated by crossover operation | Master |
| 15 | Nmu individuals newly generated by mutation operation | Master |
| 16 | End | |
| 17 | End |
| Parameters and Results | Case 1-1 | Case 1-2 | Case 1-3 | Case 1-4 |
|---|---|---|---|---|
| Population size (Ntotal) | 50 | 100 | 150 | 200 |
| Nelite | 30% of Ntotal | |||
| Nco | 60% of Ntotal | |||
| Nmu | 10% of Ntotal | |||
| Average calculation time (s) | 180.09 | 264.05 | 387.16 | 483.86 |
| Result 1 (MWh) | 197.96 | 198.27 | 198.27 | 198.27 |
| Result 2 (MWh) | 197.96 | 198.27 | 198.27 | 198.27 |
| Result 3 (MWh) | 197.89 | 198.27 | 198.27 | 198.27 |
| Parameters and Results | Case 2-1 | Case 2-2 | Case 2-3 | Case 2-4 |
|---|---|---|---|---|
| Population size (Ntotal) | 100 | 100 | 100 | 100 |
| Nelite | 10% of Ntotal | 30% of Ntotal | 50% of Ntotal | 70% of Ntotal |
| Nco | 80% of Ntotal | 60% of Ntotal | 40% of Ntotal | 20% of Ntotal |
| Nmu | 10% of Ntotal | 10% of Ntotal | 10% of Ntotal | 10% of Ntotal |
| Average calculation time (s) | 300.28 | 264.05 | 201.84 | 147.01 |
| Result 1 (MWh) | 197.94 | 198.27 | 198.27 | 198.27 |
| Result 2 (MWh) | 198.15 | 198.27 | 198.15 | 197.89 |
| Result 3 (MWh) | 197.90 | 198.27 | 197.89 | 198.08 |
| Parameters | Parameter 1 | Parameter 2 | Parameter 3 |
|---|---|---|---|
| Smax (%) | 80 | 80 | 90 |
| Smin (%) | 30 | 30 | 40 |
| Sn (%) | 60 | 70 | 65 |
| D | Parameter 1 | Parameter 2 | Parameter 3 | |||
|---|---|---|---|---|---|---|
| EObj (MWh) | Life (year) | EObj (MWh) | Life (year) | EObj (MWh) | Life (year) | |
| 1 | 470 | 0.29 | 517 | 0.32 | 502 | 0.31 |
| 2 | 1373 | 0.85 | 1402 | 0.88 | 1404 | 0.87 |
| 5 | 5127 | 3.19 | 5017 | 3.16 | 5136 | 3.20 |
| 7 | 8155 | 5.09 | 7894 | 4.97 | 8111 | 5.06 |
| 10 | 13,214 | 8.27 | 12,618 | 7.98 | 13,053 | 8.17 |
| Cases | Methods | Smin (%) | Smax (%) | Sn (%) | Eobj (MWh) |
|---|---|---|---|---|---|
| Case 1 12 MW/4.5 MWh | Method in Reference [21] | 39 | 100 | 75 | 30,316 |
| Proposed MSPGA | 20 | 100 | 43 | 34,178 | |
| Case 2 12 MW/6 MWh | Method in Reference [21] | 33 | 99 | 66 | 34,778 |
| Proposed MSPGA | 16 | 85 | 34 | 39,305 | |
| Case 3 12 MW/9 MWh | Method in Reference [21] | 21 | 95 | 54 | 41,587 |
| Proposed MSPGA | 4 | 90 | 26 | 45,643 |
| Method | Cases | Time (h) | Smin (%) | Smax (%) | Sn (%) | EObj. (MWh) | Life (Year) |
|---|---|---|---|---|---|---|---|
| MSPGA | 1 | 22.0 | 20 | 96 | 43 | 34,178.3 | 21.7 |
| 2 | 18.3 | 20 | 100 | 43 | 34,178.3 | 21.7 | |
| 3 | 17.2 | 20 | 100 | 43 | 34,178.3 | 21.7 | |
| Average | 19.2 | - | - | - | 34,178.3 | 21.7 | |
| GA | 1 | 61.0 | 20 | 99 | 43 | 34,178.3 | 21.7 |
| 2 | 61.5 | 20 | 94 | 43 | 34,178.3 | 21.7 | |
| 3 | 65.3 | 20 | 82 | 43 | 34,178.3 | 21.7 | |
| Average | 62.6 | - | - | - | 34,178.3 | 21.7 |
| ESS Models | ESS1 | ESS2 | ESS3 |
|---|---|---|---|
| Degradation model | Model 1 | Model 2 | Model 3 |
| Pr | 12 MW | 12 MW | 12 MW |
| Erated | 4.5 MWh | 4.5 MWh | 4.5 MWh |
| Cases | ESS1 | ESS2 | ESS3 | Sum | |
|---|---|---|---|---|---|
| Case 1 | Smin, Smax, Sn | {20, 88, 43} | {16, 89, 40} | {22, 91, 43} | |
| EObj | 34,178 | 29,496 | 34,178 | 97,852 | |
| Case 2 | Smin, Smax, Sn | {20, 88, 43} | |||
| EObj | 34,178 | 29,432 | 34,169 | 97,779 | |
| Case 3 | Smin, Smax, Sn | {16, 89, 40} | |||
| EObj | 34,097 | 29,496 | 34,084 | 97,676 | |
| Case 4 | Smin, Smax, Sn | {22, 91, 43} | |||
| EObj | 34,177 | 29,428 | 34,178 | 97,783 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, S.-M.; Kim, J.-C.; Yun, S.-Y. Optimum State-of-Charge Operating Range for Frequency Regulation of Energy Storage Systems Using a Master–Slave Parallel Genetic Algorithm. Electronics 2020, 9, 1298. https://doi.org/10.3390/electronics9081298
Cho S-M, Kim J-C, Yun S-Y. Optimum State-of-Charge Operating Range for Frequency Regulation of Energy Storage Systems Using a Master–Slave Parallel Genetic Algorithm. Electronics. 2020; 9(8):1298. https://doi.org/10.3390/electronics9081298
Chicago/Turabian StyleCho, Sung-Min, Jae-Chul Kim, and Sang-Yun Yun. 2020. "Optimum State-of-Charge Operating Range for Frequency Regulation of Energy Storage Systems Using a Master–Slave Parallel Genetic Algorithm" Electronics 9, no. 8: 1298. https://doi.org/10.3390/electronics9081298
APA StyleCho, S.-M., Kim, J.-C., & Yun, S.-Y. (2020). Optimum State-of-Charge Operating Range for Frequency Regulation of Energy Storage Systems Using a Master–Slave Parallel Genetic Algorithm. Electronics, 9(8), 1298. https://doi.org/10.3390/electronics9081298






