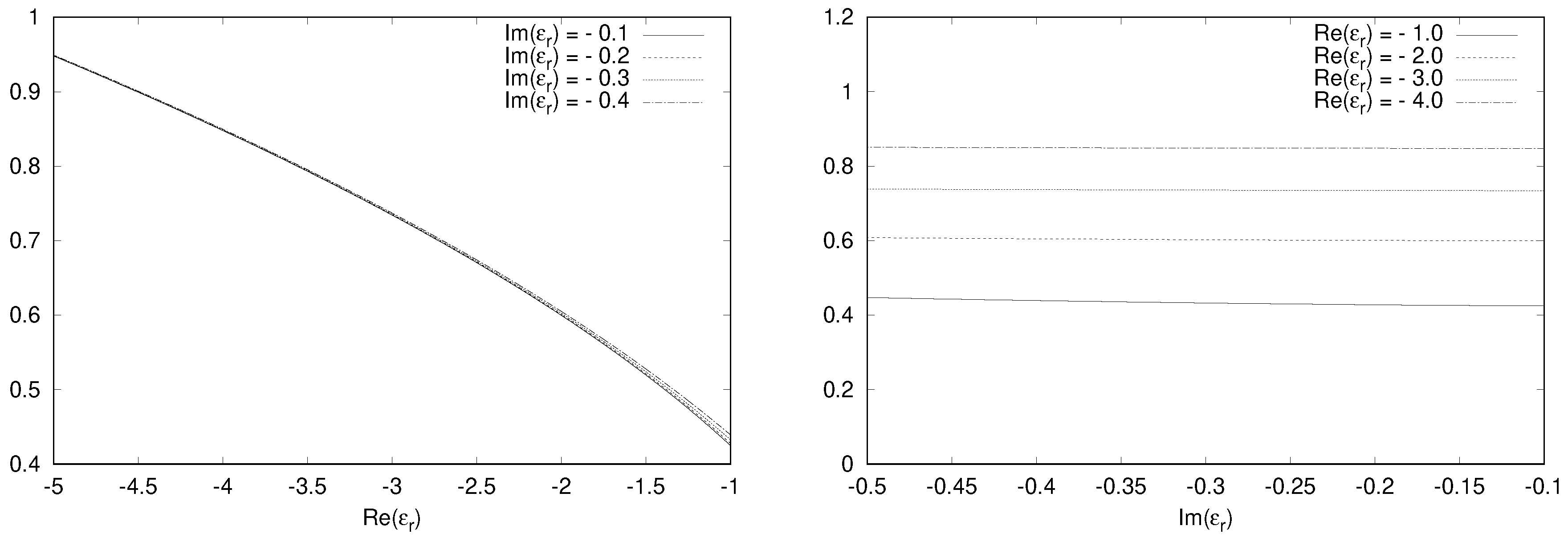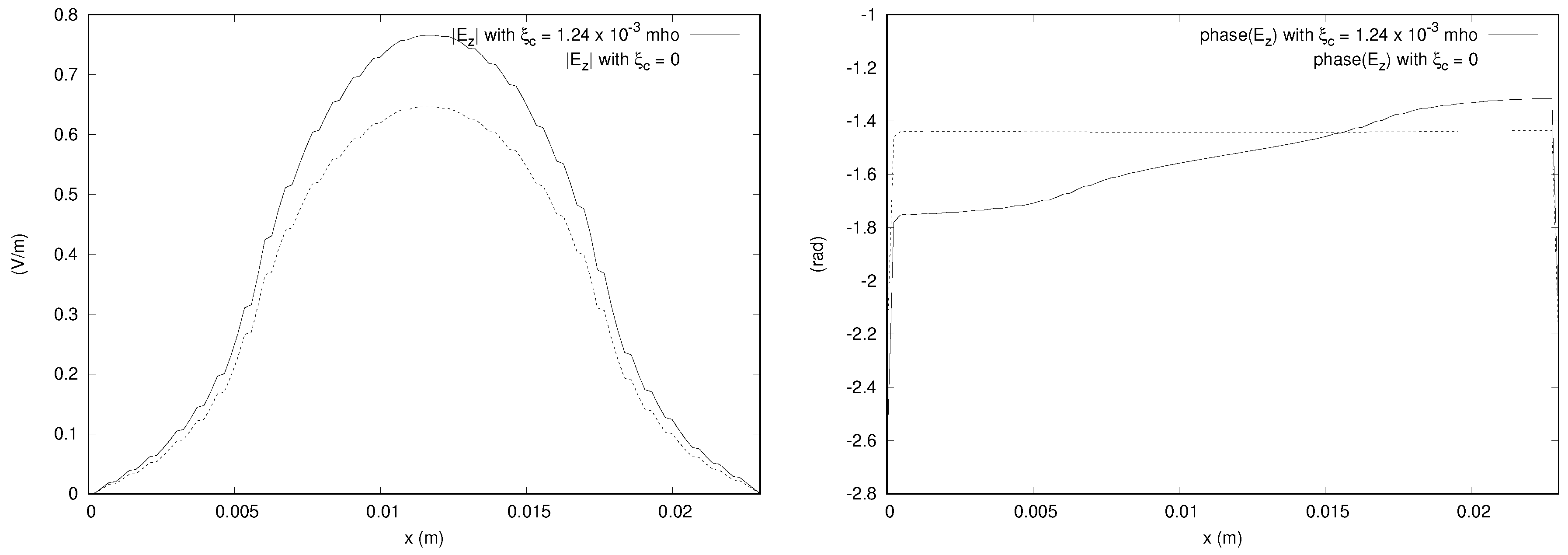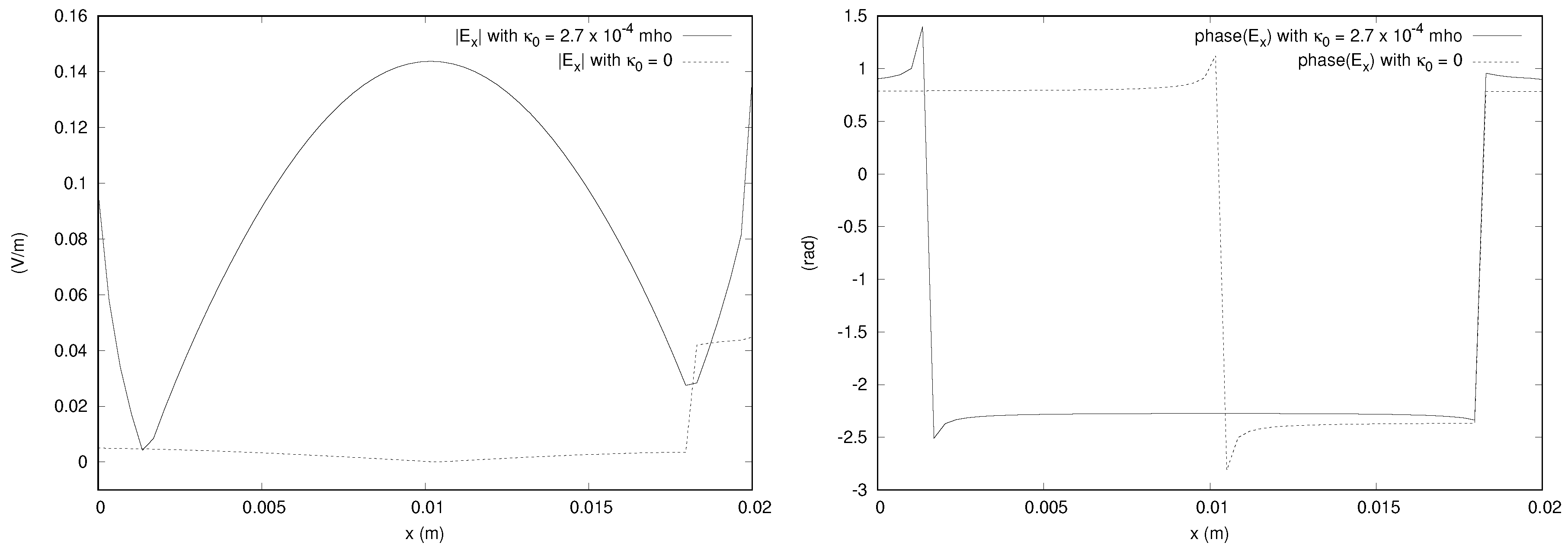Three-Dimensional Time-Harmonic Electromagnetic Scattering Problems from Bianisotropic Materials and Metamaterials: Reference Solutions Provided by Converging Finite Element Approximations

Abstract

A recently developed theory is applied to deduce the well posedness and the finite element approximability of time-harmonic electromagnetic scattering problems involving bianisotropic media in free-space or inside waveguides. In particular, three example problems are considered of which one deals with scattering from plasmonic gratings that exhibit bianisotropy while the other two deal with bianisotropic obstacles inside waveguides. The hypotheses that guarantee the reliability of the numerical results are verified, and the ranges of the constitutive parameters of the media involved for which the finite element solutions are guaranteed to be reliable are deduced. It is shown that, within these ranges, there can be significant bianisotropic effects for the practical media considered as examples. The ensured reliability of the obtained results can make them useful as benchmarks for other numerical approaches. To the best of our knowledge, no other tool can guarantee reliable solutions.

1. Introduction

Bianisotropic media have important applications in numerous practical problems ranging from the microwave to photonic frequency bands [1,2,3,4]. The electromagnetic problems involving such media admit analytical solutions only in very specialized cases, and numerical simulators are necessary to solve the vast majority of them.

In this context, the reliability of the numerical solvers is of utmost importance, and results guaranteeing the well posedness of the problems and the convergence of the numerical solutions are crucial. Some of the previous papers that addressed this issue were limited in their applications [5,6,7,8]. For instance, the work in [5] made strong assumptions on the losses to guarantee the reliability of the results. The results in [6] were derived for two-dimensional problems involving axially moving cylinders, whereas [7] dealt only with evolution problems inside cavities. As for [8], the constitutive parameters were taken to be smooth, which did not allow applications to radiation and scattering problems.

A considerable generalization of the conditions that allow ensuring the well posedness of the problems and the convergence of the finite element solutions was recently achieved in [9]. A set of non-restrictive hypotheses was shown to guarantee such results for three-dimensional time-harmonic problems involving bianisotropic media. The authors applied the theory to rotating axisymmetric objects, where the effect of motion induced bianisotropy. However, the theoretical results derived were applicable to a much wider range of bianisotropic materials and metamaterials.

In this paper, we exploit the recently developed theory to obtain novel results. We consider examples of practical problems discussed in the open literature for which, to the best of our knowledge, none of the previous theories were able to guarantee the reliability of the numerical results. In particular, we study the electromagnetic scattering from plasmonic gratings, which exhibits bianisotropy [1], and from bianisotropic obstacles in waveguides [10,11]. We demonstrate the application of the theory in [9] to derive the conditions on the constitutive parameters of these problems that guarantee the reliability of the results. The numerical solutions of the problems are calculated under such conditions, which, owing to the reliability assured by the theory, can be used as references for other numerical solvers. As far as we are aware, no other tool is available that allows obtaining benchmark solutions for these problems.

The paper is organized as follows. In Section 2, the problem is defined and the theory is summarized to guide the reader in its application. Section 3 contains the main results of the paper, where the application of the theory is demonstrated and reliable solutions are obtained. Section 4 provides the conclusions.

2. Mathematical Description of the Problem

In this paper, we are interested in electromagnetic problems that involve bianisotropic media under time-harmonic excitation, which were studied in [9]. While the full details of the problem definition and results are available in the reference, here we provide a summary of the main points in order to ease the understanding of the present developments.

The problem is formulated in an open, bounded, and connected domain $\Omega \in {\mathbb{R}}^3$, which has a Lipschitz continuous stationary boundary denoted by $\Gamma$. To take into account electromagnetic problems involving inhomogeneous materials, we assume that $\Omega$ can be decomposed into m subdomains (see HD3 of [9]) denoted ${\Omega }_i$, $i\in I=\{1,\dots ,m\}$.

The time-harmonic sources imply that all the resulting fields are in turn time-harmonic and the assumed factor $e^{j\omega t}$ is ubiquitous and is suppressed. The media involved in the problem are linear and time-invariant and are considered to satisfy the following constitutive relations:

$$\left\{\begin{array}{ll}\mathbf{D}=(1/c_0)P\mathbf{E}+L\mathbf{B}& \mathrm{in}\Omega ,\\ \mathbf{H}=M\mathbf{E}+c_{0}Q\mathbf{B}& \mathrm{in}\Omega .\end{array}\right.$$

(1)

In the above equation, $\mathbf{E}$, $\mathbf{B}$, $\mathbf{D}$, and $\mathbf{H}$ are complex valued functions defined in $\Omega$ and represent, respectively, the electric field, magnetic induction, electric displacement, and magnetic field, while $c_0$ is the speed of light in a vacuum. The space where we will seek $\mathbf{E}$ and $\mathbf{H}$ is [12] (p. 82; see also p. 69):

$$U=H_{L^2,\Gamma }(\mathrm{curl},\Omega )=\{\mathbf{v}\in H(\mathrm{curl},\Omega )|\mathbf{v}\times \mathbf{n}\in L_t^2(\Gamma )\},$$

(2)

where [12] (p. 48):

$$L_t^2(\Gamma )=\{\mathbf{v}\in {\left(L^2(\Gamma )\right)}^3|\mathbf{v}·\mathbf{n}=0\mathrm{almost} \mathrm{everywhere} \mathrm{on} \Gamma \}.$$

(3)

Based on Maxwell’s equations, boundary conditions, and constitutive relations, the following variational formulation of the problem can be deduced [5]: given $\omega >0$, the electric and magnetic current densities prescribed by the sources ${\mathbf{J}}_e,{\mathbf{J}}_m\in {\left(L^2(\Omega )\right)}^3$ and the known term ${\mathbf{f}}_R\in L_t^2(\Gamma )$, involved in admittance boundary condition, find $\mathbf{E}\in U$ such that:

$$a(\mathbf{E},\mathbf{v})=l\left(\mathbf{v}\right)\forall \mathbf{v}\in U,$$

(4)

where:

$$\begin{array}{cc}{\displaystyle a(\mathbf{u},\mathbf{v})=c_0{\left(Q\mathrm{curl}\mathbf{u},\mathrm{curl}\mathbf{v}\right)}_{0,\Omega }-\frac{{\omega }^2}{c_0}{\left(P\mathbf{u},\mathbf{v}\right)}_{0,\Omega }-j\omega {\left(M\mathbf{u},\mathrm{curl}\mathbf{v}\right)}_{0,\Omega }}& \hfill \\ -j\omega {\left(L\mathrm{curl}\mathbf{u},\mathbf{v}\right)}_{0,\Omega }+j\omega {\left(Y(\mathbf{n}\times \mathbf{u}\times \mathbf{n}),\mathbf{n}\times \mathbf{v}\times \mathbf{n}\right)}_{0,\Gamma },\hfill \end{array}$$

(5)

and:

$$l\left(\mathbf{v}\right)=-j\omega {\left({\mathbf{J}}_e,\mathbf{v}\right)}_{0,\Omega }-c_0{\left(Q{\mathbf{J}}_m,\mathrm{curl}\mathbf{v}\right)}_{0,\Omega }+j\omega {\left(L{\mathbf{J}}_m,\mathbf{v}\right)}_{0,\Omega }-j\omega {\left({\mathbf{f}}_R,\mathbf{n}\times \mathbf{v}\times \mathbf{n}\right)}_{0,\Gamma }.$$

(6)

In [9], we derived a set of sufficient conditions that guarantee the well posedness and finite element approximability of the problem. The developed theory was applied to problems involving rotating axisymmetric objects. In this paper, we apply the theory to a wider range of problems involving bianisotropic materials and metamaterials demonstrating the generality of the developments and obtaining interesting new solutions [1,10,11].

We recall important definitions and hypotheses to fix the notations that are required for proceeding with the application of the theory. The subscript $i\in I$ identifying the subdomain ${\Omega }_i$ may belong to two subsets, $I_a$ and $I_b$ of I, according to the properties of the media involved: $i\in I_a$ when they are anisotropic (that is, with $L=M=0$) and $i\in I_b$ when they are bianisotropic. Any matrix A with complex entries can be split into $A=A_s-j{A}_{ss}$ with $A_s=\frac{A+A^{*}}{2}$ and $A_{ss}=\frac{A^{*}-A}{2j}$. Some of the hypotheses will be stated using the alternative form of constitutive relations defined by:

$$\left\{\begin{array}{ll}\mathbf{E}=\kappa \mathbf{D}+\chi \mathbf{B}& \mathrm{in}\Omega ,\\ \mathbf{H}=\gamma \mathbf{D}+\nu \mathbf{B}& \mathrm{in}\Omega .\end{array}\right.$$

(7)

where the constitutive matrices are given by [13] $\kappa =c_0{P}^{-1}$, $\chi =-c_0{P}^{-1}L$, $\gamma =c_{0}M{P}^{-1}$, and $\nu =c_0(Q-M{P}^{-1}L)$.

As mentioned in Section 6 of [9], most of the hypotheses are readily satisfied for important practical problems. That leaves us with seven critical hypotheses (HM9–HM15 in [9]) on the media involved in the problem that need to be verified. Among them, HM9–HM12 of [9] are stated in terms of the constitutive relations involving $\kappa$, $\nu$, $\chi$, and $\gamma$ and are restated here as H1–H4.

Hypothesis 1 (H1).

$\exists \exists C_{\kappa ,d}>0,C_{\nu ,d}>0:|determinant\left(\kappa \right)|\ge C_{\kappa ,d},\left|determinant\left(\nu \right)\right|\ge C_{\nu ,d},\forall \mathbf{x}\in {\overline{\Omega }}_i,\forall i\in I$,

Hypothesis 2 (H2).

${\mathbf{l}}_{1,3}^T{\kappa }^{-1}{\mathbf{l}}_{1,3}\ne 0,{\mathbf{l}}_{1,3}^T{\nu }^{-1}{\mathbf{l}}_{1,3}\ne 0\forall {\mathbf{l}}_{1,3}\in {\mathbb{R}}^3,{\mathbf{l}}_{1,3}\ne 0,\forall \mathbf{x}\in {\overline{\Omega }}_i,\forall i\in I_a$,

Hypothesis 3 (H3).

$\exists \exists C_{\kappa ,r}>0,C_{\nu ,r}>0:|{\mathbf{l}}_{1,3,n}^T{\kappa }^{-1}{\mathbf{l}}_{1,3,n}|\ge C_{\kappa ,r},|{\mathbf{l}}_{1,3,n}^T{\nu }^{-1}{\mathbf{l}}_{1,3,n}|\ge C_{\nu ,r}\forall {\mathbf{l}}_{1,3,n}\in {\mathbb{R}}^3:{\Vert {\mathbf{l}}_{1,3,n}\Vert }_2=1,\forall \mathbf{x}\in {\overline{\Omega }}_i,\forall i\in I_b$,

Hypothesis 4 (H4).

$\exists \exists C_{\kappa ,s}>0,C_{\nu ,s}>0$:

$$\left(\sum _{i,j=1}^3\left|{\kappa }_{ij}\right|\right)-{\displaystyle \underset{i=1,2,3}{min}}\left|{\kappa }_{ii}\right|\le C_{\kappa ,s}\forall \mathbf{x}\in {\overline{\Omega }}_k,\forall k\in I_b,$$

(8)

$$\left(\sum _{i,j=1}^3\left|{\nu }_{ij}\right|\right)-{\displaystyle \underset{i=1,2,3}{min}}\left|{\nu }_{ii}\right|\le C_{\nu ,s}\forall \mathbf{x}\in {\overline{\Omega }}_k,\forall k\in I_b,$$

(9)

and κ, χ, γ, and ν satisfy:

$$\frac{4\left(\left({\sum }_{i,j=1}^3\left|{\gamma }_{ij}\right|\right)-{min}_{i=1,2,3}\left|{\gamma }_{ii}\right|\right)\left(\left({\sum }_{i,j=1}^3\left|{\chi }_{ij}\right|\right)-{min}_{i=1,2,3}\left|{\chi }_{ii}\right|\right)}{\left(-C_{\kappa ,s}+\sqrt{C_{\kappa ,s}^2+4C_{\kappa ,d}{C}_{\kappa ,r}}\right)\left(-C_{\nu ,s}+\sqrt{C_{\nu ,s}^2+4C_{\nu ,d}{C}_{\nu ,r}}\right)}<1$$

(10)

$\forall \mathbf{x}\in {\overline{\Omega }}_k,\forall k\in I_b$.

Among the above hypotheses, H2 needs to hold only in the subdomains ${\Omega }_i$, $i\in I_a$. H1 can be verified separately in any subdomain ${\Omega }_i$, $i\in I$, whereas H3 and H4 are to be defined and verified only locally on any subdomain ${\Omega }_i$, $i\in I_b$ (see Remark 1 of [9]).

The local continuity of the tensors P, Q, L, and M can be assumed in most practical problems, which allows the definition of the following constants.

• $\exists C_L>0$: ${|(L\mathrm{curl}\mathbf{u},\mathbf{v})}_{0,\Omega }|\le C_L{\Vert \mathrm{curl}\mathbf{u}\Vert }_{0,\Omega }{\Vert \mathbf{v}\Vert }_{0,\Omega }$ for all $\mathbf{u}\in H(\mathrm{curl},\Omega )$ and $\mathbf{v}\in {\left(L^2(\Omega )\right)}^3$,
• $\exists C_M>0$: ${|(M\mathbf{u},\mathrm{curl}\mathbf{v})}_{0,\Omega }|\le C_M{\Vert \mathbf{u}\Vert }_{0,\Omega }{\Vert \mathrm{curl}\mathbf{v}\Vert }_{0,\Omega }$ for all $\mathbf{u}\in {\left(L^2(\Omega )\right)}^3$ and $\mathbf{v}\in H(\mathrm{curl},\Omega )$.

Finally, HM13–HM15 of [9] are reported here as H5–H7.

Hypothesis 5 (H5).

We can find $C_{PS}>0$ such that ${|(P\mathbf{u},\mathbf{u})}_{0,\Omega }|\ge C_{PS}{\Vert \mathbf{u}\Vert }_{0,\Omega }^2$ for all $\mathbf{u}\in {\left(L^2(\Omega )\right)}^3$.

Hypothesis 6 (H6).

We can find $C_{QS}>0$ such that ${|(Q\mathrm{curl}\mathbf{u},\mathrm{curl}\mathbf{u})}_{0,\Omega }|\ge C_{QS}{\Vert \mathrm{curl}\mathbf{u}\Vert }_{0,\Omega }^2$ for all $\mathbf{u}\in H(\mathrm{curl},\Omega )$.

Hypothesis 7 (H7).

$C_{PS}$, $C_{QS}$, $C_L$, and$C_M$(i.e., all media involved) are such that$C_{QS}-\frac{C_L{C}_M}{C_{PS}}>0$.

We refer to Section 6 of [9] for some hints about the calculation of the constants involved in the above conditions. In particular, we recall here Lemma 1 of [9] for easy reference, which is helpful in finding the constant involved in H5.

Lemma 1.

Suppose that$P_{ss}$is uniformly positive definite in${\Omega }_{el}\subset \Omega$, that is$\exists C_1>0$such that:

$${\int }_{{\Omega }_{el}}{\mathbf{u}}^{*}{P}_{ss}\mathbf{u}\ge C_1{\int }_{\Omega el}{\left|\mathbf{u}\right|}^2=C_1{\left|\right|\mathbf{u}\left|\right|}_{0,{\Omega }_{el}}^2\forall \mathbf{u}\in {\left(L^2(\Omega )\right)}^3.$$

(11)

whenever${\Omega }_{el}=\Omega$, we can simply define$C_{PS}=C_1$.

Whenever${\Omega }_{el}$is not the whole Ω, suppose that, in the complementary region,$P_s$is uniformly positive or negative definite, that is$\exists C_5>0$such that:

$$\left|{\int }_{\Omega \backslash {\Omega }_{el}}{\mathbf{u}}^{*}{P}_s\mathbf{u}\right|\ge C_5{\left|\right|\mathbf{u}\left|\right|}_{0,\Omega \backslash {\Omega }_{el}}^2.$$

(12)

whenever${\Omega }_{el}=\varnothing$, we simply have$C_{PS}=C_5$, and we can set:

$$C_{PS}={\displaystyle \underset{i\in I}{min}}{\displaystyle \underset{\mathbf{x}\in {\Omega }_i}{inf}}{\lambda }_{min}\left(P_s\right),$$

(13)

where${\lambda }_{min}$denotes the minimum of the magnitudes of the eigenvalues of the Hermitian symmetric matrix$P_s$.

Finally, whenever${\Omega }_{el}$is neither the empty set nor the whole domain, under assumptions HM2 and HM3 of [9], condition H5 is satisfied with$C_{PS}$given by:

$$C_{PS}=\frac{1}{\sqrt{2}}min\left(\sqrt{(1-\alpha )}{C}_5,\sqrt{C_1^2+(1-\frac{1}{\alpha })C_3^2}\right),$$

(14)

where$C_3>0$is defined by:

$$\left|{\int }_{{\Omega }_{el}}{\mathbf{u}}^{*}{P}_s\mathbf{u}\right|\le C_3{\Vert \mathbf{u}\Vert }_{0,{\Omega }_{el}}^2$$

(15)

and α is such that$1>\alpha >\frac{C_3^2}{C_1^2+C_3^2}>0$.

Analogously, by replacing P with Q in Equations (11), (12), and (15), we define, respectively, ${\Omega }_{ml}$ and the constants $C_2>0$, $C_4>0$, and $C_6>0$ and deduce that condition H6 is satisfied if we set:

$$C_{QS}={\displaystyle \underset{i\in I}{min}}{\displaystyle \underset{\mathbf{x}\in {\Omega }_i}{inf}}{\lambda }_{min}\left(Q_s\right),$$

(16)

whenever ${\Omega }_{ml}=\varnothing$, $C_{QS}=C_2$ whenever ${\Omega }_{ml}=\Omega$, or:

$$C_{QS}=\frac{1}{\sqrt{2}}min\left(\sqrt{(1-\alpha )}{C}_6,\sqrt{C_2^2+(1-\frac{1}{\alpha })C_4^2}\right),$$

(17)

$\alpha$ being such that $1>\alpha >\frac{C_4^2}{C_2^2+C_4^2}>0$, when ${\Omega }_{ml}\ne \Omega$ and ${\Omega }_{ml}\ne \varnothing$.

With respect to the H4, if we define:

$$C_{\chi ,s}={\displaystyle \underset{i\in I_b}{max}}{\displaystyle \underset{\mathbf{x}\in {\Omega }_i}{sup}}\left((\sum _{i,j=1}^3|{\chi }_{ij}|)-{\min }_{i=1,2,3}\left|{\chi }_{ii}\right|\right),$$

(18)

$$C_{\gamma ,s}=\underset{i\in I_b}{max}\underset{\mathbf{x}\in {\Omega }_i}{sup}\left((\sum _{i,j=1}^3|{\gamma }_{ij}|)-{\min }_{i=1,2,3}\left|{\gamma }_{ii}\right|\right),$$

(19)

the sufficient condition guaranteeing the validity of the inequality in the hypothesis can be expressed as:

$$K_u=\frac{4C_{\chi ,s}{C}_{\gamma ,s}}{\left(-C_{\kappa ,s}+\sqrt{C_{\kappa ,s}^2+4C_{\kappa ,d}{C}_{\kappa ,r}}\right)\left(-C_{\nu ,s}+\sqrt{C_{\nu ,s}^2+4C_{\nu ,d}{C}_{\nu ,r}}\right)}<1.$$

(20)

3. Results and Discussion

In this section, we apply the theory developed in [9] to several classes of problems that could not be managed with the previous theories [5,6,7,8]. The conditions are established on the constitutive parameters of such problems, under which the well posedness and finite element approximability can be guaranteed. In particular, we apply the theory and obtain solutions for three examples of bianisotropic media, which are found in the open literature. The first one is that introduced in [1] where the authors considered plasmonic gratings, which are represented by an equivalent bianisotropic media. In this case, we study the scattering from a slab of the equivalent medium, which is placed in empty space, in accordance with the setup considered by the authors [1]. Next, the media introduced in [10,11] are analyzed. The authors there considered the scattering from the bianisotropic obstacles placed inside hollow waveguides. Although we stick to the original configurations proposed by the authors, our tools can be used to analyze other problems involving these media.

Under the conditions that guarantee that hypotheses H1–H7 are satisfied, the numerical solutions of these problems are computed. They can be used as reference solutions for other approaches and simulators because, on the one hand, for each problem, our theory guarantees the convergence of the sequence of approximations, and on the other hand, we verify that the outcome we present is close to the limit of the sequence by a stability analysis of the numerical solutions.

We use a first order edge element based Galerkin finite element simulator to obtain the solutions as described in Section 5 of [9].

3.1. Scattering from Plasmonic Gratings Behaving as Bianisotropic Metamaterials

In [1], the authors considered a plasmonic grating that exhibits bianisotropy at visible wavelengths. The bianisotropic media considered there are of the form:

$$\left\{\begin{array}{l}\mathbf{D}=\epsilon \mathbf{E}+\xi \mathbf{H},\\ \mathbf{B}=\zeta \mathbf{E}+\mu \mathbf{H},\end{array}\right.$$

(21)

with:

$$\epsilon ={\epsilon }_0\left[\begin{array}{ccc}{\epsilon }_x& 0& 0\\ 0& {\epsilon }_y& 0\\ 0& 0& {\epsilon }_z\end{array}\right],\mu ={\mu }_0\left[\begin{array}{ccc}{\mu }_x& 0& 0\\ 0& {\mu }_y& 0\\ 0& 0& {\mu }_z\end{array}\right],$$

(22)

$$\xi =\frac{1}{c_0}\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& j{\xi }_0& 0\end{array}\right],\zeta =\frac{1}{c_0}\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& -j{\xi }_0\\ 0& 0& 0\end{array}\right].$$

(23)

Here, ${\epsilon }_x$, ${\epsilon }_y$, and ${\epsilon }_z$ are complex valued functions and are set to be equal to a unique value ${\epsilon }_r$. Moreover, ${\mu }_x$, ${\mu }_y$, and ${\mu }_z$ are each set equal to one, and ${\xi }_0$ is taken to be real valued. The region occupied by the scatterer may be denoted as ${\Omega }_s\subset \Omega$. The above form can be converted into the alternative form of constitutive relations [13] involving the P, Q, L, and M matrices defined in Equation (1), and the final result is shown in the following equations:

$$P=c_0{\epsilon }_0\left[\begin{array}{ccc}{\epsilon }_r& 0& 0\\ 0& {\epsilon }_r& 0\\ 0& 0& {\epsilon }_r-{\xi }_0^2\end{array}\right],$$

(24)

$$Q=\frac{1}{c_0{\mu }_0}{I}_3,$$

(25)

$$L=M^T=\frac{j{\xi }_0}{{\mu }_0{c}_0}\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 1& 0\end{array}\right].$$

(26)

Here, $I_3$ is the three by three identity matrix. The complementary region $\Omega \backslash {\Omega }_s$ is occupied by the empty space, which is characterized by $P=c_0{\epsilon }_0{I}_3$, $Q=\frac{1}{c_0{\mu }_0}{I}_3$, $L=M=0$. This problem cannot be managed by the previous theories and, in particular, by the theory in [5], which relied on strong hypothesis about losses.

The bianisotropic medium is lossy with the imaginary part $Im\left({\epsilon }_r\right)<0$, whereas ${\xi }_0$ is assumed real here to avoid some longer calculations. Now, Lemma 1 can be applied to verify hypothesis H5. Inside ${\Omega }_s$, P can be decomposed as $P=P_s-j{P}_{ss}$ with:

$$P_s=\frac{P+P^{*}}{2}=c_0{\epsilon }_0\left[\begin{array}{ccc}Re\left({\epsilon }_r\right)& 0& 0\\ 0& Re\left({\epsilon }_r\right)& 0\\ 0& 0& Re\left({\epsilon }_r\right)-{\xi }_0^2\end{array}\right],$$

(27)

and $P_{ss}=\frac{P^{*}-P}{2j}=-c_0{\epsilon }_{0}Im\left({\epsilon }_r\right)I_3$. Hence, we have ${\Omega }_{el}={\Omega }_s$, the lossy region where $P_{ss}$ is uniformly positive definite and the complementary region with the free space where $P_s$ is uniformly positive definite. This means that the conditions of Lemma 1 are satisfied, and as a result, H5 is valid.

From the definitions (see Equations (11), (12), and (15)), $C_1=c_0{\epsilon }_0\left|Im\left({\epsilon }_r\right)\right|$, $C_5=c_0{\epsilon }_0$, and $C_3=c_0{\epsilon }_{0}max\left(\right|Re\left({\epsilon }_r\right)-{\xi }_0^2|,|Re\left({\epsilon }_r\right)\left|\right)$. To find the minimum of the two expressions in Equation (14), we note that, in the valid range, the value of the first expression decreases monotonically with $\alpha$, whereas that of the second expression increases with it. The highest estimate for $C_{PS}$ is obtained when the two expressions have the same value. The value of $\alpha$ at which this happens can be evaluated by equating the two expressions and finding the positive root of the resulting quadratic equation. This value of $\alpha$, denoted as ${\alpha }_{opt}$, is given by:

$${\alpha }_{opt}=\frac{C_5^2-C_1^2-C_3^2+\sqrt{{(C_5^2-C_1^2-C_3^2)}^2+4C_5^2{C}_3^2}}{2C_5^2}.$$

(28)

Thus, we may simply write:

$$C_{PS}=\sqrt{\frac{1-{\alpha }_{opt}}{2}}{c}_0{\epsilon }_0.$$

(29)

As mentioned in [9], this does not mean that a better value of $C_{PS}$ cannot be found. For example, if $Re\left({\epsilon }_r\right)-{\xi }_0^2>0$, then $P_s$ is uniformly positive definite in $\Omega$, and we can find another candidate for $C_{PS}$, namely $C_7=c_0{\epsilon }_{0}min(1,|Re\left({\epsilon }_r\right)-{\xi }_0^2\left|\right)$ (see Equation (31) of [9]). In particular, when $Re\left({\epsilon }_r\right)-{\xi }_0^2>\frac{1}{\sqrt{2}}$, $C_7$ is always going to give a value for $C_{PS}$ that is higher than that obtained from the lemma.

In the rest of the subsection, the discussion focuses on the cases with $Re\left({\epsilon }_r\right)<0$, which gives a non-definite $P_s$ in $\Omega$. For this case, $C_3=c_0{\epsilon }_0|Re\left({\epsilon }_r\right)-{\xi }_0^2|$, and we can directly use the value of $C_{PS}$ in Equation (29). Since the material is assumed to be non-magnetic, the direct application of the definition gives $C_{QS}=\frac{1}{c_0{\mu }_0}$, and H6 is valid. Likewise, for the continuity constants $C_L$ and $C_M$, we can choose the value $\frac{|{\xi }_0|}{c_0{\mu }_0}$. Then, the inequality in H7 becomes $C_{QS}-\frac{C_L{C}_M}{C_{PS}}=\frac{1}{c_0{\mu }_0}(1-\frac{{\xi }_0^2\sqrt{2}}{\sqrt{1-{\alpha }_{opt}}})>0$, which gives:

$$|{\xi }_0|<{\left(\frac{1-{\alpha }_{opt}}{2}\right)}^{1/4}.$$

(30)

Since the right-hand side of Equation (30) also depends on ${\xi }_0$ due to the presence of $C_3$ in the expression for ${\alpha }_{opt}$, we do not have a closed-form expression on the limit on ${\xi }_0$ below which H7 is satisfied. However, a graphical analysis can be done for estimating such a limit on $|{\xi }_0|$, as shown in Figure 1. The value of $Re\left({\epsilon }_r\right)$ is varied in the range $(-5.0,-1.0)$, whereas $Im\left({\epsilon }_r\right)$ assumes values in the range $(-0.5,-0.1)$. It can be observed that for a fixed value of $Im\left({\epsilon }_r\right)$, the range of ${\xi }_0$ over which H7 is valid steadily decreases as $\left|Re\right({\epsilon }_r\left)\right|$ increases. As for the dependence on $Im\left({\epsilon }_r\right)$, the corresponding range increases when the medium becomes lossier due to higher $\left|Im\right({\epsilon }_r\left)\right|$, as expected.

Since outside the region occupied by the bianisotropic media ($\Omega \backslash {\Omega }_s$), we just have the empty space, H1 and H2 are trivially satisfied there. By Remark 1 of [9], since H1, H3, and H4 need to hold only locally, now we have to just analyze them inside ${\Omega }_s$ occupied by the bianisotropic medium. We consider the alternative form of constitutive relations, which for the medium inside ${\Omega }_s$ becomes as in Equations (31) to (33), for examining the validity of H1, H3 and H4 [13]:

$$\kappa =\frac{1}{{\epsilon }_0{\epsilon }_r}\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& \frac{{\epsilon }_r}{{\epsilon }_r-{\xi }_0^2}\end{array}\right],$$

(31)

$$\nu =\frac{1}{{\mu }_0}\left[\begin{array}{ccc}1& 0& 0\\ 0& \frac{{\epsilon }_r}{{\epsilon }_r-{\xi }_0^2}& 0\\ 0& 0& 1\end{array}\right],$$

(32)

$$\gamma =-{\chi }^T=\frac{j{\xi }_0{c}_0}{{\epsilon }_r-{\xi }_0^2}\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right].$$

(33)

The constants of interest can be evaluated directly from the definitions. The determinants of $\kappa$ and $\nu$ are, respectively, $\frac{1}{{\left({\epsilon }_0{\epsilon }_r\right)}^3(1-\frac{{\xi }_0^2}{{\epsilon }_r})}$ and $\frac{1}{{\left({\mu }_0\right)}^3(1-\frac{{\xi }_0^2}{{\epsilon }_r})}$, which immediately give the values of $C_{\kappa ,d}$ and $C_{\nu ,d}$.

$$C_{\kappa ,d}=\frac{1}{|{\epsilon }_0^3{\epsilon }_r^3(1-\frac{{\xi }_0^2}{{\epsilon }_r})|},$$

(34)

$$C_{\nu ,d}=\frac{1}{|{\mu }_0^3(1-\frac{{\xi }_0^2}{{\epsilon }_r})|}.$$

(35)

The inverses of the diagonal matrices $\kappa$ and $\nu$ are just the diagonal matrices with the reciprocal entries. Applying Equations (40) and (41) of [9] gives the values of $C_{\kappa ,r}$ and $C_{\nu ,r}$.

$$C_{\kappa ,r}=\left|{\epsilon }_0{\epsilon }_r\right|,$$

(36)

$$C_{\nu ,r}={\mu }_0.$$

(37)

Using Equations (36) and (37) of [9], we get $C_{\kappa ,s}$ and $C_{\nu ,s}$.

$$C_{\kappa ,s}=\frac{2}{|{\epsilon }_0{\epsilon }_r|},$$

(38)

$$C_{\nu ,s}=\frac{2}{{\mu }_0}.$$

(39)

From Equations (18) and (19), we can easily evaluate $C_{\gamma ,s}$ and $C_{\chi ,s}$.

$$C_{\chi ,s}=C_{\gamma ,s}=\left|\frac{{\xi }_0{c}_0}{{\epsilon }_r-{\xi }_0^2}\right|.$$

(40)

The hypotheses H1 and H3 are valid due to the existence of the above constants. Using these constants, the value of $K_u$ can be calculated from Equation (20). The critical value of $|{\xi }_0|$ below which the condition in H4 is satisfied is plotted in Figure 2, with respect to either $Re\left({\epsilon }_r\right)$ or $Im\left({\epsilon }_r\right)$. The results show that the range of ${\xi }_0$ for which H4 holds true increases with the increase in $\left|Re\right({\epsilon }_r\left)\right|$, while it is practically independent of $Im\left({\epsilon }_r\right)$.

Let us try to understand the implications of the theory by applying it to the numerical solution of a specific problem involving the medium of interest. We consider the region with the scatterer ${\Omega }_s$ to be a cube filled with homogeneous bianisotropic media. The surrounding region is filled with empty space, and the overall domain of numerical investigation, $\Omega$, has a cubic shape as well and is concentric to ${\Omega }_s$. In the following, $\Omega$ and ${\Omega }_s$ are characterized by sides of length 2 $\mathsf{\mu }$m and 0.8 $\mathsf{\mu }$m, respectively. The axes are taken along the sides of the cubic domain $\Omega$, and the excitation is with a plane wave incident along the x axis, with the electric field polarized along the z axis, having a magnitude of 1 V/m and wavelength of 1 $\mathsf{\mu }$m.

Inside ${\Omega }_s$, the medium is characterized by ${\epsilon }_r=-1-j0.4$, ${\mu }_r=1$, and ${\xi }_0=-0.41$. This value is such that the hypotheses required for well posedness and finite element approximability are satisfied. In fact, for the ${\epsilon }_r$ considered, condition H4 is valid for $|{\xi }_0|<0.4393$, and condition H7 is valid for $|{\xi }_0|<0.4235$.

The solutions are obtained with a first order edge element based Galerkin finite element method. The boundary condition is enforced with Y equal to the admittance of a vacuum and with an inhomogeneous term ${\mathbf{f}}_R$, taking into account the incident field.

The domain is discretized uniformly using tetrahedral meshes. The meshing is done by first dividing the domain into small identical cubes, each of which is in turn divided into six tetrahedra. The parameter h denotes the maximum diameter of all the elements of the mesh [14] (p. 131), and in this case, it is simply given by the side of the small cubes times $\sqrt{3}$. To study the stability of the solution, we consider different levels of refinement of meshes ranked in order of h, ranging from “very coarse” to “very fine”. For example, the mesh denoted as very coarse is characterized by cubes of sides 200 nm, and the resulting mesh has 1331 nodes, 6000 tetrahedral elements, and 1200 boundary faces. A summary of the information related to the four different refinements of the meshes that were used is given in

Table 1. Details of the different meshes used.

Type of Mesh	Maximum Diameter of the Mesh (h in nm)	Number of Nodes	Number of Elements	Number of Boundary Faces
Very coarse	200 $\sqrt{3}$	1331	6000	1200
Coarse	100 $\sqrt{3}$	9261	48,000	4800
Fine	50 $\sqrt{3}$	68,921	384,000	19,200
Very fine	25 $\sqrt{3}$	531,441	3,072,000	76,800

.

The outcomes related to the stability of the results of the simulations are shown in Figure 3 by plotting the magnitude of the z component of the electric field along a line parallel to the y axis and passing through the center of gravity of the domain. The difference between successive refinements progressively decreases, and the fine and very fine meshes give stable solutions. The well posedness and convergence result that was predicted using the theory guarantee that our solutions are reliable.

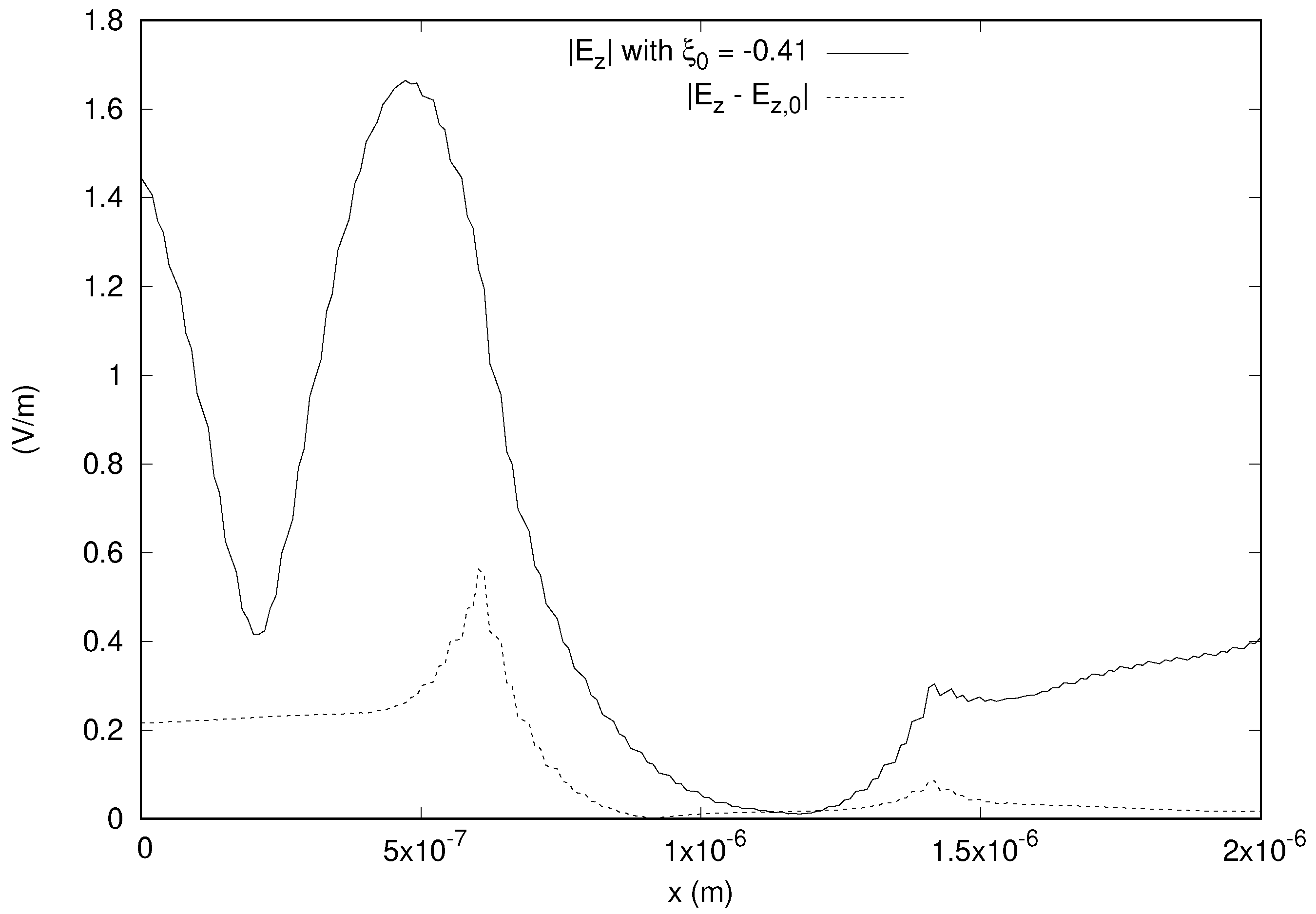
Figure 4 shows the significance of the bianisotropic effect on the z component of the electric field along a line parallel to the x axis and passing through the center of gravity of the domain. Here, $E_z$ denotes the solution obtained with ${\xi }_0=-0.41$, and $E_{z,0}$ is the solution when ${\xi }_0=0$, while the plot shows the magnitude of the difference $|E_z-E_{z,0}|$ along with $|E_z|$. The magnitude of the difference is as large as 50% of the incident field. 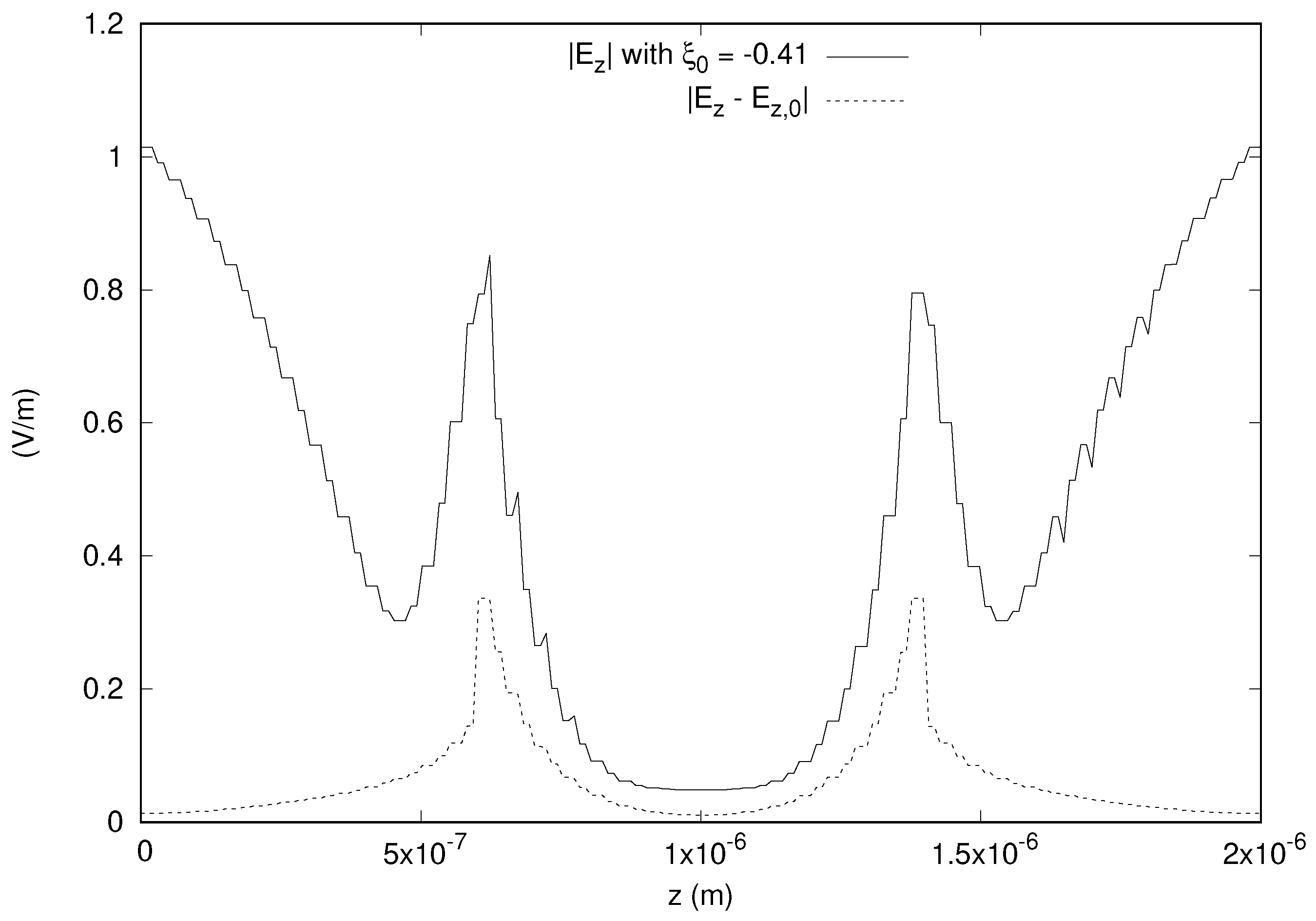Similarly, the results along a line parallel to the z axis and passing through the center of gravity of the domain are shown in Figure 5, and we get a difference of around 30% of the incident field.

These non-negligible effects imply that to get accurate results, it is necessary to consider the bianisotropy of the medium. Hence, the reliability of the finite element solution in the presence of bianisotropy is important for getting good results for these problems. The application of our theory gives the conditions under which we can guarantee such reliability. The solutions obtained can serve as references for other approaches.

3.2. Scattering from Chiral Obstacles in a Waveguide

In [10], the authors considered a metallic waveguide, which was hollow except for an obstacle characterized by a chiral medium with the following constitutive relations.

$$\left\{\begin{array}{l}\mathbf{D}={\epsilon }_0{\epsilon }_r{I}_3\mathbf{E}-j{\xi }_c{I}_3\mathbf{B},\\ \mathbf{H}=-j{\xi }_c{I}_3\mathbf{E}+\frac{1}{{\mu }_0{\mu }_r}{I}_3\mathbf{B}.\end{array}\right.$$

(41)

Here, ${\epsilon }_r$, ${\mu }_r$, and ${\xi }_c$ are strictly positive real quantities. Thus, from Equation (1), we can easily identify P, Q, L, and M, which are given below:

$$P={\epsilon }_0{\epsilon }_r{c}_0{I}_3,$$

(42)

$$Q=\frac{1}{{\mu }_0{\mu }_r{c}_0}{I}_3,$$

(43)

$$L=M=-j{\xi }_c{I}_3.$$

(44)

In Section 6 of [5], it was shown that this media could not be managed by the theory developed there, independently of the value of ${\xi }_c\in \mathbb{R}$ and of any other material involved in the model of interest. However, we show that the generality of the recently developed theory in [9] allows us to apply it to obtain the conditions for well posedness and finite element approximability for this kind of problem of practical interest.

Let us analyze the validity of the hypotheses by considering, as did the authors in [10], ${\epsilon }_r\ge 1$ and ${\mu }_r=1$. We can make use of Lemma 1 of [9] to check H5. $P_s=P$ and is equal to ${\epsilon }_0{\epsilon }_r{c}_0$ inside the material and simply ${\epsilon }_0{c}_0$ outside. Since ${\Omega }_{el}=\varnothing$, a value of $C_{PS}$ can be found by using Equation (13). In particular, H5 is satisfied for $C_{PS}={\epsilon }_0{c}_0$. The hypothesis H6 is also trivially valid with $C_{QS}=\frac{1}{{\mu }_0{c}_0}$. By Equations (32) and (33) of [9], $C_L=C_M={\xi }_c$. Then, the inequality in hypothesis H7 becomes $C_{QS}-\frac{C_L{C}_M}{C_{PS}}=c_0({\epsilon }_0-{\mu }_0{\xi }_c^2)>0$, which implies:

$${\xi }_c<\sqrt{\frac{{\epsilon }_0}{{\mu }_0}}=2.654\times {10}^{-3}\mathrm{mho}.$$

(45)

This is not a small value considering the chiral effects reported in [10]. As the region outside the obstacle is empty space, H2 is trivially satisfied, and by Remark 1 of [9], we need to verify that the hypotheses H1, H3, and H4 hold true locally inside the region occupied by the bianisotropic medium. To do this, the suitable form of constitutive relations is in terms of $\kappa$, $\nu$, $\gamma$, and $\chi$, which are given by the following [13]:

$$\kappa =\frac{1}{{\epsilon }_0{\epsilon }_r}{I}_3,$$

(46)

$$\nu =\frac{{\epsilon }_0{\epsilon }_r+{\mu }_0{\xi }_c^2}{{\mu }_0{\epsilon }_0{\epsilon }_r}{I}_3,$$

(47)

$$\chi =-\gamma =\frac{j{\xi }_c}{{\epsilon }_0{\epsilon }_r}{I}_3.$$

(48)

$\kappa$ and $\nu$ are multiples of the identity matrix with eigenvalues $\frac{1}{{\epsilon }_0{\epsilon }_r}$ and $\left(\frac{{\epsilon }_0{\epsilon }_r+{\mu }_0{\xi }_c^2}{{\mu }_0{\epsilon }_0{\epsilon }_r}\right)$, respectively. The determinants are just the cubes of the eigenvalues, and hence, according to Equations (34) and (35) of [9], we get the values of $C_{\kappa ,d}$ and $C_{\nu ,d}$.

$$C_{\kappa ,d}={\left(\frac{1}{{\epsilon }_0{\epsilon }_r}\right)}^3,$$

(49)

$$C_{\nu ,d}={\left(\frac{{\epsilon }_0{\epsilon }_r+{\mu }_0{\xi }_c^2}{{\mu }_0{\epsilon }_0{\epsilon }_r}\right)}^3.$$

(50)

$C_{\kappa ,s}$ and $C_{\nu ,s}$, by Equations (36) and (37) of [9], are in this case simply twice the eigenvalue of the corresponding diagonal matrix:

$$C_{\kappa ,s}=\frac{2}{{\epsilon }_0{\epsilon }_r},$$

(51)

$$C_{\nu ,s}=2\frac{{\epsilon }_0{\epsilon }_r+{\mu }_0{\xi }_c^2}{{\mu }_0{\epsilon }_0{\epsilon }_r}.$$

(52)

The inverse of the matrices is also trivial, and Equations (40) and (41) of [9] simply evaluate to the reciprocals of the eigenvalues of $\kappa$ and $\nu$, respectively giving $C_{\kappa ,r}$ and $C_{\nu ,r}$:

$$C_{\kappa ,r}={\epsilon }_0{\epsilon }_r,$$

(53)

$$C_{\nu ,r}=\frac{{\mu }_0{\epsilon }_0{\epsilon }_r}{{\epsilon }_0{\epsilon }_r+{\mu }_0{\xi }_c^2}.$$

(54)

From Equations (18) and (19), we get:

$$C_{\chi ,s}=C_{\gamma ,s}=\frac{2{\xi }_c}{{\epsilon }_0{\epsilon }_r}.$$

(55)

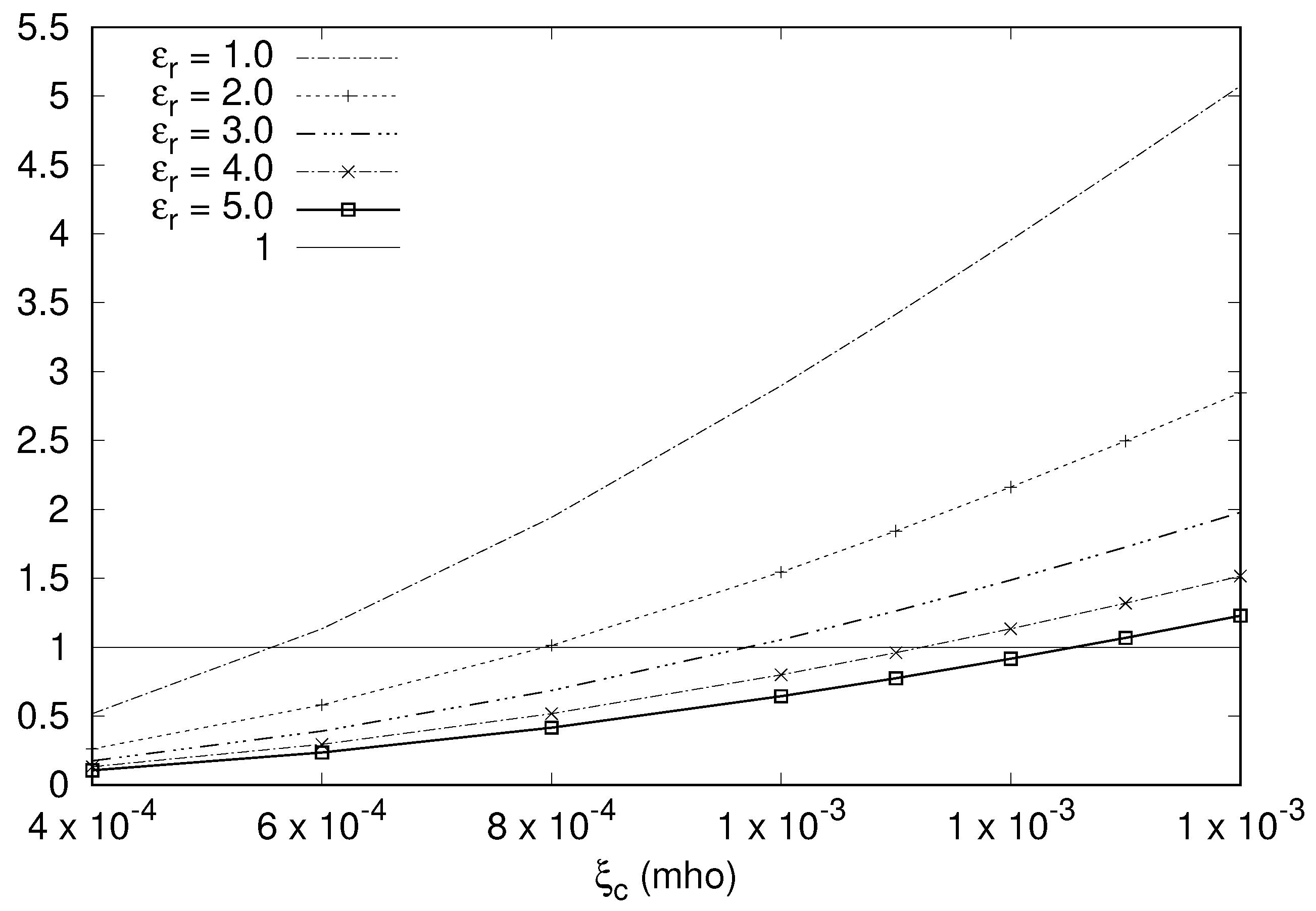
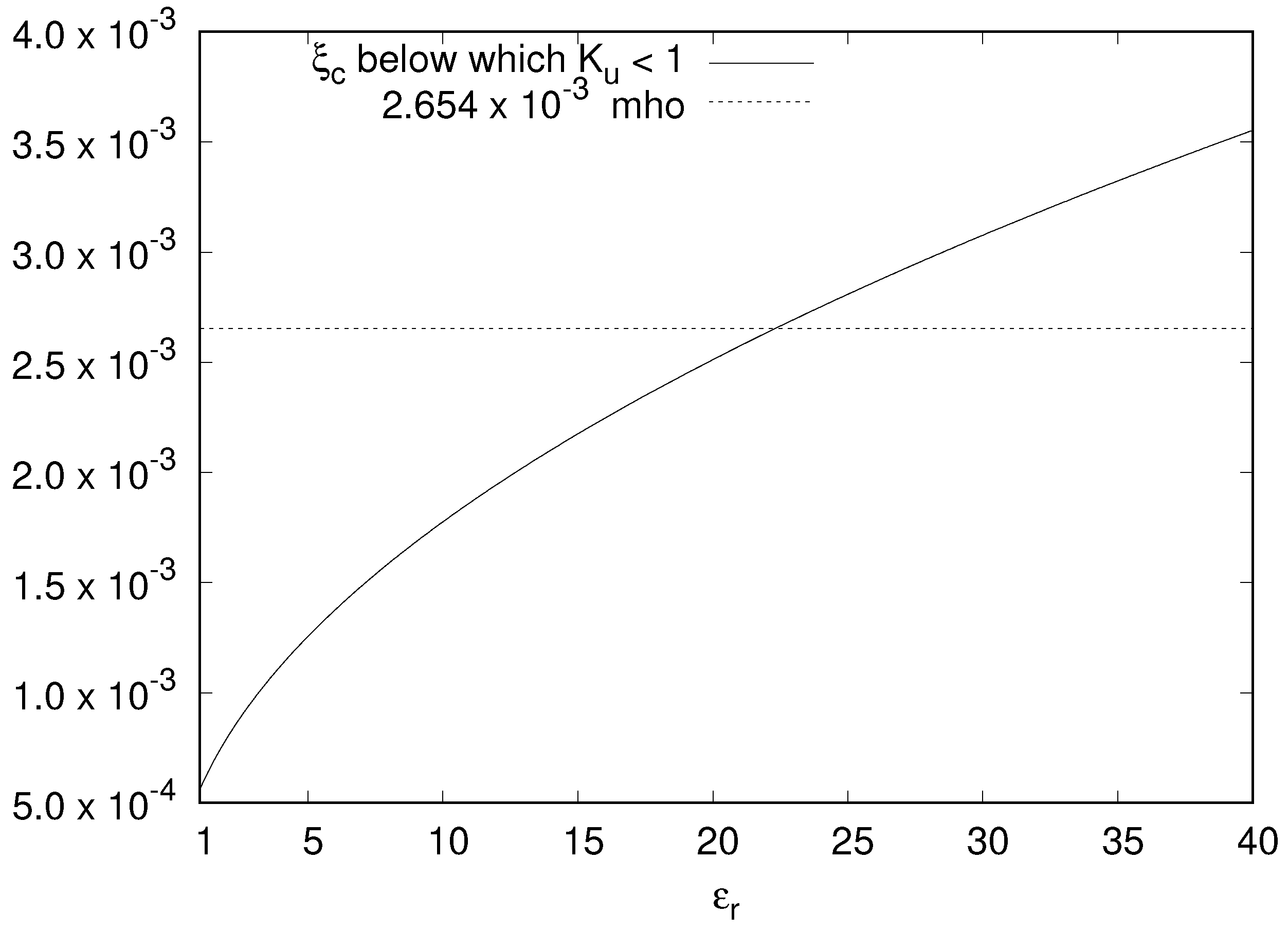
Having shown that the hypotheses H1 and H3 are satisfied, we can use the above constants to calculate $K_u$ to verify H4. Figure 6 shows the dependence of $K_u$ on ${\xi }_c$ for various values of ${\epsilon }_r$. As the value of ${\epsilon }_r$ increases, the hypothesis H4 remains valid for higher and higher values of ${\xi }_c$. Figure 7 shows the plot of the critical value of ${\xi }_c$ below which H4 is satisfied against ${\epsilon }_r$. The limit of $2.654\times {10}^{-3}$ mho, arising from Equation (45) required to satisfy H7, is also shown in the same figure. It is seen that for low values of ${\epsilon }_r$, the tighter condition arises from the need to satisfy H4. For example, the limiting value is $5.6\times {10}^{-4}$ mho for ${\epsilon }_r=1$, increases with ${\epsilon }_r$, and is $1.78\times {10}^{-3}$ mho for ${\epsilon }_r=10$. The curve crosses the $2.654\times {10}^{-3}$ mho line at around ${\epsilon }_r=22.3$, and above that value, Equation (45) imposes the stricter limit.

Now, we consider a specific numerical problem for which the solution is calculated using our finite element simulator. A rectangular waveguide with a discontinuity due to a block of bianisotropic medium is considered as shown in Figure 8. In the simulation, the rectangular waveguide is characterized by $a=23$ mm, $b=10$ mm and has a length $l=40$ mm. The obstacle is a parallelepiped with $c=11$ mm, $d=5$ mm and a length $w=10$ mm. The origin of the axis is at the lower right corner of the near face of the waveguide shown in Figure 8. The obstacle ranges from $x=6$ mm to $x=17$ mm along the x axis, from $y=0$ to $y=5$ mm along the y axis, and from $z=15$ mm to $z=25$ mm along the z axis. The bianisotropic medium making up the obstacle is characterized by ${\epsilon }_r=5$ and ${\xi }_c=1.24\times {10}^{-3}$ mho. For this medium, $K_u=0.98<1$, and also, Equation (45) is satisfied; hence, all the hypotheses required to guarantee the well posedness and convergence of finite element solutions hold true. The waveguide is excited with $T{E}_{10}$ mode having an amplitude of 1 V/m and a frequency of 9 GHz. The input port is on the x-y plane, and the output port is closed on a matched homogeneous admittance boundary condition for the $T{E}_{10}$ mode in the empty waveguide.

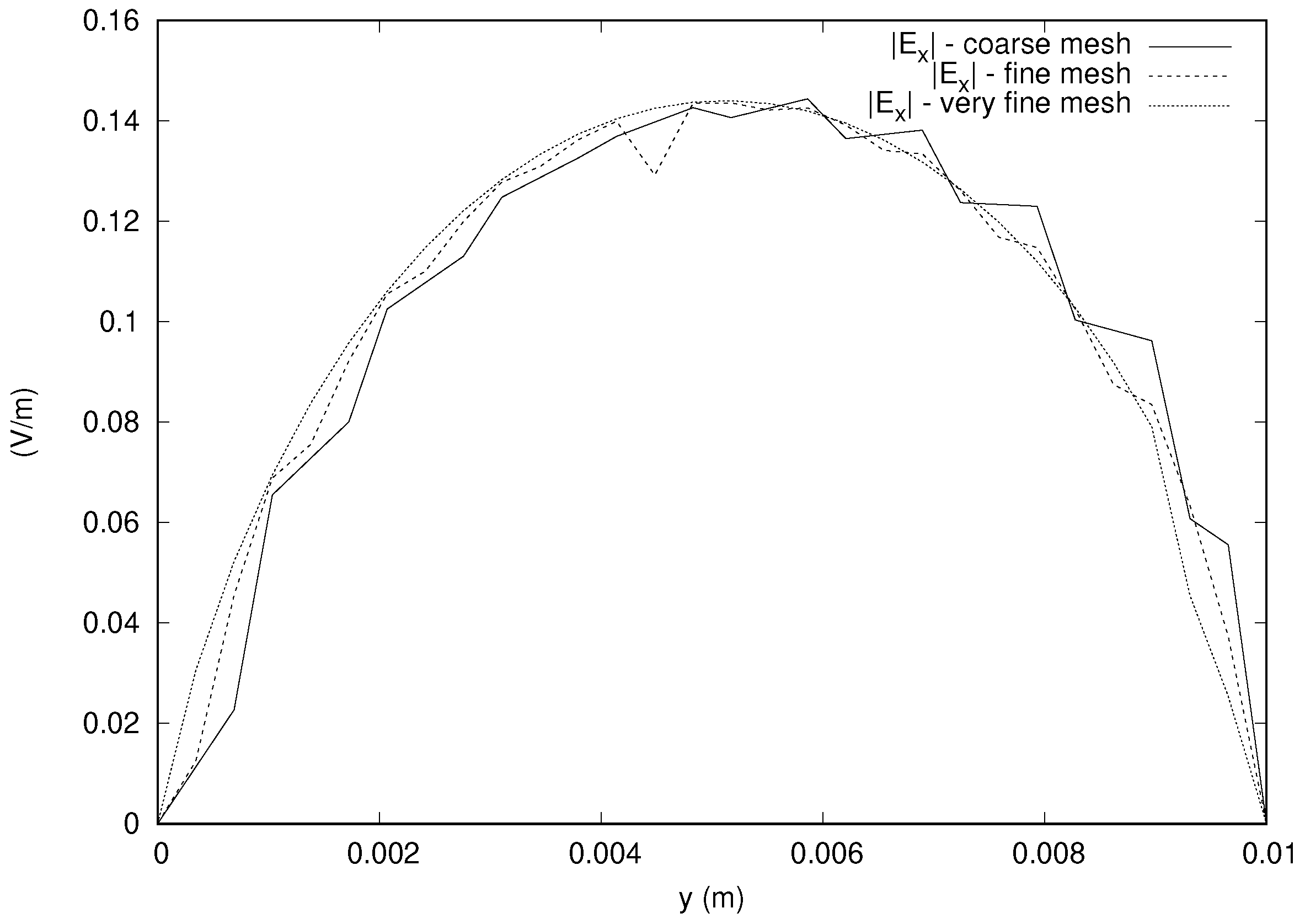
The details of the Galerkin finite element solver is the same as before. The tetrahedral meshes are obtained as discussed in the previous subsection by dividing the domain into small cubes, each of which is in turn subdivided into six tetrahedra. 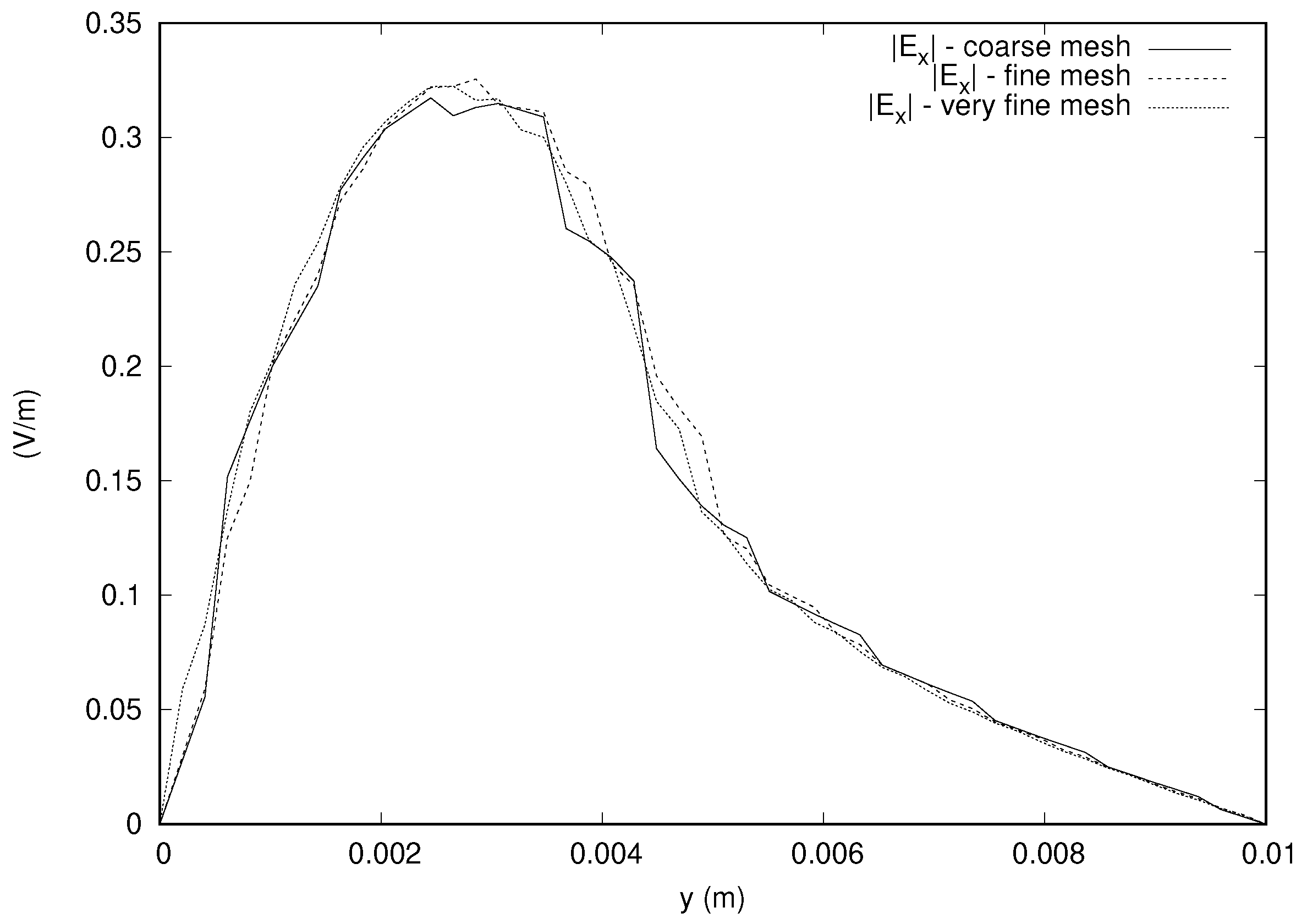The stability of the solution is verified by checking the solutions for three different meshes, which are characterized by small cubes of sides $\frac{1}{2}$ mm, $\frac{1}{4}$ mm, and $\frac{1}{6}$ mm, which are referred to as, respectively, “coarse”, “fine”, and “very fine” meshes. There are 10,824 nodes, 55,200 elements, and 6200 boundary faces in the coarse mesh, whereas the fine mesh has 79,947 nodes, 441,600 elements, and 24,800 boundary faces, and finally, the very fine mesh has 262,570 nodes, 1,490,400 elements, and 55,800 boundary faces. It was verified that the solutions obtained with these meshes are stable. For example, Figure 9 shows the magnitude of the x component of the electric field along a line parallel to the y axis and passing through the center of gravity of the domain with the different meshes and illustrates the stability of the result. It is noted that the x component of the electric field along this line is zero for the achiral case (${\xi }_c=0$), and there is a difference of more than 30% of the incident field, which is induced by the bianisotropy.

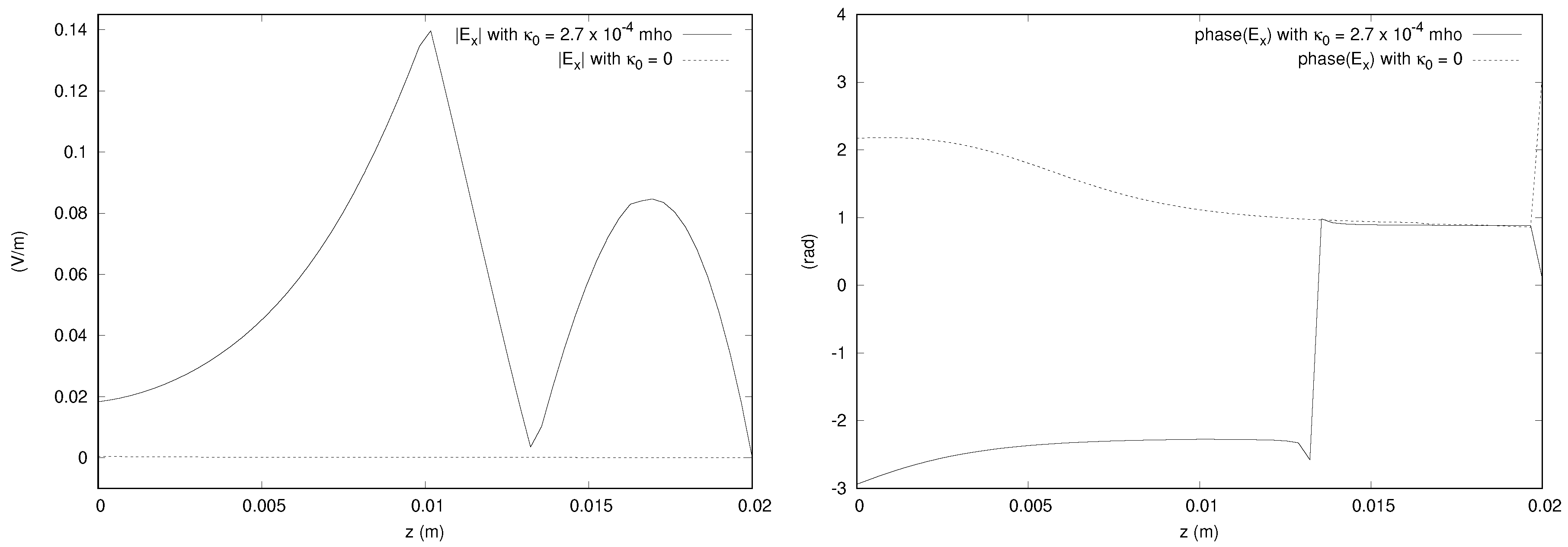
Figure 10 shows the result for the magnitude and phase of the x component of the electric field along the line parallel to the x axis and passing through the center of gravity of the domain. We have a difference of 20% of the magnitude of the incident field for the x component of the electric field along this line. Similarly, Figure 11 shows that the bianisotropic effect for the x component of the field along the line parallel to the z axis and passing through the center of gravity of the domain causes a difference in the magnitude of the electric field of around 13% of the incident field.

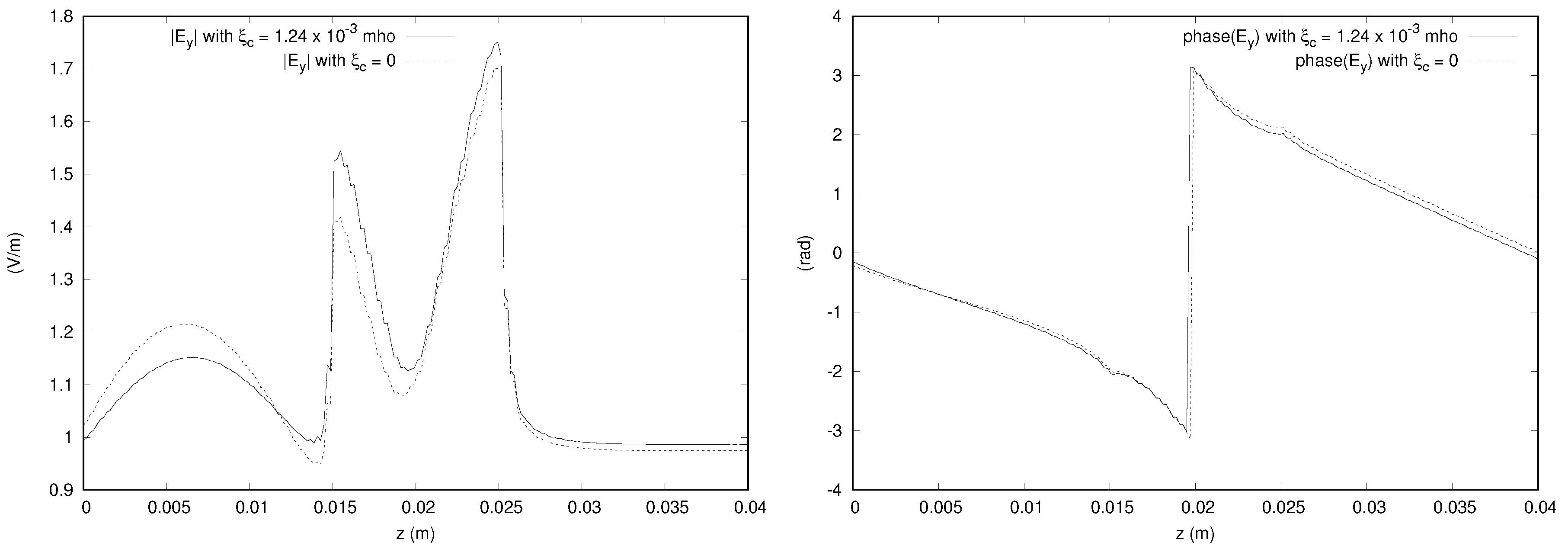
Figure 12 shows the y component of the electric field along a line parallel to the z axis and passing through the center of gravity of the domain. The bianisotropic effect is again not negligible and causes a difference of more than 10% of the incident field. A similar effect is present in the z component as can be seen in the plot along a line parallel to the x axis and passing through the center of gravity of the domain, which is given in Figure 13. We do not show the other figures to save space, but it is noted that the y component of electric field along the lines through the center of the domain and parallel to the x and y axes shows small differences in magnitude between the chiral and achiral cases, being less than five percent of the incident field. The z component on the other hand along the lines parallel to the y and z axes and passing through the center of the domain shows a difference of more than 15% of the incident field.

Together, these results provide a point of reference for other approaches of solving such problems, owing to the reliability of the results provided here, which is guaranteed by the recently developed theory. The previous theory [5] was not able to manage these problems, and our results are therefore novel. In fact, to the best of our knowledge, there are no other approaches that are available to get reliable results for benchmarking. The significant bianisotropic effects demonstrated in the results show the practical importance of the theory for such media.

3.3. Reflection by a Short-Circuited Waveguide Half Filled with Bianisotropic Media

Another relevant bianisotropic medium was discussed in [11], where the authors considered a short-circuited rectangular waveguide, half of which was empty and the other half filled with a lossless bianisotropic material characterized by:

$$P={\epsilon }_0{c}_0{I}_3,$$

(56)

$$Q=\frac{1}{{\mu }_0{c}_0}{I}_3,$$

(57)

$$L=M=j{\kappa }_{0}A,$$

(58)

where A is the matrix given by:

$$A=\left[\begin{array}{ccc}1& 1& 0\\ 1& 1& 0\\ 0& 0& 1\end{array}\right],$$

(59)

and ${\kappa }_0$ is a positive real number.

The hypotheses H5 and H6 are trivially valid with $C_{PS}={\epsilon }_0{c}_0$ and $C_{QS}=\frac{1}{{\mu }_0{c}_0}$. Further, $L^{*}L=M^{*}M={\kappa }_0^2{A}^2$ whose eigenvalues are zero, ${\kappa }_0^2$, and $4{\kappa }_0^2$. Therefore, by Equations (32) and (33) of [9], we get $C_L=C_M=2{\kappa }_0$. The condition in hypothesis H7 then becomes $C_{QS}-\frac{C_L{C}_M}{C_{PS}}=\frac{1}{{\mu }_0{c}_0}-\frac{4{\kappa }_0^2}{{\epsilon }_0{c}_0}>0$, which gives the following limit on ${\kappa }_0$:

$${\kappa }_0<\frac{1}{2}\sqrt{\frac{{\epsilon }_0}{{\mu }_0}}=1.327\times {10}^{-3}\mathrm{mho}.$$

(60)

The hypothesis H2 holds true since the anisotropic part is just empty space. H1, H3, and H4 can be studied using the alternative form of constitutive relations, which is characterized by the following matrices [13]:

$$\kappa =\frac{1}{{\epsilon }_0}{I}_3,$$

(61)

$$\nu =\frac{1}{{\mu }_0}{I}_3+\frac{{\kappa }_0^2}{{\epsilon }_0}{A}^2,$$

(62)

$$\chi =-\gamma =\frac{-j{\kappa }_0}{{\epsilon }_0}A.$$

(63)

The determinants of $\kappa$ and $\nu$ can be readily calculated, and by using Equations (34) and (35) of [9], we get $C_{\kappa ,d}$ and $C_{\nu ,d}$:

$$C_{\kappa ,d}=\frac{1}{{\epsilon }_0^3},$$

(64)

$$C_{\nu ,d}=\frac{({\epsilon }_0+{\mu }_0{\kappa }_0^2)({\epsilon }_0+4{\mu }_0{\kappa }_0^2)}{{\mu }_0^3{\epsilon }_0^2}.$$

(65)

$C_{\kappa ,s}$ and $C_{\nu ,s}$ can be directly obtained from their definitions:

$$C_{\kappa ,s}=\frac{2}{{\epsilon }_0},$$

(66)

$$C_{\nu ,s}=\frac{2{\epsilon }_0+8{\mu }_0{\kappa }_0^2}{{\mu }_0{\epsilon }_0}.$$

(67)

By simple application of the definition:

$$C_{\kappa ,r}={\epsilon }_0$$

(68)

and by Equation (41) of [9], $C_{\nu ,r}$ evaluates to the reciprocal of the largest eigenvalue of the real matrix $\nu$, which is given by:

$$C_{\nu ,r}=\frac{{\mu }_0{\epsilon }_0}{{\epsilon }_0+4{\mu }_0{\kappa }_0^2}.$$

(69)

Equations (18) and (19) give:

$$C_{\chi ,s}=C_{\gamma ,s}=\frac{4{\kappa }_0}{{\epsilon }_0}.$$

(70)

The existence of the above constants verifies H1 and H3, and we can use them to calculate $K_u$ to check H4. It can be verified that $K_u$ is less than one when ${\kappa }_0\le 2.72\times {10}^{-4}$ mho, which is stricter than the limit obtained from Equation (60).

Finally, let us give some numerical solutions for this problem, which can be used as references for other approaches. The cross-section of the waveguide is 2 cm along the x axis and 1 cm along the y axis, and the length of the waveguide is 2 cm, half of which is filled with the bianisotropic medium characterized by ${\kappa }_0=2.7\times {10}^{-3}$ mho (see Figure 1 of [11]). The origin is taken on the corner of the open face of the waveguide on the empty side. $T{E}_{10}$ mode is excited in the waveguide with a source of amplitude 1 V/m and a frequency of 12 GHz.

The first order edge element based Galerkin finite element method is used to obtain the solution. The meshing is carried out by dividing the domain into identical cubes, each of which is then subdivided into six tetrahedra. The stability of the result is ensured by evaluating the solutions on three meshes, termed as “coarse”, “fine”, and “very fine”, characterized, respectively, by cubes of sides 1 mm, $\frac{1}{2}$ mm, and $\frac{1}{3}$ mm. The coarse mesh has 4852 nodes, 24,000 elements, and 3200 boundary faces. The fine mesh is composed of 35,301 nodes, 192,000 elements, and 12,800 boundary faces. The very fine mesh has 115,351 nodes, 648,000 elements, and 28,800 boundary faces. The results obtained with these meshes are stable. For example, Figure 14 shows the stability of the results obtained with the three meshes for the x component of the electric field along a line parallel to the y axis and passing through the center of gravity of the domain.

We provide the magnitudes and phases of the x component of the electric field obtained from the simulation in Figure 15, Figure 16 and Figure 17. The bianisotropy causes a difference in magnitude of up to 14% of the incident field. The phases are also significantly affected by the bianisotropy of the medium. The figures for other components are not shown to save space, but it is noted that the y component is affected by the bianisotropy, showing a difference of up to about 10% of the incident field. The z component of the field along the line parallel to the x axis passing through the center of gravity of the domain does show a difference of about 10% of the incident field, but the magnitudes along the other directions are close to zero for both values of ${\kappa }_0$ considered.

Since the theory guarantees the reliability of these results, they can be used as references for other solvers and approaches. It is to be noted that the previous theory developed in [5] could not be applied to this medium since the same reasons mentioned there with respect to the medium in [10] are valid. Hence, our results show the generality of the new theory with respect to the application to interesting bianisotropic media. The results demonstrate that our theory can be applied to problems with significant bianisotropic effects. This consideration underlines its practical importance.

4. Conclusions

In this paper, we discussed the application of a recently developed theory to electromagnetic scattering problems involving bianisotropic materials and metamaterials of practical interest. The range of constitutive parameters over which the reliability of the results was guaranteed was calculated for these problems, and the solutions were obtained. The ensured reliability of the results made them useful as benchmarks for other numerical techniques. To the best of our knowledge, none of the previous tools were able to get such benchmark solutions.