Energy Efficient Computation Offloading Mechanism in Multi-Server Mobile Edge Computing—An Integer Linear Optimization Approach

Abstract

Conserving energy resources and enhancing computation capability have been the key design challenges in the era of the Internet of Things (IoT). The recent development of energy harvesting (EH) and Mobile Edge Computing (MEC) technologies have been recognized as promising techniques for tackling such challenges. Computation offloading enables executing the heavy computation workloads at the powerful MEC servers. Hence, the quality of computation experience, for example, the execution latency, could be significantly improved. In a situation where mobile devices can move arbitrarily and having multi servers for offloading, computation offloading strategies are facing new challenges. The competition of resource allocation and server selection becomes high in such environments. In this paper, an optimized computation offloading algorithm that is based on integer linear optimization is proposed. The algorithm allows choosing the execution mode among local execution, offloading execution, and task dropping for each mobile device. The proposed system is based on an improved computing strategy that is also energy efficient. Mobile devices, including energy harvesting (EH) devices, are considered for simulation purposes. Simulation results illustrate that the energy level starts from $0.979\%$ and gradually decreases to $0.87\%$. Therefore, the proposed algorithm can trade-off the energy of computational offloading tasks efficiently.

1. Introduction

The Internet of things (IoT) is changing our lives drastically. Connectivity among people, things, and businesses are increasing exponentially. It enables flexible connectivity and exchange of data among billions of devices and processes. With the rapid increase in IoT devices, energy need is also increasing [1]. To cope with this issue, energy harvesting (EH) devices have been introduced in the market. EH capture ambient recyclable energy from the environment, such as solar radiation, wind, human motion energy, as well as ambient radio-frequency. Consequently, EH is considered one of the promising techniques to prolong the network lifetime and provide a satisfactory quality of experiences for IoT devices.

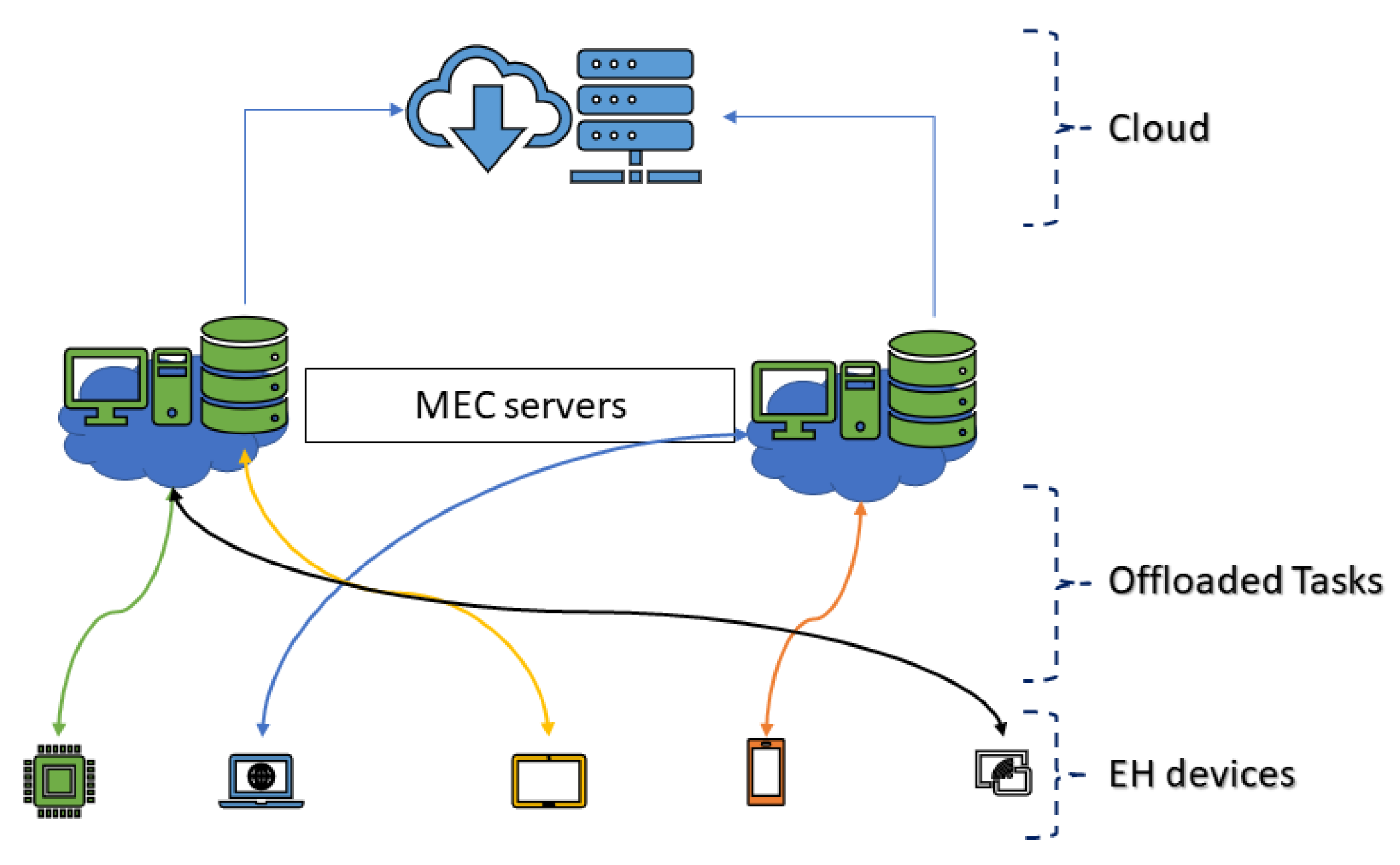
A new network paradigm known as Mobile Edge Computing (MEC) is introduced to liberate mobile devices from computationally intensive tasks. Several edge servers are deployed near the mobile devices aiming at a significant reduction in latency, congestion avoidance, and prolonging the network lifetime. Several IoT devices offload the heavy computation workload to the MEC devices such as base stations, access points, and so forth [2]. Integrating EH and MEC techniques contribute to improving computation performance and open new possibilities for cloud computing [3,4].

Computational offloading is a way to help the low memory devices by performing heavy tasks on MEC servers. Tasks are directly associated with IoT devices. A task that is going to be offloaded needs to be transmitted over a wireless access network, and time constraint must be considered during this process [5]. However, to decide computational offloading in MEC servers systems with multiple energy harvesting devices is still challenging. A critical problem in the computation offloading is to select the optimal MEC device from several candidates in the coverage radio range and data over the networks is also vulnerable to attacks [6]. There are many computational offloading schemes been presented in fog computing scenarios. Lyapunov optimization-based algorithm is used for offloading and resource allocation purposes by Chang et al. [7]. Their proposed algorithm can dynamically coordinate and allocate resources to fog nodes. They focused on subproblems such as latency, consumption of power by EH devices, and the priority of mobile devices. To address subproblems, they have minimized the upper bound Lyapunov drift plus penalty function. Liu et al. [8] have used a queuing model to achieve objective optimization in fog computing scenarios. Their proposed system can help to minimize energy consumption and improve delay performance. They also optimize the payment cost for mobile devices. A distributed computation offloading decision-making problem has been shown by Chen et al. [9]. They have formulated a problem for multi-user computation offloading to achieve nash equilibrium by using a game-theoretic approach. However, they consider the offloading decision strategy and energy control as separate issues.

It is worth noting that most of the previous works either do not consider the dynamic offloading or only consider the wireless powered single-user MEC system with binary offloading. In this paper, a smart and energy-efficient computation offloading algorithm for multi-user and multi-server MEC system is designed and which have different EH devices. The proposed algorithm is based on integer linear programming for dynamic offloading. It goes around feasible region constraint by different linear functions, and it finds the first interaction between the objective function and feasible region. The proposed algorithm allows choosing the execution mode among local execution, offloading execution, and task dropping for each mobile device. The main contributions of this Paper includes

• Proposing a dynamic framework for energy-efficient computation offloading approach based on linear programming in multi-users, multi-servers MEC environment.
• Presenting an efficient approach that allows switching between different modes (offloading execution, task dropping, and local execution) based on the executing tasks.
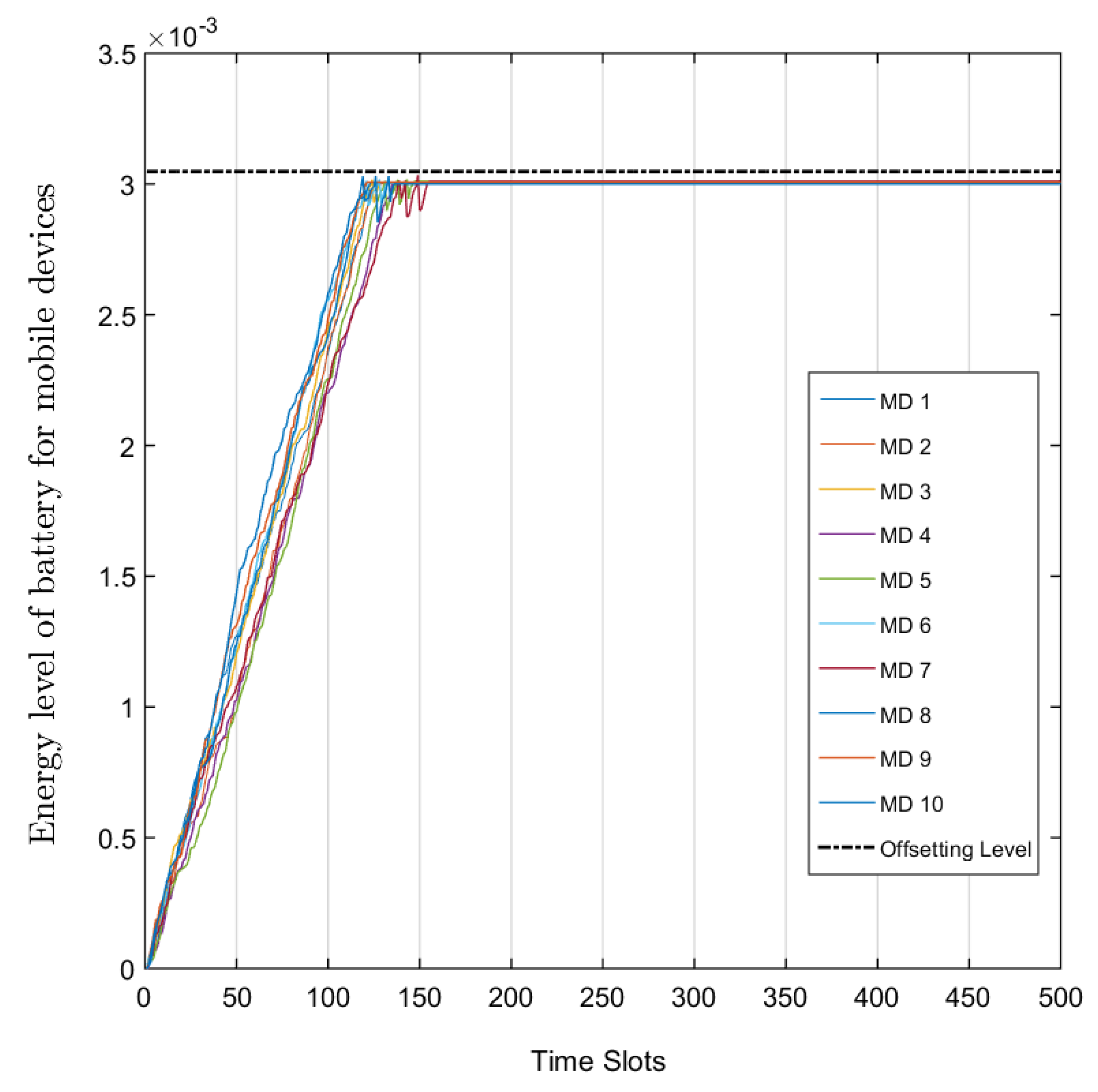
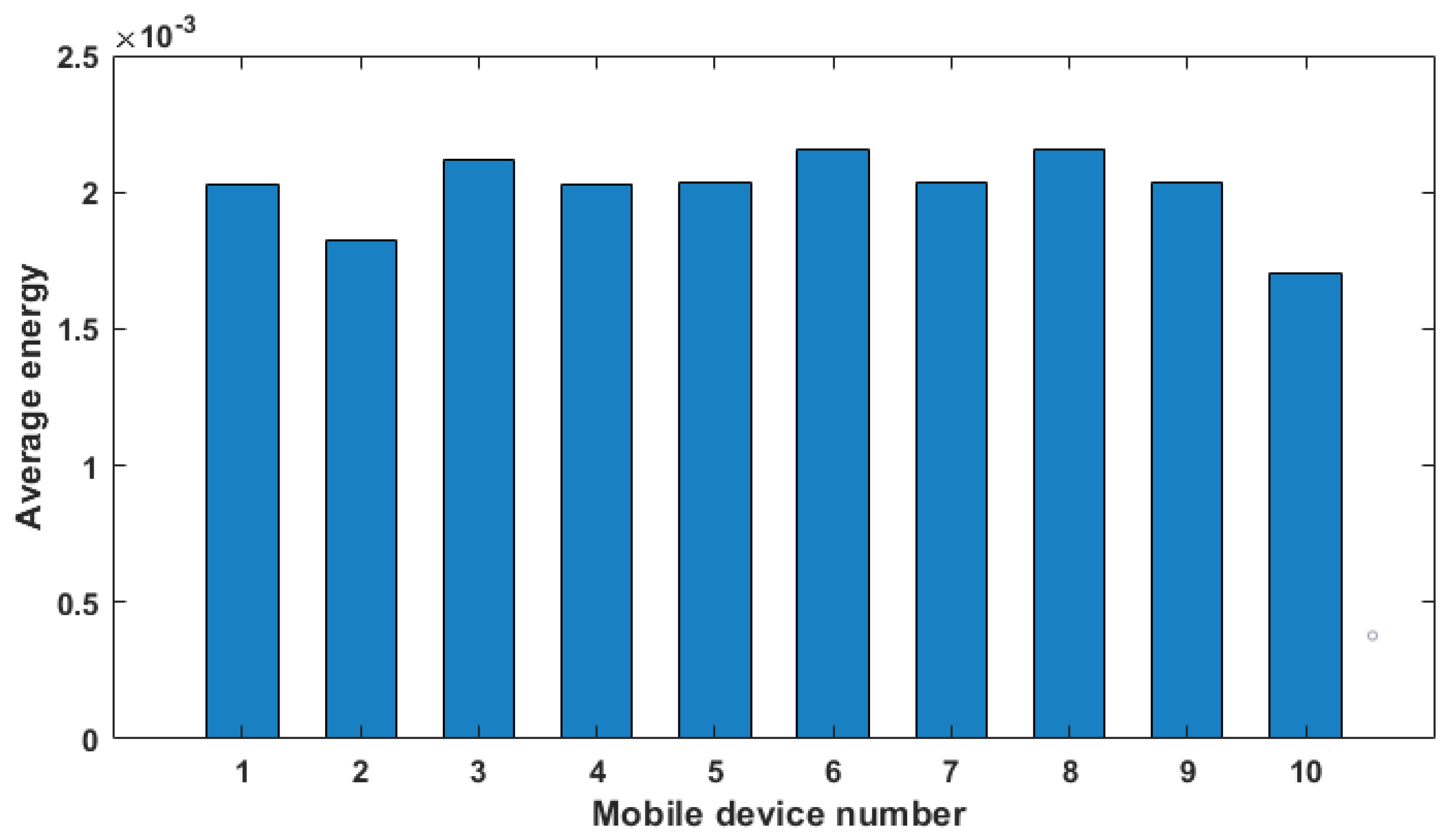
• Extensive experiments to evaluate the performance has been conducted, and it is observed that the proposed method performs well as compared to existing models.

The remainder of this paper is organized as follows. Section 2 discusses the related works of the proposed system. Section 3 introduces the design of the proposed model. Section 4 explains the proposed model using linear programming. Section 6 describes the experimental results and evaluates the performance. Some discussion in Section 7 is made, and finally, our work is concluded in Section 8.

2. Related Work

Edge computing refers to those computational tasks which are being done at or near the edge of a network. In contrast, fog computing is the connection between the edge devices and the cloud in the system. Edge computing and fog computing are beneficial technologies. Their importance and usefulness are described by Mach, P. et al. [10]. Edge computing builds the underlying architecture of computational resources at the edge, and fog computing uses this technique for computational offloading. It also enhances the network connection over different edge devices or edge servers. Sensing observations consume more energy than transmission. The energy consumption of data transmission over the cloud is less than the local execution. Hence, offloading is helpful if performing much computation by broadcasting a relatively small amount of data. It is usefull with the high computation and with small communication [11]. In the case of multiple devices, there is a need to optimize resource allocation dynamically with EH devices. Liu et al. [12]. designed a dynamic computation offloading system in the case of fog computing while considering EH devices. They took social relationship to minimize the exeectuion cost of social group while using game theoretic approach.

Table 1. Mobile Edge Computing (MEC) based research articles for offloading.

Sr#	Year	Technique	Offloading Task	User Support	Edge Computation	Remote Server	Energy Harvesting
1 [13]	2015	Sub-optimum and Optimum statistical approach	Single	Single	Single	No	No
2 [14]	2016	Microwave power transfer	Single	Single	Single	No	Yes
3 [15]	2017	Linear relaxation semi-definite relaxation	Multiple	Single	Multiple	No	No
4 [16]	2018	Binary Computation	Single	Multiple	Single	No	Yes
5 [17]	2018	Q -learning	Single	Multiple	Multiple	No	Yes
6 [18]	2019	Deep Reinforcement learning	Single	Multiple	Single	No	yes
7 [19]	2019	Semi-definite relaxation and stochastic mapping	Single	Multiple	Single	Yes	No
8 [20]	2019	Heterogeneous deep learning-based offloading	Multiple	Multiple	Multiple	Yes	No
9 [21]	2020	Deep Reinforcement Learning	Multiple	Multiple	Single	No	No
10 [Proposed]	-	Integer Linear Programming	Multiple	Multiple	Multiple	Yes	Yes

summarized the recent research articles related to MEC based offloading. These articles have been compared according to the offloading task, user support, edge computation model, and compatibility with energy harvesting devices.

Markov process is extensively appropriated in the state transitions of stochastic systems. Many researchers use Markov Decision Processes (MDP) for the modeling of application placement problems in MEC. Doshi, P. et al. [22] addresses the issue of deterministic behavior of services, which also requires extra monitoring of execution to recover from unexpected behavior of those services. They proposed an MDP-based model for the composition of the workflow. Henriques, D. et al. [23] developed an algorithm to solve the issue of non-determinism. MDP is a continuation of Markov chains. The distinction between them is the additional options and compensations for motivation. The author reduces MDP to a Markov chain and then applied statistical model checking to find the optimal solution. X. Guo and O. Hernandez Lerma, [24], wrote a book completely devoted to continuous-time MDP. They discussed the theoretical and applied implications of continuous-time MDP with advanced criteria. Schaefer, A.J. et al. [25] uses MDP for the medical treatment decisions. Such decisions are very critical because of the uncertainty nature of different patients. Those decisions should be taken in insertion and sequential environment, and the doctor must have to consider all the uncertain factors which make them complex. MDP helps to find the best treatment plan according to the disease. But there are many challenges such as low computational power and requirement of more data.

The design of efficient computation offloading strategies has drawn study concern in current ages. Most works focus on single client-server MEC systems with energy harvesting devices. There is less work done for a system with multiple users and also for numerous servers, which are more typical scenarios in the real world. Huang, D. et al. [26] proposes a time-varying wireless channel based algorithm. They used Lyapunov optimization to overcome the problem of high energy consumption. Figure 1 demonstrates a basic structure of multiple energy harvesting clients and a multi-server mobile edge computing system. Son, Y et al. [27] presented an adaptive method for offloading in a cloud converged virtual machine system. They used a hybrid deep neural network approach to obtain context required for synchronization from cloud-based offloading service.

Task scheduling policy for delay optimization for a single user was proposed by Liu, J. et al. [28]. Their proposed work determines the offloaded components of a software-based on stochastic control. The efficiency of computation offloading usually depends upon the wireless channel, and these channels should remain static during the execution process. But when the coherence time of a channel is less than the latency requirement, than it becomes difficult for channels to stay static. Optimizing the radio and computational resource usage cna be used [13]. They demonstrate that to achieve a good quality of the channel, computation offloading must be higher. They use multi-input multi-output (MIMO) channels and proved that with this, more offloading is done. Energy savings are also more significant when compared to single-input single-output (SISO) and multi-input single-output (MISO) channels. Badri, H. et al. [29], the authors designed a parallel greedy sample average approximation. They solved the problem of placement in mobile edge computing by developing a multi-stage stochastic programming method. Their primary purpose was to decrease communication, computational, and relocation cost.

Edge computing is used to overcome the limitations of mobile devices by offloading. Edge computing saves computational capabilities, battery resources, and storage availability. However, the problem is to find the optimal offloading mechanism for computational offloading. Mao, Y. et al. [30] proposed a Lyapunov optimization-based dynamic computation algorithm (LODCO) to tackle the problem of offloading mechanism in a multi-user case. It was a low complexity algorithm that reduces computation failures noticeably. Their proposed framework enables adaptive offloading powered by energy harvesting. They focused on energy harvesting MEC servers and energy harvesting mobile devices. For this purpose system operator decides the amount of computation to be offloaded. The LODCO algorithm can make the offloading decision in every time slot, and it can reduce execution time by up to 64 % by offloading to the MEC servers. Zhao, H. et al. [31] developed a system to obtain low execution cost and also perform offloading tasks based on the Lyapunov optimization dynamic computation algorithm. Their solution can improve the computation of offloading tasks, and they also focus on the quality of experience. They mainly focus on the selection of the optimal server and utilization of resources. But in their work, issues like the collaboration of cross-edge and overlapping of signal coverage are not considered.

Sardellitti, S. et al. [32] analyzed a situation designed by various mobile clients inquiring for computation offloading of their tasks to a set of edge servers. Moreover, to reduce the energy consumption of mobile devices and to further increase their battery life, which was also a severe issue. In this scenario, where multi-clouds are linked with every small cell Evolved Node B (eNodeB), the energy consumption decreases with the increment of the small cell eNodeBs. In the multi-cloud environment, each cloud is considered as a set of cloud-enabled access points clustered together, and it is regarded as a single entity. Some researchers concentrated on advancing energy harvesting or dynamic voltage scaling technologies. Many mobile applications generated on the IoT Mobile Devices, require high energy consumption because they are computationally intensive. To reduce the execution latency of MEC systems, Mao, Y. et al. [33] proposed a flow shop scheduling theory-based low-complexity solution. They optimize both allocations of transmission power and offloading tasks. But their presented algorithm can be applied only on single-user and single cloudlet environment. A significant issue among computation offloading and selection of MEC servers in a multi-user scenario is discussed by Dinh et al. [15]. They implemented a computational offloading structure by simultaneously optimizing the task allocation decision and the CPU frequency of mobile devices. They also proposed semidefinite relaxations based algorithms to find out the optimal task allocation decision while keeping in view the fixed CPU frequency and elastic CPU frequency. If the edge nodes have high computational power, it causes low computation latency. But communication delay can occur more extensively because of the weak communication link. So it is not straightforward to satisfy both latency and reliability at the same time. The increment in the number of edge nodes decreases the computation delay of the task but tends to increase the risk of error probability. This issue makes it more challenging to design an optimal offloading scheme, which takes account of computations and communications.

The integration of MEC with vehicular networks is evolving a new paradigm called vehicular edge computing. But offloading the tasks to edge vehicles poses security and privacy issues. Huang, X. et al. [34] suggested a decentralized reputation management system to implement security assurance and improve network efficiency in the implementation of vehicular edge computing. But in this scenario, roadside units are vulnerable to intrusions, so that problem still needs to be addressed. Zhang, K. et al. [35], the authors devised a contract-based computation offloading scheme in cloud-enabled vehicular networks. Their system maximized the advantage of the MEC service provider by improving the allocation of the computing resources based on the scheduling threshold. They used the MEC servers to offer computation offloading services and designed an optimal offloading algorithm. Their system considers the resource limitation of MEC servers, latency tolerance, and transmission cost. The MEC server also gets the payment from vehicles based on the computational offloading task. It uses a wireless communication service for the contract information payment. One of the main issues is to analyze the effect of transmission control between data of mobile users and vehicles. Another problem in vehicular edge computing networks is to minimize the cost of service sharing as a volunteer node. Such as providing a video streaming service that requires resources from mobile users. A valid service control mechanism was composed in an online vehicle MEC environment to address these issues by Nguyen, T. et al. [36]. They propose a video streaming service model based on the lower cost of obtaining data from nearby vehicles. They also recommend an incentive mechanism to encourage users to rent their resources. Roadside units play a vital role in vehicular edge computing networks. Liu, Q. et al. [37] proposed an adequate disseminated computation offloading algorithm to enable better offloading arrangements for the vehicle to vehicle networks. To guarantee the most beneficial use of underutilized vehicular computational resources. Feng, J. et al. [38] introduced an autonomous vehicular edge (AVE) structure in controlling the unused computational resources of vehicles. They select MEC based environment to address various network related issues in vehicular technology. The authors present an efficient scheduling and adaptive offloading scheme that reduces the computation complexities in a VANET environment.

MEC has the potential to achieve an optimal trade-off for delay-sensitive and computation- intensive tasks. Hou, X. et al. [39] observed two types of vehicles (parked vehicles and slow vehicles) as a foundation in implementing computational resources for vehicles with computation-intensive jobs in the vehicular edge computing. Vehicle to vehicle communication requires service-deployment latencies below a few tens of milliseconds. They proposed a new paradigm with the name of Vehicular Fog Computing. Their system satisfies basic requirements such as location awareness, low latency, and mobility.

The abundance of IoT devices has risen significantly in licensed and unlicensed band networks (e.g., wireless fidelity). Ho, J. et al. [40] introduced a queueing model for energy storage and battery consumption behavior of IoT devices and a low energy probability model. The proposed model provides a formula for the downlink speed of IoT devices by calculating battery exhaustion, download opportunities, and the likelihood of the initial window size of the licensed assisted access channel backoff. They have distinguished how to transmit power packs for wireless EH devices, which exist on authorized secondary access channels with WiFi channels. They continued this notion to wireless networks using the power pack concept practiced in wired networks. However, their work did not focus on diminishing interference by downloading licensed and unlicensed bands. Another offloading model for EH devices is proposed through providing sustainable energy supply and adequate computer skills in a work by Li, C. et al. [41]. Nowadays, MEC is combined with wireless power transmission to improve wireless devices’ performance in IoT systems called wirelessly powered MEC. In their work, they used non-orthogonal multiple access technologies to handle a boot collision where two or more devices could identify the same syncword. syncword is used for synchronizing data transmission. The results of theoretical performance analysis show that the power consumption of the system is performing well. But they have not considered the task dropping scenarios for mobile EH devices.

3. System Model

A multi-user, multi-server mobile edge computing systems with energy harvesting devices is considered. The proposed system model consists of N different mobile devices, and those devices have EH components. Many EH devices rely on renewable energy sources to captured stored for future use. This system also contains M MEC servers. Those servers will be used for the offloading purpose, and they are located at some distance D from EH devices. Mobile devices can use the wireless medium to access the MEC servers [42]. These servers are capable of performing computational tasks on behalf of mobile devices. In the experimental simulations, $N=\{1,2,\dots ,N\}$ mobile devices and $M=\{1,2,\dots ,M\}$ MEC servers are used. It is assumed that every device resides within the range of the MEC server. Through the proposed smart offloading strategy, the computational process can be boosted significantly. The system model of multi-server, multi-user computing systems is explained in Figure 2. Every energy harvesting device has two types of tasks. Some computation is done locally, while others will be offloaded to the server [43].

The wireless medium is identically distributed through the system, and the time slot is denoted by $\tau$ = 0.002 s. Maximum current is set to be $E_{max}$ = 3 mJ and minimum current $E_{min}$ = 0.02 mJ. The remaining notations and their values, along with their descriptions, are enlisted in

Table 2. Notations along with values used for experiments.

Sr	Notations	Description	Values
1.	K	switching power supply	${10}^{-28}$
2.	$\tau$	time slot	0.002 s
3.	$\omega$	omega	${10}^6$ Hz
4.	$\sigma$	sigma	${10}^{-13}$ W
5.	$E_{max}$	maximum current	3.00 mJ
6.	L	one bit size	1000 bit
7.	X	movement for a period of time	737.5 s
8.	$W=(L\times X)$	number of clock cycles	737,500
9.	$g_0$	Path	−40 dB
10.	N	amount of devices	10
11.	M	MEC servers	5
12.	T	Iterations	50
13.	$E_{min}$	Minimum current	0.02 mJ
14.	V	Penalty value	10${}^{-5}$ (J${}^2$/s)
15.	$\rho$	density	0.6
16.	$E{H}_{max}$	upper limit of the value	${48}^{-6}$ J
17.	$Pt{x}_{max}$	maximum movement	1 W
18.	$f_{max}$	maximum period of CPU time	1.5 GHz

.

4. Integer Linear Programming Based Computation Offloading

Integer linear programming is one of the top algorithms of the last century, which is used to solve linear problems. This algorithm goes around feasible region constraint by using different linear functions. Then it finds the first intersection between the objective function and the feasible region. It allows users to switch between different modes. Linear programming is used to switch between different states. MEC system is comprised of different modes based on executing tasks such as offloading execution, task dropping, and local execution. Integer linear programming is useful in such scenarios. The run time complexity of integer linear programming is NP-complete [44]. Let $D=(N,R)$ be an undirected graph. Define a linear program as an Equation (1) with the constraint of $x_v+x_u\ge 1$ for all $uv$ belongs to R it implies that at least one end point of every edge is included in this subset.

$$min\sum _{v\in N}{x}_v.$$

(1)

Another constraint of $x_v\ge 0$ where v belongs to N. Likewise given vertex cover that treat C, $v\in C$ can set $x_v$ to 1, and $v\notin C$ can set $x_v$ to 0. Thus giving us a feasible solution to the integer program [45].

4.1. Resolve Linear Problems for Offloading

Solving a linear problem requires three essential components. The first one is the objective function, which defines what the user wants to achieve. For example, the user wants to maximize profit or minimize time. Decision variables are the variables that are updated in search of optimal values that meet the objective function. The third is the constraints. In the real world, there are many limitations, such as insufficient running time, resources, computational power, and so on. Linear programming has two foremost objectives to deal with, inequalities and minimization. The offset point is a matrix $Ax=B$, but the only adequate solutions are non-negative. It expects $x⩾0$, meaning that no component of x can be negative. From many possible solutions, linear programming chooses the solution that minimizes the cost. The computation offloading delay comprises a couple of parts, computation time, and transmission delay [46]. There is a trade-off between the two parts due to their differences in computing capability and distances. The computational offloading problem can be formulated as Equation (2).

$$Cos{t}_{\zeta ,\eta ,\theta }=\sum _{i=1}^m\sum _{j=1}^n\left(c_{i,j}+d_{i,j}\right),$$

(2)

where $c_{i,j}$ denotes the computation time and $d_{i,j}$ denotes the transmission delay. $\zeta ,\eta ,\theta$ are used to denote the status of task offloading execution, task dropping, and local execution based on the executing tasks according to the following scenarios.

$$\zeta =\left\{\begin{array}{c}1,\mathrm{local}\mathrm{execution}\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.\eta =\left\{\begin{array}{c}1,\mathrm{offloading}\mathrm{execution}\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.\theta =\left\{\begin{array}{c}1,\mathrm{task}\mathrm{dropping}\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

(3)

This cost minimization function also involves some constraints, such as MEC server is constraint and its total number is M. Equation (5) is to represent the limitation of resources for computation offloading request. Equation (4) shows that tasks can be dropped due to lack of energy of EH device. EH devices often faces random variation in harvesting energy.

$$\sum _{i=1}^m{y}_{i,j,\theta }\le m\forall j\in [1,n]$$

(4)

$$\sum _{i=1}^m{y}_{i,j,\eta }\le min\{m,M\}\forall j\in [1,n].$$

(5)

4.2. Multiple Server and Multiple Users Scenario

In the real-time scenario, the delay-sensitive task request can be generated dynamically. The scheduling methodology for the task is handled by an integer linear programming based computational task model. The task should be executed within the required task execution time. The proposed model provides an execution slot while considering the optimization and availability of resources and the best quality of experience (QoE) provisioning. It determines a strategy to drop the task or to execute it locally. In this model, the computational task is represented as $tas{k}_i^t$ where i is the ith device and t is the time stamp at which task request is popped to be executed. Now the probability of a task popped at ith device at time slot $\tau$ is represented by Equations (6) and (7). These two equations illustrate the constraint that one module can be computed at either the mobile device or server-side. If task request arrives computation can be done by the ith device at the $\tau$ time depending on energy value which is $E_i^t$=1 and computation case can be decided as an offloading or local else if the energy of the ith device is insufficient, the value $E_i^t$=0 and task will be dropped.

$${\zeta }_i^t+{\eta }_i^t+{\theta }_i^t=1,t\in \tau ,i\in N$$

(6)

$$\zeta ,\eta ,\theta \in \{0,1\}.$$

(7)

In the proposed scenario, no task buffer is considered. Task execution is decided using indicators ($\zeta ,\eta ,\theta$). The indicators determine whether to execute locally or offload or to drop the task. The indicator determines the value of task i at time $\tau$ with computation strategy. We have three task computation approaches ($\zeta ,\eta ,\theta$) where $\zeta$ is local execution, $\eta$ is the offloading, and $\theta$ is the dropping of the task. So the indicators for the task i can be determined as ${\zeta }_i^t,{\eta }_i^t$,and ${\theta }_i^t$ and the computation probability for them is as according to Equation (6). Two main factors determine the value for each of the indicators. One is the cost of execution at local, and the other is the cost of execution in offloading. In case of offloading request the computation model can be represented as $tas{k}_{i,j}^t$ where i is the ith device, j is the jth server and $\tau$ is $\tau$th timestamp. Depending on the channelization in terms of transmission delay, computation in terms of CPU cycles, and optimize resource utilization in terms of energy consumption, the offloading cost is decided, and the model can be executed [31].

$$R_{i,\eta }^t=lo{g}_2(\frac{\sigma \times L}{\omega \times h_{i,j}^t}),t\in \tau ,i\in N,j\in M$$

(8)

$$P{L}_{\eta }=(\frac{L}{(\omega \times {\tau }_d)-1}{)}^2\times \frac{\sigma }{h_{i,j}^t}t\in \tau ,i\in N,j\in M$$

(9)

$$R_{i,\zeta }^t=\sum _v^L(f_{i,v}^t),t\in \tau ,i\in N,$$

(10)

$$P{L}_{\zeta }=\sum _v^L\times c(f_{i,v}^t),t\in \tau ,i\in N.$$

(11)

Achievable rate for $\left(R_t\right)$ can be calculated using Equation (8) where $\sigma ,\omega$ and L denote noise power, bandwidth and task bit size respectively in the case of offloading. Power needed for execution of computation task can be calculated $\left(p{L}^{\tau }\right)$ using Equation (9). In the case of local execution dynamic voltage v and frequency f is applied to get local transmission delay $R_{i,\zeta }^t$, expressed in Equation (10) and local energy consumed $P{L}_{\zeta }$, expressed in Equation (11). Where c is the coefficient of capacitance, L is the computational task in bits, $N=\{1,2,\dots ,N\}$ mobile devices and $M=\{1,2,\dots ,M\}$ MEC servers.

5. System Flow

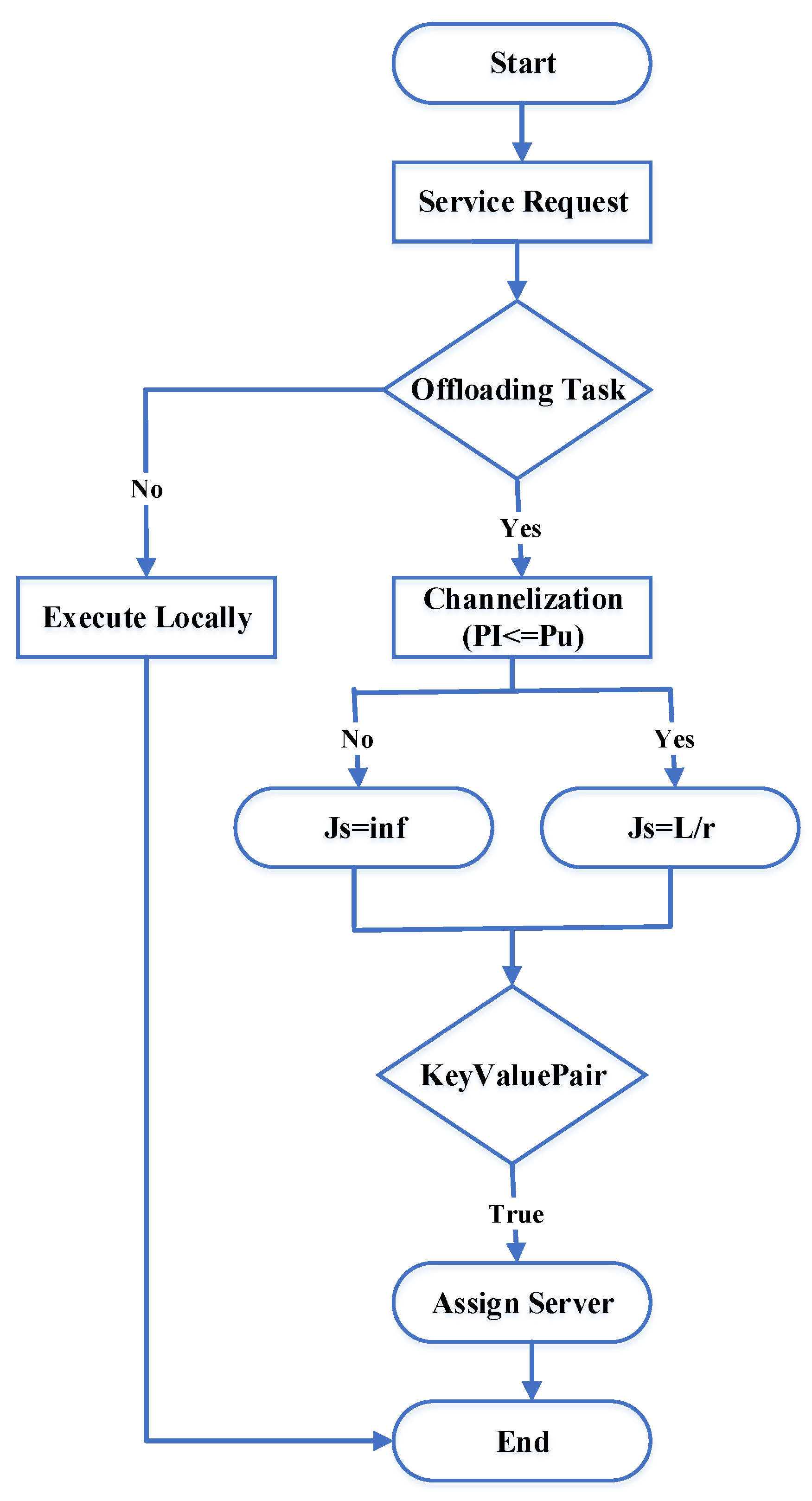
The proposed method allows switching between different modes (i.e., offloading execution, task dropping, and local execution) based on the executing tasks. Figure 3 shows the process flow diagram of the proposed system. It initializes the map of the number of EH devices. If the task is for offloading, the system will calculate the channelization of the EH device. Then it will check the status of the Boolean variable $KBoolPair$. If the status is false, then it will calculate position variable $pos$; Otherwise, it will assign the server for offloading.

The proposed methodology starts with initializing the map with null then stores the number of mobile devices connected to each MEC server. The function produces a computational task, find out the best energy harvesting devices, and then calculates the delay of execution. After that, from the first server and a mobile device that is limited to a distance within 0 to 60, it derives channelization of the mover. Then, it assigns the server or alternative mode for those tasks that users choose to uninstall to perform and finds mobile devices with minimal transmission latency of MEC server pairs. We store the values of key pair, device i, and optimal server j, in map. $mi{n}_i$ and $mi{n}_j$ is obtained corresponding to the minimum delay. At this point, only offloading or uninstall execution is considered. Then the key-value pair is removed from the map and synchronize a series of commonly maintained variables. When the mobile device has a server that can be selected, it will continually look for the shortest delay that can be found. It will then return the outermost while loop to start inspecting for the lowest $J_s$ again. It will then remove the key-value pair from the map and synchronize a series of co-maintained variables. The time complexity of Algorithm 1 is represented by $\mathcal{O}\left(T\right(EH\left)\right)$, where T and EH denote the total number of time slots and energy harvesting devices, respectively.

Detailed steps of the proposed algorithm are explained in Algorithm 1 and its sub-algorithms.

Table 3. Description of variables used in algorithms.

Sr #	Variable	Description
1	$mi{n}_i$	Minimum delay for device
2	$mi{n}_j$	Minimum delay for server
3	$E_{remotematrix}$	Current energy consumption
4	$P_{matrix}$	Best transmission power
5	$J_m$	Locally executed delay
6	$F_u$	Upper frequency of local execution
7	$F_l$	Lower frequency of local execution
8	$KBoolPair$	Boolean variable Flag
9	h	Channel power gain
10	$J_s^{matrix}$	Delay value of the current mobile device

describe the variables which are used in algorithms.

Algorithm 1 Energy-efficient computation offloading.

Ensure: Initialize flags with null

Ensure: Initialize $E_{remotematrix},P_{matrix},J_m$

while $T\ne T_{max}$do

while $E{H}_i\ne E{H}_{max}$ do

generate $f_l$ and $f_u$

if $f_l\le f_u$ then

generate $f_0$

calculate $E_{local}(t,i)$

else

set $J_m\left(i\right)$ equal to infinity

set $KBoolPair$ as true

end if

end while

calculate channelization of mover // Execute Algorithm 2

if $KBoolPair$ is false then

use integer linear programming // Execute Algorithm 3

else

assigns the server for those tasks needs to be offloaded // Execute Algorithm 4

end if

slice iteration++

end while

5.1. Computation Offloading

The primary purpose of this system is to choose the mode for offloading or local execution. In Algorithm 1, the proposed energy-efficient computation offloading mechanism is discussed. This algorithm works for every iteration of Time T initializing from 1. It starts with the mapping null and initializing flags, $E_{remotematrix},P_{matrix}$, and $J_m$. $E_{remotematrix}$ and a matrix of zeros initializes $P_{matrix}$ with the dimension of $\tau \times N$, where $\tau$ is the number of time slices, and N is the number of mobile devices. Flags are initialized with the matrix of $M\times 1$, where M is the number of MEC servers. $E_{remotematrix}$ is to save the current energy consumption of the mobile device to each MEC server separately in a matrix. $P_{matrix}$ is to save the best transmission power of the current mobile device to each MEC server separately. $J_m$ is to store the locally executed delay of each mobile device separately for use in secondary decision making. The number of devices is set as N, and a loop is initialized for every device. A variable zeta is initialized with binomial distribution and generate Lower frequency $F_l$ and upper frequency $F_u$ of local execution by N mobile devices, using Equation (12) and Equation (13) respectively. If $F_l$ is less than or equal to $F_u$, then the function will calculate the execution delay. Calculate energy consumption performed locally by $i_{th}$ mobile device $E_{local}(t,i)$ and generate $F_o$ using Equation (14). The $KBoolPair$ set to be False. However, $KBoolPair$ is True when $F_l$ is greater than $F_u$, where $J_m\left(i\right)$ is infinity otherwise $KBoolPair$ will remain False.

After that, the channelization of mover is calculated using Algorithm 2 to decide between using integer linear programming or assigning of the task to the server. After the execution of Algorithm 2 system will check the status of $KBoolPair$. If $KBoolPair$ is false, then use integer linear programming mechanism using Algorithm 3. Otherwise, the tasks that need to be offloaded are assigned to a server using Algorithm 4. In the end, the time slice iteration is incremented, and the whole procedure is repeated until the maximum time T is reached.

$$F_L=max(\sqrt{\frac{E_{min}}{k\times w}}÷\frac{w}{{\tau }_d})$$

(12)

$$F_u=min(\sqrt{\frac{E_{min}}{k\times \omega }}÷f_{max})$$

(13)

$$f_o=(\frac{v}{\theta \times {\omega }^{\Delta }\times k}{)}^{\frac{1}{3}}.$$

(14)

Algorithm 2 Calculate channelization of mobile devices.

Ensure: Initialize $h_{tmp}$

Ensure: Calculate $R_t$, $P{L}^{\tau }$

if $p_l\le p_u$then

set $j_S$ as inf

set $KBoolPair$ as true

else

calculate $J_s$ by dividing L to r;

set $KBoolPair$ as true

end if

set $J_s^{matrix}(i,j)$ as $J_s$;

calculate container number of the execution

5.2. Channelization of EH Device

One of the major reasons for anomalies is the incorrect calculation of the channels’ access mechanism. In this research, the adaptable width of channelization is calculated. It helps in minimizing performance anomalies. The calculation of the channelization of mobile devices is explained in Algorithm 2. To calculate the mover’s channelization, initialize $h_{tmp}$ with a matrix $h(i,j)$, where h is channel power gain from the mobile device to the server. Then calculate temporary achievable rate $\left(R_t\right)$ using Equation (8) and power needed for execution of computation task $\left(p{L}^{\tau }\right)$ using Equation (9). If $p_L$ is less than or equal to $p_U$, set $j_S$ as infinity and set $KBoolPair$ as true. Otherwise calculate $J_s$ by dividing L to r; and set $KBoolPair$ as true. then set $J_s^{matrix}(i,j)$ as $J_s$. If the mode is equal to two, then calculate the value of the map.

5.3. Integer Linear Programming

The use of integer linear programming is explained in Algorithm 3. For this, we initialize the target as a matrix of zeros. We also initialize variables intcon, A, b, $l_b,u_b$ and calculate an updated target and a goal. Intcon is the vector of positive integers which ranges from 1 to $N\times (M+2)$. Then, we return the calculation result of the system operation and set the value of position variable ($pos$) where system operation is true. If pos is equal to 1, then set indicator $(t,i)$ as 1. If pos is equal to 2, then set indicator $(t,i)$ as 3. Otherwise, set indicator $(t,i)$ as 2.

Algorithm 3 Use integer linear programming.

Ensure: Initialize target as a matrix of zeros

Ensure: Initialize intcon, A, b, $l_b,u_b$

while $Iter\ne 10$ do

calculate updated target and goal

returns calculation result of system operation

set pos where system operation as true

if pos is equal to 1 then

set indicator $(t,i)$ as 1;

if pos is equal to 2 then

set indicator $(t,i)$ as 3;

else

set indicator $(t,i)$ as 2;

end if

end if

end while

5.4. Assigning the Server

The steps for assigning the server for those tasks which need to be offloaded are described in Algorithm 4. For this purpose, start with setting the movement of the maximum CPU time of the server and calculate the upper bound $ub$. Then repeat the next steps until the map is not equal to null. The function to find a mobile device with minimal transmission latency also finds minimum i and j corresponding to the minimum delay. At this point, the algorithm only considers uninstalling execution tasks. If $rand$ is less than or equal to $eps$ than delete the key-value pair from the map and synchronize a series of commonly maintained variables. Corresponding to the MEC server, Increment 1 in the flag and Set $J_s^{matrix}(mi{n}_i,mi{n}_j)$ to $inf$ and if min value of $J_s^{matrix}$ is not equal to inf then return the outermost while to start looking for the smallest $J_s$ again. Otherwise, initialize the indicator variable and delete the key-value pair from the map and synchronize a series of co-maintained variables. Here, $J_s^{matrix}$ is to save the delay value of the current mobile device to each MEC server. In a case where the mode is equal to 2, the current optimal mode will still execute for uninstallation if $flag{s}_{mi{n}_j}$ are less then or similar to $ub$, than remove the key-value pair from the map and synchronize a series of commonly maintained variables. Set $J_s^{matrix}(mi{n}_i,mi{n}_j)$ to infinity, and if min value of $J_s^{matrix}$ is not equal to inf, then return the outermost variable and reset the indicator variable. After that, set the new optimal mode and initialize indicator $(t,i)$ to mode, Also remove the key-value pair from the map. This algorithm is used to assign the server or alternative mode for those tasks that users choose to uninstall to perform.

Algorithm 4 Assigns the server for those tasks needs to be offloaded.

Require: movement of maximum CPU time period of server

Ensure: Calculate $UB$

while $map\ne null$ do

Found device with minimal transmission latency

if$rand\le eps$then

if $Fla{g}^{m}i{n}_j\le UB$ then

Corresponding to the MEC server Increment 1 in flag

Set $J_s^{matrix}(mi{n}_i,mi{n}_j)=inf$

else

Reset indicator variable

end if

else

if $rand⩾eps$ then

Current optimal mode is still executed for uninstallation

if $flag{s}_{mi{n}_j}$ is less than or equal to UB then

$flag{s}_{mi{n}_j}$ 1++

Set $J_s^{matrix}(mi{n}_i,mi{n}_j)=inf$

else

if $min\left(J_s^{matrix}\right)\ne inf$ then

Returns the outermost

else

Reset indicator variable

end if

end if

else

initialize indicator $(t,i)$ to mode

Remove the key-value pair from the map

end if

end if

end while

6. Performance Evaluation

In this section, the analysis of the proposed algorithm based on parameters, enlisted in Table 2 is performed. The experiments to compare simulation results with the existing mixed-integer nonlinear program based software defined task offloading algorithm [47] and Lyapunov optimization-based genetic algorithm [31] is also conducted. The experimental system consists of the intel core i5 processor with 16 GB RAM and R2019b version of MATLAB. The active switching power supply is initialized as K = $1\times {10}^{-28}$ and server bandwidth as $\omega$ = $1\times {10}^6$ Hz. The value of tau = 0.002 and noise power, $\sigma$ = $1\times {10}^{-13}$. The movement of the maximum CPU time is initialized with $1.5\times {10}^9$ Hz, maximum current with 0.003 (j), the movement for a period of time as 737.5. $L\times X$ calculates the required number of clock cycles needed by the mobile device to perform local computing tasks. In the multi-server environment, the number of MEC servers is set as M = 8 and the number of mobile devices as N = 10. There is a penalty value in LODCO to optimize the performance of the tasks, which is V = $1\times {10}^{-3}$ [30]. Furthermore, some containers are required to store the values of run-time results such as the value of momentum, offload execution, frequency of mobile devices for local and remote execution frequency, and execution cost. Detailed values and their descriptions are given in Table 2.

6.1. Results

This section demonstrates the results of the proposed algorithm. The algorithm was implemented in MATLAB R2019b for simulation. The graphs and plots were also designed using the functions of MATLAB. For the graphs toolbox, MATLAB plot gallery [48] is used. MATLAB requires extensive execution time for solving complex problems. So only the small size of mobile devices and servers is considered.

Table 4. Simulation environment.

Sr #	Component	Description
1	CPU	Intel Core i5-8500
2	RAM	16 GB
3	OS	MS Window 10
4	IDE	Matlab 2019b
5	Graph tool	MATLAB plot gallery

shows the components used for experimental simulations

Quality of experience (QoE) cost depends upon the execution delay and cost of offloading the task. It can be calculated using Equation (15). The average QoE-cost is demonstrated in Figure 4 for all mobile devices. The proposed algorithm obtains this cost at each time slot. The average QoE cost starts with a maximum of $0.9\times {10}^{-3}$ J, and then it gradually starts decreasing. By using the proposed algorithm, a stable state of average QoE cost at the end of this graph is obtained. It shows the stability obtained by the proposed algorithm.

$$QoE={\mathrm{\Sigma }}_{iϵN}\left(w/f_i\right)/{\tau }_i$$

(15)

In Figure 5, the X-axis shows the number of time slots for energy harvesting devices, and the battery energy level is shown on Y-axis. There are 10 Mobile devices (MD) and one offsetting level. This graph depicts the variation in the level of average battery energy for different time slots. It shows significant improvement in stabilizing the energy level. It acquired the stability between 125th and 150th-time slots. The energy level starts increasing at the beginning and finally maintains an energy level close to the offsetting level for all mobile devices.

Figure 6 shows the average battery energy level of all mobile devices. The X-axis shows the index of the mobile device, and Y-axis shows the average energy level of the battery. All the devices maintained almost the same maximum level of energy, which ranges from 0.0017 J to 0.0021 J.

6.2. Comparison

To verify the effectiveness of the proposed algorithm, it is compared with the existing mixed-integer nonlinear program based software defined task offloading algorithm [47] and Lyapunov optimization-based genetic algorithm [31]. The results of the comparison are displayed in Figure 7. Lyapunov optimization-based genetic algorithm and mixed integer nonlinear program based software defined task offloading algorithm are NP-hard programs, whereas the integer programming solution is NP-complete [44]. Lyapunov optimization-based algorithm and the proposed algorithm are dynamic, but results show that proposed algorithm is taking average less energy concerning each device. The X-axis shows the number of maximum distance between every Mobile device and servers, whereas Y-axis displays the average ratio of offloading tasks. Each energy level starts from $0.979\%$ and gradually decreases to $0.87\%$. This graph depicts the variation in the level of offloading tasks to distance. When the distance increases, the average ratio of offloading tasks starts decreasing. If the distance between the MEC server and a mobile device is increased, then the channel power also amplifies, this increment in channel power requires more energy and results in the execution delay.

7. Discussion

MEC with multi servers is emerging as a new paradigm that can replace client cloud architecture. Many devices with low computational power are also included in the MEC environment. Offloading the work for such computationally intensive energy harvesting devices can increase the quality of computation experience. The authors of References [30,49] use dynamic computation offloading algorithms for MEC with energy harvesting devices. However, the presented aspects and details are not generic. The paper proposes an approach based on linear programming to improve the efficiency of energy consumption in the MEC server. A dynamic and energy-efficient computation offloading approach for multi-users and multi-servers is introduced in the mobile edge computing system. The proposed method allows switching between different modes of offloading execution, task dropping, and local execution based on the executing tasks. The reason for conducting this study is to improve the quality of experience by energy-efficient computation offloading. Simulation results illustrate that the proposed solution can trade off the energy of computational offloading tasks efficiently. During the simulation, it is observed that the energy level starts from 0.979% and gradually decreases to 0.87%. The impact of channelization is also focused on this work because the incorrect calculation of the channel’s access mechanism leads to anomalies. In this research, the adaptable width of channelization is calculated, which will help to minimize the performance anomalies. In the future, this work can be extended by considering the MEC servers with limited resources.

8. Conclusions

In this paper, a multi-user and multi-server mobile-edge computing system with energy harvesting devices is examined. An algorithm for computation offloading is proposed. Multi-server mobile edge computing has the purpose of decreasing the response rate of mobile devices, and it is getting popular day by day. The proposed system is an improved computation offloading strategy, which is also energy efficient. Experimental analysis and simulation results show that the proposed algorithm can efficiently trade-off the power of computational offloading tasks. It also requires less time for execution, and it fits very well with mobile edge computing operations. In the proposed future work strategy, we will study the resource limitations of the MEC server and provide a more general situation for mobile device users to dynamically leave during computation offloading.