Electrical Material Properties of Carbon Reinforced Concrete
Abstract
:1. Introduction
2. State of the Art
2.1. Carbon Reinforced Concrete
2.2. Characterization of RF Properties of Building Materials
3. Investigations & Setup
3.1. Reinforcement Material
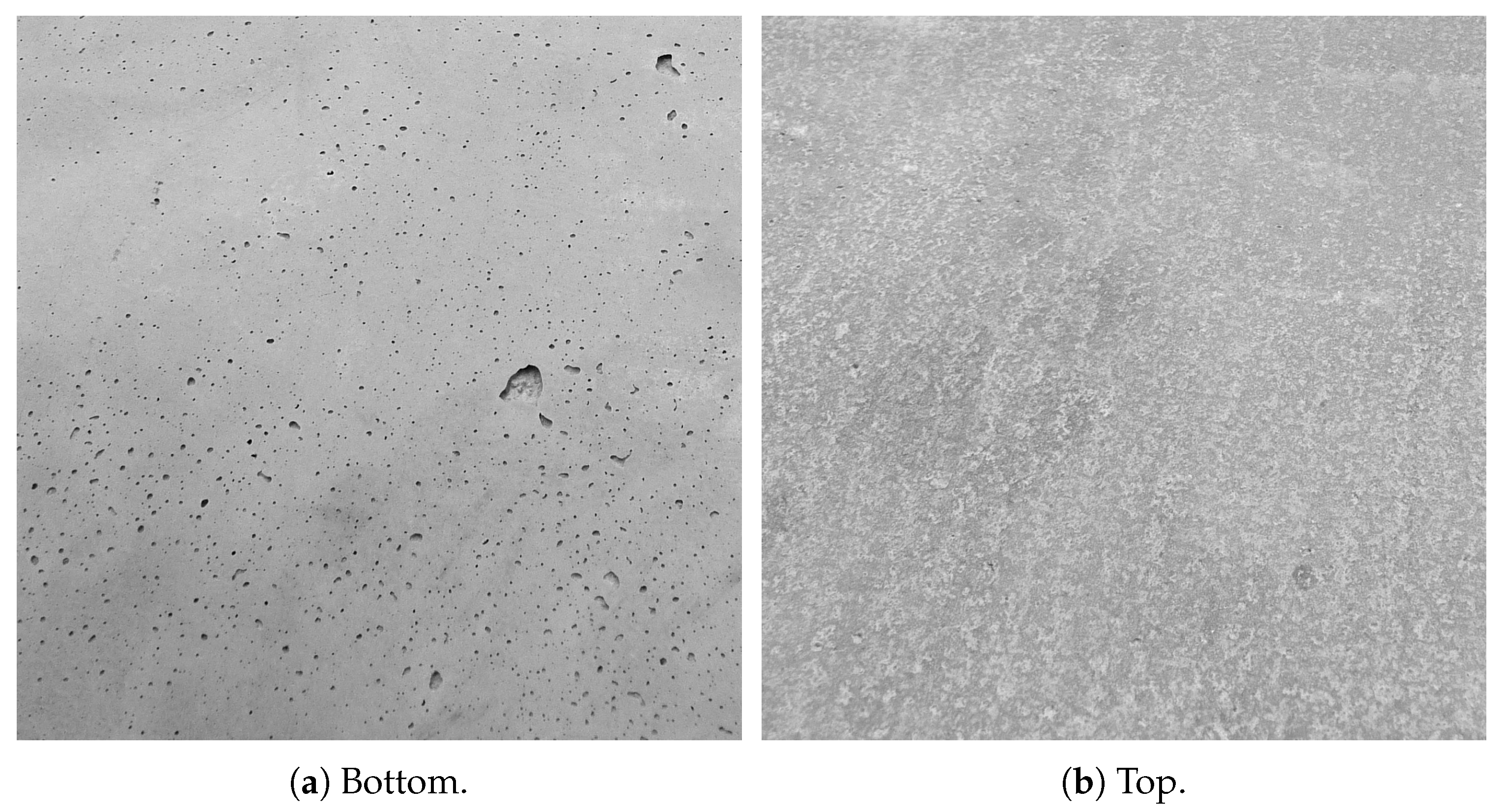
3.2. Concrete Samples & Preparation
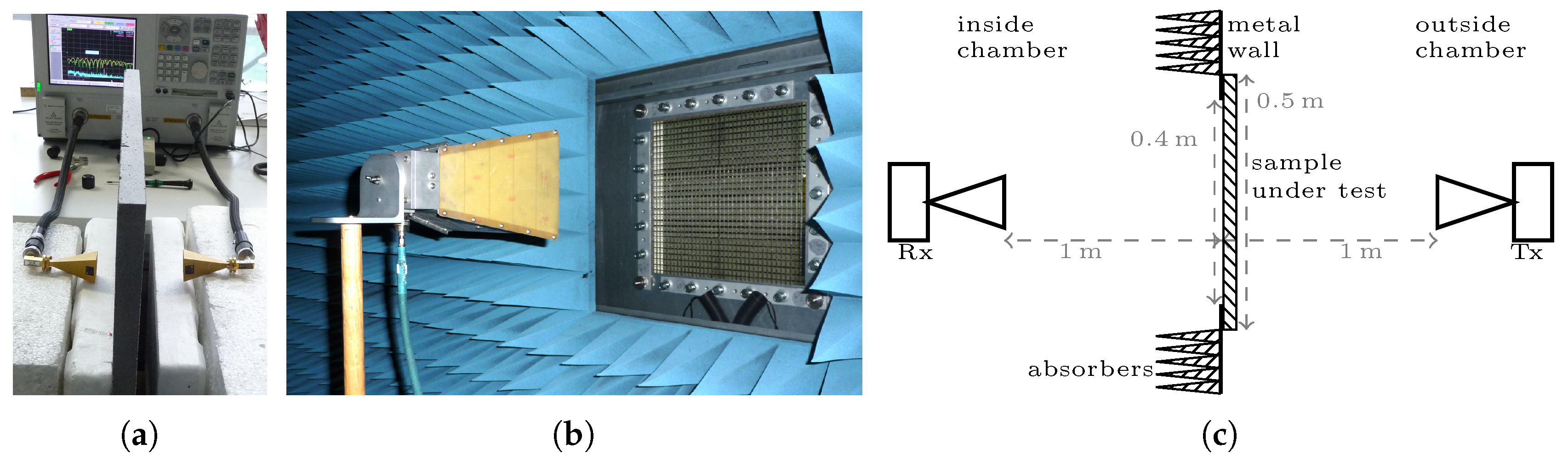
3.3. Measurement Setup
3.3.1. Measurement Window of Anechoic Chamber
3.3.2. Short-Distance Setup 50 to 67 GHz
3.4. Measurement Procedure
4. Results & Discussion
4.1. Electrical Resistance at DC
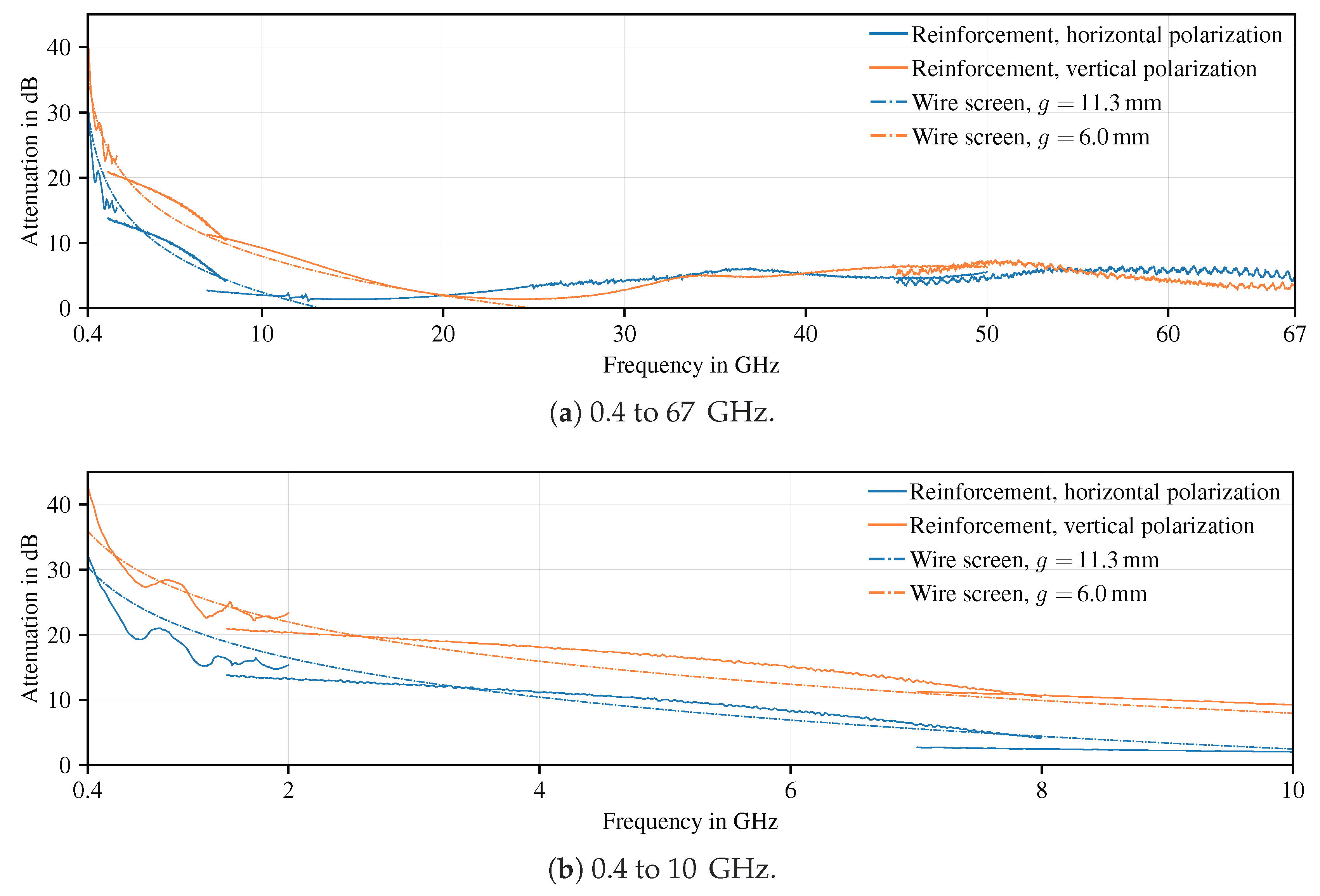
4.2. Transmission Measurements of Reinforcement Material
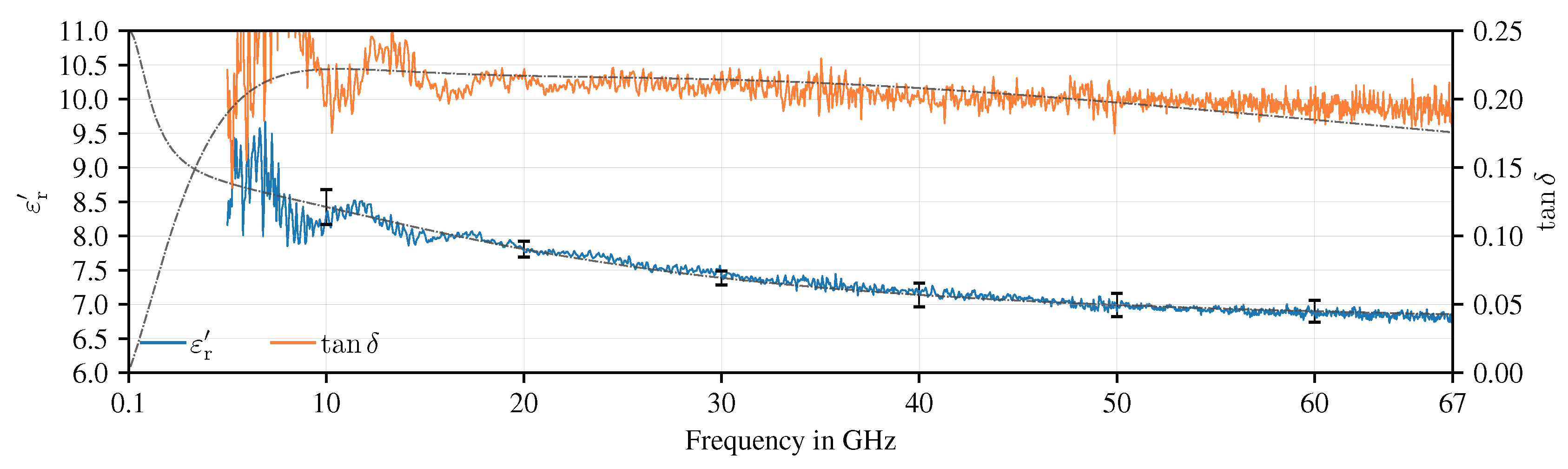
4.3. Material Properties of Concrete Samples
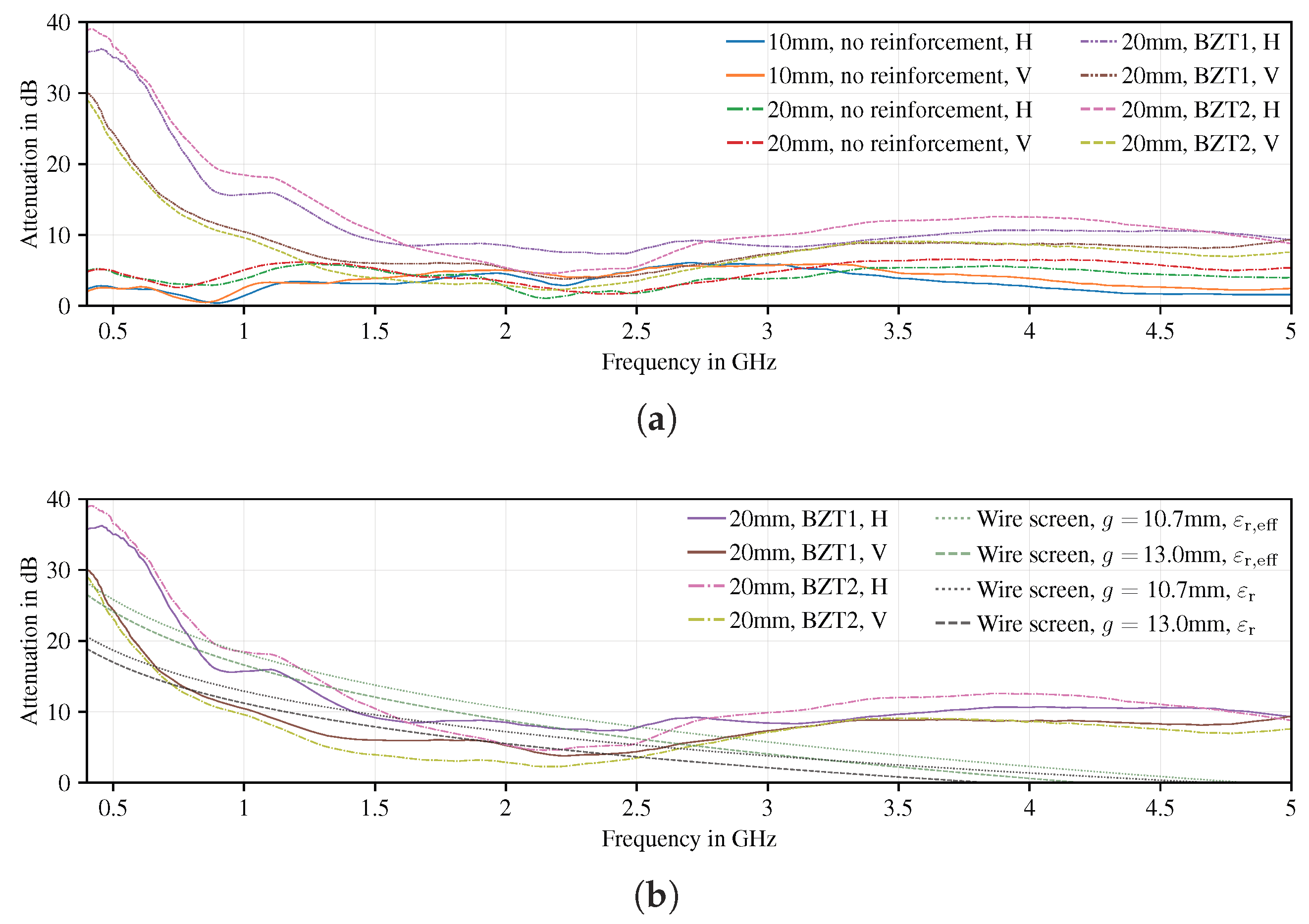
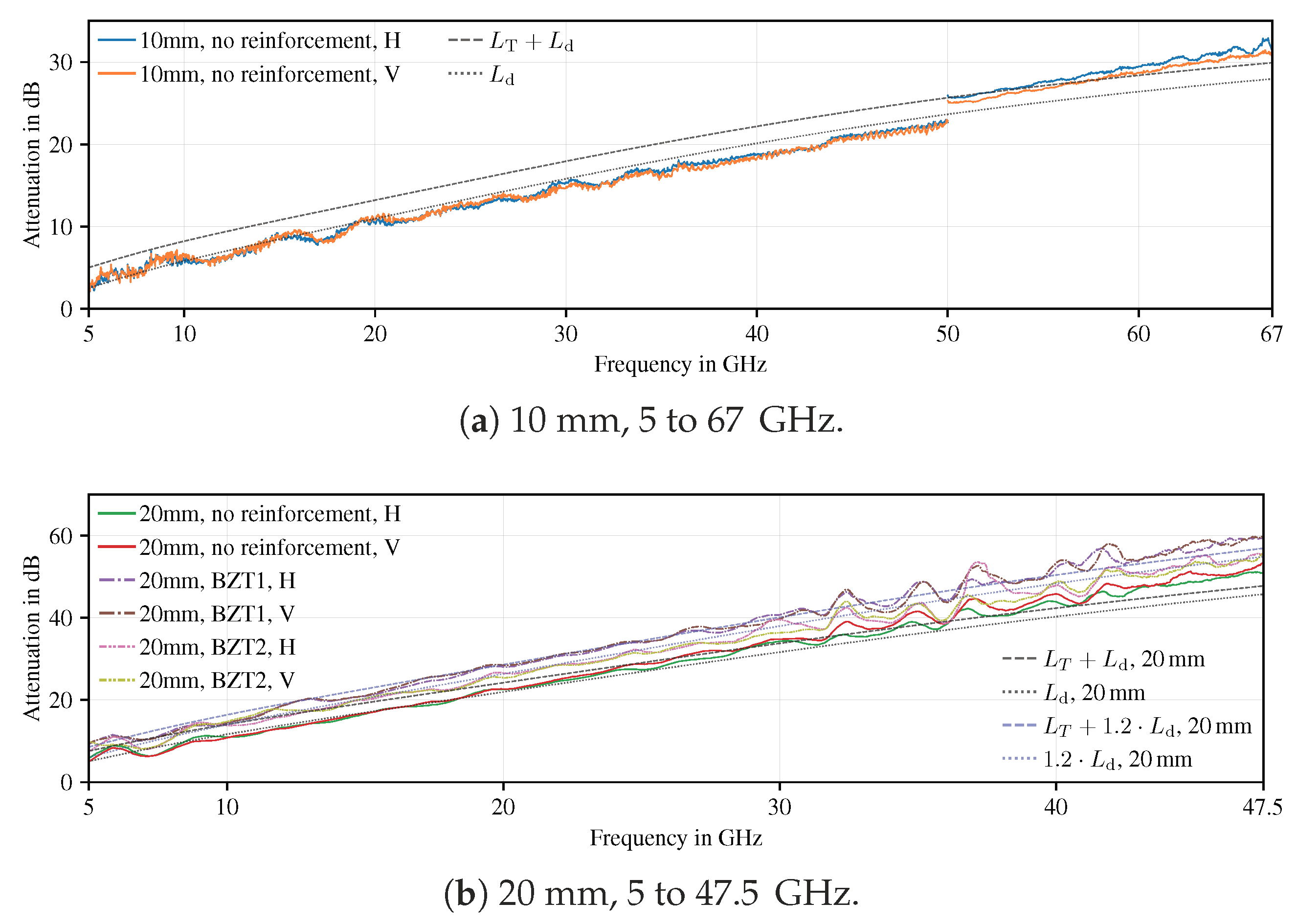
4.4. Transmission Measurements of Reinforced Concrete Slabs
4.4.1. Influence of the Carbon Fiber Reinforcement Embedded in Concrete, 0.4 to 5 GHz
4.4.2. 5 to 67 GHz
5. Conclusions and Further Work
5.1. Influence of the Reinforcement
5.2. Characterization of the Investigated Samples
5.3. Influence of the Pagel TF10 Fine Concrete
5.4. Consequences for Indoor and Urban Radio Communications Planning
5.5. Further Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FDTD | finite differences in time domain |
| FSPL | free-space path loss |
| MUT | material under test |
| RF | radio frequency |
| SE | shielding effectiveness |
| SBR | styrene-butadiene rubber |
| UHPC | Ultra high performance concrete |
References
- Moore, D. The Roman Panteon: The Triumph of Concrete; University of Guam: Mangilao, Guam, 1995. [Google Scholar]
- Scheerer, S.; Schladitz, F.; Curbach, M. Textile Reinforced Concrete–from the idea to a high performance material. In Proceedings of the FERRO-11—11th International Symposium On Ferrocement and 3rd ICTRC International Conference On Textile Reinforced Concrete, Aachen, Germany, 7–10 June 2015. [Google Scholar]
- Schumann, A.; Michler, H.; Schladitz, F.; Curbach, M. Parking Slabs Made of Carbon Reinforced Concrete. Struct. Concr. 2018, 19, 647–655. [Google Scholar] [CrossRef]
- FCC. FCC Takes Steps to Facilitate Mobile Broadband and next Generation Wireless Technologies in Spectrum above 24 GHz. 2016. Available online: https://apps.fcc.gov/edocs_public/attachmatch/DOC-340301A1.pdf (accessed on 30 April 2020).
- Nilson, A.H.; Darwin, D.; Dolan, C.W. Design of Concrete Structures, 5th ed.; McGraw Hill Higher Education: Boston, MA, USA, 2015. [Google Scholar]
- Schladitz, F.; Tietze, M.; Lieboldt, M.; Schumann, A.; Patricia, M. Carbon Reinforced Concrete in Construction Practice. In IABSE Conference Kuala Lumpur 2018—Engineering the Developing World; International Association for Bridge and Structural Engineering: Kuala Lumpur, Malaysia, 2018; pp. 348–355. [Google Scholar]
- Ezquerra, T.A.; Connor, M.T.; Roy, S.; Kulescza, M.; Fernandes-Nascimento, J.; Baltá-Calleja, F.J. Alternating-Current Electrical Properties of Graphite, Carbon-Black and Carbon-Fiber Polymeric Composites. Compos. Sci. Technol. 2001, 61, 903–909. [Google Scholar] [CrossRef]
- MatWeb. MatWeb, Your Source for Materials Information. Available online: http://matweb.com/ (accessed on 30 April 2020).
- Haynes, W.M. CRC Handbook of Chemistry and Physics, 97th ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Kirsten, M.; Freudenberg, C.; Cherif, C. Carbonfasern, der Werkstoff des 21. Jahrhunderts. Beton Und Stahlbetonbau 2015, 110, 8–15. [Google Scholar] [CrossRef]
- Helbig, T.; Unterer, K.; Kulas, C.; Rempel, S.; Hegger, J. Fuß- und Radwegbrücke aus Carbonbeton in Albstadt-Ebingen. Beton und Stahlbetonbau 2016, 111, 676–685. [Google Scholar] [CrossRef]
- Kranich, S. Building Permit Issued for the Construction of the World’s First Carbon Reinforced Concrete Building (Press Release). 2020. Available online: https://www.bauen-neu-denken.de/wp-content/uploads/2020/03/2020-02-07-PM_Baugenehmigung-EN.pdf (accessed on 30 April 2020).
- Ferreira, D.; Cuiñas, I.; Caldeirinha, R.F.S.; Fernandes, T.R. A Review on the Electromagnetic Characterisation of Building Materials at Micro- and Millimetre Wave Frequencies. In Proceedings of the 8th European Conference on Antennas and Propagation (EuCAP 2014), The Hague, The Netherlands, 6–10 April 2014; pp. 145–149. [Google Scholar]
- Inomata, M.; Ogawa, T.; Yoshino, S. Material Transmission Loss Modeling for Indoor Propagation Modeling. In Proceedings of the 2014 IEEE 25th Annual International Symposium on Personal, Indoor, and Mobile Radio Communication (PIMRC), Washington, DC, USA, 2–5 September 2014; pp. 722–726. [Google Scholar]
- Sandrolini, L.; Reggiani, U.; Ogunsola, A. Modelling the Electrical Properties of Concrete for Shielding Effectiveness Prediction. J. Phys. Appl. Phys. 2007, 40, 5366. [Google Scholar] [CrossRef]
- Rudd, R.; Craig, K.; Ganley, M.; Hartless, R. Building Materials and Propagation; Technical Report; Office of Communications (Ofcom): London, UK, 2014; Available online: https://www.ofcom.org.uk/research-anddata/technology/general/building-materials (accessed on 30 April 2020).
- Ferreira, D.; Caldeirinha, R.F.S.; Fernandes, T.R.; Cuiñas, I. Hollow Clay Brick Wall Propagation Analysis and Modified Brick Design for Enhanced Wi-Fi Coverage. IEEE Trans. Antennas Propag. 2018, 66, 331–339. [Google Scholar] [CrossRef]
- Dalke, R.A.; Holloway, C.L.; McKenna, P.; Johansson, M.; Ali, A.S. Effects of Reinforced Concrete Structures on RF Communications. IEEE Trans. Electromagn. Compat. 2000, 42, 486–496. [Google Scholar] [CrossRef]
- Weiping, Q.; Shenggao, D.; Yerong, Z. FDTD Calculation of the Effects of Reinforced Concrete Wall on Short Path Propagation of UWB Pulse. In Proceedings of the 2005 Asia-Pacific Microwave Conference Proceedings, Suzhou, China, 4–7 December 2005; Volume 4. [Google Scholar] [CrossRef]
- Choroszuho, A.; Butryło, B. Local Attenuation of Electromagnetic Field Generated by Wireless Communication System inside the Building. Przegląd Elektrotechniczny 2011, 87, 123–126. [Google Scholar]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Boston, MA, USA, 2005. [Google Scholar]
- Hintzen, W. Allgemeine Bauaufsichtliche Zulassung abZ Z-31.10-182: Verstärken von Stahlbetonbauteilen (Methods and Procedures for the Reinforcement of Concrete with Textiles). Allgemeine bauaufsichtliche Zulassung/National Technical Approval, Deutsches Institut für Bautechnik. 2017. Available online: https://www.textilbetonzentrum.de/images/AbZ_Z-3110-182.pdf (accessed on 20 May 2020).
- TF10/TUDALIT Fine Concrete Data Sheet (English). Data Sheet; PAGEL Spezialbeton GmbH & Co. KG: Essen, Germany, 2017; Available online: https://www.pagel.com/all/pdf/gb/tf10_gb.pdf (accessed on 30 April 2020).
- DIN EN 206-1: Beton: Festlegung, Eigenschaften, Herstellung Und Konformität/Concrete—Specification, Performance, Production and Conformity; Norm/Standard Specification, Deutsches Institut für Normung e.V.: Berlin, Germany, 2017.
- DIN EN 998-1: Festlegungen Für Mörtel Im Mauerwerksbau—Teil 1: Putzmörtel/Specification for Mortar for Masonry/Part 1: Rendering and Plastering Mortar; Norm/Standard Specification, Deutsches Institut für Normung e.V.: Berlin, Germany, 2017.
- DIN EN 12390-2: Prüfung von Festbeton—Teil 2: Herstellung Und Lagerung von Probekörpern Für Festigkeitsprüfungen/Testing Hardened Concrete—Part 2: Making and Curing Specimens for Strength Tests; Norm/Standard Specification, Deutsches Institut für Normung e.V.: Berlin, Germany, 2017.
- HL033 Data Sheet. Data Sheet; Rohde & Schwarz GmbH: Munich, Germany, 2018; Available online: https://cdn.rohde-schwarz.com/pws/dl_downloads/dl_common_library/dl_brochures_and_datasheets/pdf_1/service_support_30/HL033.pdf (accessed on 30 April 2020).
- 3164-06 Open Boundary Quad-Ridged Horn Data Sheet. Data Sheet; ETS-Lindgren, ESCO Technologies Inc.: St. Louis, MO, USA, 2018; Available online: http://www.ets-lindgren.com/datasheet/antennas/openboundary-quad-ridged-horn/4003/400303 (accessed on 30 April 2020).
- RFspin DRH50 Data Sheet. Data Sheet, RFspin s.r.o. 2017. Available online: https://www.rfspin.cz/en/antennas/measurement-antennas/drh50 (accessed on 30 April 2020).
- SAGE Millimeter Inc. SAR-2309-15-S2 Data Sheet. Data Sheet. 2017. Available online: https://sftp.eravant.com/content/datasheets/SAR-2309-15-S2.pdf (accessed on 20 May 2020).
- White, D.R.J. EMI Test Methods and Procedures; A Handbook Series on Electromagnetic Interference and Compatibility; Don White Consultants, Inc.: Warrenton, VA, USA, 1974; Volume 2. [Google Scholar]
- Balanis, C.A. Antenna Theory: Analysis and Design, 3rd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- White, D.R.J. Electromagnetic Shielding Materials and Performance, 2nd ed.; Don White Consultants, Inc.: Gainesville, VA, USA, 1980. [Google Scholar]
- Seiler, P.; Hegler, S.; Schladitz, F.; Plettemeier, D. Dielectric Material Characterization for 5G Propagation Modelling. In Proceedings of the 2019 IEEE 2nd 5G World Forum (5GWF), Dresden, Germany, 30 September–2 October 2019; pp. 17–21. [Google Scholar] [CrossRef]
- Seiler, P.S. Dielectric Material Characterization up to Terahertz Frequencies Using Planar Transmission Lines. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2018. Available online: https://nbnresolving.org/urn:nbn:de:bsz:14-qucosa2-339342 (accessed on 30 April 2020).
- Böttcher, C.J.F.; Bordewijk, P. Theory of Electric Polarization, Vol II: Dielectrics in Time-Dependent Fields, 2nd ed.; Elsevier Scientific Pub. Co.: Amsterdam, The Netherlands; New York, NY, USA, 1973; Volume 2. [Google Scholar]
- Ramo, S.; Whinnery, J.R.; Van Duzer, T. Fields and Waves in Communication Electronics, 3rd ed.; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Hecht, E. Optics, 5th ed.; Pearson: Boston, MA, USA, 2016. [Google Scholar]

| Material | Tensile Strength (Axial) | Young’s Modulus | Density |
|---|---|---|---|
| in | in | in | |
| Steel | 0.3 to 0.6 | 210 | 7.9 |
| AR Glass Fiber | 2.0 | 76 | 2.7 |
| Basaltic Fiber | 4.8 | 90 to 110 | 2.6 to 2.8 |
| Carbon Fiber | 3.0 to 5.0 | 240 to 600 | 1.8 |
| Prototype Material | BZT 1 | BZT 2 | ||
|---|---|---|---|---|
| Center-center | between warps | 8 | 12.7 | 12.7 |
| distance | between wefts | 12.3 | 16 | 14 to 16 |
| Carbon Fiber | warps | 2 | 2 | 2 |
| diameter | wefts | 1 | 1 | 1 |
| Gap | between warps | 6 | 10.7 | 10.7 |
| width | between wefts | 11.3 | 15 | 13 to 15 |
| Number Produced | Dimensions (x × y × z) in | Reinforcement & Positioning |
|---|---|---|
| 3 | 50 × 50 × 1 | none |
| 3 | 50 × 50 × 2 | none |
| 2 | 50 × 50 × 2 | BZT1, centered along z |
| 2 | 50 × 50 × 2 | BZT2, centered along z |
| Antenna | Frequency Range | Dimensions (w × d × h) |
|---|---|---|
| R&S HL033 [27] | 0.08 to 2 GHz | 1.96 × 1.8 × 0.1 m |
| ETS Lindgren 3164-06 [28] | 0.3 to 6 GHz | 51.4 × 50 × 50 cm |
| RFspin DRH50 [29] | 4.5 to 75 GHz | 56 × 43.6 × 37.7 cm |
| SAGE SAR-2309-15-S2 [30] | 45 to 75 GHz | 61 × 32.4 × 26.4 cm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hegler, S.; Seiler, P.; Dinkelaker, M.; Schladitz, F.; Plettemeier, D. Electrical Material Properties of Carbon Reinforced Concrete. Electronics 2020, 9, 857. https://doi.org/10.3390/electronics9050857
Hegler S, Seiler P, Dinkelaker M, Schladitz F, Plettemeier D. Electrical Material Properties of Carbon Reinforced Concrete. Electronics. 2020; 9(5):857. https://doi.org/10.3390/electronics9050857
Chicago/Turabian StyleHegler, Sebastian, Patrick Seiler, Max Dinkelaker, Frank Schladitz, and Dirk Plettemeier. 2020. "Electrical Material Properties of Carbon Reinforced Concrete" Electronics 9, no. 5: 857. https://doi.org/10.3390/electronics9050857
APA StyleHegler, S., Seiler, P., Dinkelaker, M., Schladitz, F., & Plettemeier, D. (2020). Electrical Material Properties of Carbon Reinforced Concrete. Electronics, 9(5), 857. https://doi.org/10.3390/electronics9050857






