Multi-Objective Optimal Scheduling of a Hybrid Ferry with Shore-to-Ship Power Supply Considering Energy Storage Degradation
Abstract
1. Introduction
2. Literature Review
3. Contributions
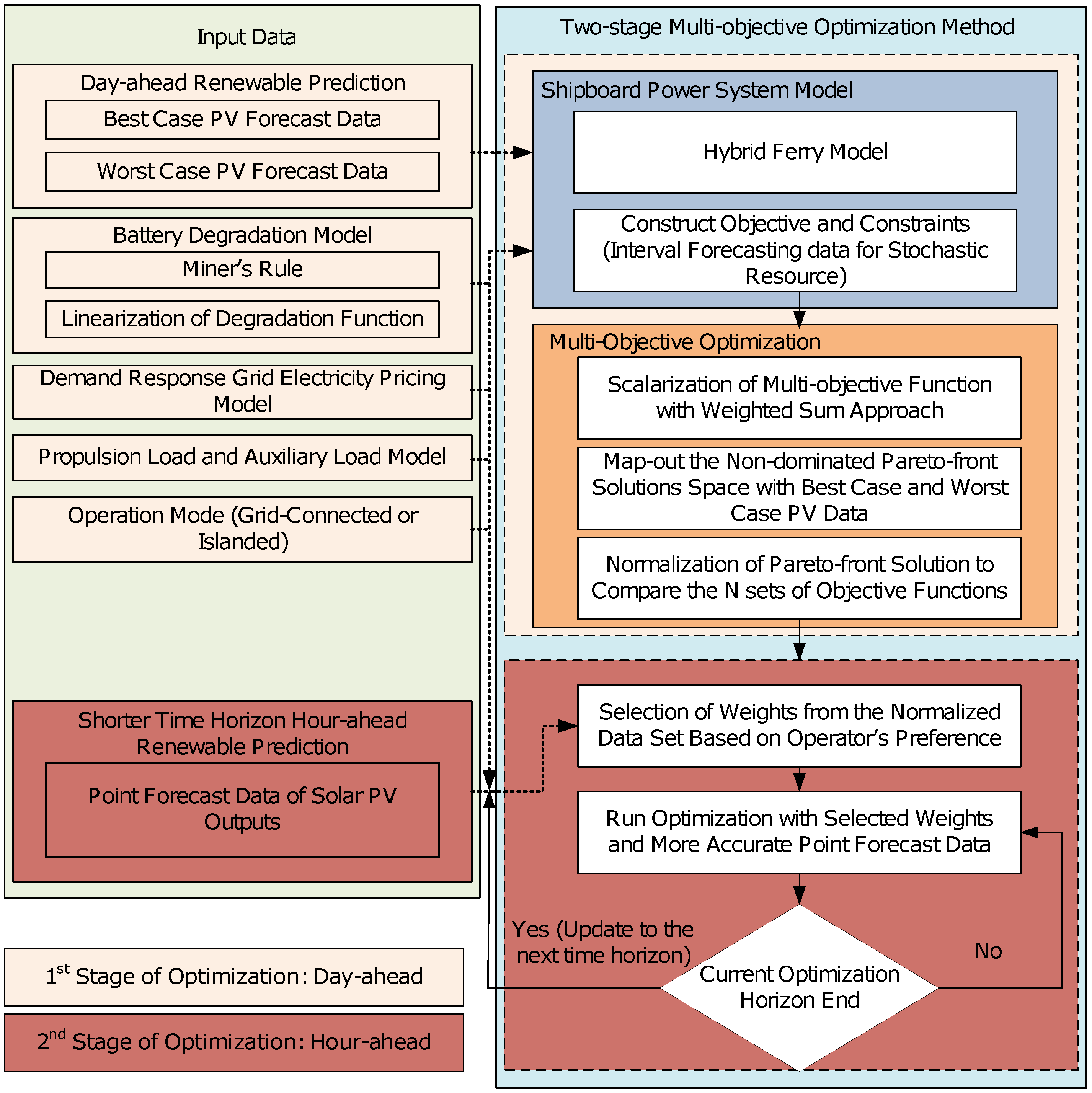
4. Proposed Optimal Dispatch Scheme of Hybrid Ferry with Shore-to-Ship Power Supply
5. Mathematical Modeling
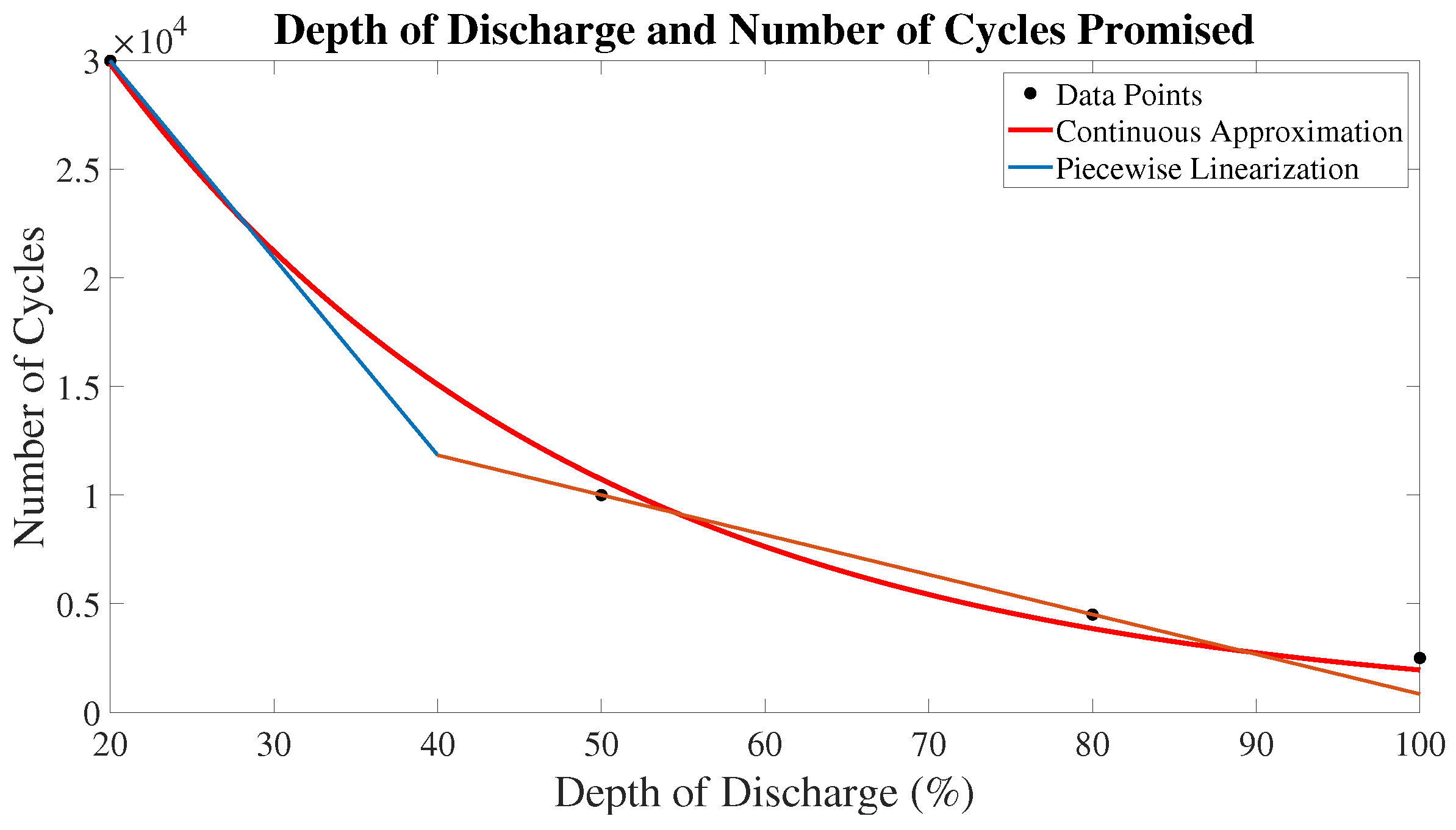
5.1. Energy Storage Degradation Model
5.2. Propulsion Load Model
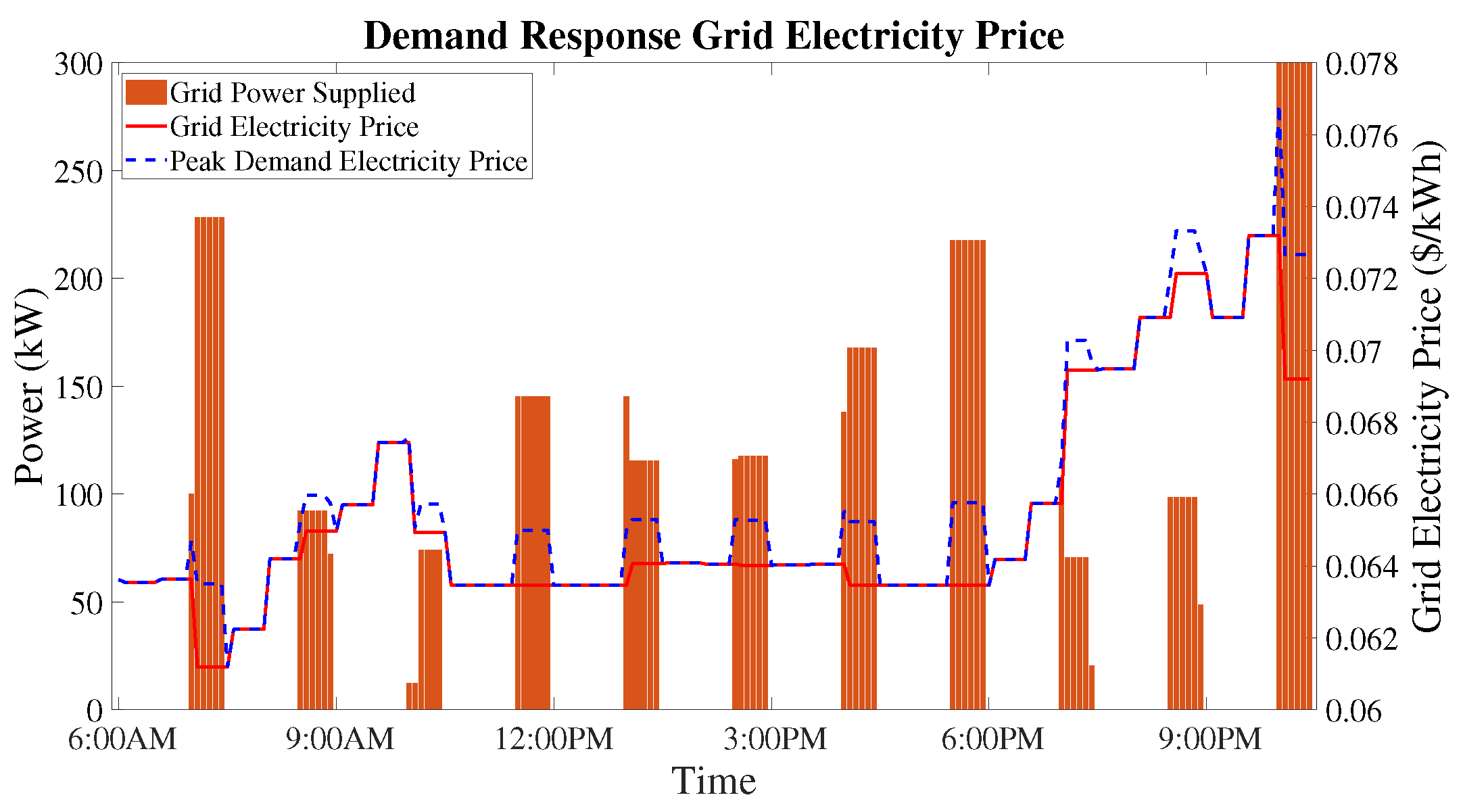
5.3. Demand Response Electricity Price Model
5.4. Hybrid Vessel Operation Model
6. Solution Methods
7. Case Study Parameters
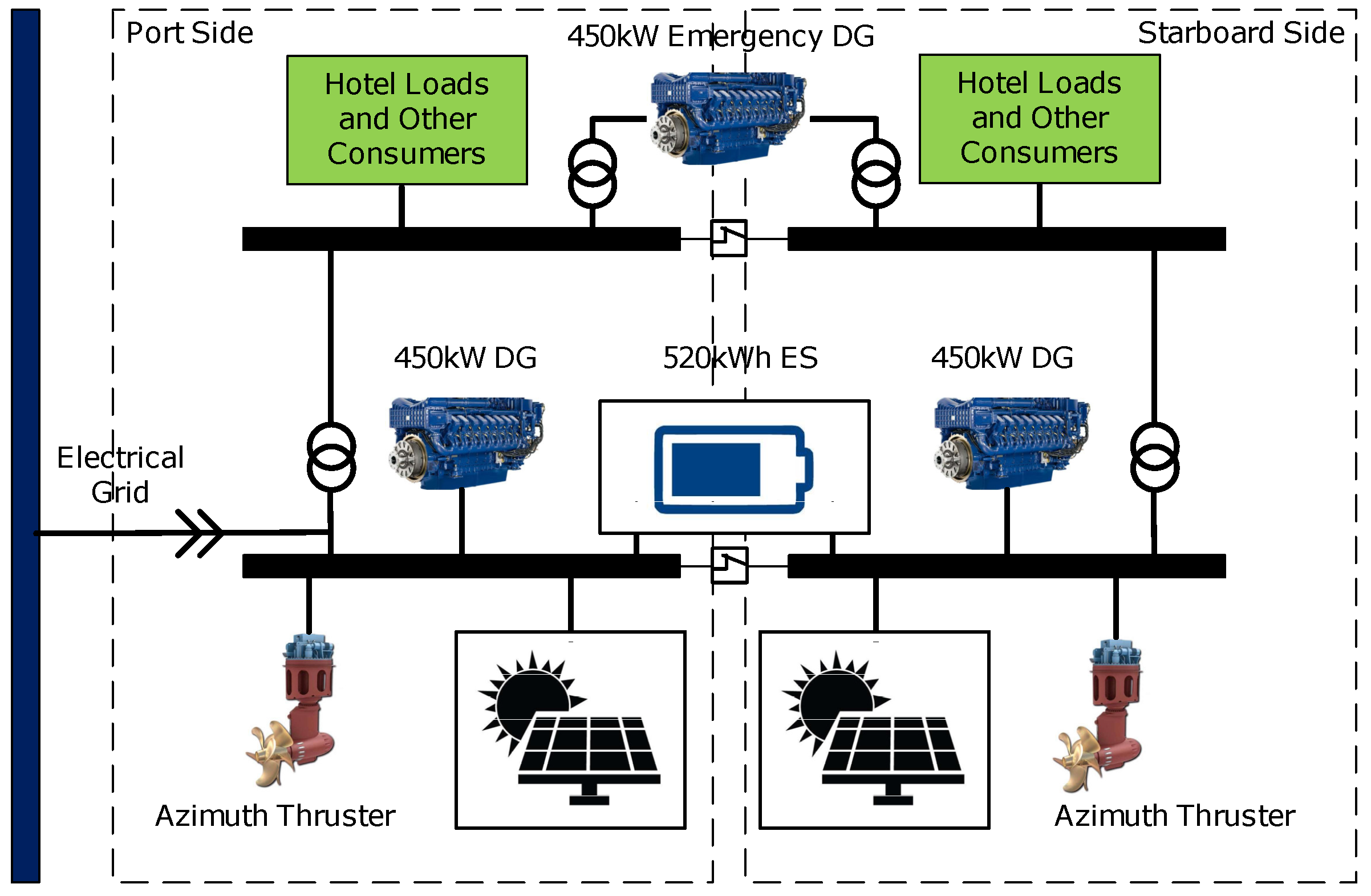
7.1. System Configuration and Parameters
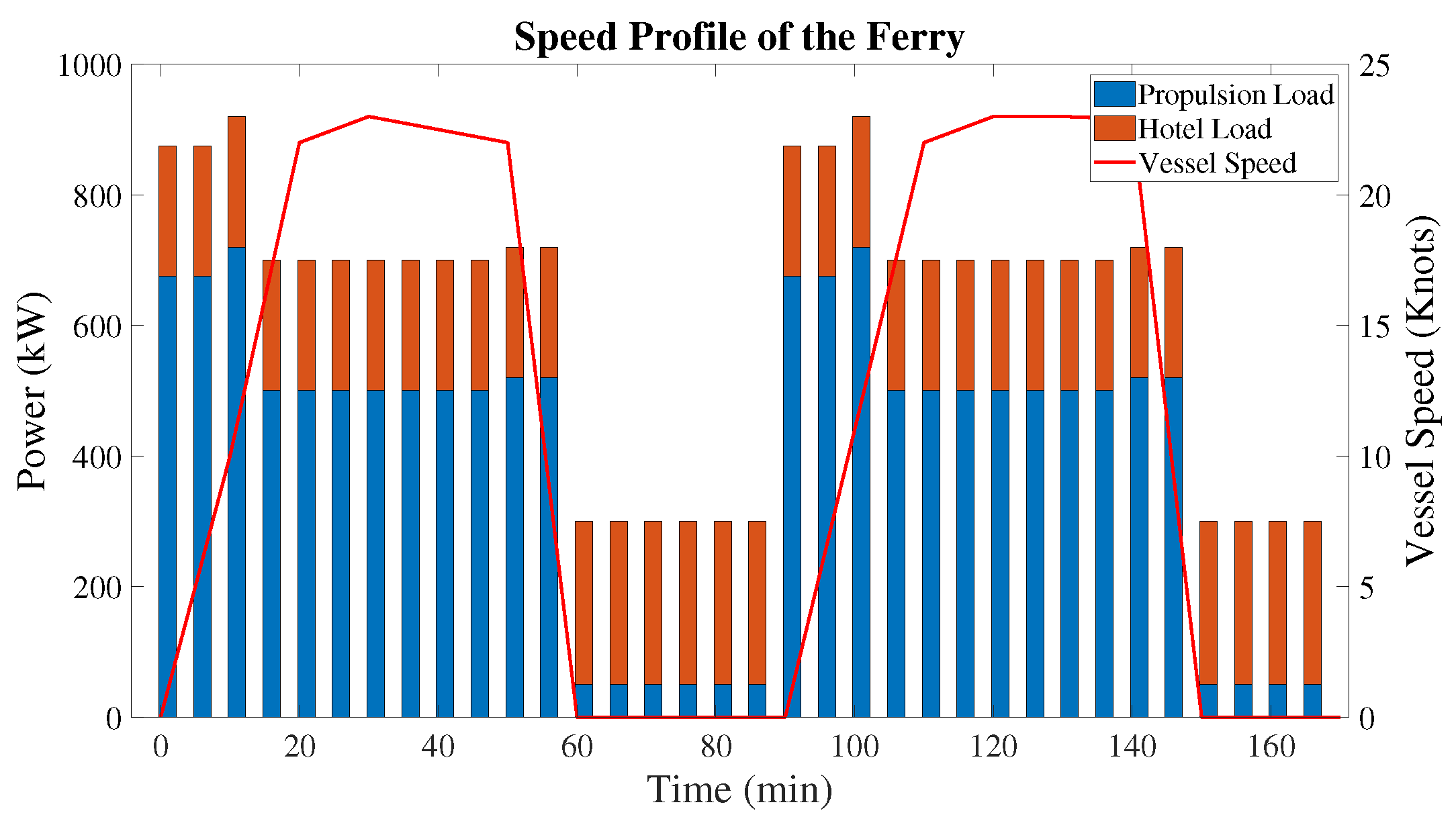
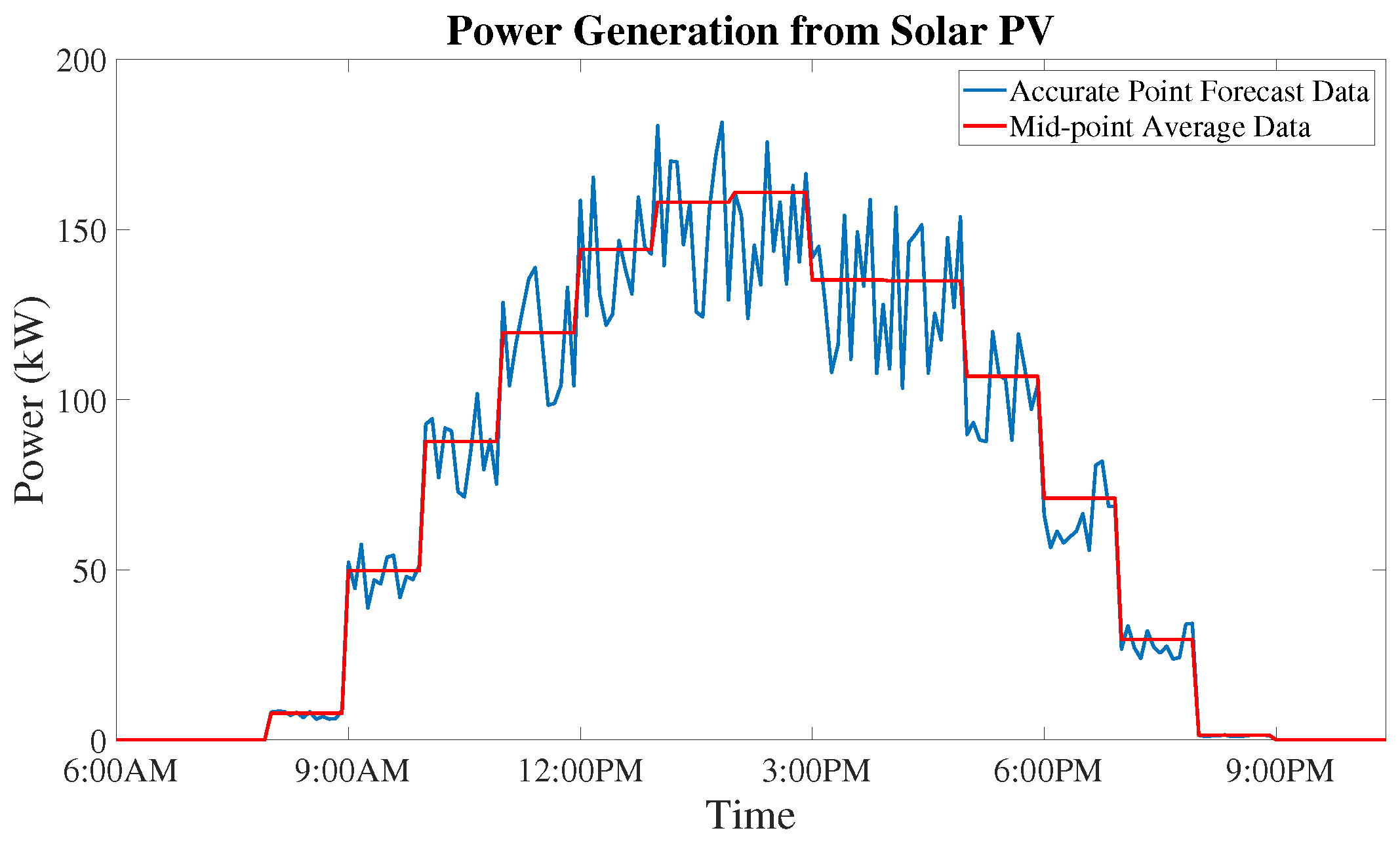
7.2. Vessel Operating Profile
8. Simulation Results
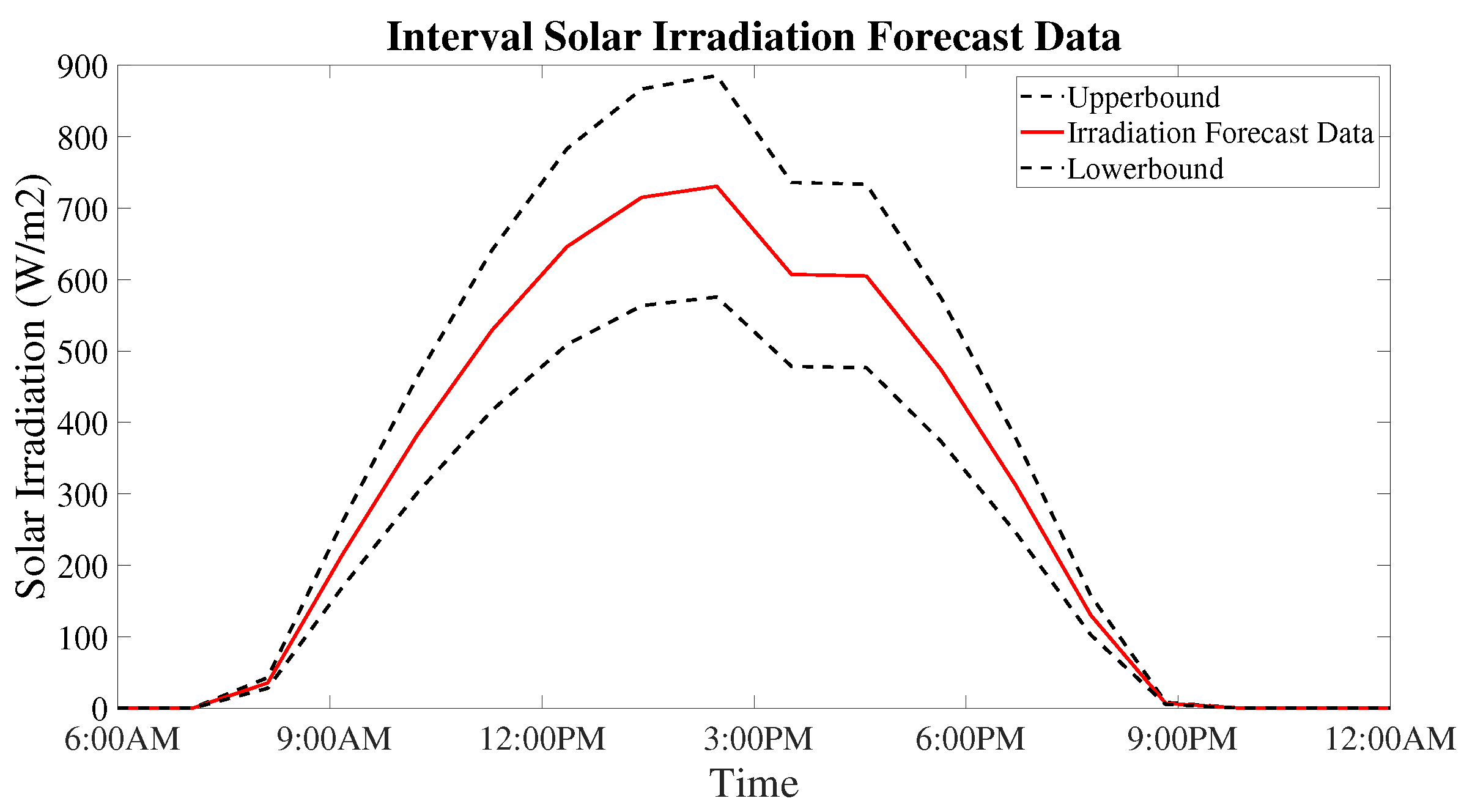
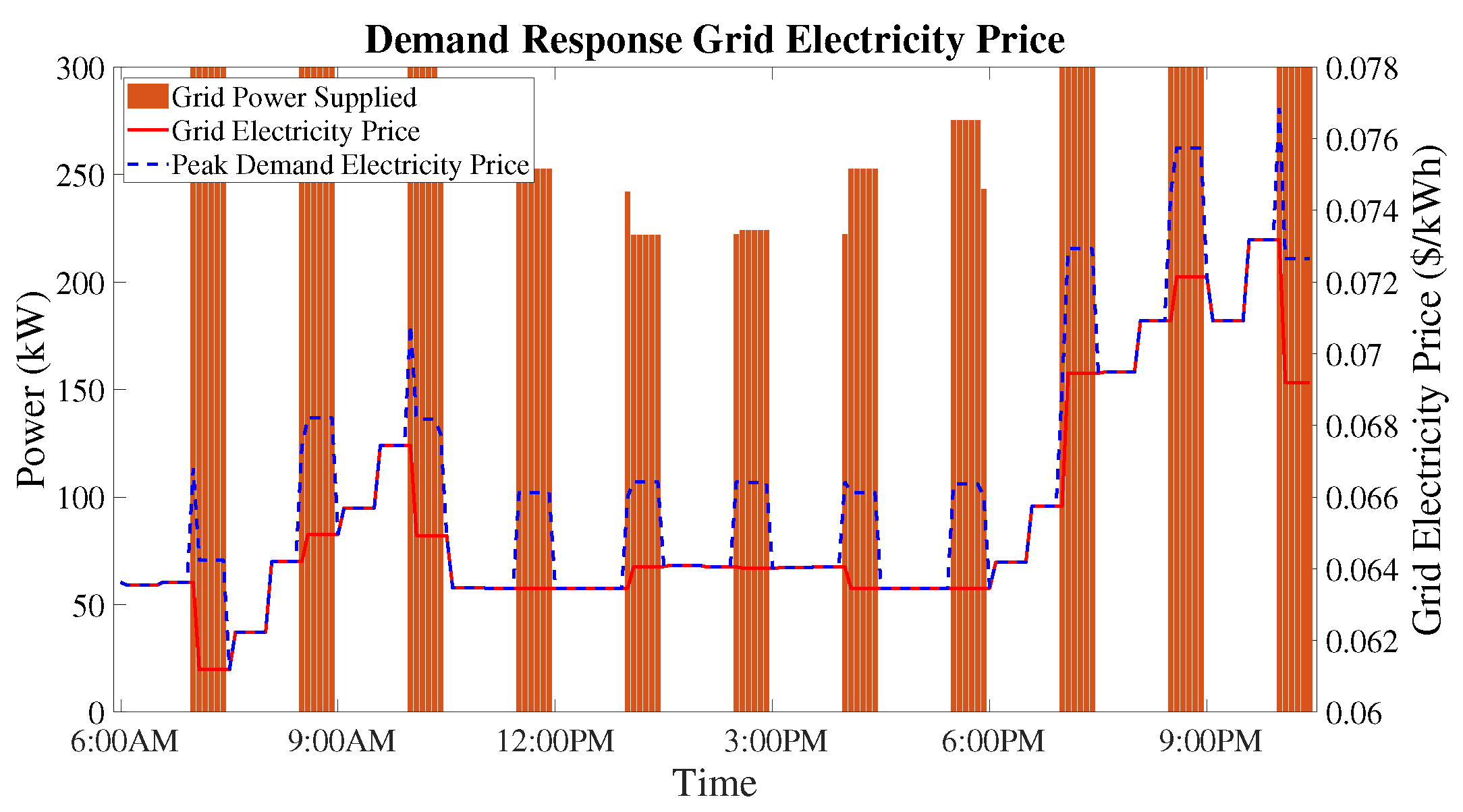
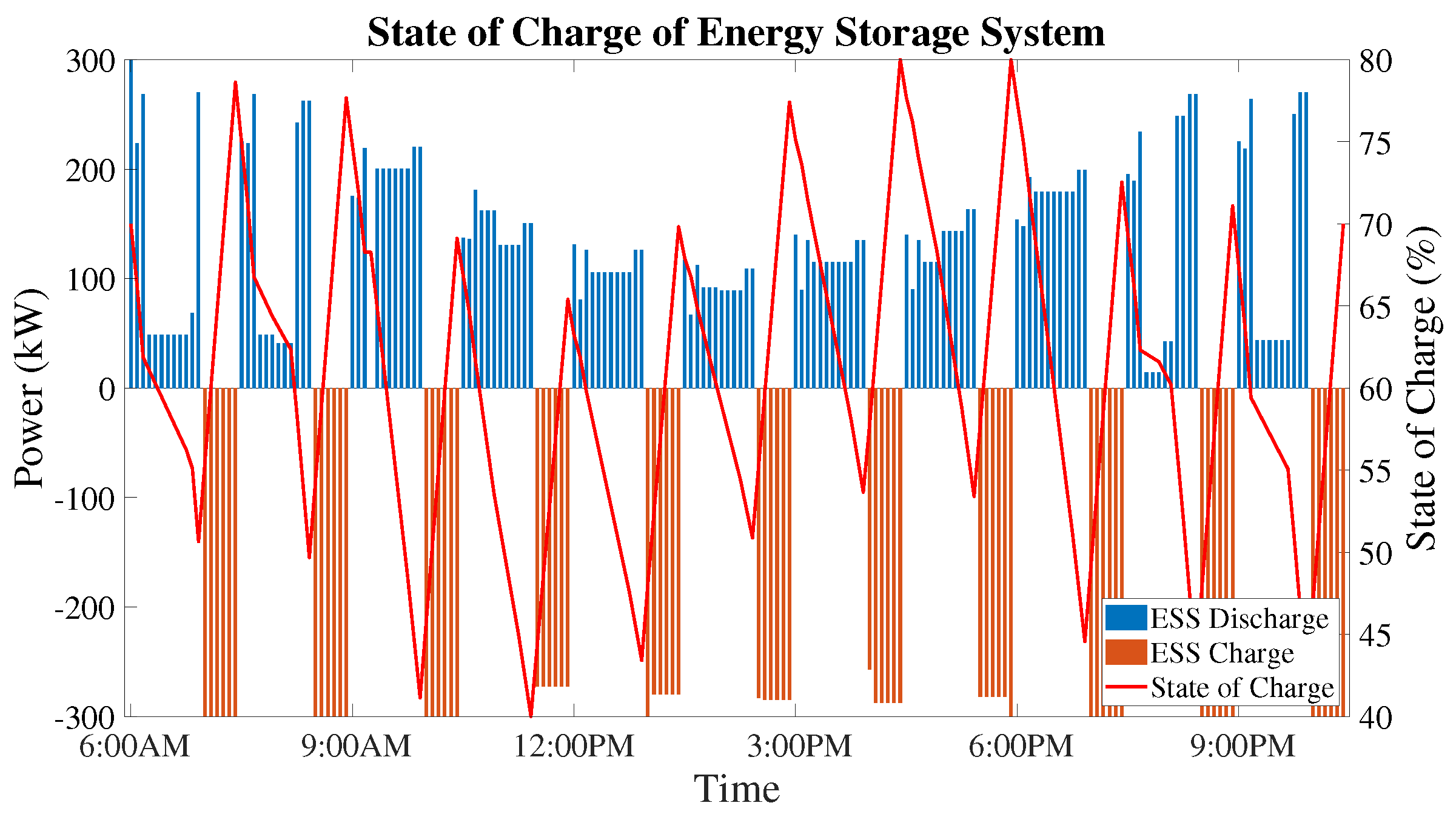
8.1. First Stage of Optimal Dispatch—Day-Ahead
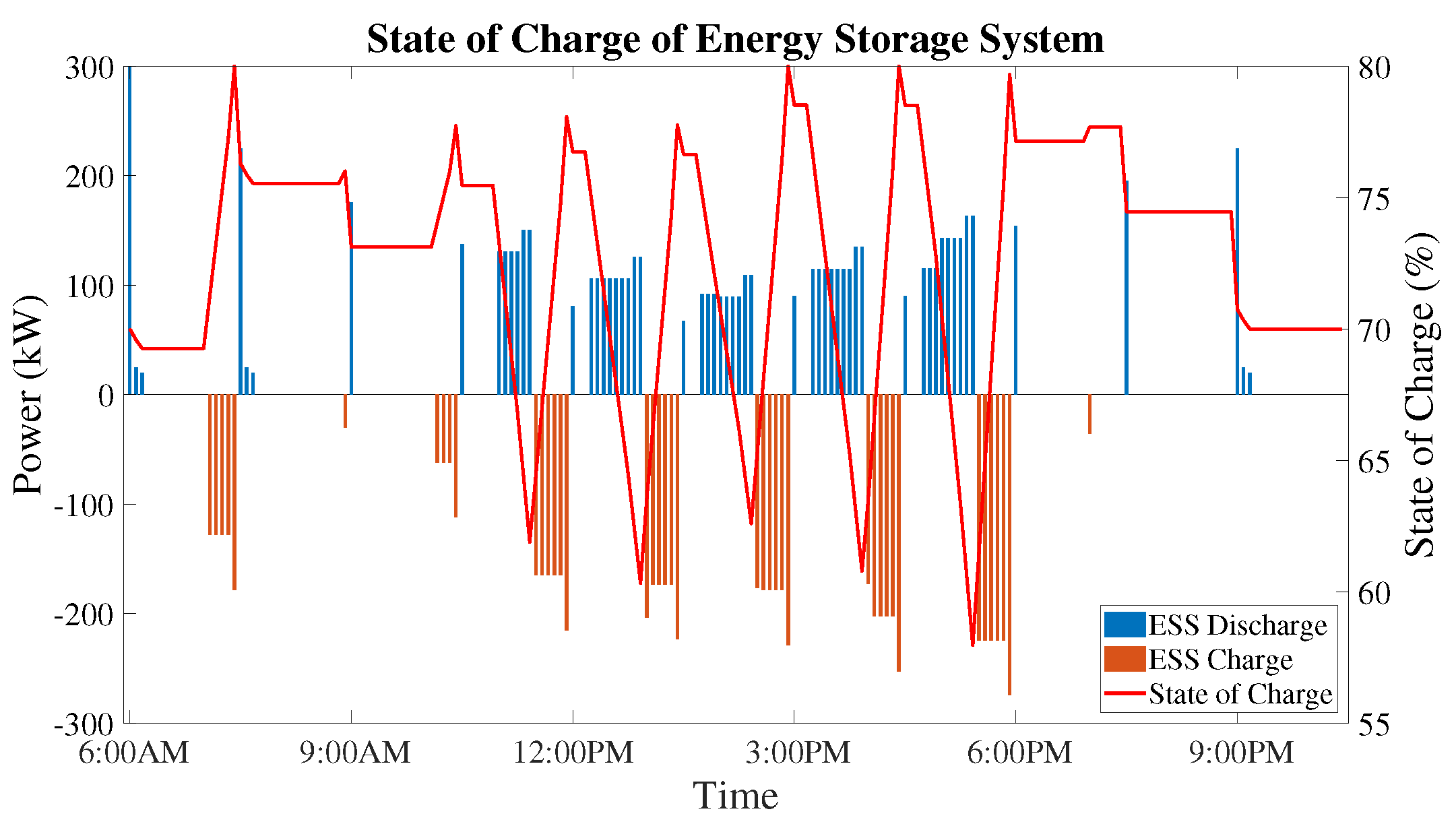
8.2. Second Stage of Economic Dispatch—Hour-Ahead
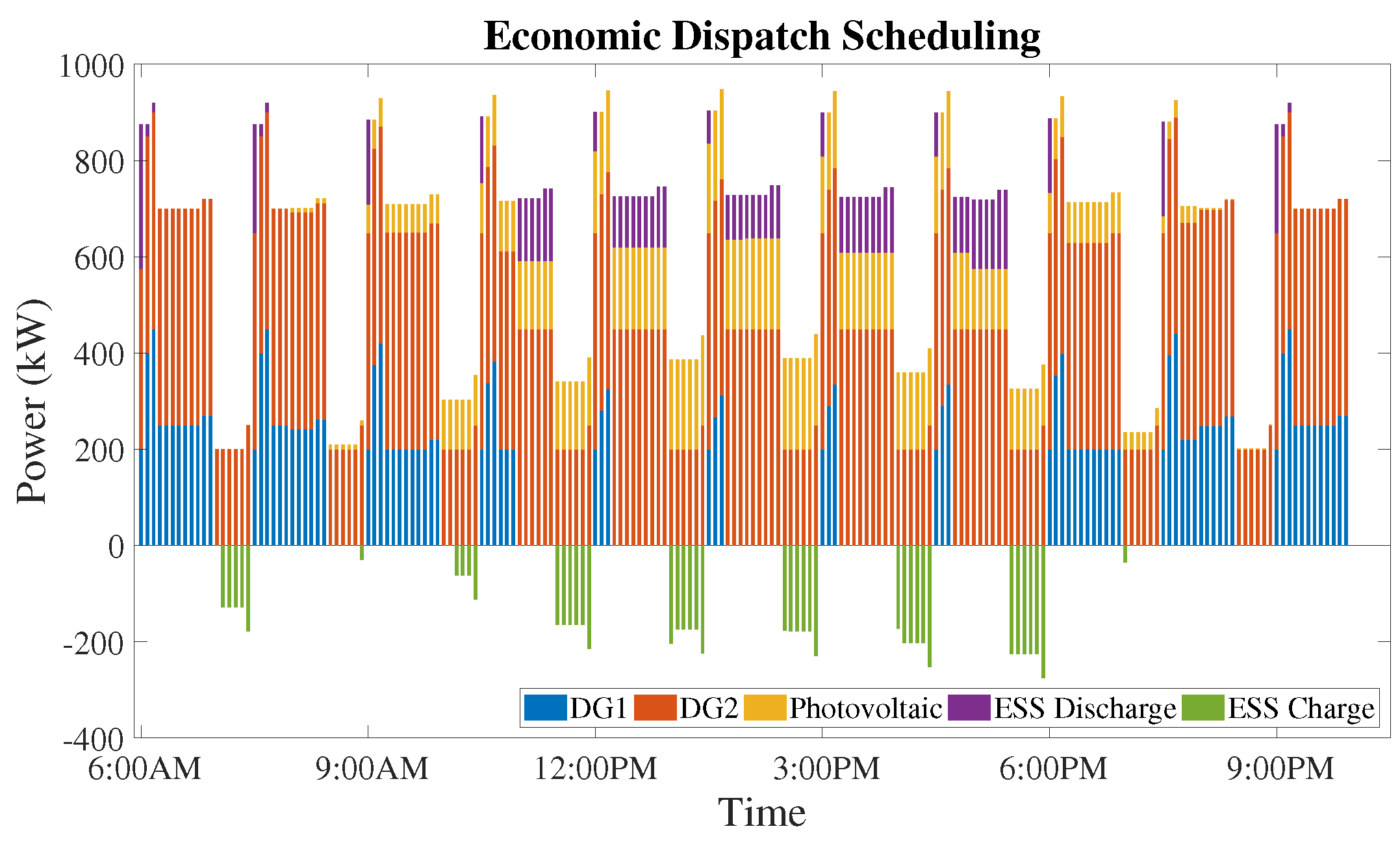
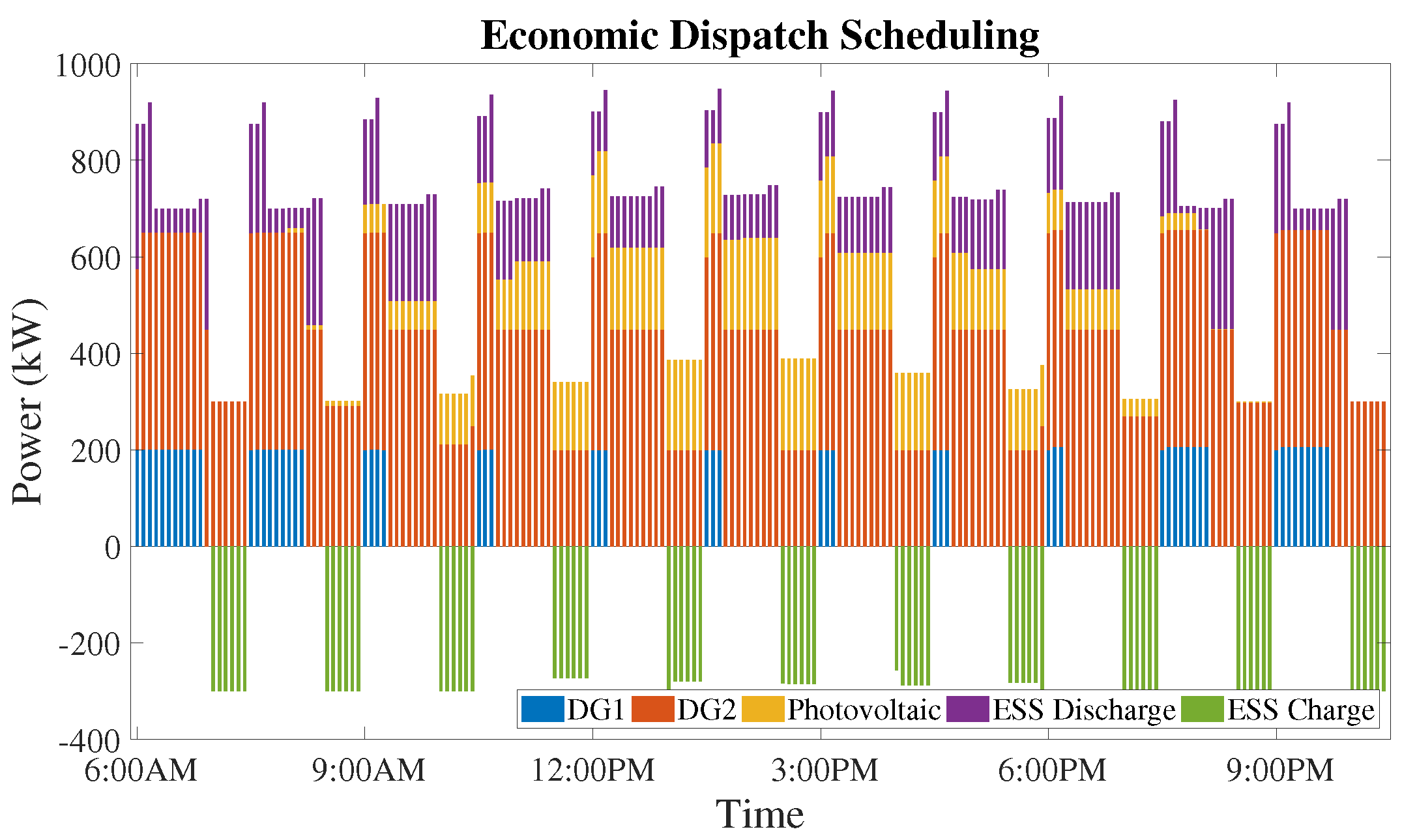
8.2.1. Case Study 1—w1 = 0.65 and w2 = 0.35
8.2.2. Case Study 2—w1 = 0.85 and w2 = 0.15
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Min/max | Minimum and Maximum Values |
| rated | Rated value |
| t | tth time step |
| T | Optimization time horizon (h) |
| Time step size (min) | |
| ES/ESS | Energy Storage System |
| DGs | Diesel Generators |
| S2S | Shore-to-ship power supply |
| The following input parameters are used in this manuscript: | |
| Total installed area of the PV modules (m2) | |
| nth DG’s fuel consumption coefficient | |
| Curve fitting coefficients | |
| Exponential Curve fitting coefficients | |
| Propulsion power and speed correlation coefficient, and hull-dependent coefficient | |
| Rated ES Size (kWh) | |
| Cost of diesel fuel ($/L) | |
| State transition cost of DGs ($/transition) | |
| Maintenance cost of DGs and PV ($/kW) | |
| Carbon credit cost per unit mass ($/kg) | |
| Time of use electricity price ($/kWh) | |
| Irradiation data (W/m2) | |
| Investment cost of ES ($/kWh) | |
| N | Number of DGs |
| Number of half cycles allowed for ES at a given depth of discharge | |
| Total number of half cycles lost from static degradation of ES | |
| Average cycle used per year for ES | |
| Normalized Solution Vector | |
| Operation and maintenance cost ($/kWh) | |
| Ramp rate limits of DG (kW/Δt) | |
| Propulsion power requirement of ferry (kW) | |
| Ferry Load Profile (kW) | |
| Solar power generation (kW) | |
| r | Interest rate (%) |
| Salvage cost ($) | |
| Investment cost of ES ($) | |
| Minimum on/off time of the DG (minutes) | |
| v | Velocity of the ferry (knots) |
| Weighted coefficient of the objective i | |
| Efficiency (%) | |
| Scaling factor of grid electricity price | |
| The following variables are used in this manuscript: | |
| cost | Total fuel consumption cost ($) |
| cost | Total startup and shutdown cost of DGs ($) |
| cost | Total maintenance cost of the DGs ($) |
| cost | Total maintenance cost of the PV ($) |
| cost | Total cost of charging from grid ($) |
| cost | Total cost of carbon tax for emission ($) |
| cost | Total cost of ES degradation ($) |
| Fuel Consumption of nth DG (liter/kW) | |
| Demand response electricity price ($/kWh) | |
| Objective function j in ith solution set ($) | |
| Output power of nth DG (kW) | |
| Power supplied from the grid (kW) | |
| Charge and discharge power from ES (kW) | |
| SOC | State of Charge of ES (%) |
| Lifetime of ES (years) | |
| Binary on/off status of the DG | |
| () | State transition time instance on to off |
| () | State transition time instance off to on |
| Static degradation of ES | |
| Dynamic degradation of ES | |
| Accumulated degradation of ES | |
References
- International Maritime Organization. Third IMO GHG Study 2014 Executive Summary and Final Reports; International Maritime Organization: London, UK, 2015. [Google Scholar]
- European Commission. EU Strategy for Liquefied Natural Gas and Gas Storage; European Commission: Brussels, Belgium, 2016. [Google Scholar]
- International Maritime Organization. Prevention of Air Pollution from Ships MARPOL ANNEX VL; International Maritime Organization: London, UK, 1997. [Google Scholar]
- International Maritime Organization. Energy Efficiency Measures—Amendments MARPOL ANNEX VL; International Maritime Organization: London, UK, 2013. [Google Scholar]
- European Commission. Roadmap to a Single European Transport Area—Towards a Competitive and Resource Efficient Transport System; European Commission: Brussels, Belgium, 2011. [Google Scholar]
- Corvus Energy. World’s First All-Electric Car Ferry—Vessels and Shore Charging Stations. Available online: https://corvusenergy.com/ (accessed on 5 April 2020).
- Koller, M.; Borsche, T.; Ulbig, A.; Andersson, G. Defining a degradation cost function for optimal control of a battery energy storage system. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar]
- Perez, A.; Moreno, R.; Moreira, R.; Orchard, M.; Strbac, G. Effect of Battery Degradation on Multi-Service Portfolios of Energy Storage. IEEE Trans. Sustain. Energy 2016, 7, 1718–1729. [Google Scholar] [CrossRef]
- Abdulla, K.; De Hoog, J.; Muenzel, V.; Suits, F.; Steer, K.; Wirth, A.; Halgamuge, S. Optimal Operation of Energy Storage Systems Considering Forecasts and Battery Degradation. IEEE Trans. Smart Grid 2018, 9, 2086–2096. [Google Scholar] [CrossRef]
- Ju, C.; Wang, P.; Goel, L.; Xu, Y. A two-layer energy management system for microgrid with hybrid energy storage considering degradation costs. IEEE Trans. Smart Grid 2018, 9, 6047–6057. [Google Scholar] [CrossRef]
- Kumar, J.; Kumpulainen, L.; Kauhaniemi, K. Technical design aspects of harbour area grid for shore to ship power: State of the art and future solutions. Int. J. Electr. Power Energy Syst. 2019, 104, 840–852. [Google Scholar] [CrossRef]
- Sciberras, E.A.; Zahawi, B.; Atkinson, D.J. Reducing shipboard emissions—Assessment of the role of electrical technologies. Transp. Res. Part D Transp. Environ. 2017, 51, 227–239. [Google Scholar] [CrossRef]
- Kanellos, F.D.; Prousalidis, J.M.; Tsekouras, G.J. Control system for fuel consumption minimization-gas emission limitation of full electric propulsion ship power systems. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2014, 228, 17–28. [Google Scholar] [CrossRef]
- Shang, C.; Srinivasan, D.; Reindl, T. Economic and Environmental Generation and Voyage Scheduling of All-Electric Ships. IEEE Trans. Power Syst. 2016, 31, 4087–4096. [Google Scholar] [CrossRef]
- Boveri, A.; Silvestro, F.; Molinas, M.; Skjong, E. Optimal Sizing of Energy Storage Systems for Shipboard Applications. IEEE Trans. Energy Convers. 2018, 34, 801–811. [Google Scholar] [CrossRef]
- Yao, C.; Chen, M.; Hong, Y.Y. Novel Adaptive Multi-Clustering Algorithm-Based Optimal ESS Sizing in Ship Power System Considering Uncertainty. IEEE Trans. Power Syst. 2018, 33, 307–316. [Google Scholar] [CrossRef]
- Shang, C.; Srinivasan, D.; Reindl, T. NSGA-II for joint generation and voyage scheduling of an all-electric ship. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016. [Google Scholar]
- Jaurola, M.; Hedin, A.; Tikkanen, S.; Huhtala, K. Optimising design and power management in energy-efficient marine vessel power systems: A literature review. J. Mar. Eng. Technol. 2018, 18, 92–101. [Google Scholar] [CrossRef]
- Kanellos, F.; Anvari-Moghaddam, A.; Guerrero, J. Smart Shipboard Power System Operation and Management. Inventions 2016, 18, 92–101. [Google Scholar] [CrossRef]
- Hein, K.; Xu, Y. Hybrid Energy Storage System in Naval Vessel with 2-Stage Power-sharing Algorithm. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 3607–3612. [Google Scholar]
- Kanellos, F.D. Optimal power management with GHG emissions limitation in all-electric ship power systems comprising energy storage systems. IEEE Trans. Power Syst. 2014, 29, 330–339. [Google Scholar] [CrossRef]
- Al-Falahi, M.D.A.; Nimma, K.S.; Jayasinghe, S.D.G.; Enshaei, H.; Guerrero, J.M. Power management optimization of hybrid power systems in electric ferries. Energy Convers. Manag. 2018, 172, 50–66. [Google Scholar] [CrossRef]
- Wen, S.; Lan, H.; Hong, Y.Y.; Yu, D.C.; Zhang, L.; Cheng, P. Allocation of ESS by interval optimization method considering impact of ship swinging on hybrid PV/diesel ship power system. Appl. Energy 2016, 175, 158–167. [Google Scholar] [CrossRef]
- Kanellos, F.D.; Tsekouras, G.J.; Hatziargyriou, N.D. Optimal demand-side management and power generation scheduling in an all-electric ship. IEEE Trans. Sustain. Energy 2014, 5, 1166–1175. [Google Scholar] [CrossRef]
- Huang, Y.; Lan, H.; Hong, Y.Y.; Wen, S.; Fang, S. Joint voyage scheduling and economic dispatch for all-electric ships with virtual energy storage systems. Energy 2020, 190, 116268. [Google Scholar] [CrossRef]
- Zhengmao, L.; Yan, X.; Sidun, F.; Yu, W. Multi-objective Coordinated Energy Dispatch and Voyage Scheduling for a Multi-energy Cruising Ship. In Proceedings of the 2019 IEEE/IAS 55th Industrial and Commercial Power Systems Technical Conference (I&CPS), Calgary, AB, Canada, 5–8 May 2019; pp. 1–8. [Google Scholar]
- LithiumWerks. Lithium Phosphate Battery. Available online: https://lithiumwerks.com/technology/ (accessed on 5 April 2020).
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar]
- Energy Market Authority. Renewable Energy: Solar Generation Profile. Available online: https://www.ema.gov.sg/Renewable_Energy.aspx (accessed on 5 April 2020).
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No.04CH37508), New Orleans, LA, USA, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Studio-CPLEX, IBM ILOG CPLEX Optimization. User’s Manual-Version 12. Available online: https://www.ibm.com/ (accessed on 5 April 2020).
- MQ Power. 500 kW Diesel on-Site Power Industrial Generator. Available online: http://www.powertechengines.com/MQP-DataSheets/ (accessed on 5 April 2020).
- Cummins. Triton Power TP-C500-T1-60. Available online: https://www.americasgenerators.com/ (accessed on 5 April 2020).
- Lai, C.S.; McCulloch, M.D. Levelized cost of electricity for solar photovoltaic and electrical energy storage. Appl. Energy 2017, 150, 191–203. [Google Scholar] [CrossRef]

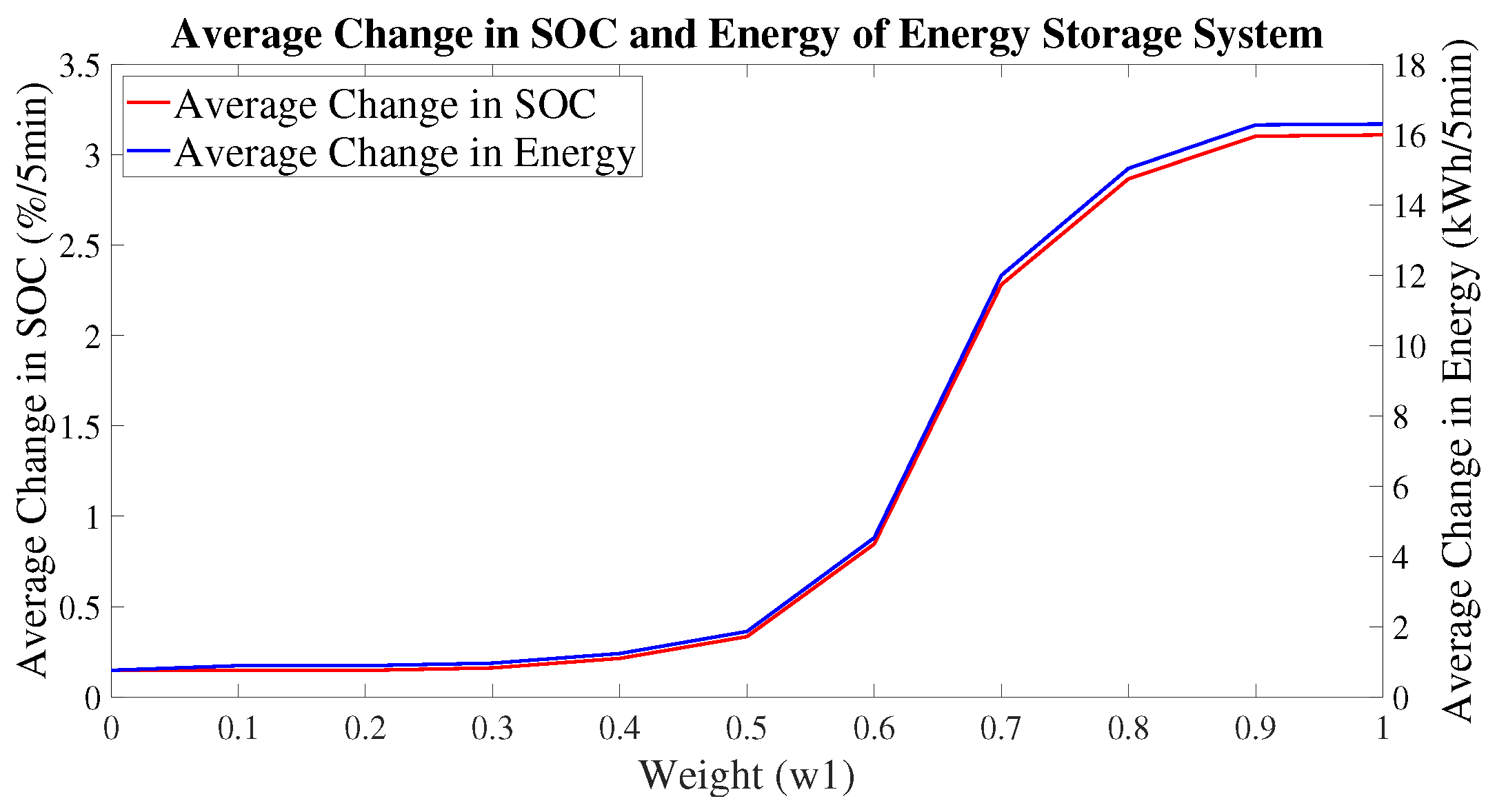
| Unit | Pmax (kW) | Pmin (kW) | Tmin (min) | Pramp,max |
|---|---|---|---|---|
| DG1 | 450 | 200 | 15 | 200 (kW/Δt) |
| DG2 | 450 | 200 | 15 | 200 (kW/Δt) |
| Grid | 300 | 0 | – | – |
| DG1 | a = 1.568 × 10−4, b = 0.592, c = 0.0001 | |||
| DG2 | a = 6.72 × 10−5, b = 0.160, c = −0.0001 | |||
| Ffuel = 0.83 $/L, FCO2 = 30 $/ton, Ftrans = 10 $/transition | ||||
| FDG,mai = 0.007 $/kWh, FPV,mai = 0.05 $/kWh, Δt = 5 min | ||||
| 300 kW | 0 kW | 97% | 40% | 80% |
| 520 kWh | 10/year | −0.03411 | 59,070 | −908 |
| T | ||||
| 4.816 × 104 | −183.3 | 1.917 × 104 | 10 | 1500 $/kWh |
| r | ||||
| 1000 | $78,000 | 0.12 $/kWh | 5% | 14.55 $/kW |
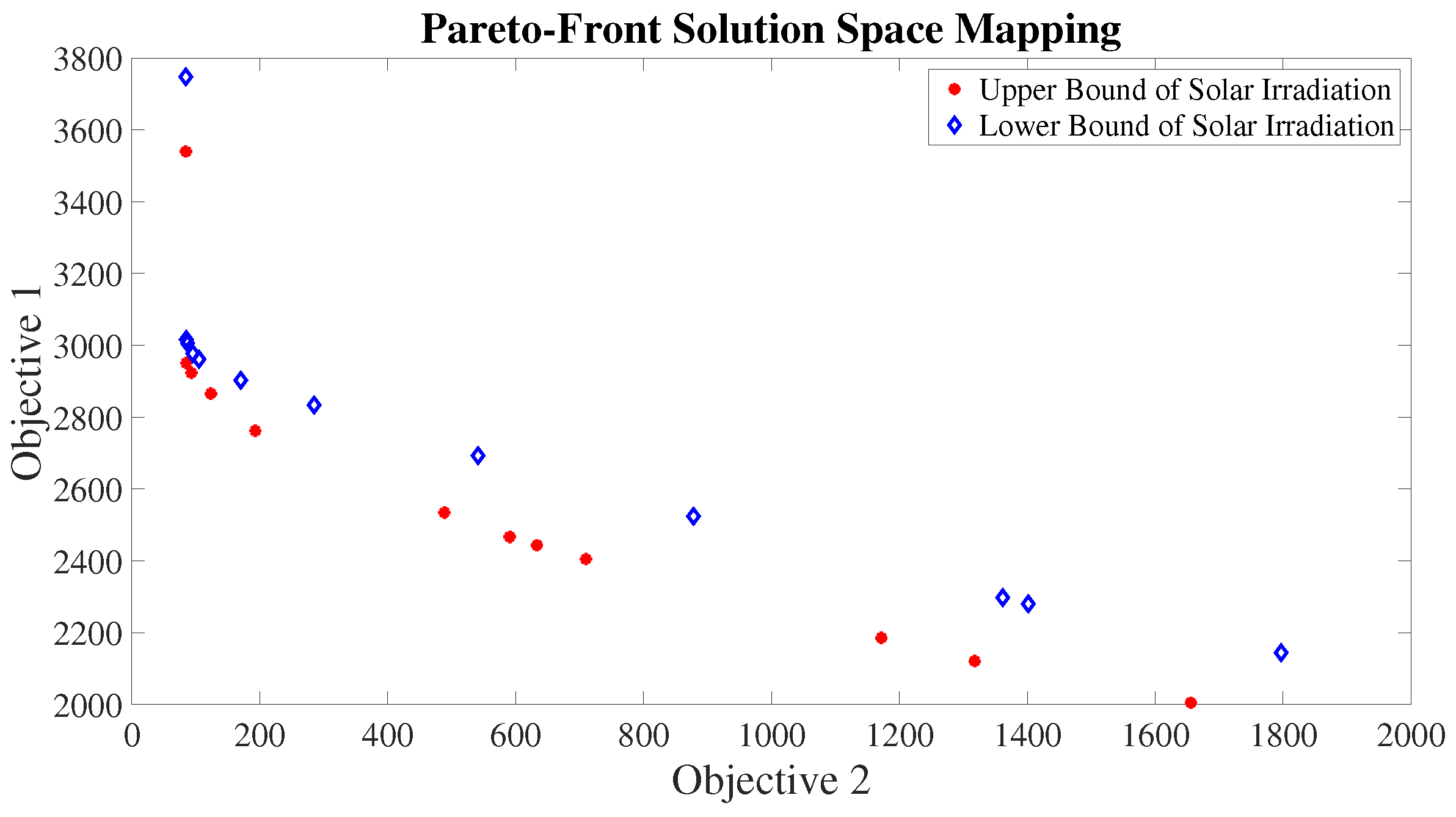
| Weight (w) | PV Bound | Objective 1-Emission, Fuel Consumption and O&M Cost $ | Objective 2-Energy Storage Degradation Cost $ | Simulation Time (s) |
|---|---|---|---|---|
| w1 = 1.0 w2 = 0 | Upper | 1.99 × 103 | 1.80 × 103 | 0.80 |
| Lower | 2.14 × 103 | 1.80 × 103 | 0.87 | |
| w1 = 0.9 w2 = 0.1 | Upper | 1.98 × 103 | 1.79 × 103 | 1.93 |
| Lower | 2.14 × 103 | 1.80 × 103 | 1.83 | |
| w1 = 0.8 w2 = 0.2 | Upper | 2.00 × 103 | 1.66 × 103 | 3.48 |
| Lower | 2.14 × 103 | 1.80 × 103 | 3.45 | |
| w1 = 0.7 w2 = 0.3 | Upper | 2.12 × 103 | 1.32 × 103 | 5.36 |
| Lower | 2.28 × 103 | 1.40 × 103 | 5.38 | |
| w1 = 0.6 w2 = 0.4 | Upper | 2.53 × 103 | 488.78 | 9.61 |
| Lower | 2.90 × 103 | 170.00 | 9.60 | |
| w1 = 0.5 w2 = 0.5 | Upper | 2.76 × 103 | 193.18 | 14.94 |
| Lower | 2.96 × 103 | 105.15 | 15.21 | |
| w1 = 0.4 w2 = 0.6 | Upper | 2.87 × 103 | 123.60 | 10.81 |
| Lower | 2.96 × 103 | 105.15 | 11.21 | |
| w1 = 0.3 w2 = 0.7 | Upper | 2.92 × 103 | 93.21 | 5.27 |
| Lower | 2.98 × 103 | 95.47 | 5.39 | |
| w1 = 0.2 w2 = 0.8 | Upper | 2.95 × 103 | 85.19 | 2.95 |
| Lower | 3.00 × 103 | 87.27 | 3.21 | |
| w1 = 0.1 w2 = 0.9 | Upper | 2.95 × 103 | 85.19 | 1.59 |
| Lower | 3.02 × 103 | 85.22 | 1.68 | |
| w1 = 0 w2 = 1.0 | Upper | 3.54 × 103 | 84.58 | 0.78 |
| Lower | 3.75 × 103 | 84.49 | 0.81 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hein, K.; Yan, X.; Wilson, G. Multi-Objective Optimal Scheduling of a Hybrid Ferry with Shore-to-Ship Power Supply Considering Energy Storage Degradation. Electronics 2020, 9, 849. https://doi.org/10.3390/electronics9050849
Hein K, Yan X, Wilson G. Multi-Objective Optimal Scheduling of a Hybrid Ferry with Shore-to-Ship Power Supply Considering Energy Storage Degradation. Electronics. 2020; 9(5):849. https://doi.org/10.3390/electronics9050849
Chicago/Turabian StyleHein, Kyaw, Xu Yan, and Gary Wilson. 2020. "Multi-Objective Optimal Scheduling of a Hybrid Ferry with Shore-to-Ship Power Supply Considering Energy Storage Degradation" Electronics 9, no. 5: 849. https://doi.org/10.3390/electronics9050849
APA StyleHein, K., Yan, X., & Wilson, G. (2020). Multi-Objective Optimal Scheduling of a Hybrid Ferry with Shore-to-Ship Power Supply Considering Energy Storage Degradation. Electronics, 9(5), 849. https://doi.org/10.3390/electronics9050849





