Gaussian-Process-Based Surrogate for Optimization-Aided and Process-Variations-Aware Analog Circuit Design
Abstract
1. Introduction
1.1. Motivation
1.2. Our Approach and Contributions
- A high-accuracy surrogate model for circuit optimization with low-computational effort compared with circuit simulations.
- The use of Gaussian processes regression models for high accuracy prediction of device parameters across corners based on the technology characterization.
- A flexible optimization framework easily configurable for different fabrication processes, circuit topologies, and optimization algorithms.
2. Multi-Objective Constrained Optimization for Automatic Circuit Design
2.1. Multi-Objective Optimization
2.1.1. Gradient-Based Optimization Algorithms
2.1.2. Evolutionary Optimization Algorithms
2.2. Analog Circuit Design as an Optimization Problem
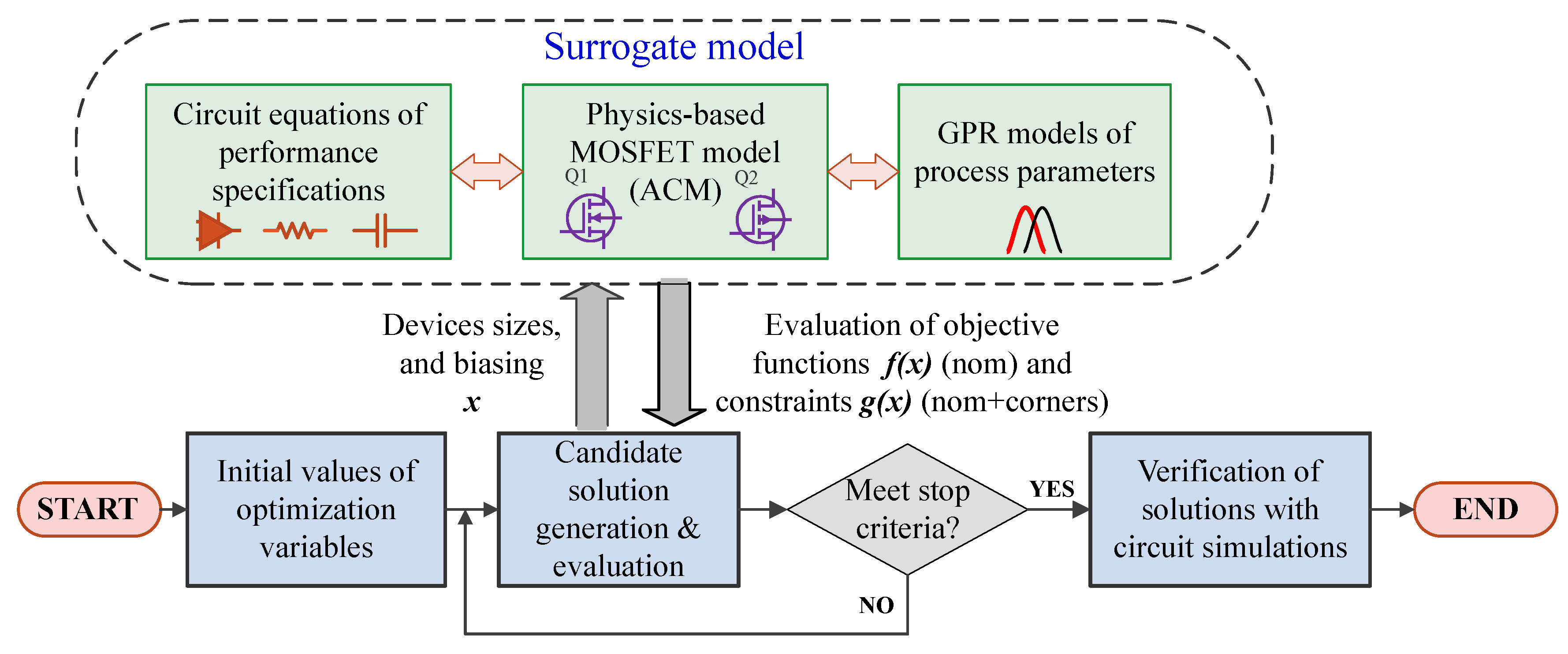
3. Proposed Surrogate Model for Optimization-Based EDA Tools
3.1. General Optimization Architecture
- The Gaussian process regression models of parameters of the process technology trained from characterization data.
- The physics-based model of the parameters of the MOS transistor.
- The circuit equations of the performance metrics of the circuit topology.
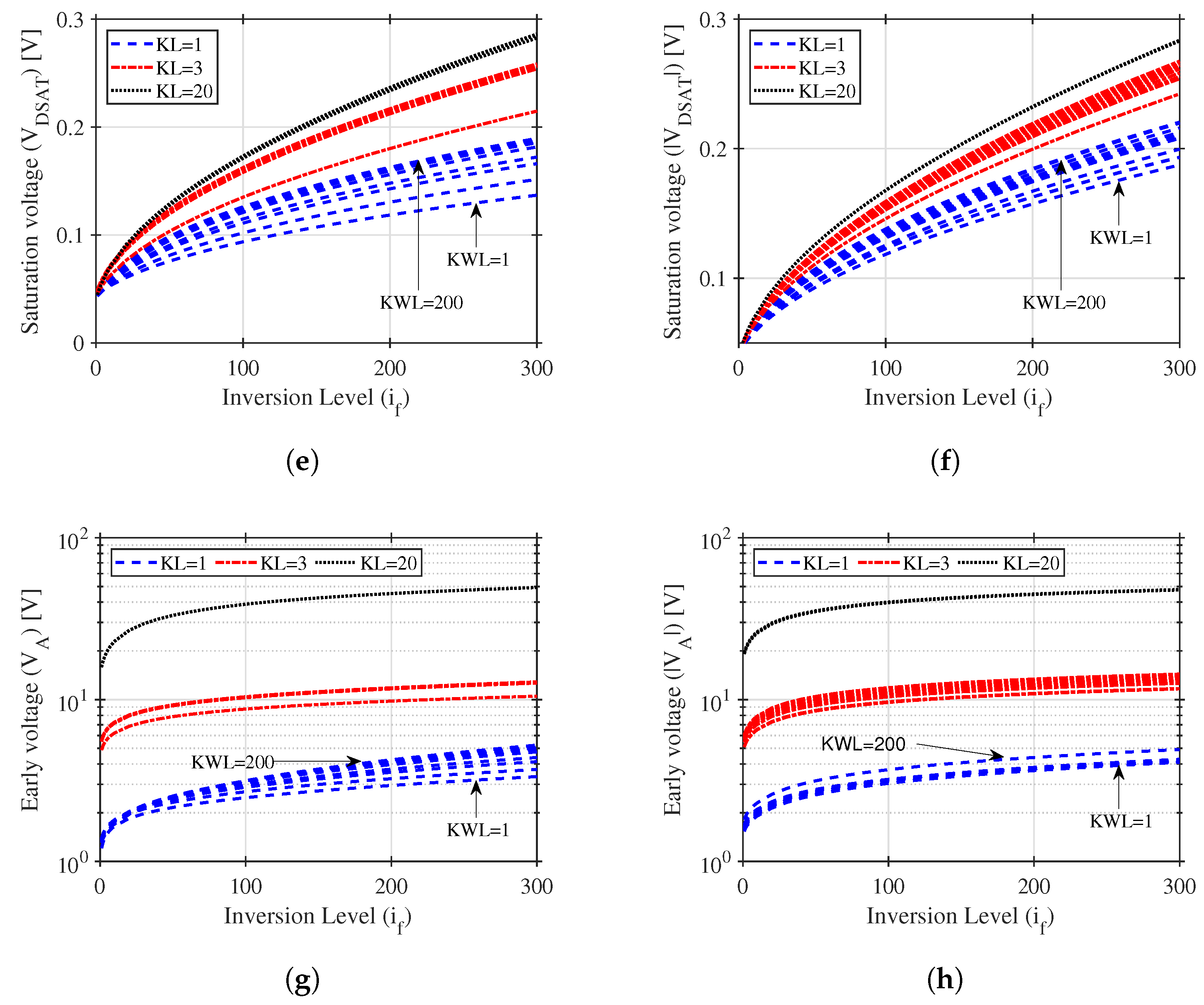
3.2. Advanced Compact MOSFET (ACM) Model
3.3. Gaussian Process-Based Regression Models of the Process Characterization
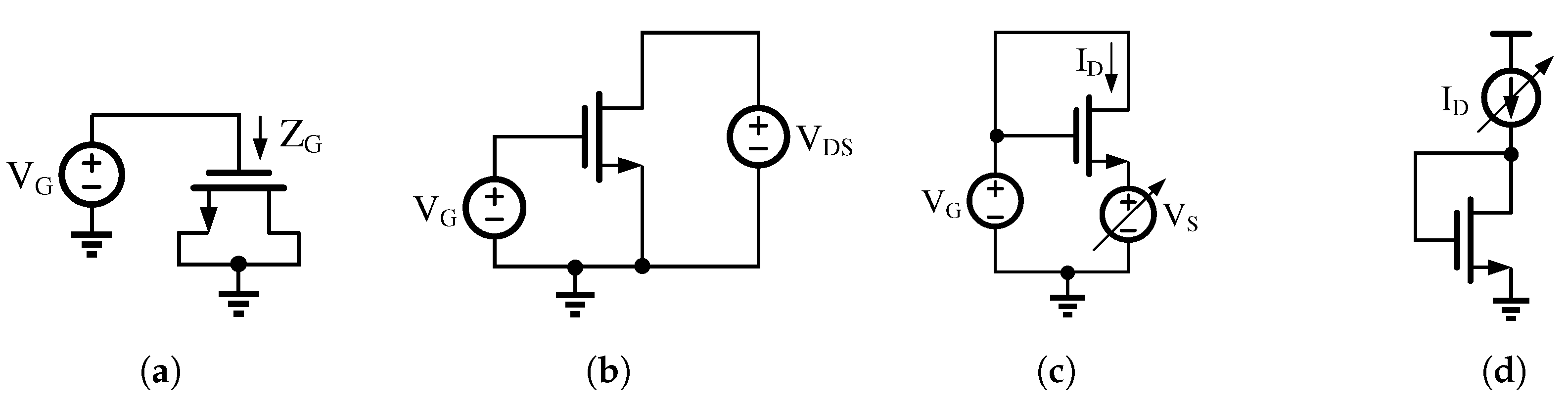
3.3.1. Characterization of the Parameters of CMOS Transistors
3.3.2. Gaussian-Processes-Based Regression Models
3.4. Circuit Performance Equation-Based Model
3.5. Process Variations-Aware Automatic Design
4. Experimental Results
4.1. Error of the GPR-Based Surrogate Model
4.2. Experimental Setup
4.3. Active-RC Second Order Filter
4.3.1. Surrogate of the Filter’s Performance Metrics
4.3.2. Results of Filter’s Automatic Design
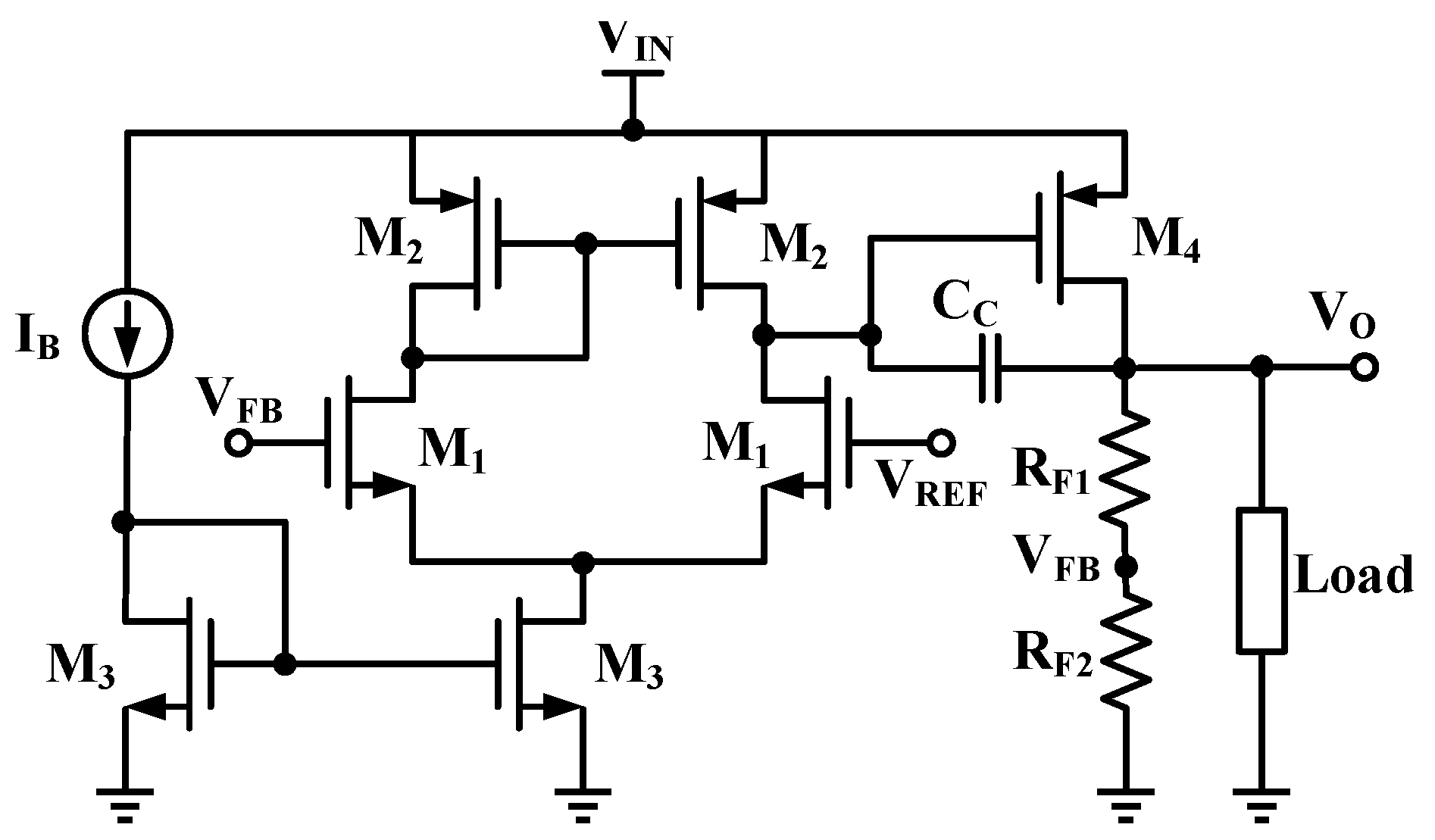
4.4. Capacitor-Less Low-Dropout (CL-LDO) Voltage Regulator
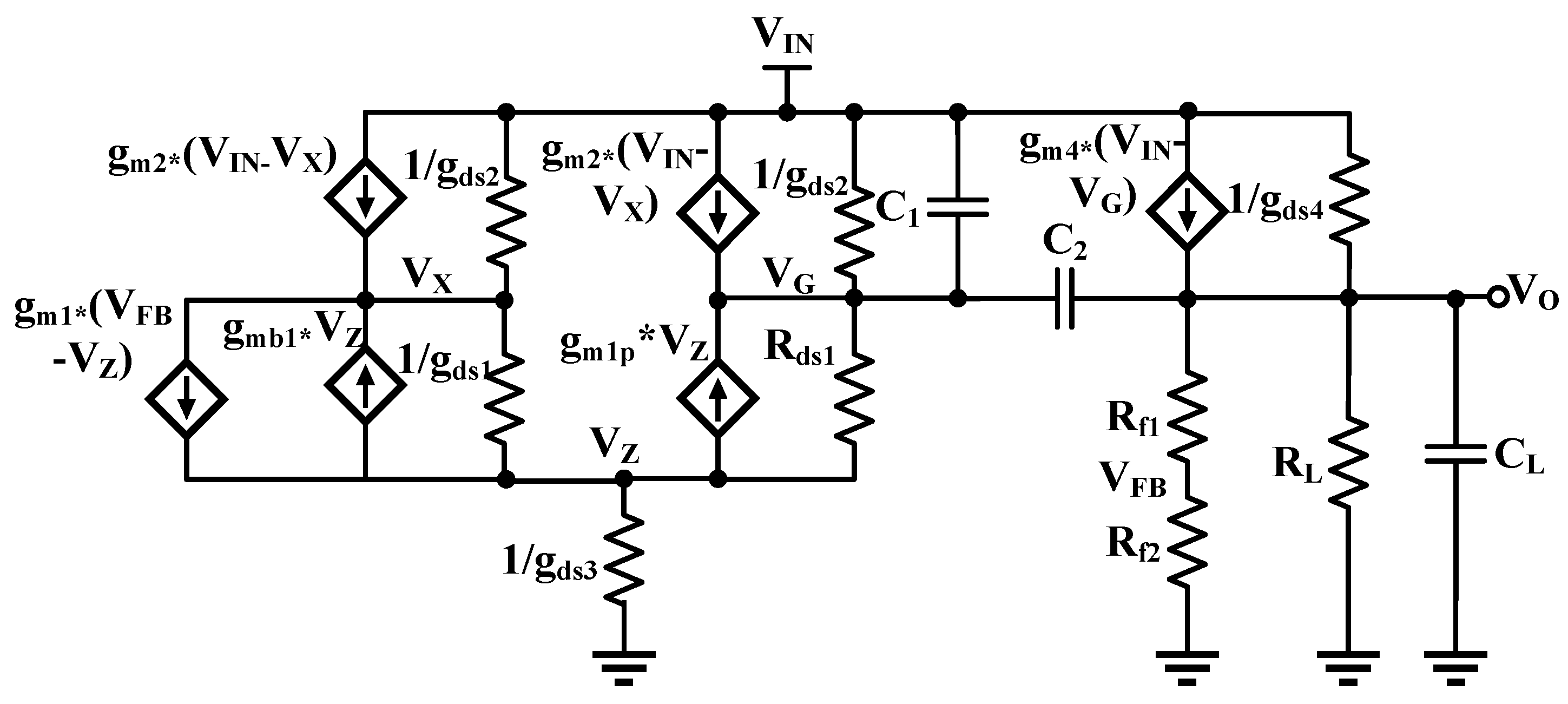
4.4.1. Surrogate of the LDO’s Performance Metrics
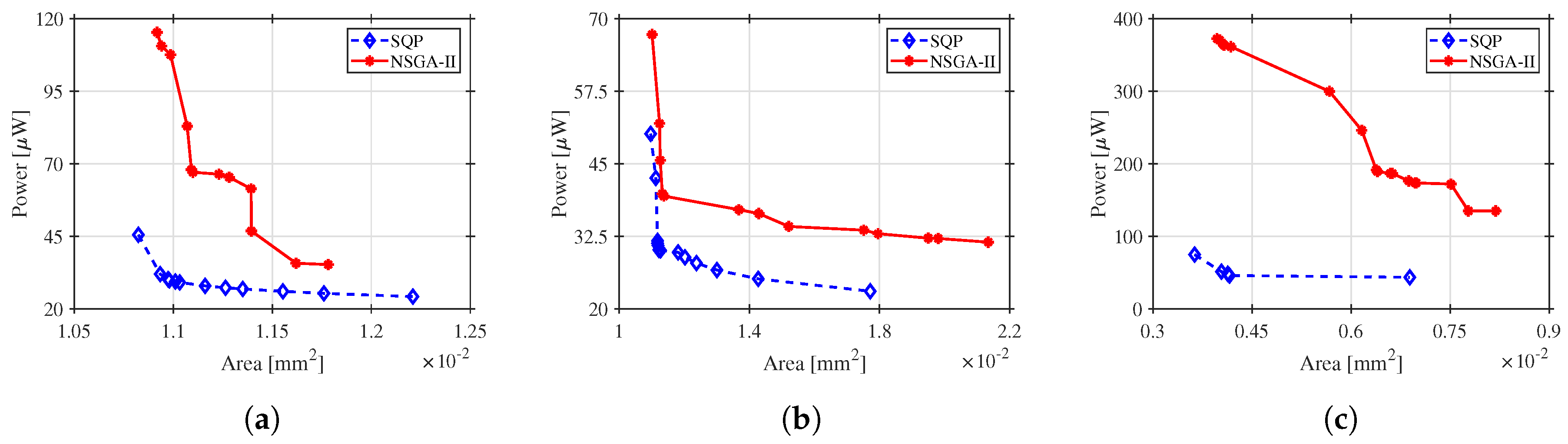
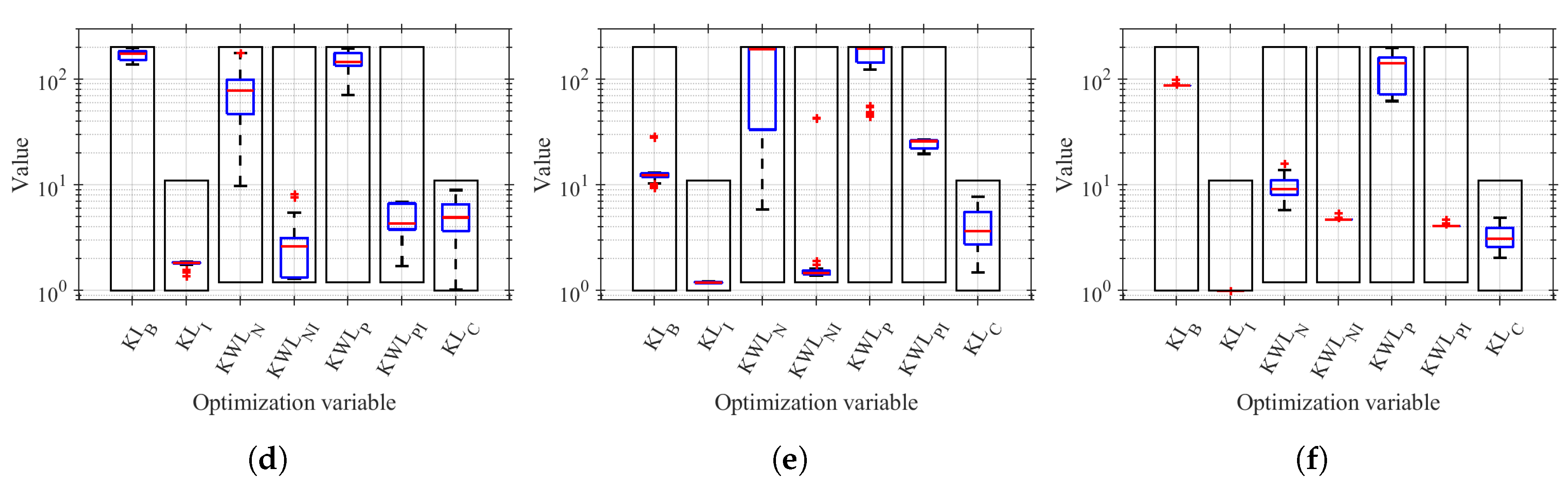
4.4.2. Results of the LDO’s Automatic Design
4.5. Current-Starved Voltage Controlled Oscillator (CSVCO)
4.5.1. Surrogate of the CSVCO’s Performance Metrics
4.5.2. Results of the CSVCO’s Automatic Design
4.6. Summary
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Scheffer, L.; Lavagno, L.; Martin, G. EDA for IC implementation, circuit design, and process technology. In Electronic Design Automation for Integrated Circuits Handbook; Scheffer, L., Lavagno, L., Martin, G., Eds.; CRC Taylor & Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Razavi, B. Design of Analog CMOS Integrated Circuits; McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]
- Gielen, G.G.E.; Rutenbar, R.A. Computer-aided design of analog and mixed-signal integrated circuits. Proc. IEEE 2000, 88, 1825–1854. [Google Scholar] [CrossRef]
- Fakhfakh, M.; Cooren, Y.; Sallem, A.; Loulou, M.; Siarry, P. Analog circuit design optimization through the particle swarm optimization technique. Analog Integr. Circuits Signal Process. 2010, 63, 71–82. [Google Scholar] [CrossRef]
- Fakhfakh, M.; Tlelo-Cuautle, E.; Siarry, P. Computational Intelligence in Analog and Mixed-Signal (AMS) and Radio-Frequency (RF) Circuit Design; Springer: Cham, Switzerland, 2015; pp. 1–491. [Google Scholar]
- Rutenbar, R.A.; Gielen, G.G.E.; Roychowdhury, J. Hierarchical Modeling, Optimization, and Synthesis for System-Level Analog and RF Designs. Proc. IEEE 2007, 95, 640–669. [Google Scholar] [CrossRef]
- Goswami, M.; Kundu, S. Constrained Low-power CMOS Analog Circuit Design via All-Inversion Region MOS Model. In Proceedings of the 2014 IEEE Fourth International Conference on Consumer Electronics Berlin (ICCE-Berlin), Berlin, Germany, 7–10 September 2014; pp. 277–278. [Google Scholar]
- Rocha, F.; Martins, R.; Lourenço, N.; Horta, N. Electronic Design Automation of Analog ICs Combining Gradient Models with Multi-Objective Evolutionary Algorithms; Springer Briefs in Applied Sciences and Technology; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Lyu, W.; Xue, P.; Yang, F.; Yan, C.; Hong, Z.; Zeng, X.; Zhou, D. An efficient Bayesian optimization approach for automated optimization of analog circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 1954–1967. [Google Scholar] [CrossRef]
- Kubar, M.; Jakovenko, J. A Powerful Optimization Tool for Analog Integrated Circuits Design. Radioengineering 2013, 22, 921–931. [Google Scholar]
- Binkley, D.M.; Hopper, C.E.; Tucker, S.D.; Moss, B.C.; Rochelle, J.M.; Foty, D.P. A CAD methodology for optimizing transistor current and sizing in analog CMOS design. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2003, 22, 225–237. [Google Scholar] [CrossRef]
- Ochotta, E.S.; Rutenbar, R.A.; Carley, L.R. Synthesis of high-performance analog circuits in ASTRX/OBLX. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1996, 15, 273–294. [Google Scholar] [CrossRef]
- De Smedt, B.; Gielen, G.G.E. WATSON: Design space boundary exploration and model generation for analog and RFIC design. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2003, 22, 213–224. [Google Scholar] [CrossRef]
- Sanabria Borbon, A.; Tlelo-Cuautle, E.; de la Fraga, L. Optimal Sizing of Amplifiers by Evolutionary Algorithms with Integer Encoding and gm/ID Design Method. In NEO 2016. Studies in Computational Intelligence; Maldonado, Y., Trujillo, L., Schütze, O., Riccardi, A., Vasile, M., Eds.; Springer: Cham, Switzerland, 2018; Volume 731, pp. 263–279. [Google Scholar]
- Jespers, P.; Murmann, B. Systematic Design of Analog CMOS Circuits; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Soto-Aguilar, S.; Sanabria-Borbón, A.; Sánchez-Sinencio, E. Surrogate-based Optimization-aided Design for Low Power Analog Circuits. In Proceedings of the 2018 IEEE 61st International Midwest Symposium on Circuits and Systems (MWSCAS), Windsor, ON, Canada, 5–8 August 2018; pp. 566–569. [Google Scholar]
- Graeb, H.; Schlichtmann, U. Pareto optimization of analog circuits considering variability. Int. J. Circuit Theory Appl. 2009, 22, 283–299. [Google Scholar] [CrossRef]
- Mueller-Gritschneder, D.; Graeb, H. Computation of yield-optimized pareto fronts for analog integrated circuit specifications. In Proceedings of the Design, Automation and Test in Europe, DATE, EDAA, Dresden, Germany, 8–12 March 2010; pp. 1088–1093. [Google Scholar]
- Damera-Venkata, N.; Evans, B.L. An automated framework for multicriteria optimization of analog filter designs. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1999, 46, 981–990. [Google Scholar] [CrossRef]
- Hershenson, M.D.M.; Boyd, S.P.; Lee, T.H. Optimal design of a CMOS op-amp via geometric programming. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2001, 20, 1–21. [Google Scholar] [CrossRef]
- Rout, P.K.; Acharya, D.P.; Panda, G. A Multiobjective Optimization Based Fast and Robust Design Methodology for Low Power and Low Phase Noise Current Starved VCO. IEEE Trans. Semicond. Manuf. 2014, 27, 43–50. [Google Scholar] [CrossRef]
- Mandal, P.; Visvanathan, V. CMOS op-amp sizing using a geometric programming formulation. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2001, 20, 22–38. [Google Scholar] [CrossRef]
- Liu, B.; Gielen, G.; Fernández, F.V. Automated Design of Analog and High-frequency Circuits. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2014; Volume 501. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Nocedal, J., Wright, S.J., Eds.; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, USA, 2006. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Sanabria-Borbon, A.C. Optimising operational amplifiers by evolutionary algorithms and gm/Id method. Int. J. Electron. 2016, 103, 1665–1684. [Google Scholar] [CrossRef]
- Lourenço, N. GENOM-POF: Multi-Objective Evolutionary Synthesis of Analog ICs with Corners Validation. In Proceedings of the 14th International Conference on Genetic and Evolutionary Computation (GECCO), Philadelphia, PA, USA, 7–11 July 2012; pp. 1119–1126. [Google Scholar]
- Mohanty, S.P. Nanoelectronic Mixed-Signal System Design; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Schneider, M.C.; Galup-Montoro, C. CMOS Analog Design Using All-Region MOSFET Modeling; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Cunha, A.I.A.; Schneider, M.C.; Galup-Montoro, C. An MOS transistor model for analog circuit design. IEEE J. Solid-State Circuits 1998, 33, 1510–1519. [Google Scholar] [CrossRef]
- Radin, R.L.; Moreira, G.L.; Galup-Montoro, C.; Schneider, M.C. A simple modeling of the early voltage of MOSFETs in weak and moderate inversion. In Proceedings of the 2008 IEEE International Symposium on Circuits and Systems, Seattle, WA, USA, 18–21 May 2008; pp. 1720–1723. [Google Scholar]
- Binkley, D.M. Tradeoffs and Optimization in Analog CMOS Design; John Wiley and Sons Ltd.: Chichester, UK, 2008. [Google Scholar]
- Liu, B.; He, Y.; Reynaert, P.; Gielen, G. Global optimization of integrated transformers for high frequency microwave circuits using a Gaussian process based surrogate model. In Proceedings of the 2011 Design, Automation Test in Europe, Grenoble, France, 14–18 March 2011; pp. 1–6. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Zhang, S.; Lyu, W.; Yang, F.; Yan, C.; Zhou, D.; Zeng, X.; Hu, X. An Efficient Multi-Fidelity Bayesian Optimization Approach for Analog Circuit Synthesis. In Proceedings of the 56th Annual Design Automation Conference 2019 (DAC’19), Las Vegas, NV, USA, 2–6 June 2019; Association for Computing Machinery: New York, NY, USA, 2019. [Google Scholar]
- Matworks. Matlab Documentation R2019b. Available online: https://www.mathworks.com/help/releases/R2019b/index.html (accessed on 10 January 2020).
- Gielen, G.G.; Sansen, W.M. Symbolic Analysis for Automated Design of Analog Integrated Circuits; Kluwer Academic Publishers: Norwell, MA, USA, 1991. [Google Scholar]
- Franco, S. Design with Operational Amplifiers and Analog Integrated Circuits, 4th ed.; McGraw-Hill, Inc.: New York, NY, USA, 2015. [Google Scholar]
- Vereecken, W.; Steyaert, M. Ultra-Wideband Pulse-based Radio, 1st ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Bruton, L.T.; Trofimenkoff, F.N.; Treleaven, D.H. Noise performance of low-sensitivity active filters. IEEE J. Solid-State Circuits 1973, 8, 85–91. [Google Scholar] [CrossRef]
- Torres, J.; El-Nozahi, M.; Amer, A.; Gopalraju, S.; Abdullah, R.; Entesari, K.; Sanchez-Sinencio, E. Low Drop-Out Voltage Regulators: Capacitor-less Architecture Comparison. IEEE Circuits Syst. Mag. 2014, 14, 6–26. [Google Scholar] [CrossRef]
- Razavi, B. RF Microelectronics; Prentice Hall Communications Engineering and Emerging Technologies Series; Prentice Hall: New York, NY, USA, 2012. [Google Scholar]
- Hajimiri, A.; Limotyrakis, S.; Lee, T.H. Jitter and phase noise in ring oscillators. IEEE J. Solid-State Circuits 1999, 34, 790–804. [Google Scholar] [CrossRef]
- Ghai, D.; Mohanty, S.P.; Kougianos, E. Design of Parasitic and Process-Variation Aware Nano-CMOS RF Circuits: A VCO Case Study. IEEE Trans. Very Large Scale Integr. Syst. 2009, 17, 1339–1342. [Google Scholar] [CrossRef]

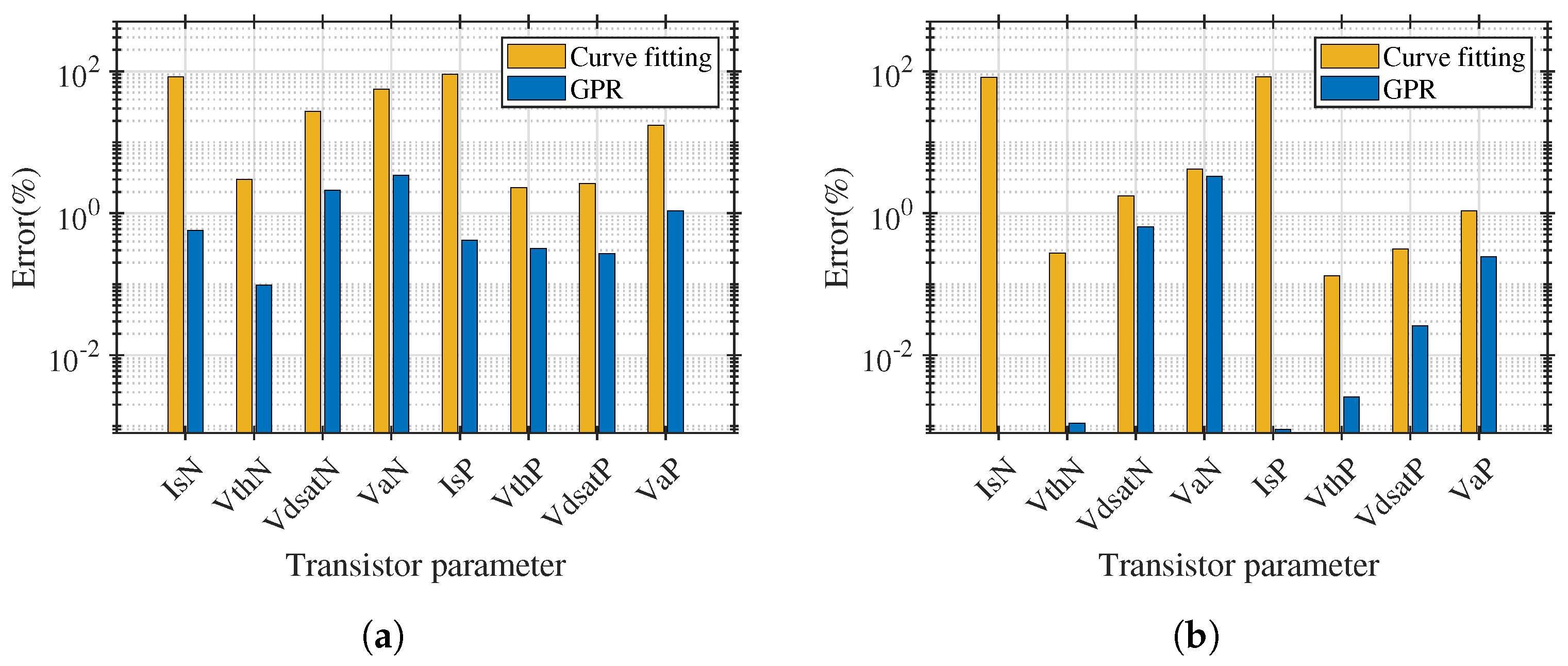









NMOS | PMOS | NMOS | PMOS | NMOS | PMOS | NMOS | PMOS | |
|---|---|---|---|---|---|---|---|---|
| KernelFunc | Exp. | ArdExp. | ArdExp. | ArdExp. | Exp. | Exp. | Exp. | ArdExp. |
| BasisFunc | Linear | None | Constant | None | Constant | Constant | None | None |
| FitMethod | Fic | Fic | Sr | Sr | Sd | Sd | Fic | Sr |
| ActiveSetMethod | Sgma | Sgma | Random | Random | Entropy | Random | Sgma | Random |
| PredictMethod | Exact | Exact | Exact | Exact | Exact | Exact | Exact | Exact |
| ResubLoss | 1.37 × 10 | 3.5 × 10 | 6.26 × 10 | 11.52 × 10 | 5.18 × 10 | 2.35 × 10 | 6.29 × 10 | 2.47 × 10 |
| Parameter of the Algorithm | SQP | NSGA-II |
|---|---|---|
| Algorithm implementation | fmincon: sqp [36] | NSGA2 toolbox [25] |
| Multi-start/Runs | 10 | 10 |
| Stop criteria | Function tolerance = 1 × 10 | Max. generations = 500 |
| Max. Fun. evaluations = 8 × 10 | Population size = 30 | |
| Other parameters | Max. iterations = 2 × 10 | Dist. index for crossover = 20 |
| Constraint tolerance = 1 × 10 | Dist. index for mutation = 20 |
| Parameter | Spec | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min | Mean | Max | Min | Mean | Max | Min | Mean | Max | ||
| [dB] | >40 | 55.54 | 57.59 | 61.35 | 52.21 | 55.69 | 58.58 | 42.47 | 45.65 | 49.24 |
| >10 | 19.28 | 20.98 | 31.87 | 13.59 | 15.03 | 16.26 | 11.71 | 12.27 | 13.34 | |
| [°] | >40 | 42.17 | 45.49 | 48.16 | 42.31 | 45.75 | 49.21 | 44.62 | 46.91 | 48.68 |
| [V] | >0.6 | 1.14 | 1.18 | 1.23 | 1.11 | 1.20 | 1.30 | 0.76 | 0.85 | 0.95 |
| [V] | >1 | 1.29 | 1.36 | 1.65 | 1.25 | 1.32 | 1.37 | 1.39 | 1.43 | 1.47 |
| [V/s] | >0.4 | 2.13 | 2.38 | 3.63 | 10.40 | 12.24 | 15.06 | 85.84 | 91.49 | 103.63 |
| 0.56 | 0.66 | 1.15 | 4.73 | 5.53 | 6.41 | 56.02 | 57.15 | 60.07 | ||
| [V/] | <2 | 0.89 | 1.04 | 1.22 | 1.22 | 1.34 | 1.41 | 1.05 | 1.11 | 1.18 |
| Process | PSR@1 kHz | PSR@10 kHz | PSR@100 kHz | PM | |||||
|---|---|---|---|---|---|---|---|---|---|
| TSMC 180 nm | 1.8 V | 1.6 V | 100 pF | 533.3 A | 5.3 mA | <−50 dB | <−45 dB | <−25 dB | >45° |
| IBM 130 nm | 1.2 V | 1 V | 100 pF | 333.3 A | 3.3 mA | <−40 dB | <−40 dB | <−25 dB | >45° |
| TSMC 65 nm | 1.2 V | 1 V | 100 pF | 333.3 A | 3.3 mA | <−40 dB | <−40 dB | <−25 dB | >45° |
| Metric | Spec. | Low Load | High Load | ||||
|---|---|---|---|---|---|---|---|
| Min | Mean | Max | Min | Mean | Max | ||
| |PSR@1kHz| [dB] | >40 | 40.26 | 48.81 | 54.40 | 48.62 | 54.08 | 63.18 |
| |PSR@10kHz| [dB] | >40 | 40.04 | 45.58 | 50.71 | 44.77 | 48.67 | 54.41 |
| |PSR@100kHz |[dB] | >25 | 27.87 | 30.99 | 34.51 | 27.02 | 30.74 | 35.29 |
| Phase Margin [°] | >45 | 49.33 | 59.91 | 68.62 | 73.40 | 81.07 | 85.64 |
| Metric | Spec. | Low Load | High Load | ||||
|---|---|---|---|---|---|---|---|
| Min | Mean | Max | Min | Mean | Max | ||
| |PSR@1kHz| [dB] | >40 | 40.37 | 48.97 | 59.72 | 45.78 | 56.67 | 74.05 |
| |PSR@10kHz| [dB] | >40 | 40.19 | 47.12 | 54.45 | 45.31 | 50.60 | 56.27 |
| |PSR@100kHz |[dB] | >25 | 31.54 | 33.75 | 36.49 | 31.71 | 33.93 | 37.06 |
| Phase margin [°] | >45 | 50.39 | 53.32 | 55.99 | 70.85 | 73.78 | 77.42 |
| Circuit | No. of Design Variables | No. of Constraints | Evaluation Time Surrogate [s] | Evaluation Time Simulation [s] | Evaluation Time Improvement |
|---|---|---|---|---|---|
| Filter | 9 | 21 | |||
| LDO | 10 | 24 | |||
| VCO | 7 | 15 | 18 |
| Circuit | TSMC180 | IBM130 | TSMC65 | |||
|---|---|---|---|---|---|---|
| SQP | NSGA-II | SQP | NSGA-II | SQP | NSGA-II | |
| Filter | 90.48% | 68.57% | 100.00% | 100.00% | 57.14% | 100.00% |
| LDO | 76.67% | 70.00% | 70.00% | 83.33% | 56.67% | 75.45% |
| VCO | 60.00% | 66.67% | 70.00% | 93.33% | 86.67% | 60.00% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanabria-Borbón, A.C.; Soto-Aguilar, S.; Estrada-López, J.J.; Allaire, D.; Sánchez-Sinencio, E. Gaussian-Process-Based Surrogate for Optimization-Aided and Process-Variations-Aware Analog Circuit Design. Electronics 2020, 9, 685. https://doi.org/10.3390/electronics9040685
Sanabria-Borbón AC, Soto-Aguilar S, Estrada-López JJ, Allaire D, Sánchez-Sinencio E. Gaussian-Process-Based Surrogate for Optimization-Aided and Process-Variations-Aware Analog Circuit Design. Electronics. 2020; 9(4):685. https://doi.org/10.3390/electronics9040685
Chicago/Turabian StyleSanabria-Borbón, Adriana C., Sergio Soto-Aguilar, Johan J. Estrada-López, Douglas Allaire, and Edgar Sánchez-Sinencio. 2020. "Gaussian-Process-Based Surrogate for Optimization-Aided and Process-Variations-Aware Analog Circuit Design" Electronics 9, no. 4: 685. https://doi.org/10.3390/electronics9040685
APA StyleSanabria-Borbón, A. C., Soto-Aguilar, S., Estrada-López, J. J., Allaire, D., & Sánchez-Sinencio, E. (2020). Gaussian-Process-Based Surrogate for Optimization-Aided and Process-Variations-Aware Analog Circuit Design. Electronics, 9(4), 685. https://doi.org/10.3390/electronics9040685





