Hardware in the Loop Implementation of the Oscillator-based Heart Model: A Framework for Testing Medical Devices
Abstract
1. Introduction
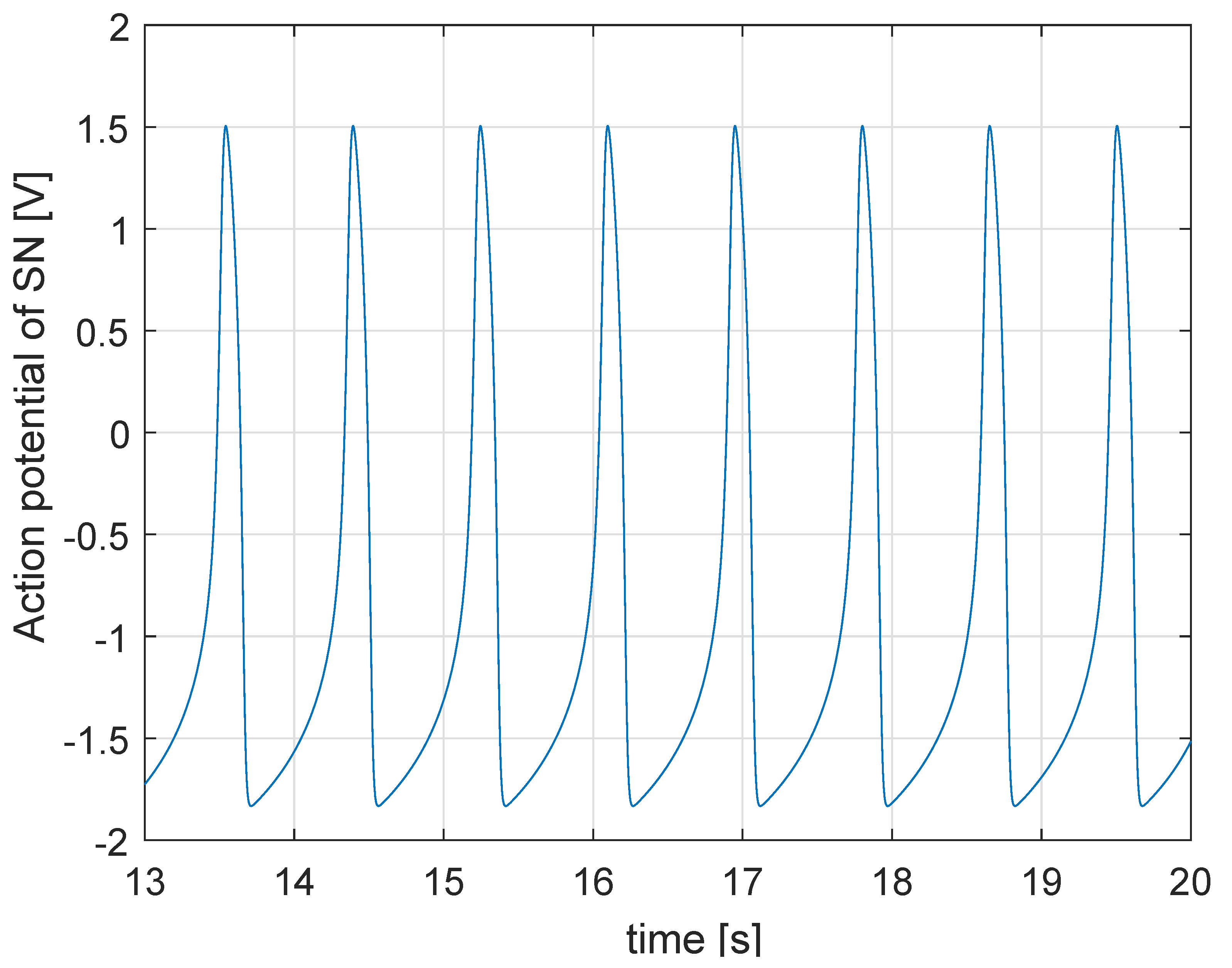
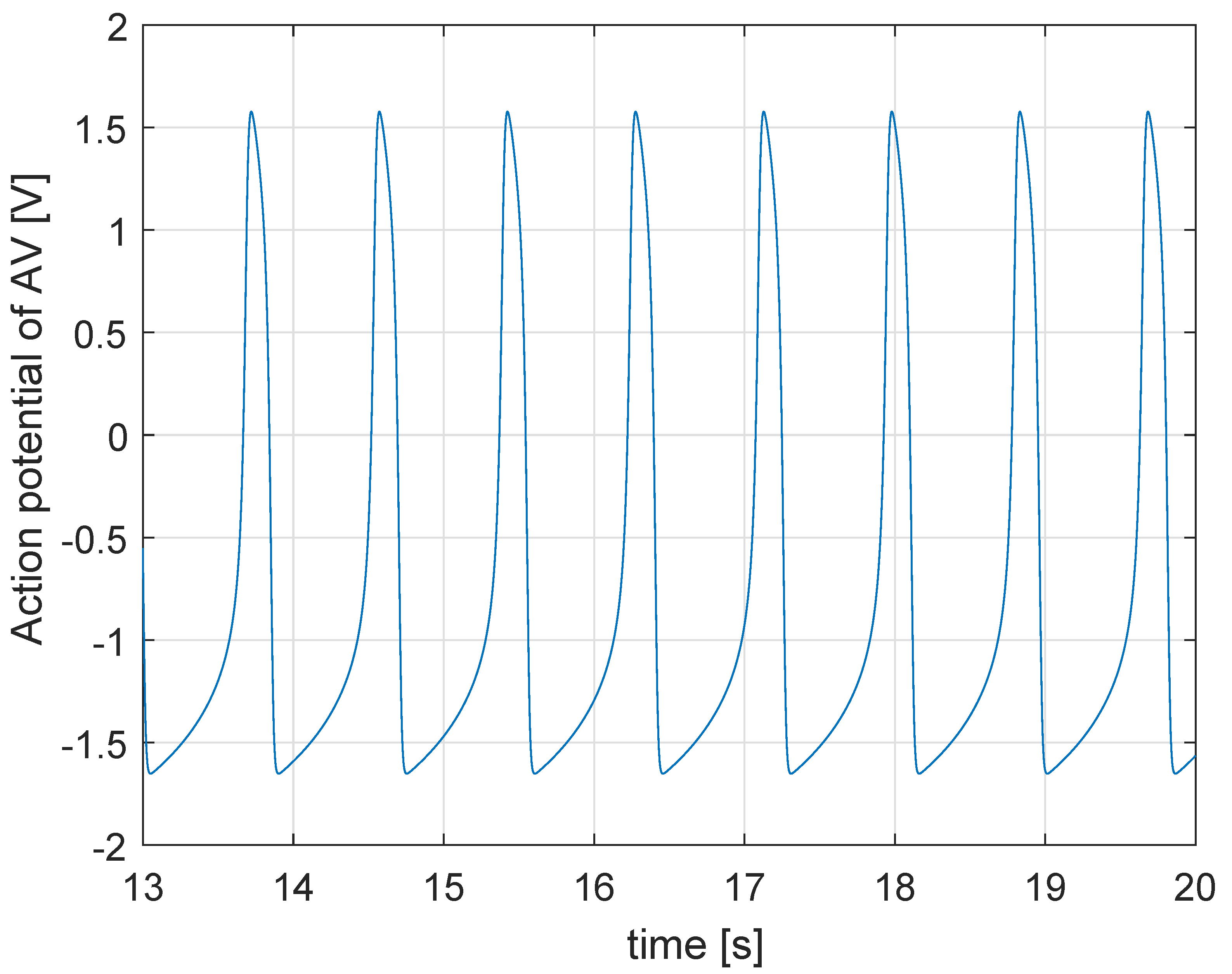
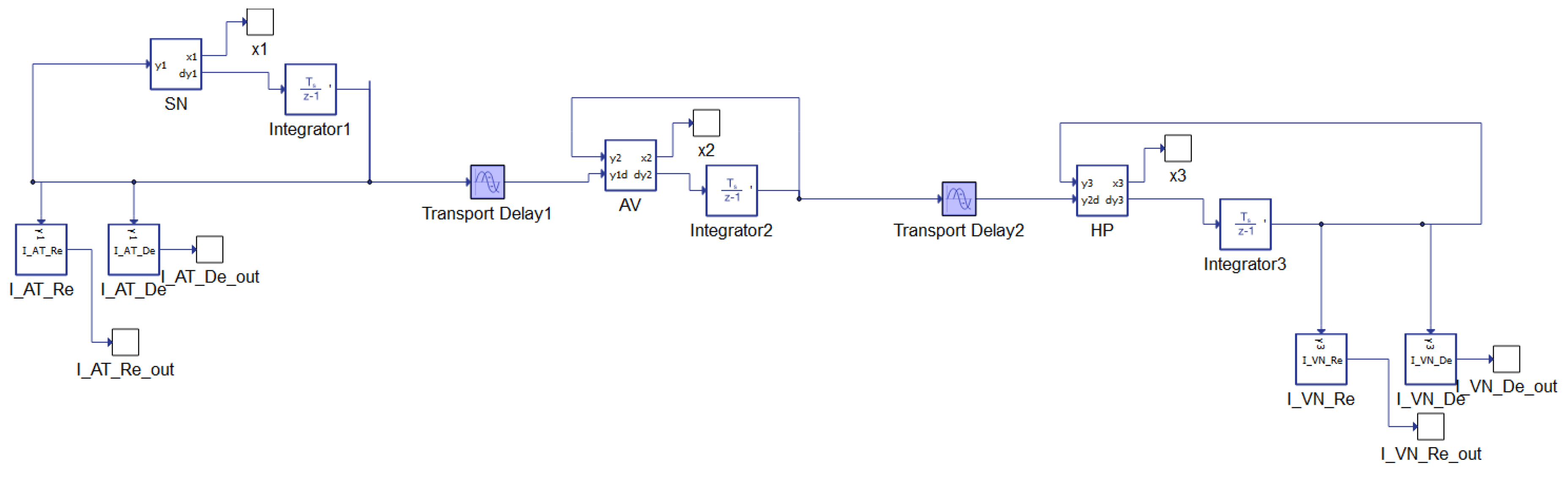
2. Physiology of the Heart: The State of the Art of the Mathematical Model
- A voltage variable that allows regenerative self-excitation through a positive feedback. It is a cubic term and it represents the non linearity of the system;
- A recovery variable, that provides a negative feedback. It is slower and it is the linear part of the system.
- Damping coefficients for the pacemaker, , , ;
- Parameters defining the amplitude of a pulse, , , ;
- Parameters changing the rest state and dynamics, , , ;
- Parameters controlling the hyper-polarization of the excitation variable, , , ;
- Parameters controlling excitation threshold, , , ;
- Parameters controlling excited state, , ,
- Coupling coefficients , .
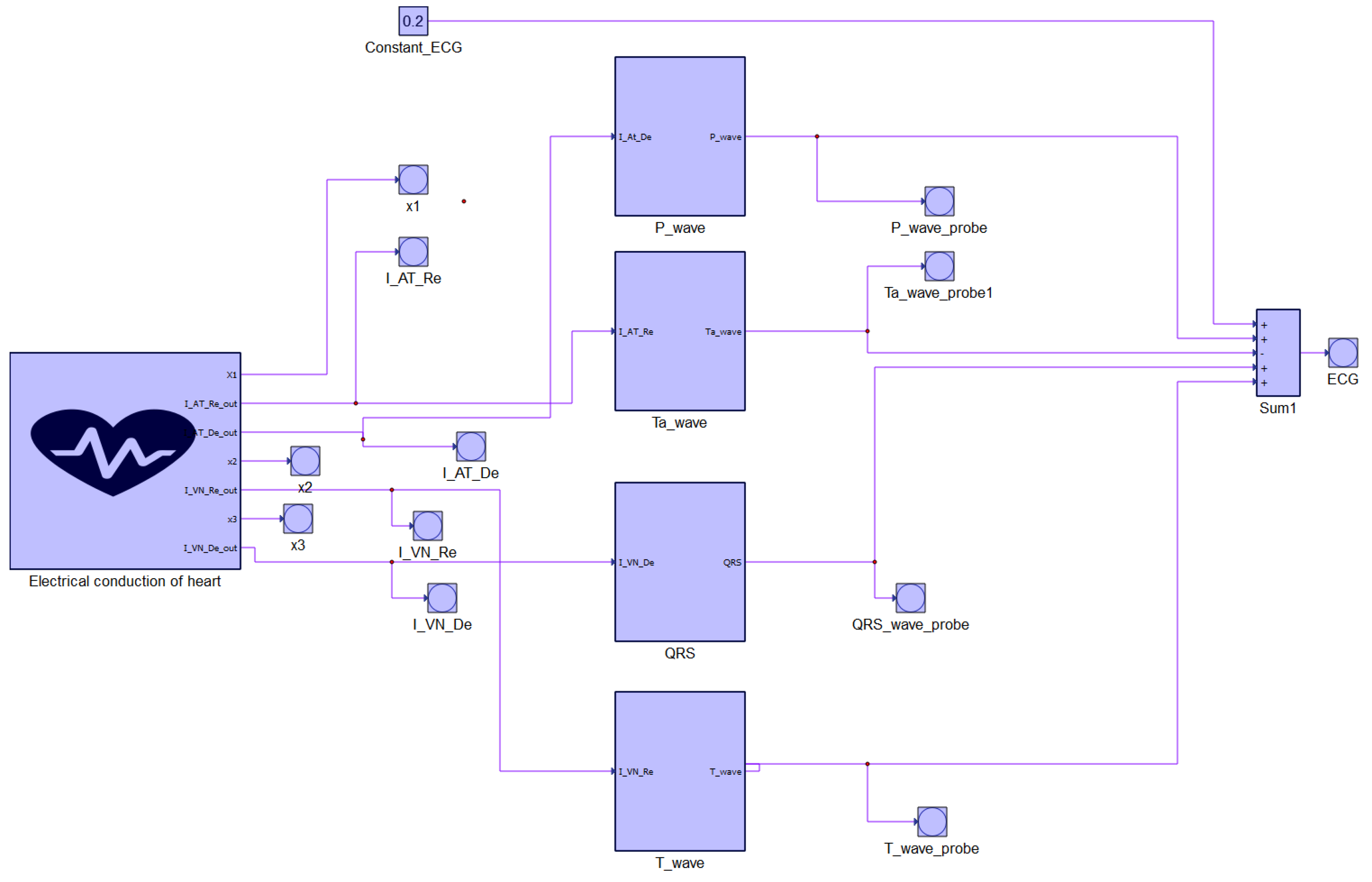
- P wave:
- Ta wave:
- QRS complex:
- T wave
- Scaling coefficients: , , , ;
- Parameters defining the amplitude of a pulse: , , , ;
- Parameters changing the rest state and dynamics: , , , ;
- Parameters controlling the hyperpolarization of the excitation variable: , , , ;
- Parameters representing excitability and controlling the abruptness of activation and the duration of the action potential: , , , ;
- Parameters changing the rest state and dynamics: , , , ;
- Parameters controlling excitation threshold: , , , ;
- Parameters controlling excited state: , , , ;
- Coupling coefficient for P wave: ;
- Coupling coefficient for Ta wave: ;
- Coupling coefficient for QRS complex: ;
- Coupling coefficient for T wave: .
- :
- :
- :
- :
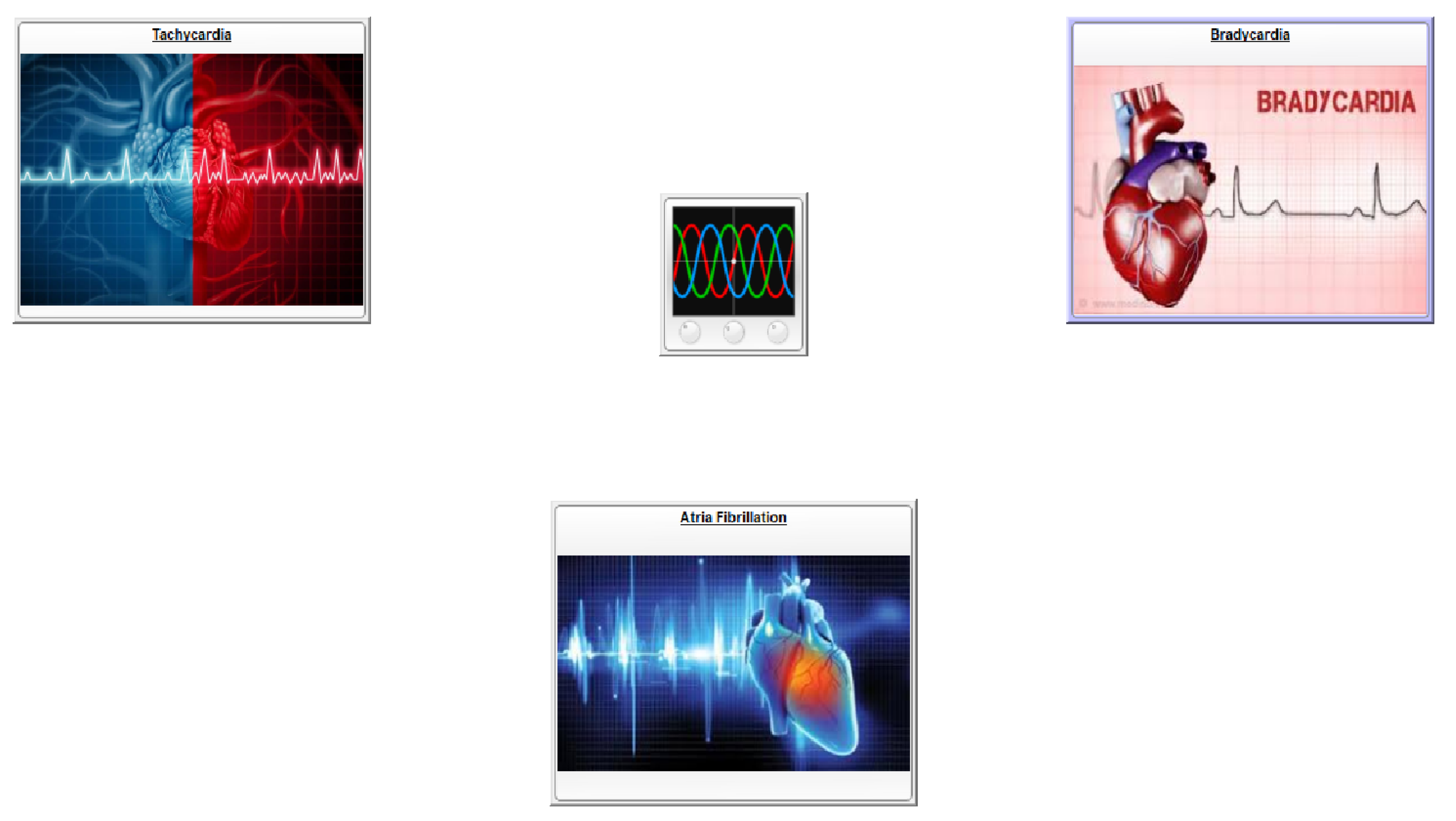
3. Analysis of the Diseases Detectable by an ECG
3.1. Tachycardia
3.2. Bradycardia
3.3. Atrial Fibrillation
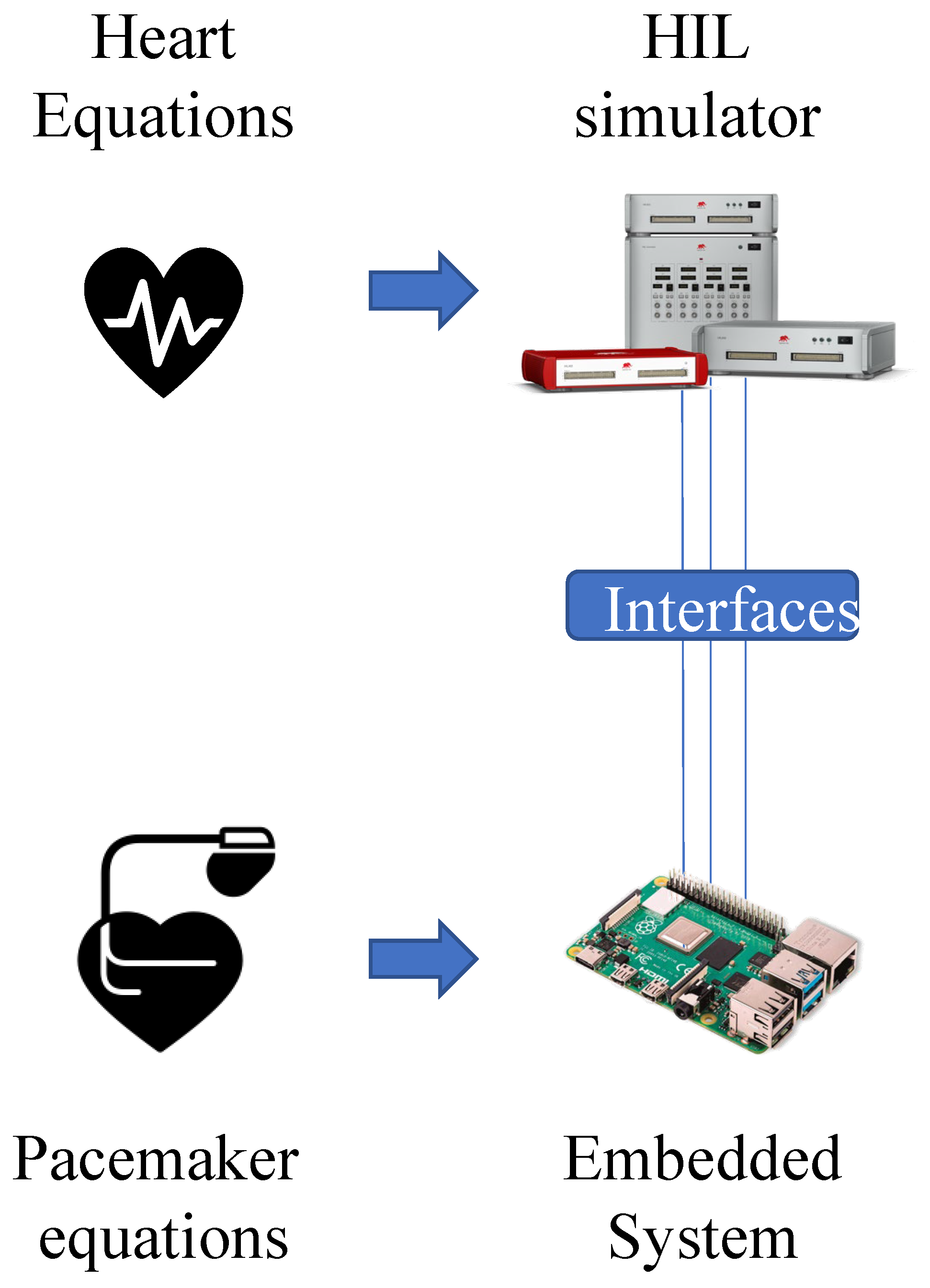
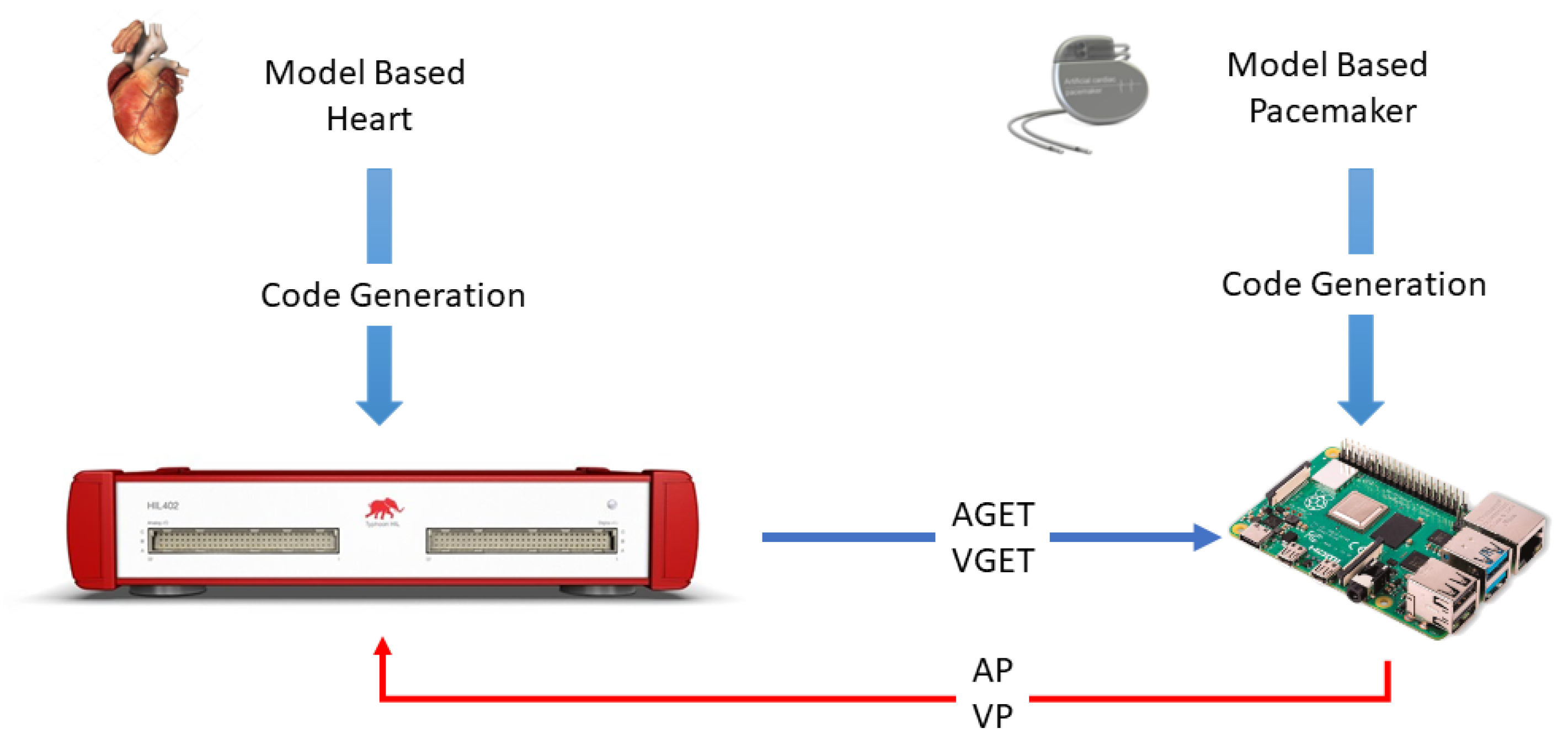
4. Hardware in the Loop Model
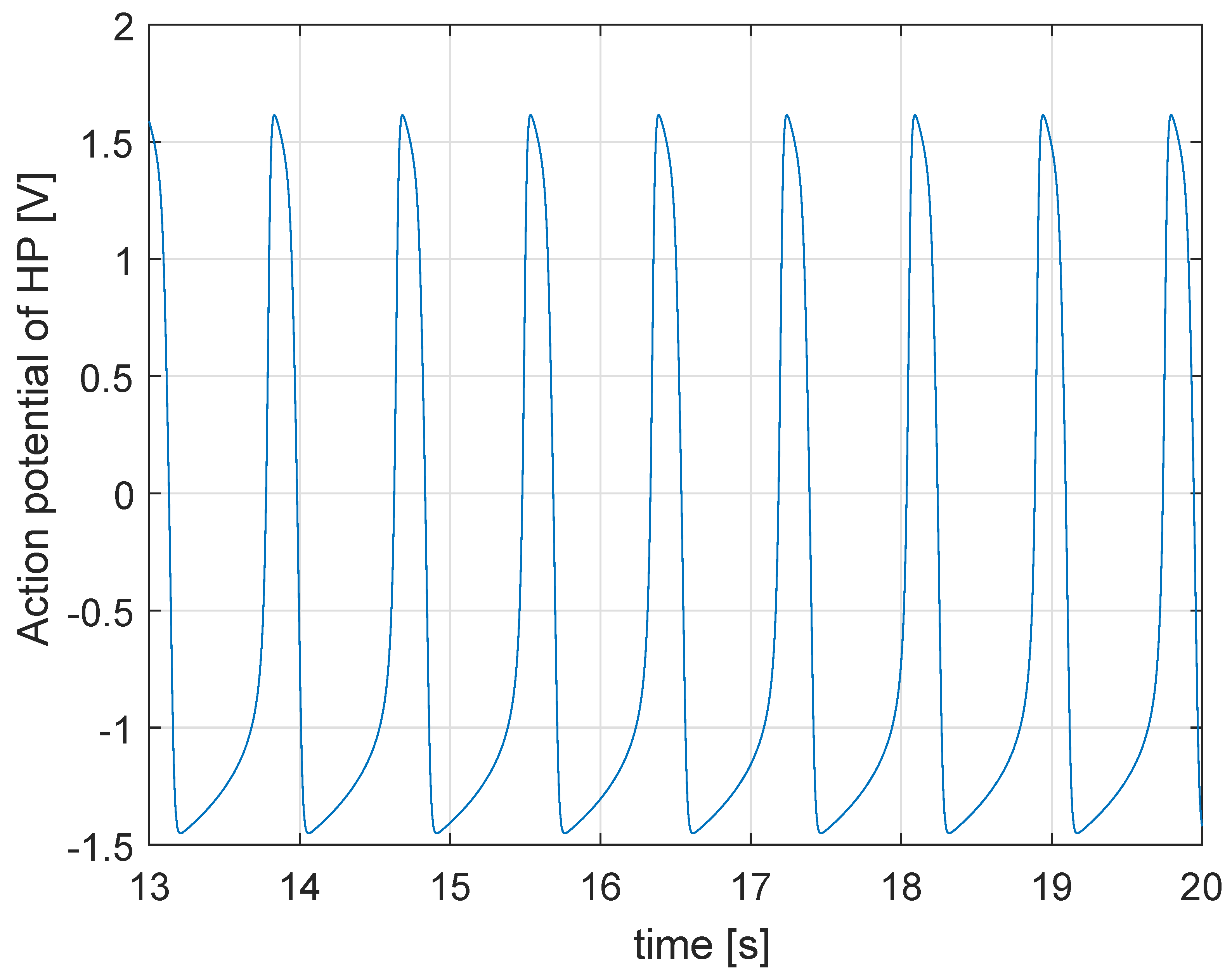
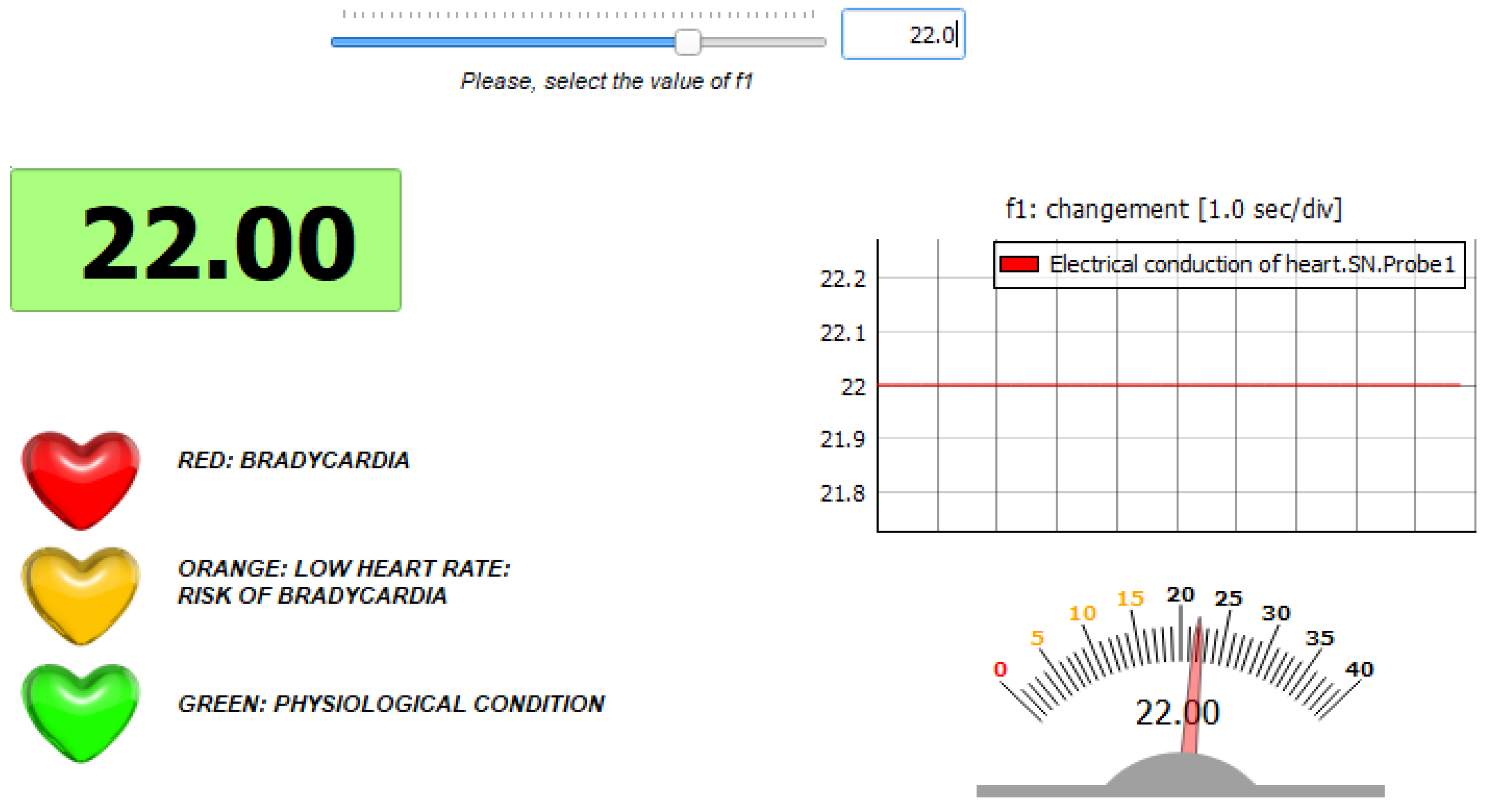
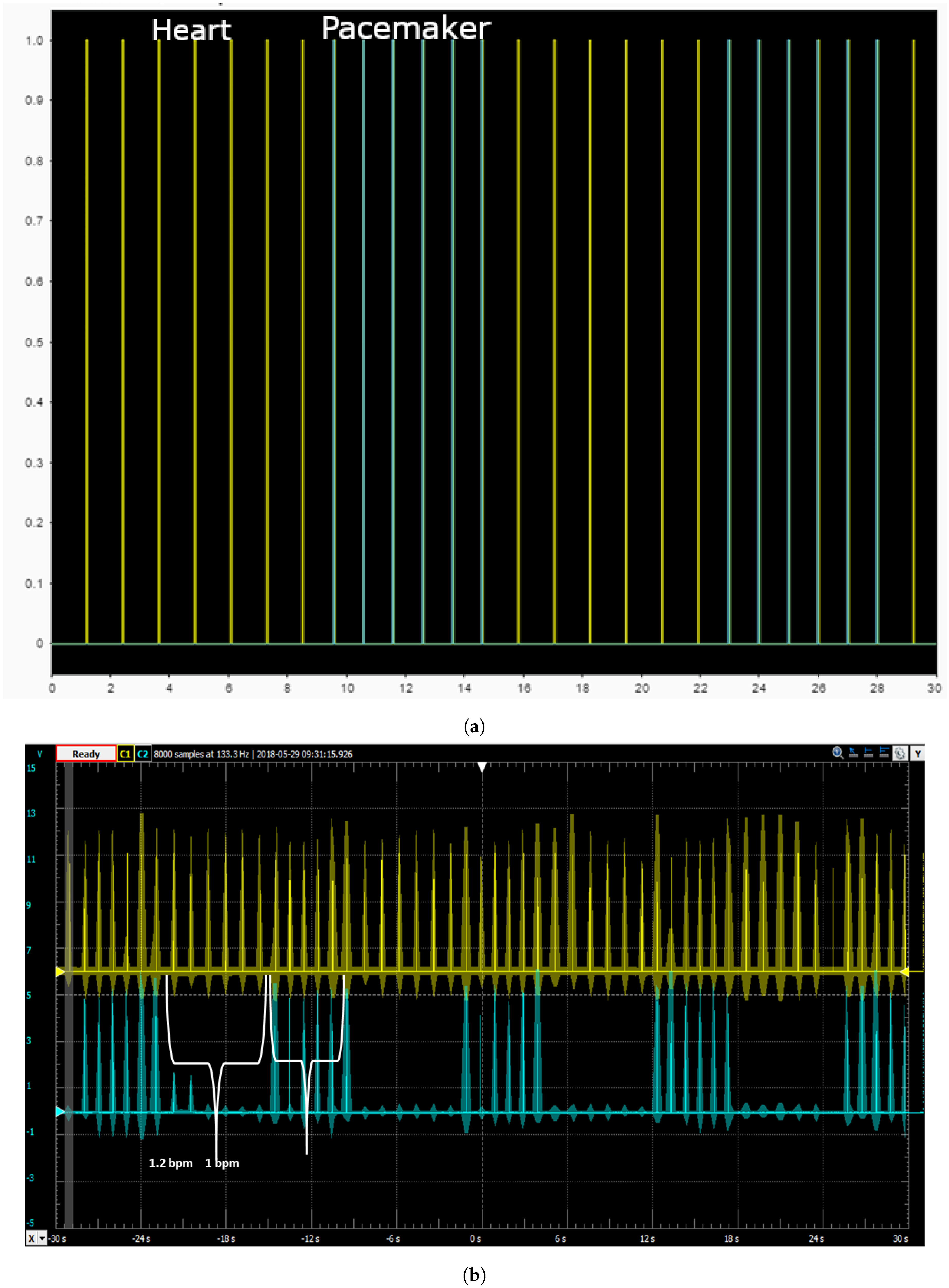
5. Application: Test of a Pacemaker
- Lower Rate Interval (LRI): This component keeps the heart rate above a minimum value.
- Atrio-Ventricular Interval (AVI): The function of the AVI component is to maintain the appropriate delay between the atria and the ventricles.
- Post Ventricular Atrial Refractory Period (PVARP), to filter noise, and Post Ventricular Atrial Blanking (PVAB): the PVARP and the PVAB are initialized by ventricular events.
- Ventricular Refractory Period (VRP): Along with the PVARP and PVAB, the VRP is used to filter noise and early events which could otherwise cause undesired pacemaker behavior.
- Physiological condition: the parameter is set to its original value ();
- Condition of bradycardia: the parameter is set to a value different from the original one ().
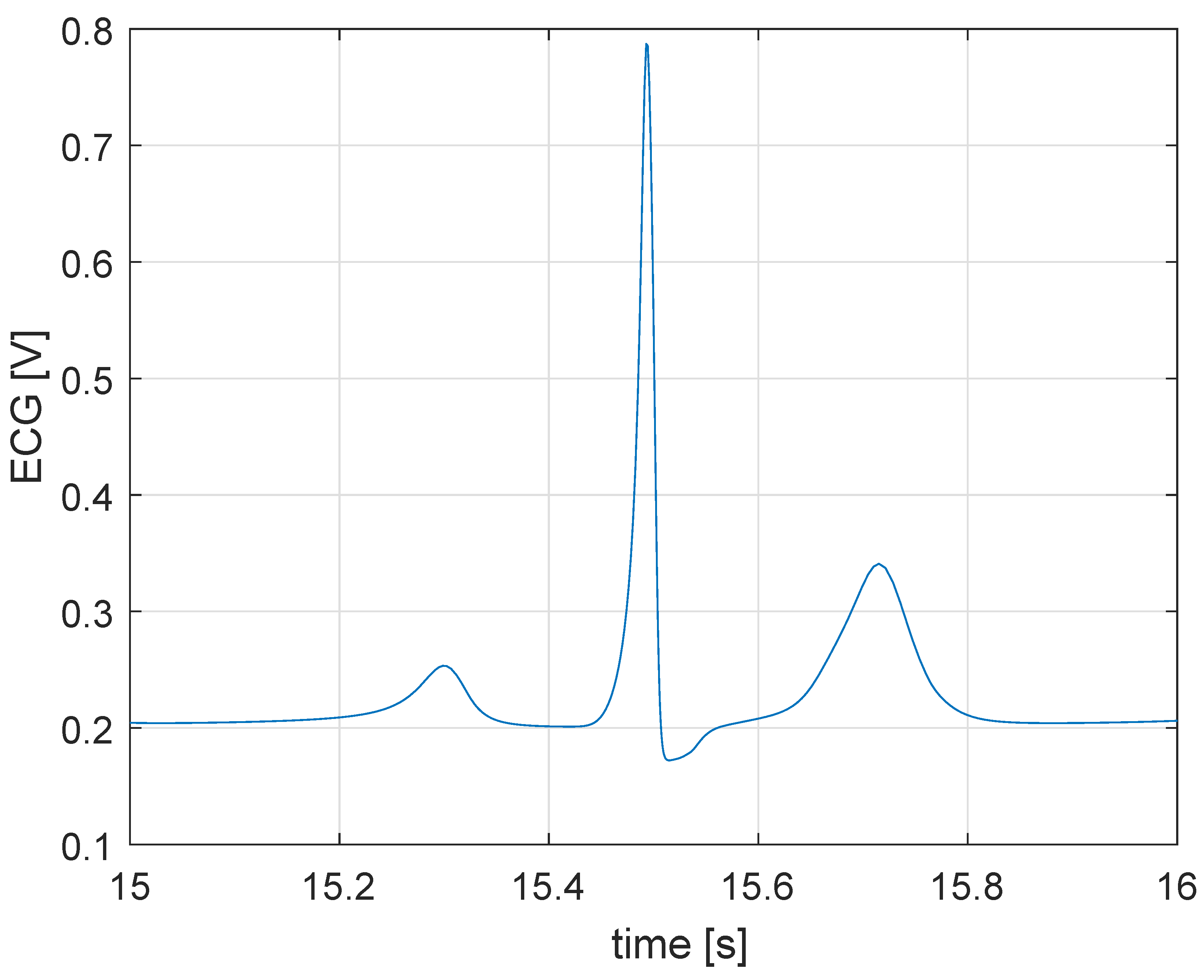
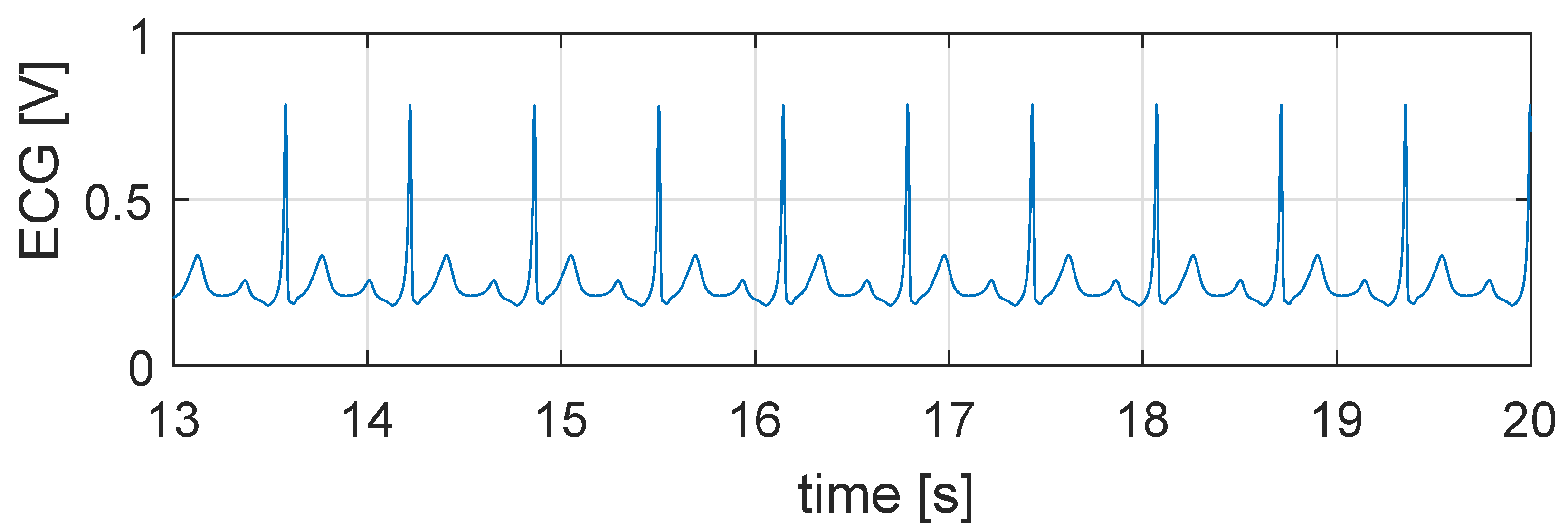
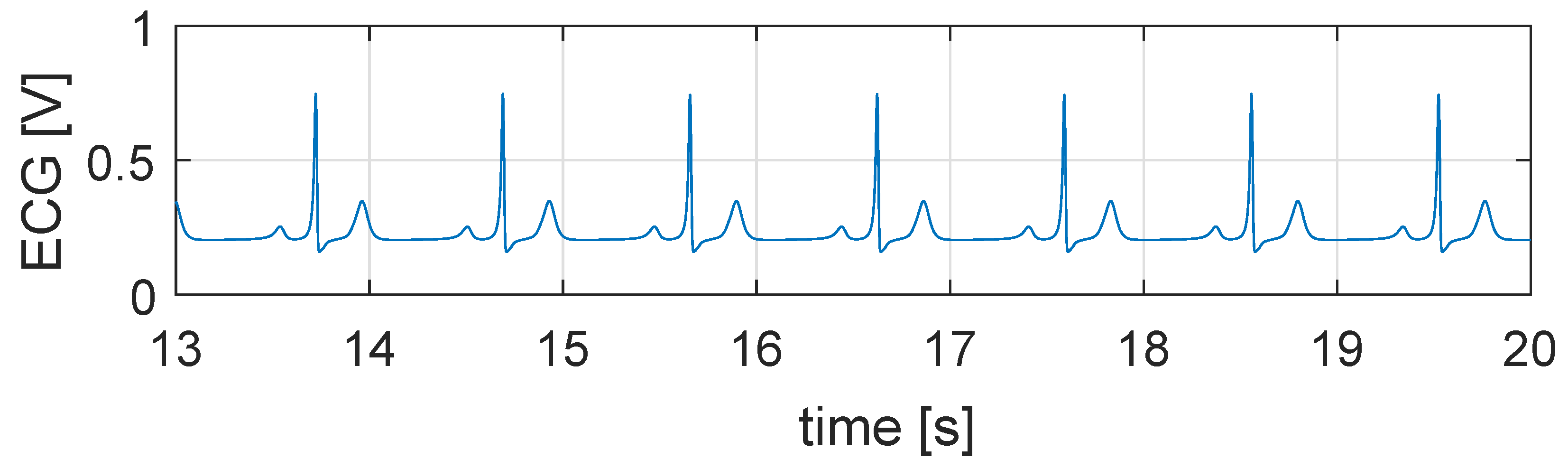
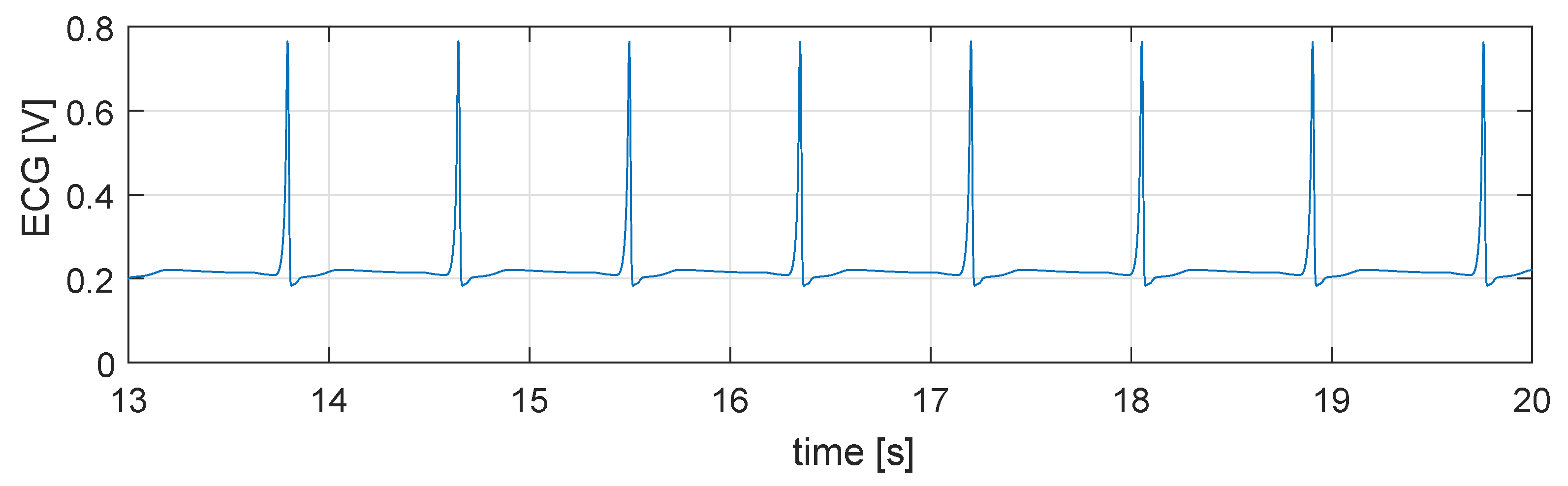
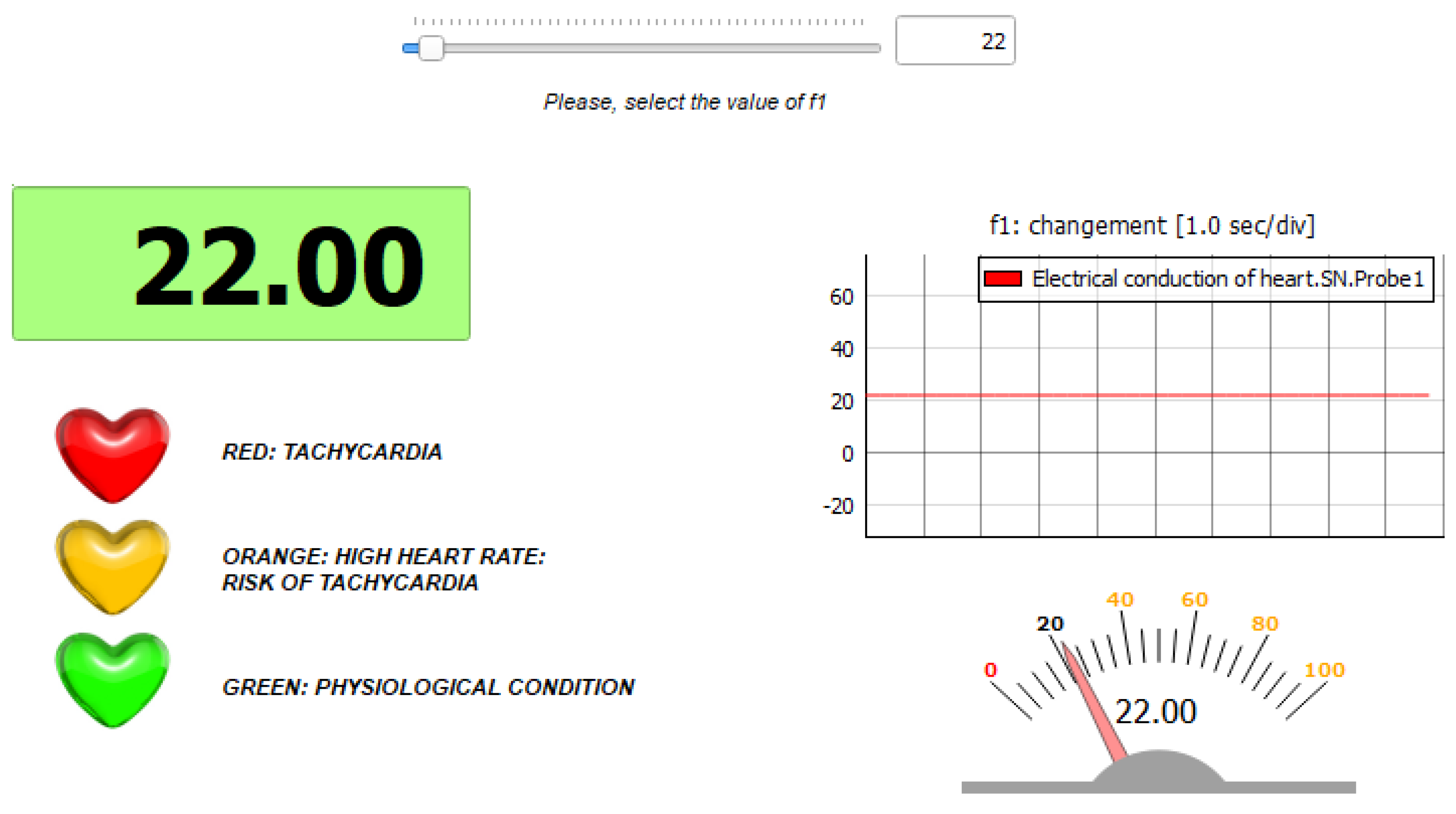
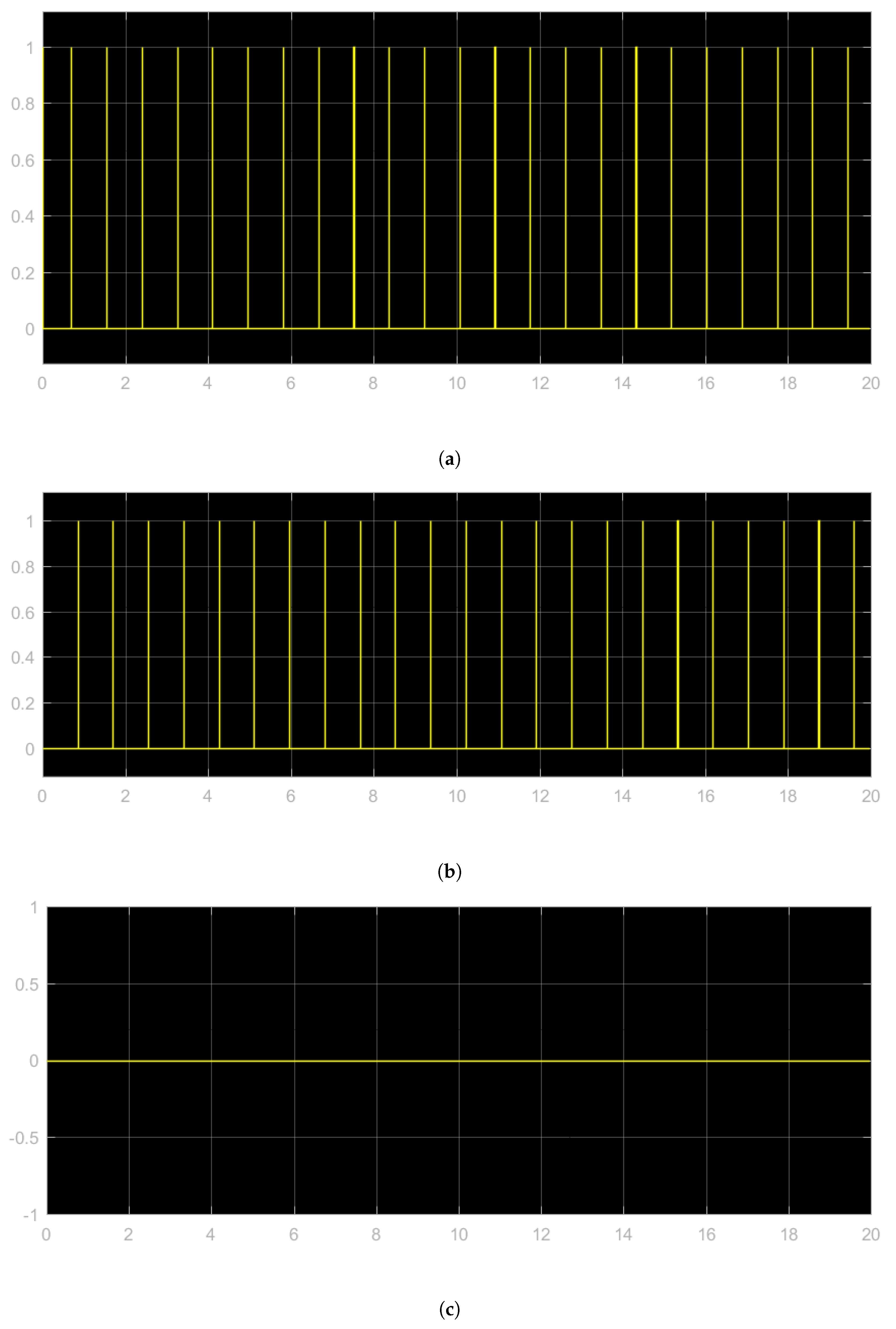
5.1. Simulation in Physiological Condition
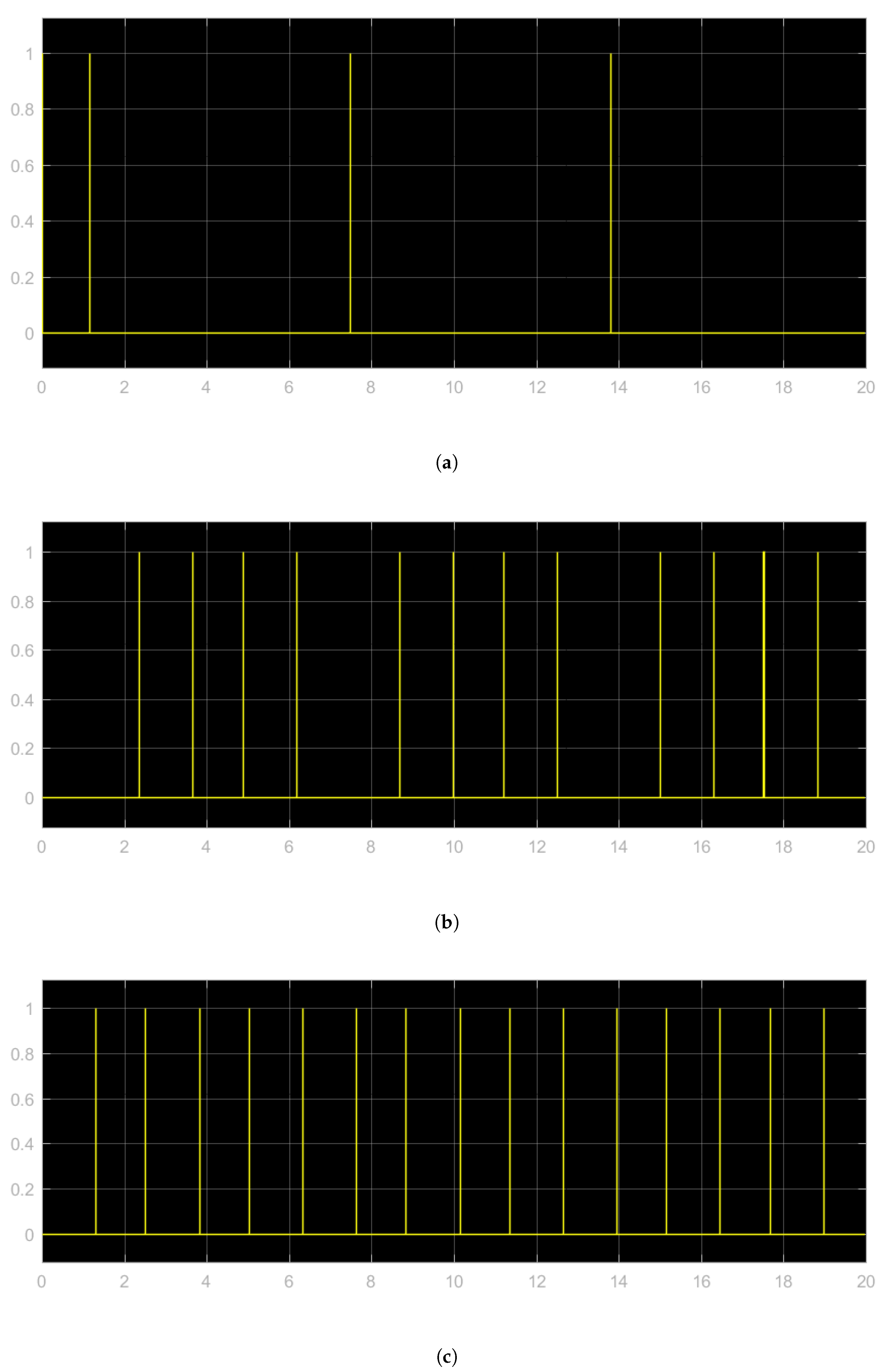
5.2. Simulation in Case of Bradycardia
5.3. Closed Loop Simulation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Friedenthal, S.; Moore, A.; Steiner, R. Chapter 18—Integrating SysML into a Systems Development Environment. In A Practical Guide to SysML, 3rd ed.; Steiner, R., Moore, A., Friedenthal, S., Eds.; Morgan Kaufmann Publishers: Burlington, MA, USA, 2014; pp. 507–541. [Google Scholar]
- Ellis, G. Chapter 13—Model Development and Verification. In Control System Design Guide, 4th ed.; Ellis, G., Ed.; Butterworth-Heinemann: Oxford, UK, 2012; pp. 261–282. [Google Scholar]
- Mai, X.H.; Kwak, S.-K.; Jung, J.-H.; Kim, K.A. Comprehensive Electric-Thermal Photovoltaic Modeling for Power-Hardware-in-the-Loop Simulation (PHILS) Applications. IEEE Trans. Ind. Electron. 2017, 64, 6255–6264. [Google Scholar] [CrossRef]
- Lauss, G.; Strunz, K. Multirate Partitioning Interface for Enhanced Stability of Power Hardware-in-the-Loop Real-Time Simulation. IEEE Trans. Ind. Electron. 2019, 66, 595–605. [Google Scholar] [CrossRef]
- Schlager, M.; Elmenreich, W.; Wenzel, I. Interface Design for Hardware-in-the-Loop Simulation. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; pp. 1554–1559. [Google Scholar]
- Walter, M.; Eisenbrand, S.; Kopp, R.; Leonhardt, S. Hardware-in-the-loop test bench for artificial lungs. In Proceedings of the XIV RUSSIAN-GERMANY CONFERENCE ON BIOMEDICAL ENGINEERING (RGC-2019), St. Petersburg, Russia, 3–6 July 2019; Potrakhov, N.N., Gryaznov, A.Y., Kostrin, D.K., Eds.; American Institute of Physics: College Park, MD, USA, 2019; Volume 2140, p. 020078. [Google Scholar] [CrossRef]
- Kung, E.; Farahmand, M.; Gupta, A. A Hybrid ExperimentalComputational Modeling Framework for Cardiovascular Device Testing. J. Biomech. Eng. 2019, 141. [Google Scholar] [CrossRef] [PubMed]
- Justino da Silva, S.; Scardovelli, T.; Boschi, S.; Rodrigues, S.; Silva, A. Simple adaptive PI controller development and evaluation for mean arterial pressure regulation. Res. Biomed. Eng. 2019, 35, 157–165. [Google Scholar] [CrossRef]
- Di Bernardo, D.; Signorini, M. A model of two nonlinear coupled oscillators for the study of heartbeat dynamics. Int. J. Bifurcation Chaos 1998, 8, 1975–1985. [Google Scholar] [CrossRef]
- Signorini, M.G.; di Bernardo, D. Simulation of heartbeat dynamics: A nonlinear model. Int. J. Bifurc. Chaos 1998, 8, 1725–1731. [Google Scholar] [CrossRef]
- Ryzhii, M.; Ryzhii, E. Simulink heart model for simulation of the effect of external signals. In Proceedings of the 2016 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Chiang Mai, Thailand, 5–7 October 2016; pp. 1–5. [Google Scholar]
- Ryzhii, E.; Ryzhii, M. Formation of second-degree atrioventricular blocks in the cardiac heterogeneous oscillator model. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; p. 15585163. [Google Scholar]
- Ryzhii, E.; Ryzhii, M. Modeling of Heartbeat Dynamics with a System of Coupled Nonlinear Oscillators. In Biomedical Informatics and Technology, Proceedings of First International Conference, ACBIT 2013, Aizu-Wakamatsu, Japan, 16–17 September 2013; Pham, T.D., Ichikawa, K., Oyama-Higa, M., Coomans, D., Jiang, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 67–75. [Google Scholar]
- Ryzhii, E.; Ryzhii, M. A heterogeneous coupled oscillator model for simulation of ECG signals. Comput. Methods Programs Biomed. 2014, 117, 40–49. [Google Scholar]
- Andalam, S.; Roop, P.; Malik, A.; Trew, M. Rethinking the Validation Process for Medical Devices: A Cardiac Pacemaker Case Study. In Proceedings of the 2018 IEEE 21st International Symposium on Real-Time Distributed Computing (ISORC), Singapore, 29–31 May 2018; p. 17962934. [Google Scholar]
- Barker, C.; Kwiatkowska, M.; Mereacre, A.; Paoletti, N.; Patanè, A. Hardware-in-the-loop simulation and energy optimization of cardiac pacemakers. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; p. 15585183. [Google Scholar]
- Jiang, Z.; Pajic, M.; Moarref, S.; Alur, R.; Mangharam, R. Modeling and Verification of a Dual Chamber Implantable Pacemaker. In Tools and Algorithms for the Construction and Analysis of Systems, Proceedings of the 18th International Conference, TACAS 2012, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2012, Tallinn, Estonia, 24 March–1 April, 2012; Flanagan, C., König, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 188–203. [Google Scholar]
- Quiroz-Juárez, M.; Jiménez-Ramírez, O.; Aragón, J.; Del Río-Correa, J.L.; Vázquez-Medina, R. Periodically kicked network of RLC oscillators to produce ECG signals. Comput. Biol. Med. 2019, 104, 87–96. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Binczak, S.; Jacquir, S.; Pont, O.; Yahia, H. Parameters analysis of FitzHugh-Nagumo model for a reliable simulation. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 4334–4337. [Google Scholar]
- Burns, E. ECG Library. Available online: http://lifeinthefastlane.com/ecg-library (accessed on 20 February 2020).
- PhysioNet: The Research Resource for Complex Physiologic Signals. Available online: https://physionet.org/ (accessed on 20 February 2020).
- Typhoon Hil Documentation. Available online: https://www.typhoon-hil.com/ (accessed on 25 February 2020).


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mascio, C.D.; Gruosso, G. Hardware in the Loop Implementation of the Oscillator-based Heart Model: A Framework for Testing Medical Devices. Electronics 2020, 9, 571. https://doi.org/10.3390/electronics9040571
Mascio CD, Gruosso G. Hardware in the Loop Implementation of the Oscillator-based Heart Model: A Framework for Testing Medical Devices. Electronics. 2020; 9(4):571. https://doi.org/10.3390/electronics9040571
Chicago/Turabian StyleMascio, Chiara Di, and Giambattista Gruosso. 2020. "Hardware in the Loop Implementation of the Oscillator-based Heart Model: A Framework for Testing Medical Devices" Electronics 9, no. 4: 571. https://doi.org/10.3390/electronics9040571
APA StyleMascio, C. D., & Gruosso, G. (2020). Hardware in the Loop Implementation of the Oscillator-based Heart Model: A Framework for Testing Medical Devices. Electronics, 9(4), 571. https://doi.org/10.3390/electronics9040571





