Complex Dynamics of a Novel Chaotic System Based on an Active Memristor
Abstract
1. Introduction
2. Memristor Model and its Emulator
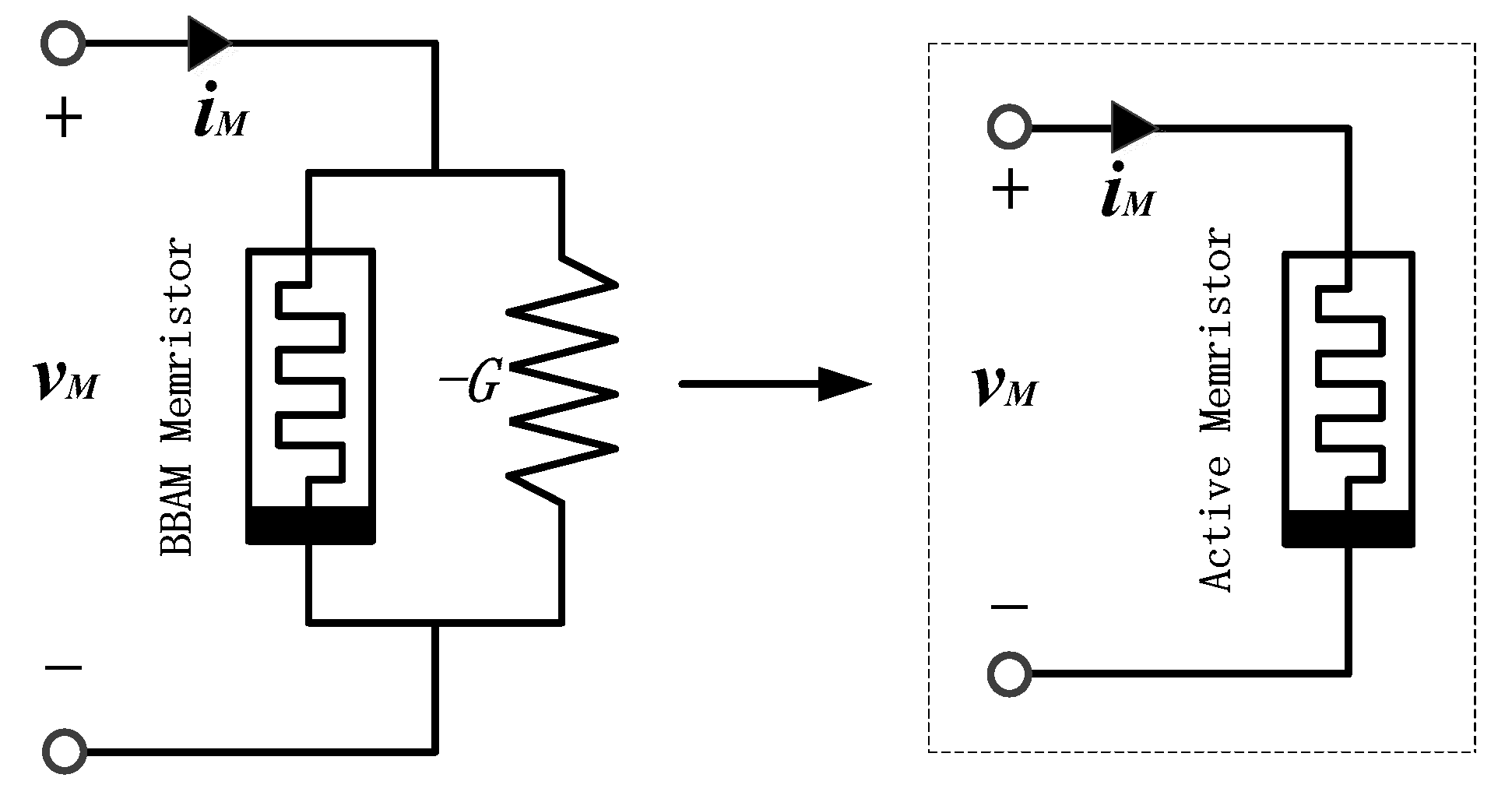
2.1. An Active Memristor
2.2. Memristive Emulator
3. Chaotic Circuit Topology and Circuit Dynamics
3.1. Chaotic Circuit Ttopology
3.2. Stability of the System
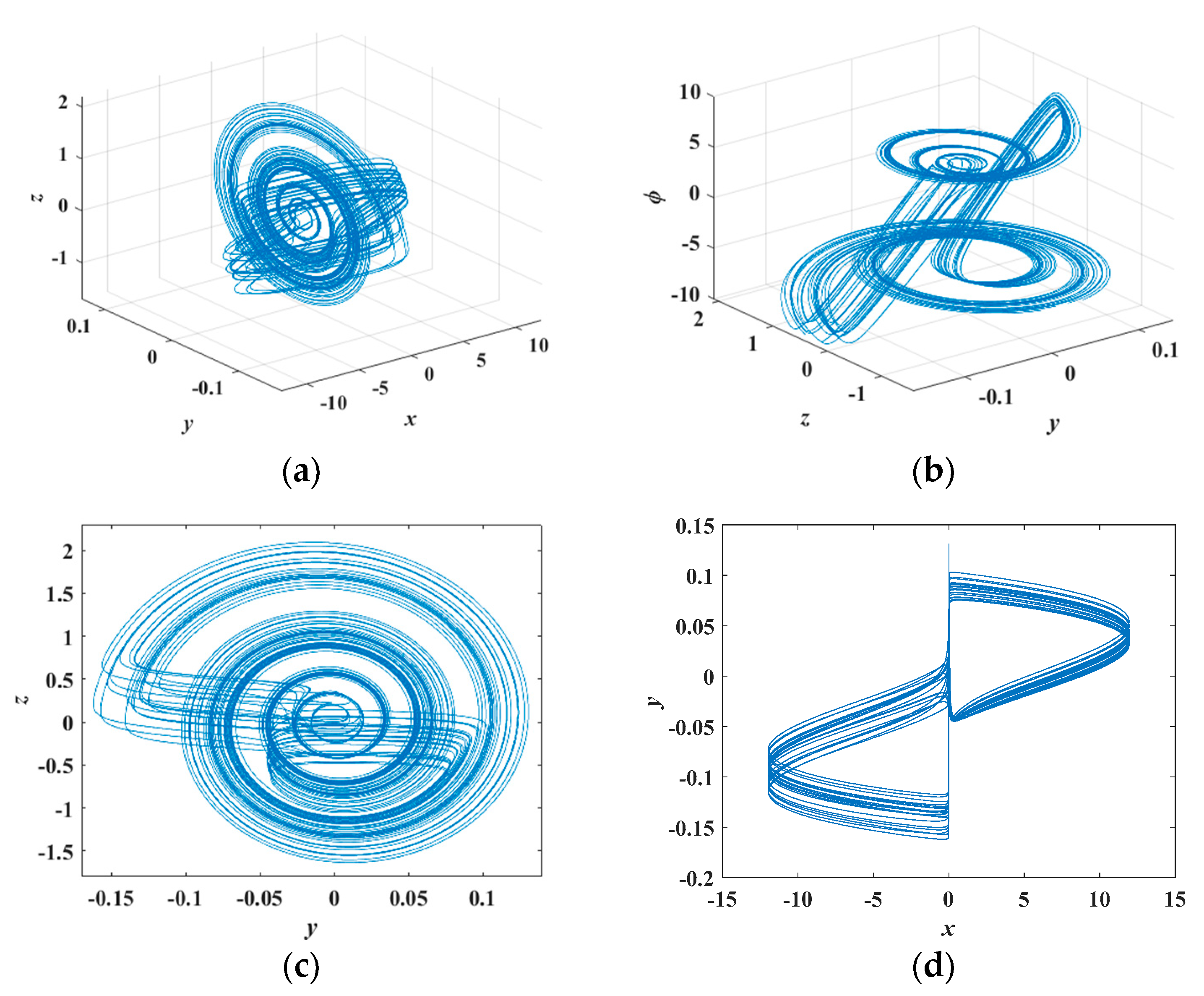
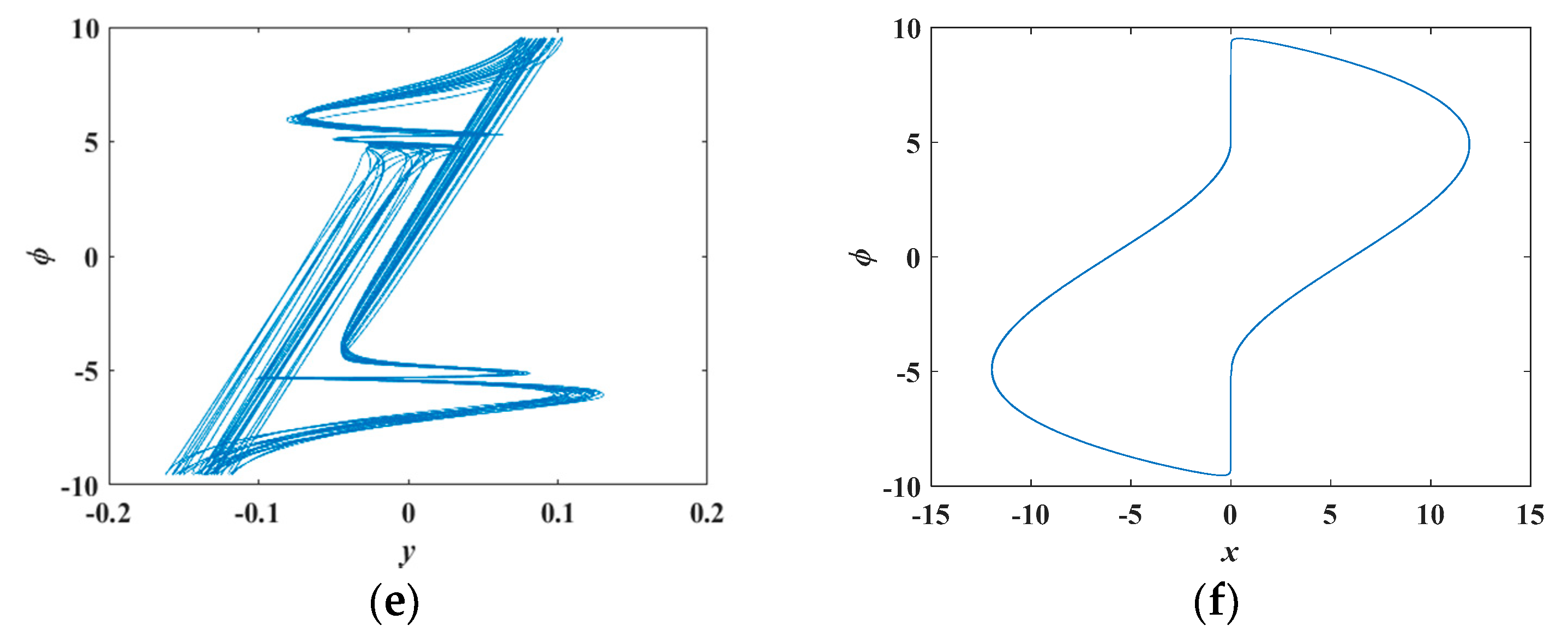
4. Dynamics of the Memristor-Based Oscillator
4.1. Symmetry
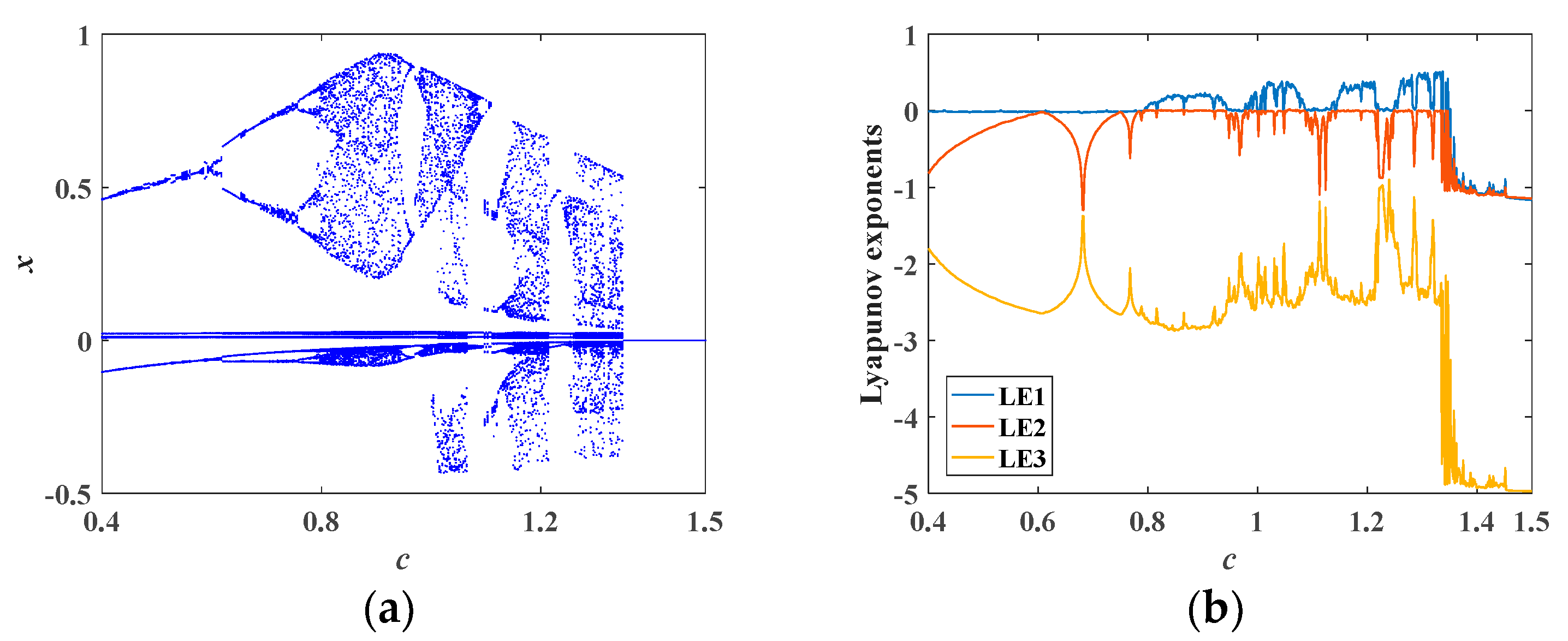
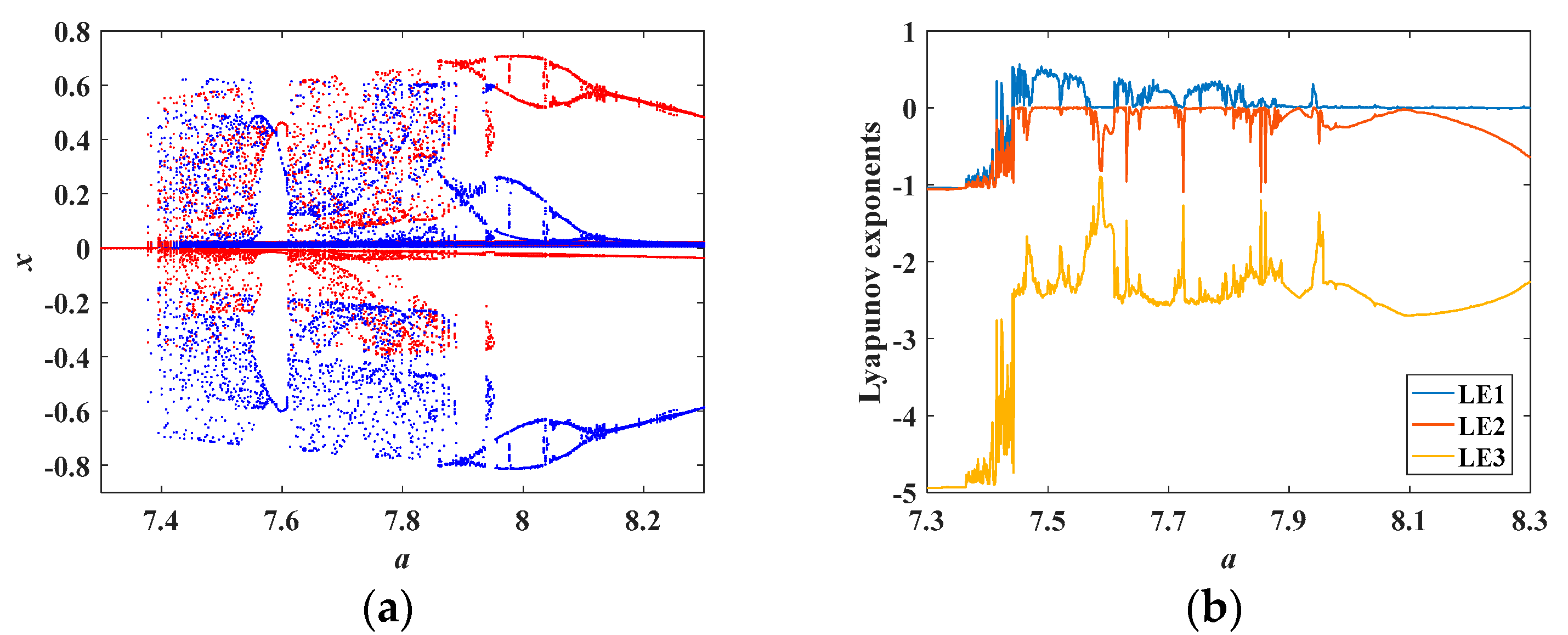
4.2. Dynamics of the Memristor-Based Oscillator with the Varying Parameter c
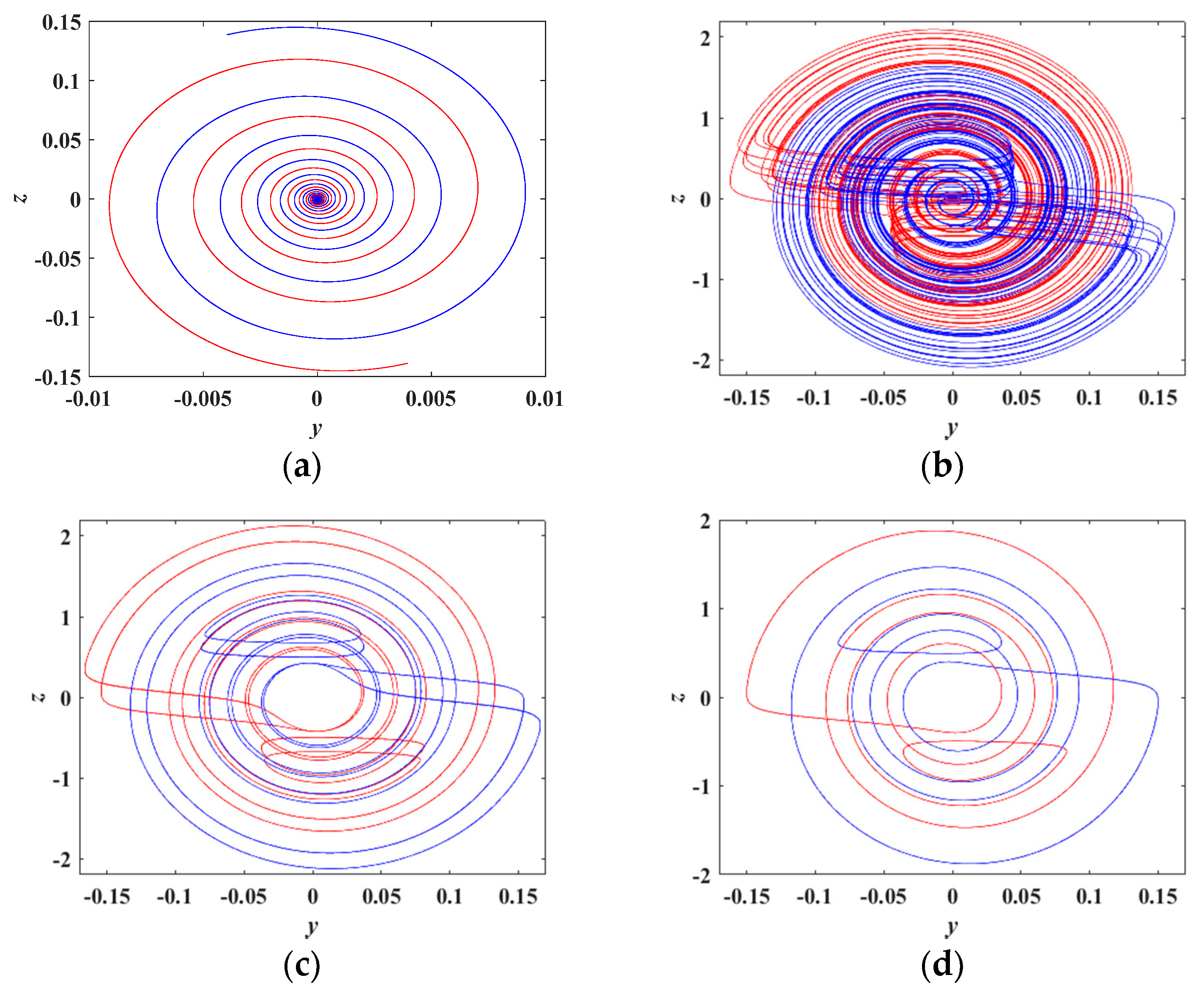
4.3. Coexisting Bifurcation and Coexisting Attractors with the Varying Parameter a
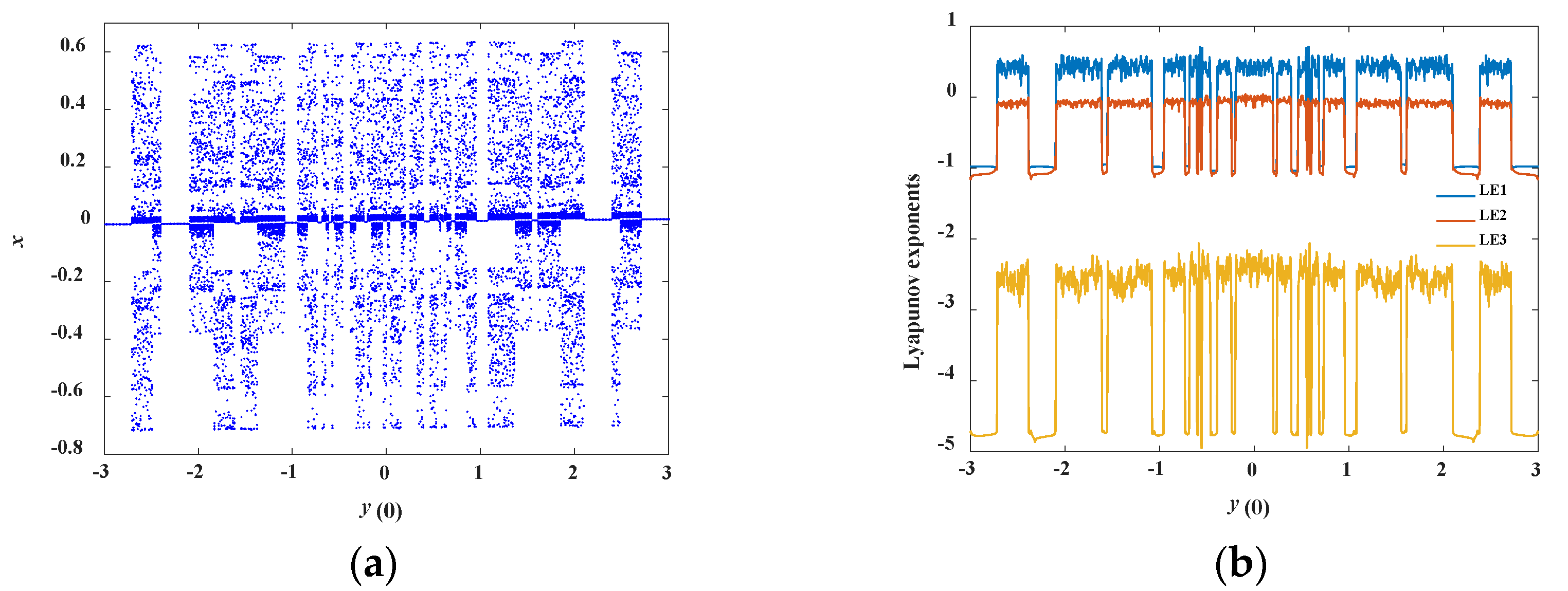
4.4. Heterogeneous Multistability
4.5. Transient Chaos
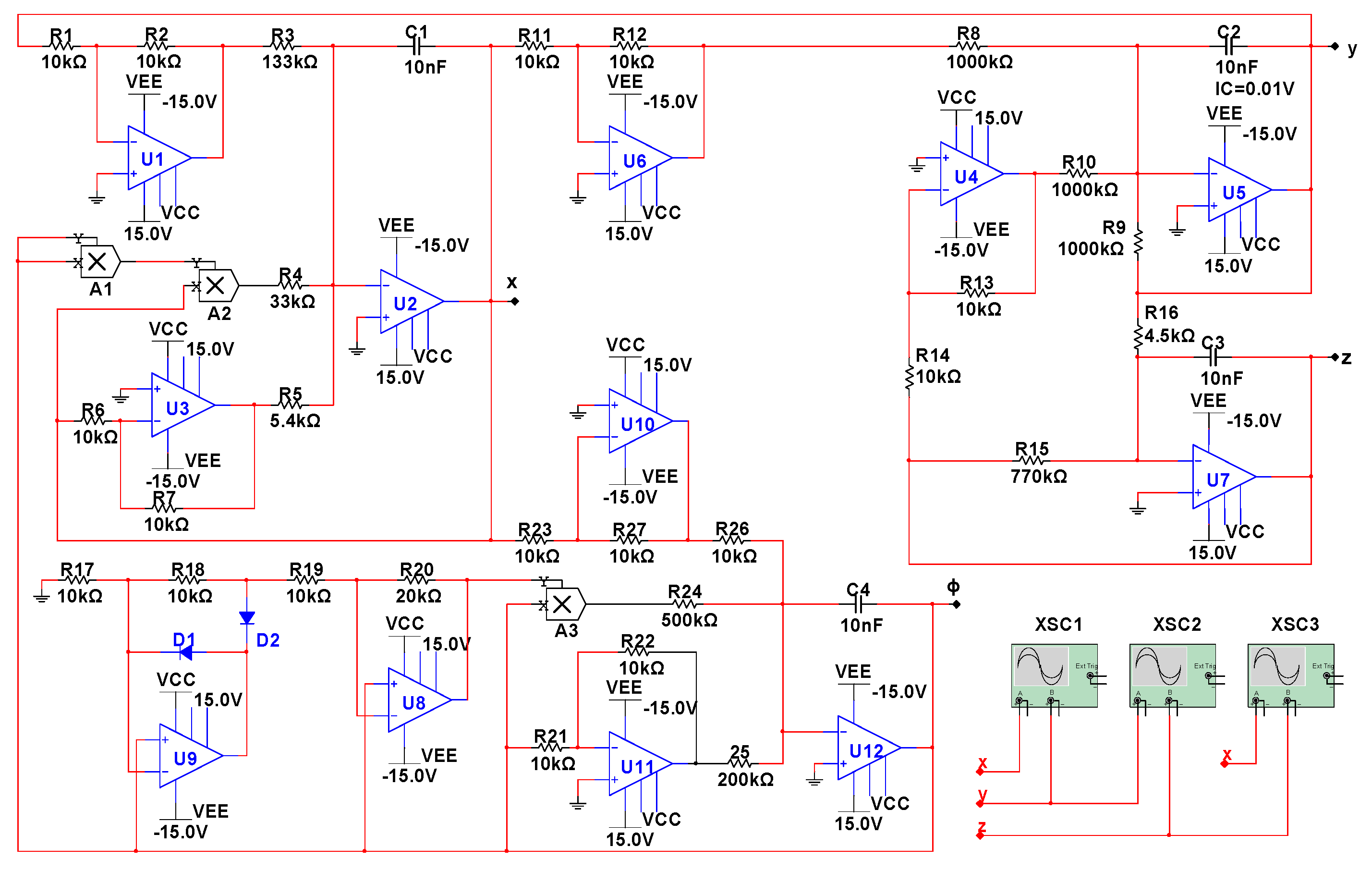
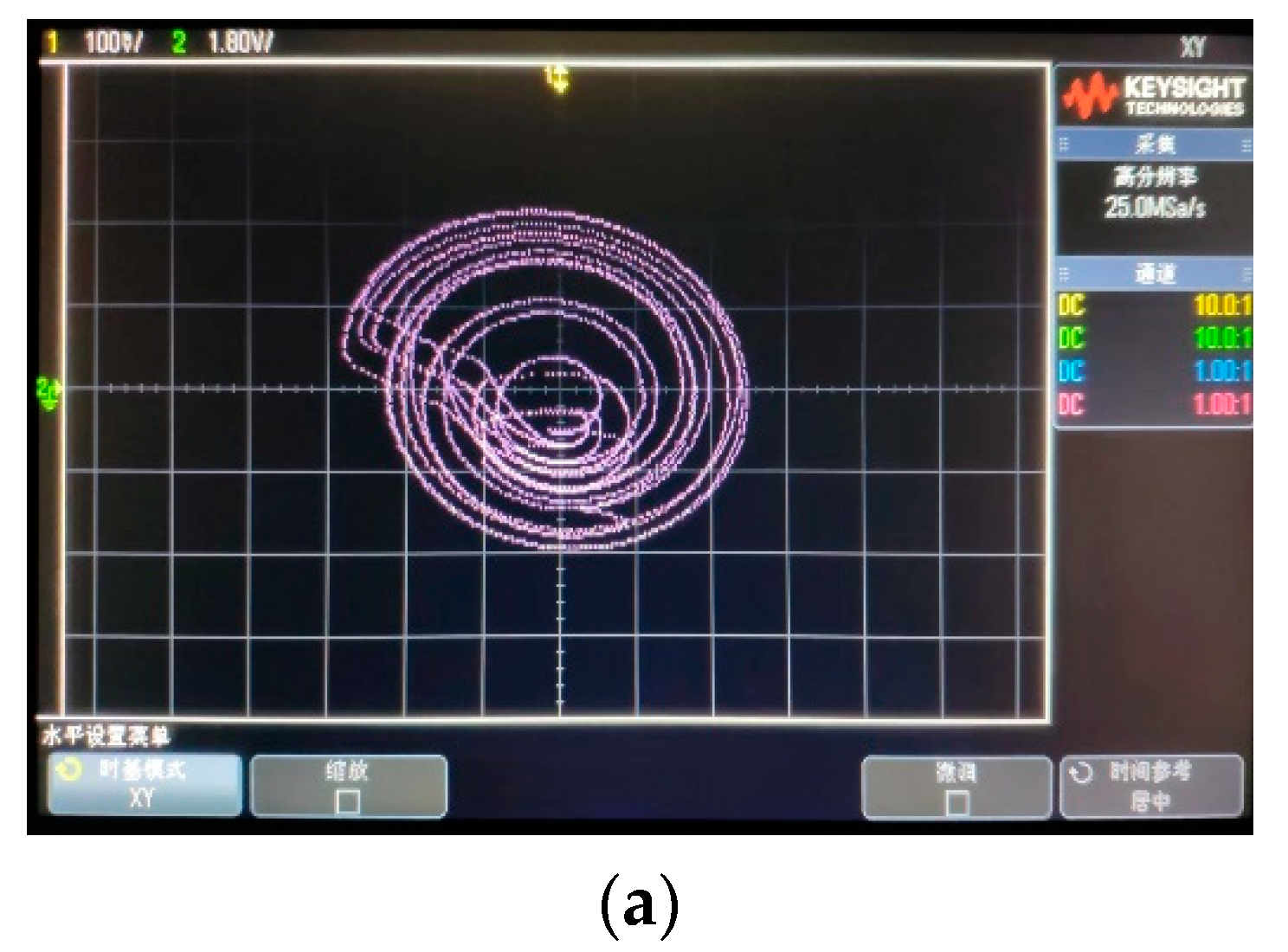
5. The Physical Realization of the Memristor-Based Chaotic System
- ,
- ,
- , , , , , ,
- , , .
6. Implementation of the Chaotic System by DSP Technology
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Corinto, F.; Gilli, M.; Forti, M. Flux-charge description of circuits with non-volatile switching memristor devices. IEEE Trans. Circuits Syst. II 2018, 65, 642–646. [Google Scholar] [CrossRef]
- Duan, S.K.; Hu, X.F.; Wang, L.D. Analog memristive memory with applications in audio signal processing. Sci. China Inform. Sci. 2014, 57, 1–15. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Y.; Fardad, M. A memristor-based optimization framework for artificial intelligence applications. IEEE Circ. Syst. Mag. 2018, 18, 29–44. [Google Scholar] [CrossRef]
- Ge, J.; Zhang, S.; Liu, Z. Flexible artificial nociceptor using a biopolymer-based forming-free memristor. Nanoscale 2019, 11, 6591–6601. [Google Scholar] [CrossRef]
- Huang, X.; Fan, Y.; Jia, J.; Wang, Z.; Li, Y. Quasi-synchronization of fractional-order memristor-based neural networks with parameter mismatches. IET Control Theory Appl. 2017, 11, 2317–2327. [Google Scholar] [CrossRef]
- Yuan, F.; Huang, X.; Wang, Z. Nonlinear dynamics and chaos in a simplified memristor-based fractional-order neural network with discontinuous memductance function. Nonlinear Dynam. 2018, 93, 611–627. [Google Scholar]
- Li, Y.; Huang, X.; Song, Y. A new fourth-order memristive chaotic system and its generation. Int. J. Bifurc. Chaos 2015, 25, 1550151. [Google Scholar] [CrossRef]
- Chang, H.; Song, Q.; Li, Y. Unstable limit cycles and singular attractors in a two-dimensional memristor-based dynamic system. Entropy 2019, 21, 415. [Google Scholar] [CrossRef]
- Huang, X.; Jia, J.; Li, Y. Complex nonlinear dynamics in fractional and integer order memristor-based systems. Neurocomputing 2016, 218, 296–306. [Google Scholar] [CrossRef]
- Guo, M.; Xue, Y.; Gao, Z.; Zhang, Y.; Dou, G.; Li, Y. Dynamic analysis of a physical SBT memristor-based chaotic circuit. Int. J. Bifurc. Chaos 2018, 27, 1730047. [Google Scholar] [CrossRef]
- Wen, S.; Zeng, Z.; Huang, T. Fuzzy modeling and synchronization of different memristor-based chaotic circuits [J]. Phys. Lett. A 2013, 377, 2016–2021. [Google Scholar] [CrossRef]
- Itoh, M.; Chua, L.O. Memmristor osillators. Int. J. Bifurc. Chaos 2008, 18, 3183–3206. [Google Scholar] [CrossRef]
- Muthuswamy, B.; Kokate, P. Memristor-based chaotic circuits. IETE Tech. Rev. 2009, 26, 417. [Google Scholar] [CrossRef]
- Muthuswamy, B.; Chua, L.O. Simplest chaotic circuit. Int. J. Bifurc. Chaos 2010, 20, 1567–1580. [Google Scholar] [CrossRef]
- Chang, H.; Zhen, W.; Li, Y. Dynamic analysis of a bistable bi-local active memristor and its associated oscillator system. Int. J. Bifurc. Chaos 2018, 28, 1850105. [Google Scholar] [CrossRef]
- Nguomkam, N.A.; Kengne, J. A minimal three-term chaotic flow with coexisting routes to chaos, multiple solutions, and its analog circuit realization. Analog Integr. Circuits Signal Process. 2019, 101, 415–429. [Google Scholar] [CrossRef]
- Wang, G.; Yuan, F.; Chen, G. Coexisting multiple attractors and riddled basins of a memristive system. Chaos 2018, 28, 013125. [Google Scholar] [CrossRef]
- Zhou, C.; Li, Z.; Zeng, Y. A novel 3D fractional-order chaotic system with multifarious coexisting attractors. Int. J. Bifurc. Chaos 2019, 29, 1950004. [Google Scholar] [CrossRef]
- Chang, H.; Li, Y.; Yuan, F. Extreme multistability with hidden attractors in a simplest memristor-based circuit. Int. J. Bifurc. Chaos 2019, 29, 1950086. [Google Scholar] [CrossRef]
- Han, B.; Tao, J.; Kaibin, C. Memristor-based canonical Chua’s circuit: Extreme multistability in voltage-current domain and its controllability in flux-charge domain. Complexity 2018, 2018, 1–13. [Google Scholar]
- Buscarino, A.; Fortuna, L.; Frasca, M.; Valentina Gambuzza, L. A chaotic circuit based on Hewlett-Packard memristor. Chaos 2012, 22, 023136. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Abdolmohammadi, H.R.; Alsaadi, F.E. A new oscillator with infinite coexisting asymmetric attractors. Chaos Soliton. Fract. 2018, 110, 252–258. [Google Scholar] [CrossRef]
- Rajagopal, K.; Khalaf, A.J.M.; Wei, Z.; Pham, V.T.; Alsaedi, A.; Hayat, T. Hyperchaos and coexisting attractors in a memristor Van der Pol–Duffing oscillator. Int. J. Bifurc. Chaos 2019, 29, 1950067. [Google Scholar] [CrossRef]
- Alombah, N.H.; Fotsin, H.; Romanic, K.K. Coexistence of multiple attractors, metastable chaos and bursting oscillations in a multiscroll memristive chaotic circuit. Int. J. Bifurc. Chaos 2017, 27, 1750067. [Google Scholar] [CrossRef]
- Lai, Q.; Nestor, T.; Kengne, J. Coexisting attractors and circuit implementation of a new 4D chaotic system with two equilibria. Chaos Soliton. Fract. 2018, 107, 92–102. [Google Scholar] [CrossRef]
- Varshney, V.; Sabarathinam, S.; Prasad, A. Infinite number of hidden attractors in memristor-based autonomous Duffing oscillator. Int. J. Bifurc. Chaos 2018, 28, 1850013. [Google Scholar] [CrossRef]
- Wang, G.Y.; Shi, C.B.; Wang, X.W.; Yuan, F. Coexisting oscillation and extreme multistability for a memcapacitor based circuit. Math. Probl. Eng. 2017, 2017, 6504969. [Google Scholar] [CrossRef]
- Karthikeyan, R.; Jafari, S.; Karthikeyan, A. Hyperchaotic memcapacitor oscillator with infinite equilibria and coexisting attractors. Circ. Syst. Signal Pr. 2018, 37, 3702–3724. [Google Scholar]
- Tang, Y.X.; Abdul, J.M.K.; Rajagopal, K. A new nonlinear oscillator with infinite number of coexisting hidden and self-excited attractors. Chin. Phys. B 2018, 27, 040502. [Google Scholar] [CrossRef]
- Galias, Z. Numerical study of multiple attractors in the parallel inductor–capacitor–memristor circuit. Int. J. Bifurc. Chaos 2017, 27, 1730036. [Google Scholar] [CrossRef]
- Li, C.; Thio, W.J.C.; Lu, H.H.C.; Lu, T. A memristive chaotic oscillator with increasing amplitude and frequency. IEEE Access 2018, 6, 12945–12950. [Google Scholar] [CrossRef]
- Chua, L.O.; Kang, S.M. Memristive devices and systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Yuan, F.; Deng, Y.; Li, Y. The amplitude, frequency and parameter space boosting in a memristor-meminductor-based circuit. Nonlinear Dynam. 2019, 96, 389–405. [Google Scholar] [CrossRef]







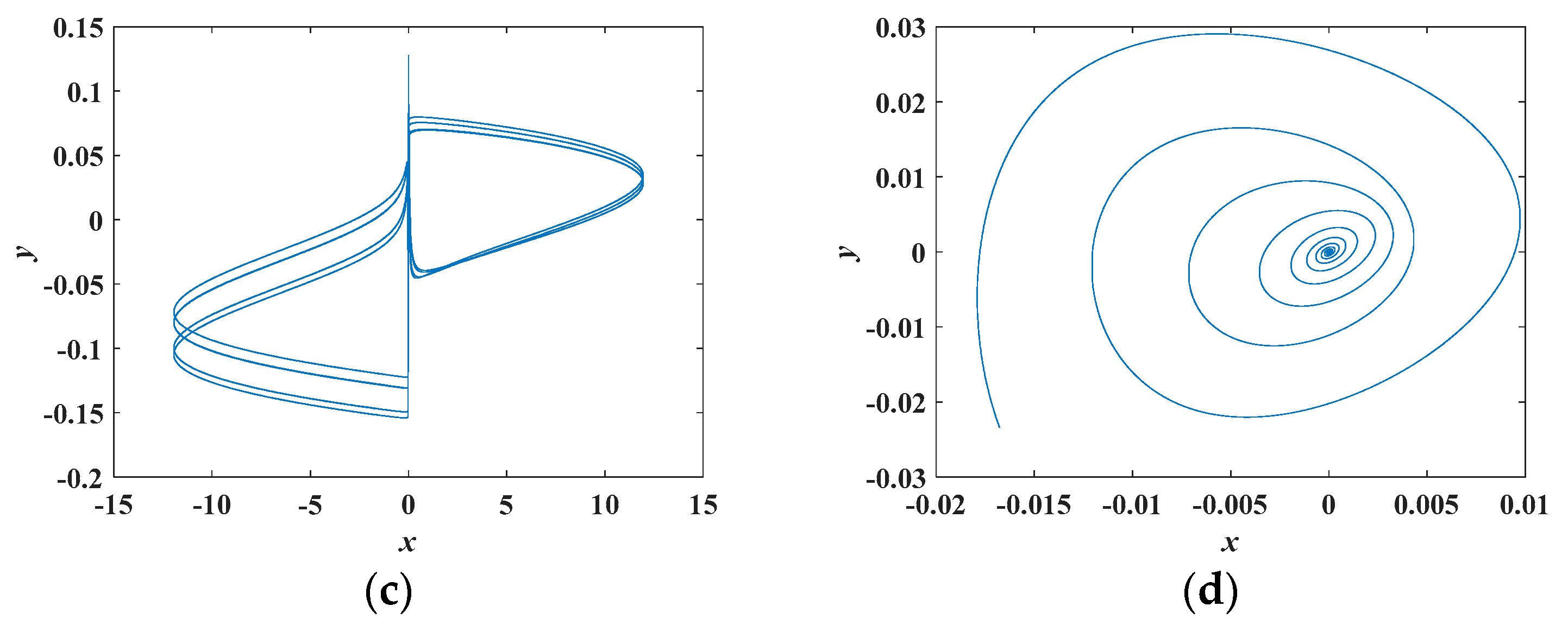





| Parameters | a | b | c | h | A | B |
| Values | 7.5 | 199 | 1.3 | 25 | 5 | 100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Q.; Chang, H.; Li, Y. Complex Dynamics of a Novel Chaotic System Based on an Active Memristor. Electronics 2020, 9, 410. https://doi.org/10.3390/electronics9030410
Song Q, Chang H, Li Y. Complex Dynamics of a Novel Chaotic System Based on an Active Memristor. Electronics. 2020; 9(3):410. https://doi.org/10.3390/electronics9030410
Chicago/Turabian StyleSong, Qinghai, Hui Chang, and Yuxia Li. 2020. "Complex Dynamics of a Novel Chaotic System Based on an Active Memristor" Electronics 9, no. 3: 410. https://doi.org/10.3390/electronics9030410
APA StyleSong, Q., Chang, H., & Li, Y. (2020). Complex Dynamics of a Novel Chaotic System Based on an Active Memristor. Electronics, 9(3), 410. https://doi.org/10.3390/electronics9030410




