A Formal Verification Framework for Security Issues of Blockchain Smart Contracts
Abstract
1. Introduction
2. Related Work
3. Background
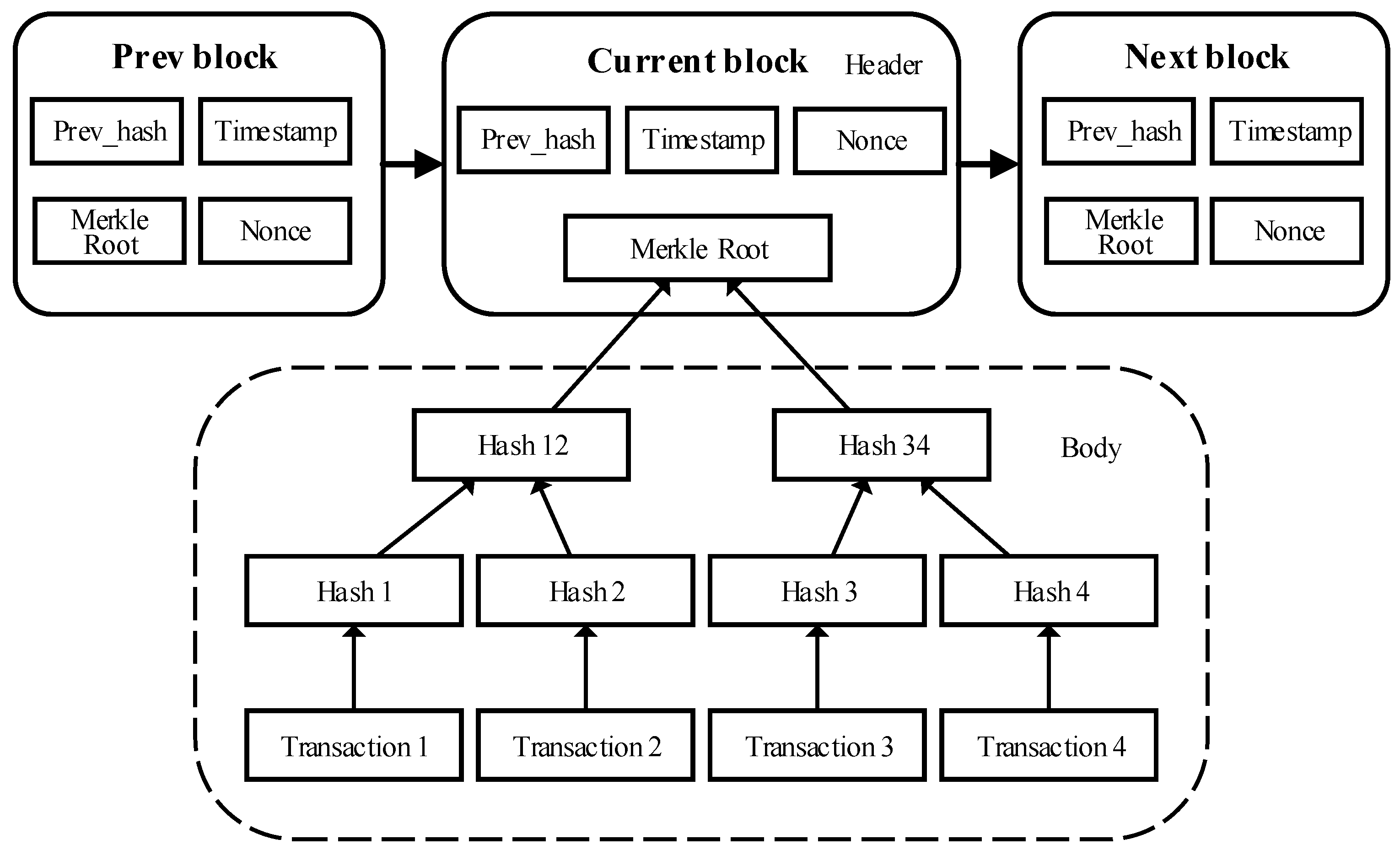
3.1. Blockchain Technology
3.2. Smart Contracts
3.3. Coq Proof Assistant
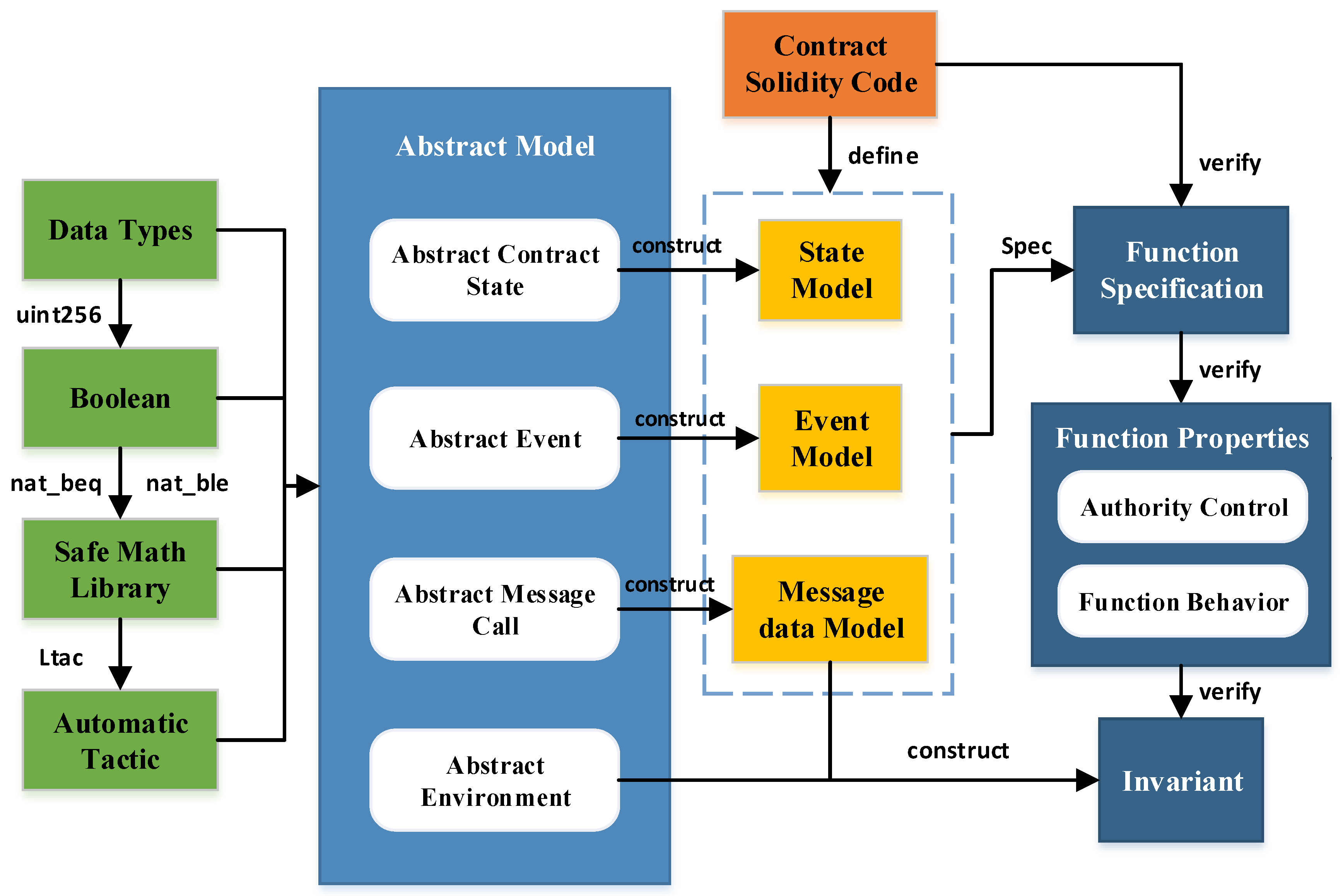
4. Formal Verification Framework
4.1. Security Issues of Smart Contracts
4.1.1. Integer Overflow
4.1.2. Function Specification Issue
4.1.3. Invariant Issue
4.1.4. Authority Control Issue
4.1.5. Behavior of the Specific Function
4.2. Formal Verification Framework for Blockchain Smart Contracts
5. Formal Verification of BNB Contract
5.1. Model of BNB Contract
5.2. Verification of Function Specification
5.3. Verification of Invariant
5.4. Contract Properties
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| EVM | Ethereum Virtual Machine |
| BNB | Binance Coin |
| BTC | Bitcoin |
| ETH | Ethereum |
| LTC | Litecoin |
| DSL | Domain Specific Language |
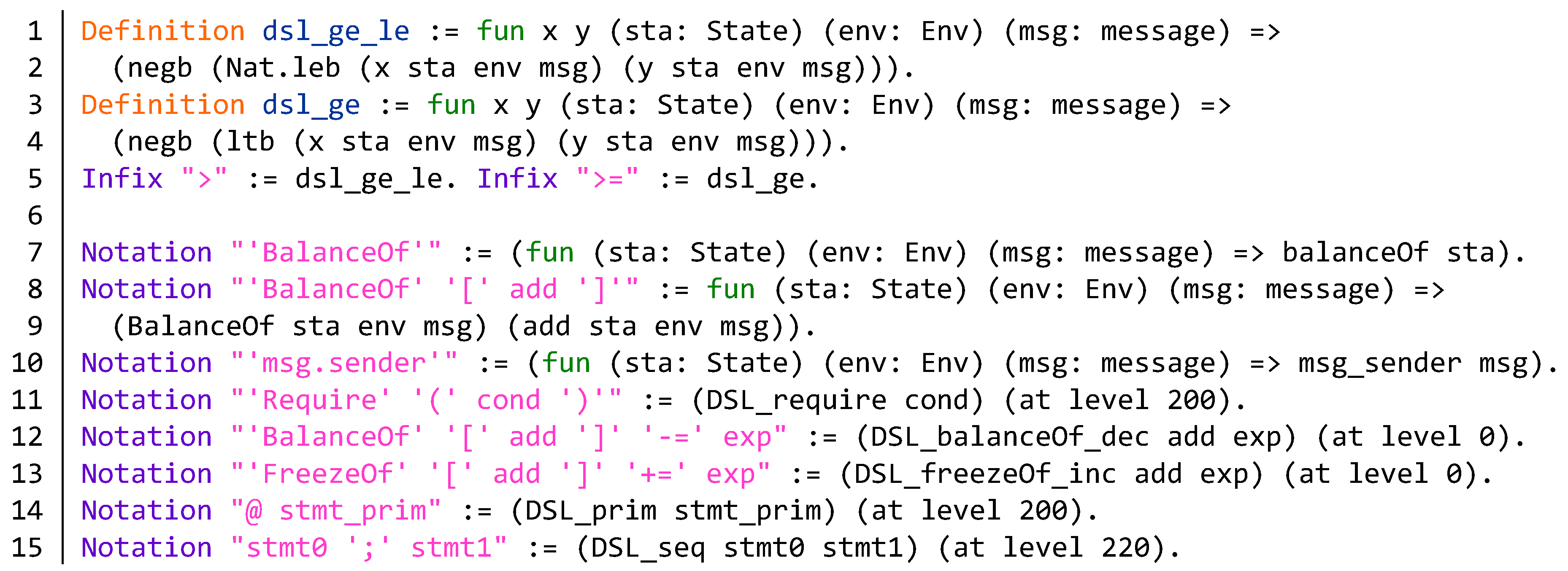
Appendix A. Semantics of DSL Statements and Evaluation Step of the BNB Contract


Appendix B. Source Code of the BNB Contract
| Algorithm A1 Partial source code of BNB contract. |
|
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 18 May 2008).
- Buterin, V. Ethereum: A next-generation smart contract and decentralized application platform. Available online: https://github.com/ethereum/wiki/wiki/White-Paper (accessed on 18 May 2019).
- Ethereum Solidity Documentation. Available online: https://Solidity.readthedocs.io/en/develop/ (accessed on 12 December 2019).
- Luu, L.; Chu, D.H.; Olickel, H.; Saxena, P.; Hobor, A. Making smart contracts smarter. In Proceedings of the ACM SIGSAC Conf. Comput. Commun. Securit, New York, NY, USA, 24–28 October 2016; pp. 254–269. [Google Scholar]
- Atzei, N.; Bartoletti, M.; Cimoli, T. A Survey of Attacks on Ethereum Smart Contracts (SoK). In Proceedings of the Int. Conf. Princ. Secur. Trust, Uppsala, Sweden, 22–29 April 2017; pp. 164–186. [Google Scholar]
- The DAO Attacked: Code Issue Leads to $60 Million Ether Theft. Available online: https://www.coindesk.com/dao-attacked-code-issue-leads-60-million-ether-theft/ (accessed on 17 June 2017).
- Liu, J.; Liu, Z.T. A Survey on Security Verification of Blockchain Smart Contracts. IEEE Access 2019, 7, 77894–77904. [Google Scholar] [CrossRef]
- The Coq Proof Assistant Reference Manual. Available online: https://coq.inria.fr/distrib/current/refman/ (accessed on 20 May 2019).
- Bertot, Y.; Castéran, P. Interactive Theorem Proving and Program Development, Coq’Art: The Calculus of Inductive Constructions; Springer: Heidelberg, Germany, 2004. [Google Scholar]
- Nipkow, T.; Paulson, L.C.; Wenzel, M. Isabelle/HOL: A Proof Assistant for Higher-Order Logic; Springer-Verlag: Berlin, Germany, 2002. [Google Scholar]
- Avigad, J. The Mechanization of Mathematics. Notices Am. Math. Soc. 2018, 65, 681–690. [Google Scholar] [CrossRef]
- Gonthier, G. Formal proof—The Four Color Theorem. Notices Am. Math. Soc. 2008, 55, 1382–1393. [Google Scholar]
- Gonthier, G.; Asperti, A.; Avigad, J.; Bertot, Y.; Cphen, C.; Garillot, F.; Roux, S.; Mahboubi, A.; Connor, R.; Biha, O. Machine-checked proof of the Odd Order Theorem. In Proceedings of the Interactive Theorem Proving, Rennes, France, 23–26 July 2013; pp. 163–179. [Google Scholar]
- Hales, T.C. Formal proof. Notices Am. Math. Soc. 2008, 55, 1370–1380. [Google Scholar]
- Wiedijk, F. Formal proof – getting started. Notices Am. Math. Soc. 2008, 55, 1408–1414. [Google Scholar]
- The CompCert C verified Compiler: Documentation and User’s Manual. Available online: http://compcert.inria.fr/man/manual.pdf (accessed on 17 September 2019).
- Gu, R.H.; Shao, Z.; Chen, H.; Wu, X.; Kim, J.; Sjoberg, V.; Costanzo, D. CertiKOS: An Extensible Architecture for Building Cerified Concurrent OS Kernels. In Proceedings of the USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 653–669. [Google Scholar]
- Appel, A.W.; Beringer, L.; Chlipala, A.; Pierce, B.C.; Shao, Z.; Weirich, S.; Zdancewic, S. Position paper: The science of deep specifcation. Philos. Trans. R. Soc. A 2017, 375, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Alharby, M.; Moorsel, A.V. Blockchain-based smart contracts: A systematic mapping study. In Proceedings of the Fourth International Conference on Computer Science and Information Technology (CSIT 2017), Yerevan, Armenia, 25–29 September 2017; pp. 125–140. [Google Scholar]
- Torres, C.F.; Schütte, J.; State, R. Osiris: Hunting for integer bugs in ethereum smart contracts. In Proceedings of the Annual Computer Security Applications Conference, San Juan, PR, USA, 3–7 December 2018; pp. 19–34. [Google Scholar]
- Bragagnolo, S.; Rocha, H.; Denker, M.; Ducasse, S. SmartInspect: Solidity smart contract inspector. In Proceedings of the International Workshop Blockchain Oriented Software Engineering, Campobasso, Italy, 20 March 2018; pp. 9–18. [Google Scholar]
- Bartoletti, M.; Pompianu, L. An empirical analysis of smart contracts: Platforms, applications, and design patterns. In Proceedings of the International Conference on Financial Cryptography and Data Security, Sliema, Malta, 3–7 April 2017; pp. 494–509. [Google Scholar]
- Coblenz, M. Obsidian: A safer blockchain programming language. In Proceedings of the IEEE/ACM 39th International Conference on Software Engineering Companion (ICSE-C), Buenos Aires, Argentina, 20–28 May 2017; pp. 1–11. [Google Scholar]
- Magazzeni, D.; Mcburney, P.; Nash, W. Validation and verification of smart contracts: A research agenda. Computer 2017, 50, 50–57. [Google Scholar] [CrossRef]
- Bhargavan, K.; DelignatLavaud, A.; Fournet, C.; Gollamudi, A.; Gonthier, G.; Kobeissi, N.; Kulatova, N.; Rastogi, A.; Sibut-Pinote, T.; Swamy, N. Short Paper: Formal verification of smart contracts. In Proceedings of the 2016 ACM Workshop on Programming Languages and Analysis for Security, Vienna, Austria, 24 October 2016; pp. 91–96. [Google Scholar]
- Hirai, Y. Formal Verification of Deed Contract in Ethereum Name Service. Available online: https://yoichihirai.com/deed.pdf (accessed on 1 November 2016).
- Hirai, Y. Defining the ethereum virtual machine for interactive theorem provers. In Proceedings of the Int. Conf. Financial Cryptogr. Data Secur., Sliema, Malta, 7 April 2017; pp. 520–535. [Google Scholar]
- Amani, S.; Begel, M.; Bortin, M.; Staples, M. Towards verifying ethereum smart contract bytecode in Isabelle/Hol. In Proceedings of the ACM Sigplan International Conference, Los Angeles, CA, USA, 8–9 January 2018; pp. 66–77. [Google Scholar]
- Grishchenko, I.; Maffei, M.; Schneidewind, C. A Semantic Framework for the Security Analysis of Ethereum smart contracts. In Proceedings of the Principles of Security and Trust, Thessaloniki, Greece, 14–20 April 2018; pp. 243–269. [Google Scholar]
- SECBIT. Correctness Proofs of Ethereum Token Contracts. Available online: https://github.com/sec-bit/tokenlibs-with-proofs (accessed on 20 July 2018).
- Yang, Z.; Lei, H. FEther: An Extensible Definitional Interpreter for Smart-Contract Verifications in Coq. IEEE Access 2019, 7, 37770–37791. [Google Scholar] [CrossRef]
- Szabo, N. Smart Contracts: Building Blocks for Digital Markets. Available online: https://kameir.com/smart-contracts/ (accessed on 20 June 1996).





















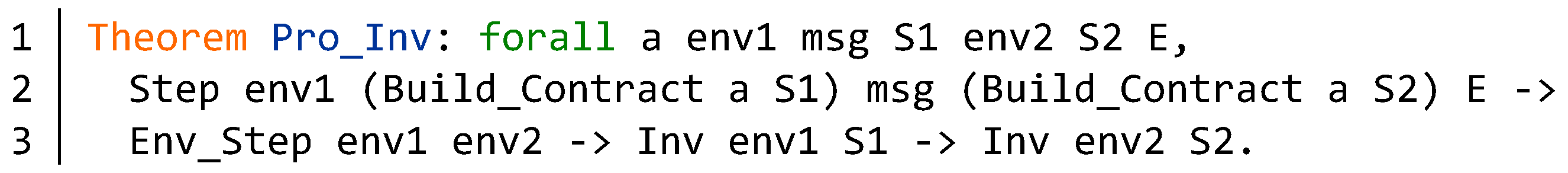


| File | Reference | Specification | Proof |
|---|---|---|---|
| Data_Types.v | Section 4.1 | 10 | 0 |
| Boolean.v | Section 4.1 | 300 | 150 |
| Safe_Math.v | Section 4.1 | 200 | 150 |
| Abstract_Model.v | Section 4.1 | 50 | 0 |
| Automatic.v | Section 4.2 | 150 | 60 |
| Model.v | Section 5.1 | 40 | 0 |
| Specification.v | Section 5.2 | 750 | 720 |
| Invariant.v | Section 5.3 | 150 | 400 |
| Properties.v | Section 5.4 | 40 | 300 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Yu, W. A Formal Verification Framework for Security Issues of Blockchain Smart Contracts. Electronics 2020, 9, 255. https://doi.org/10.3390/electronics9020255
Sun T, Yu W. A Formal Verification Framework for Security Issues of Blockchain Smart Contracts. Electronics. 2020; 9(2):255. https://doi.org/10.3390/electronics9020255
Chicago/Turabian StyleSun, Tianyu, and Wensheng Yu. 2020. "A Formal Verification Framework for Security Issues of Blockchain Smart Contracts" Electronics 9, no. 2: 255. https://doi.org/10.3390/electronics9020255
APA StyleSun, T., & Yu, W. (2020). A Formal Verification Framework for Security Issues of Blockchain Smart Contracts. Electronics, 9(2), 255. https://doi.org/10.3390/electronics9020255





