Coordinated Control Scheme of Battery Storage System to Augment LVRT Capability of SCIG-Based Wind Turbines and Frequency Regulation of Hybrid Power System
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Reviews
1.3. Contribution
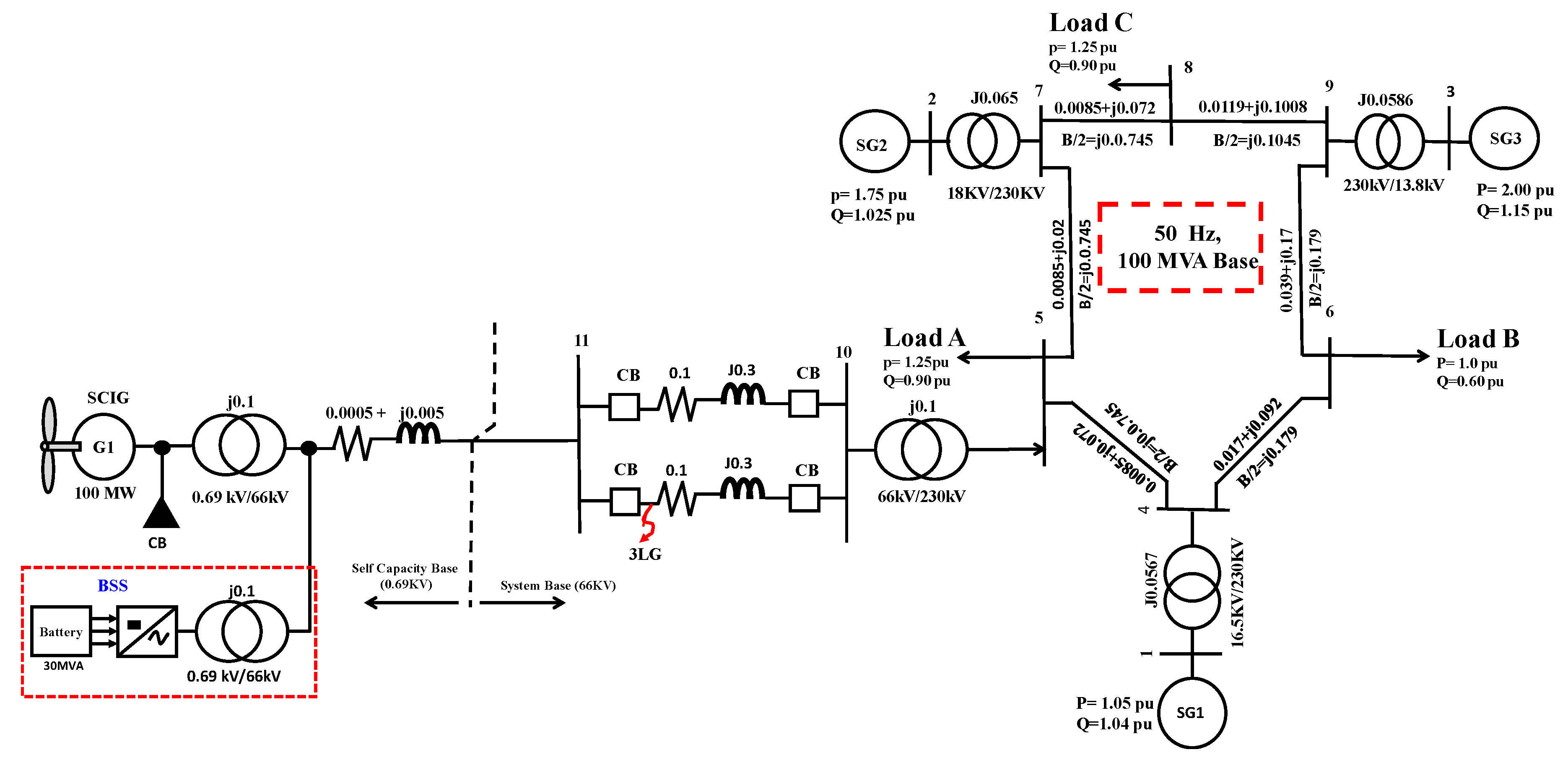
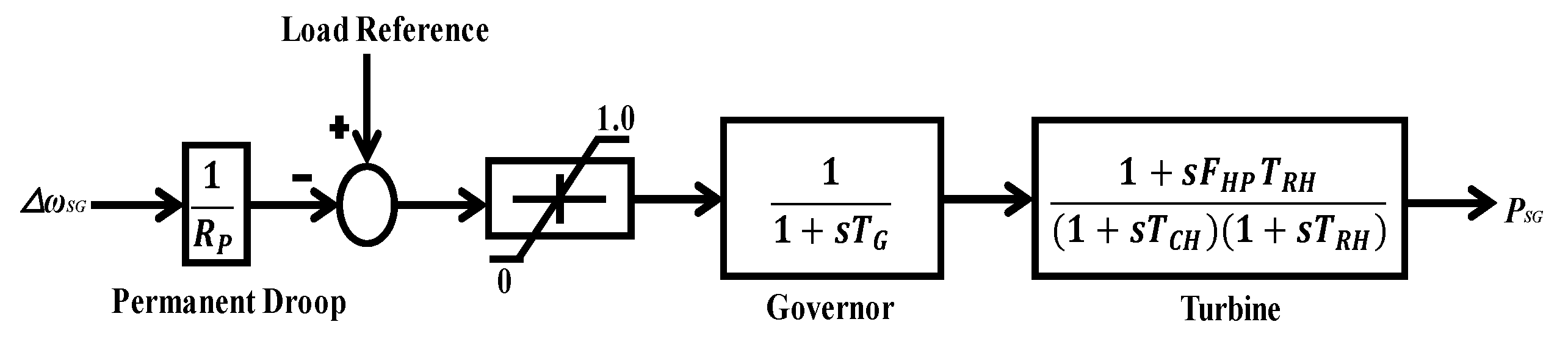
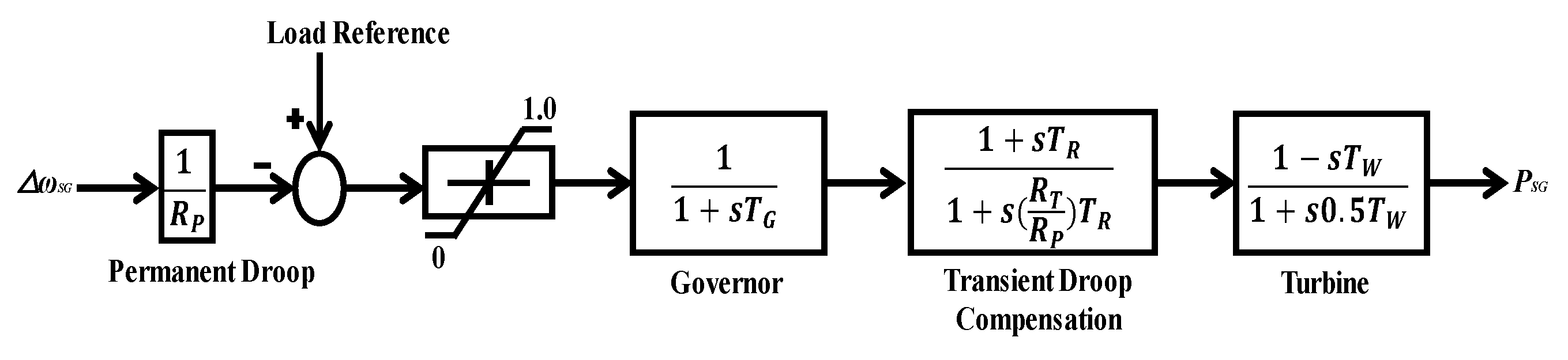
2. Model of a Hybrid Power System
3. Model of a Wind Turbine
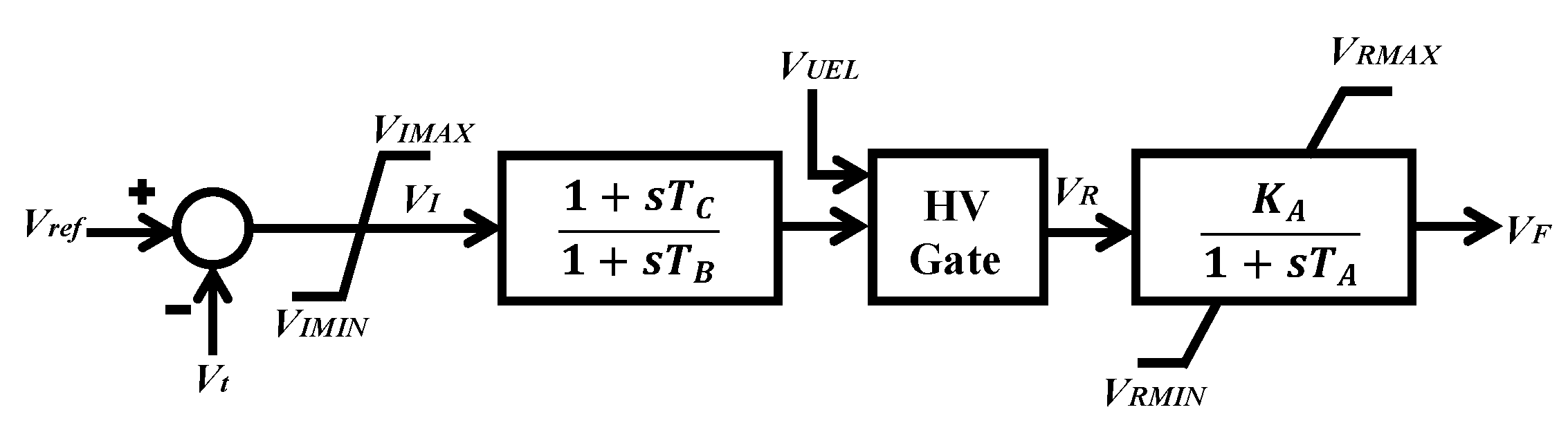
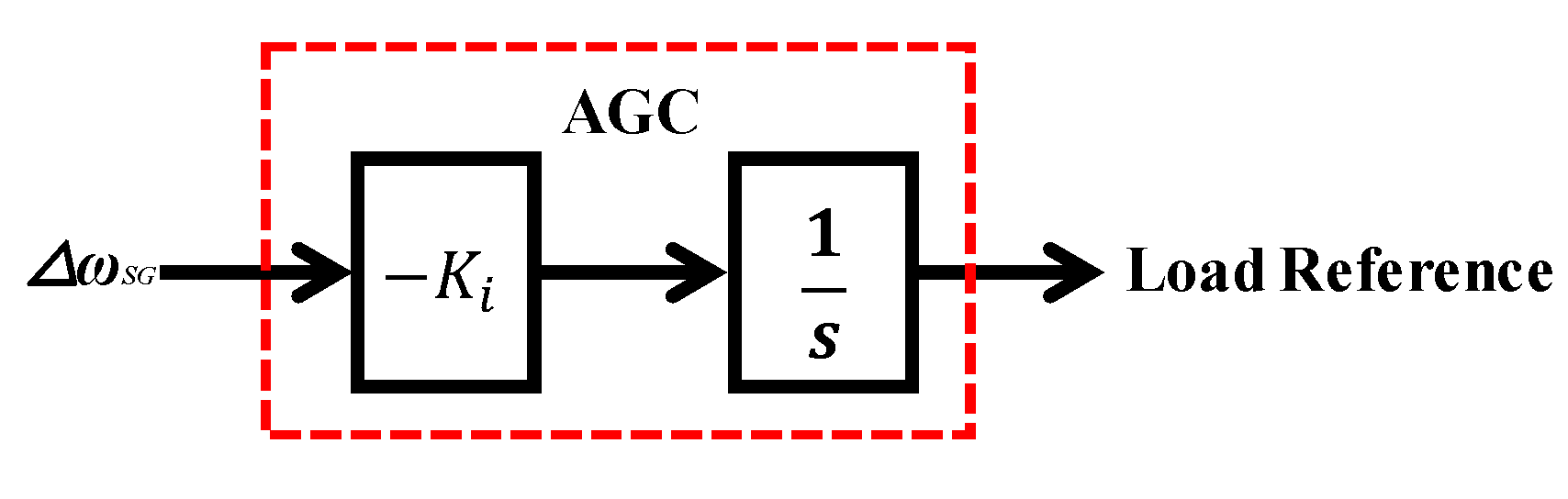
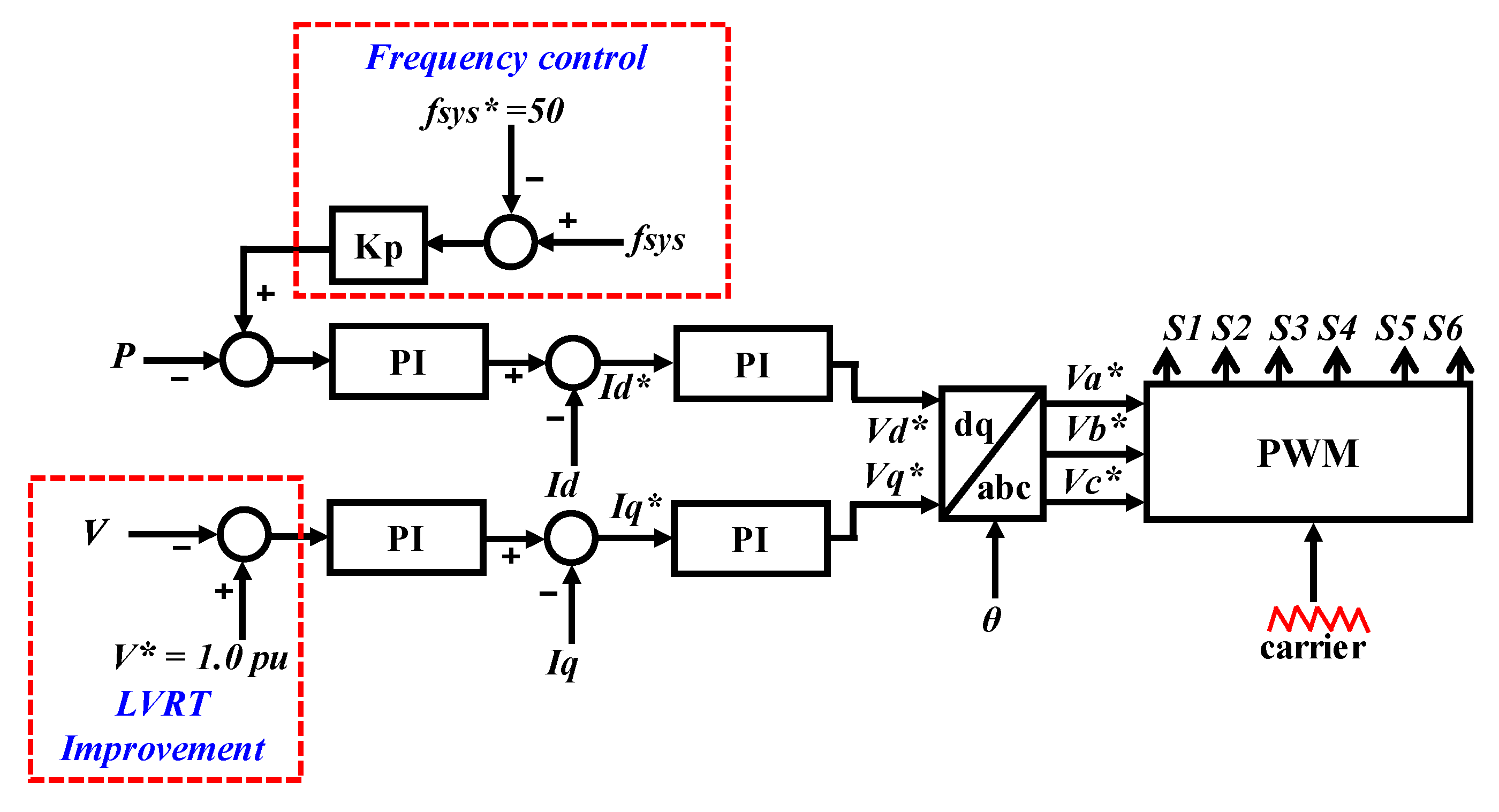
4. Proposed Coordinated Control of Battery Storage System
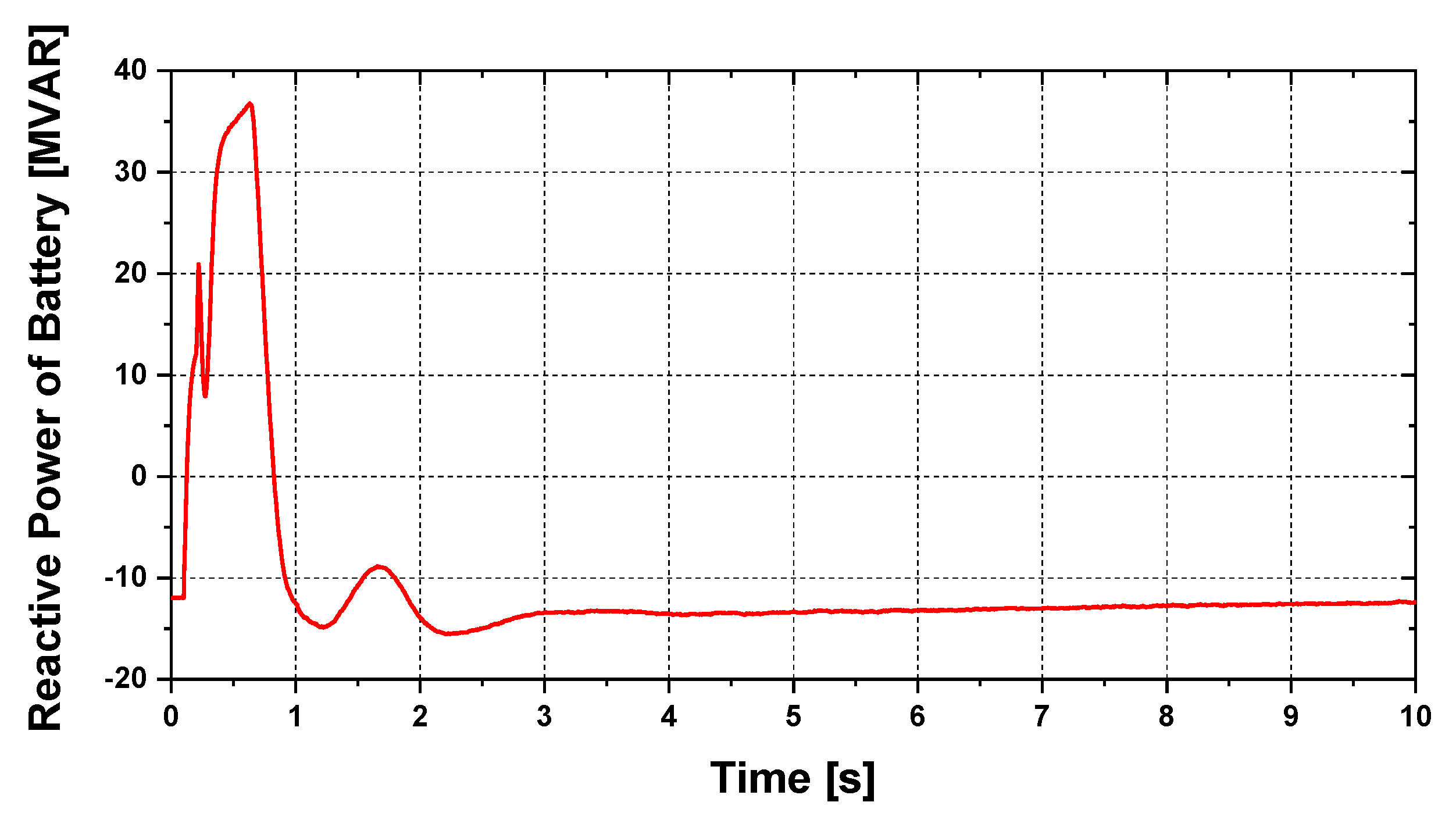
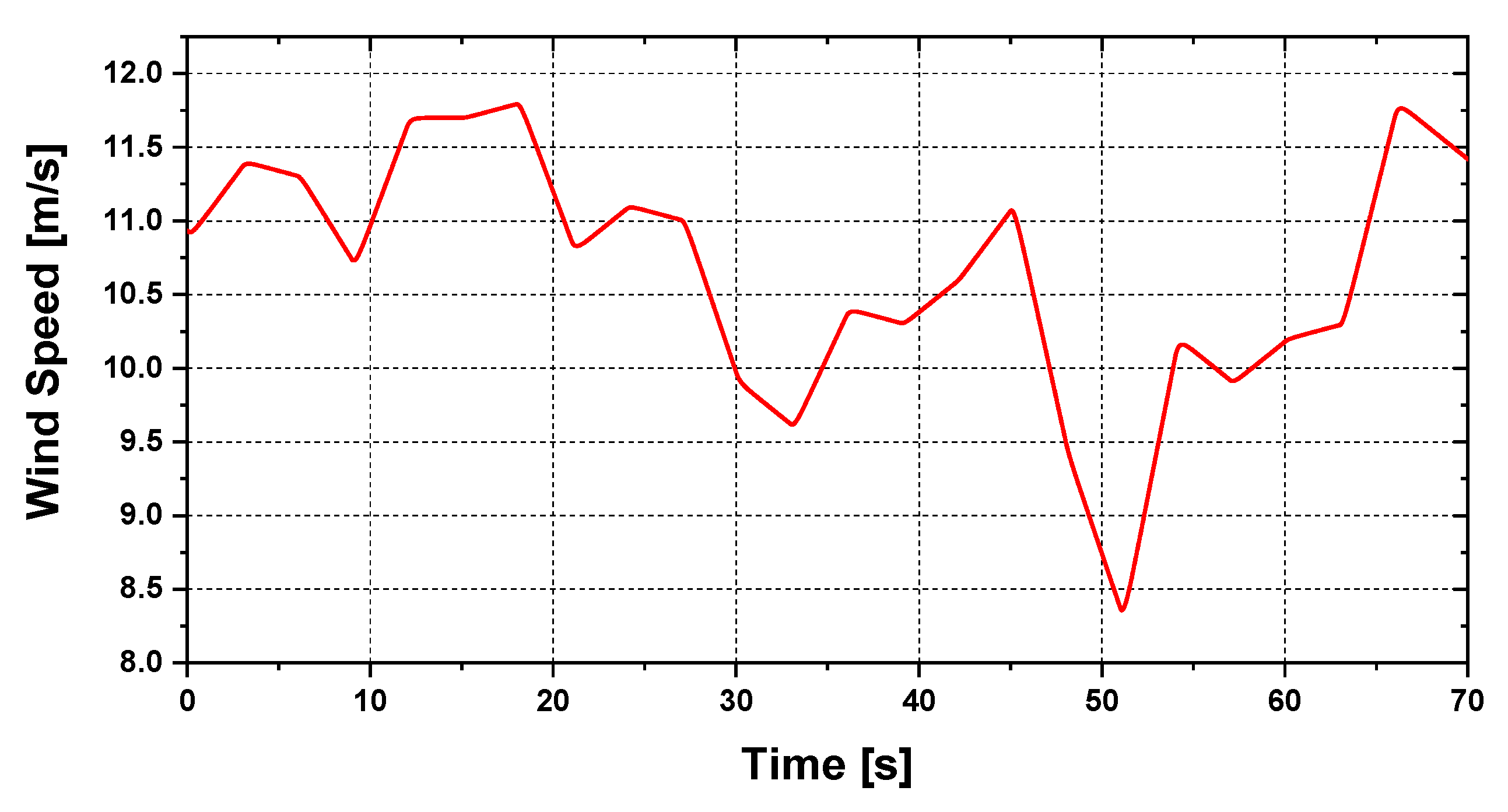
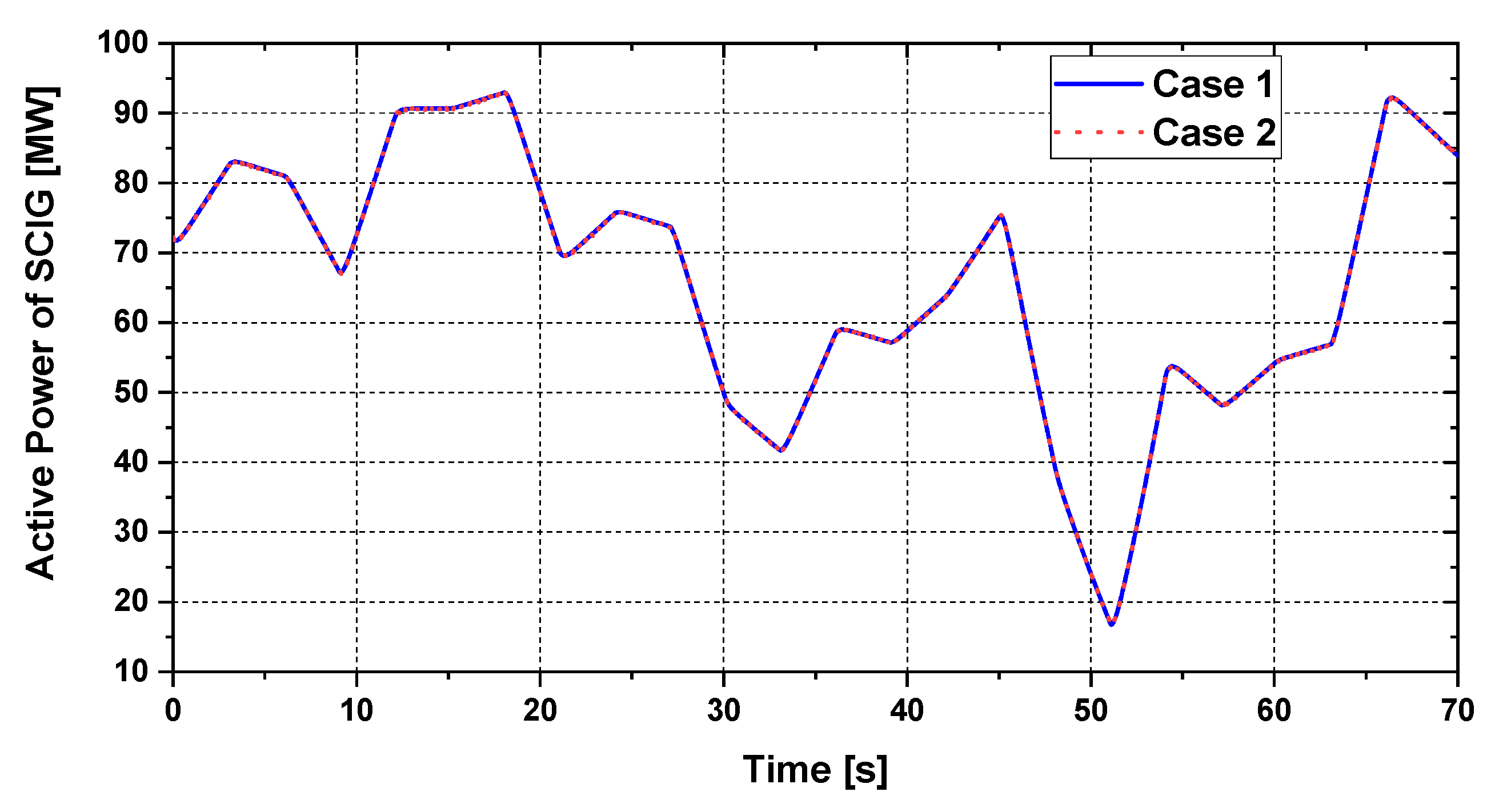
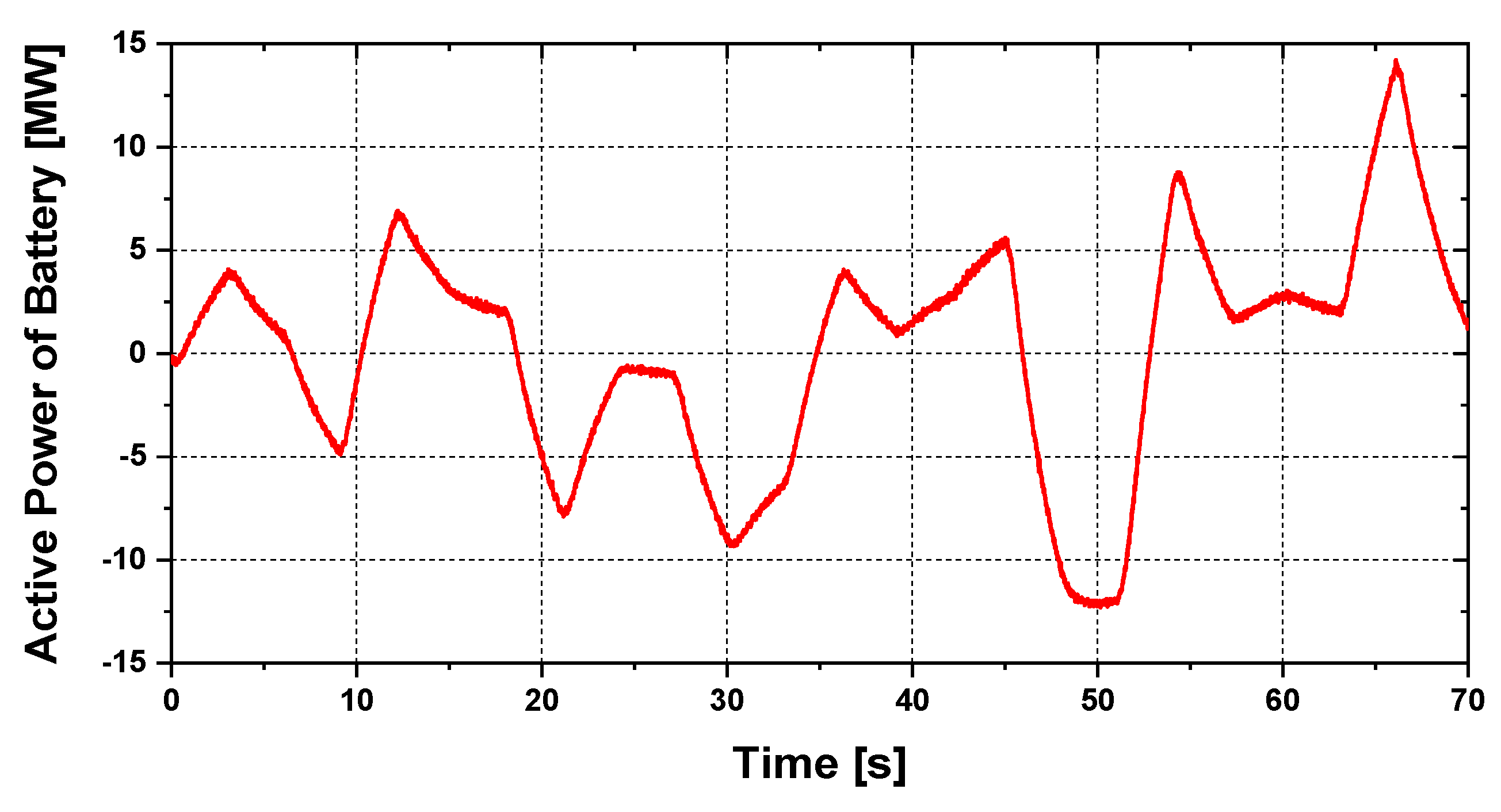
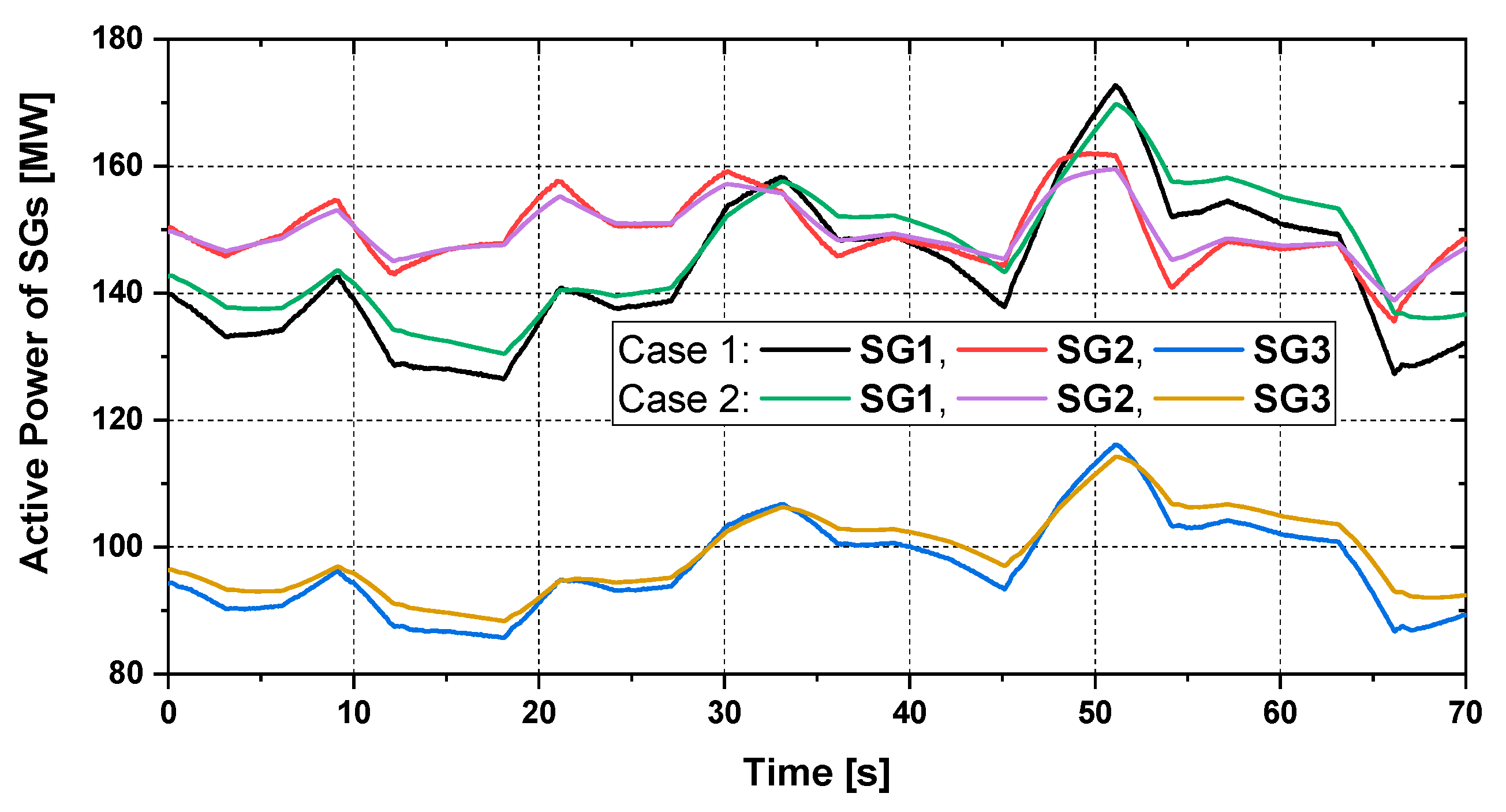
5. Simulation Results
5.1. Transient Stability Analysis
5.2. Steady-State Stability Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Parameter | SG1 (Thermal) | SG2 (Thermal) | SG3 (Hydro) |
|---|---|---|---|
| Voltage | 16.5 kV | 18 kV | 13.8 kV |
| Ra | 0.003 pu | 0.003 pu | 0.003 pu |
| Xl | 0.1 pu | 0.1 pu | 0.1 pu |
| Xd | 2.11 pu | 2.11 pu | 1.20 pu |
| Xq | 2.05 pu | 2.05 pu | 0.700 pu |
| X’d | 0.25 pu | 0.25 pu | 0.24 pu |
| X’’d | 0.21 pu | 0.21 pu | 0.20 pu |
| X’’q | 0.21 pu | 0.21 pu | 0.20 pu |
| T’do | 6.8 s | 7.4 s | 7.2 s |
| T’’do | 0.033 s | 0.033 s | 0.031 s |
| T’’qo | 0.030 s | 0.030 s | 0.030 s |
| H | 4.0 s | 4.0 s | 4.0 s |
| Squirrel Cage Induction Generator (SCIG) | |
|---|---|
| R1 | 0.01 pu |
| X1 | 0.1 pu |
| Xm | 3.5 pu |
| R21 | 0.035 pu |
| R22 | 0.014 pu |
| X21 | 0.03 pu |
| X22 | 0.089 pu |
| H | 1.5 s |
References
- Ula, A.H.M.S. Global warming and electric power generation: What is the connection? IEEE Trans. Energy Convers. 1991, 6, 599–604. [Google Scholar] [CrossRef]
- Global Status Report 2017. Available online: https://www.worldgbc.org/sites/default/files/UNEP%20188_GABC_en%20%28web%29.pdf (accessed on 10 January 2020).
- Global Wind Energy Council (GWEC). Annual Market Update 2015, Global Wind Report 2015. Available online: http://www.gwec.net/ (accessed on 15 October 2017).
- Global Wind Energy Council (GWEC). Global Wind Energy Outlook 2016: Wind Power to Dominate Power Sector Growth 2016. Available online: http://www.gwec.net/ (accessed on 25 November 2019).
- Hazari, M.; Mannan, M.; Umemura, A.; Takahashi, R.; Tamura, J. Stabilization of Wind Farm by Using PMSG Based Wind Generator Taking Grid Codes into Consideration. J. Power Energy Eng. 2018, 6, 40–52. [Google Scholar] [CrossRef][Green Version]
- Priyavarthini, S.; Nagamani, C.; Ilango, G.S.; Rani, M.A.A. An improved control for simultaneous sag/swell mitigation and reactive power support in a grid-connected wind farm with DVR. Int. J. Electr. Power Energy Syst. 2018, 101, 38–49. [Google Scholar] [CrossRef]
- Mohammadpour, H.A.; Ghaderi, A.; Mohammadpour, H.; Ali, M.H. Low voltage ride-through enhancement of fixed-speed wind farms using series FACTS controllers. Sustain. Energy Technol. Assess. 2015, 9, 12–21. [Google Scholar] [CrossRef]
- Wei, Y.; Kang, L.; Qi, R.; Wen, M.; Cheng, M.M. Optimal control of SVC-MERS and application in SCIG powered micro-grid. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 3367–3373. [Google Scholar]
- Gatavi, E.; Hellany, A.; Nagrial, M.; Rizk, J. Improved Low Voltage Ride-Through capability of DFIG-based wind turbine with breaking resistor and converter control. In Proceedings of the 2018 IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG 2018), Doha, Qatar, 10–12 April 2018; pp. 1–6. [Google Scholar]
- Kamel, R.M. Three fault ride through controllers for wind systems running in isolated micro-grid and Effects of fault type on their performance: A review and comparative study. Renew. Sustain. Energy Rev. 2014, 37, 698–714. [Google Scholar] [CrossRef]
- Marei, M.I.; El-Goharey, H.S.K.; Toukhy, R.M. Fault ride-through enhancement of fixed speed wind turbine using bridge-type fault current limiter. J. Electr. Syst. Inf. Technol. 2016, 3, 119–126. [Google Scholar] [CrossRef]
- Heydari-doostabad, H.; Khalghani, M.R.; Khooban, M.H. A novel control system design to improve LVRT capability of fixed speed wind turbines using STATCOM in presence of voltage fault. Int. J. Electr. Power Energy Syst. 2016, 77, 280–286. [Google Scholar] [CrossRef]
- Ren, J.; Hu, Y.; Wang, J.; Ji, Y. Principle of low voltage ride-through ability realization of fixed speed wind generator using series reactor and SVC. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; Volume 3, pp. 2173–2177. [Google Scholar]
- Kalsi, S.; Madura, D.; Howard, R.; Snitchler, G.; MacDonald, T.; Bradshaw, D.; Grant, I.; Ingram, M. Superconducting dynamic synchronous condenser for improved grid voltage support. In Proceedings of the 2003 IEEE PES Transmission and Distribution Conference and Exposition (IEEE Cat. No.03CH37495), Dallas, TX, USA, 7–12 September 2003; Volume 2, pp. 742–747. [Google Scholar]
- Farias, M.F.; Battaiotto, P.E.; Cendoya, M.G.; de Ingeniería, F. Investigation of UPQC for sag compensation in wind farms to weak grid connections. In Proceedings of the 2010 IEEE International Conference on Industrial Technology, Vina del Mar, Chile, 14–17 March 2010; pp. 937–942. [Google Scholar]
- Mahela, O.P.; Gupta, N.; Khosravy, M.; Patel, N. Comprehensive Overview of Low Voltage Ride Through Methods of Grid Integrated Wind Generator. IEEE Access 2019, 7, 99299–99326. [Google Scholar] [CrossRef]
- He, G.; Chen, Q.; Kang, C.; Xia, Q.; Poolla, K. Cooperation of Wind Power and Battery Storage to Provide Frequency Regulation in Power Markets. IEEE Trans. Power Syst. 2017, 32, 3559–3568. [Google Scholar] [CrossRef]
- Nguyen, C.L.; Lee, H.H. A Novel Dual-Battery Energy Storage System for Wind Power Applications. IEEE Trans. Ind. Electron. 2016, 63, 6136–6147. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability & Control; McGraw-Hill Inc.: New York, NY, USA, 1994. [Google Scholar]
- Rosyadi, M.; Umemura, A.; Takahashi, R.; Tamura, J.; Uchiyama, N.; Ide, K. Simplified Model of Variable Speed Wind Turbine Generator for Dynamic Simulation Analysis. IEEJ Trans. Power Energy 2015, 135, 538–549. [Google Scholar] [CrossRef]
- Muyeen, S.M.; Tamura, J.; Murata, T. Stability Augmentation of a Grid Connected Wind Farm; Springer: London, UK, 2009. [Google Scholar]
- Hazari, M.R.; Mannan, M.A.; Muyeen, S.M.; Umemura, A.; Takahashi, R.; Tamura, J. Stability Augmentation of a Grid-Connected Wind Farm by Fuzzy-Logic-Controlled DFIG-Based Wind Turbines. Appl. Sci. 2018, 8, 20. [Google Scholar] [CrossRef]
- E. ON NETZ GmbH. Grid Connection Regulation for High and Extra High Voltage; E. ON NETZ GmbH: Essen, Germany, 2006. [Google Scholar]



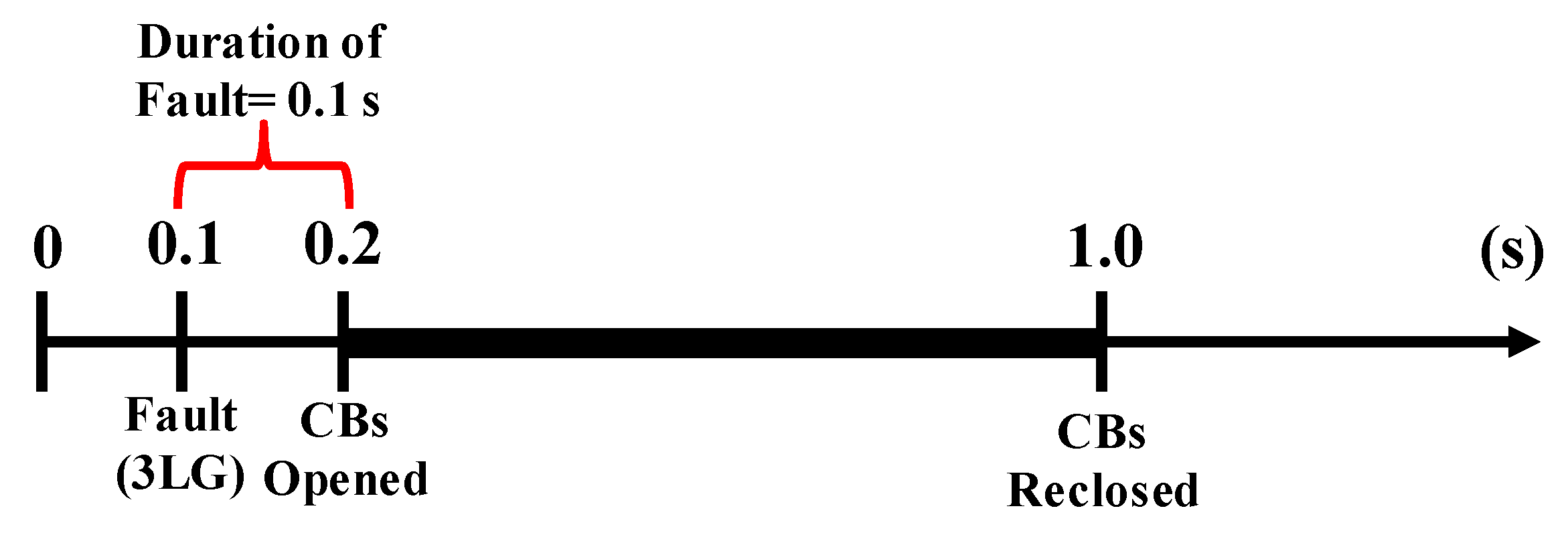
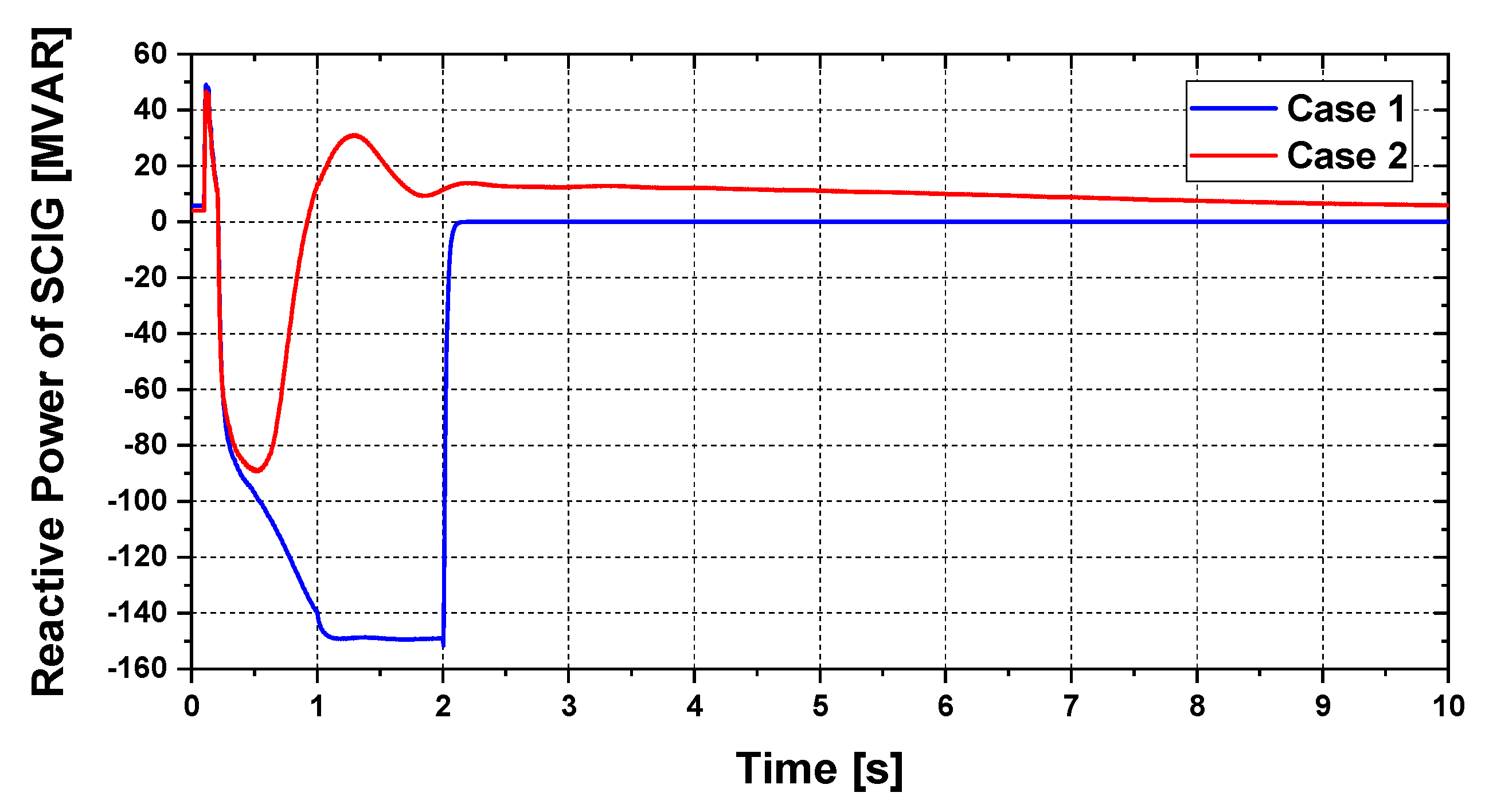
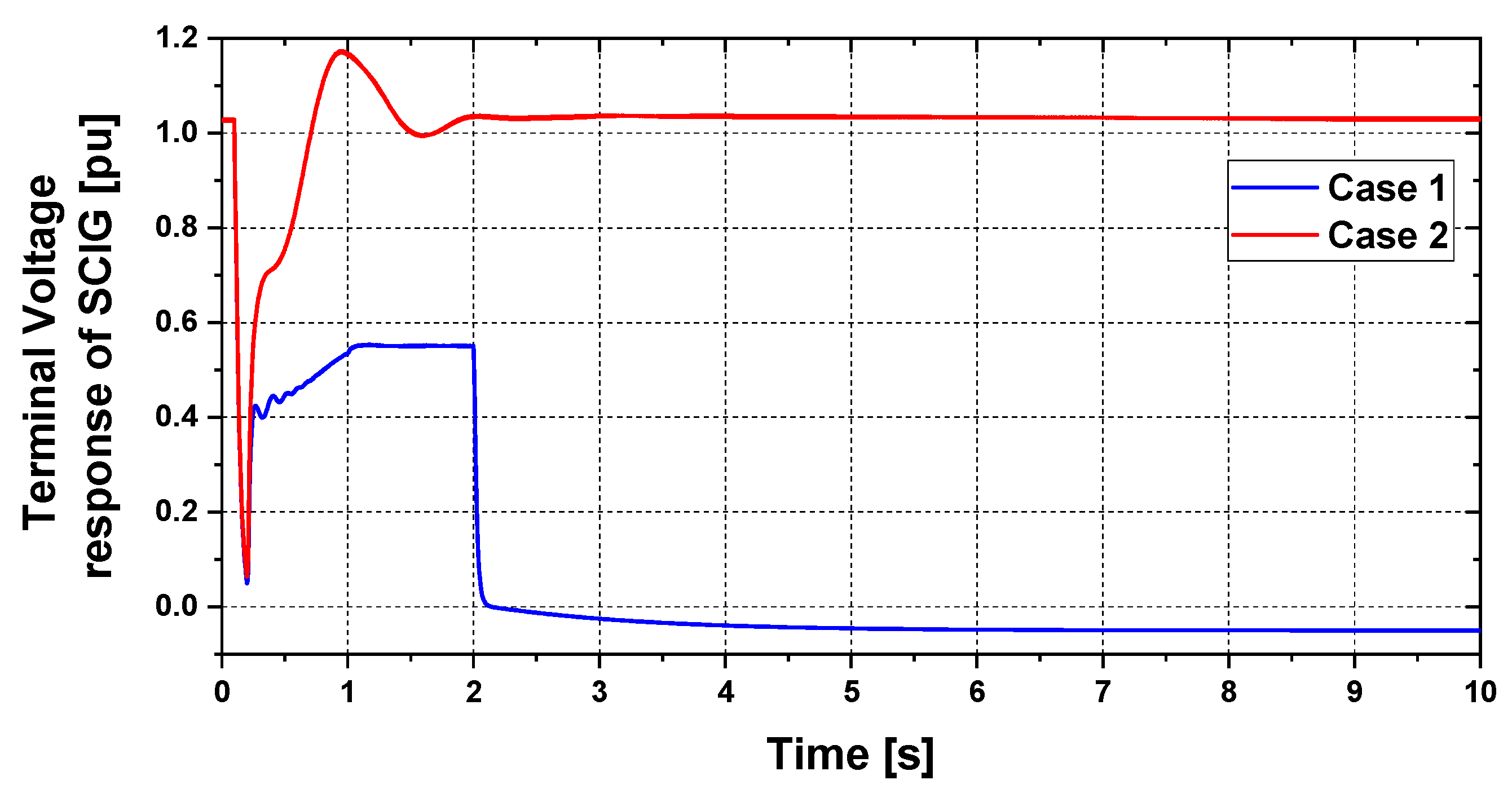

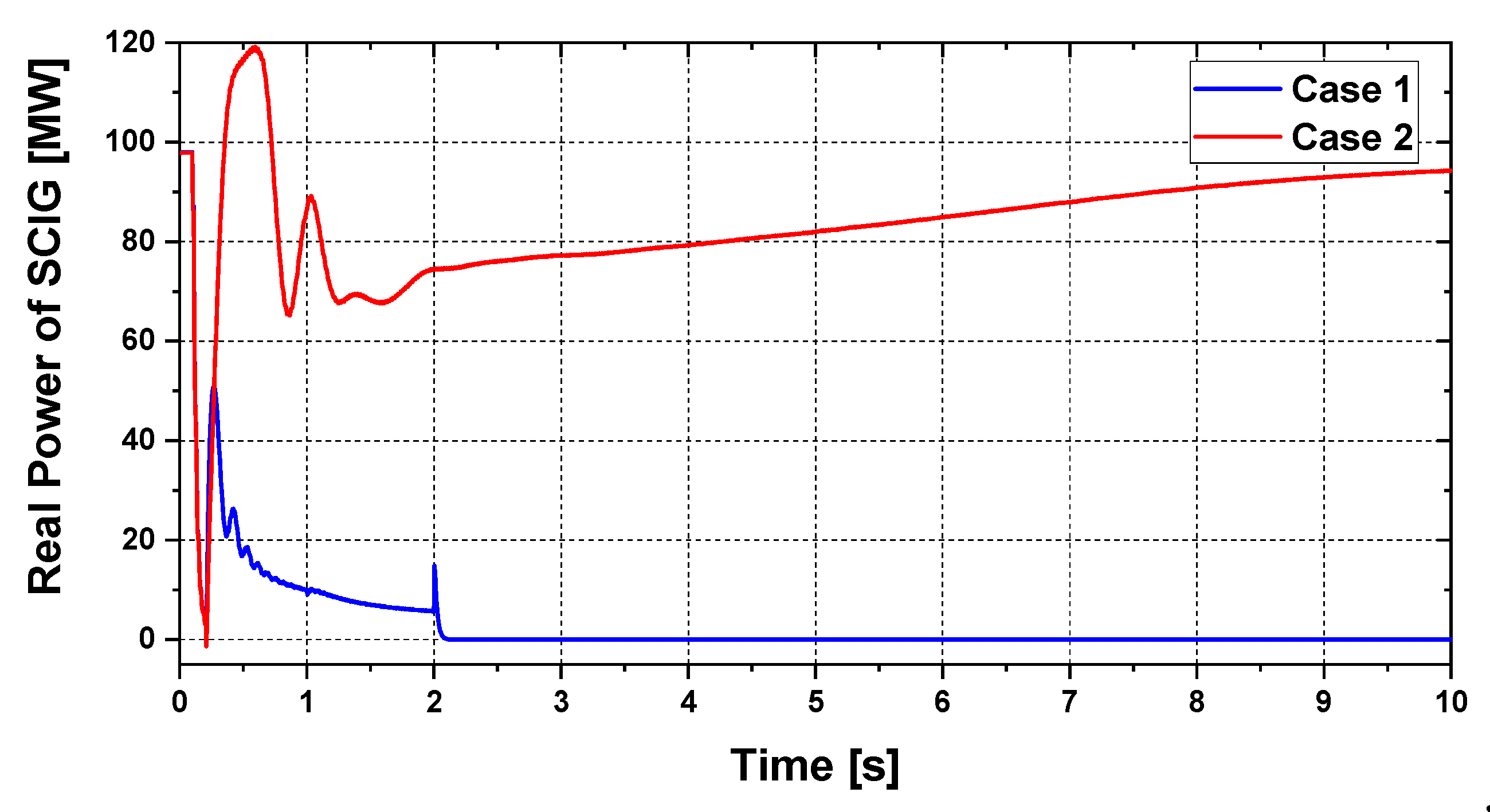
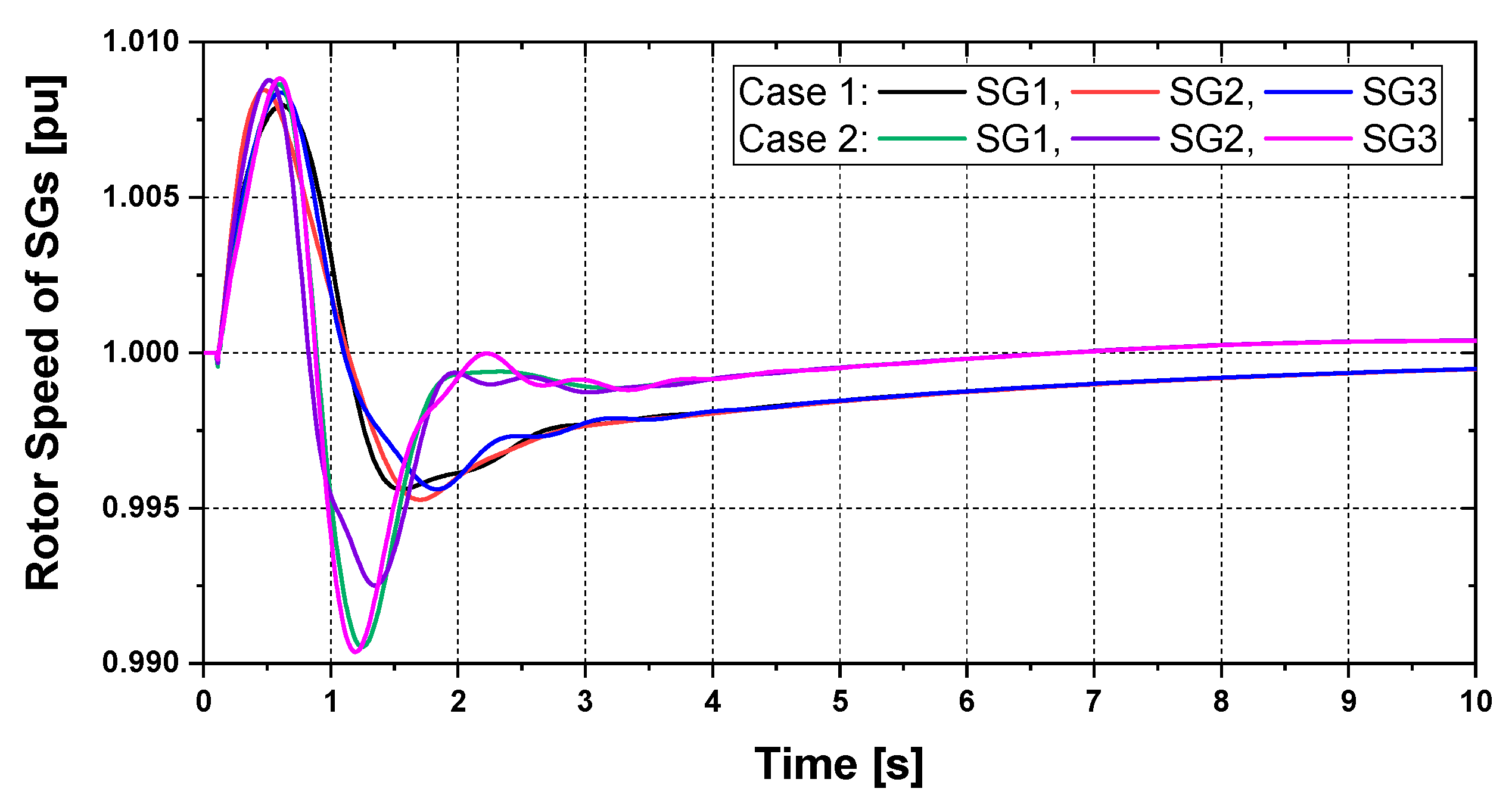
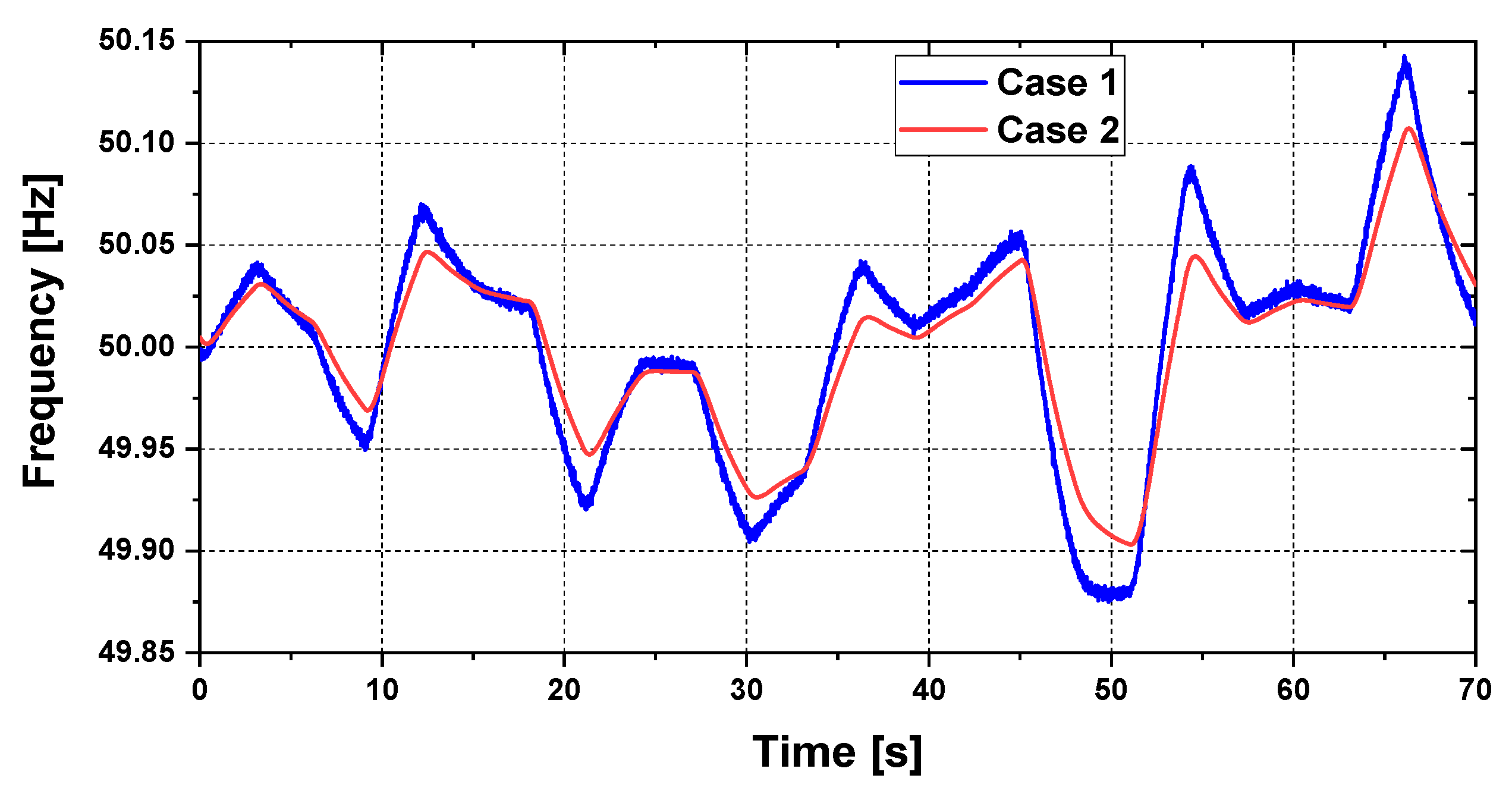

| Parameters of frequency | Case 1 | Case 2 |
|---|---|---|
| Maximum frequency deviation in positive direction (+Δf) | 0.1428 | 0.1072 |
| Maximum frequency deviation in negative direction (−Δf) | −0.1249 | −0.0969 |
| Standard deviation (σ) | 0.0536 | 0.0419 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hazari, M.R.; Jahan, E.; Mannan, M.A.; Tamura, J. Coordinated Control Scheme of Battery Storage System to Augment LVRT Capability of SCIG-Based Wind Turbines and Frequency Regulation of Hybrid Power System. Electronics 2020, 9, 239. https://doi.org/10.3390/electronics9020239
Hazari MR, Jahan E, Mannan MA, Tamura J. Coordinated Control Scheme of Battery Storage System to Augment LVRT Capability of SCIG-Based Wind Turbines and Frequency Regulation of Hybrid Power System. Electronics. 2020; 9(2):239. https://doi.org/10.3390/electronics9020239
Chicago/Turabian StyleHazari, Md. Rifat, Effat Jahan, Mohammad Abdul Mannan, and Junji Tamura. 2020. "Coordinated Control Scheme of Battery Storage System to Augment LVRT Capability of SCIG-Based Wind Turbines and Frequency Regulation of Hybrid Power System" Electronics 9, no. 2: 239. https://doi.org/10.3390/electronics9020239
APA StyleHazari, M. R., Jahan, E., Mannan, M. A., & Tamura, J. (2020). Coordinated Control Scheme of Battery Storage System to Augment LVRT Capability of SCIG-Based Wind Turbines and Frequency Regulation of Hybrid Power System. Electronics, 9(2), 239. https://doi.org/10.3390/electronics9020239







