Sensitivity Analysis of Exact Tracking Error Dynamics Passive Output Control for a Flat/Partially Flat Converter Systems
Abstract
1. Introduction
2. Development of ETEDPOF Control Law for Fourth and Sixth Order Systems
2.1. General Procedure for ETEDPOF Development
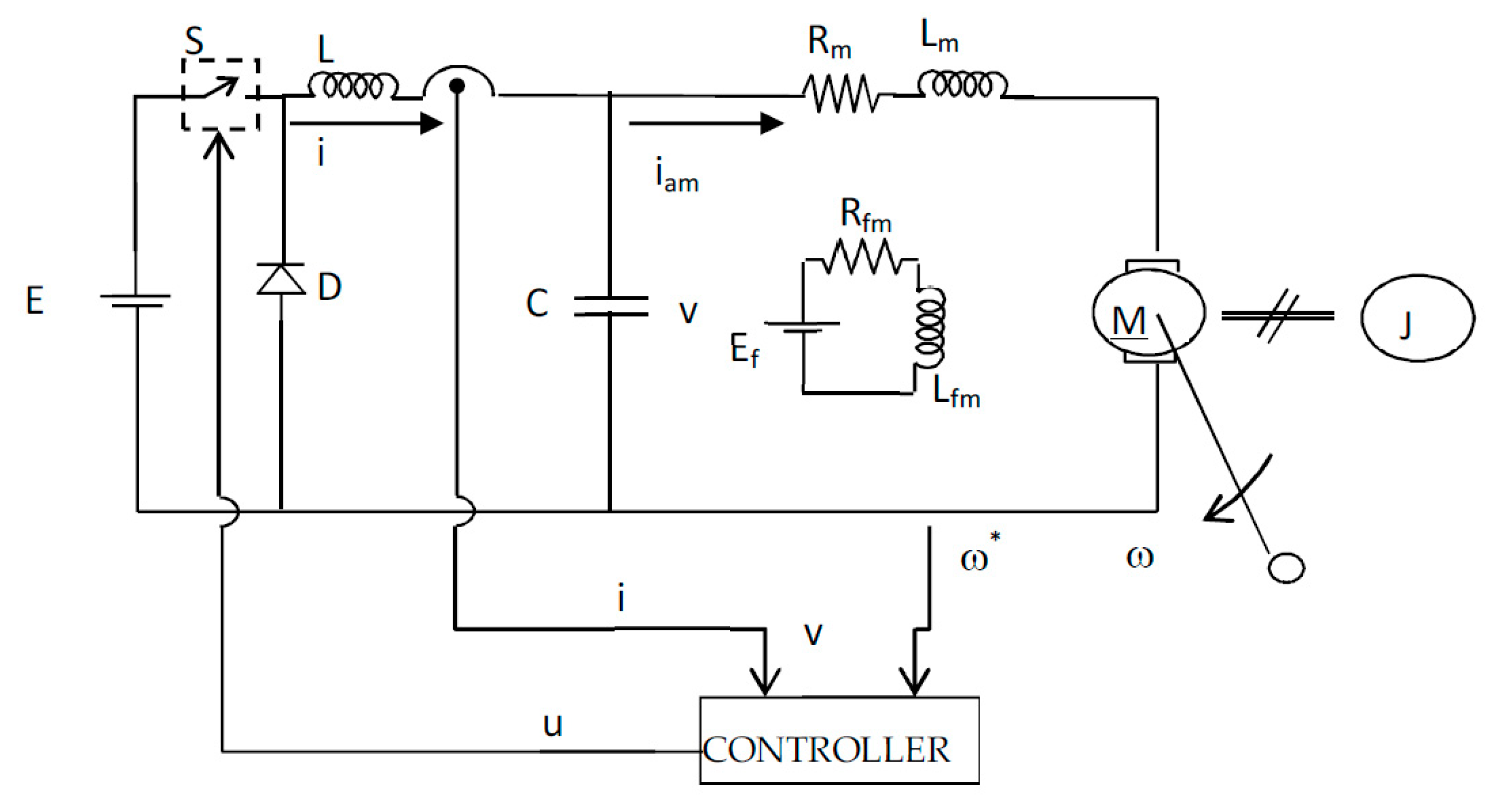
2.2. ETEDPFO for Buck Converter with Dynamic Load
- k—Torque constant (N·m/A)
- L—Buck converter inductance (henry)
- C—Buck converter capacitance (farad)
- Rm—Motor armature resistance (Ohm)
- Lm—Motor armature inductance (henry)
- u—Average control input
- i—Input current (ampere)
- v—Armature voltage or converter output voltage (volt)
- ω—Angular velocity of the motor shaft
- TL—Load torque (Nm)
- iam—Motor armature current (ampere)
- N—Speed of the motor shaft (RPM)
- J—Motor Inertia (kg·m2)
- B—Frictional coefficient (N·m·s)
- E—Input voltage (volt)
2.2.1. ETEDPOF Design
2.2.2. Stability Proof
2.3. ETEDPOF for Boost Converter
- L—Boost converter inductance (Henry)
- C—Boost converter capacitance (Farad)
- Rm—Motor armature resistance (Ohm)
- Lm—Motor armature inductance (Henry)
- u—Average control input
- i—Input current (Ampere)
- v—Armature voltage or converter output voltage (Volt)
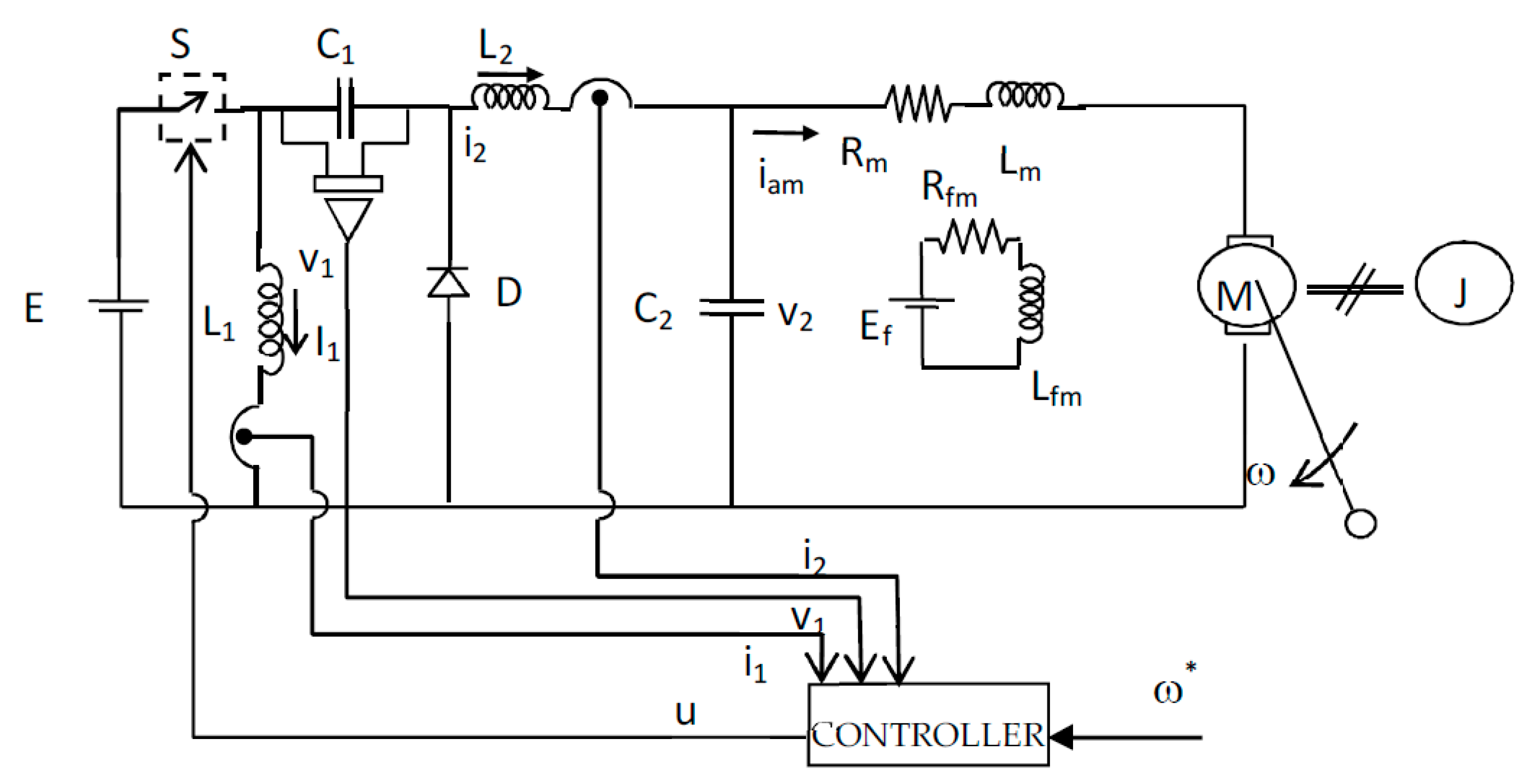
2.4. ETEDPOF for a Luo Converter System
- —Inductor () current (Ampere)
- —Inductor () current (Ampere)
- —Capacitor () voltage (Volt)
- —Capacitor () voltage (Volt)
- —Motor armature current (Ampere)
- u—Control input
- E—Supply voltage (Volt)
3. Sensitivity Analysis
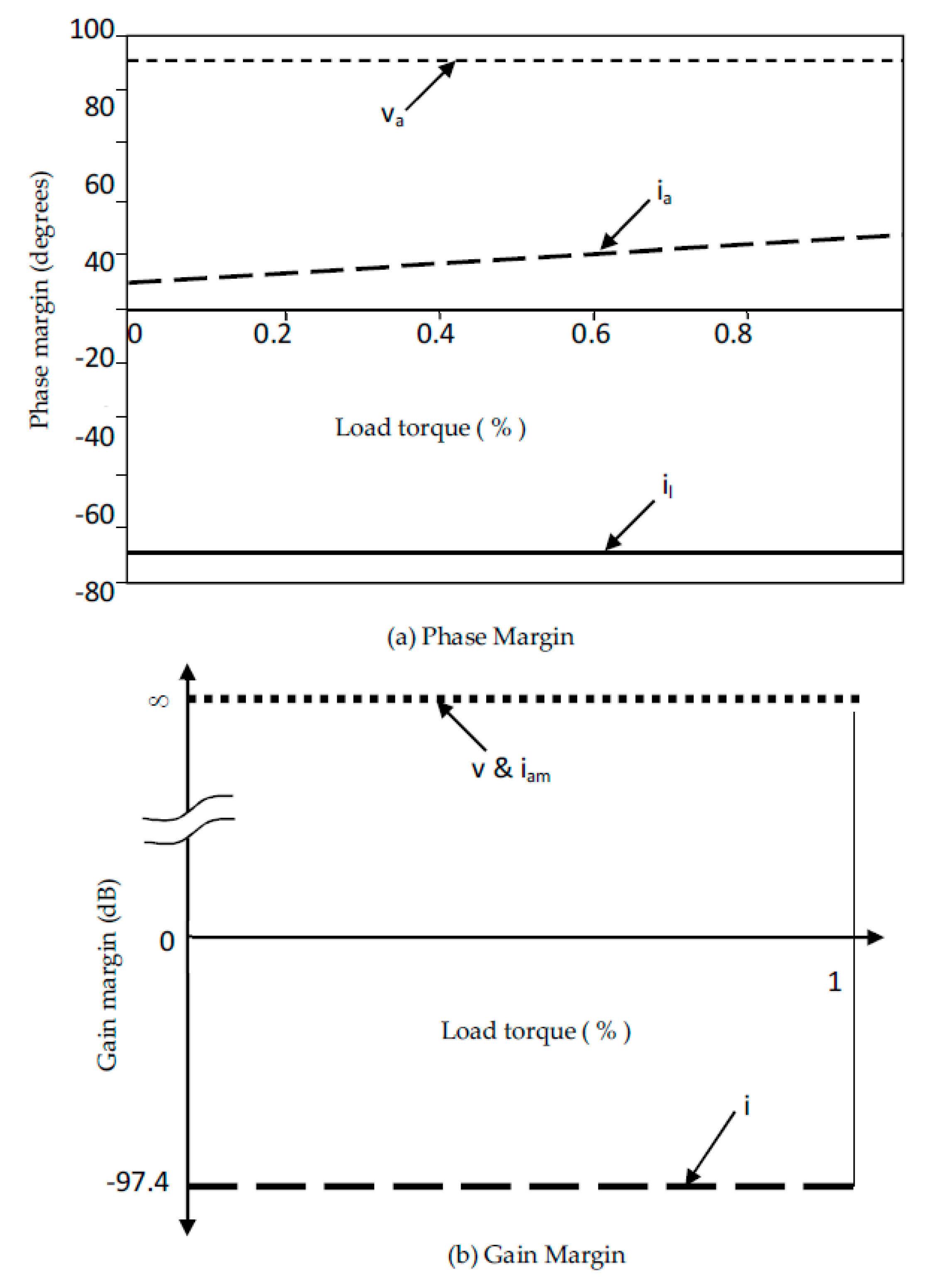
3.1. Sensitivity Analysis of Buck Converter
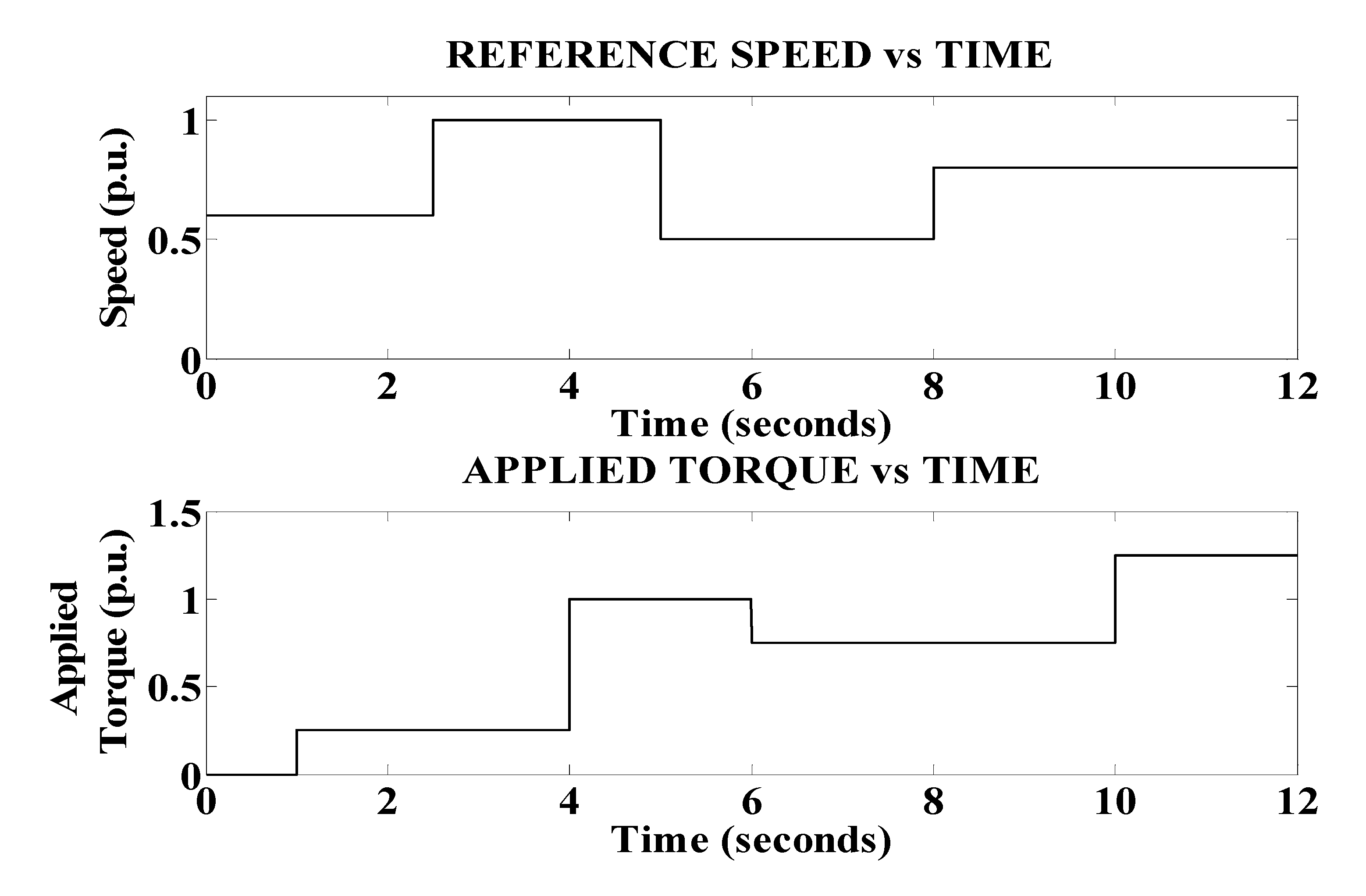
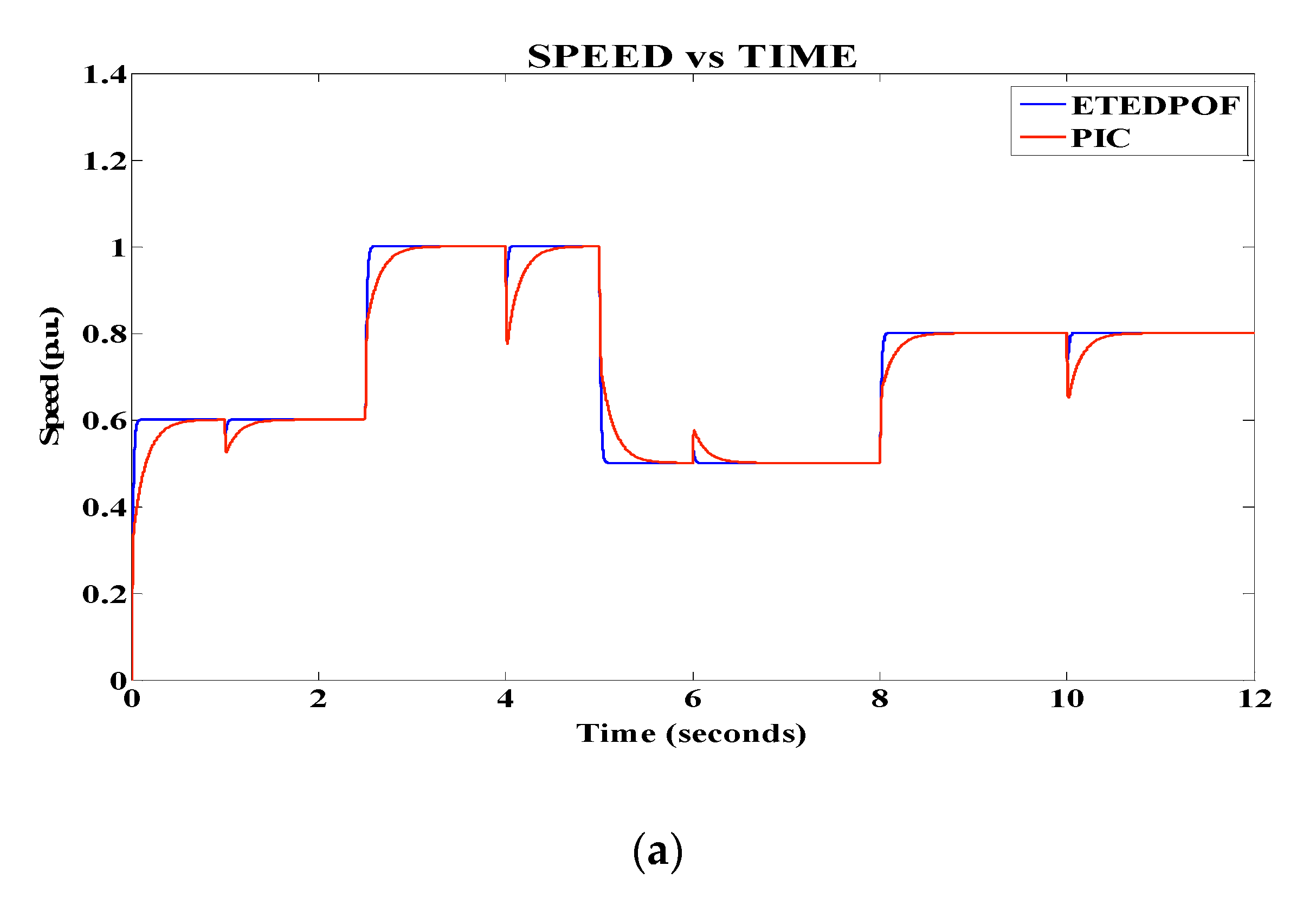
Comparison of ETEDPOF and PIC
3.2. Sensitivity Analysis of Boost Converter
3.3. Sensitivity Analysis of a Luo Converter
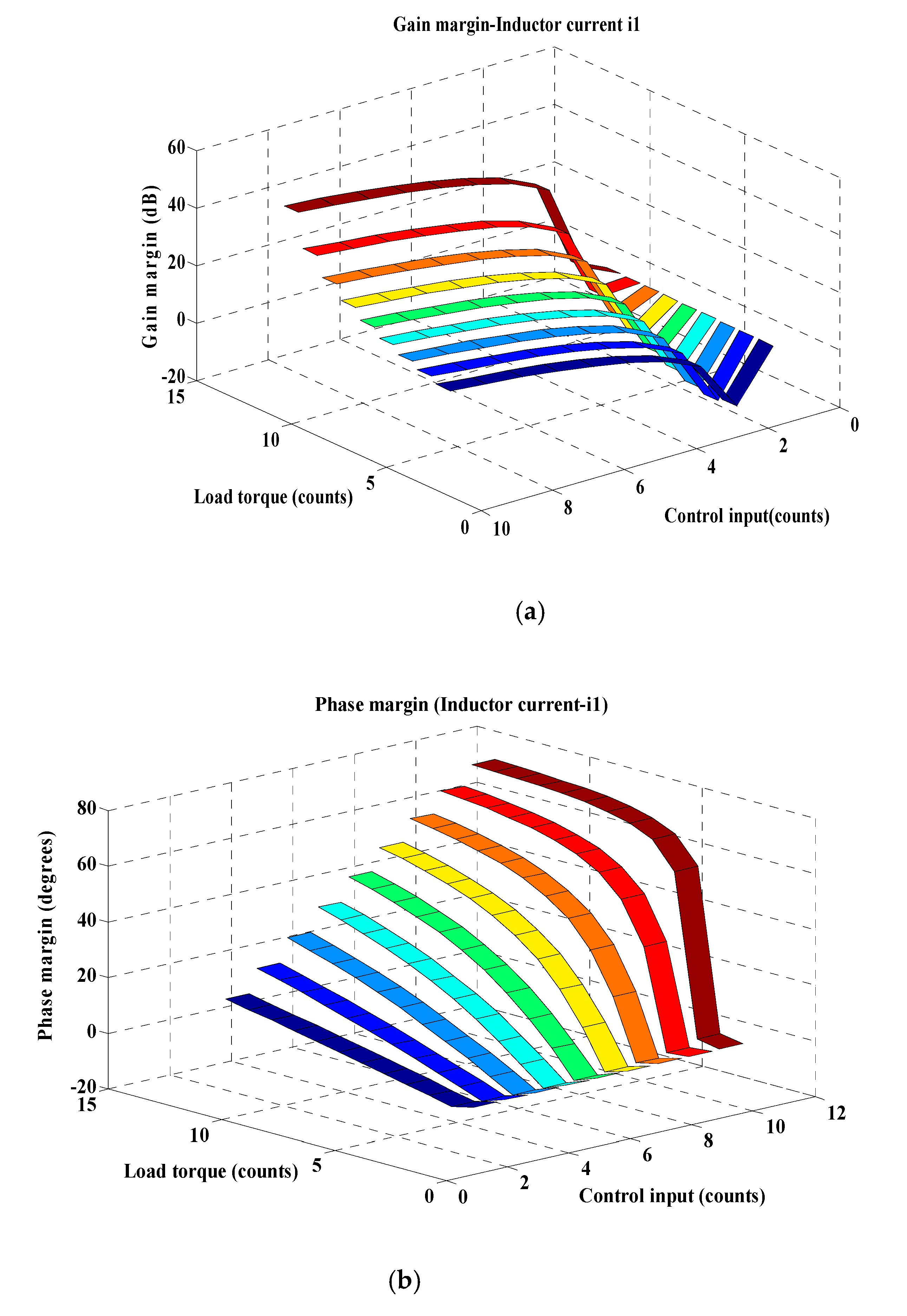
- The frequency response of inductor current (i1) is shown in Figure 11. Though the gain margin remains positive, the phase margin assumes a low value for smaller values of load torque. Therefore, it can be considered as one of the sensitive variables;
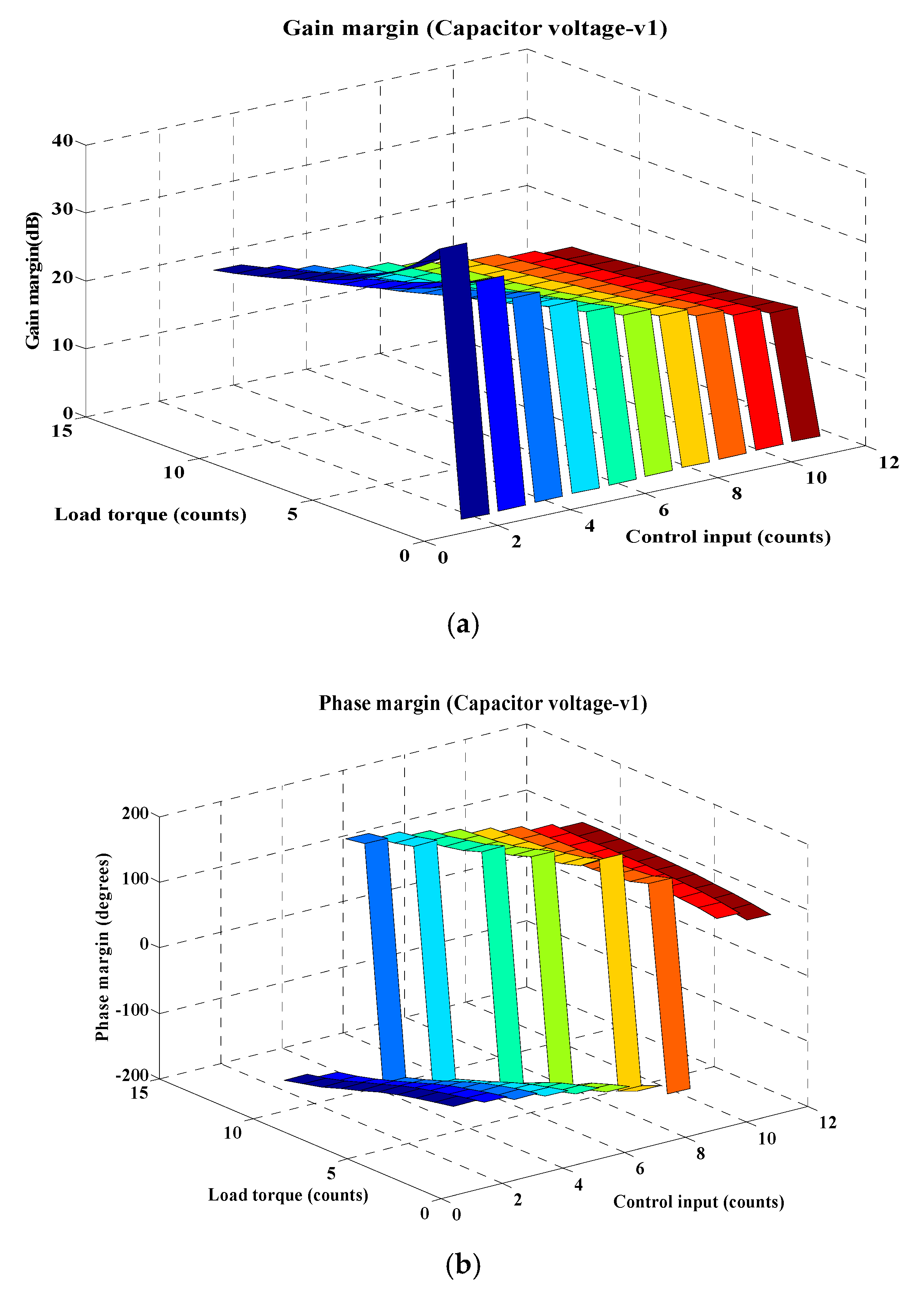
- The frequency response of capacitor voltage v1 is shown in Figure 12. The gain margin for v1 becomes low for smaller values of load torque, and phase margin value becomes positive to negative when the load torque moves from low to high value. As both gain and phase margin variations are opposite to each other, v1 is considered as a sensitive variable;
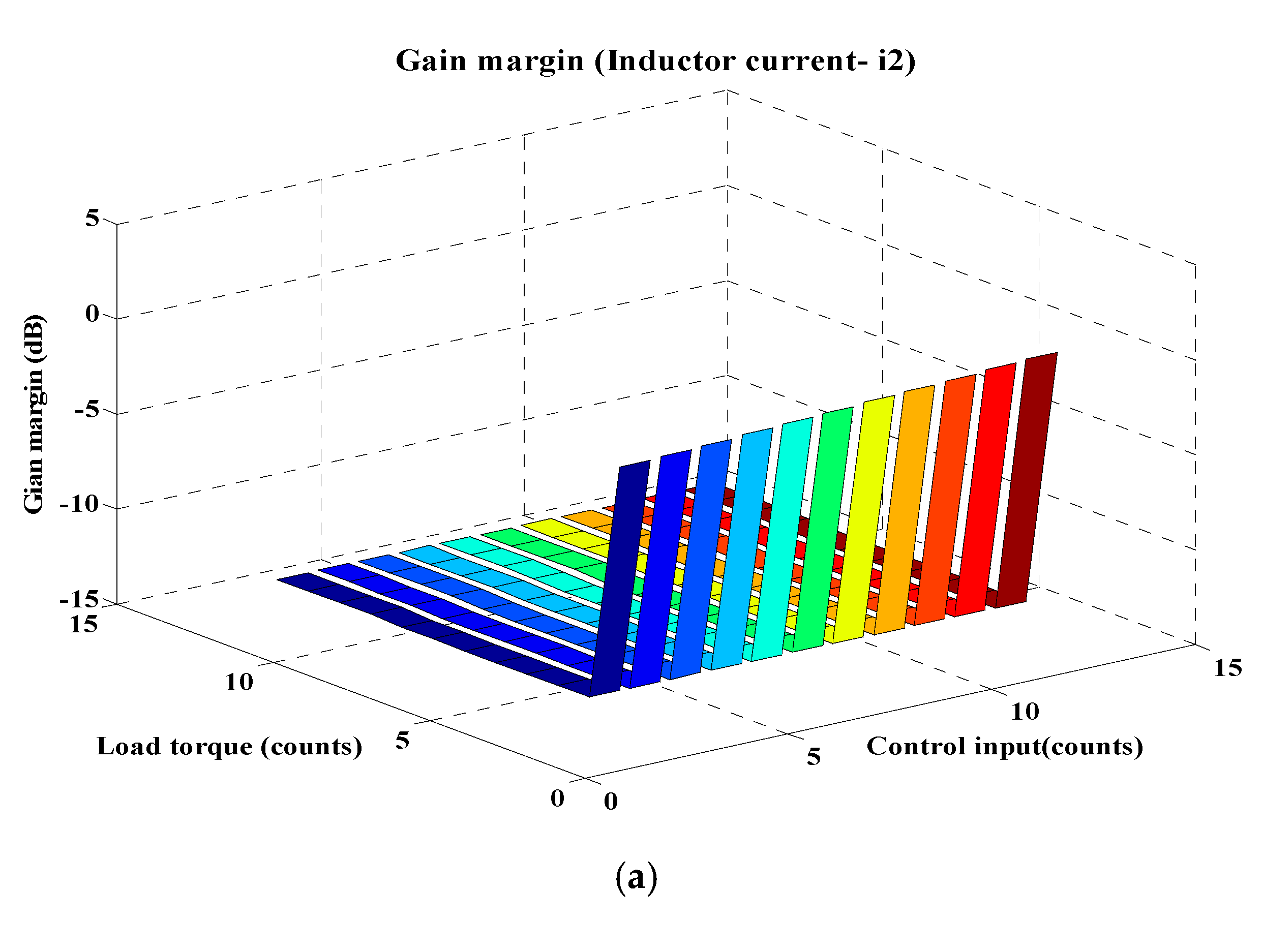
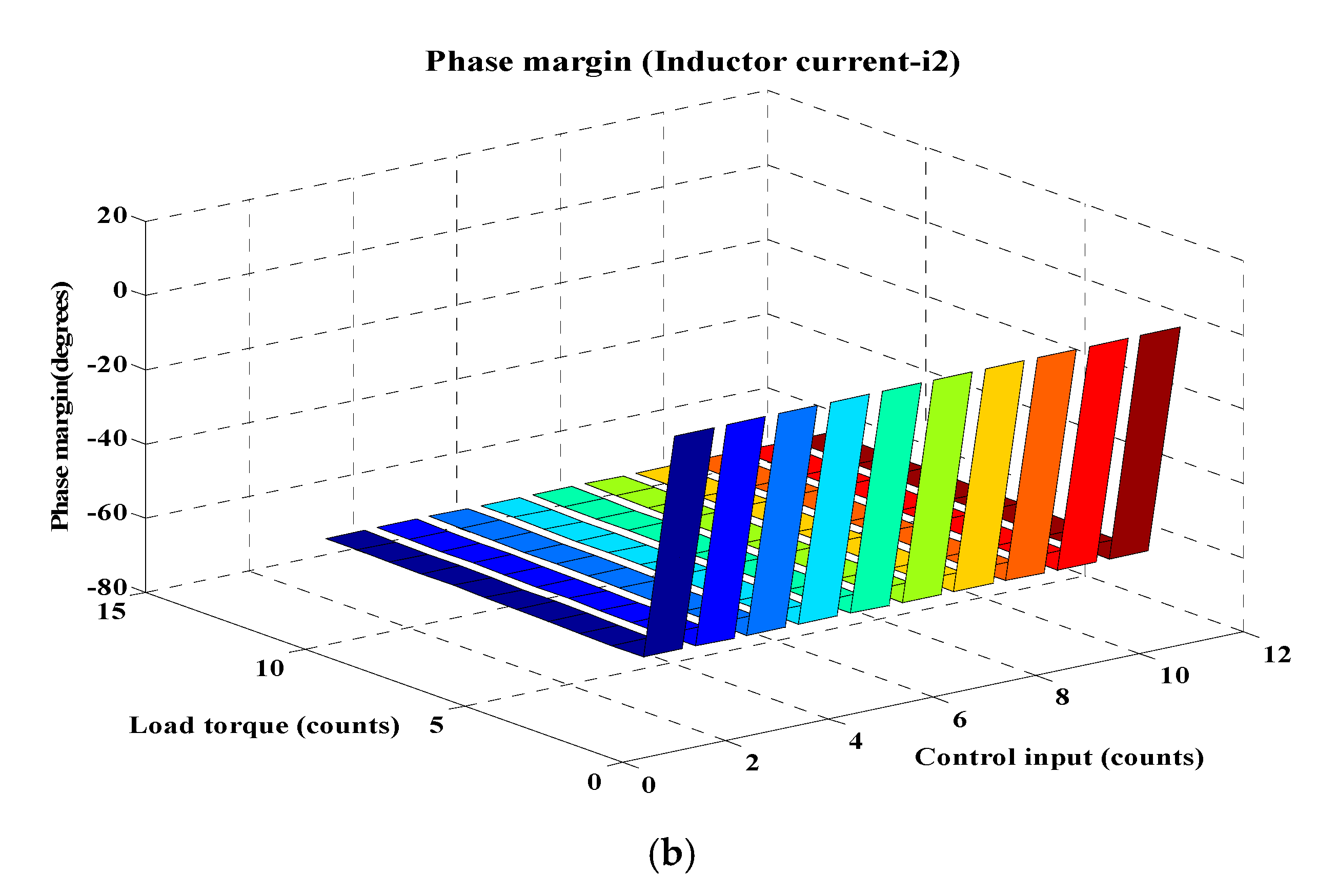
- Bode plot response for inductor current (i2) is shown in Figure 13, which indicates that both margin values are negative and thus it makes i2 as a sensitive variable;
- Figure 14 confirms that the variables ‘v1′ and ‘iam’ are not sensitive due to positive margin values.
4. Conclusions
- (a)
- In a buck converter with a dynamic load, the inductor current is considered as the sensitive variable;
- (b)
- In order to verify the sensitivity nature, ETEDPOF is compared with PIC in the above-mentioned system. The results confirm the superiority of ETEDPOF against PIC for various speed references and different load torque conditions;
- (c)
- In a boost converter, the current flow through the boost inductor and the voltage across the load are confirmed as sensitive;
- (d)
- In a luo converter, the capacitor voltage (v1) or capacitor voltages (v2), inductor current (i1) and inductor current (i2) are considered as more sensitive variables.
Author Contributions
Funding
Conflicts of Interest
References
- Linares-Flores, J.; Sira-Ramírez, H.; Yescas, E.; Sanjuan, J.J.V. A Comparison Between the Algebraic and the Reduced Order Observer Approaches for on-Line Load Torque Estimation in a Unit Power Factor Rectifier-DC Motor System. Asian J. Control 2010, 14, 45–57. [Google Scholar] [CrossRef]
- Linares-Flores, J.; Sira-Ramirez, H.; Cuevas-Lopez, E.F.; Contreras-Ordaz, M.A. Sensorless Passivity Based Control of a DC Motor via a Solar Powered Sepic Converter-Full Bridge Combination. J. Power Electron. 2011, 11, 743–750. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.; Oliver-Salazar, M.A.; Leyva-Ramos, J. Voltage Regulation of a Fuel Cell-Boost Converter System: A Proportional Integral Exact Tracking Error Dynamics Passive Output Feedback Control Approach. In Proceedings of the 2012 American Control Conference (ACC), Montereal, QC, Canada, 27–29 June 2012; pp. 2153–2158. [Google Scholar]
- Chu, C.-C.; Tsai, H.-C. Passivity-Based Control of UPFCs. In Proceedings of the International Conference on Power Electronics and Drive Systems (PEDS), Taipei, Taiwan, 2–5 November 2009; pp. 794–799. [Google Scholar]
- Lee, T.-S. Lagrangian Modeling and Passivity-Based Control of Three-Phase AC/DC Voltage-Source Converters. IEEE Trans. Ind. Electron. 2004, 51, 892–902. [Google Scholar] [CrossRef]
- Tofighi, A.; Kalantar, M. Power Management of PV/Battery Hybrid Power Source via Passivity-Based Control. Renew. Energy 2011, 36, 2440–2450. [Google Scholar] [CrossRef]
- Komurcugil, H. Steady-State Analysis and Passivity-Based Control of Single-Phase PWM Current-Source Inverters. IEEE Trans. Ind. Electron. 2009, 57, 1026–1030. [Google Scholar] [CrossRef]
- Escobar, G.; Ortega, R.; Sira-Ramirez, H.; Vilain, J.; Zein, I. An Experimental Comparison of Several Nonlinear Controllers for Power Converters. IEEE Control Syst. Mag. 1999, 19, 66–82. [Google Scholar]
- Kumar, S.G.; Thilagar, S.H. Sensorless Load Torque Estimation and Passivity Based Control of Buck Converter Fed DC Motor. Sci. World J. 2015, 2015, 1–15. [Google Scholar] [CrossRef]
- Kumar, S.G.; Thilagar, S.H. Soft Sensing of Speed in Load Torque Estimation for Boost Converter Fed DC Motor. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–14 November 2013; pp. 3758–3763. [Google Scholar]
- Ganesh, K.S.; Hosimin Thilagar, S. Development of Load Torque Estimation and Passivity Based Control for DC Motor Drive Systems with Reduced Sensor Count. In Emerging Issues in Science and Technology; Book Publisher International: Kolkata, India, 2020; Volume 3, pp. 1–25. [Google Scholar]
- Hou, R.; Song, H.; Nguyen, T.-T.; Qu, Y.; Kim, H.-M. Robustness Improvement of Superconducting Magnetic Energy Storage System in Microgrids Using an Energy Shaping Passivity-Based Control Strategy. Energies 2017, 10, 671. [Google Scholar] [CrossRef]
- Huang, J.; Wang, H.; Wang, C. Passivity-Based Control of a Doubly Fed Induction Generator System under Unbalanced Grid Voltage Conditions. Energies 2017, 10, 1139. [Google Scholar] [CrossRef]
- Li, T.; Cheng, Q.; Sun, W.; Chen, L. Grid-Connected Control Strategy of Five-Level Inverter Based on Passive E-L Model. Energies 2017, 10, 1657. [Google Scholar] [CrossRef]
- Rosa, A.; De Souza, T.M.; Morais, L.M.F.; Seleme, I.S., Jr. Adaptive and Nonlinear Control Techniques Applied to SEPIC Converter in DC-DC, PFC, CCM and DCM Modes Using HIL Simulation. Energies 2018, 11, 602. [Google Scholar] [CrossRef]
- Kim, S.-K. Passivity-Based Robust Output Voltage Tracking Control of DC/DC Boost Converter for Wind Power Systems. Energies 2018, 11, 1469. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, H.; Yu, J.; Wu, H.; Liu, X. Trajectory Tracking of Flexible-Joint Robots Actuated by PMSM via a Novel Smooth Switching Control Strategy. Appl. Sci. 2019, 9, 4382. [Google Scholar] [CrossRef]
- Guerrero-Sánchez, M.E.; Hernández-González, O.; Lozano, R.; García-Beltrán, C.D.; Valencia-Palomo, G.; López-Estrada, F. Energy-Based Control and LMI-Based Control for a Quadrotor Transporting a Payload. Mathematics 2019, 7, 1090. [Google Scholar] [CrossRef]
- Rymarski, Z.; Bernacki, K.; Dyga, L.; Davari, P. Passivity-Based Control Design Methodology for UPS Systems. Energies 2019, 12, 4301. [Google Scholar] [CrossRef]
- Jung, D.; Bang, S. Posture Stabilization of Wheeled Mobile Robot Based on Passivity-Based Robust Switching Control With Model Uncertainty Compensation. Appl. Sci. 2019, 9, 5233. [Google Scholar] [CrossRef]
- Travieso-Torres, J.C.; Vilaragut-Llanes, M.; Costa-Montiel, Á.; Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Contreras-Jara, C.; Álvarez-Gracia, A. New Adaptive High Starting Torque Scalar Control Scheme for Induction Motors Based on Passivity. Energies 2020, 13, 1276. [Google Scholar] [CrossRef]
- Yang, W.; Meng, F.; Sun, M.; Liu, K. Passivity-Based Control Design for Magnetic Levitation System. Appl. Sci. 2020, 10, 2392. [Google Scholar] [CrossRef]
- Gil-González, W.; Serra, F.M.; Montoya, O.D.; Ramírez-Vanegas, C.; Orozco-Henao, C. Direct Power Compensation in AC Distribution Networks With SCES Systems via PI-PBC Approach. Symmetry 2020, 12, 666. [Google Scholar] [CrossRef]
- Ryalat, M.; Damiri, H.S.; ElMoaqet, H.; Alrabadi, I. An Improved Passivity-Based Control of Electrostatic MEMS Device. Micromachines 2020, 11, 688. [Google Scholar] [CrossRef]
- Rymarski, Z.; Bernacki, K. Different Features of Control Systems for Single-Phase Voltage Source Inverters. Energies 2020, 13, 4100. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Ramírez-Vanegas, C. Discrete-Inverse Optimal Control Applied to the Ball and Beam Dynamical System: A Passivity-Based Control Approach. Symmetry 2020, 12, 1359. [Google Scholar] [CrossRef]
- Rajeev, V.K.A.; Rivera, M.; Kumar, S.G. Investigation on Passivity Based Control for Electrical Applications. In Proceedings of the Chilean Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Pucon, Chile, 18–20 October 2017; pp. 1–6. [Google Scholar]
- Singer, R. Selecting State Variables to Minimize Eigenvalue Sensitivity of Multivariable Systems. Automatica 1969, 5, 85–93. [Google Scholar] [CrossRef]
- Wong, K. Stability Study of a Voltage-Mode Buck Regulator Using System Poles Approach. In Proceedings of the IEEE International Symposium on Circuits and Systems, Bangkok, Thailand, 25–28 May 2003; pp. 817–820. [Google Scholar]
- Serra, F.M.; Fernández, L.M.; Montoya, O.D.; Gil-González, W.; Hernández, J. Nonlinear Voltage Control for Three-Phase DC-AC Converters in Hybrid Systems: An Application of the PI-PBC Method. Electronics 2020, 9, 847. [Google Scholar] [CrossRef]
- Sang, Y.; Yang, B.; Fu, Y.; An, N.; Zeng, F.; Yu, T. Passive Current Control Design for MMC in HVDC Systems through Energy Reshaping. Electronics 2019, 8, 967. [Google Scholar] [CrossRef]
- Landi, C.T.; Ferraguti, F.; Fantuzzi, C.; Secchi, C. A Passivity-Based Strategy for Manual Corrections in Human-Robot Coaching. Electronics 2019, 8, 320. [Google Scholar] [CrossRef]
- Lu, Y.; Cheng, K.W.E.; Ho, S.L.; Pan, J.F. Examination of H-Bridge Resonant Converter Using Passivity Based Control. In Proceedings of the International Conference on Power Electronics Systems and Applications (ICPESA), Hong Kong, China, 9–11 November 2004; pp. 235–242. [Google Scholar]
- Wei, M.-Y.; Liu, T.-H.; Lin, C.-K. Design and Implementation of a Passivity-Based Controller for Sensorless Synchronous Reluctance Motor Drive Systems. IET Electr. Power Appl. 2011, 5, 335. [Google Scholar] [CrossRef]
- Kumar, S.G.; Thilagar, S.H. Comparative study of proportional integral and passivity based control for buck converter. In Proceedings of the 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications, Noordwijkerhout, The Netherlands, 29–31 July 2011; pp. 309–314. [Google Scholar]
- Gensior, A.; Sira-Ramirez, H.; Rudolph, J.; Guldner, H. On Some Nonlinear Current Controllers for Three-Phase Boost Rectifiers. IEEE Trans. Ind. Electron. 2008, 56, 360–370. [Google Scholar] [CrossRef]
- Lee, S.; Chung, H.; Wong, B. Computation of the Cycle State-Variable Sensitivity Matrix of PWM DC/DC Converters and Its Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2000, 47, 1542–1548. [Google Scholar] [CrossRef]
- Gupta, P.; Patra, A. Super-Stable Energy Based Switching Control Scheme for DC-DC Buck Converter Circuits. In Proceedings of the IEEE International Symposium on Circuits and Systems, Kobe, Japan, 23–26 May 2005; pp. 3063–3066. [Google Scholar]
- Hiskens, I.A. Stability of Hybrid System Limit Cycles: Application to the Compass Gait Biped robot. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 774–779. [Google Scholar]
- Prempraneerach, P.; Hover, F.; Triantafyllou, M.; Chryssostomidis, C.; Karniadakis, G. Sensitivity Analysis and Low-Dimensional Stochastic Modeling of Shipboard Integrated Power Systems. In Proceedings of the IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 1999–2003. [Google Scholar]
- Feng, Q.; Nelms, R.; Hung, J. Posicast-Based Digital Control of the Buck Converter. IEEE Trans. Ind. Electron. 2006, 53, 759–767. [Google Scholar] [CrossRef]
- Mallada, U.R.; Leyva, R.; Garcés, P. Sensitivity Analysis in Dc-Dc Converter Optimal Design. In Proceedings of the IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 358–364. [Google Scholar]
- Kumar, S.G.; Hosimin Thilagar, S.; Rivera, M. Low Cost Implementation of Passivity Based Control and Estimation of Load Torque for a Luo Converter With Dynamic Load. Electronics 2020. (Accepted for publication). [Google Scholar]
- Donde, V.; Hiskens, I.A. Analysis of Tap-Induced Oscillations Observed in an Electrical Distribution System. IEEE Trans. Power Syst. 2007, 22, 1881–1887. [Google Scholar] [CrossRef]
- Hiskens, I.A.; Pai, M. Sensitivity Analysis of Power System Trajectories: Recent Results. In Proceedings of the IEEE International Symposium on Circuits and Systems (Cat. No.98CH36187), Monterey, CA, USA, 31 May–3 June 1998; pp. 439–443. [Google Scholar]
- Fukuyama, T.; Kato, T. Tolerance Computation of a Power Electronic Circuit by Higher Order Sensitivity Analysis Method. IEEJ Trans. Ind. Appl. 2001, 121, 835–840. [Google Scholar] [CrossRef][Green Version]
- Figueres, E.; Garcerá, G.; Pascual, M. Comparative Analysis of ACC Control Loops of DC-DC Converters by Means of Robust Parametric Control Theory. In Proceedings of the 31st Annual Power Electronics Specialists Conference, Galway, Ireland, 23 June 2002; pp. 1403–1407. [Google Scholar]
- Bekey, G.; Tomovic, R. Sensitivity of Discrete Systems to Variation of Sampling Interval. IEEE Trans. Autom. Control. 1966, 11, 284–287. [Google Scholar] [CrossRef]
- Kumar, S.G.; Hosimin-Thilagar, S.; Rivera, M. Cost Effective Control of a Partially Flat Boost Converter Fed DC Motor. In Proceedings of the IEEE International Conference on Automatica (ICA-ACCA), Curico, Chile, 19–21 October 2016; pp. 1–7. [Google Scholar]
- Ganesh, S.K.; Hosimin, S.T. Passivity Based Control of Luo Converter. J. Electr. Eng. 2013, 13, 159–166. [Google Scholar]







| S. No | Buck Converter | Motor | ||
|---|---|---|---|---|
| Symbol | Value | Symbol | Value | |
| 1. | L | 0.42 mH | Po | 18 W |
| 2. | Rated current | 4A (Base value) | E | 12 V (base value) |
| 3. | C | 50 µF | Iam | 1.5 A |
| 4. | Switching frequency | 50 kHz | N | 1500 RPM (base value) |
| 5. | Vin | 24 V | Lm | 712.85 mH |
| S.No | % Load Torque | Armature Voltage | Armature Current | Inductor Current | |||
|---|---|---|---|---|---|---|---|
| GM | PM | GM | PM | GM | PM | ||
| (dB) | (degrees) | (dB) | (degrees) | (dB) | (degrees) | ||
| 1. | 0 | ∞ | 9.88 | ∞ | 90.1 | −97.4 | −88.9 |
| 2. | 0.1 | ∞ | 10.9 | ∞ | 90.1 | −97.4 | −88.9 |
| 3. | 0.2 | ∞ | 11.9 | ∞ | 90.2 | −97.4 | −88.9 |
| 4. | 0.3 | ∞ | 12.9 | ∞ | 90.2 | −97.4 | −88.9 |
| 5. | 0.4 | ∞ | 13.9 | ∞ | 90.2 | −97.4 | −88.9 |
| 6. | 0.5 | ∞ | 14.9 | ∞ | 90.2 | −97.4 | −88.9 |
| 7. | 0.6 | ∞ | 15.9 | ∞ | 90.2 | −97.4 | −88.9 |
| 8. | 0.7 | ∞ | 16.9 | ∞ | 90.2 | −97.4 | −88.9 |
| 9. | 0.8 | ∞ | 17.8 | ∞ | 90.3 | −97.4 | −88.9 |
| 10. | 0.9 | ∞ | 18.8 | ∞ | 90.3 | −97.4 | −88.9 |
| 11. | 1.0 | ∞ | 19.7 | ∞ | 90.3 | −97.4 | −88.9 |
| S.No | Dynamic Load | 2nd Order Converter | ||||
|---|---|---|---|---|---|---|
| Symbol | Value | Symbol | Value | Symbol | Value | |
| 1. | Po | 18 W | T | 1 Kgcm | L | 0.62 mH |
| 2. | Vdc | 12 Volts | J | 0.886138 × 10−4 kgm2 | Rated Current | 5 A |
| 3. | Ia | 1.5 A | B | 96.894 × 10−6 Nm/rad | C | 5 × 10−5 F |
| 4. | N | 1500 RPM | k | 0.05022 Nm/A | f | 50 × 103 Hz |
| 5. | La | 712.85 × 10−3 H | E | 4.0 V | ||
| 6. | Ra | 26 × 10−1 Ω | 12.5 × 10−2 | |||
| S. No | Luo Converter | Armature Side | DC Motor | |||
|---|---|---|---|---|---|---|
| Field Side | ||||||
| Symbol | Value | Symbol | Value | Symbol | Value | |
| 1. | L1 | 18 mH | Po | 1 HP | Rfm | 696.1 Ω |
| 2. | C1 | 200 µF | Ea | 180 Volts | Lfm | 25.023 H |
| 3. | L2 | 20.769 mH | Iam | 5.1 A | Ef | 180 V |
| 4. | C2 | 440.1 µF | N | 1500 RPM | Base Values | |
| 5. | Rated current | 7 A | Lm | 111.6 mH | Speed | 1500 RPM |
| 6. | DC Supply voltage | 220 V | Rm | 6.1 Ω | Current | 5.1 A |
| Laf | 3.44 H | Voltage | 220 V | |||
| 7. | Switching frequency | 32 kHz | B | 2.7 × 10−3 Nm/rad | ||
| 8. | J | 3.4 × 10−3 kgm2 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srinivasan, G.K.; Srinivasan, H.T.; Rivera, M. Sensitivity Analysis of Exact Tracking Error Dynamics Passive Output Control for a Flat/Partially Flat Converter Systems. Electronics 2020, 9, 1942. https://doi.org/10.3390/electronics9111942
Srinivasan GK, Srinivasan HT, Rivera M. Sensitivity Analysis of Exact Tracking Error Dynamics Passive Output Control for a Flat/Partially Flat Converter Systems. Electronics. 2020; 9(11):1942. https://doi.org/10.3390/electronics9111942
Chicago/Turabian StyleSrinivasan, Ganesh Kumar, Hosimin Thilagar Srinivasan, and Marco Rivera. 2020. "Sensitivity Analysis of Exact Tracking Error Dynamics Passive Output Control for a Flat/Partially Flat Converter Systems" Electronics 9, no. 11: 1942. https://doi.org/10.3390/electronics9111942
APA StyleSrinivasan, G. K., Srinivasan, H. T., & Rivera, M. (2020). Sensitivity Analysis of Exact Tracking Error Dynamics Passive Output Control for a Flat/Partially Flat Converter Systems. Electronics, 9(11), 1942. https://doi.org/10.3390/electronics9111942






