Fast Preconditioner Computation for BICGSTAB-FFT Method of Moments with NURBS in Large Multilayer Structures
Abstract
1. Introduction
2. Description of the Problem
3. Numerical Results
3.1. Focused Beam Reflectarray Made of Two Sets of Four Parallel Dipoles with Small Rotations
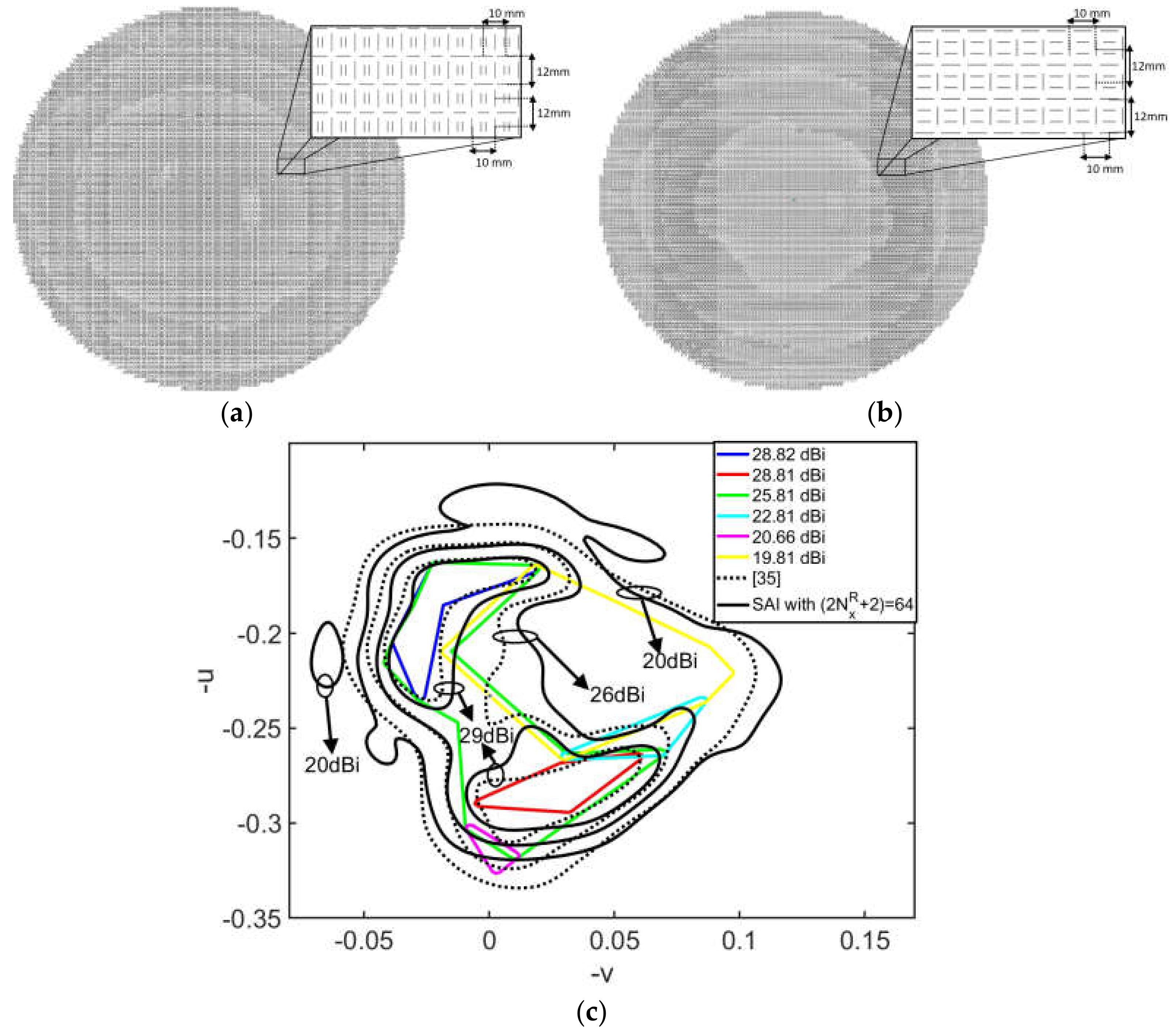
3.2. Reflectarray Made of Two Orthogonal Sets of Four Parallel Dipoles to Generate South American Coverage
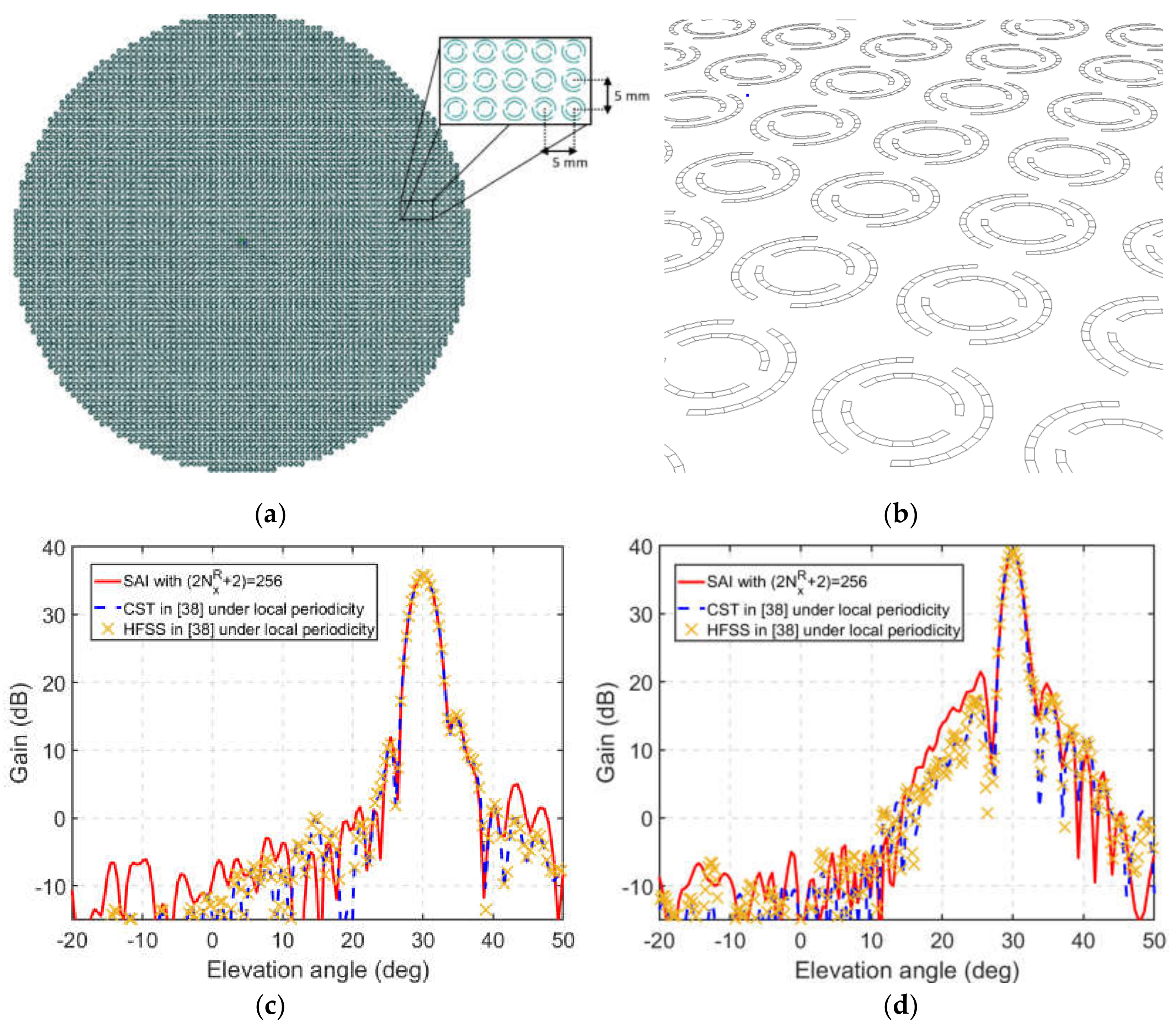
3.3. Dual Band Circular Polarized Focused Beam Reflectarray Made of Dual Concentric Split Rings
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, J.; Encinar, J.A. Reflectarray Antennas; IEEE Press/Wiley: Piscataway, NJ, USA, 2008. [Google Scholar]
- Ben, A.M. Frequency Selective Surfaces; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Minatti, G.; Caminita, F.; Casaletti, M.; Maci, S. Spiral leaky wave antennas based on modulated surface impidance. IEEE Trans. Antennas Propag. 2011, 59, 4436–4444. [Google Scholar] [CrossRef]
- Valle, L.; Rivas, F.; Cátedra, M.F. Combining the Moment Method with Geometrical Modelling by NURBS Surfaces and Bézier Patches. IEEE Trans. Antennas Propag. 1994, 42, 373–381. [Google Scholar] [CrossRef]
- Bézier, P. The Mathematical Basis of the UNISURF CAD System; Butterworths: London, UK, 1986. [Google Scholar]
- Lorentz, G. Bernstein Polynomials; Toronto Press: Toronto, ON, Canada, 1953. [Google Scholar]
- Itoh, T. Numerical Techniques for Microwave and Millimeter-Wave Passive Structures; John Wiley and Sons: New York, NJ, USA, 1989. [Google Scholar]
- Miller, E.K.; Deadrick, F.J. Numerical and Asymptotic Techniques in Electromagnetics; Springer: New York, NY, USA, 1975. [Google Scholar]
- Stutzman, W.L.; Thiele, G.A. Antenna Theory and Design; John Wiley and Sons: New York, NY, USA, 1981. [Google Scholar]
- Sarkar, T.K.; Siarkiewicz, K.R.; Stratton, R.F. Survey of Numerical Methods for Solution of Large System of Linear Equations for Electromagnetic Field Problems. IEEE Trans. Antennas Propag. 1981, 29, 847–856. [Google Scholar] [CrossRef]
- Sarkar, T.K.; Rao, S.M. The Application of the Conjugate Gradient Method for the Solution of the Electromagnetic Scattering from Arbitrarily Oriented Wire Antennas. IEEE Trans. Antennas Propag. 1984, 32, 398–403. [Google Scholar] [CrossRef]
- Van den Berg, P.M. Iterative Computational Techniques in Scattering Based upon the Integrated Square Error Criterion. IEEE Trans. Antennas Propag. 1981, 32, 1063–1071. [Google Scholar] [CrossRef]
- Cátedra, M.F. Solution to Some Electromagnetics Problems Using Fast Fourier Transform with Conjugate Gradient Method. Electron. Lett. 1986, 22, 1049–1051. [Google Scholar] [CrossRef]
- Cátedra, M.F.; Torres, R.P.; Basterrechea, J.; Gago, E. CG-FFT Method, Application Signal Proccesing Techniques to Electromagnetics; Artech House: Norwood, MA, USA, 1995. [Google Scholar]
- Zhao, J.S.; Chew, W.C.; Lu, C.C.; Michielssen, E.; Song, J. Thin-Stratified Medium Fast-Multipole Algorithm for Solving Microstrip Structures. IEEE Trans. Microw. Theory Tech. 1998, 46, 395–403. [Google Scholar] [CrossRef]
- Ling, F.; Wang, C.F.; Jin, J.M. An Efficient Algorithm for Analyzing Large-Scale Microstrip Structures Using Adaptive Integral Method Combined with Discrete Complex-Image Method. IEEE Trans. Microw. Theory Tech. 2000, 48, 832–839. [Google Scholar] [CrossRef]
- Lu, C.C.; Chew, W.C. A multilevel algorithm for solving boundary integral equations of wave scattering. Microw. Opt. Tech. Lett. 1994, 7, 466–470. [Google Scholar] [CrossRef]
- Bleszynsky, E.; Bleszynsky, M.; Jaroszewicz, T. AIM: Adaptative integral method for solving large scale electromagnetic scattering and radiation problems. Radio Sci. 1996, 31, 1225–1251. [Google Scholar] [CrossRef]
- Okhmatovski, V.; Yuan, M.; Jeffrey, I.; Phelps, R. A Three-Dimensional Precorrected FFT Algorithm for Fast Method of Moments Solutions of the Mixed-Potential Integral Equation in Layered Media. IEEE Trans. Microw. Theory Tech. 2009, 57, 3505–3517. [Google Scholar] [CrossRef]
- Yang, K.; Yılmaz, A.E. FFT-accelerated analysis of scattering from three-dimensional structures residing in multiple layers. In Proceedings of the CEM’13 Computational Electromagnetics International Workshop, Izmir, Turkey, 2–5 August 2013; pp. 4–8. [Google Scholar]
- Rao, S.M.; Wilton, D.R.; Glisson, A.W. Electromagnetic scattering by surfaces of arbitrary shapes. IEEE Trans. Antennas Propag. 1982, 30, 409–418. [Google Scholar] [CrossRef]
- Phillips, J.R.; White, J.K. A precorrected-FFT method for electrostatic analysis of complicated 3-D structures. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1997, 16, 1059–1072. [Google Scholar] [CrossRef]
- Florencio, R.; Somolinos, A.; González, I.; Cátedra, M.F. BICGSTAB-FFT Method of Moments with NURBS for Analysis of Planar Generic Layouts Embedded in Large Multilayer Structures. Electronics 2020, 9, 1476. [Google Scholar] [CrossRef]
- Georgakis, I.P.; Giannakopoulos, I.I.; Litsarev, M.S.; Polimeridis, A.G. A Fast Volume Integral Equation Solver with Linear Basis Functions for the Accurate Computation of Electromagnetic Fields in MRI. arXiv 2019, arXiv:1902.02196. [Google Scholar]
- Benzi, M.; Tuma, M. A sparse approximate inverse preconditioner for non-symmetric linear systems. SIAM J. Sci. Comput. 1996, 19, 968–994. [Google Scholar] [CrossRef]
- Lee, J.; Zhang, J.; Lu, C.C. Sparse Inverse Preconditioning of Multilevel Fast Multipole Algorithm for Hybrid Integral Equations in Electromagnetics. IEEE Trans. Antennas Propag. 2004, 52, 2277–2287. [Google Scholar] [CrossRef]
- Delgado, C.; Moreno, J.; Cátedra, F. Application of a Sparsity Pattern and Region Clustering for Near Field Sparse Approximate Inverse Preconditioners in Method of Moments Simulations. Int. J. Antennas Propag. 2017, 2017, 1–7. [Google Scholar] [CrossRef]
- Michalski, K.A.; Zheng, D. Electromagnetic scattering and radiation by surfaces of arbitrary shape in layered media, part I: Theory. IEEE Trans. Antennas Propag. 1990, 38, 335–344. [Google Scholar] [CrossRef]
- Florencio, R.; Boix, R.R.; Encinar, J.A. Fast and accurate MoM analysis of periodic arrays of multilayered stacked rectangular patches with application to the design of reflectarray antennas. IEEE Trans. Antennas Propag. 2015, 63, 2558–2571. [Google Scholar] [CrossRef]
- Boix, R.R.; Fructos, A.L.; Mesa, F. Closed Form Uniform Asymptotic Expansions of Green’s Functions in Layered Media. IEEE Trans. Antennas Propag. 2010, 58, 2934–2945. [Google Scholar] [CrossRef]
- Van der Vorst, H.A. Bi-CGSTAB: A Fast and Smoothly Converging Variant of Bi-CG for the Solution of Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 1992, 13, 631–644. [Google Scholar] [CrossRef]
- Florencio, R.; Somolinos, A.; González, I.; Cátedra, M.F. Method of Moments Based on Equivalent Periodic Problem and FFT with NURBS Surfaces for Analysis of Multilayer Periodic Structures. Electronics 2020, 9, 234. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions, 9th ed.; National Institute of Standards and Technology (NBS): New York, NY, USA, 1970. [Google Scholar]
- Florencio, R.; Encinar, J.A.; Boix, R.R.; Pérez-Palomino, G.; Toso, G. Cross-polar reduction in reflectarray antennas by means of element rotation. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–5. [Google Scholar]
- Florencio, R.; Boix, R.R.; Encinar, J.A.; Toso, G. Optimized Periodic MoM for the Analysis and Design of Dual Polarization Multilayered Reflectarray Antennas Made of Dipoles. IEEE Trans. Antennas Propag. 2017, 65, 3623–3637. [Google Scholar] [CrossRef]
- Encinar, J.A.; Arrebola, M.; de la Fuente, L.F.; Tosso, G. A transmit-receive reflectarray antenna for direct broadcast satellite applications. IEEE Trans. Antennas Propag. 2011, 59, 3255–3264. [Google Scholar] [CrossRef]
- Florencio, R.; Encinar, J.A.; Boix, R.R.; Losada, V.; Toso, G. Reflectarray antennas for dual polarization and broadband telecom satellite applications. IEEE Trans. Antennas Propag. 2015, 63, 1234–1246. [Google Scholar] [CrossRef]
- Florencio, R.; Boix, R.R.; Encinar, J.A. Efficient Spectral Domain MoM for the Design of Circularly Polarized Reflectarray Antennas Made of Split Rings. IEEE Trans. Antennas Propag. 2018, 67, 1760–1771. [Google Scholar] [CrossRef]
- Smith, T.; Gothelf, U.V.; Kim, O.S.; Breinbjerg, O. Design, manufacturing, and testing of a 20/30 GHz dual-band circularly polarized reflectarray antenna in submission. IEEE Antennas Wireless Propag. Lett. 2013, 12, 1480–1483. [Google Scholar] [CrossRef]
- Huang, J.; Pogorzelski, R.J. A Ka-band microstrip reflectarray with elements having variable rotation angles. IEEE Trans. Antennas Propag. 1998, 46, 650–656. [Google Scholar] [CrossRef]
- Martynyuk, A.E.; Lopez, J.I.M.; Martynyuk, N.A. Spiraphase-type reflectarrays based on loaded ring slot resonators. IEEE Trans. Antennas Propag. 2004, 52, 142–153. [Google Scholar] [CrossRef]
- Intel. Available online: https://software.intel.com/content/www/us/en/develop/documentation/mkl-developer-reference-fortran/top/lapack-routines/lapack-linear-equation-routines/lapack-linear-equation-computational-routines/estimating-the-condition-number-lapack-computational-routines/gecon.html (accessed on 9 November 2020).
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]


| 2Nx + 2 | CPU Time (s) |
|---|---|
| 32 | 19 |
| 64 | 47 |
| 128 | 278 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Florencio, R.; Somolinos, Á.; González, I.; Cátedra, F. Fast Preconditioner Computation for BICGSTAB-FFT Method of Moments with NURBS in Large Multilayer Structures. Electronics 2020, 9, 1938. https://doi.org/10.3390/electronics9111938
Florencio R, Somolinos Á, González I, Cátedra F. Fast Preconditioner Computation for BICGSTAB-FFT Method of Moments with NURBS in Large Multilayer Structures. Electronics. 2020; 9(11):1938. https://doi.org/10.3390/electronics9111938
Chicago/Turabian StyleFlorencio, Rafael, Álvaro Somolinos, Iván González, and Felipe Cátedra. 2020. "Fast Preconditioner Computation for BICGSTAB-FFT Method of Moments with NURBS in Large Multilayer Structures" Electronics 9, no. 11: 1938. https://doi.org/10.3390/electronics9111938
APA StyleFlorencio, R., Somolinos, Á., González, I., & Cátedra, F. (2020). Fast Preconditioner Computation for BICGSTAB-FFT Method of Moments with NURBS in Large Multilayer Structures. Electronics, 9(11), 1938. https://doi.org/10.3390/electronics9111938






