Systematic Study of the Influence of the Angle of Incidence Discretization in Reflectarray Analysis to Improve Support Vector Regression Surrogate Models
Abstract
1. Introduction
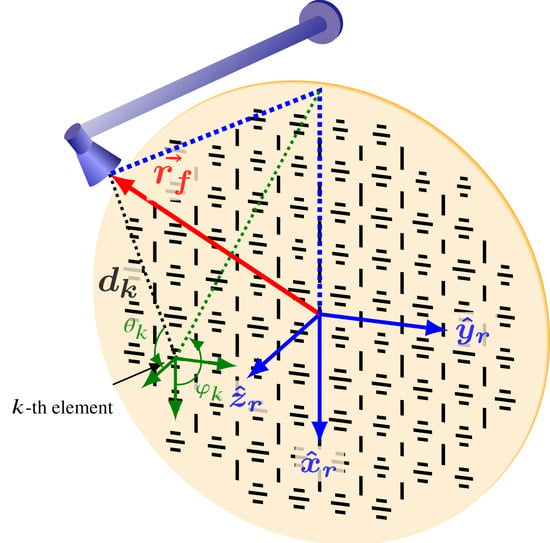
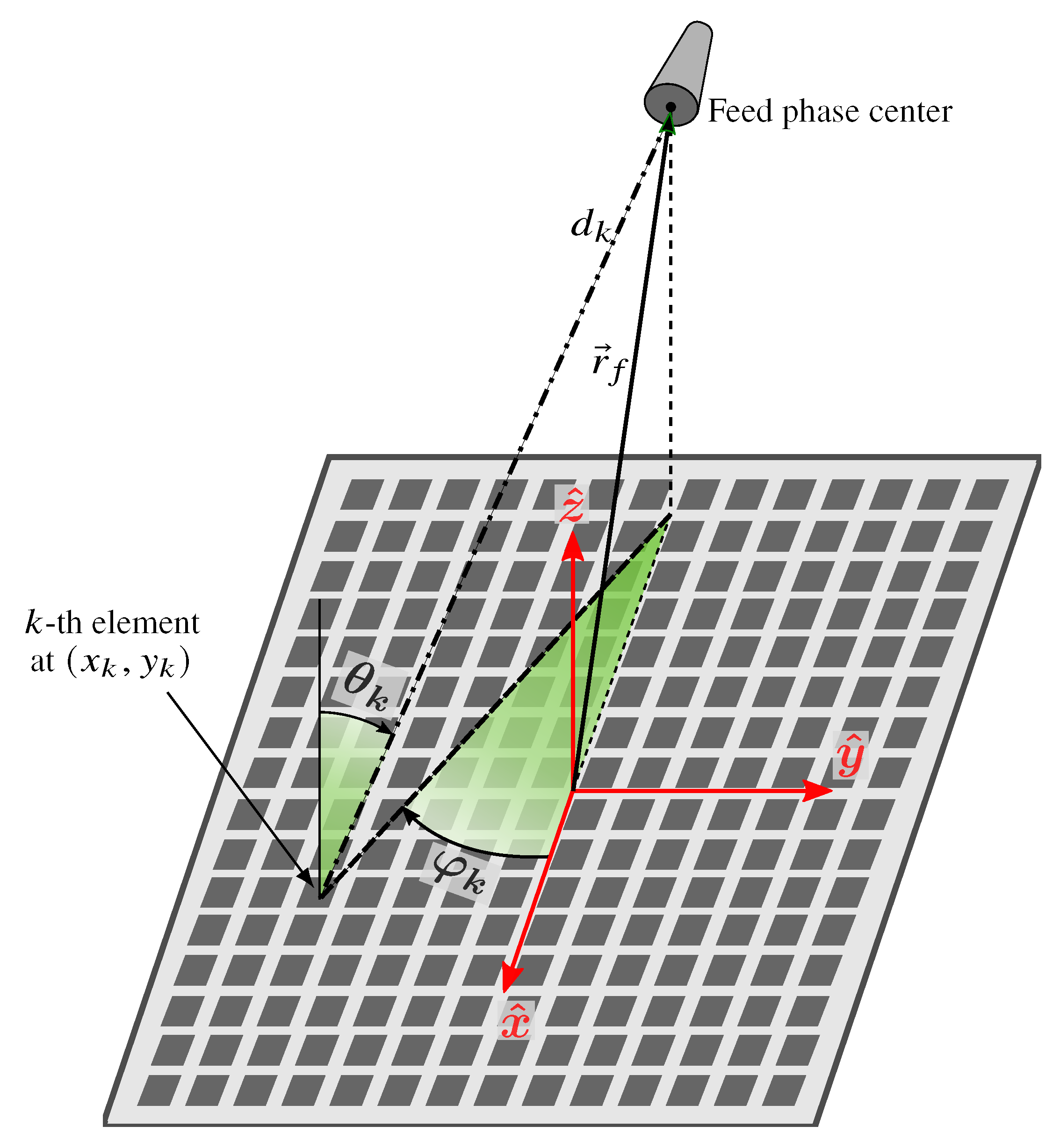
2. Problem Statement
3. Surrogate Modeling Based on SVR
3.1. Model Definition
3.2. Sources of Error in the Reflectarray Analysis Due to the SVR Modeling
4. Systematic Study of the Influence of the Discretization of the Angles of Incidence
4.1. Discretization of the Angles of Incidence
4.2. Testing Conditions for the Accuracy of the Discretizations
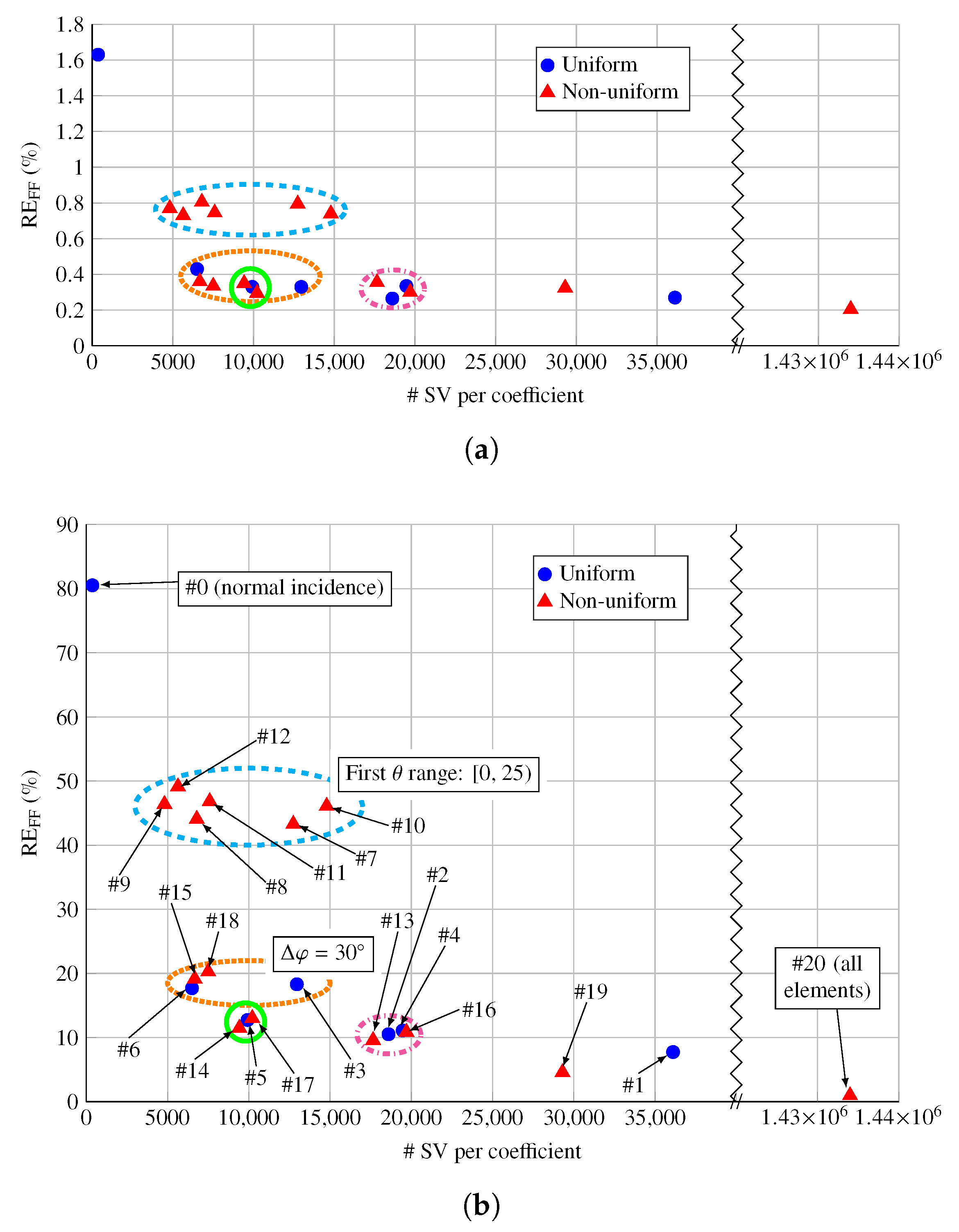
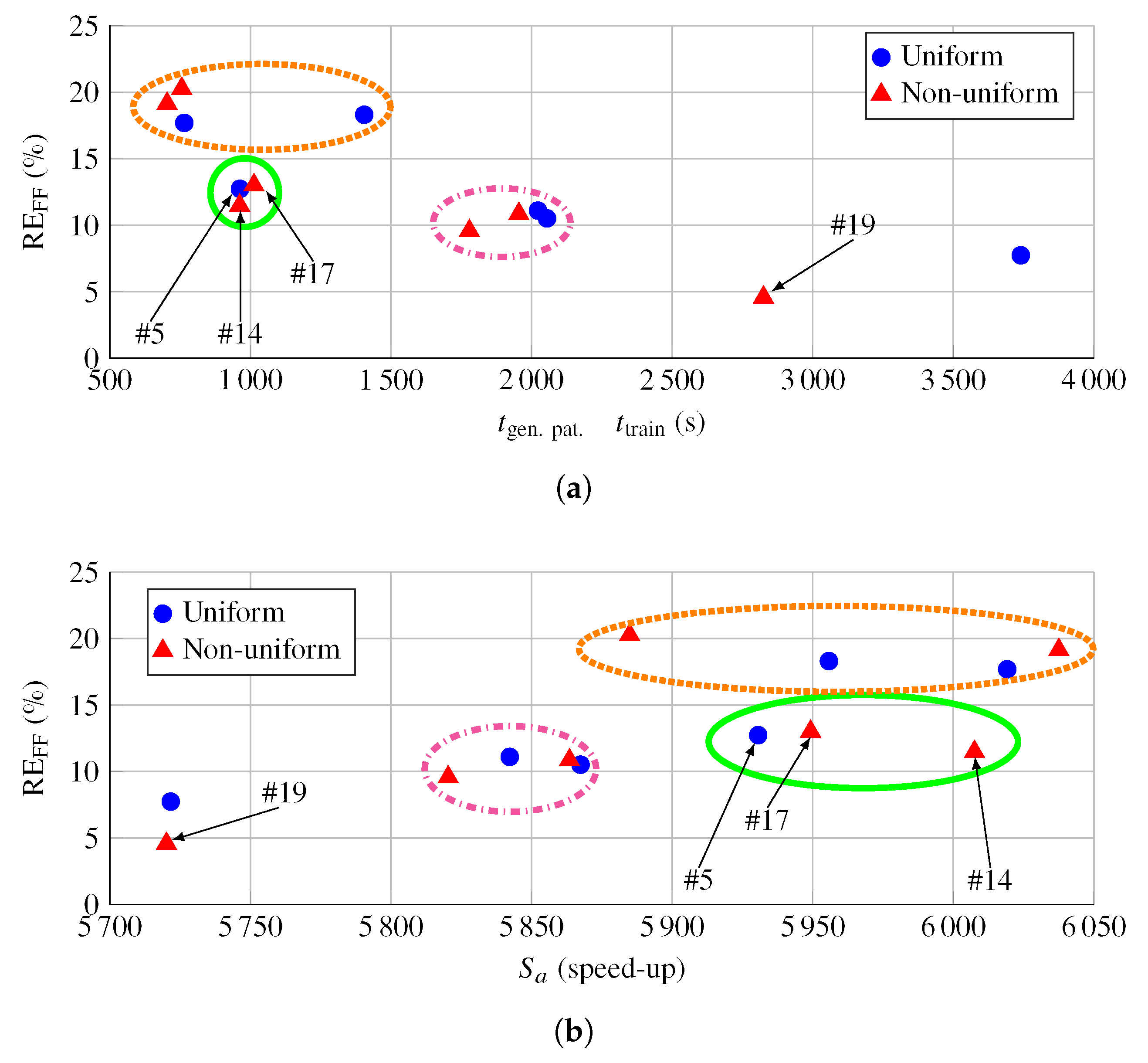
4.3. Analysis of the Results
4.4. Further Discussion
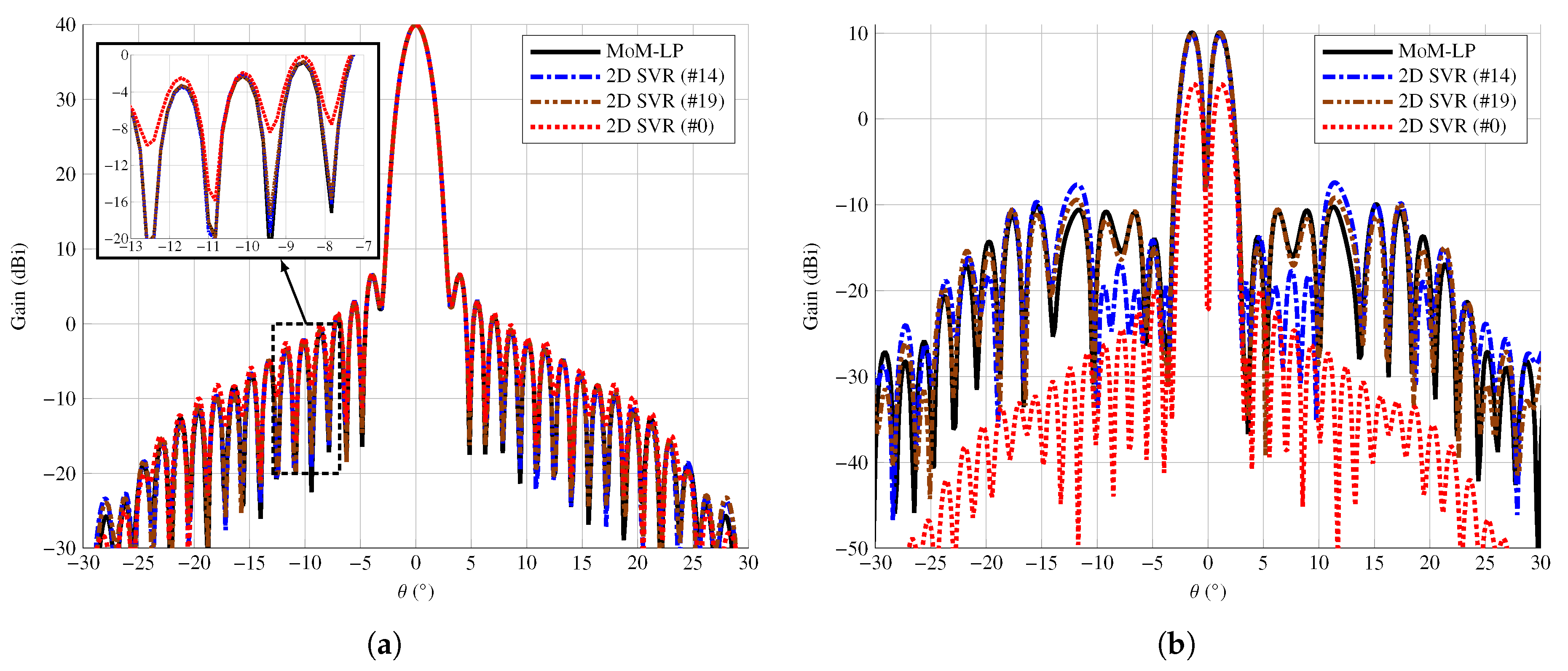
5. Effect of the Discretization on Several Radiation Patterns
- Pencil beam pattern in boresight direction.
- Shaped-beam reflectarray with a sectored beam pattern in azimuth and a squared-cosecant pattern in elevation. This radiation pattern presents a dynamic range in the coverage zone of almost 15 dB in elevation, where the copolar component has to smoothly decrease over an angular span of .
- Contoured beam with European coverage for direct-to-home (DTH) applications. This kind of application has very tight cross-polarization requirements. Thus, it is necessary to accurately predict the crosspolar pattern. This is the same radiation pattern considered in previous sections.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| CP | Copolar |
| DTH | Direct-to-home |
| FW-LP | Full-Wave analysis technique based on Local-Periodicity |
| MoM-LP | Method of Moments based on Local-Periodicity |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| XP | Crosspolar |
References
- Freni, A.; Mussetta, M.; Pirinoli, P. Neural network characterization of reflectarray antennas. Int. J. Antennas Propag. 2012, 2012, 1–10. [Google Scholar] [CrossRef]
- Robustillo, P.; Zapata, J.; Encinar, J.A.; Rubio, J. ANN Characterization of Multi-Layer Reflectarray Elements for Contoured-Beam Space Antennas in the Ku-Band. IEEE Trans. Antennas Propag. 2012, 60, 3205–3214. [Google Scholar] [CrossRef]
- Güneş, F.; Nesil, S.; Demirel, S. Design and Analysis of Minkowski Reflectarray Antenna Using 3-D CST Microwave Studio-Based Neural Network Model with Particle Swarm Optimization. Int. J. RF Microw. Comput. Eng. 2013, 23, 272–284. [Google Scholar] [CrossRef]
- Salucci, M.; Tenuti, L.; Oliveri, G.; Massa, A. Efficient Prediction of the EM Response of Reflectarray Antenna Elements by an Advanced Statistical Learning Method. IEEE Trans. Antennas Propag. 2018, 66, 3995–4007. [Google Scholar] [CrossRef]
- Prado, D.R.; López-Fernández, J.A.; Barquero, G.; Arrebola, M.; Las-Heras, F. Fast and Accurate Modeling of Dual-Polarized Reflectarray Unit Cells Using Support Vector Machines. IEEE Trans. Antennas Propag. 2018, 66, 1258–1270. [Google Scholar] [CrossRef]
- Shi, L.P.; Zhang, Q.H.; Zhang, S.H.; Liu, G.X.; Yi, C. Application of Machine Learning Method to the Prediction of EM Response of Reflectarray Antenna Elements. In Proceedings of the 2019 Photonics & Electromagnetics Research Symposium-Fall (PIERS-Fall), Xiamen, China, 17–20 December 2019; pp. 2671–2676. [Google Scholar] [CrossRef]
- Pozar, D.M.; Targonski, S.D.; Syrigos, H.D. Design of millimeter wave microstrip reflectarrays. IEEE Trans. Antennas Propag. 1997, 45, 287–296. [Google Scholar] [CrossRef]
- Huang, J.; Encinar, J.A. Reflectarray Antennas; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Johansson, F.S. A new planar grating-reflector antenna. IEEE Trans. Antennas Propag. 1990, 38, 1491–1495. [Google Scholar] [CrossRef]
- Cervellera, C.; Maccio, D. Learning With Kernel Smoothing Models and Low-Discrepancy Sampling. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 504–509. [Google Scholar] [CrossRef]
- Chaharmir, M.R.; Shaker, J.; Legay, H. Broadband Design of a Single Layer Large Reflectarray Using Multi Cross Loop Elements. IEEE Trans. Antennas Propag. 2009, 57, 3363–3366. [Google Scholar] [CrossRef]
- Xue, F.; Wang, H.J.; Yi, M.; Liu, G.; Dong, X.C. Design of a Broadband Single-Layer Linearly Polarized Reflectarray Using Four-Arm Spiral Elements. IEEE Antennas Wireless Propag. Lett. 2017, 16, 696–699. [Google Scholar] [CrossRef]
- Nayeri, P.; Yang, F.; Elsherbeni, A.Z. Design of Single-Feed Reflectarray Antennas With Asymmetric Multiple Beams Using the Particle Swarm Optimization Method. IEEE Trans. Antennas Propag. 2013, 61, 4598–4605. [Google Scholar] [CrossRef]
- Prado, D.R.; López-Fernández, J.A.; Arrebola, M.; Goussetis, G. Support Vector Regression to Accelerate Design and Crosspolar Optimization of Shaped-Beam Reflectarray Antennas for Space Applications. IEEE Trans. Antennas Propag. 2019, 67, 1659–1668. [Google Scholar] [CrossRef]
- Prado, D.R.; López-Fernández, J.A.; Arrebola, M.; Goussetis, G. On the Use of the Angle of Incidence in Support Vector Regression Surrogate Models for Practical Reflectarray Design. IEEE Trans. Antennas Propag. 2020. [Google Scholar] [CrossRef]
- Prado, D.R.; Arrebola, M.; Pino, M.R.; Florencio, R.; Boix, R.R.; Encinar, J.A.; Las-Heras, F. Efficient Crosspolar Optimization of Shaped-Beam Dual-Polarized Reflectarrays Using Full-Wave Analysis for the Antenna Element Characterization. IEEE Trans. Antennas Propag. 2017, 65, 623–635. [Google Scholar] [CrossRef]
- Pozar, D.M.; Metzler, T.A. Analysis of a reflectarray antenna using microstrip patches of variable size. Electron. Lett. 1993, 29, 657–658. [Google Scholar] [CrossRef]
- Encinar, J.A.; Arrebola, M.; Dejus, M.; Jouve, C. Design of a 1-metre reflectarray for DBS application with 15% bandwidth. In Proceedings of the First European Conference on Antennas and Propagation (EuCAP), Nice, France, 6–10 November 2006; pp. 1–5. [Google Scholar] [CrossRef]
- Pozar, D.M.; Targonski, S.D.; Pokuls, R. A shaped-beam microstrip patch reflectarray. IEEE Trans. Antennas Propag. 1999, 47, 1167–1173. [Google Scholar] [CrossRef]
- Encinar, J.A. Design of a dual frequency reflectarray using microstrip stacked patches of variable size. Electron. Lett. 1996, 32, 1049–1050. [Google Scholar] [CrossRef]
- Encinar, J.A. Design of two-layer printed reflectarrays using patches of variable size. IEEE Trans. Antennas Propag. 2001, 49, 1403–1410. [Google Scholar] [CrossRef]
- Headland, D.; Carrascoo, E.; Nirantar, S.; Withayachumnankul, W.; Gutruf, P.; Schwarz, J.; Abbott, D.; Bhaskaran, M.; Sriram, S.; Perruisseau-Carrier, J.; et al. Dielectric Resonator Reflectarray as High-Efficiency Nonuniform Terahertz Metasurface. ACS Photonics 2016, 3, 1019–1026. [Google Scholar] [CrossRef]
- Zhou, M.; Sørensen, S.B.; Kim, O.S.; Jørgensen, E.; Meincke, P.; Breinbjerg, O. Direct Optimization of Printed Reflectarrays for Contoured Beam Satellite Antenna Applications. IEEE Trans. Antennas Propag. 2013, 61, 1995–2004. [Google Scholar] [CrossRef]
- Imaz-Lueje, B.; Prado, D.R.; Arrebola, M.; Pino, M.R. Reflectarray antennas: A smart solution for new generation satellite mega-constellations in space communications. Sci. Rep. 2020. [Google Scholar] [CrossRef]
- Vaquero, A.F.; Arrebola, M.; Pino, M.R.; Florencio, R.; Encinar, J.A. Demonstration of a Reflectarray with Near-field Amplitude and Phase Constraints as Compact Antenna Test Range Probe for 5G New Radio Devices. IEEE Trans. Antennas Propag. 2020. [Google Scholar] [CrossRef]
- Prado, D.R.; Arrebola, M.; Pino, M.R.; Goussetis, G. Contoured-Beam Dual-Band Dual-Linear Polarized Reflectarray Design Using a Multi-Objective Multi-Stage Optimization. IEEE Trans. Antennas Propag. 2020, 68, 7682–7687. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27:1–27:27. Available online: https://www.csie.ntu.edu.tw/~cjlin/libsvm (accessed on 24 September 2020). [CrossRef]
- Florencio, R.; Boix, R.R.; Encinar, J.A. Enhanced MoM Analysis of the Scattering by Periodic Strip Gratings in Multilayered Substrates. IEEE Trans. Antennas Propag. 2013, 61, 5088–5099. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels, 1st ed.; The MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Platt, J.C. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines; Technical Report MSR-TR-98-14; Microsoft Research: Redmond, WA, USA, 1998. [Google Scholar]
- Prado, D.R.; López-Fernández, J.A.; Arrebola, M.; Pino, M.R.; Goussetis, G. General Framework for the Efficient Optimization of Reflectarray Antennas for Contoured Beam Space Applications. IEEE Access 2018, 6, 72295–72310. [Google Scholar] [CrossRef]
- Prado, D.R.; López-Fernández, J.A.; Arrebola, M.; Pino, M.R.; Goussetis, G. Wideband Shaped-Beam Reflectarray Design Using Support Vector Regression Analysis. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2287–2291. [Google Scholar] [CrossRef]





| Unit Cell | Frequency | Periodicity | Substrate Characteristics | ||
|---|---|---|---|---|---|
| Relative Permittivity | Loss Tangent | Thickness | |||
| Figure 3a | 28 GHz | 4.29 mm | |||
| () | |||||
| Figure 3b | 17 GHz | 8.82 mm | |||
| () | |||||
| Figure 3c | 29 GHz | 5.0 mm | |||
| () | |||||
| Figure 3d | 11.85 GHz | 12.0 mm | |||
| () | |||||
| # | Type | () | Set () | () | Pairs |
|---|---|---|---|---|---|
| 0 | NI | - | {0} | - | 1 |
| 1 | U | 5 | {2, 7, 12, 17, 22, 27, 32, 37} | 10 | 190 |
| 2 | U | 5 | {2, 7, 12, 17, 22, 27, 32, 37} | 20 | 98 |
| 3 | U | 5 | {2, 7, 12, 17, 22, 27, 32, 37} | 30 | 68 |
| 4 | U | 10 | {5, 15, 25, 35} | 10 | 102 |
| 5 | U | 10 | {5, 15, 25, 35} | 20 | 52 |
| 6 | U | 10 | {5, 15, 25, 35} | 30 | 34 |
| 7 | NU | - | {12, 29, 36} | 10 | 64 |
| 8 | NU | - | {12, 29, 36} | 20 | 34 |
| 9 | NU | - | {12, 29, 36} | 30 | 24 |
| 10 | NU | - | {12, 27, 32, 37} | 10 | 74 |
| 11 | NU | - | {12, 27, 32, 37} | 20 | 38 |
| 12 | NU | - | {12, 27, 32, 37} | 30 | 28 |
| 13 | NU | - | {7, 20, 29, 36} | 10 | 90 |
| 14 | NU | - | {7, 20, 29, 36} | 20 | 52 |
| 15 | NU | - | {7, 20, 29, 36} | 30 | 34 |
| 16 | NU | - | {7, 20, 27, 32, 37} | 10 | 100 |
| 17 | NU | - | {7, 20, 27, 32, 37} | 20 | 52 |
| 18 | NU | - | {7, 20, 27, 32, 37} | 30 | 38 |
| 19 | NU | - | {5, 10, 17, 23, 29, 35, 40} | 10 | 152 |
| 20 | NU | Surrogate models for all reflectarray elements | 7052 | ||
| SVR | Variable | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| #14 | −81.7 | −82.0 | −38.1 | −38.5 | −39.2 | −38.6 | −38.3 | −38.4 | −38.6 | −38.7 | |
| #19 | −82.4 | −82.5 | −38.1 | −38.5 | −39.2 | −38.7 | −38.2 | −38.3 | −38.6 | −38.7 | |
| #14 | 645 | 689 | 1 019 | 1 027 | 916 | 978 | 990 | 1 192 | 838 | 961 | |
| #19 | 1 833 | 2 122 | 3 067 | 3 175 | 2 799 | 3 044 | 2 985 | 3 586 | 2 457 | 2 823 |
| Discretization | Pencil Beam | Shaped-Beam | Contoured-Beam | |||
|---|---|---|---|---|---|---|
| CP | XP | CP | XP | CP | XP | |
| #0 | 1.02 | 78.13 | 2.54 | 82.18 | 1.63 | 80.52 |
| #14 | 0.11 | 7.20 | 0.91 | 8.32 | 0.36 | 11.54 |
| #19 | 0.21 | 2.14 | 0.91 | 3.47 | 0.51 | 4.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prado, D.R.; López-Fernández, J.A.; Arrebola, M. Systematic Study of the Influence of the Angle of Incidence Discretization in Reflectarray Analysis to Improve Support Vector Regression Surrogate Models. Electronics 2020, 9, 2105. https://doi.org/10.3390/electronics9122105
Prado DR, López-Fernández JA, Arrebola M. Systematic Study of the Influence of the Angle of Incidence Discretization in Reflectarray Analysis to Improve Support Vector Regression Surrogate Models. Electronics. 2020; 9(12):2105. https://doi.org/10.3390/electronics9122105
Chicago/Turabian StylePrado, Daniel R., Jesús A. López-Fernández, and Manuel Arrebola. 2020. "Systematic Study of the Influence of the Angle of Incidence Discretization in Reflectarray Analysis to Improve Support Vector Regression Surrogate Models" Electronics 9, no. 12: 2105. https://doi.org/10.3390/electronics9122105
APA StylePrado, D. R., López-Fernández, J. A., & Arrebola, M. (2020). Systematic Study of the Influence of the Angle of Incidence Discretization in Reflectarray Analysis to Improve Support Vector Regression Surrogate Models. Electronics, 9(12), 2105. https://doi.org/10.3390/electronics9122105