Aspects of Efficiency Enhancement in Reflectarrays with Analytical Investigation and Accurate Measurement
Abstract
1. Introduction
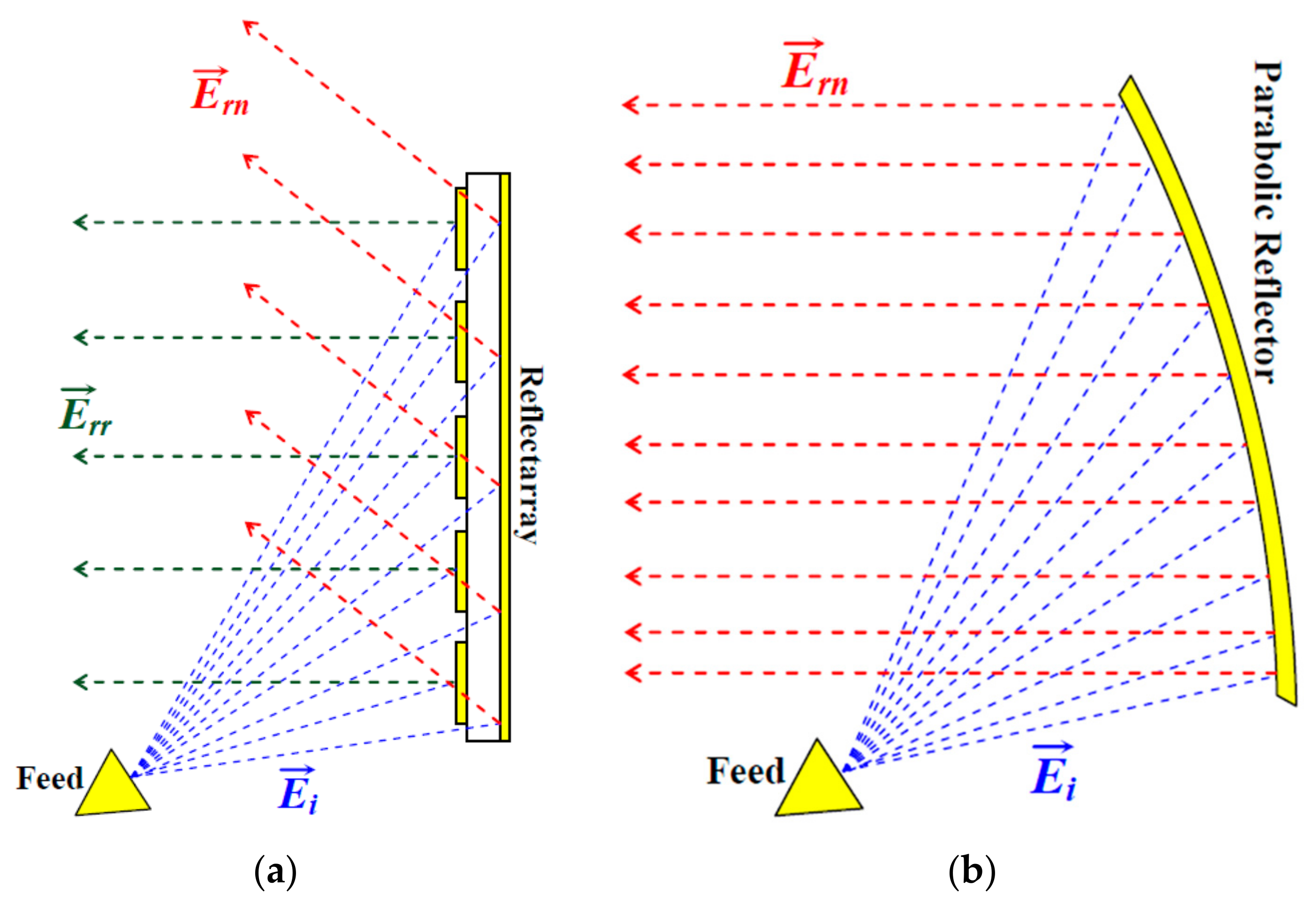
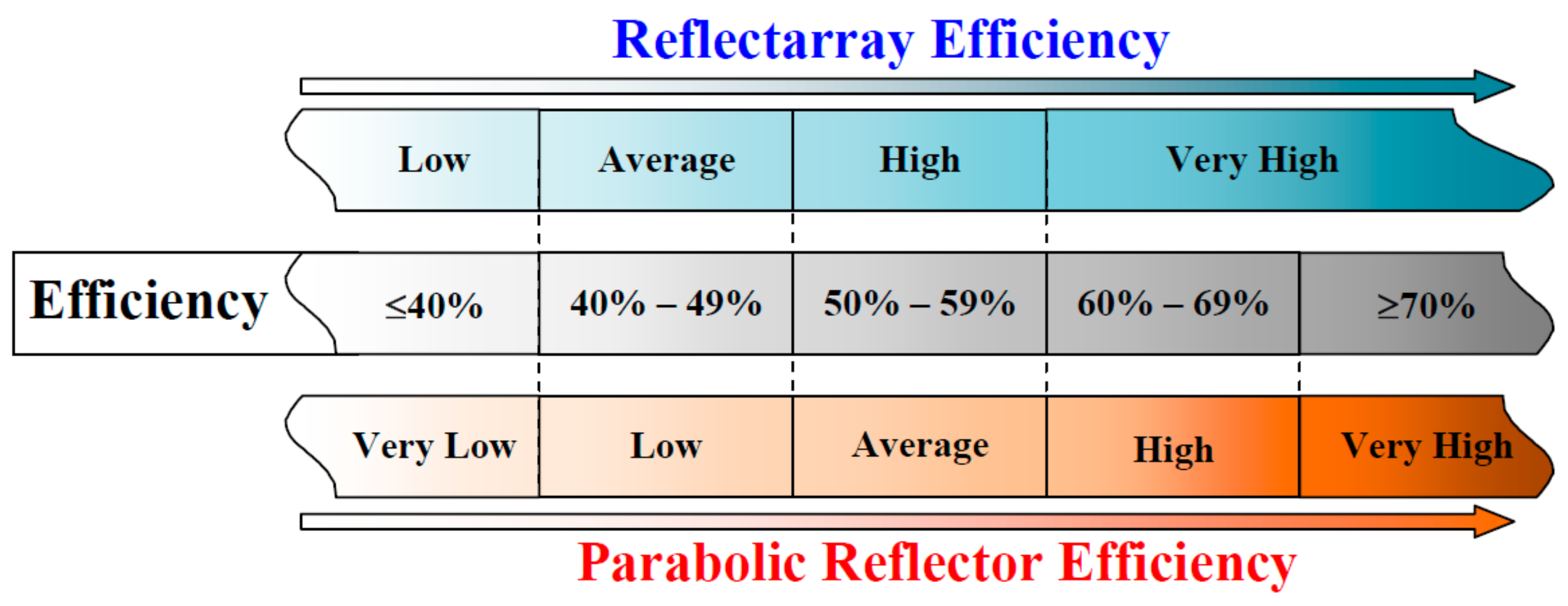
2. Loss Quantification of Reflectarray Antenna
3. Background of the Common Techniques of Efficiency Improvement in Reflectarrays
3.1. Elements with Low Loss and Wide Reflection Phase Range
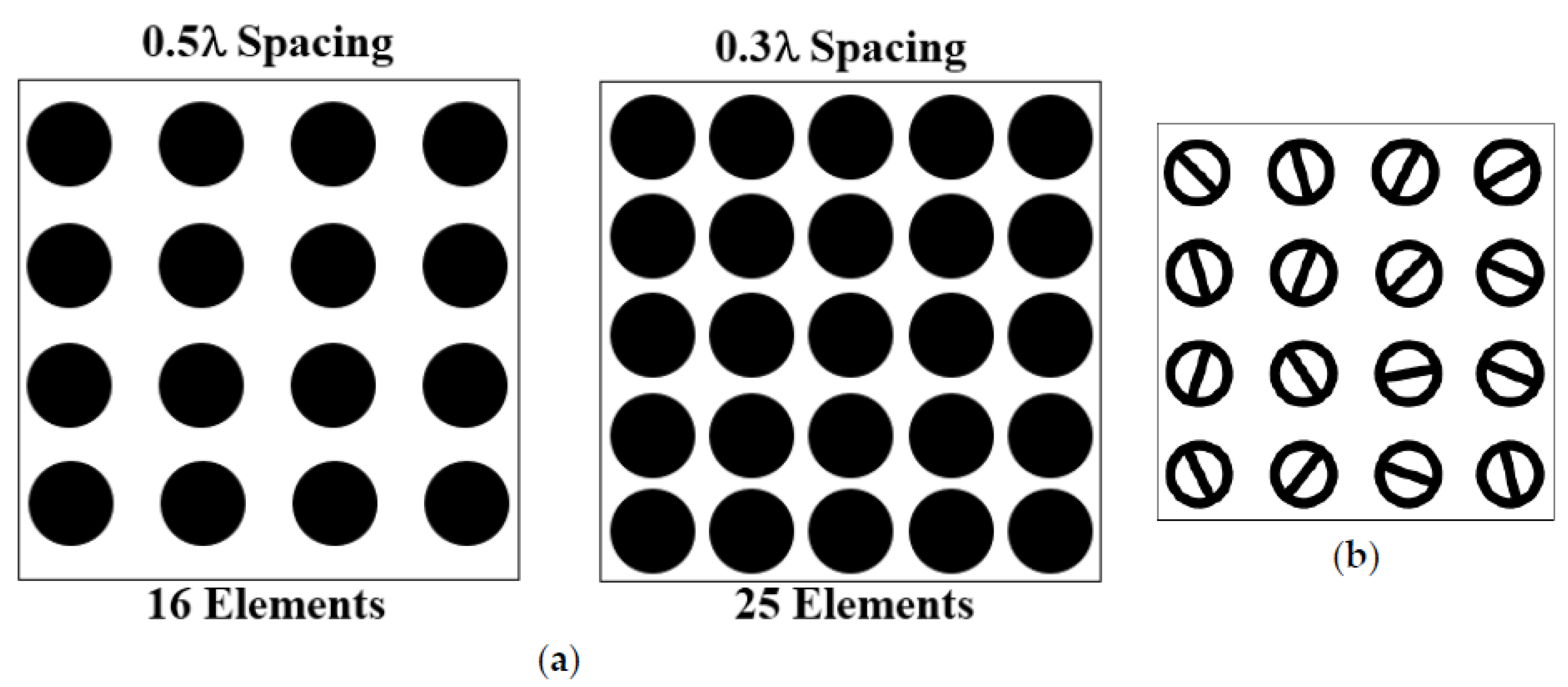
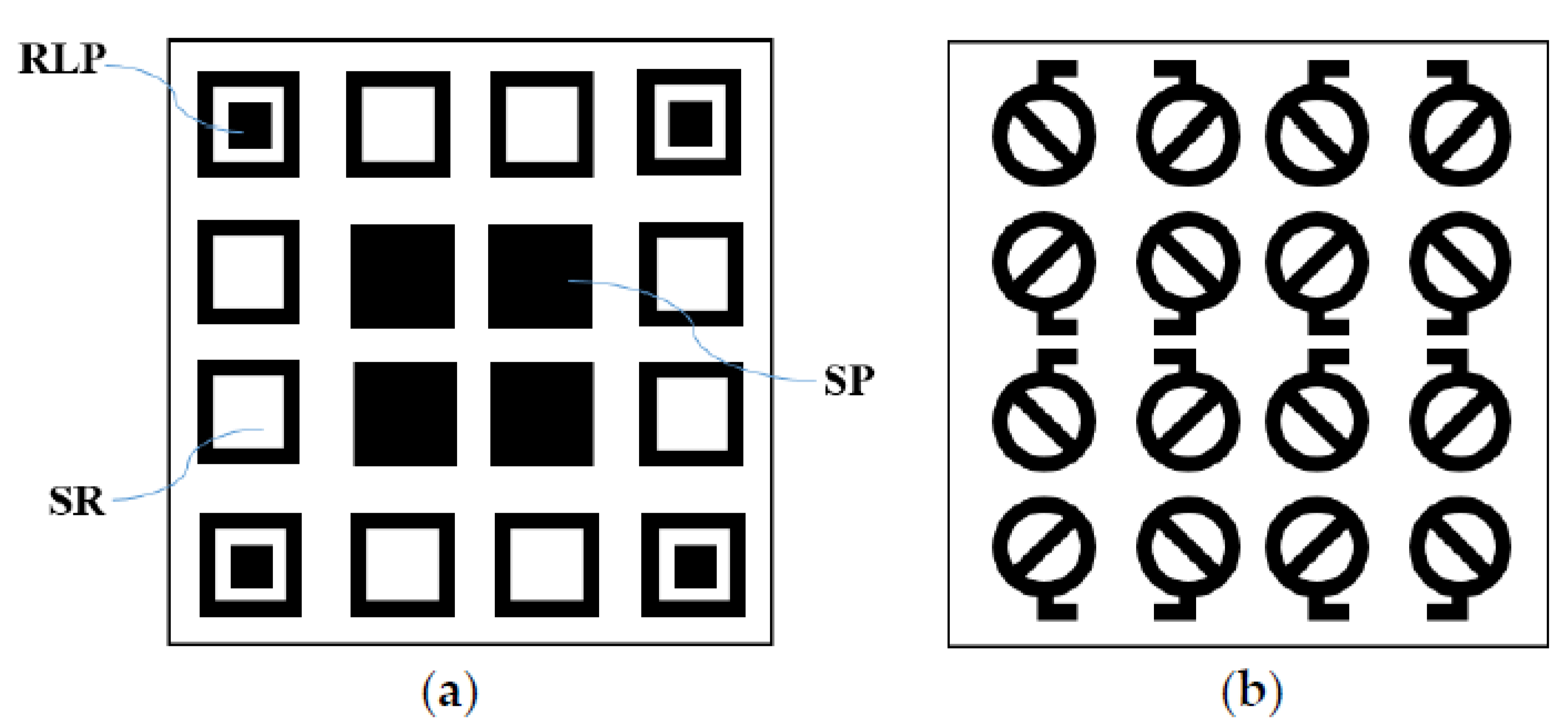
3.2. Sub-Wavelength Elements for Loss Reduction
3.3. Strategic Feeding Mechanism for Aperture Loss Reduction
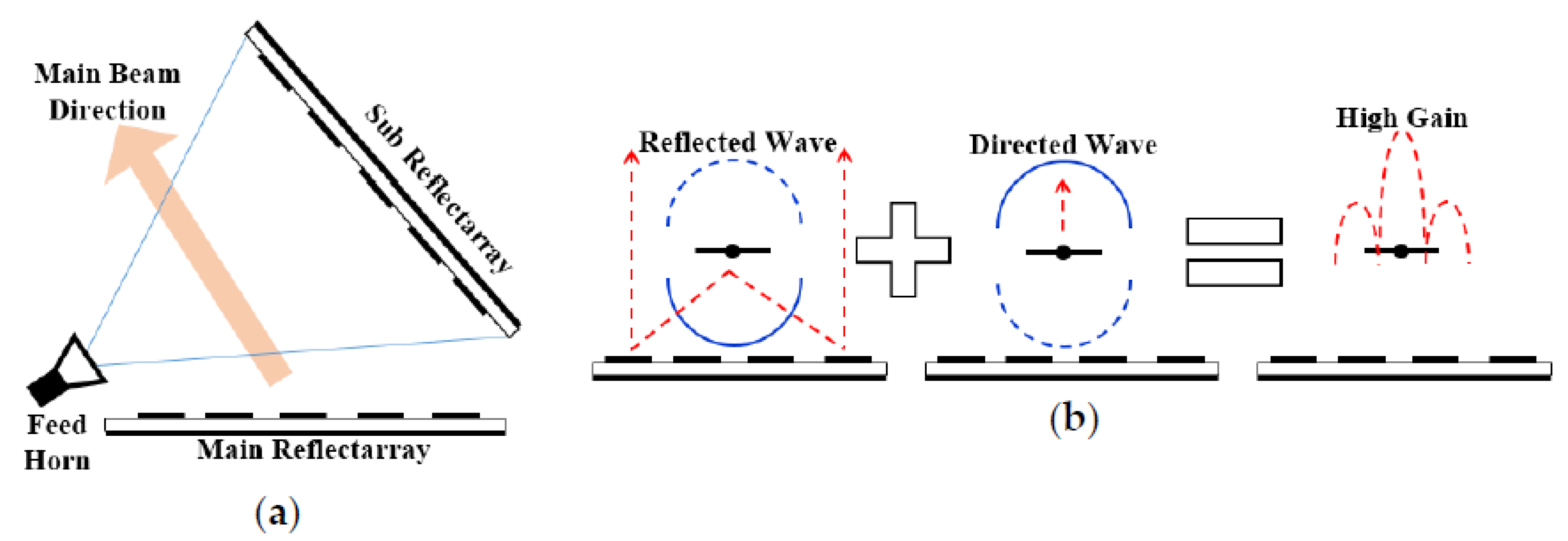
3.4. Some Advanced Types of Reflectarray
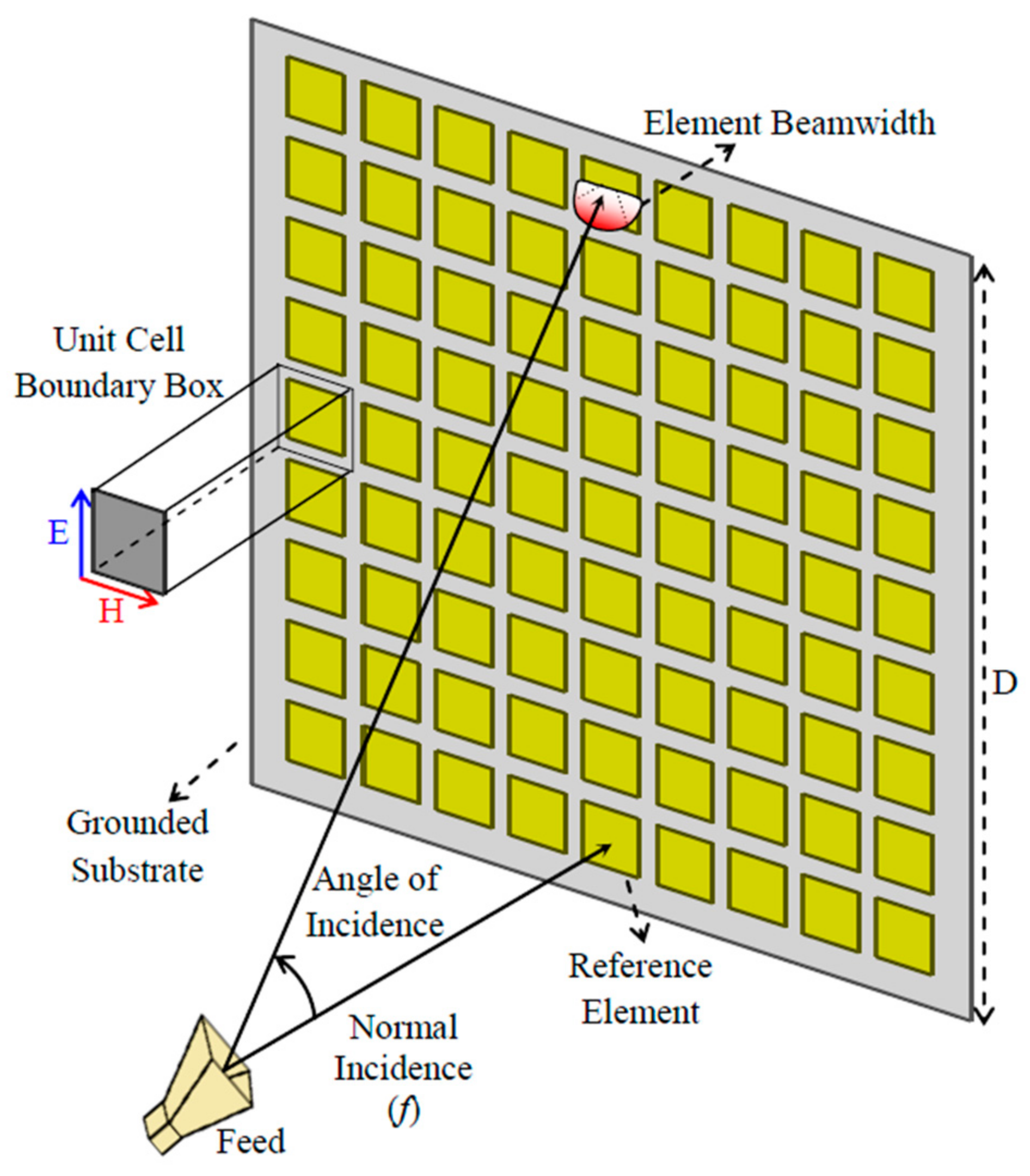
4. Factors Affecting the Aperture Efficiency of the Circular Aperture Reflectarray Antenna
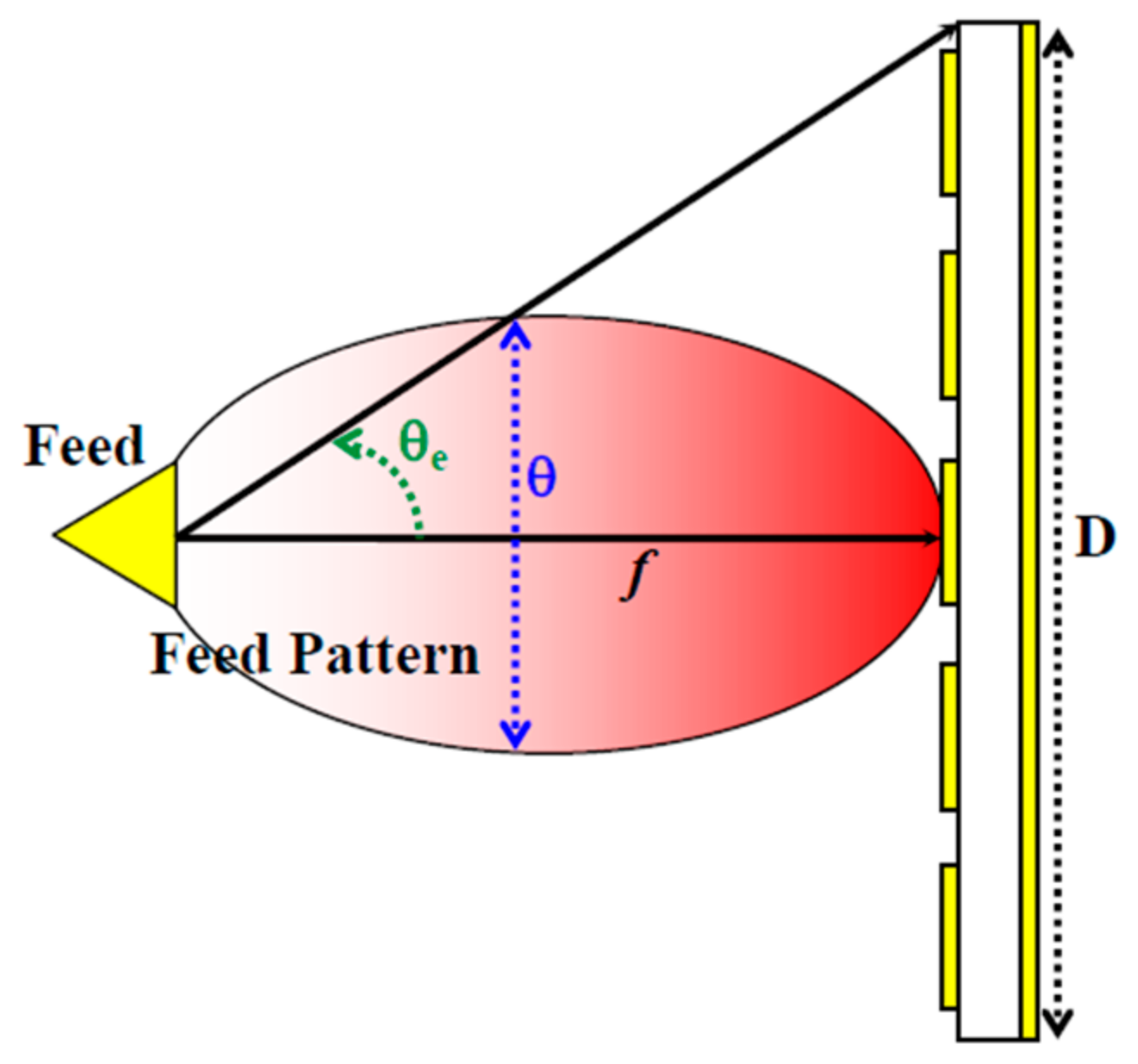
4.1. Effects of Different Feeds on the Aperture Efficiency
4.2. The Effect of Different Feed Distances on the Aperture Efficiency
4.3. The Effect of the Feed Footprint on the Aperture Efficiency
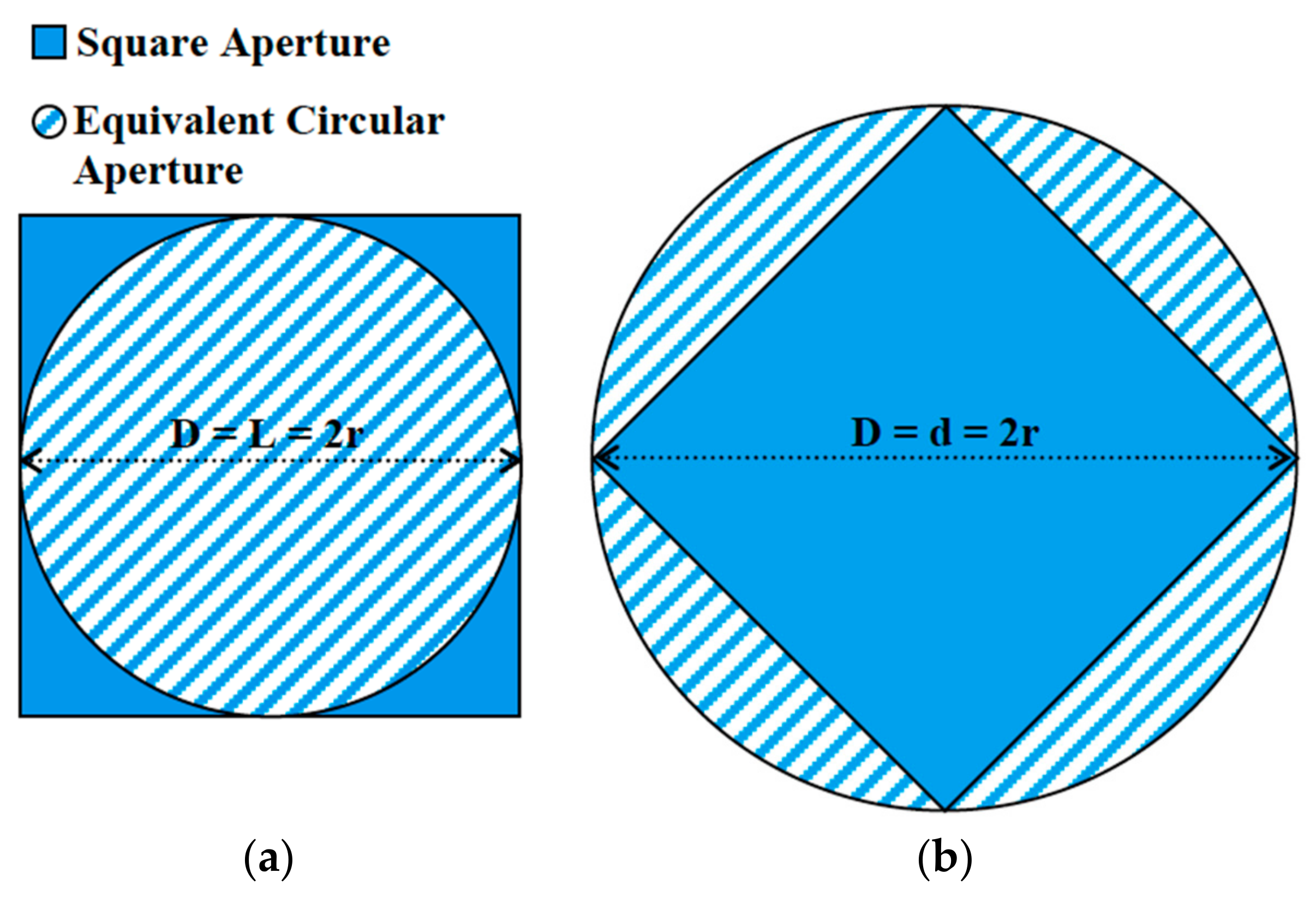
5. Aperture Efficiency of the Square Aperture Reflectarray Antenna
5.1. Aperture Efficiency of the Conventional Square Aperture
5.2. Aperture Efficiency of the Square Aperture in a Diamond Shape
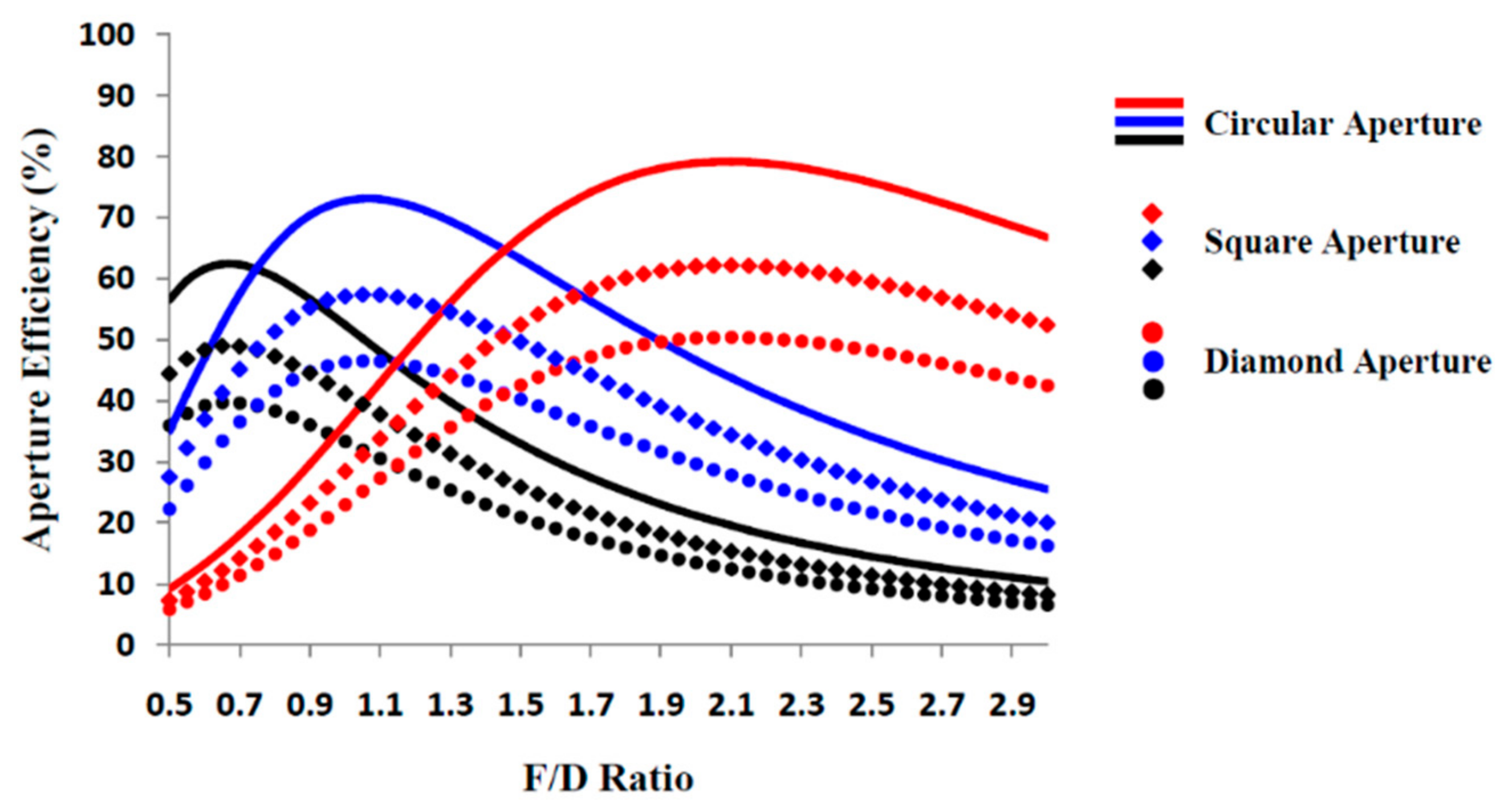
5.3. Aperture Efficiency Comparison between Circular and Square Aperture Reflectarrays
6. A Practical Method to Accurately Predict and Measure the Efficiency of a Reflectarray Antenna
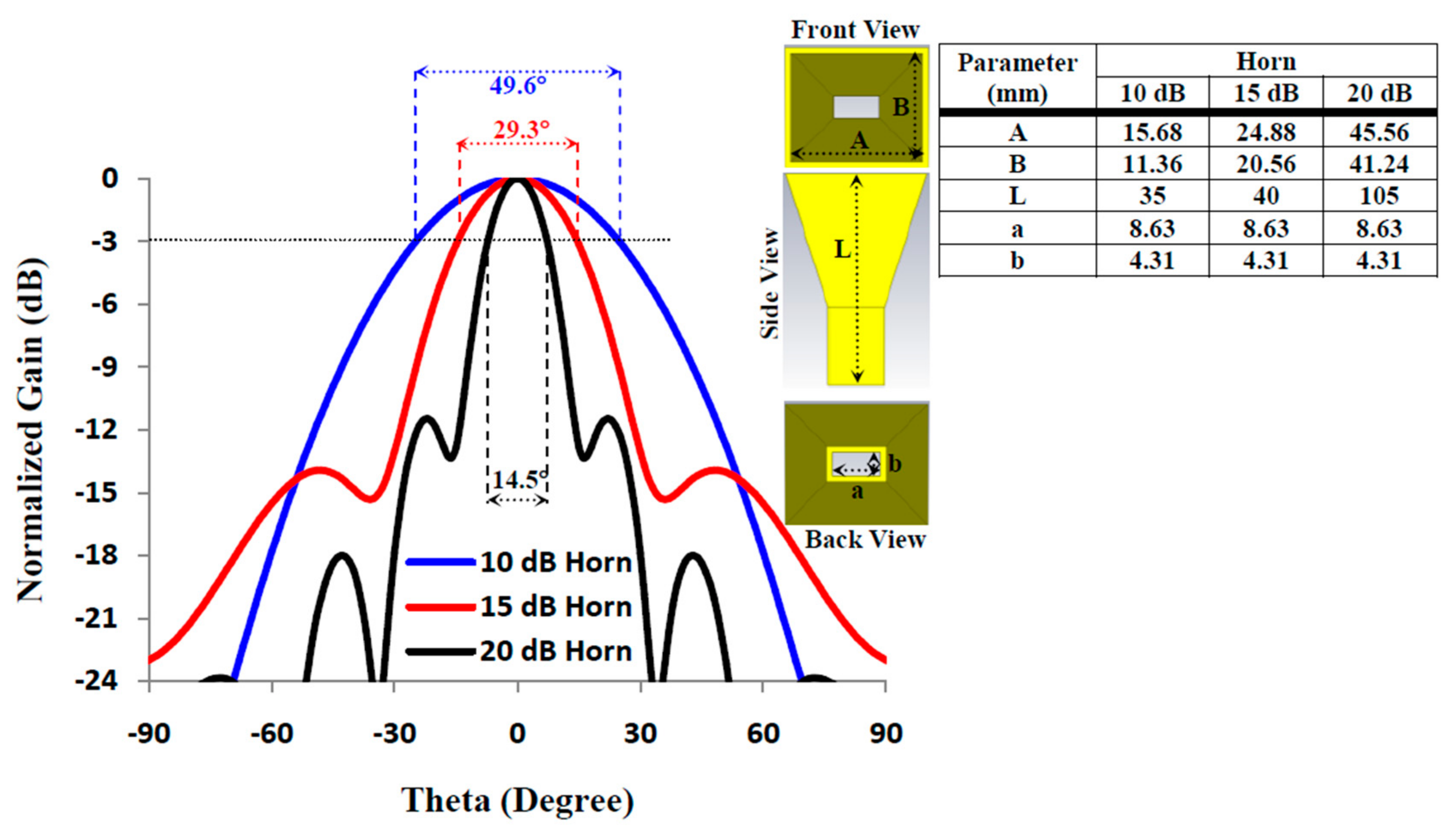
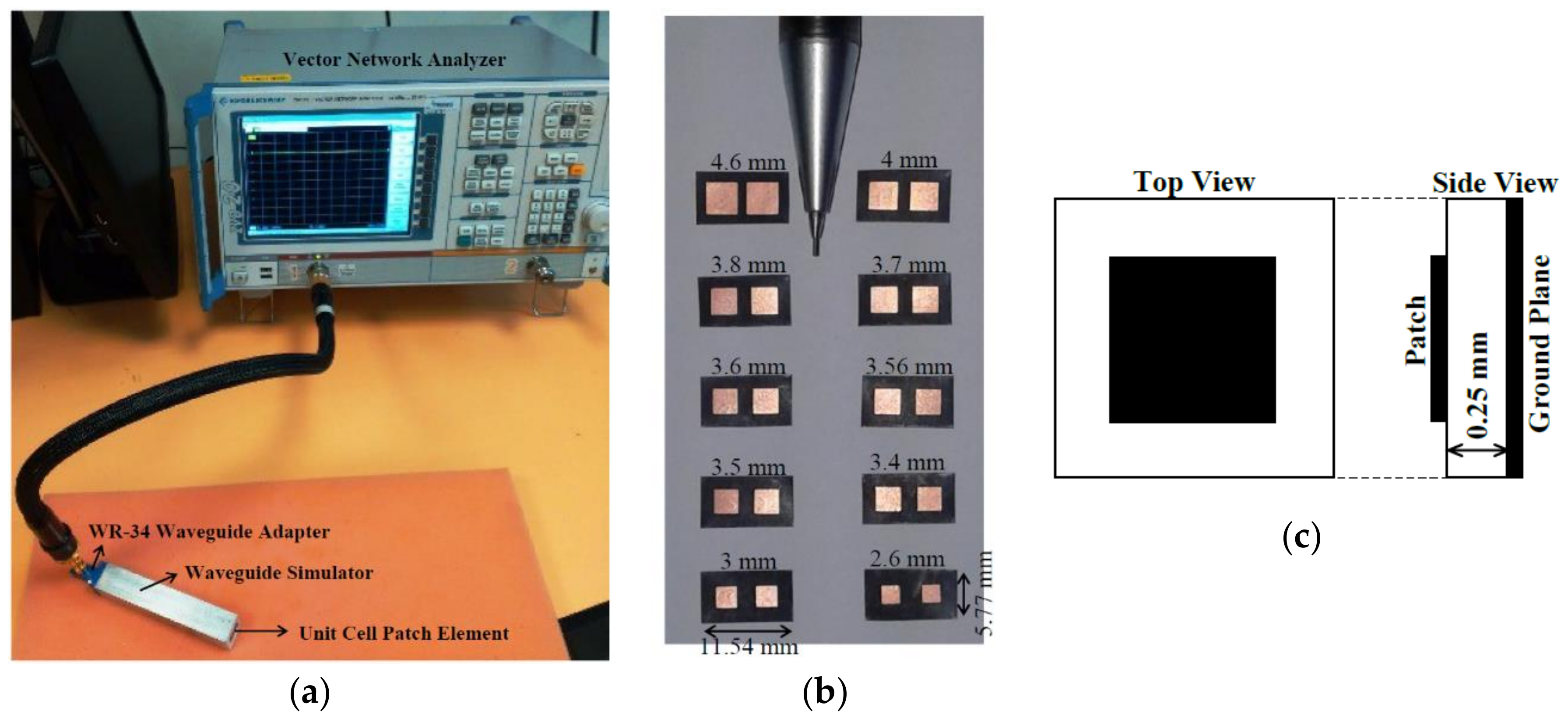
6.1. Design and Analysis of the Pyramidal Horn Feed
6.2. Design Characteristics of the Unit Cell Patch Element
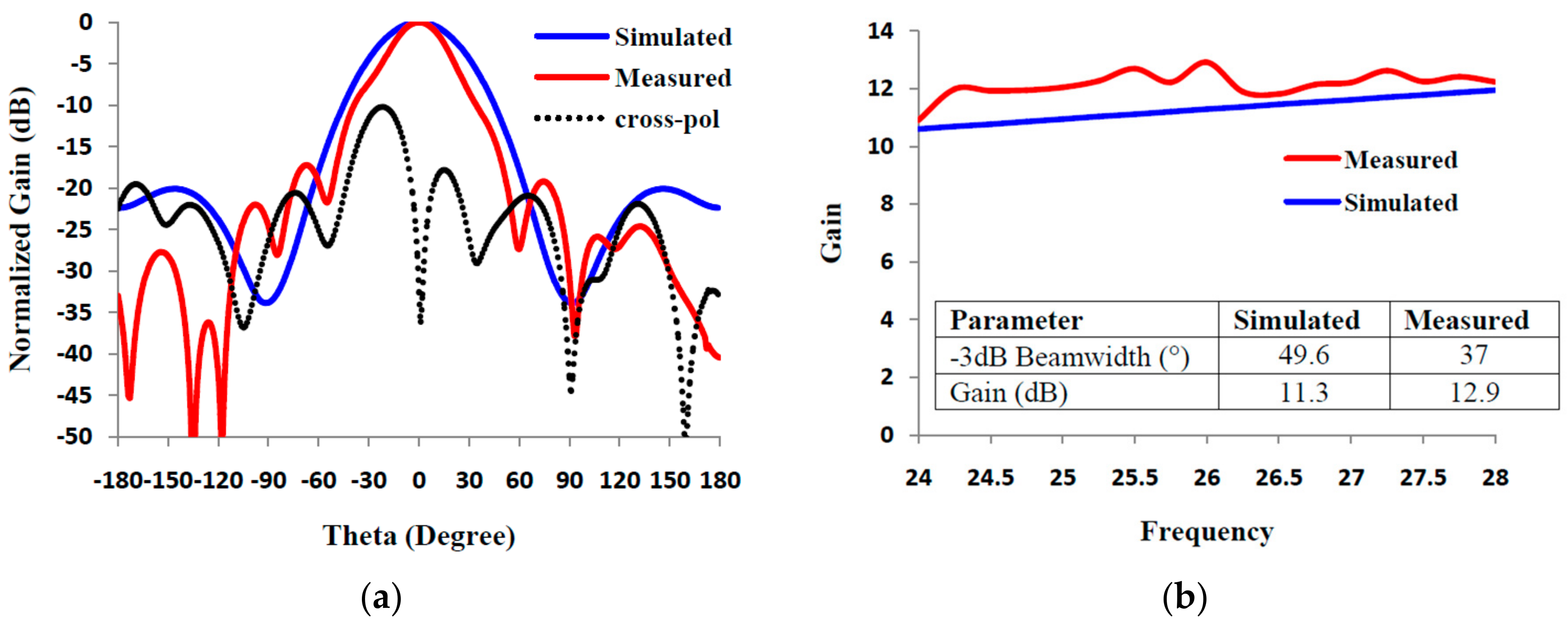
6.3. Design and Validation of the Circular and Square Aperture Reflectarrays
6.4. Efficiency Prediction by Gain-Directivity Relation
6.5. Efficiency Prediction by Loss Quantification
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pozar, D.M.; Metzler, T.A. Analysis of a reflectarray antenna using microstrip patches of variable size. Electron. Lett. 1993, 29, 657–658. [Google Scholar] [CrossRef]
- Inam, M.; Dahri, M.H.; Jamaluddin, M.H.; Seman, N.; Kamarudin, M.R.; Sulaiman, N.H. Design and characterization of millimeter wave planar reflectarray antenna for 5G communication systems. Int. J. RF Microw. Comput. Eng. 2019, 29, 29. [Google Scholar] [CrossRef]
- Huang, J.; Encinar, J. Reflectarray Antennas; Wiley Inter Science: Hoboken, NJ, USA, 2007. [Google Scholar]
- Hashim Dahri, M.; Jamaluddin, M.H.; Khalily, M.; Abbasi, M.I.; Selvaraju, R.; Kamarudin, M.R. Polarization Diversity and Adaptive Beamsteering for 5G Reflectarrays: A Review. IEEE Access 2018, 6, 19451–19464. [Google Scholar] [CrossRef]
- Berry, D.C.; Malech, R.G.; Kennedy, W.A. The reflectarray antenna. IEEE Trans. Antennas Propag. 1963, 11, 645–651. [Google Scholar] [CrossRef]
- Yi, M.; Lee, W.; Yoon, Y.J.; So, J. Non-resonant conductor reflectarray element for linear reflection phase. Electron. Lett. 2015, 51, 669–671. [Google Scholar]
- Abd-Elhady, M.; Hong, W.; Zhang, Y. A Ka-band reflectarray implemented with a single-layer perforated dielectric substrate. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 600–603. [Google Scholar] [CrossRef]
- Mei, P.; Zhang, S.; Pedersen, G.F. A Low-Cost, High-Efficiency and Full-Metal Reflectarray Antenna with Mechanically 2-D Beam-Steerable Capabilities for 5G Applications. IEEE Trans. Antennas Propag. 2020, 68, 6997–7006. [Google Scholar] [CrossRef]
- Abbasi, M.I.; Dahri, M.H.; Jamaluddin, M.H.; Seman, N.; Kamarudin, M.R.; Sulaiman, N.H. Millimeter Wave Beam Steering Reflectarray Antenna Based on Mechanical Rotation of Array. IEEE Access 2019, 7, 145685–145691. [Google Scholar] [CrossRef]
- Huang, J.; Pogorzelski, R. A Ka-band microstrip reflectarray with elements having variable rotation angles. IEEE Trans. Antennas Propag. 1998, 46, 650–656. [Google Scholar] [CrossRef]
- Florencio, R.; Martínez-De-rioja, D.; Martínez-De-rioja, E.; Encinar, J.A.; Boix, R.R.; Losada, V. Design of ku-and ka-band flat dual circular polarized reflectarrays by combining variable rotation technique and element size variation. Electronics 2020, 9, 985. [Google Scholar] [CrossRef]
- Ismail, M.Y.; Inam, M. Resonant Elements for Tunable Reflectarray Antenna Design. Int. J. Antennas Propag. 2012, 2012, 1–6. [Google Scholar] [CrossRef]
- Chang, D.-C.; Huang, M.-C. Multiple-polarization microstrip reflectarray antenna with high efficiency and low cross-polarization. IEEE Trans. Antennas Propag. 1995, 43, 829–834. [Google Scholar] [CrossRef]
- Costanzo, S.; Member, S.; Venneri, F.; Borgia, A.; Massa, G.D.I.; Member, L.S. Dual-Band Dual-Linear Polarization Reflectarray for mmWaves/5G Applications. IEEE Access 2020, 8, 78183–78192. [Google Scholar] [CrossRef]
- Jamaluddin, M.H.; Gillard, R.; Sauleau, R.; Milon, M.-A. Perturbation Technique to Analyze Mutual Coupling in Reflectarrays. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 697–700. [Google Scholar] [CrossRef]
- Miao, Z.W.; Hao, Z.C.; Wang, Y.; Jin, B.B.; Wu, J.B.; Hong, W. A 400-GHz High-Gain Quartz-Based Single Layered Folded Reflectarray Antenna for Terahertz Applications. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 78–88. [Google Scholar] [CrossRef]
- Huang, J. Analysis of microstrip reflectarray antenna for microspacecraft applications. Telecommun. Data Acquis. Prog. Rep. 1994, 42–120, 153–173. [Google Scholar]
- Greco, F.; Boccia, L.; Arnieri, E. A Ka-Band Cylindrical Paneled Reflectarray Antenna. Electronics 2019, 8, 654. [Google Scholar] [CrossRef]
- Yang, X.; Xu, S.; Yang, F.; Li, M.; Hou, Y.; Jiang, S.; Liu, L. A Broadband High-Efficiency Reconfigurable Reflectarray Antenna Using Mechanically Rotational Elements. IEEE Trans. Antennas Propag. 2017, 65, 3959–3966. [Google Scholar] [CrossRef]
- Chen, Q.-Y.; Qu, S.-W.; Zhang, X.-Q.; Xia, M.Y. Low-Profile Wideband Reflectarray by Novel Elements with Linear Phase Response. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1545–1547. [Google Scholar] [CrossRef]
- Dahri, M.H.; Inam, M.; Jamaluddin, M.H.; Kamarudin, M.R. A Review of High Gain and High Efficiency Reflectarrays for 5G Communications. IEEE Access 2017, 6, 5973–5985. [Google Scholar] [CrossRef]
- Tahseen, M.M.; Kishk, A.A. Ka-Band Circularly Polarized High Efficiency Wide Band Reflectarray Using Cross Bow-Tie Elements. Prog. Electromagn. Res. 2015, 153, 1–10. [Google Scholar] [CrossRef]
- Vosoogh, A.; Keyghobad, K.; Khaleghi, A.; Mansouri, S. A High-Efficiency Ku-Band Reflectarray Antenna Using Single-Layer Multiresonance Elements. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 891–894. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Yu, A.; Yang, F.; Elsherbeni, A.Z.; Huang, J.; Samii, Y.R. Aperture efficiency analysis of reflectarray antennas. Microw. Opt. Technol. Lett. 2010, 52, 364–372. [Google Scholar] [CrossRef]
- Pasku, V.; Fravolini, M.L.; Moschitta, A. Effects of antenna directivity on RF ranging when using space diversity techniques. Measurement 2017, 98, 429–438. [Google Scholar] [CrossRef]
- Rajagopalan, H.; Rahmat-Samii, Y. Dielectric and conductor loss quantification for microstrip reflectarray: Simulations and measurements. IEEE Trans. Antennas Propag. 2008, 56, 1192–1196. [Google Scholar] [CrossRef]
- Ethier, J.; Chaharmir, M.R.; Shaker, J. Loss Reduction in Reflectarray Designs Using Sub-Wavelength Coupled-Resonant Elements. IEEE Trans. Antennas Propag. 2012, 60, 5456–5459. [Google Scholar] [CrossRef]
- Costa, F.; Monorchio, A. Closed-Form Analysis of Reflection Losses in Microstrip Reflectarray Antennas. IEEE Trans. Antennas Propag. 2012, 60, 4650–4660. [Google Scholar] [CrossRef]
- Chen, L.; Qu, S.W.; Chen, B.J.; Bai, X.; Ng, K.B.; Chan, C.H. Terahertz metasurfaces for absorber or reflectarray applications. IEEE Trans. Antennas Propag. 2017, 65, 234–241. [Google Scholar] [CrossRef]
- Ethier, J.; Chaharmir, M.R.; Shaker, J.; Lee, D. Development of Novel Low-Cost Reflectarrays [Antenna Applications Corner]. IEEE Antennas Propag. Mag. 2012, 54, 277–287. [Google Scholar] [CrossRef]
- Ethier, J.; Chaharmir, M.R.; Shaker, J. Reflectarray thinning using sub-wavelength coupled-resonant elements. Electron. Lett. 2012, 48, 359–360. [Google Scholar] [CrossRef]
- Mohammadirad, M.; Komjani, N.; Chaharmir, M.R.; Shaker, J.; Sebak, A.R. Phase error analysis of the effect of feed movement on bandwidth performance of a broadband X-Ku band reflectarray. Int. J. RF Microw. Comput. Eng. 2013, 23, 517–526. [Google Scholar] [CrossRef]
- Pozar, D.M.; Targoski, S.D.; Syrigos, H.D. Design of millimeter wave microstrip reflectarrays. IEEE Trans. Antennas Propag. 1997, 45, 287–296. [Google Scholar] [CrossRef]
- Pozar, D.M. Wideband reflectarrays using artificial impedance surfaces. Electron. Lett. 2007, 43, 148–149. [Google Scholar] [CrossRef]
- Ismail, M.Y.; Dahri, M.H. Tunable Reflectarray Resonant Elements based on Non-linear Liquid Crystals. J. Adv. Mater. Res. 2013, 746, 357–362. [Google Scholar] [CrossRef]
- Liu, D.; Pfeiffer, U.; Grzyb, J.; Gaucher, B. Advanced Millimeter-Wave Technologies: Antennas, Packaging and Circuits; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Dahri, M.H.; Jamaluddin, M.H.; Seman, F.C.; Inam, M.; Ashyap, A.Y.I.; Kamarudin, M.R.; Hayat, O. A Novel Asymmetric Patch Reflectarray Antenna with Ground Ring Slots for 5G Communication Systems. Electronics 2020, 9, 1450. [Google Scholar] [CrossRef]
- Dahri, M.H.; Ismail, M.Y. Performance Analysis of Reflectarray Resonant Elements based on Dielectric Anisotropic Materials. Procedia Eng. 2013, 53, 203–207. [Google Scholar] [CrossRef]
- Chen, X.; Chen, Q.; Feng, P.; Huang, K. Efficient design of the microstrip reflectarray antenna by optimizing the reflection phase curve. Int. J. Antennas Propag. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Pozar, D.M.; Targonski, S.D.; Syrigos, H.D. Analysis and design of millimeter wave microstrip reflectarrays. IEEE Antennas Propag. Soc. Int. Symp. 1995 Dig. 1995, 1, 287–296. [Google Scholar]
- Park, J.H.; Choi, H.K.; Kim, S.H. Design of Ku-band reflectarray using hexagonal patch with crossed slots. Microw. Opt. Technol. Lett. 2012, 54, 2383–2387. [Google Scholar] [CrossRef]
- Da, X.; Wu, J.; Zhao, J.; Baoqin, L.; Wu, K. Single-Layer Circularly Polarized Wide Band Reflectarray Antenna with High Aperture Efficiency. Int. J. Antennas Propag. 2018, 2018, 1–7. [Google Scholar] [CrossRef]
- Pérez, J.G.; Tayebi, A.; Diego, I.G.; Pérez, F.C. Broadband reflectarray antenna composed of single-layer concentric rings. J. Electromagn. Waves Appl. 2013, 27, 2166–2175. [Google Scholar] [CrossRef]
- Florencio, R.; Boix, R.R.; Carrasco, E.; Encinar, J.A.; Barba, M.; Pérez-Palomino, G. Broadband reflectarrays made of cells with three coplanar parallel dipoles. Microw. Opt. Technol. Lett. 2014, 56, 748–753. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, H.; Liu, T. A high efficiency reflectarray antenna design based on incident field. J. Commun. 2017, 12, 532–537. [Google Scholar] [CrossRef]
- Jeong, J.G.; Park, N.J.; Yoon, Y.J. Aperture efficiency improvement of folded reflectarray using rectangle and split-ring combined element. Electron. Lett. 2018, 54, 797–798. [Google Scholar] [CrossRef]
- Maddahali, M.; Forooraghi, K. High efficiency reflectarray using smooth tapering in phase pattern on antenna surface. Microw. Opt. Technol. Lett. 2013, 55, 747–753. [Google Scholar] [CrossRef]
- Xue, F.; Wang, H.; Wang, Y.; Zhang, L. Broadband and high efficiency single-layer reflectarray using circular ring attached two sets of phase-delay lines. Prog. Electromagn. Res. M 2018, 66, 193–202. [Google Scholar]
- Oh, S.W.; Ahn, C.H.; Chang, K. Reflectarray element using variable ring with slot on ground plane. Electron. Lett. 2009, 45, 1206–1207. [Google Scholar] [CrossRef]
- Pochiraju, T.; Fusco, V. Amplitude and phase controlled reflectarray element based on an impedance transformation unit. IEEE Trans. Antennas Propag. 2009, 57, 3821–3826. [Google Scholar] [CrossRef]
- Nayeri, P.; Yang, F.; Elsherbeni, A.Z. A broadband microstrip reflectarray using sub-wavelength patch elements. In Proceedings of the IEEE Antennas and Propagation Society, AP-S International Symposium (Digest), Charleston, SC, USA, 1–5 June 2009; pp. 1–4. [Google Scholar]
- Jo, E.S.; Cho, S.B.; Kim, D. Bandwidth enhancement of a miniaturized reflectarray antenna using sub-wavelength meander-line cells. Microw. Opt. Technol. Lett. 2017, 59, 1553–1557. [Google Scholar] [CrossRef]
- Guo, L.; Tan, P.K.; Chio, T.-H. Investigations on Beam-Scanning Improvement of Reflectarrays Using Single-Layered Sub-Wavelength Elements. Prog. Electromagn. Res. C 2014, 51, 139–147. [Google Scholar] [CrossRef][Green Version]
- Qin, P.Y.; Guo, Y.J.; Weily, A.R. Broadband reflectarray antenna using sub-wavelength elements based on double square meander-line rings. IEEE Trans. Antennas Propag. 2016, 64, 378–383. [Google Scholar] [CrossRef]
- Pattanayak, A.; Rana, G.; Duttagupta, S.P.; Gandhi, P.S.; Deshmukh, A.A. Design of a 5 GHz reflectarray with reduced size unit cell and extremely low phase sensitivity. Radioengineering 2018, 27, 718–723. [Google Scholar] [CrossRef]
- Konno, K.; Chen, Q. Enhancing Aperture Efficiency of reflectarray by accurately evaluating mutual coupling of reflectarray elements. IEICE Commun. Express 2016, 5, 341–346. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X. A low mutual coupling reflectarray antenna using sub-wavelength fragmented elements with isolation walls based on H-shaped unit cells. Electromagnetics 2018, 38, 260–271. [Google Scholar] [CrossRef]
- Wu, J.; Da, X.; Lin, B.; Zhao, J.; Wu, K. Circularly polarized low-cost wide band reflectarray antenna constructed with subwavelength elements. Int. J. RF Microw. Comput. Eng. 2018, 28, 1–7. [Google Scholar] [CrossRef]
- Tahseen, M.M.; Kishk, A.A. Feed Matching Improvement for Center Fed Reflectarray. Prog. Electromagn. Res. M 2017, 54, 67–74. [Google Scholar] [CrossRef][Green Version]
- Cai, T.; Wang, G.M.; Liang, J.G. High-efficiency reflectarray antenna using a compact focusing meta-lens. Appl. Phys. A 2017, 123, 159. [Google Scholar] [CrossRef]
- Hu, W.; Arrebola, M.; Cahill, R.; Encinar, J.A.; Fusco, V.; Gamble, H.S.; Alvarez, Y.; Las-Heras, F. 94 GHz dual-reflector antenna with reflectarray subreflector. IEEE Trans. Antennas Propag. 2009, 57, 3043–3050. [Google Scholar]
- Tienda, C.; Encinar, J.A.; Arrebola, M.; Barba, M.; Carrasco, E. Design, manufacturing and test of a dual-reflectarray antenna with improved bandwidth and reduced cross-polarization. IEEE Trans. Antennas Propag. 2013, 61, 1180–1190. [Google Scholar] [CrossRef]
- Kim, D.; Park, I.Y. A Miniaturized Reflectarray Antenna for Scanned Beam Applications. IEEE Trans. Antennas Propag. 2016, 64, 960–967. [Google Scholar] [CrossRef]
- Yoon, J.H.; So, J.; Yoon, Y.J.; Kim, J.; Lee, W. Single-layer reflectarray with combination of element types. Electron. Lett. 2014, 50, 574–576. [Google Scholar] [CrossRef]
- Derafshi, I.; Komjani, N.; Ghasemi-Mizuji, E. Analytical method for designing fss-backed reflectarray antenna using transmission line approach. J. Microw. Optoelectron. Electromagn. Appl. 2017, 16, 529–541. [Google Scholar] [CrossRef][Green Version]
- Hasani, H.; Kamyab, M.; Mirkamali, A. Low cross-polarization reflectarray antenna. IEEE Trans. Antennas Propag. 2011, 59, 1752–1756. [Google Scholar] [CrossRef]
- Headland, D.; Carrasco, E.; Nirantar, S.; Withayachumnankul, W.; Gutruf, P.; Schwarz, J.; Abbott, D.; Bhaskaran, M.; Sriram, S.; Perruisseau-carrier, J.; et al. Dielectric resonator reflectarray as high-efficiency non-uniform terahertz metasurface. ACS Photonics 2016, 3, 1019–1026. [Google Scholar] [CrossRef]
- Nayeri, P.; Liang, M.; Sabory-Garcia, R.A.; Tuo, M.; Yang, F.; Gehm, M.; Xin, H.; Elsherbeni, A.Z. 3D printed dielectric reflectarrays: Low-cost high-gain antennas at sub-millimeter waves. IEEE Trans. Antennas Propag. 2014, 62, 2000–2008. [Google Scholar] [CrossRef]
- Wang, J.; Member, Y.Z.; Gao, S. An Efficiency-Improved Tightly Coupled Dipole Reflectarray Antenna Using Variant-Coupling- Capacitance Method. IEEE Access 2020, 8, 37314–37320. [Google Scholar] [CrossRef]
- Yi, M.; Lee, W.; So, J. Design of cylindrically conformed metal reflectarray antennas for millimetre-wave applications. Electron. Lett. 2014, 50, 1409–1410. [Google Scholar] [CrossRef]
- An, W.; Xu, S.; Yang, F. A Metal-Only Reflectarray Antenna Using Slot-Type Elements. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1553–1556. [Google Scholar] [CrossRef]
- Venneri, F.; Costanzo, S.; Di Massa, G.; Marozzo, E.; Borgia, A.; Corsonello, P.; Salzano, M.; Venneri, F.; Costanzo, S.; Di Massa, G.; et al. Beam-Scanning Reflectarray Based on a Single Varactor-Tuned Element. Int. J. Antennas Propag. 2012, 2012, 1–5. [Google Scholar] [CrossRef]
- Abbasi, M.I.; Ismail, M.Y. Reflection loss and bandwidth performance of X-band infinite reflectarrays: Simulations and measurements. Microw. Opt. Technol. Lett. 2011, 53, 77–80. [Google Scholar] [CrossRef]
- Rajagopalan, H.; Rahmat-Samii, Y. On the reflection characteristics of a reflectarray element with low-loss and high-loss substrates. IEEE Antennas Propag. Mag. 2010, 52, 73–89. [Google Scholar] [CrossRef]
- Ashraf, M.A.; Abdel-rahman, M.R.; Haraz, O.A.; Alshawi, T.; Sethi, W.T.; Alshebeili, S.A. Multi-feature radiation pattern measurement apparatus operative up to 67-GHz band. Measurement 2020, 153, 107405. [Google Scholar] [CrossRef]




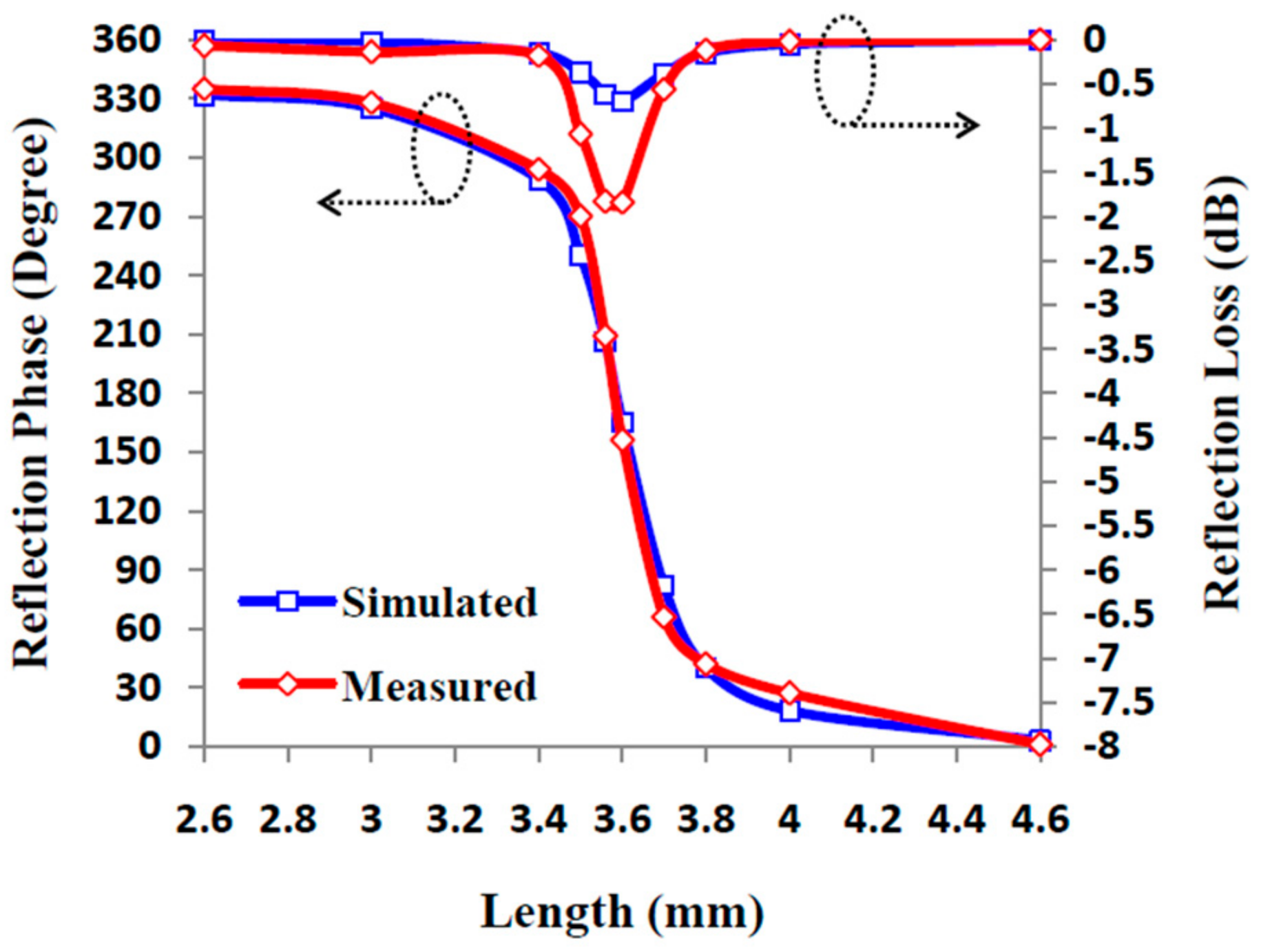
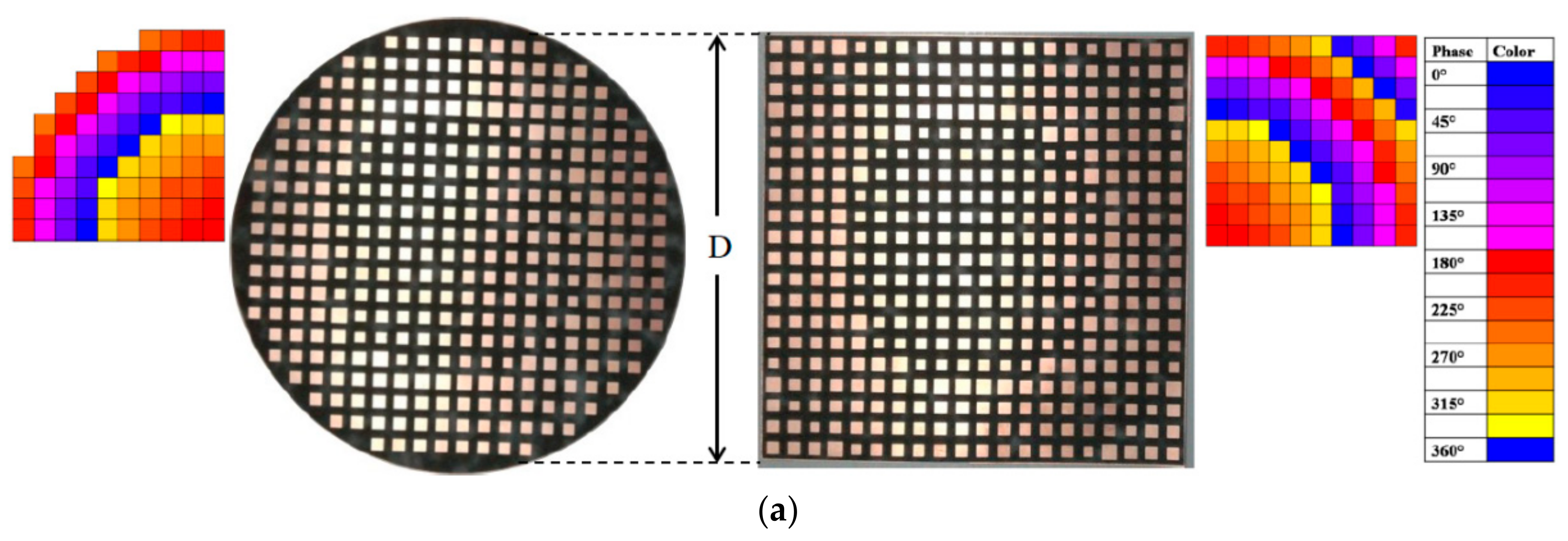

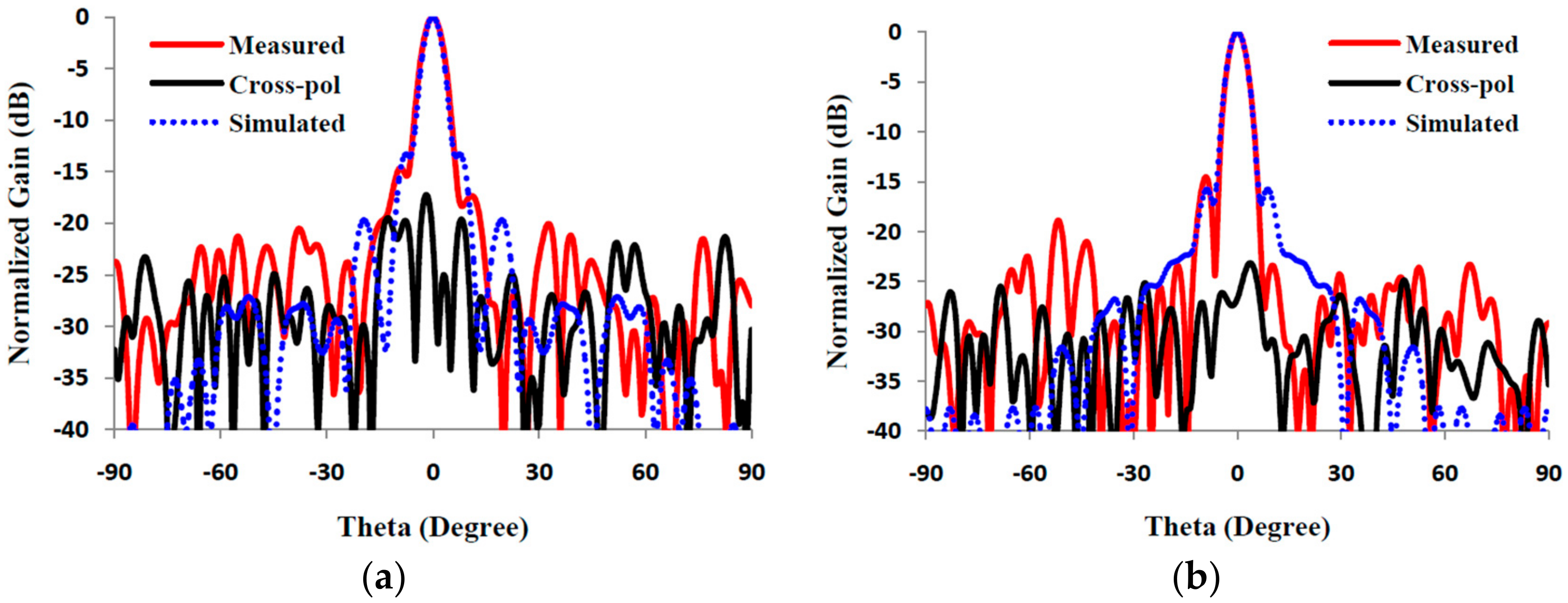

| Element Type | Design | Loss (dB) | Phase Range (°) | Aperture Size (λ2) | Efficiency (%) |
|---|---|---|---|---|---|
| Hexagonal [42] |  | N.A | 360 | 69.4 | 60 |
| Bow-tie [22,43] |  | −0.4 | 360 | 39 | 57 |
| I-Shaped [20] |  | N.A | 360 | 75.7 | 50 |
| Dual Rings [44] |  | N.A | 360 | 250 | 52 |
| Parallel Dipoles [45] |  | −0.2 | 360 | 180 | 65 |
| Two Rings and Patch [46] |  | N.A | 360 | 130 | 64 |
| Three Rings [23] |  | N.A | 500 | 163 | 66 |
| Split Ring [47] |  | −0.3 | 360 | 187 | 55 |
| Fractal [48] |  | −0.45 | 700 | 54.5 | 66 |
| Ring with Phase Delay Lines [49] |  | −0.05 | 460 | 78 | 57.3 |
| f/D | q | Max. Aperture Efficiency (%) | Feed Beamwidth (°) |
|---|---|---|---|
| 0.4 | 2 | 50 | 66 |
| 0.5 | 3 | 57 | 55 |
| 0.6 | 4.5 | 62 | 45 |
| 0.7 | 5.5 | 66 | 41 |
| 0.8 | 7 | 69 | 36 |
| 0.9 | 9 | 71 | 32 |
| 1.0 | 11 | 73 | 29 |
| 1.1 | 13 | 74 | 27 |
| 1.2 | 15 | 75 | 25 |
| 1.3 | 17.5 | 76 | 23 |
| Parameter | Circular Aperture | Square Aperture | |
|---|---|---|---|
| Predicted | Max. Directivity (dB) | 29.94 | 31 |
| Simulated | Gain (dB) | 27.03 | 27.2 |
| Efficiency (dB) | −2.91 (51.2%) | −3.8 (41.7%) | |
| Measured | Gain (dB) | 27.3 | 27.4 |
| Efficiency (dB) | −2.64 (54.4%) | −3.6 (43.6%) | |
| Type of Loss | Circular Aperture | Square Aperture | ||
|---|---|---|---|---|
| Simulated | Measured | Simulated | Measured | |
| Feed (dB) | −0.1 | −0.36 | −0.1 | −0.36 |
| Patch (dB) | −0.7 | −0.84 | −0.7 | −0.84 |
| Illumination (dB) | −0.91 | −1.19 | −1.96 | −2.21 |
| Spillover (dB) | −1.3 | −0.41 | −1.3 | −0.41 |
| Total (dB) | −3.01 | −2.8 | −4.06 | −3.82 |
| Total Efficiency | 50% | 52.5% | 39.3% | 41.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dahri, M.H.; Jamaluddin, M.H.; Seman, F.C.; Abbasi, M.I.; Sallehuddin, N.F.; I. Ashyap, A.Y.; Kamarudin, M.R. Aspects of Efficiency Enhancement in Reflectarrays with Analytical Investigation and Accurate Measurement. Electronics 2020, 9, 1887. https://doi.org/10.3390/electronics9111887
Dahri MH, Jamaluddin MH, Seman FC, Abbasi MI, Sallehuddin NF, I. Ashyap AY, Kamarudin MR. Aspects of Efficiency Enhancement in Reflectarrays with Analytical Investigation and Accurate Measurement. Electronics. 2020; 9(11):1887. https://doi.org/10.3390/electronics9111887
Chicago/Turabian StyleDahri, M. Hashim, M. Haizal Jamaluddin, Fauziahanim C. Seman, M. Inam Abbasi, N. Fazreen Sallehuddin, Adel Y. I. Ashyap, and M. Ramlee Kamarudin. 2020. "Aspects of Efficiency Enhancement in Reflectarrays with Analytical Investigation and Accurate Measurement" Electronics 9, no. 11: 1887. https://doi.org/10.3390/electronics9111887
APA StyleDahri, M. H., Jamaluddin, M. H., Seman, F. C., Abbasi, M. I., Sallehuddin, N. F., I. Ashyap, A. Y., & Kamarudin, M. R. (2020). Aspects of Efficiency Enhancement in Reflectarrays with Analytical Investigation and Accurate Measurement. Electronics, 9(11), 1887. https://doi.org/10.3390/electronics9111887











