Modelling Neural Dynamics with Optics: A New Approach to Simulate Spiking Neurons through an Asynchronous Laser

Abstract

In this paper, we propose a novel approach for implementing spiking neurons through an optical system. Spiking neurons are a new approach to emulate the neural processes that occur in the brain, known as the third generation of artificial neural networks. They have been successfully used to build a new technology called neuromorphic engineering, which looks for a better performance than traditional computing in tasks usually performed by AI-based systems. Our optical system consists of a low-cost laser source, based on a microcontroller and a continuous-wave laser diode; the microcontroller allows producing synchronous or asynchronous pulses with complex time profiles. Here, through said system we have successfully reproduced most of the neural dynamics observed in biological neurons. These dynamics have been reproduced using a very simple optical array with a great potential for the development of neuromorphic systems. The optical system has been experimentally validated.

1. Introduction

In the last few decades, spiking neurons, one of the main branches of the computational neuroscience, have been successfully used to model some important regions of the brain [1,2,3] due to their biological plausibility. This biological plausibility has different levels of complexity, from the most complex in the the Hodgkin and Huxley model [4] to the simpler approach in the Izhikevich model [5]. The latest demonstrated that a “simple” model is able to reproduce precise firing patterns like those found in neurons of the mammalian brain. The validation of a neuron model is given by its capacity to reproduce as many neuronal firing patterns as possible. To facilitate such validation, several software packages have been developed. Among the most known and used, we found the NEURON simulator [6], which is a C-based simulator with a high-level description for single neuron models or a full neural network. Due to the fact that NEURON is written in C, it offers a high computational efficiency, which is of particular interest for large neural networks with complex neuron models, e.g., the Hodgkin and Huxley model. BRIAN [7] is another widely used simulator, which compared with NEURON is better at simulating spiking neurons. This fact is mainly due to BRIAN being written in Python, a high level description language with a large community supporting and developing new and more efficient libraries every day. PyNN [8] is a Python-based and simulator-independent package for building neuronal network models, meaning that it can be simulated in one of the aforementioned simulators. Finally, we have NEST, a simulator for spiking neural network models that focuses on the dynamics, size and structure of neural systems rather than on the exact morphology of individual neurons [9]. NEST has a large library of spiking neuron models and it combines the high level description (in Python) with a highly optimised simulation kernel written in C++.

Albeit software implementations permit the simulation of detailed neural networks with impressive results, the energetic efficiency of such simulators is still far away from that achieved by the brain. That is the reason why neuromorphic engineering has born [10]. Neuromorphic engineering is a term conceived by Caver Mead in the late 1980s and published for the first time in [11]. It is a new approach to efficiently simulating spiking neuron models with the aid of specialised hardware architectures that are compatible with the main programming languages, e.g., Python and C/C++ for high level neural network descriptions. Among the most popular neuromorphic platforms we found the SpiNNaker chip [12], developed by Steve Furber et al., at the University of Manchester. The SpiNNaker platform aims to deliver a massively parallel million-core hardware to simulate large-scale spiking neural networks in biological real time. SpiNNaker is an ARM-based scalable platform which goes from 72 up to 1,036,800 ARM processor cores in its larger board. One of the main advantages of this platform is its compatibility with the main available software for spiking neuron descriptions, such as PyNN and NEST. TrueNorth [13] and Loihi [14] are other neuromorphic systems developed by IBM and Intel respectively. TrueNorth is considered the most efficient platform in terms of energy consumption, and Loihi the most recent platform. These two platforms use specialised hardware developed by the two big companies. It is true that the main goals of neuromorphic hardware are to aid scientists in understanding the complex processes that occur in the brain [15] and to solve problems in areas such as the artificial intelligence, machine learning and robotics in a more efficient way [16].

Despite the development of neuromorphic systems, their adoption is still far from being a reality, mainly because these platforms are not commercially available. In this regard, several groups have developed their own technology, most of them using FPGAs (field programmable gate arrays). The use of FPGAs in the development of neural processing systems is very popular, mainly due to their reconfigurability and scalability, processing speed and portability, but especially because they are commercially available at very low prices. Some implementation of FPGA-based systems for artificial neural networks (including deep neural networks) can be found in [17,18,19] and for spiking neural networks [20,21,22]. In these implementations, the common goal is to develop FPGA-based architectures to speed up applications in the field of neural networks.

As a matter of fact, that most of the research on hardware implementations of neural networks has been done in FPGAs for the aforementioned reasons, and more recently using neuromorphic systems. However, there is also an emerging piece of technology based on optical systems, which aims not only to replicate the basis of electronics components and their applications (specially in computing), but also to be a new paradigm in the study of the brain. At present, the main application of optical-based systems has been in treatment of brain damage through the stimulation of neurons using low level laser (light) in the damage region, showing impressive improvements [23]. However, recent studies show that neurons and some learning rules can be emulated through optic systems such as the brain does [24,25,26,27,28,29]. In this regard, we aim to contribute in this field with a novel approach to experimentally generate different neural dynamics, all of them observed in the brain [5]. Our main contribution compared to those aforementioned is that we propose a basic optical system that is able to generate biological-like patterns of neural activity and to be a basic element to build larger optical neural networks.

2. Materials and Methods

2.1. Spiking Neurons and Neural Dynamics

Spiking neurons are mathematical expressions that mimic the behaviour of biological neurons at different complexity levels. This complexity level depends on the capacity of the model to simulate the electrical and chemical variables observed in the brain. For example, the Hodgkin and Huxley model [30] is considered one of the most complex neuron models due that it uses nonlinear differential equations to approximate the electrochemical characteristics of neurons. Integrate and fire models [31] are simpler and are commonly used in the development of neuromorphic systems. Models of that kind use a linear differential equation to describe the evolution of the membrane potential and the fact that action potentials of a given neuron have the same form. If the shape of an action potential is always the same, then the shape cannot be used to transmit information: instead information is contained in the presence or absence of a spike. Therefore, action potentials are reduced to “events” that happen at a precise moment in time. These events have specific patterns according to measurements made in biological neurons. 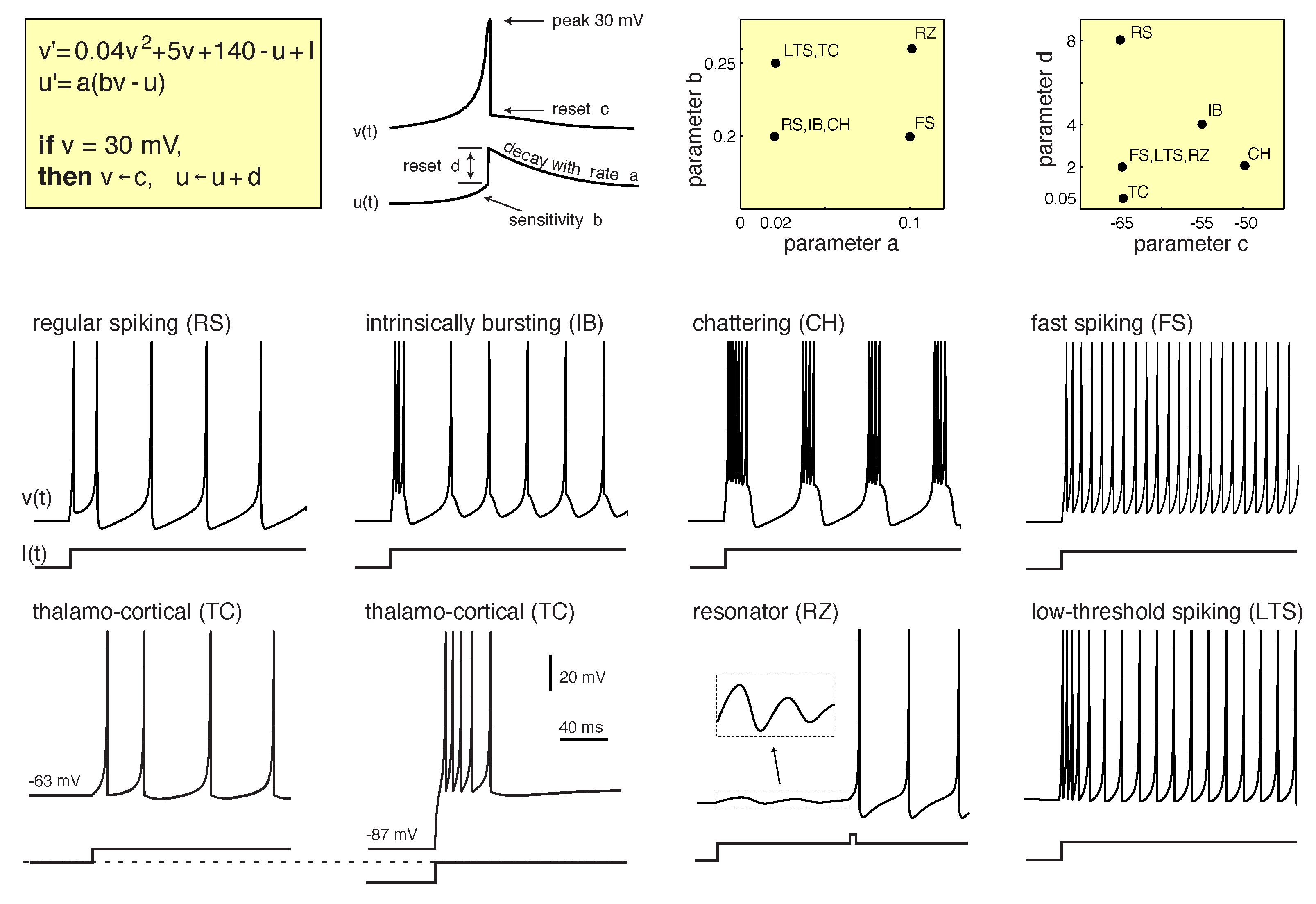In Figure 1, we can observe a chart with the different spike patterns observed in the brain and reproduced by the Izhikevich model presented in [5]. The Izhikevich model is a simple model of spiking neurons that reproduces spiking and bursting behaviour of known types of cortical neurons. The model combines the biologically plausibility of Hodgkin–Huxley-type dynamics and the computational efficiency of integrate-and-fire neurons. Thus, the Izhikevich neuron model’s equations read:

$$v^{\prime }=0.04v^2+5v+140-u+I$$

(1)

$$u^{\prime }=a(bv-u)$$

(2)

with the auxiliary after-spike resetting

$$\mathrm{if}v\le 30\mathrm{mV},\mathrm{then}\left\{\begin{array}{c}\hfill v\leftarrow c\\ \hfill u\leftarrow u+d\end{array}\right.$$

(3)

Here, v and u are dimensionless variables; a, b, c and d are dimensionless parameters; and ${}^{\prime }=d/dt$, where t is the time. The variable v represents the membrane potential of the neuron and u represents a membrane recovery variable.

In this work, we attempted to replicate experimentally the dynamics observed in Figure 1 through an optical system. These dynamics were numerically generated in [5] using the Izhikevich neuron model, which is described by Equations (1)–(3). A Euler discretisation of these equations has been implemented in this work. More information about the model and Matlab code can be found directly from the site of the author in the following link: https://www.izhikevich.org/publications/spikes.htm.

2.2. Experimental Setup

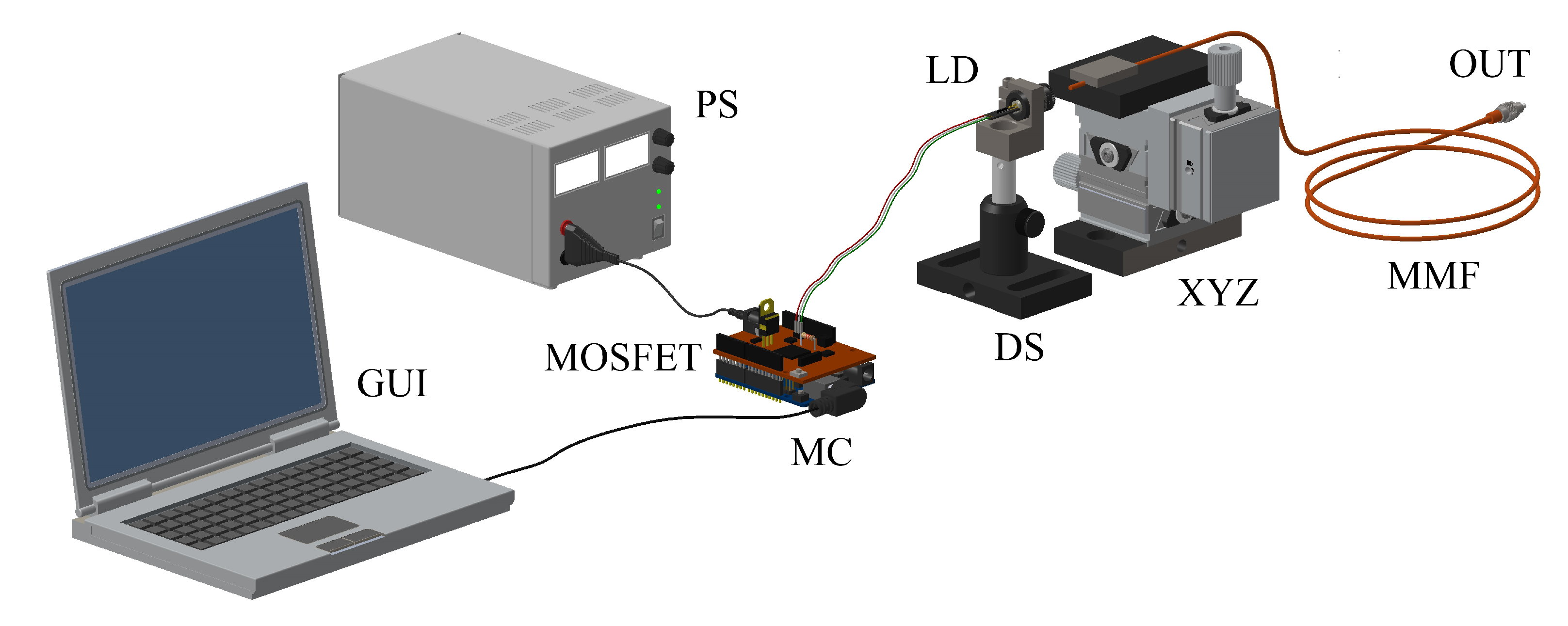
The experimental scheme for the generation of neuronal responses through a low-cost light-based system is depicted in Figure 2. It was formed by a low-cost laser diode (green laser pointer) operating at a wavelength of 532 nm, a regulated power supply, an optocoupler, an amplification-switching stage, a control based on a graphical user interface (GUI) and a microcontroller (the central part of the control), a standard multimode optical fibre (50/125 $\mathsf{\mu }$m) used as waveguide of the signal and a sensing stage at the fibre output.

Regarding the laser power supply, the optocoupler isolates the feeding stage of the pulses control since it operates at different voltages: 3.7 V of the CW laser diode (LD) and 5 V of the commercial microcontroller (Arduino Uno). Besides, the MOSFET (with a voltage of 5 V in the gate terminal, and a maximum current of 4 A in the drain terminal) is used as a switch, allowing saturation or cut-off mode to control the obtained current (by applying a voltage on the gate terminal with respect to the source terminal). The amplification stage increases the current and voltage, modulating the pulse width.

The microcontroller implements a Euler discretisation of the Izhikevich neuron model described in Section 2.1. Thus, once the input and output gates have been coordinated with the corresponding voltages, the microcontroller’s task is to turn on and off the CW laser diode; i.e., when the CW laser diode is activated a light pulse (or spike) is generated.

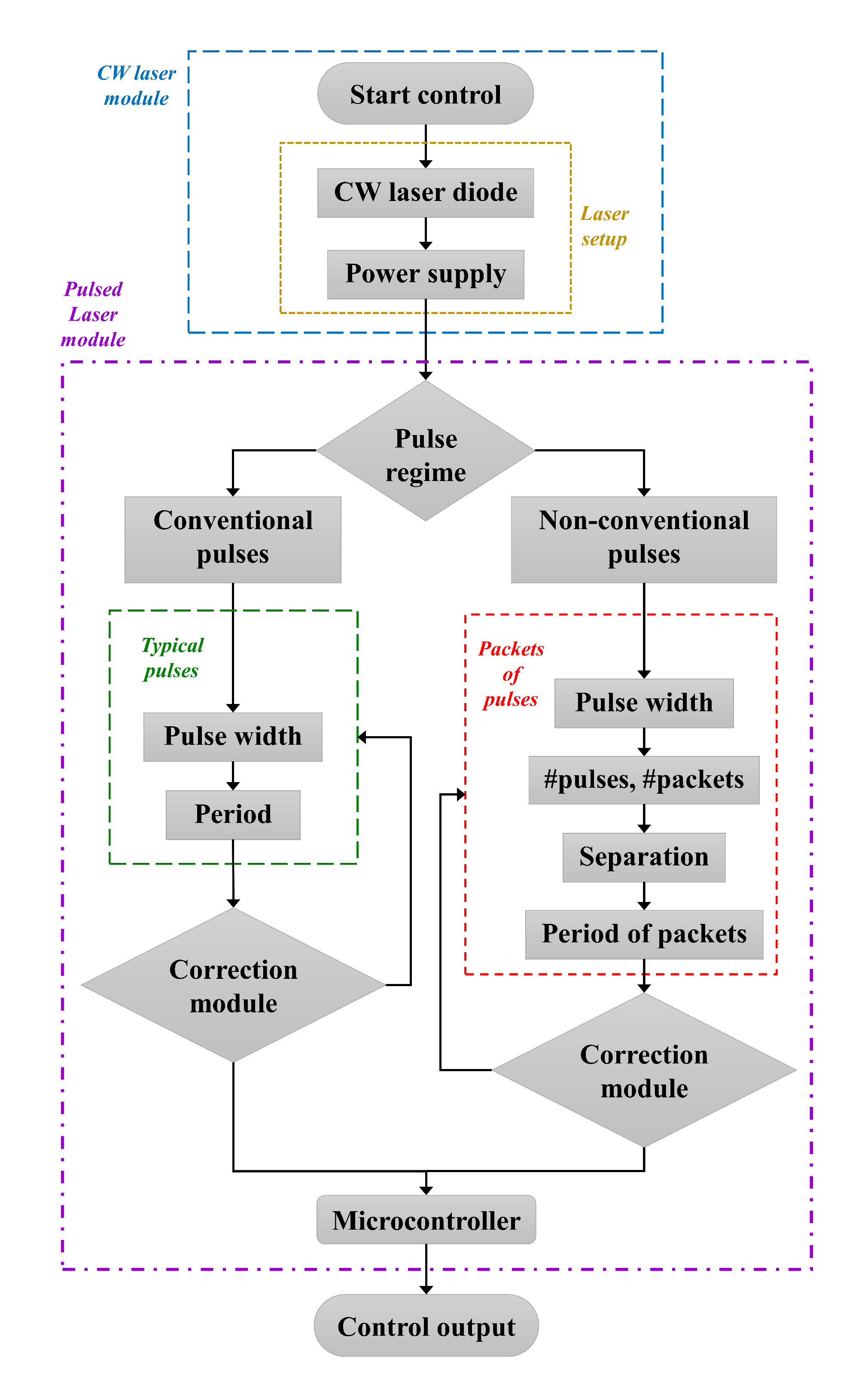
A flowchart describing the generation of pulses from the continuous emission of the laser diode is depicted in Figure 3. From the GUI and without the need to modify the experimental arrangement, the type of pulse is chosen: conventional pulses (reproducing the behaviour of mode-locked lasers) or packets of pulses of the same duration. In the first case, only the temporal pulse width and the period are defined. For the second option, in addition to defining the time duration of each pulse, the number of pulses per packet, the spacing between pulses and the period between packets are defined. This information is sent to the microcontroller, which is responsible of turning the laser diode off and on (with a minimum time response of 250 $\mathsf{\mu }$s, limited by the microcontroller’s clock), which is fed through a regulated power supply.

2.3. Methodology

The communication with the microcontroller is carried out through a GUI, which allows one to control digitally the modulation of the laser pulses. Our code generates the GUI and serial communication with the microcontroller (operating with a clock frequency of 16 MHz), sending 1-bit information in a sequential manner and in the desired time between a receiver and a transmitter. In addition, this system has the advantage of showing a digital control panel, with which the user has control over the modulation of the pulses of the neuronal temporal response, and a visual aid through a digital display.

The regulated power supply was used to power the laser diode at 3.7 V, whereas the optocoupler was used to protect the computer and the microcontroller against high voltage peaks. The design of the amplification-switching stage was done by means of a MOSFET transistor, whose objective is to control high currents; when a MOSFET is used as a switch, it works in cut-off or saturation mode, and finally the control of the current is obtained by applying a voltage on the gate terminal with respect to the source terminal called VGS. The stage of amplification and switching is used to increase the current and voltage, allowing one to modulate by pulse width the green laser pointer that initially works in the continuous regime.

To have accurate and independent control, a MOSFET transistor (IRF640) was used as a switch controlled (in the order of $\mathsf{\mu }$s) by the signal generated from the microcontroller, which was applied to the gate terminal. The MOSFET operates in the cutoff region (off switch), behaving as an open circuit between the source and the drain terminals, and it operates in the saturation region (on switch) behaving as a short circuit between the source and the drain terminals, with a very small resistance value.

The next step was to mount the laser at a suitable height and through a lens system, to attach the light in the multimode fibre to transmit the optical signal. Then, the pertinent calibration was made to let the largest amount of light into the optical fibre, through a XYZ translation stage platform. Finally, the optical signal was converted to an electrical one by means of a photodetector, operating in the visible wavelength range, allowing us to visualise the neuronal response in the oscilloscope. Although any laser diode can be used as an optical source, and in particular in the visible range, we decided to use one at 532 nm (green) because this is more sensitive than the other wavelengths and provides a better signal-to-noise ratio for the available photodetector.

3. Experimental Results

Through our experimental arrangement, we reproduced as the first result, from a laser diode in continuous wave regime, the behaviour of a conventional pulsed laser. These dynamics can be observed in Figure 4 for a regular spike train and they are similar to those observed in the cerebral cortex and presented in Figure 1. In the regular spiking regime, neurons fire a few spikes with short interspike periods, and then the period could increase.

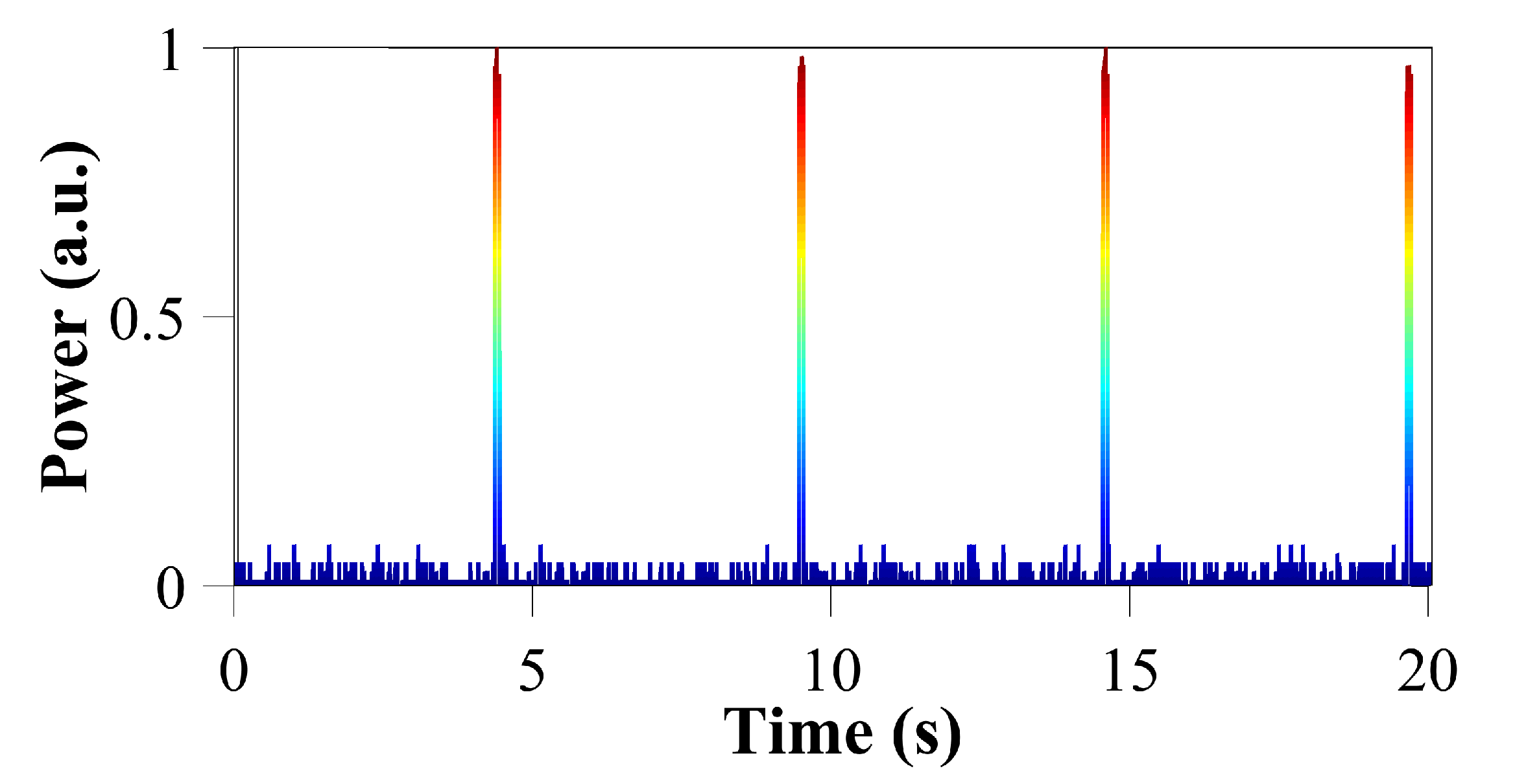
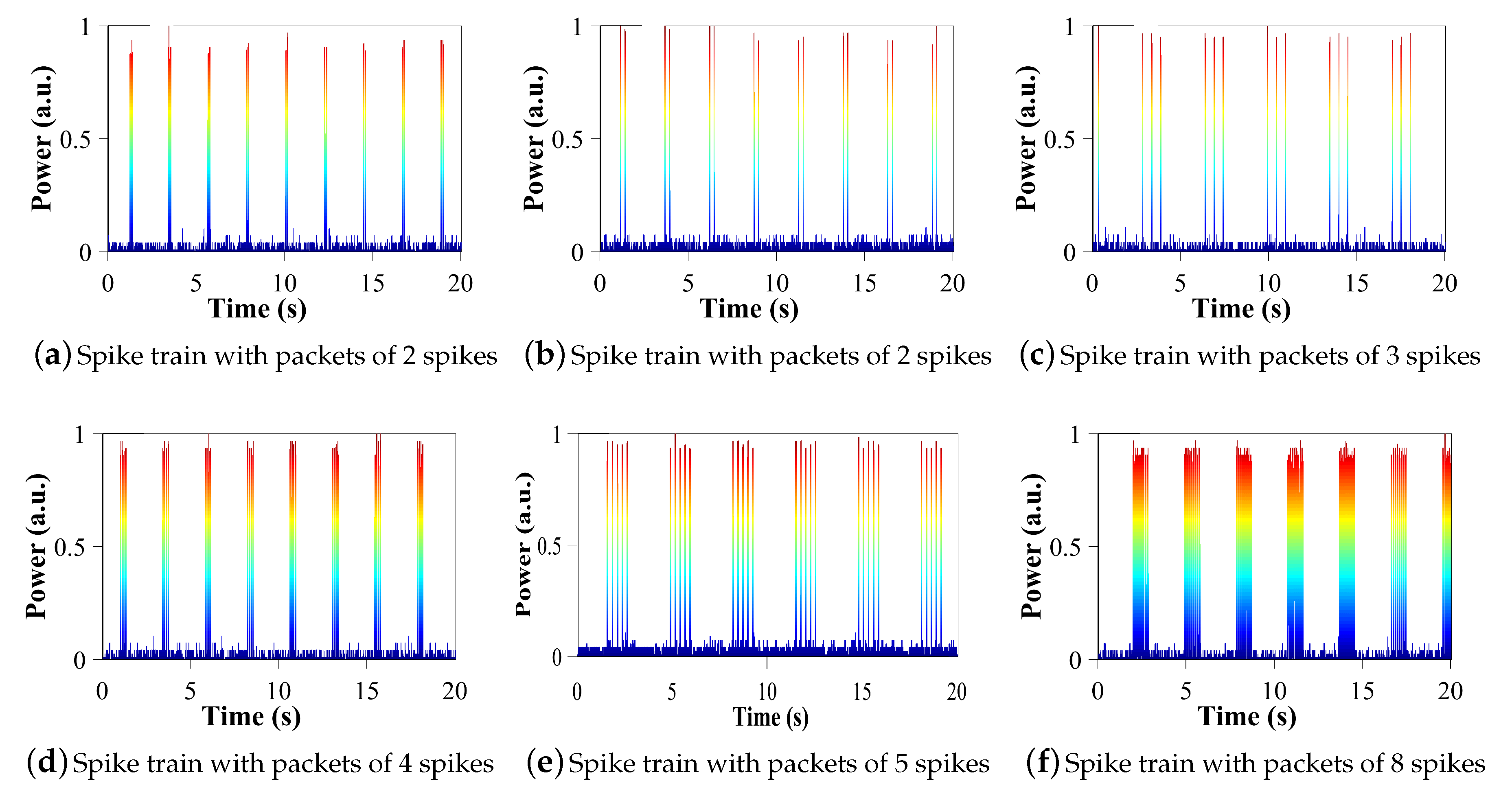
Besides, because we can control the activation of the laser in the order of ms, we can generate several non-conventional trains of pulses such as those observed in Figure 5. In this figure, we show some of the spike trains generated with two, three, four, five and eight pulses (spikes) per packet. These dynamics are of particular interest for the generation of chattering or the initialisation of intrinsically bursting dynamics. These two dynamics are produced by specialised excitatory cortical neurons, and in both cases these neurons can fire stereotypical bursts of closely spaced spikes.

Focusing, for example, on Figure 5e, we observe a spike train with packets of five pulses, each with a duration of 10 ms per pulse, a spacing of 0.25 s between the pulses of each packet and a period of 3.3 s (between packets). This information can be found for each spike train of Figure 5 in

Table 1. Data from measurements performed during the experiments.

Pulses per Packet	Pulse Width (ms)	Spacing (ms)	Period per Packet (s)	Frequency per Packet (Hz)	Figure Number
1	80	5	5	0.200	Figure 4
2	20	100	2.2	0.455	Figure 5a
2	20	260	2.53	0.395	Figure 5b
3	20	260	2.79	0.358	Figure 5c
4	30	100	2.4	0.417	Figure 5d
5	10	25	3.3	0.303	Figure 5e
8	50	110	2.92	0.342	Figure 5f
2	500	250	3.5	0.286	Figure 6

.

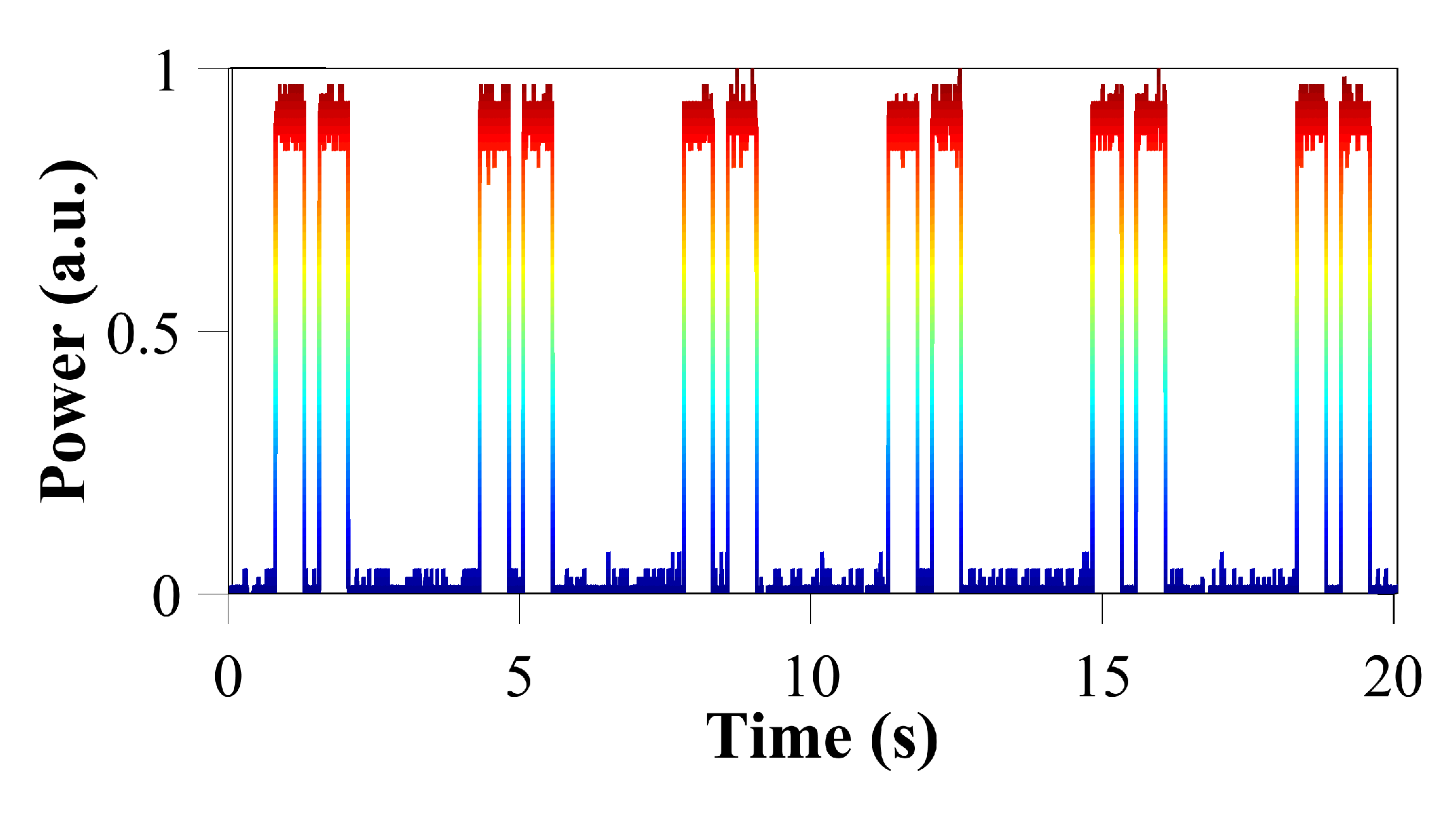
Likewise, we generated packets of two long pulses of 0.5 s in duration, as shown in Figure 6. The spacing between the pulses of the packet was defined as 0.25 s and the period of T = 3.5 s (f = 0.286 Hz). These dynamics can used for modelling the charging/discharging of the cell.

In Table 1, we present a summary of some measurements performed during the experiments and shown in Figure 5. This information could be useful to understand better the relationship between our data and the neural dynamics shown in Figure 1 and to reproduce such dynamics more precisely in further experiments. From said table it can be observed that the duration of the pulses is larger than that observed in biological neurons (1–2 ms according to [31]). The main reason for doing this is because we look for prosthetic applications where this kind of pulse can be used for neuroestimulation (further information is given in Section 5).

It should be stated that, although the pulsed laser emulates the behaviour of a mode-locked laser, the spectrum of the laser remains unaffected, since nonlinear phenomena does not participate in the process of obtaining pulses observed in the figures, regardless of their duration.

After demonstrating that our laser is able to produce periodic pulses and pulse packets, we established the appropriate parameters to produce asynchronous pulses, not periodic, with the intention of generating binary chains that can be interpreted as specific commands, as the central pattern generator does in the generation of walking patterns in humans and animals. This central pattern generator has also motivated the development of bio-inspired walking systems for robots [32]. 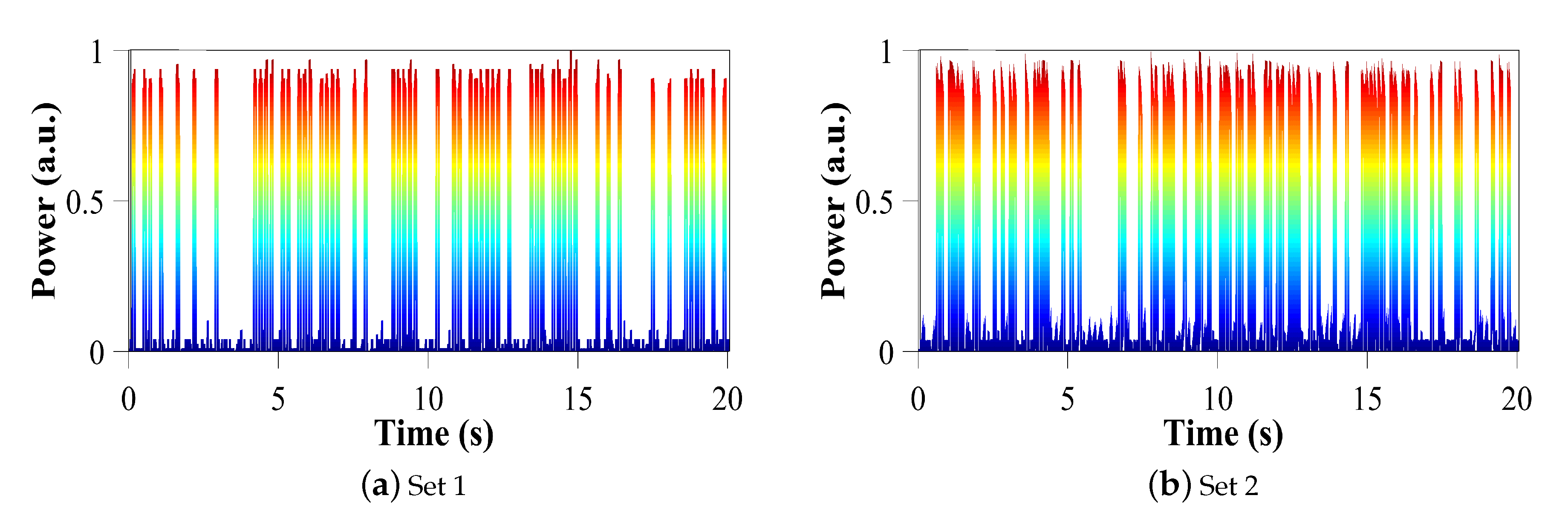Figure 7 shows two sets of asynchronous pulses, where each pulse has a duration of 70 ms an adequate time response for legged robots. Considering pulses as 1 and the laser off as 0, we have for set 1 the binary string:

$$\begin{gathered} 0100000100100000100000001000000 \\ 0100000001000000000000010101010, \end{gathered}$$

which corresponds to the first 6 seconds, presented in Figure 7a. For set 2, the corresponding binary string is:

$$\begin{gathered} 0001010010101010010100010010010 \\ 1000100101010100010010010010000, \end{gathered}$$

which also corresponds to the first 6 seconds, presented in Figure 7b.

4. Discussion

Neuromorphic systems have at least two decades of development and their goal is to help researchers in understanding the brain functioning through the simulation of complex neural networks. The main achievements of these systems are their energy efficiency, the capacity to simulate a large number of neurons and the processing speed. Albeit these characteristics have been widely demonstrated and presented in a large number of papers, there is still a lack of studies showing the capacity of these systems to simulate the main areas of the brain. We believe that this is mainly due to the natural complexity of the brain by itself, which has an impact on the experiments, theories, models and obviously the development of these neuromorphic systems. However, even if the study of the brain is still unclear, there is a new area of application for these systems: artificial intelligence, and more specifically, the simulations of deep neural networks (DNN). In the last few years, the number of publications wherein DNNs were being simulated using neuromorphic hardware considerably increased. Deep neural networks exploit the computing capacity of neuromorphic systems and leave aside the biological principles of the models. In this regard, the development of new neuromorphic systems is justified by the necessity of systems with specific characteristics to process large neural networks with a large amount of data. Thus, these neuromorphic systems will need components/elements to keep increasing their capabilities at the same time as new and more complex models of DNN appear. Our proposal presents two aspects that contribute to the aforementioned goal: On the one hand to the basic elements for the development of new low-cost neuromorphic systems that can help to simulate models for the understanding of the brain. On the other hand, a component of the existent neuromorphic systems, e.g., a communication element among the internal cores of such systems, given that our system is based on optics and has the ability to mimic the main dynamics observed in the brain.

5. Future Perspectives and Applications

A future perspective of this work is the exploration of the system scalability, e.g., to build a neural network. Once a neuron model has been numerically or experimentally validated, the next step will be to analyse its behaviour in a network. In this regard, a valid experiment might be a comparison between our system and the well-known and widely used perceptron model. The perceptron model was introduced in [33] and it consists of a single neuron which performs a binary classification. Some experiments to be performed are the implementations of logic gates, AND, OR and NOT, for a single perceptron, and XOR for a multilayer perceptron (three neurons).

A more complex application to test our system is the development of a central pattern generator. Central pattern generators are a group of neurons responsible for producing rhythmic outputs in any living entity (humans and animals). These rhythmic outputs correspond to the activity generated in the brain when a human or any other animal is walking, swimming, breathing, etc. In this regard, taking in consideration the dynamics generated in this work, we will be able to generate such rhythmic outputs and provide locomotion to a legged robot (biped, quadruped or hexapod robot). In this experiment, 6, 12 and 18 neurons (three for each leg, which correspond to femur, tibia and cox, and thus six for a biped, 12 for a quadruped and 16 for a hexapod) are necessary to coordinate the locomotion of the robot. See [34] for more details about this application.

Another application where we look to validate our system is the neuroestimulation of a prosthetic arm. In [35], a low-cost 7-DOF prosthetic arm for shoulder disarticulation has been proposed by our research group. In future work, the idea is to tackle the problem of its control through the proposed optical system. The challenge will be to identify the specific spiking pattern that generates the desired activity in the prosthetic arm. For this purpose, we can make use of EEG signals obtained from healthy people performing any activities with their arms and then translate them into a spiking pattern that can be generated for our optical system.

The cases aforementioned are examples of applications of our system that we plan to develop in the near future. However, this research has been also developed to be a complement to the existent neuromorphic systems. In particular, we are interested in developing a very fast communication system to link the different neuromorphic systems. Currently, this communication is performed by FPGAs; however, the limitation of the communication systems based on FPGA is known, i.e., the limitation in the amount of information which can be transmitted.

6. Conclusions

In this paper, we have introduced for the first time, to the best of our knowledge, an optical system able to mimic different neural dynamics observed in the brain and modelled through spiking neuron models (mathematical expressions derived mainly from an RC circuit). It can be considered as a basic unit to build more complex optical spiking neural networks. The main advantage of this system is its low-cost compared to a FPGA or even a neuromorphic system. The second main advantage is that, given that the system uses optical components, it can speed up the existing hardware systems. With this work we aim to contribute in the development of more efficient and less costly neuromorphic systems.