Modeling and Optimal Controller Based on Disturbance Detector for the Stabilization of a Three-link Inverted Pendulum Mobile Robot
Abstract
1. Introduction
2. Dynamic Model of the Mobile Robot
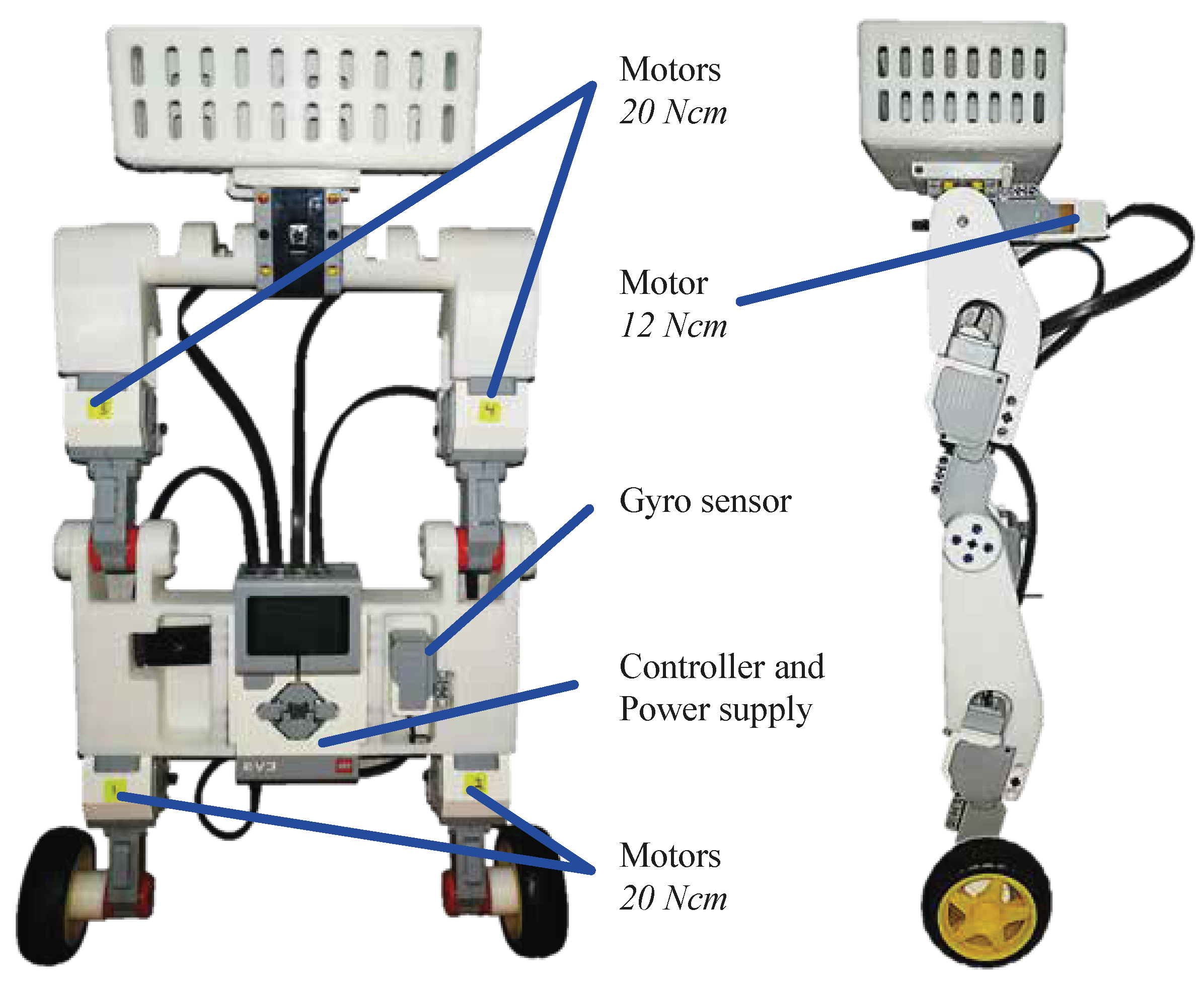
3. Design and Assembly of the Mobile Robot with Five Degrees of Freedom
4. Motors Control of the Mobile Robot
Torque Equation
5. Optimal Stabilization
5.1. State Variables Model of Mobile Robot
5.2. Optimal Control for Systems with Disturbances
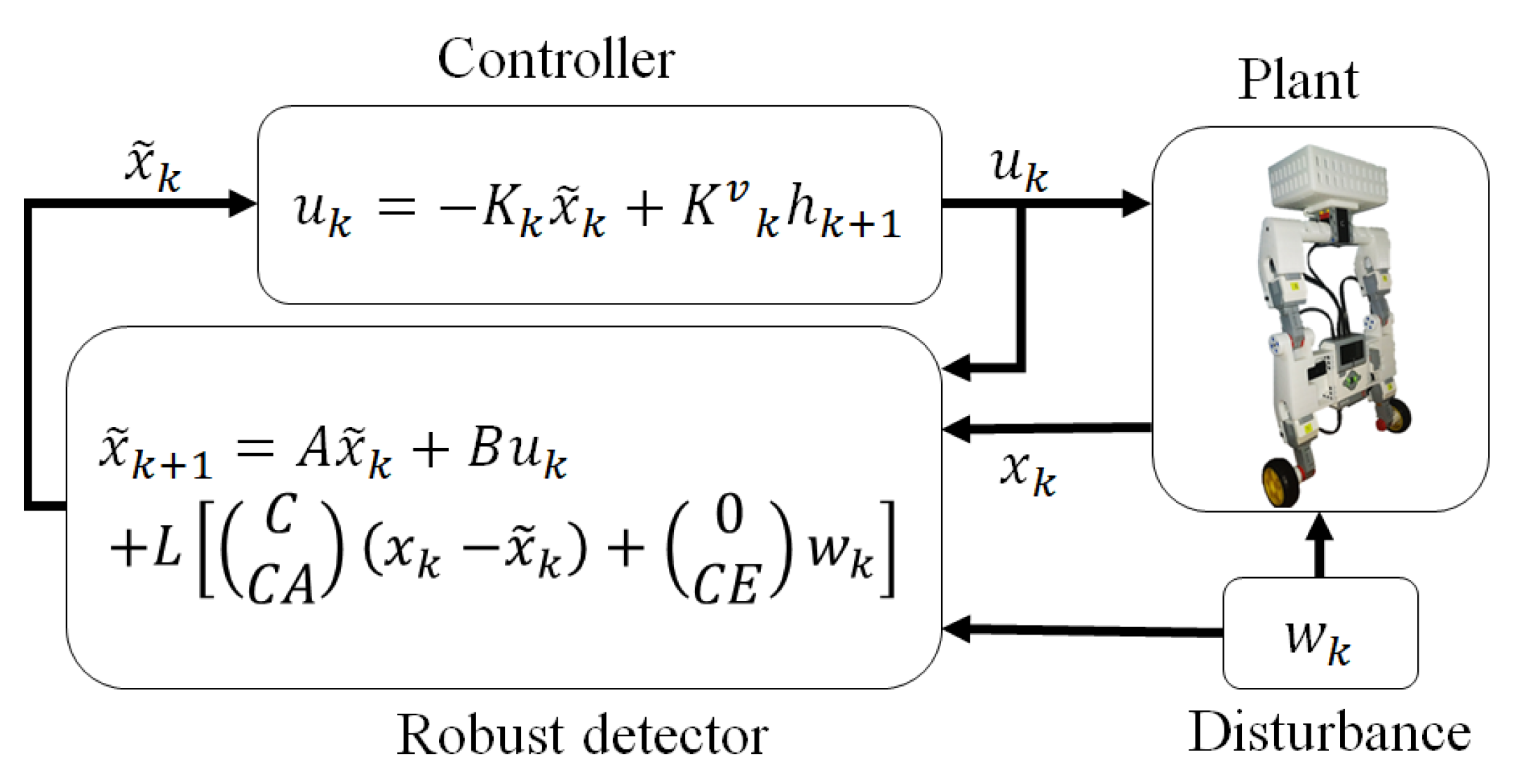
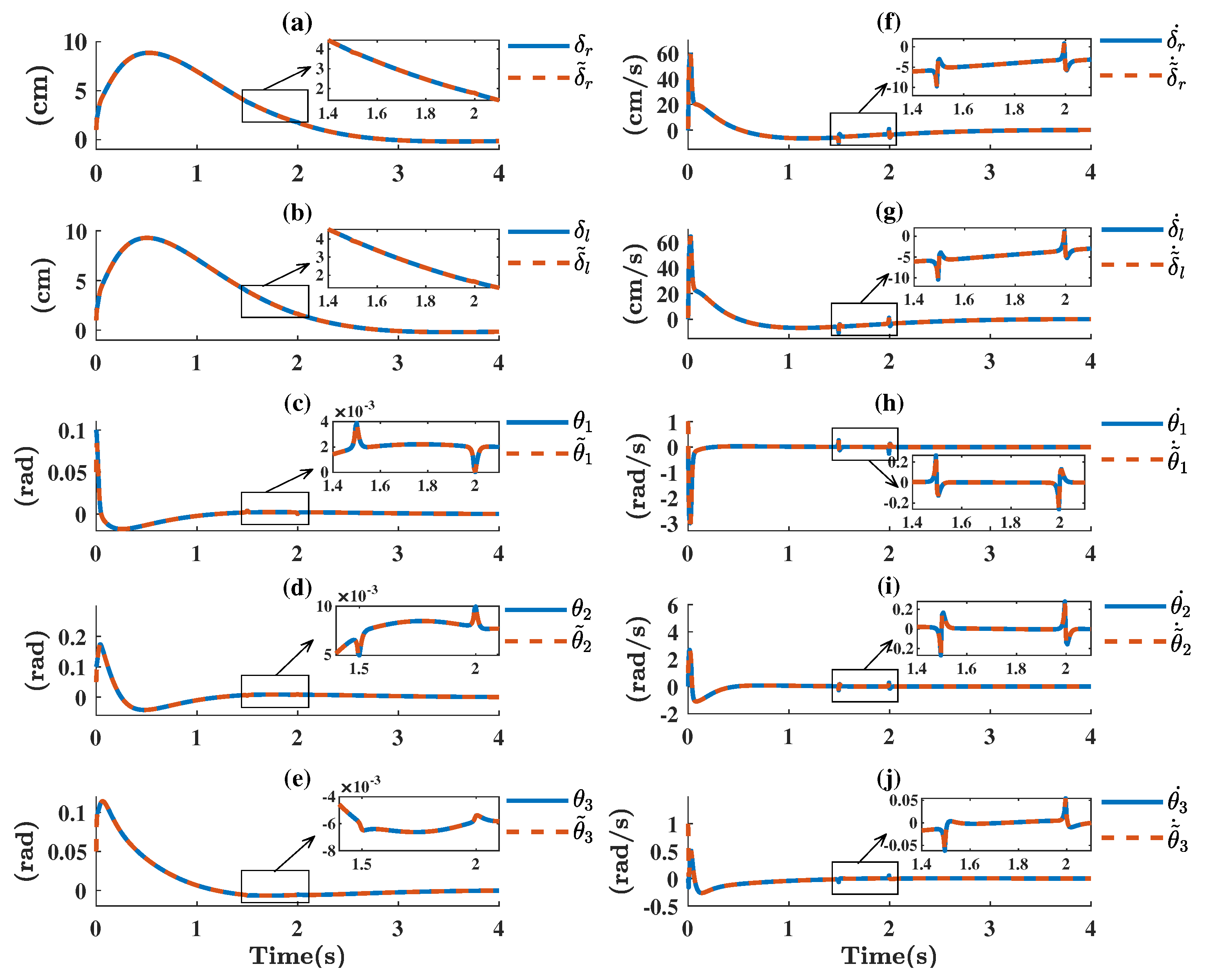
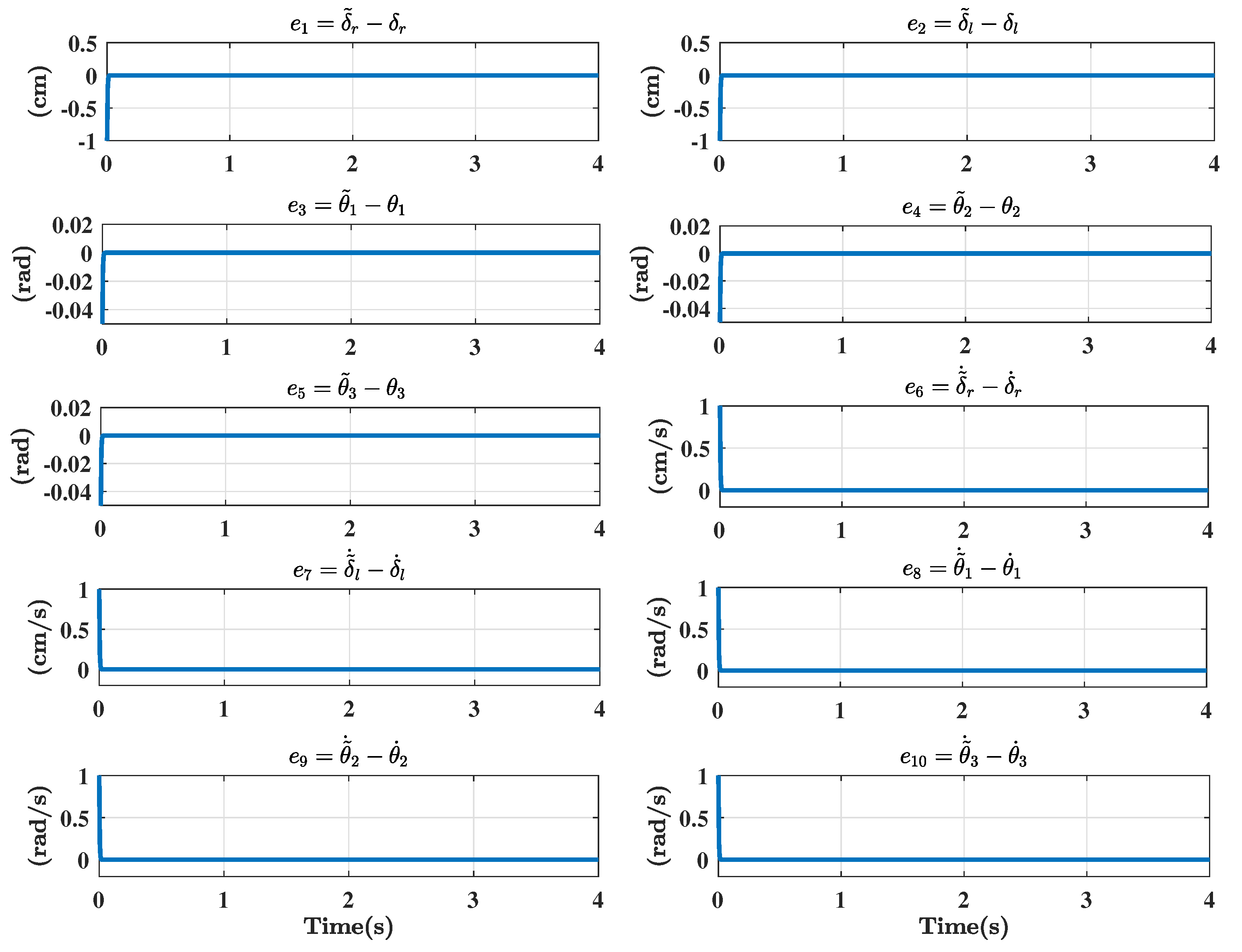
6. Robust Detector for Systems with Disturbances
Synthesis of a Robust Detector for Disturbances
7. Optimal Control Design Based on a Disturbance Detector to Stabilize the Mobile Robot
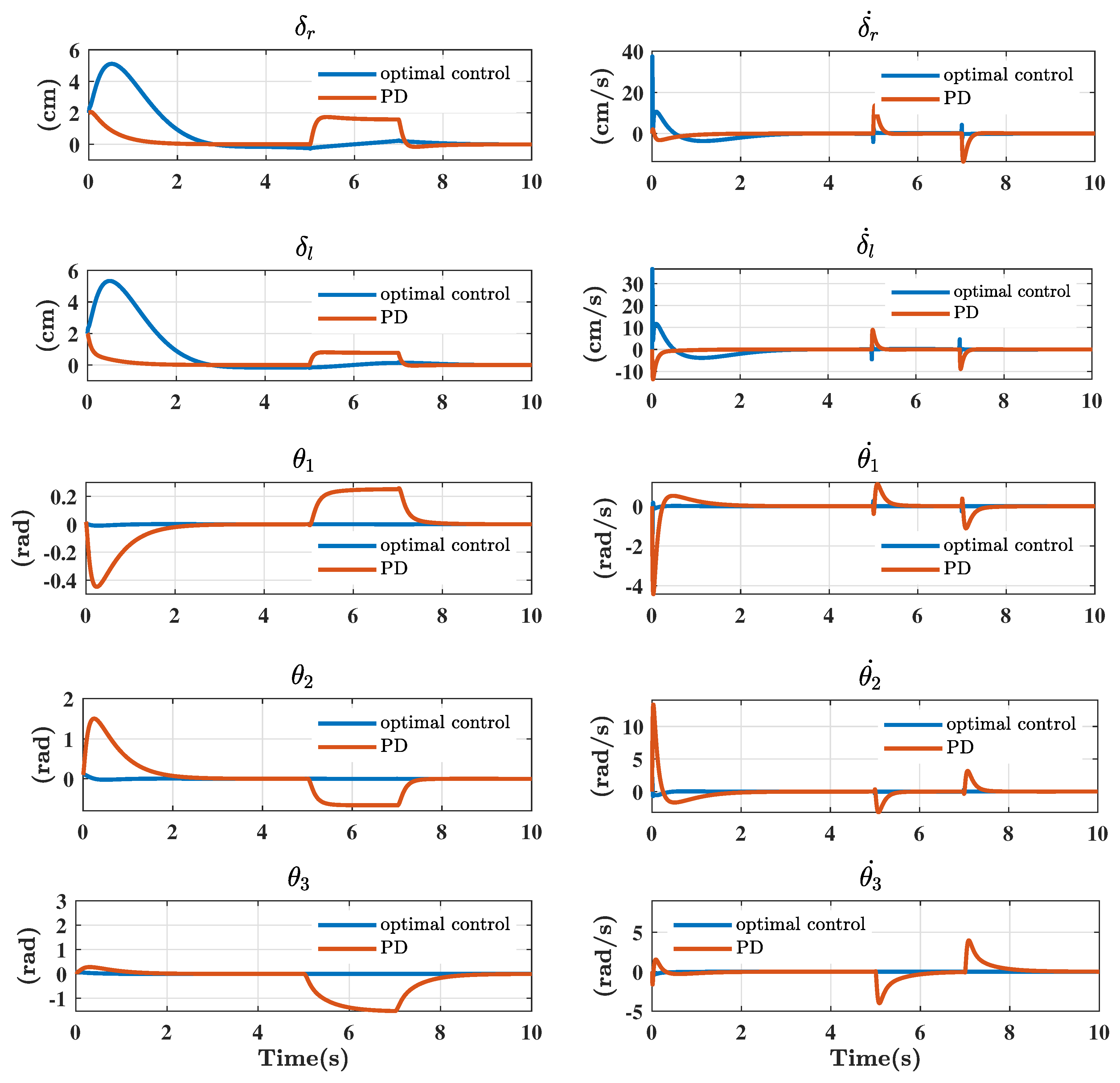
Simulations
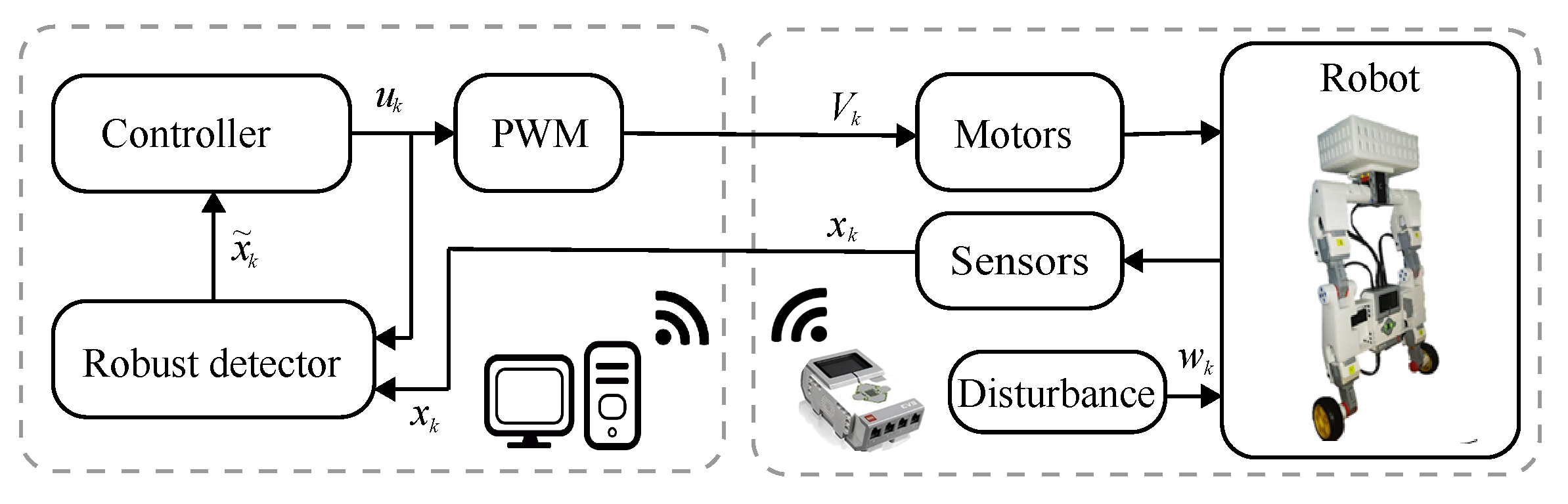
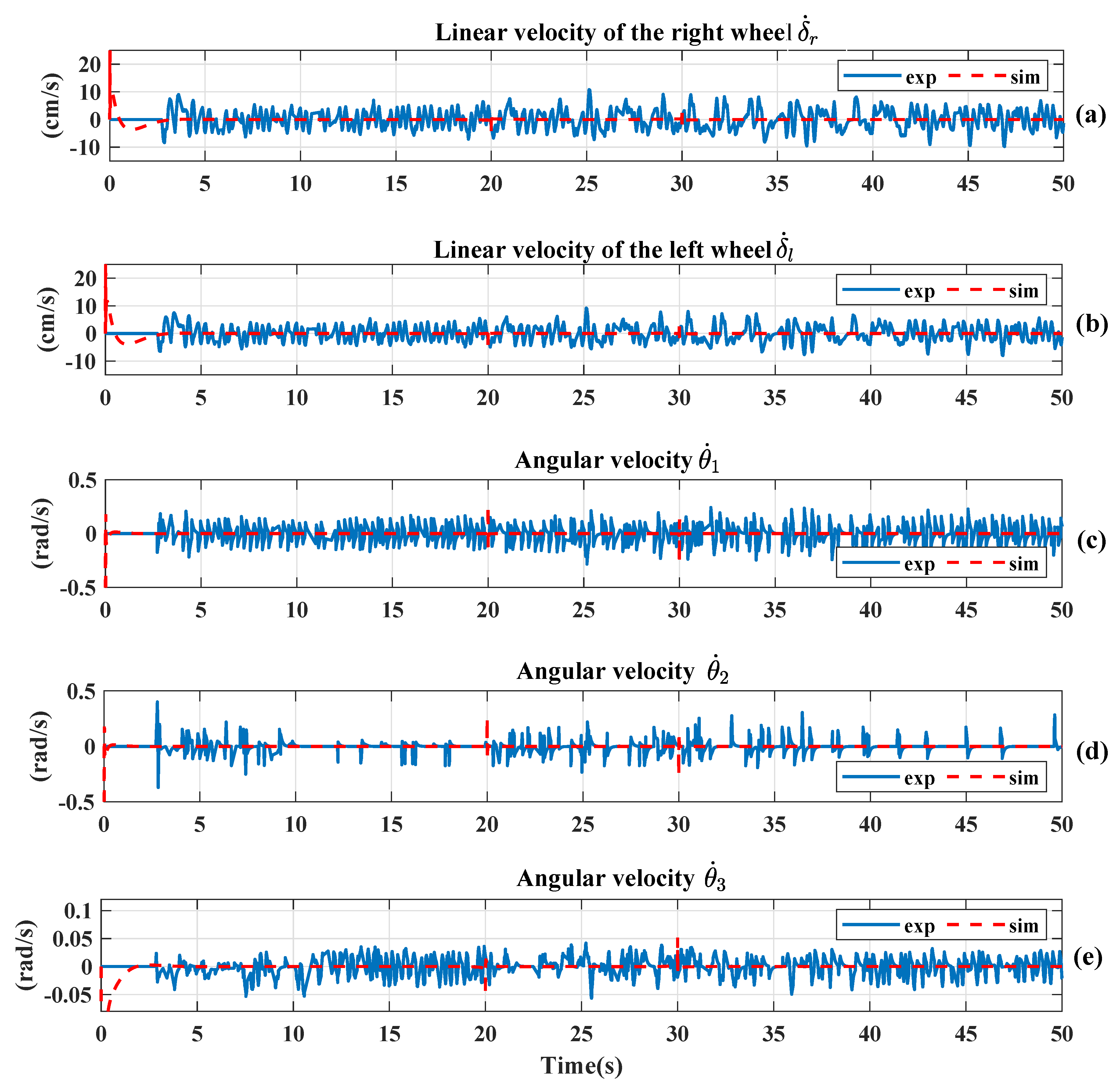
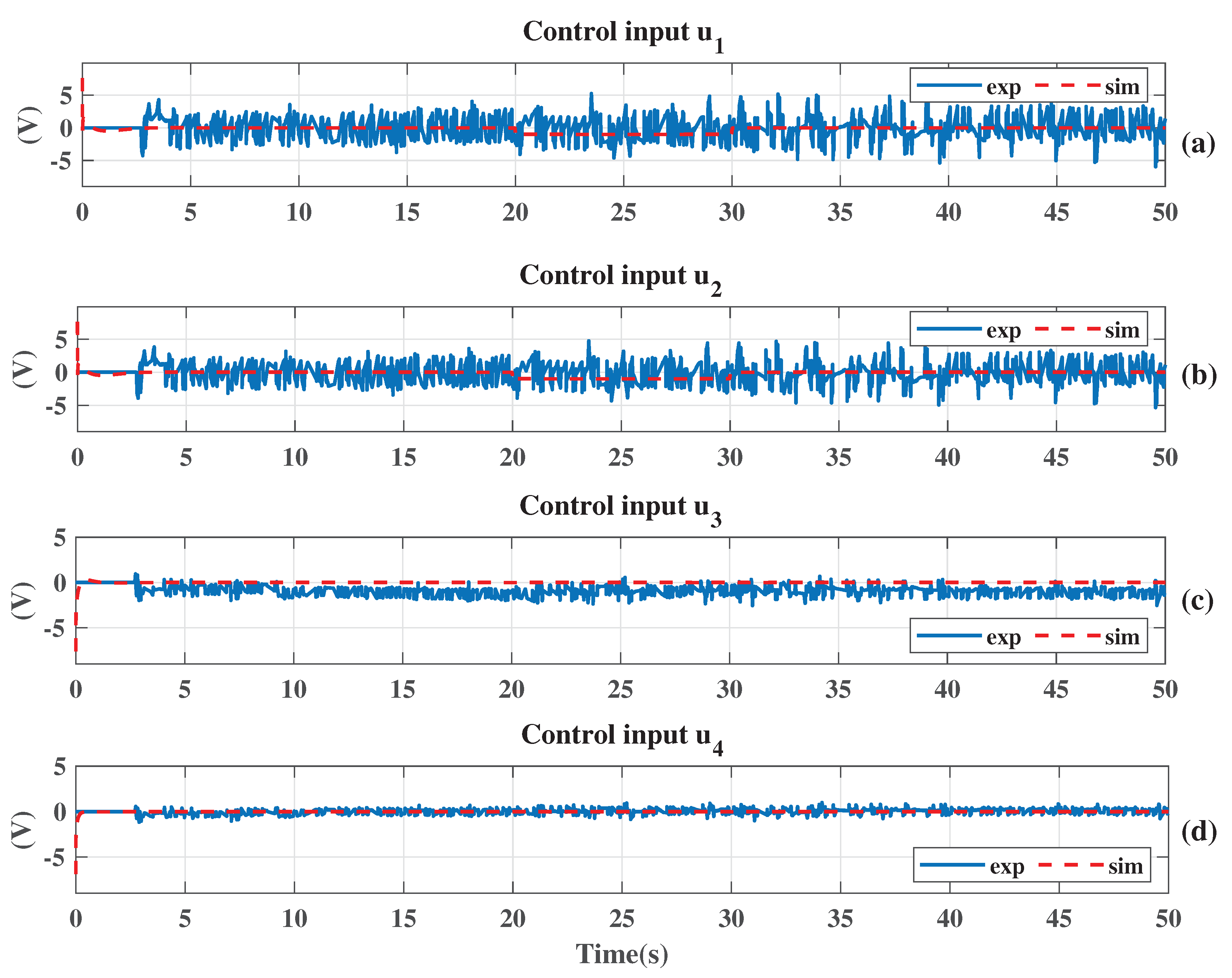
8. Real-Time Experimentation
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Control Systems
Appendix B. Matrices of the Mobile Robot Non-Lnear Model
Appendix C. Numerical Matrices of the Mobile Robot
Appendix D. Optimal Controller Based on Disturbance Detector vs. PD Controller
Abbreviations
| PID | Proportional-Integral-Derivative |
| PD | Proportional-Derivative |
| LQR | Linear Quadratic Regulator |
| CG | Center of Gravity |
| CM | Center of Mass |
| PLA | Polylactic Acid |
| RPM | Revolutions per minute |
| EMF | Electromotive Force |
| PWM | Pulse Width Modulation |
References
- Gopikrishnan, S.; Kesarkar, A.A.; Selvaganesan, N. Design of fractional controller for cart-pendulum SIMO system. In Proceedings of the IEEE International Conference on Advanced Communication Control and Computing Technologies (ICACCCT), Ramanathapuram, India, 23–25 August 2012; pp. 170–174. [Google Scholar]
- Inoue, A.; Deng, M.; Tanabe, T. Practical swing-up control system design of cart-type double inverted pendulum. In Proceedings of the IEEE Chinese Control Conference, Harbin, China, 7–11 August 2006; pp. 2141–2146. [Google Scholar]
- Eom, M.; Chwa, D. Robust swing-up and balancing control using a nonlinear disturbance observer for the pendubot system with dynamic friction. IEEE Trans. Robot. 2015, 31, 331–343. [Google Scholar] [CrossRef]
- Cao, J.-Q.; Lai, X.-Z.; Min, W. Position control method for a planar Acrobot based on fuzzy control. In Proceedings of the IEEE 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 923–927. [Google Scholar]
- Lee, H.J.; Kim, H.W.; Jung, S. Development of a mobile inverted pendulum robot system as a personal transportation vehicle with two driving modes: TransBOT. In Proceedings of the IEEE World Automation Congress, Kobe, Japan, 19–23 September 2010; pp. 1–5. [Google Scholar]
- Mohamed, S.A.; Maged, S.A.; Awad, M.I. Design and Control of the Lower Part of Humanoid Biped Robot. In Proceedings of the IEEE 3rd International Conference on Robotics and Automation Engineering (ICRAE), Guangzhou, China, 17–19 November 2018; pp. 19–23. [Google Scholar]
- Hamatani, S.; Murakami, T. A novel steering mechanism of two-wheeled wheel chair for stability improvement. In Proceedings of the IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 2154–2159. [Google Scholar]
- Solis, J.; Nakadate, R.; Yoshimura, Y.; Hama, Y.; Takanishi, A. Development of the two-wheeled inverted pendulum type mobile robot WV-2R for educational purposes. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 2347–2352. [Google Scholar]
- Reck, R.M.; Sreenivas, R.S. Developing an affordable and portable control systems laboratory kit with a Raspberry Pi. Electronics 2016, 5, 36. [Google Scholar] [CrossRef]
- Ordóñez Cerezo, J.; Castillo Morales, E.; Cañas Plaza, J.M. Control system in open-source FPGA for a self-balancing robot. Electronics 2019, 8, 198. [Google Scholar] [CrossRef]
- Yamamoto, Y. NXTway-GS Model-Based Design-Control of Self-Balancing Two-Wheeled Robot Built with LEGO Mindstorms NXT. Available online: https://la.mathworks.com/matlabcentral/fileexchange/19147-nxtway-gs-self-balancing-two-wheeled-robot-controller-design (accessed on 17 August 2020).
- Nawawi, S.W.; Ahmad, M.N.; Osman, J.H.S. Control of two-wheels inverted pendulum mobile robot using full order sliding mode control. In Proceedings of the International Conference on Man-Machine Systems, Budapest, Hungary, 9–12 October 2006; pp. 15–16. [Google Scholar]
- Chhotray, A.; Parhi, D. Navigational control analysis of two-wheeled self-balancing robot in an unknown terrain using back-propagation neural network integrated modified DAYANI approach. Robotica 2019, 37, 1346–1362. [Google Scholar] [CrossRef]
- Odry, À.; Fullér, R. Comparison of optimized PID and fuzzy control strategies on a mobile pendulum robot. In Proceedings of the IEEE 12th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 17–19 May 2018; pp. 207–212. [Google Scholar]
- Raffo, G.V.; Ortega, M.G.; Madero, V.; Rubio, F.R. Two-wheeled self-balanced pendulum workspace improvement via underactuated robust nonlinear control. Control. Eng. Pract. 2019, 44, 231–242. [Google Scholar] [CrossRef]
- Trentin, J.; Da Silva, S.; Ribeiro, J.M.D.S.; Schaub, H. Inverted Pendulum Nonlinear Controllers Using Two Reaction Wheels: Design and Implementation. IEEE Access 2020, 8, 74922–74932. [Google Scholar] [CrossRef]
- Hsu, C.F.; Kao, W.F. Double-loop fuzzy motion control with CoG supervisor for two-wheeled self-balancing assistant robots. Int. J. Dyn. Control. 2020, 8, 851–866. [Google Scholar] [CrossRef]
- Li, Z.; Yang, C.; Fan, L. Advanced Control of Wheeled Inverted Pendulum Systems; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Odry, Á.; Fullér, R.; Rudas, I.J.; Odry, P. Fuzzy control of self-balancing robots: A control laboratory project. Comput. Appl. Eng. Educ. 2020, 28, 512–535. [Google Scholar] [CrossRef]
- Lin, S.; Tsai, C. Development of a self-balancing human transportation vehicle for the teaching of feedback control. IEEE TRansactions Educ. 2008, 52, 157–168. [Google Scholar] [CrossRef]
- Reyes, F. Robótica: Control de Robots Manipuladores; Alfaomega Grupo Editor: Mexico city, Mexico, 2011. [Google Scholar]
- Garber, G. Learning LEGO Mindstorms EV3; Packt Publishing Ltd.: Birmingham, UK, 2015. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Sinha, A. Linear Systems: Optimal and Robust Control; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Kiumarsi-Khomartash, B.; Lewis, F.L.; Naghibi-Sistani, M.B.; Karimpour, A. Optimal tracking control for linear discrete-time systems using reinforcement learning. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 3845–3850. [Google Scholar]
- Ding, X. Steven Model-Based Fault Diagnosis Techniques; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 9783540763031. [Google Scholar]
- Ogata, K. Discrete-Time Control Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1995; Volume 2. [Google Scholar]
- Kailath, T. Linear Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1980; Volume 156. [Google Scholar]
- Fortuna, L.; Frasca, M. Optimal and Robust Control: Advanced Topics with Matlab; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Fadali, M.S.; Visioli, A. Digital Control Engineering: Analysis and Design; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
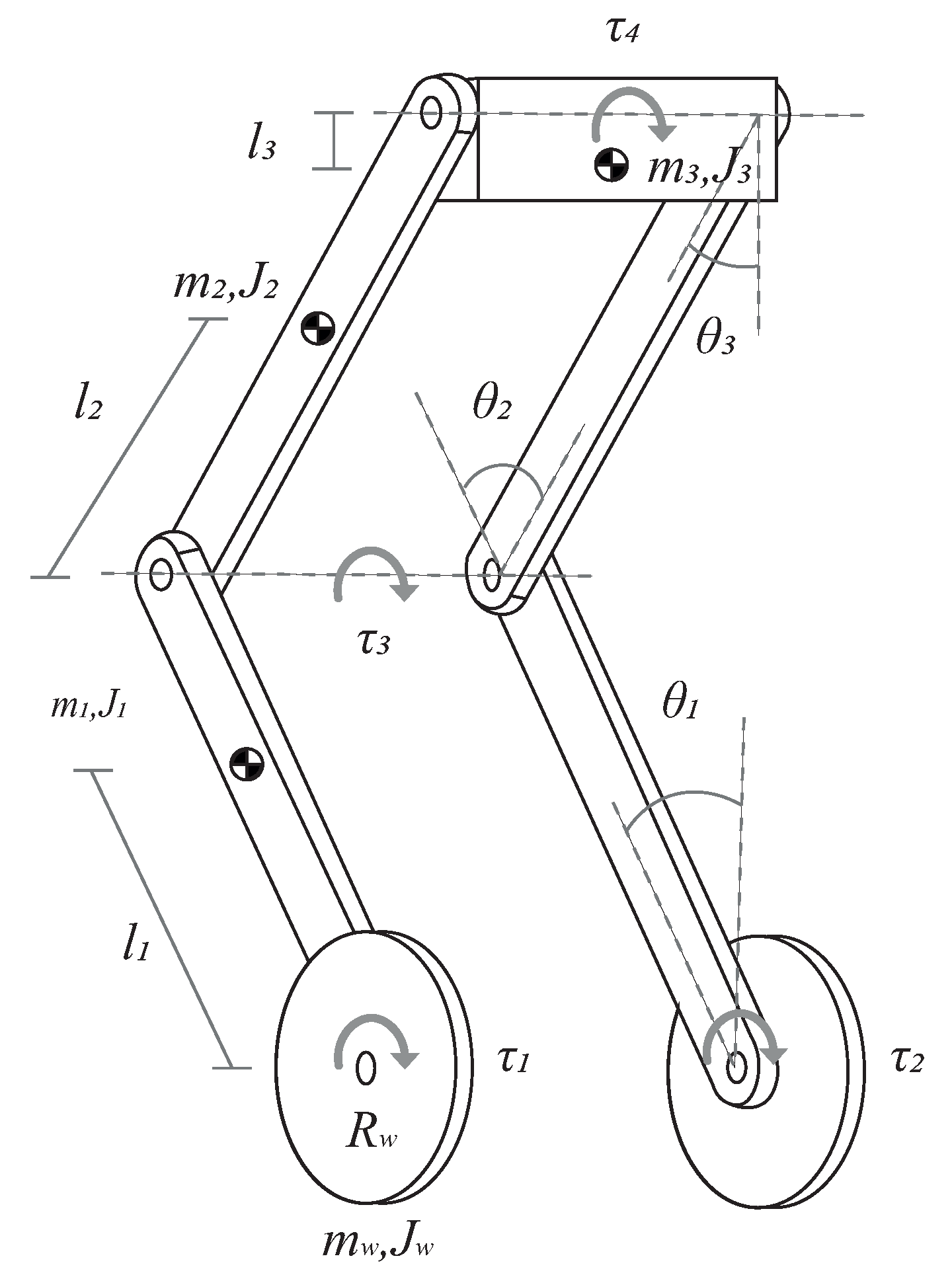



| Parameter | Description | Value |
|---|---|---|
| Length to CG of link 1 | 10 cm | |
| Length to CG of link 2 | 7.5 cm | |
| Length to CG of link 3 | 5 cm | |
| Mass of link 1 | 663 g | |
| Mass of link 2 | 290 g | |
| Mass of link 3 | 205 g | |
| Mass of the wheel | 53 g | |
| Radius of the wheel | 3.4 cm | |
| H | Distance between the wheels | 25.5 cm |
| Moment of inertia around the CM of link 1 | 22,100 gcm | |
| Moment of inertia around the CM of link 2 | 5437.5 gcm | |
| Moment of inertia around the CM of link 3 | 1708.3 gcm | |
| Moment of inertia of the wheel | 306.34 gcm |
| Motor 1 | ||||||
| Motor 2 | ||||||
| Motor 3 | ||||||
| Motor 4 | ||||||
| Motor 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jordán-Martínez, L.A.; Figueroa-García, M.G.; Pérez-Cruz, J.H. Modeling and Optimal Controller Based on Disturbance Detector for the Stabilization of a Three-link Inverted Pendulum Mobile Robot. Electronics 2020, 9, 1821. https://doi.org/10.3390/electronics9111821
Jordán-Martínez LA, Figueroa-García MG, Pérez-Cruz JH. Modeling and Optimal Controller Based on Disturbance Detector for the Stabilization of a Three-link Inverted Pendulum Mobile Robot. Electronics. 2020; 9(11):1821. https://doi.org/10.3390/electronics9111821
Chicago/Turabian StyleJordán-Martínez, Luis Alfonso, Maricela Guadalupe Figueroa-García, and José Humberto Pérez-Cruz. 2020. "Modeling and Optimal Controller Based on Disturbance Detector for the Stabilization of a Three-link Inverted Pendulum Mobile Robot" Electronics 9, no. 11: 1821. https://doi.org/10.3390/electronics9111821
APA StyleJordán-Martínez, L. A., Figueroa-García, M. G., & Pérez-Cruz, J. H. (2020). Modeling and Optimal Controller Based on Disturbance Detector for the Stabilization of a Three-link Inverted Pendulum Mobile Robot. Electronics, 9(11), 1821. https://doi.org/10.3390/electronics9111821





