GPU Accelerated Nonlinear Electronic Circuits Solver for Transient Simulation of Systems with Large Number of Components
Abstract
1. Introduction
2. Methodology
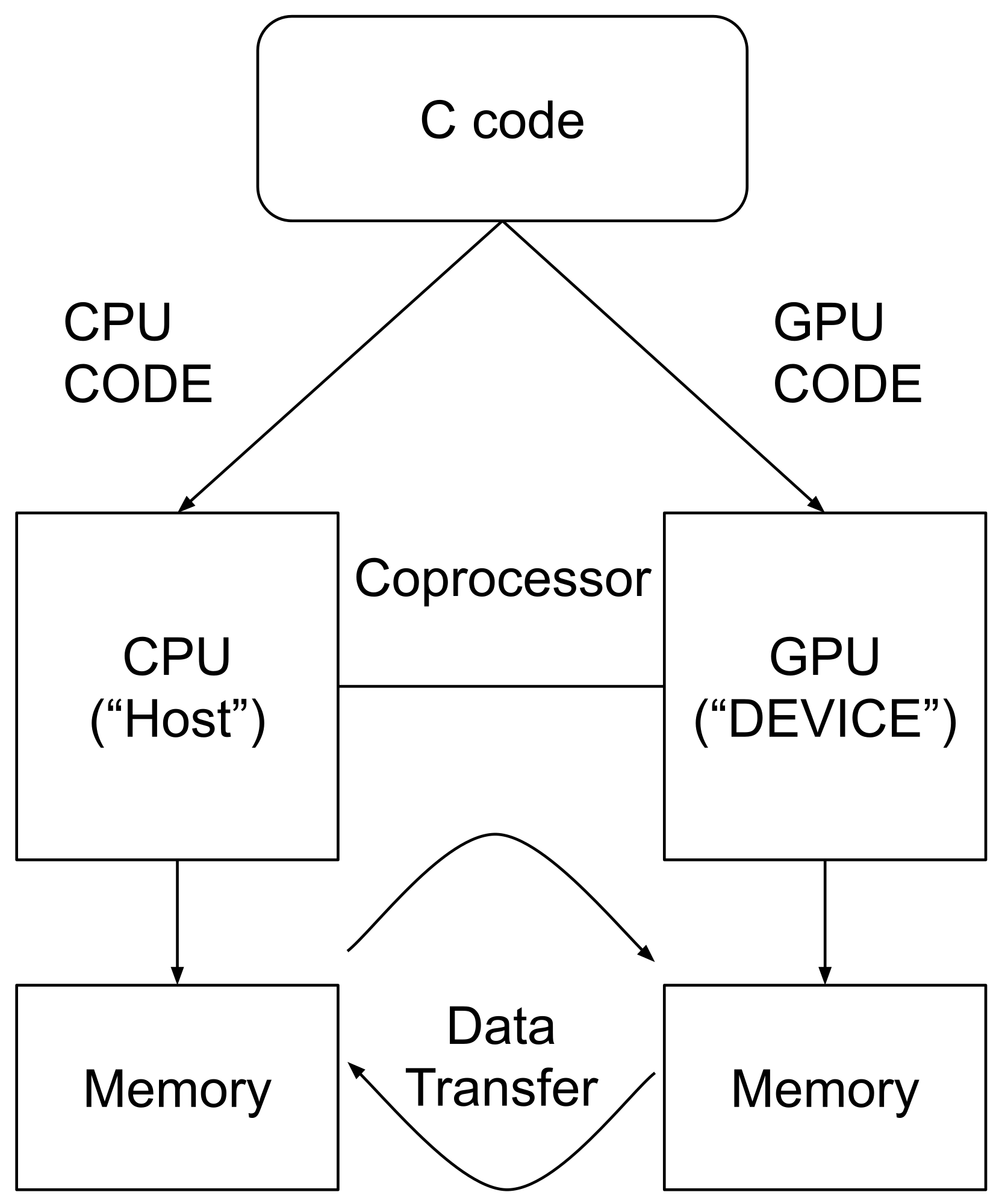
2.1. Simulation
2.2. Parallelization
2.3. Accuracy
| Algorithm 1 Biconjugate Gradient Stabilized Method Algorithm [2]. |
| for do |
| if then |
| break |
| end if |
| end for |
2.4. Setup
3. Implementation
| Algorithm 2 Transient analysis process using CUDA parallel calculation of LU factorization on a graphics card. |
| MNA (HOST) |
| Initial Matrix Composition (HOST) |
| Device Memory and Data Copy from HOST to DEVICE |
| Pivoting, Reordering (DEVICE) |
| for Timeline do |
| Linear system (LU Factorization) (DEVICE) |
| repeat {Nonlinear system (Newton-Raphson) (DEVICE) } |
| Jacobian matrix (LU Factorization) (DEVICE) |
| Next estimate (vector-matrix product) (DEVICE) |
| Residual (vector norm) (DEVICE) |
| Copy result from DEVICE to HOST |
| until Stopping criteria |
| if not (Convergence) then |
| return Convergence problem |
| end if |
| Adaptive Memory Realocation (DEVICE) |
| Optional Pivoting and Reordering (DEVICE) |
| end for |
| Free DEVICE memory |
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lippuner, J. NVIDIA CUDA; Technical Report; Los Alamos National Laboratory (LANL): Los Alamos, NM, USA, 2019.
- Van der Vorst, H.A. Bi-CGSTAB: A Fast and Smoothly Converging Variant of Bi-CG for the Solution of Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 1992, 13, 631–644. [Google Scholar] [CrossRef]
- Garg, A.; Gupta, D.; Sahadev, P.P.; Saxena, S. Comprehensive analysis of the uses of GPU and CUDA in soft-computing techniques. In Proceedings of the 2019 6th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 7–8 March 2019; pp. 584–589. [Google Scholar]
- Myasishchev, A.; Lienkov, S.; Dzhulii, V.; Muliar, I. Using GPU NVIDIA for Linear Algebra Problems. In Collection of scientific Works of the Military Institute of Kyiv National Taras Shevchenko University; Taras Shevchenko National University of Kyiv: Kyiv, Ukraine, 2019. [Google Scholar]
- Tsai, Y.M.; Cojean, T.; Anzt, H. Sparse linear algebra on AMD and NVIDIA GPUS–the race is on. In Proceedings of the International Conference on High Performance Computing, Frankfurt am Main, Germany, 22–25 June 2020; pp. 309–327. [Google Scholar]
- Yang, C. Hierarchical Roofline Analysis: How to Collect Data using Performance Tools on Intel CPUs and NVIDIA GPUs. arXiv 2020, arXiv:2009.02449. [Google Scholar]
- Li, H.; Ge Li, K.; An, J.; Ge Li, K. An Online and Scalable Model for Generalized Sparse Non-negative Matrix Factorization in Industrial Applications on Multi-GPU. IEEE Trans. Ind. Informat. 2019, 1. [Google Scholar] [CrossRef]
- Lee, J.; Kang, S.; Yu, Y.; Jo, Y.; Kim, S.; Park, Y. Optimization of GPU-based Sparse Matrix Multiplication for Large Sparse Networks. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 925–936. [Google Scholar]
- Dufrechou, E.; Ezzatti, P. Solving Sparse Triangular Linear Systems in Modern GPUs: A Synchronization-Free Algorithm. In Proceedings of the 2018 26th Euromicro International Conference on Parallel, Distributed and Network-based Processing (PDP), Cambridge, UK, 21–23 March 2018; pp. 196–203. [Google Scholar]
- Aslam, M.; Riaz, O.; Mumtaz, S.; Asif, A.D. Performance Comparison of GPU-Based Jacobi Solvers Using CUDA Provided Synchronization Methods. IEEE Access 2020, 8, 31792–31812. [Google Scholar] [CrossRef]
- Dziekonski, A.; Fotyga, G.; Mrozowski, M. Preconditioners With Low Memory Requirements for Higher-Order Finite-Element Method Applied to Solving Maxwell’s Equations on Multicore CPUs and GPUs. IEEE Access 2018, 6, 53072–53079. [Google Scholar] [CrossRef]
- Thuerck, D.; Naumov, M.; Garland, M.; Goesele, M. A Block-Oriented, Parallel and Collective Approach to Sparse Indefinite Preconditioning on GPUs. In Proceedings of the 2018 IEEE/ACM 8th Workshop on Irregular Applications: Architectures and Algorithms (IA3), Dallas, TX, USA, 12 November 2018; pp. 1–10. [Google Scholar]
- He, G.; Yin, R.; Gao, J. An efficient sparse approximate inverse preconditioning algorithm on GPU. Concurr. Comput. Pract. Exp. 2020, 32, e5598. [Google Scholar] [CrossRef]
- Lee, W.; Achar, R.; Nakhla, M.S. Dynamic GPU Parallel Sparse LU Factorization for Fast Circuit Simulation. IEEE Trans. Very Large Scale Integr. Syst. 2018, 26, 2518–2529. [Google Scholar] [CrossRef]
- Santen, V.; Amrouch, H.; Henkel, J. Reliability Estimations of Large Circuits in Massively-Parallel GPU-SPICE. In Proceedings of the 2018 IEEE 24th International Symposium on On-Line Testing And Robust System Design (IOLTS), Platja d’Aro, Spain, 2–4 July 2018; pp. 143–146. [Google Scholar] [CrossRef]
- Lannutti, F.; Menichelli, F.; Olivieri, M. CUSPICE: The revolutionary NGSPICE on CUDA Platforms. In Proceedings of the 12th MOS-AK ESSDERC/ESSCIRC Workshop, Venice Lido, Italy, 26 September 2014. [Google Scholar]
- Ho, C.; Ruehli, A.E.; Brennan, P.A. The Modified Nodal Approach to Network Analysis. IEEE Trans. Circuits Syst. 1975, 22, 504–509. [Google Scholar]
- Černỳ, D.; Dobeš, J. Common LISP as Simulation Program (CLASP) of Electronic Circuits. Radioengineering 2011, 20, 880–889. [Google Scholar]
- Cerny, D.; Dobes, J. Adaptive sparse matrix indexing technique for simulation of electronic circuits based on λ-calculus. In Proceedings of the 2015 European Conference on Circuit Theory and Design (ECCTD), Trondheim, Norway, 24–26 August 2015; pp. 1–4. [Google Scholar]
- Corporation, N. Incomplete-LU and Cholesky Preconditioned Iterative Methods Using cuSPARSE and cuBLAS. Available online: https://docs.nvidia.com/cuda/incomplete-lu-cholesky/index.html (accessed on 15 October 2020).
- De Paula, L.; Soares, A. Parallel Implementation of the BiCGStab(2) Method in GPU Using CUDA and Matlab for Solution of Linear Systems. J. Commun. Comput. 2015, 11, 339–346. [Google Scholar] [CrossRef]
- Gubian, P.; Zanella, M. Stability properties of integration methods in SPICE transient analysis. In Proceedings of the IEEE International Sympoisum on Circuits and Systems, Singapore, 11–14 June 1991. [Google Scholar]
- Vogt, H.; Hendrix, M.; Nenzi, P.; Warning, D. Ngspice Users Manual Version 33. Available online: http://ngspice.sourceforge.net/ (accessed on 18 October 2020).
- Dobes, J. A modified Markowitz criterion for the fast modes of the LU factorization. In Proceedings of the 48th Midwest Symposium on Circuits and Systems, Covington, KY, USA, 7–10 August 2005; Volume 2, pp. 955–959. [Google Scholar]
- Grigori, L.; Cosnard, M.; Ng, E. On the row merge tree for sparse LU factorization with partial pivoting. BIT Numer. Math. 2006, 47, 45–76. [Google Scholar] [CrossRef]
- Bateman, D.; Adler, A. Sparse Matrix Implementation in Octave. arXiv 2006, arXiv:cs/0604006. [Google Scholar]
- Gulati, K.; Croix, J.; Khatri, S.; Shastry, R. Fast circuit simulation on graphics processing units. In Proceedings of the 2009 Asia and South Pacific Design Automation Conference, Yokohama, Japan, 19–22 January 2009; pp. 403–408. [Google Scholar] [CrossRef]
- Jagtap, S.; Rao, Y. GPU accelerated circuit analysis using machine learning-based parallel computing model. SN Appl. Sci. 2020, 2, 883. [Google Scholar] [CrossRef]
- Lei, C.U.; Man, K.; Zhang, N.; Wu, Y. GPU-Accelerated Non-Linear Analog and Mixed-Signal Circuit Transient Simulation. In Proceedings of the International MultiConference of Engineers and Computer Scientists 2012 (IMECS 2012), Hong Kong, China, 14–16 March 2012; Volume 2, pp. 1151–1152. [Google Scholar]
- Lee, K. Nvidia GeForce RTX 2080 Ti Review. Available online: https://www.techradar.com/reviews/nvidia-geforce-rtx-2080-ti-review (accessed on 1 January 2020).
- Zhao, Z.; Zhang, Q.; Tan, G.; Xu, J.M. A new preconditioner for CGS iteration in solving large sparse nonsymmetric linear equations in semiconductor device simulation. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1991, 10, 1432–1440. [Google Scholar] [CrossRef]
- Cerny, D.; Dobes, J. Composing Scalable Solver for Simulation of Electronic Circuits in SPICE. In Proceedings of the 2018 International Conference on Intelligent and Innovative Computing Applications (ICONIC), Plaine Magnien, Mauritius, 6–7 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Dobes, J.; Cerny, D.; Biolek, D. Efficient procedure for solving circuit algebraic-differential equations with modified sparse LU factorization improving fill-in suppression. In Proceedings of the 20th European Conference on Circuit Theory and Design (ECCTD), Linkoping, Sweden, 29–31 August 2011; pp. 689–692. [Google Scholar] [CrossRef]
- Blackford, L.S.; Petitet, A.; Pozo, R.; Remington, K.; Whaley, R.C.; Demmel, J.; Dongarra, J.; Duff, I.; Hammarling, S.; Henry, G.; et al. An updated set of basic linear algebra subprograms (BLAS). ACM Trans. Math. Softw. 2002, 28, 135–151. [Google Scholar]
- Langdon, W.B. A many threaded CUDA interpreter for genetic programming. In European Conference on Genetic Programming; Springer: Berlin/Heidelberg, Germany, 2010; pp. 146–158. [Google Scholar]
- Chen, X.; Ren, L.; Wang, Y.; Yang, H. GPU-Accelerated Sparse LU Factorization for Circuit Simulation with Performance Modeling. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 786–795. [Google Scholar] [CrossRef]
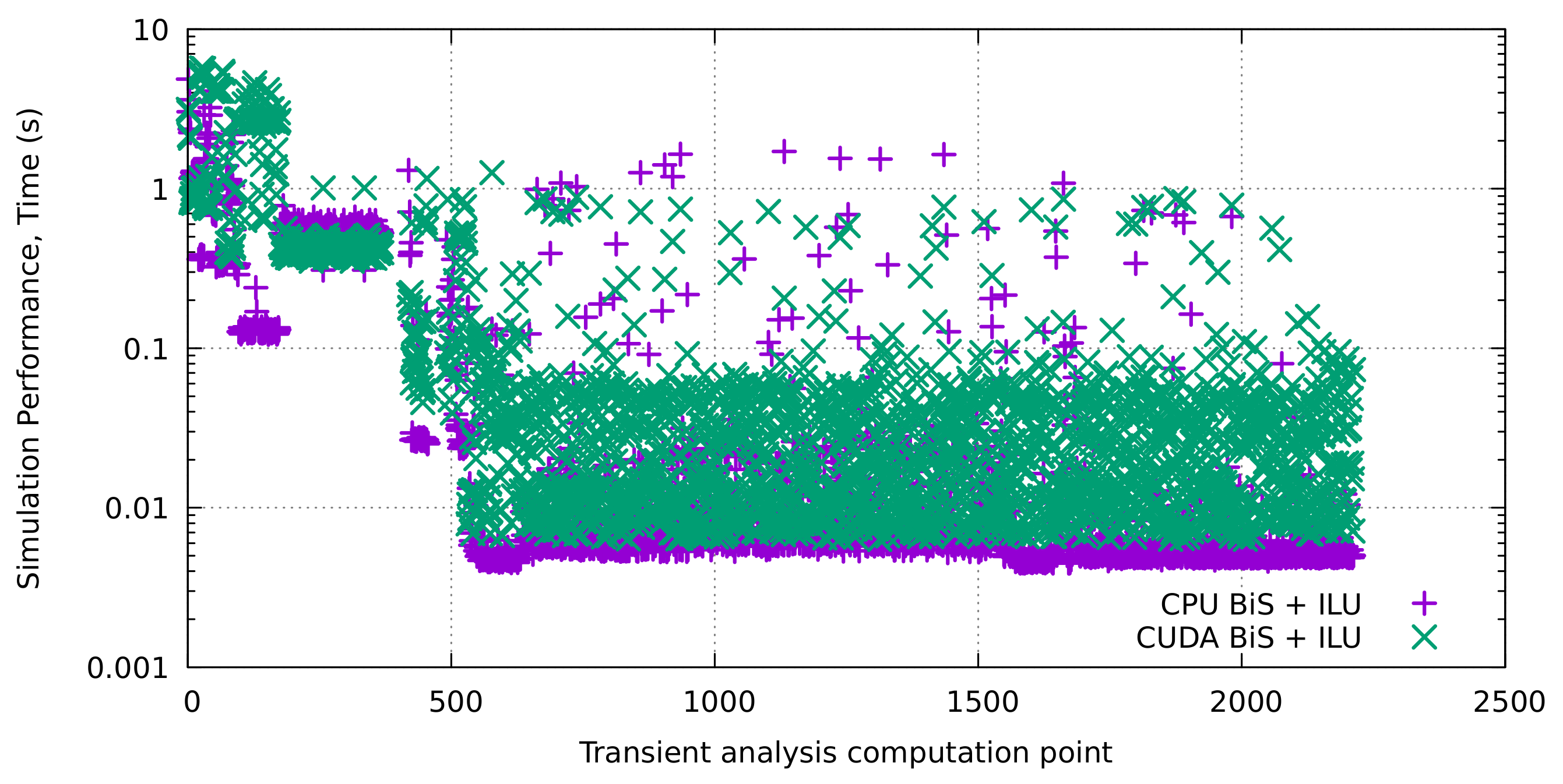
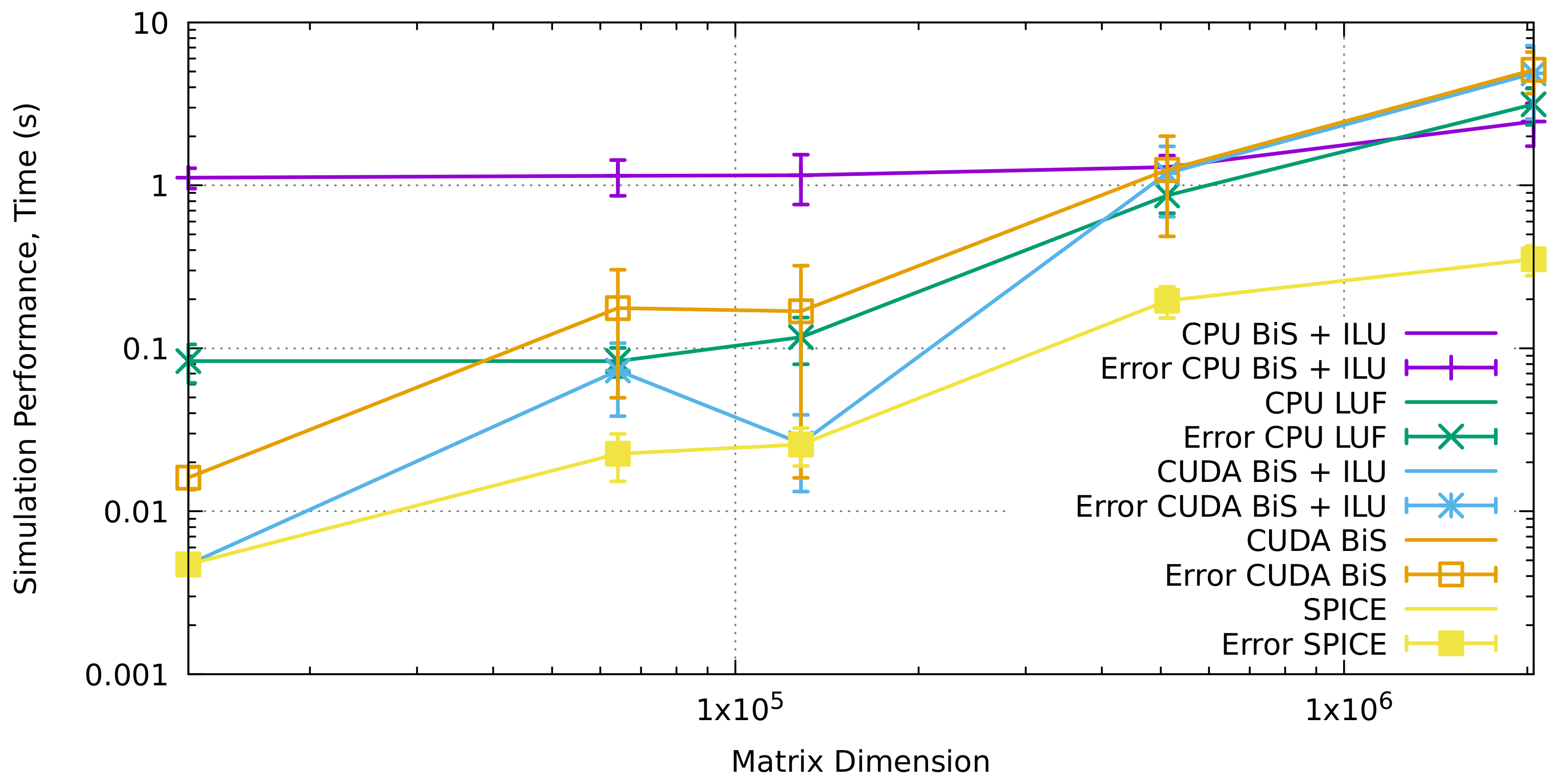
| Matrix Dimension | nnz | Factorization Time (s) |
|---|---|---|
| 2,048,129 | 10,581,374 | 2220.86 |
| 1,024,129 | 5,297,272 | 540.19 |
| 512,129 | 2,679,498 | 71.79 |
| 128,129 | 661,994 | 8.27 |
| 64,129 | 338,004 | 1.12 |
| 12,629 | 65,248 | 0.098 |
| Simulation Accuracy | ||||||
|---|---|---|---|---|---|---|
| Dimension | nnz | CPU BiS + ILU | CPU LUF | CUDA BiS + ILU | CUDA BiS | SPICE LUF |
| 12,629 | 65,248 | |||||
| 64,129 | 331,124 | |||||
| 128,129 | 661,994 | |||||
| 512,129 | 2,707,540 | |||||
| 2,048,129 | 10,581,374 | |||||
| Simulation Performance, Time (s) | ||||||
| Dimension | nnz | CPU BiS + ILU | CPU LUF | CUDA BiS + ILU | CUDA BiS | SPICE LUF |
| 12,629 | 65,248 | 1.115227 | 0.083508 | 0.004725 | 0.0161 | 0.004726 |
| 64,129 | 331,124 | 1.145234 | 0.083578 | 0.07299 | 0.176499 | 0.022568 |
| 128,129 | 661,994 | 1.152585 | 0.117093 | 0.026133 | 0.168729 | 0.025677 |
| 512,129 | 2,707,540 | 1.293445 | 0.867127 | 1.187724 | 1.245928 | 0.195807 |
| 2,048,129 | 10,581,374 | 2.462626 | 3.14092 | 4.873112 | 5.117584 | 0.352128 |
| Matrix Dimension | Grid Size | Block Size |
|---|---|---|
| 5,295,952 | (128,005, 1, 1) | (128, 1, 1) |
| 2,647,976 | (64,005, 1, 1) | (128, 1, 1) |
| 1,323,988 | (32,005, 1, 1) | (128, 1, 1) |
| 661,994 | (16,005, 1, 1) | (128, 1, 1) |
| 338,004 | (8005, 1, 1) | (128, 1, 1) |
| 130,496 | (4005, 1, 1) | (128, 1, 1) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Černý, D.; Dobeš, J. GPU Accelerated Nonlinear Electronic Circuits Solver for Transient Simulation of Systems with Large Number of Components. Electronics 2020, 9, 1819. https://doi.org/10.3390/electronics9111819
Černý D, Dobeš J. GPU Accelerated Nonlinear Electronic Circuits Solver for Transient Simulation of Systems with Large Number of Components. Electronics. 2020; 9(11):1819. https://doi.org/10.3390/electronics9111819
Chicago/Turabian StyleČerný, David, and Josef Dobeš. 2020. "GPU Accelerated Nonlinear Electronic Circuits Solver for Transient Simulation of Systems with Large Number of Components" Electronics 9, no. 11: 1819. https://doi.org/10.3390/electronics9111819
APA StyleČerný, D., & Dobeš, J. (2020). GPU Accelerated Nonlinear Electronic Circuits Solver for Transient Simulation of Systems with Large Number of Components. Electronics, 9(11), 1819. https://doi.org/10.3390/electronics9111819





