Neural Network-Based Aircraft Conflict Prediction in Final Approach Maneuvers
Abstract
1. Introduction
2. Neural Networks Basics
- will be the weight that connects the neuron in the layer with the neuron of the layer.
- will be the bias of the neuron of the layer.
- will be the activation of the neuron of the layer.
- will be what is called the weighted input. This will be used to sum up the following formula: .
- will be the error of the layer.
- . Simply put, this means that the error of any layer can be computed as the derivatives of the cost function in that activation layer multiplied by the derivative of the activation function of that layer.
- . This one means that the error of a layer can be computed as the error of the following layer multiplied by the weights of the following layer, multiplied by the derivative of the activation function of the current layer. This will be a key concept, because it gives a way of computing the error of a layer having the error of the following one.
- . In this case, the rate of change of the cost with respect to any bias is exactly the same as the error of that neuron.
- . Lastly, the rate of change of the cost with respect to any weight can be computed as the activation of its input layer multiplied by the error of its output layer.
- Feedforward: For each , compute and .
- Output error: Compute the error of the last layer as . Using the MSE as the cost error, and the sigmoid as the activation function, the derivatives are as easy as: , where is the expected output for the network in array format.
- Backpropagate the error: Compute the error of every layer using the error of the following one. As the error of the last layer can be easily known, the rest of them can be computed iteratively. This is where the power of the algorithm lays: Just with a forward and a backward pass, which can have roughly the same computational cost, the weights are adjusted closer to the final result. As stated before, the error of the hidden layers can be computed as . For the last layer, , that is, the input values.
- Compute the gradient and update the weights and biases. By putting everything together, the result is:
3. Conflict Detection in Approach Phase
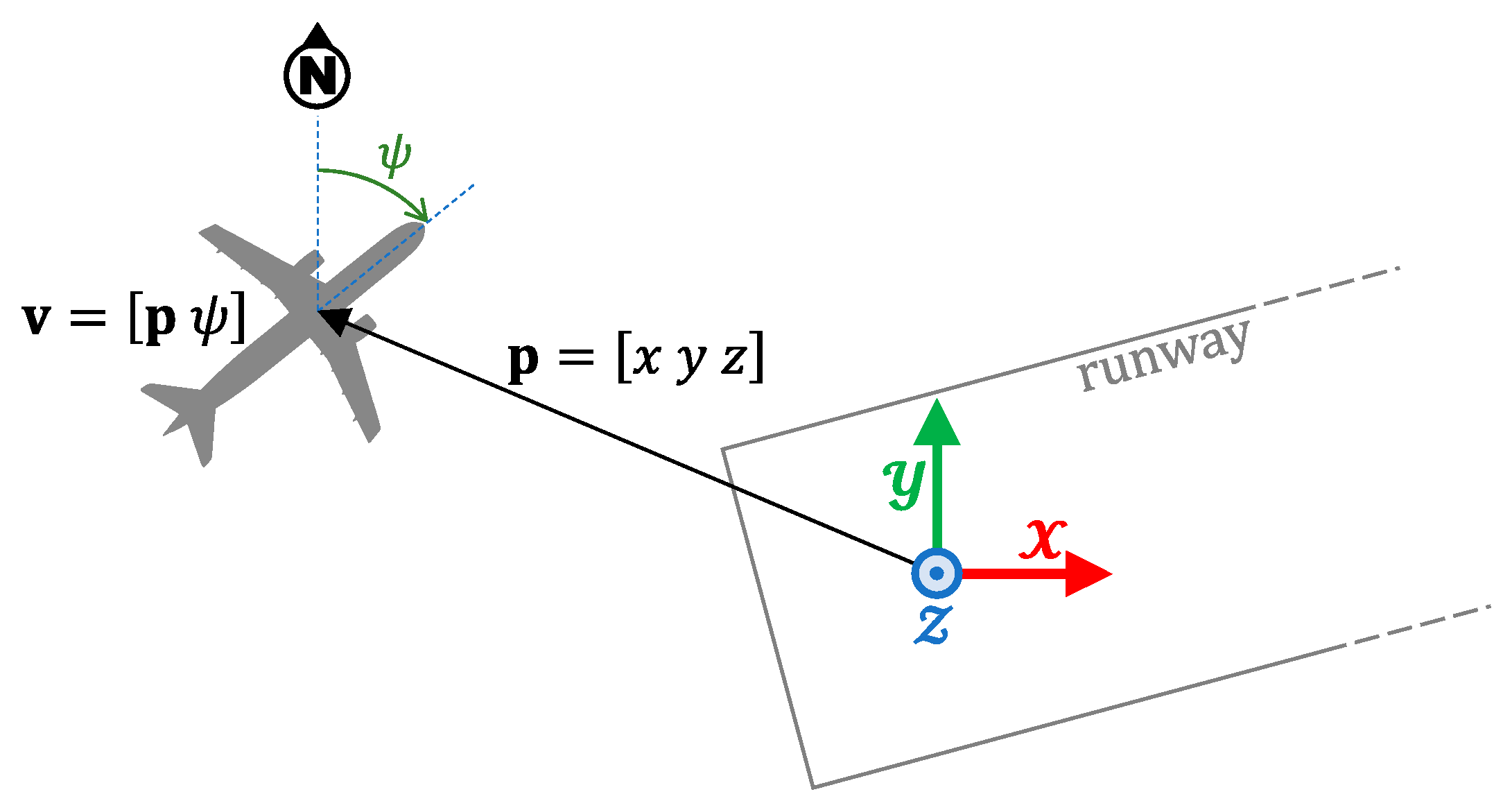
3.1. Aircraft Dynamics
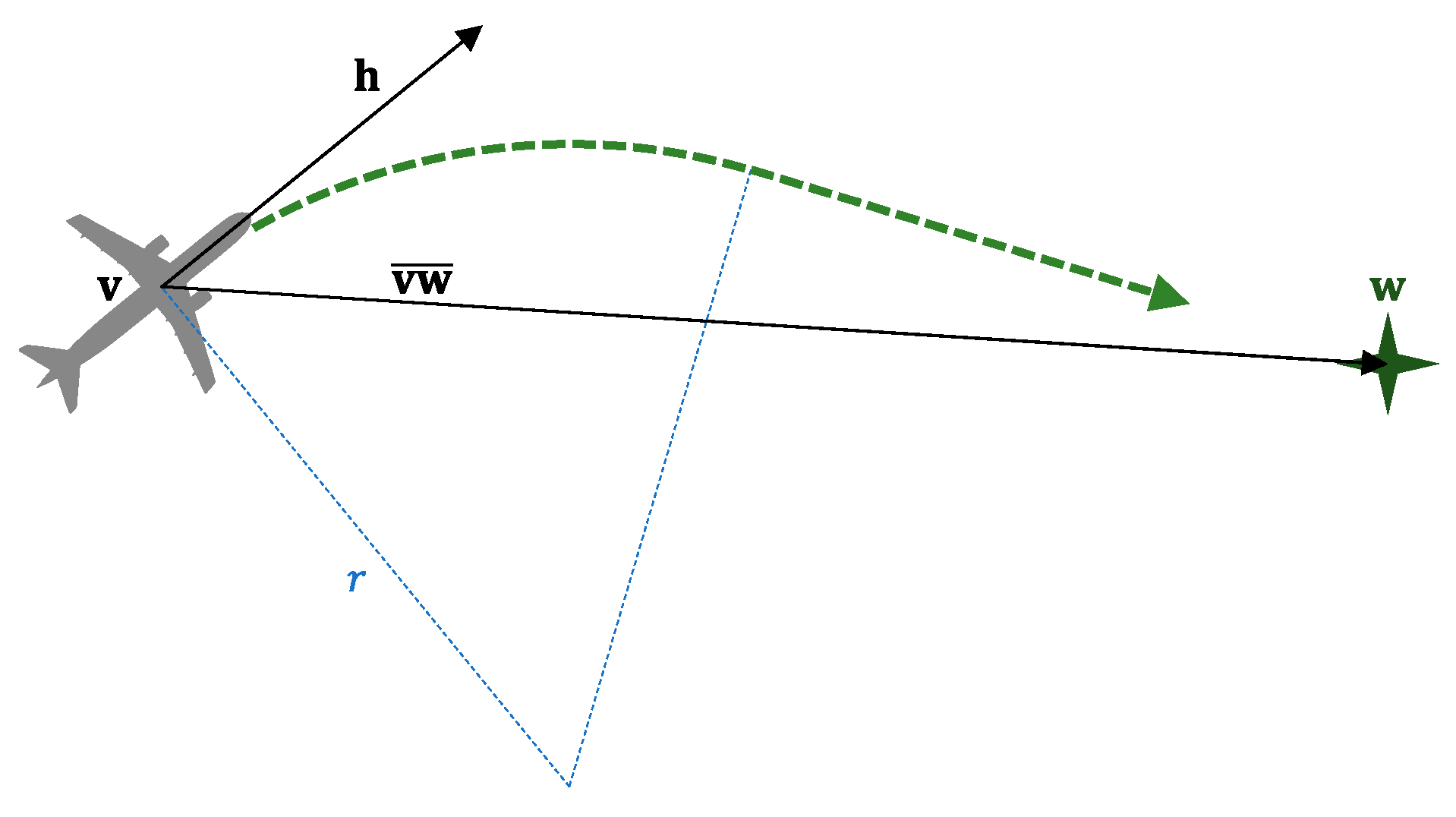
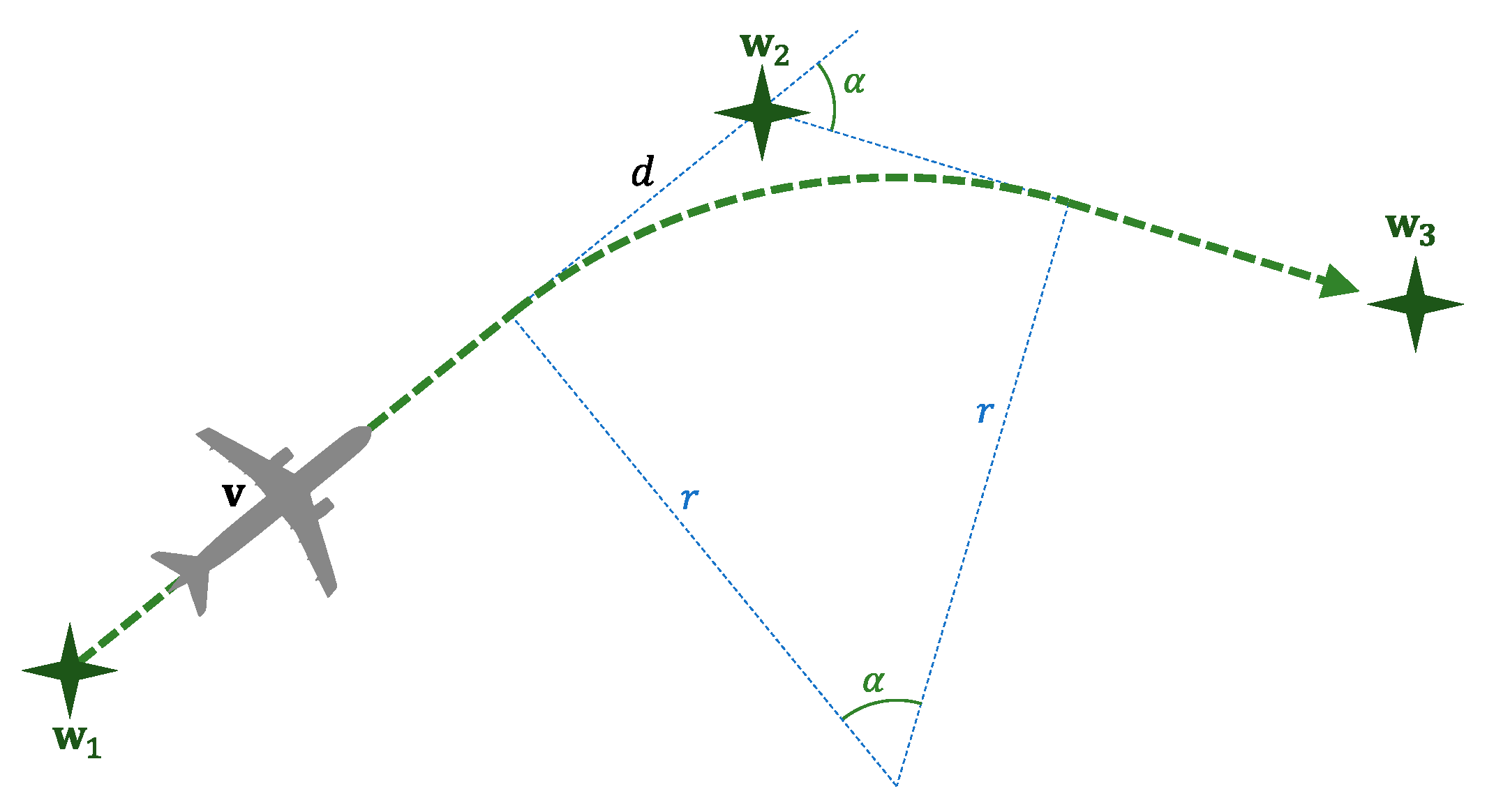
3.2. Pilot’s Behavior
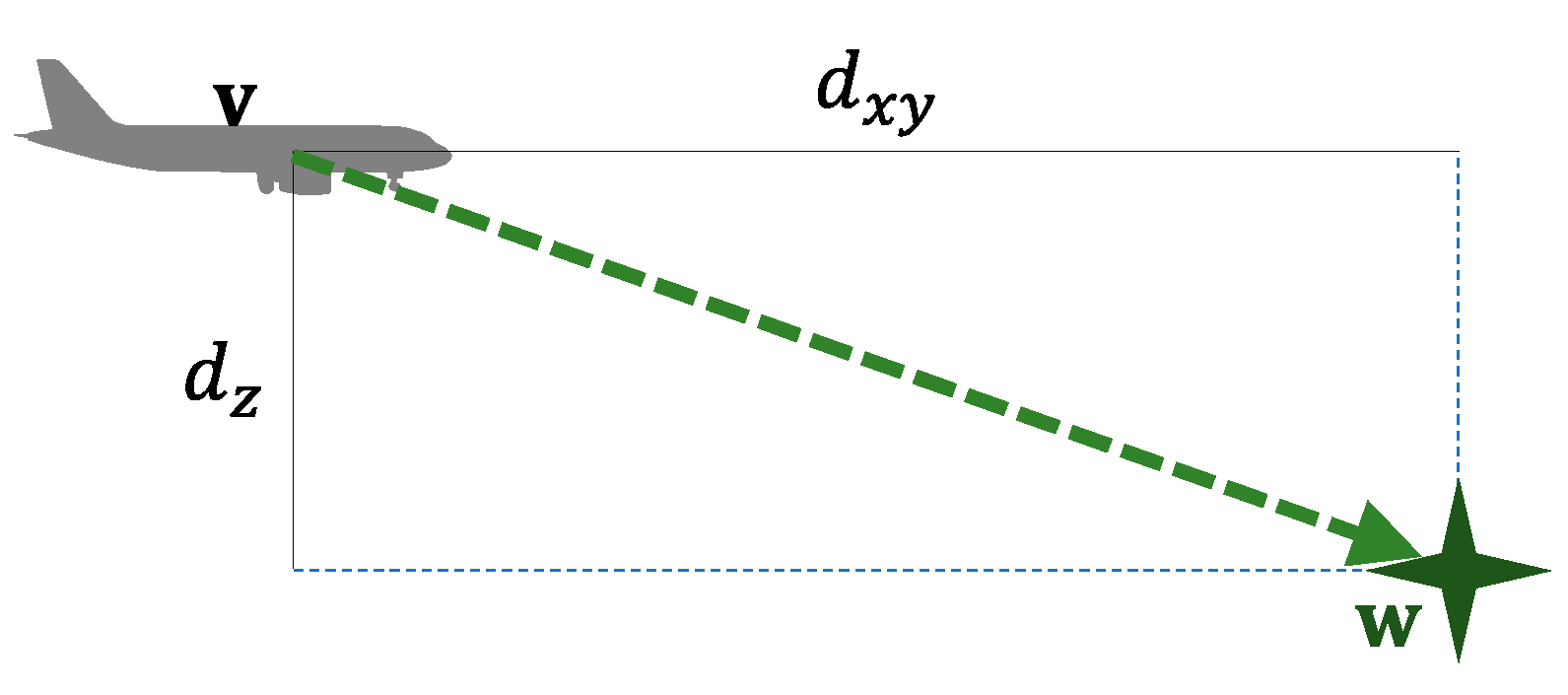
3.3. Conflict Detection
4. Conflict Prediction Based on Neural Network
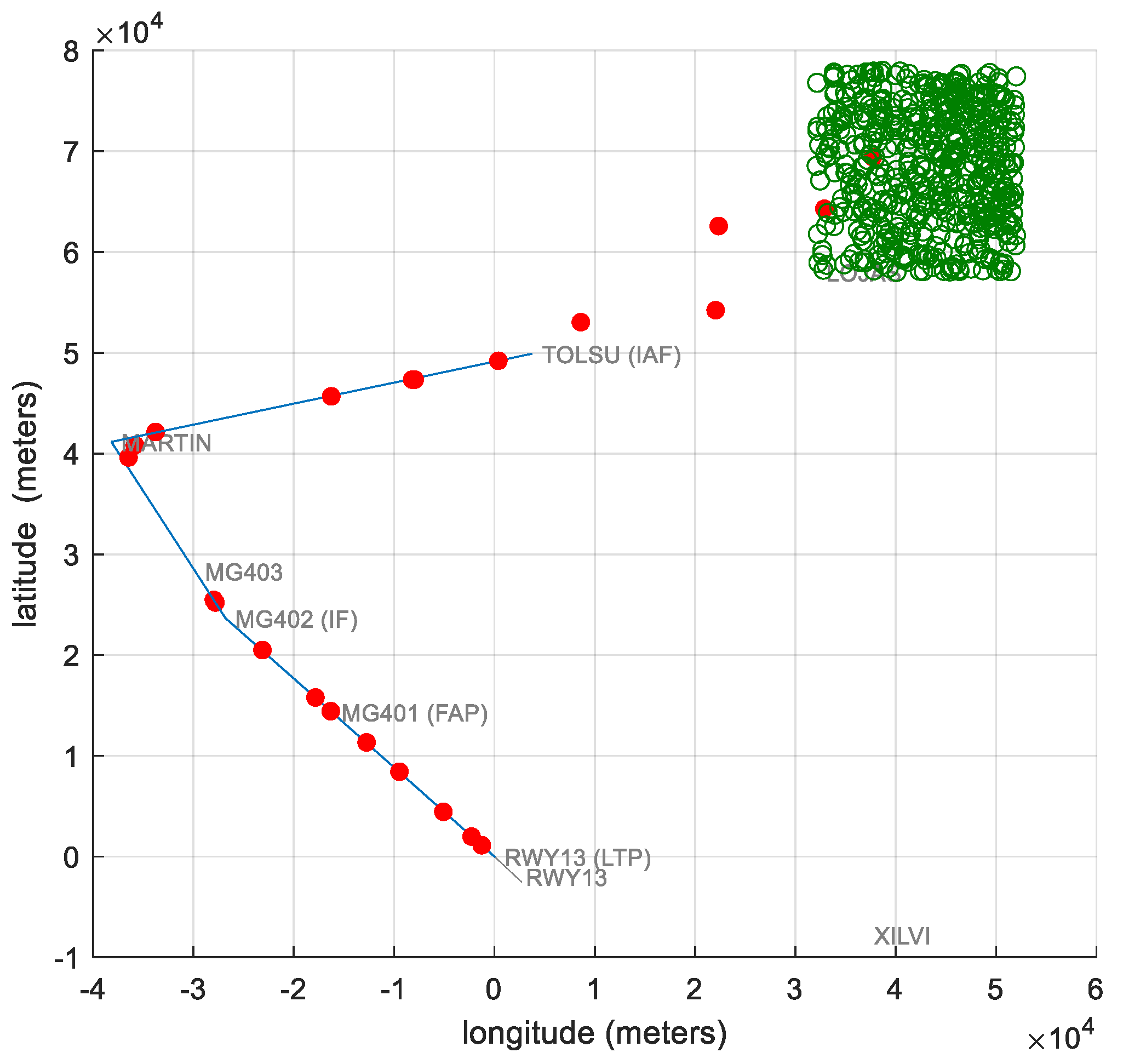
4.1. Airport Scenario
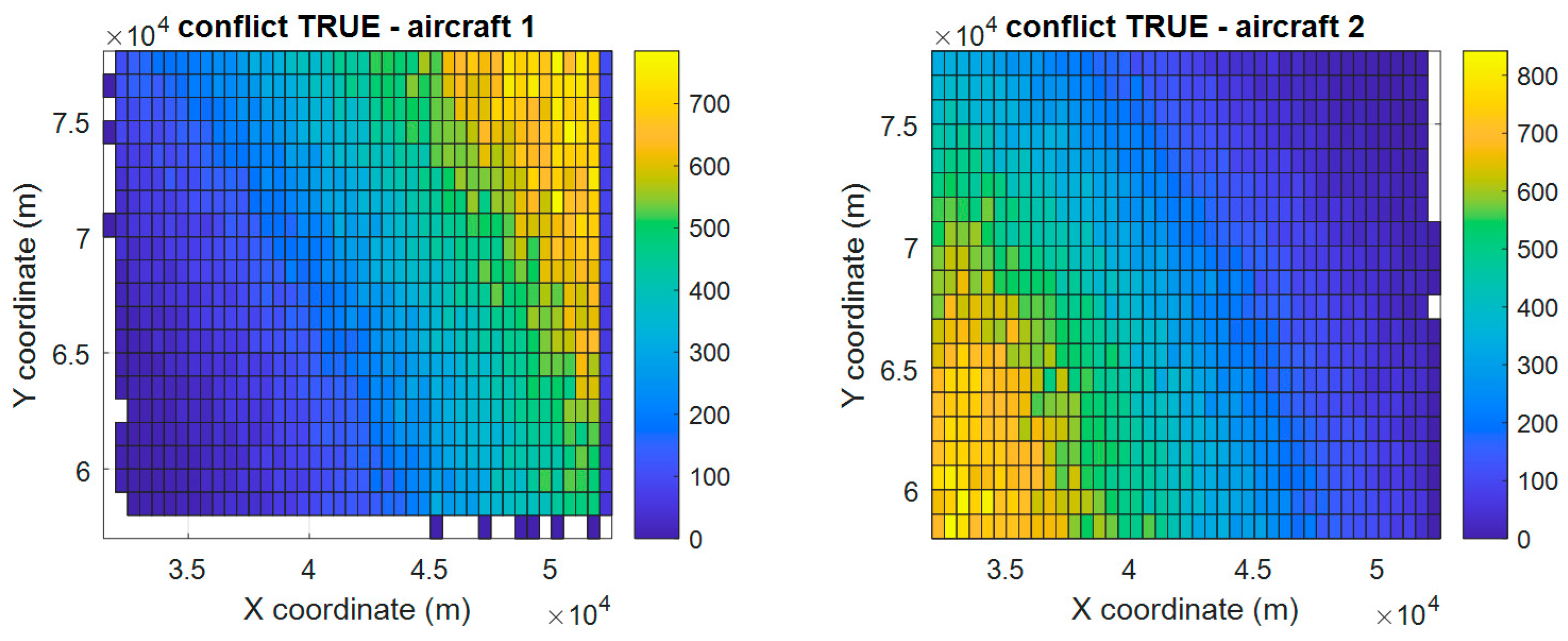
4.2. Training Database
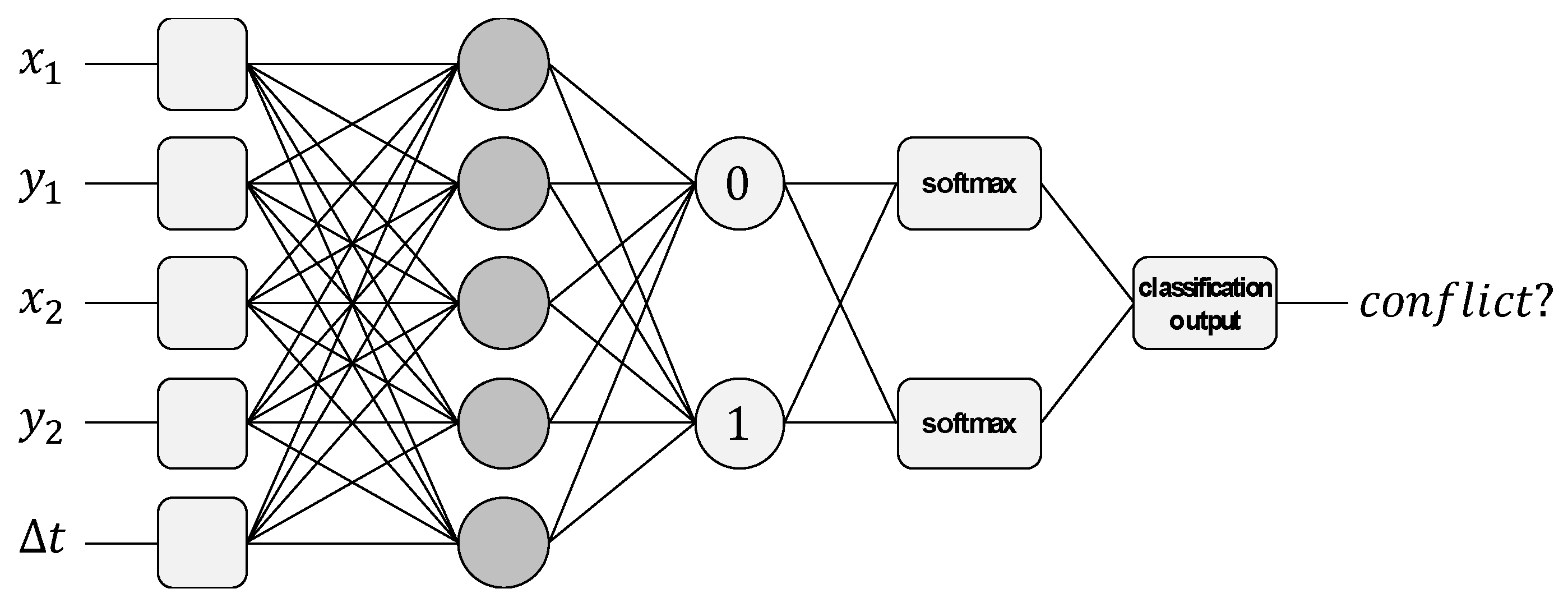
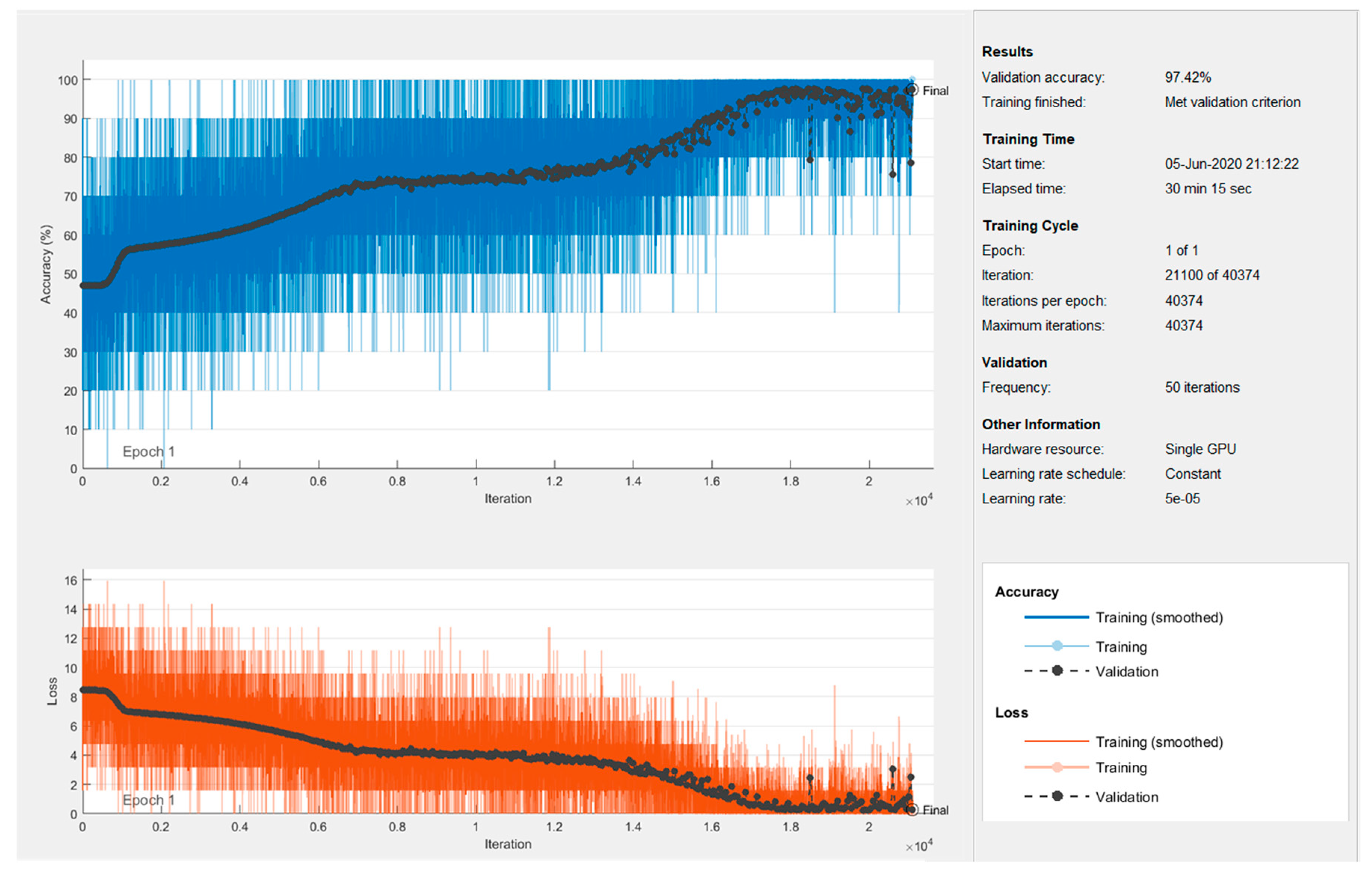
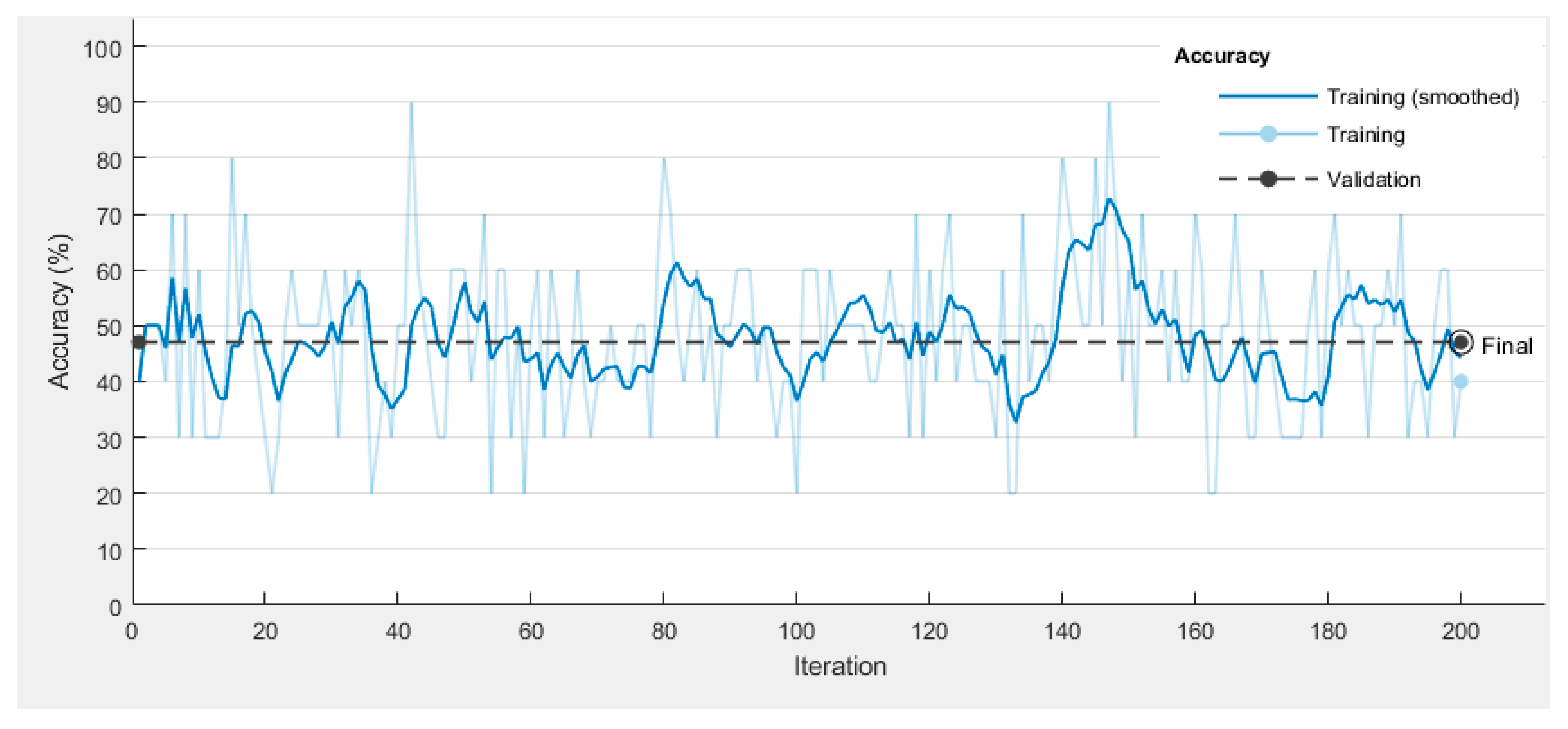
4.3. Neural Network Design and Training
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- ICAO. Traffic Growth and Airline Profitability Were Highlights of Air Transport in 2016. 2017. Available online: http://www.icao.int/Newsroom/Pages/traffic-growth-and-airline-profitability-were-highlights-of-air-transport-in-2016.aspx (accessed on 1 October 2020).
- ICAO. Doc 4444–PANS-ATM, Procedures for Air Navigation Services—Air Traffic Management; ICAO: Montreal, QC, Canada, 2016. [Google Scholar]
- Tang, J. Conflict Detection and Resolution for Civil Aviation: A literature survey. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 20–35. [Google Scholar] [CrossRef]
- Kuchar, J.K.; Yang, L.C. A Review of Conflict Detection and Resolution Modeling Methods. IEEE Trans. Intell. Transp. Syst. 2000, 1, 179–189. [Google Scholar] [CrossRef]
- Geser, A.; Muñoz, C. A geometric approach to strategic conflict detection and resolution. In Proceedings of the AIAA/IEEE Digital Avionics Systems Conference-Proceedings, Irvine, CA, USA, 27–31 October 2002; Volume 1. [Google Scholar] [CrossRef]
- Niu, H.; Ma, C.; Han, P.; Lv, J. An airborne approach for conflict detection and resolution applied to civil aviation aircraft based on ORCA. In Proceedings of the 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference, ITAIC 2019, Chongqing, China, 24–26 May 2019; pp. 686–690. [Google Scholar] [CrossRef]
- Chiang, Y.J.; Klosowski, J.T.; Lee, C.; Mitchell, J.S.B. Geometric algorithms for conflict detection/resolution in air traffic management. In Proceedings of the IEEE Conference on Decision and Control, San Diego, CA, USA, 12 December 1997; Volume 2, pp. 1835–1840. [Google Scholar] [CrossRef]
- Prandini, M.; Hu, J.; Lygeros, J.; Sastry, S. A probabilistic approach to aircraft conflict detection. IEEE Trans. Intell. Transp. Syst. 2000, 1, 199–220. [Google Scholar] [CrossRef]
- Liu, W.; Hwang, I. Probabilistic Trajectory Prediction and Conflict Detection for Air Traffic Control. J. Guid. Control. Dyn. 2011, 34, 1779–1789. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Cai, K.-Q.; Prandini, M. Multi-aircraft Conflict Detection and Resolution Based on Probabilistic Reach Sets. IEEE Trans. Control. Syst. Technol. 2017, 25, 309–316. [Google Scholar] [CrossRef]
- Moir, I.; Seabridge, A.; Jukes, M. Civil Avionics Systems; John Wiley & Sons, Ltd.: Chichester, UK, 2013. [Google Scholar]
- Beasley, J.; Howells, H.; Sonander, J. Improving short-term conflict alert via tabu search. J. Oper. Res. Soc. 2002, 53, 593–602. [Google Scholar] [CrossRef]
- Tang, J. Review: Analysis and Improvement of Traffic Alert and Collision Avoidance System. IEEE Access 2017, 5, 21419–21429. [Google Scholar] [CrossRef]
- Chaloulos, G.; Roussos, G.P.; Lygeros, J.; Kyriakopoulos, K.J. Mid and short term conflict resolution in autonomous aircraft operations. In Proceedings of the 8th Innovative Research Workshop and Exhibition, Proceedings, Brétigny-sur-Orge, France, 1–3 December 2009; pp. 221–226. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- FAA. Instrument Procedures Handbook (IPH). 2017. Available online: https://www.faa.gov/regulations_policies/handbooks_manuals/aviation/instrument_procedures_handbook/ (accessed on 1 October 2020).
- Boeing. Statistical Summary of Commercial Jet Airplane Accidents Worldwide Operations | 1959–2018. 2019. Available online: https://www.boeing.com/resources/boeingdotcom/company/about_bca/pdf/statsum.pdf (accessed on 1 October 2020).
- Chen, M.Q. Flight conflict detection and resolution based on neural network. In Proceedings of the Proceedings—2011 International Conference on Computational and Information Sciences, ICCIS 2011, Chengdu, China, 21–23 October 2011; pp. 860–862. [Google Scholar] [CrossRef]
- Kaidi, R.; Lazaar, M.; Ettaouil, M. Neural network apply to predict aircraft trajectory for conflict resolution. In Proceedings of the 2014 9th International Conference on Intelligent Systems: Theories and Applications (SITA-14), Rabat, Morocco, 7–8 May 2014. [Google Scholar] [CrossRef]
- Le Fablec, Y.; Alliot, J.M. Using Neural Networks to predict aircraft trajectories. In In Proceedings of the International Conference on Artificial Intelligence, Las Vegas, NA, USA, 28 June–1 July 1999; pp. 524–529. [Google Scholar]
- Wang, Z.; Liang, M.; Delahaye, D. Data-driven Conflict Detection Enhancement in 3D Airspace with Machine Learning. In Proceedings of the 2020 International Conference on Artificial Intelligence and Data Analytics for Air Transportation (AIDA-AT), Singapore, 3–4 February 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Wu, Z.; Tian, S.; Ma, L. A 4D Trajectory Prediction Model Based on the BP Neural Network. J. Intell. Syst. 2019, 29, 1545–1557. [Google Scholar] [CrossRef]
- Zhao, Z.; Zeng, W.; Quan, Z.; Chen, M.; Yang, Z. Aircraft trajectory prediction using deep long short-term memory networks. In Proceedings of the CICTP 2019: Transportation in China—Connecting the World—Proceedings of the 19th COTA International Conference of Transportation Professionals, Nanjing, China, 6–8 July 2019; pp. 124–135. [Google Scholar] [CrossRef]
- Ma, L.; Tian, S. A Hybrid CNN-LSTM Model for Aircraft 4D Trajectory Prediction. IEEE Access 2020, 8, 134668–134680. [Google Scholar] [CrossRef]
- Durand, N.; Alliot, J.-M.; Médioni, F. Neural Nets Trained by Genetic Algorithms for Collision Avoidance. Appl. Intell. 2000, 13, 205–213. [Google Scholar] [CrossRef]
- Alam, S.; McPartland, M.; Barlow, M.; Lindsay, P.; Abbass, H.A.; Bossomaier, T.; Wiles, J. Chapter 2 Neural Evolution for Collision Detection & Resolution in a 2D Free Flight Environment. In Recent Advances in Artificial Life; World Scientific Pub. Co. Pte. Lt.: Singapore, 2005; pp. 13–28. [Google Scholar]
- Christodoulou, M.; Kontogeorgou, C. Collision Avoidance in Commercial Aircraft Free Flight via Neural Networks and Non-Linear Programming. Int. J. Neural Syst. 2008, 18, 371–387. [Google Scholar] [CrossRef] [PubMed]
- Pham, D.T.; Tran, N.P.; Alam, S.; Duong, V.; Delahaye, D. A Machine Learning Approach for Conflict Resolution in Dense Traffic Scenarios with Uncertainties; Thirteenth USA/Europe Air Traffic Management Research and Development Seminar: Vienne, Austria, 2019. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biol. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Werbos, P.J. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- The MathWorks Inc. Matlab. Available online: https://www.mathworks.com (accessed on 1 October 2020).
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- ICAO. Required Navigation Performance Authorization Required (RNP AR) Procedure Design Manual; ICAO: Montreal, QC, Canada, 2016. [Google Scholar]
- The MathWorks Inc. “Simulink.”. Available online: https://www.mathworks.com/products/simulink.html (accessed on 1 October 2020).
- The MathWorks Inc. Deep Learning Toolbox. Available online: https://www.mathworks.com/products/deep-learning.html (accessed on 1 October 2020).
- Google. TensorFlow. Available online: https://www.tensorflow.org (accessed on 1 October 2020).
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Tijmen, T.; Hinton, G.; Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural Networks for Machine Learning. 2012. Available online: https://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf (accessed on 1 October 2020).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]



| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. | |
| 9. | |
| 10. |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | if then |
| 6. | |
| 7. | else if then |
| 8. | |
| 9. | else |
| 10. | |
| 11. | end if |
| 12. | if and then |
| 13. | |
| 14. | else |
| 15. | |
| 16. | end if |
| Aeronautical Notation | Standard Notation | |||||||
|---|---|---|---|---|---|---|---|---|
| Waypoint Name | Latitude | Longitude | Height (ft) | Speed (kt) | X (m) | Y (m) | Z (m) | Speed (m/s) |
| LOJAS | 37°12′26″ N | 4°09′14″ W | 7000 | 240 | 32,115.94 | 57,950.47 | 2133.60 | 123.47 |
| TOLSU (IAF) | 37°08′03″ N | 4°28′15″ W | 7000 | 240 | 3788.66 | 49,848.85 | 2133.60 | 123.47 |
| MARTIN | 37°03′19″ N | 4°56′23″ W | 7000 | 240 | −38,123.21 | 41,103.20 | 2133.60 | 123.47 |
| MG 403 | 36°56′23″ N | 4°50′47″ W | 5000 | 240 | −29,788.86 | 28,279.77 | 1524 | 123.47 |
| MG 402 (IF) | 36°53′52″ N | 4°48′45″ W | 5000 | 160 | −26,759.25 | 23,616.67 | 1524 | 82.31 |
| MG 401 (FAP) | 36°48′50″ N | 4°41′39″ W | 4200 | 160 | −16,175.05 | 14,299.41 | 1280.16 | 82.31 |
| RWY 13 (LTP) | 36°41′04″ N | 4°30′45″ W | 52 | 140 | 55.74 | −53.08 | 15.85 | 72.02 |
| RWY 13 | 36°40′00″ N | 4°29′20″ W | 52 | 50 | 2179.44 | −2035.92 | 15.85 | 25.72 |
| XILVI | 36°36′52″ N | 4°06′01″ W | 2200 | 220 | 36,907.56 | −7831.11 | 670.56 | 113.18 |
| Training Set | Validation Set | Test Set | Total Entries | |||||
|---|---|---|---|---|---|---|---|---|
| Conflict TRUE | 189,881 | 37.62% | 23,735 | 4.70% | 23,735 | 4.70% | 237,351 | 47.03% |
| Conflict FALSE | 213,863 | 42.38% | 26,733 | 5.30% | 26,733 | 5.30% | 267,329 | 52.97% |
| Dataset | 403,744 | 80.00% | 50,468 | 10.00% | 50,468 | 10.00% | 504,680 | 100.00% |
| Neuron | |||||||
|---|---|---|---|---|---|---|---|
| Layer 2 | 1 | 0.2880 | −0.4528 | 0.1627 | 0.4580 | −0.2579 | 0.0730 |
| 2 | −0.5185 | 0.4227 | −0.2851 | 0.4557 | 0.5900 | −0.0624 | |
| 3 | 0.6004 | 0.5419 | 0.5054 | −0.7232 | −0.3032 | −0.0663 | |
| 4 | −0.0130 | 0.3251 | 0.0855 | 0.2882 | 0.5579 | −0.0674 | |
| 5 | 0.3818 | 0.7761 | 0.3995 | −0.4928 | −0.8459 | 0.0723 | |
| Layer 3 | 1 | −0.4830 | 0.3597 | −0.4186 | 0.0510 | −0.1376 | −0.0702 |
| 2 | −0.2686 | 0.4050 | −0.9013 | −0.4604 | 0.5170 | 0.0702 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casado, R.; Bermúdez, A. Neural Network-Based Aircraft Conflict Prediction in Final Approach Maneuvers. Electronics 2020, 9, 1708. https://doi.org/10.3390/electronics9101708
Casado R, Bermúdez A. Neural Network-Based Aircraft Conflict Prediction in Final Approach Maneuvers. Electronics. 2020; 9(10):1708. https://doi.org/10.3390/electronics9101708
Chicago/Turabian StyleCasado, Rafael, and Aurelio Bermúdez. 2020. "Neural Network-Based Aircraft Conflict Prediction in Final Approach Maneuvers" Electronics 9, no. 10: 1708. https://doi.org/10.3390/electronics9101708
APA StyleCasado, R., & Bermúdez, A. (2020). Neural Network-Based Aircraft Conflict Prediction in Final Approach Maneuvers. Electronics, 9(10), 1708. https://doi.org/10.3390/electronics9101708






