Pulse Pattern Optimization Based on Brute Force Method for Medium-Voltage Three-Level NPC Converter with Active Front End
Abstract
1. Introduction
2. Selective Harmonic Elimination
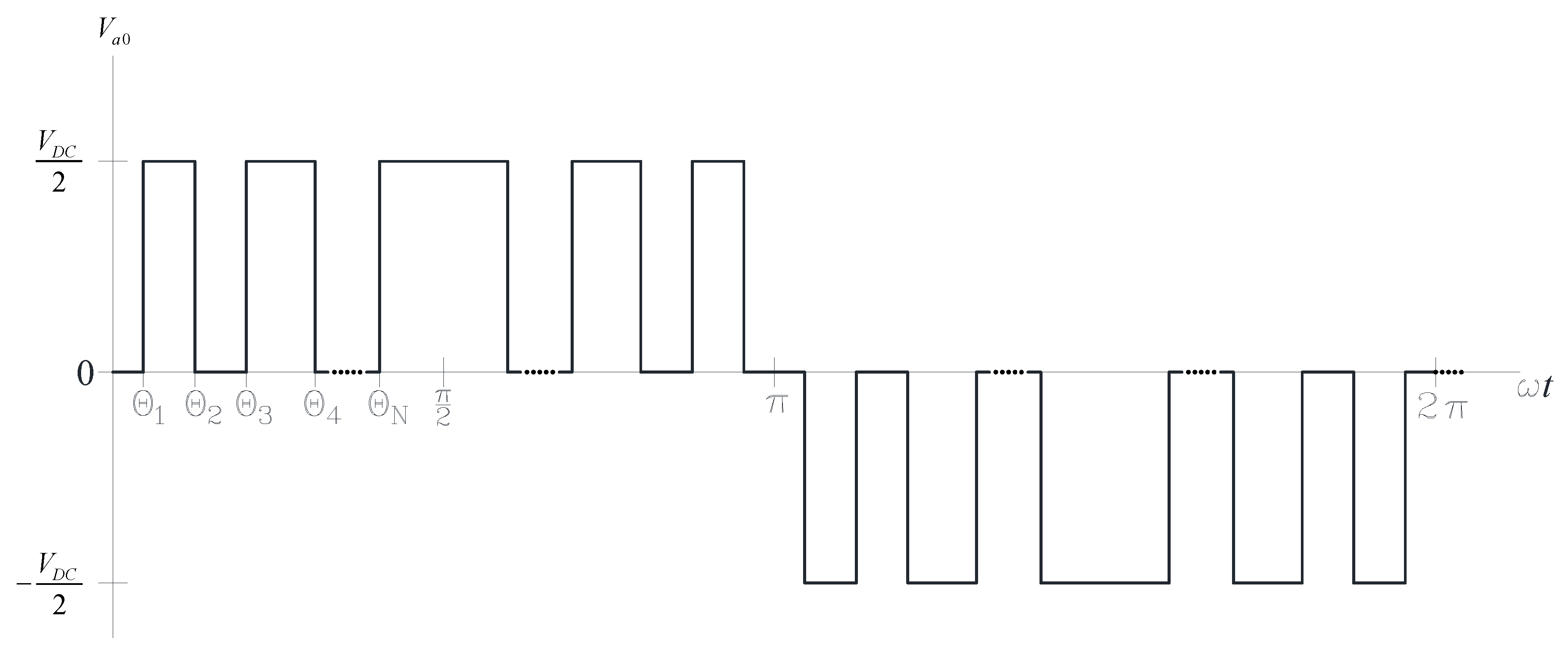
2.1. Fundamentals of Selective Harmonic Elimination
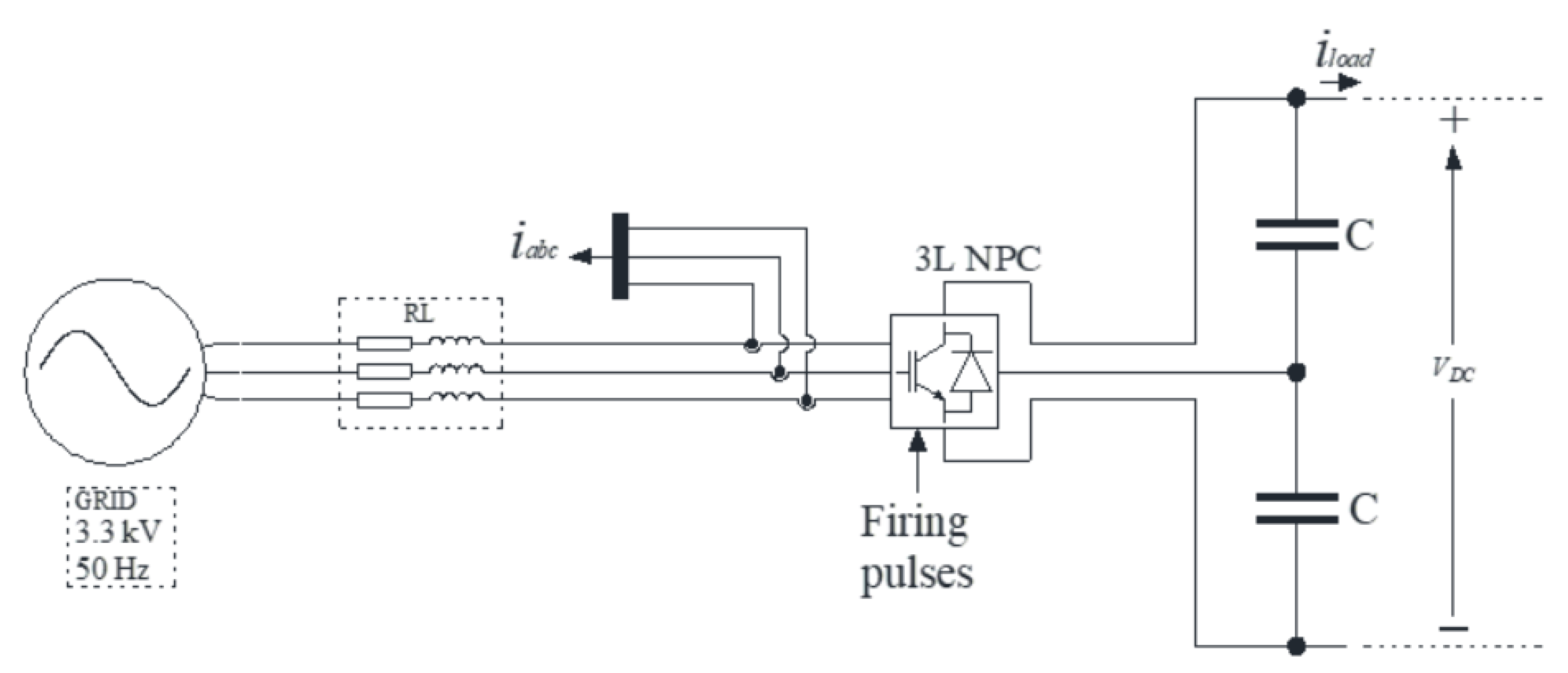
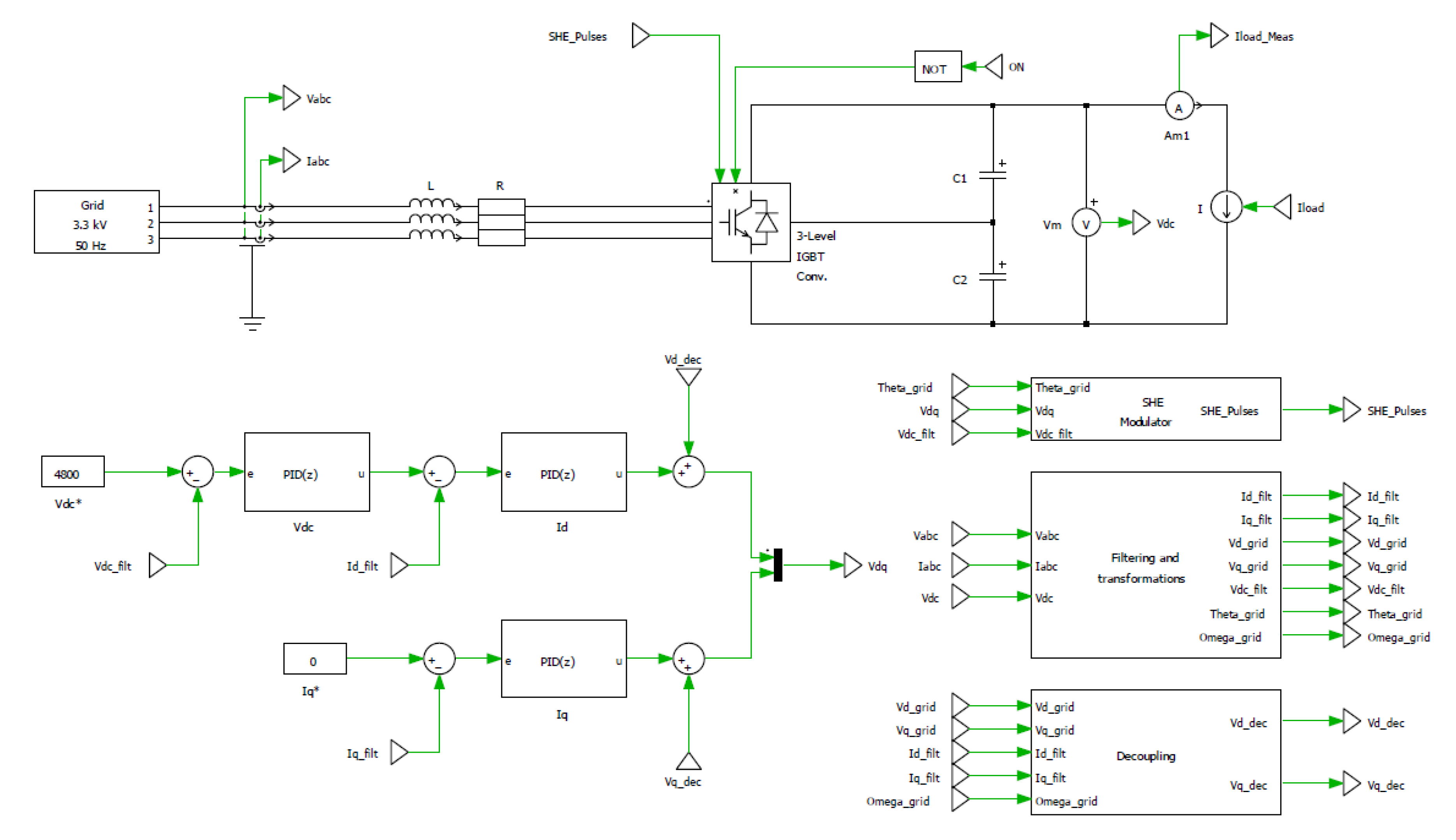
2.2. System Design and Problem Statement
3. Brute Force Method
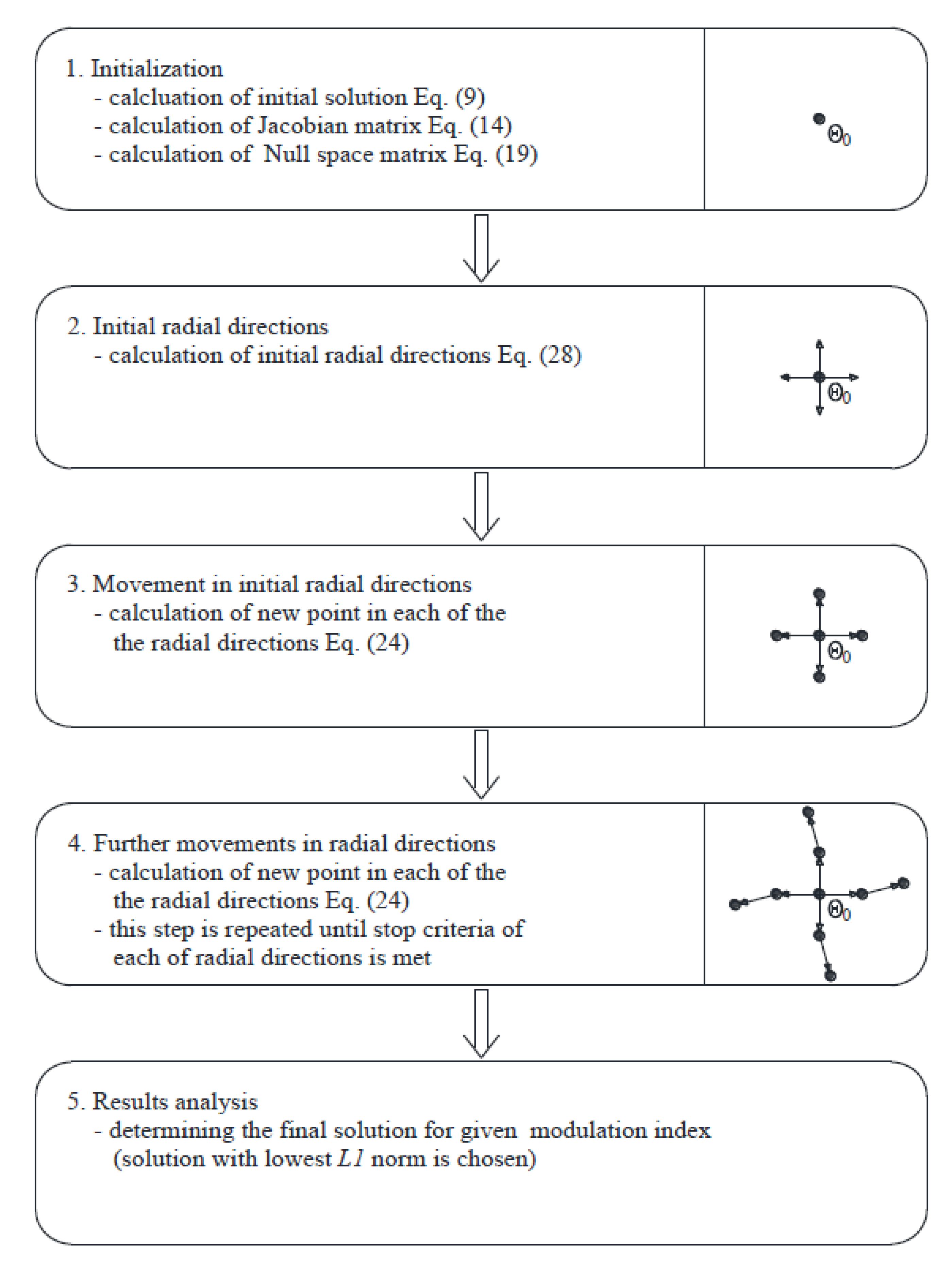
3.1. Algorithm for the Brute Force Method
3.2. Search Direction of the Brute Force Method
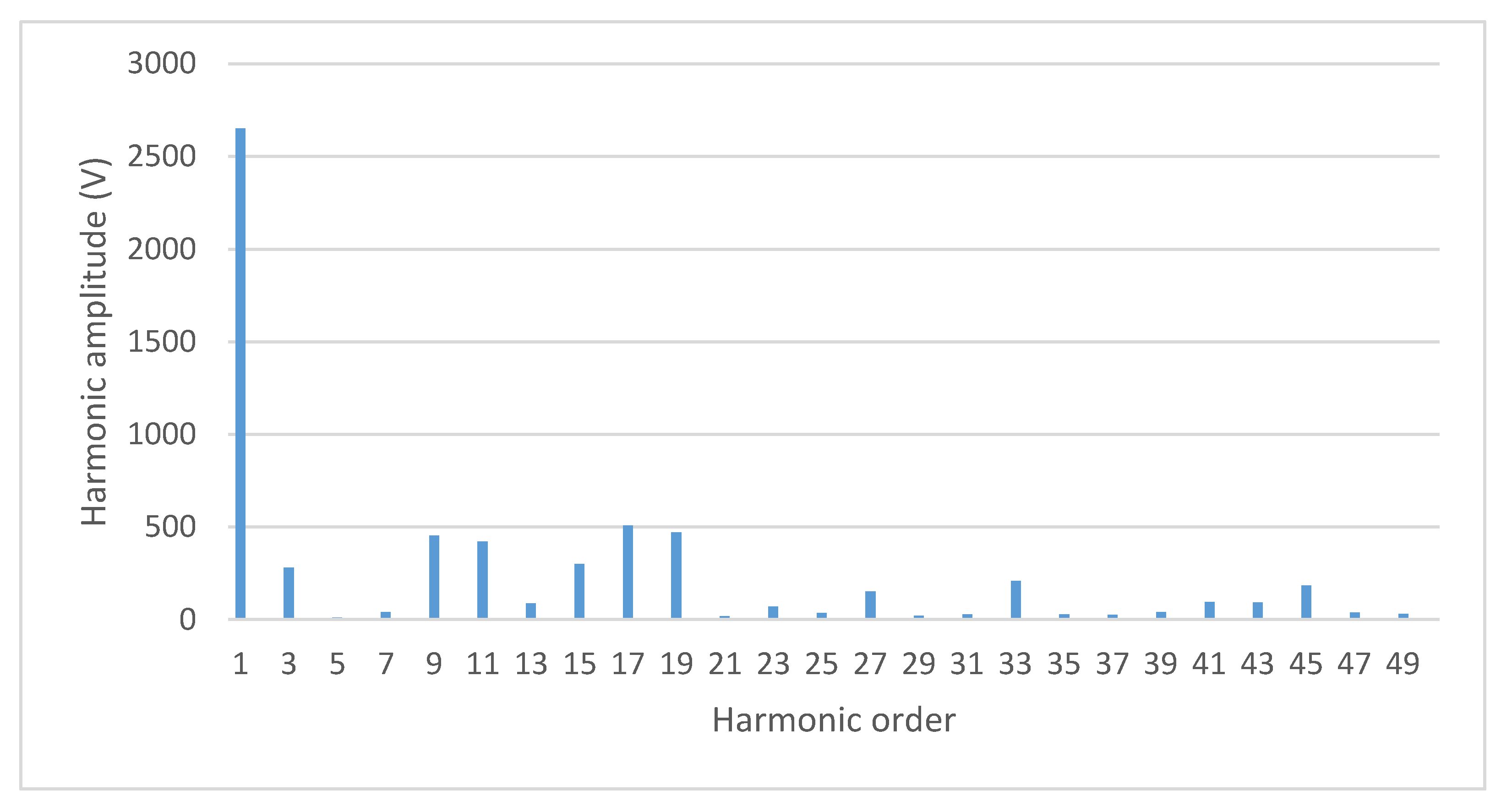
4. Obtained Results with the Brute Force Method
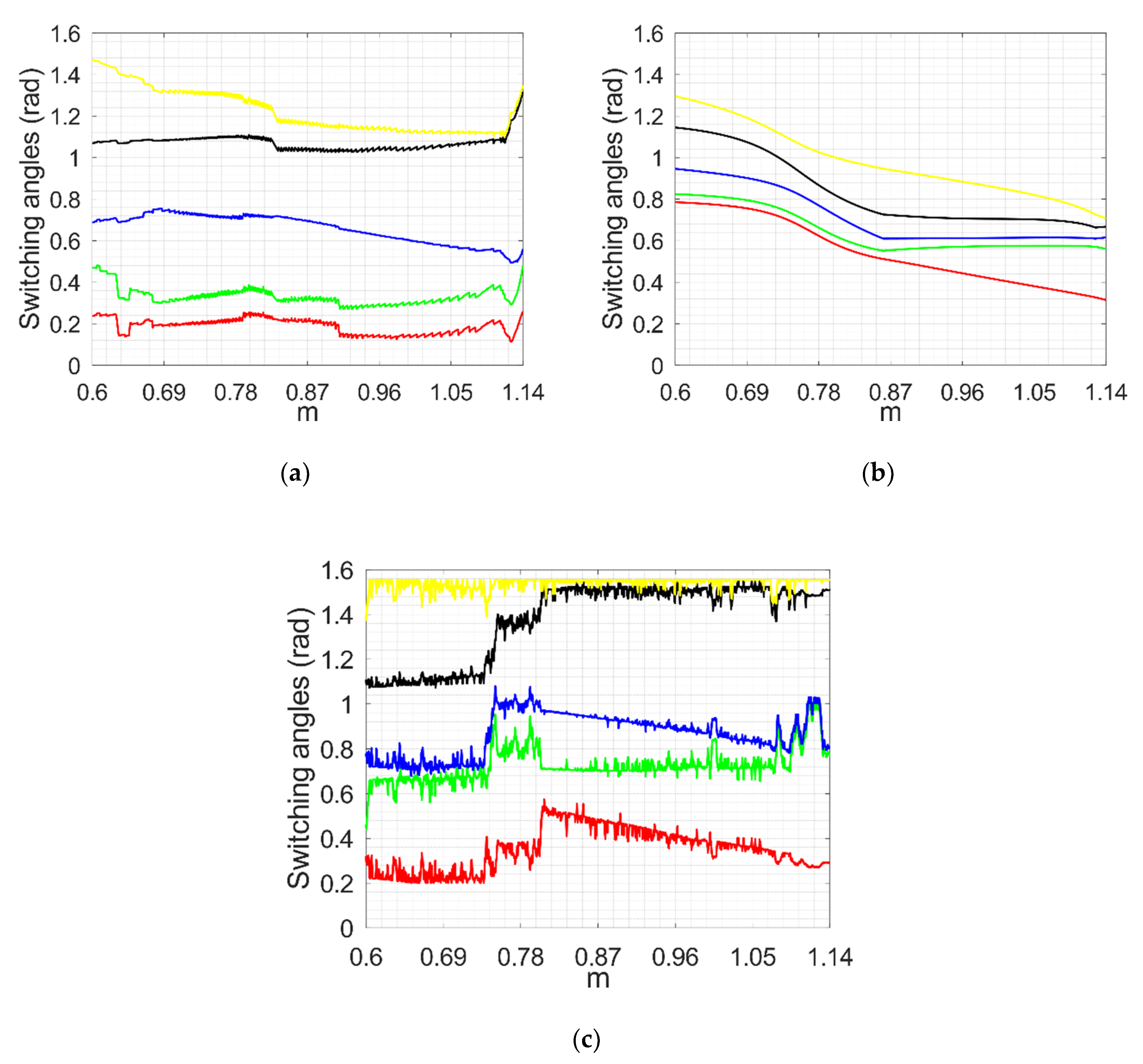
4.1. Determined Pulse Patterns and Comparison with Other Methods
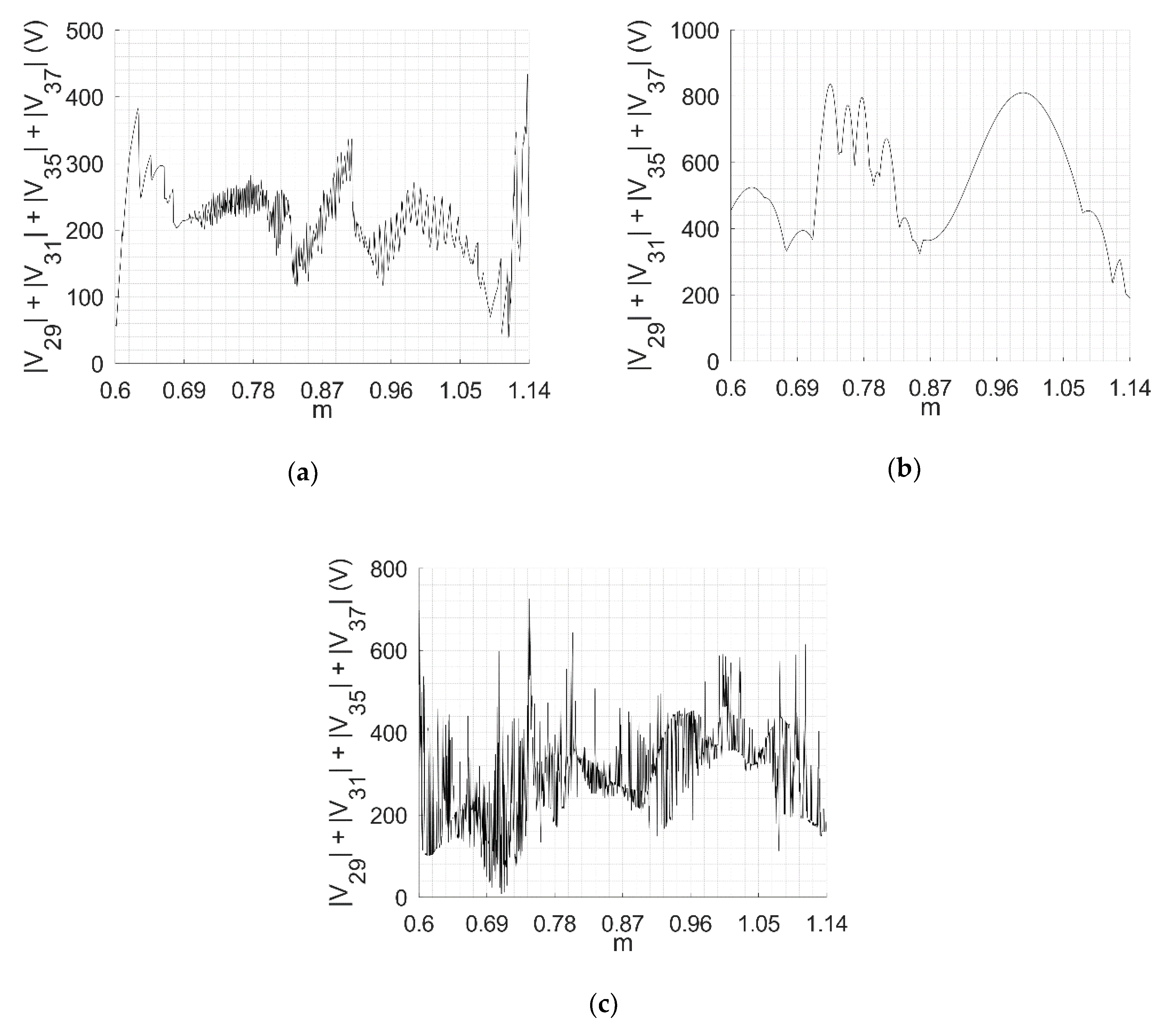
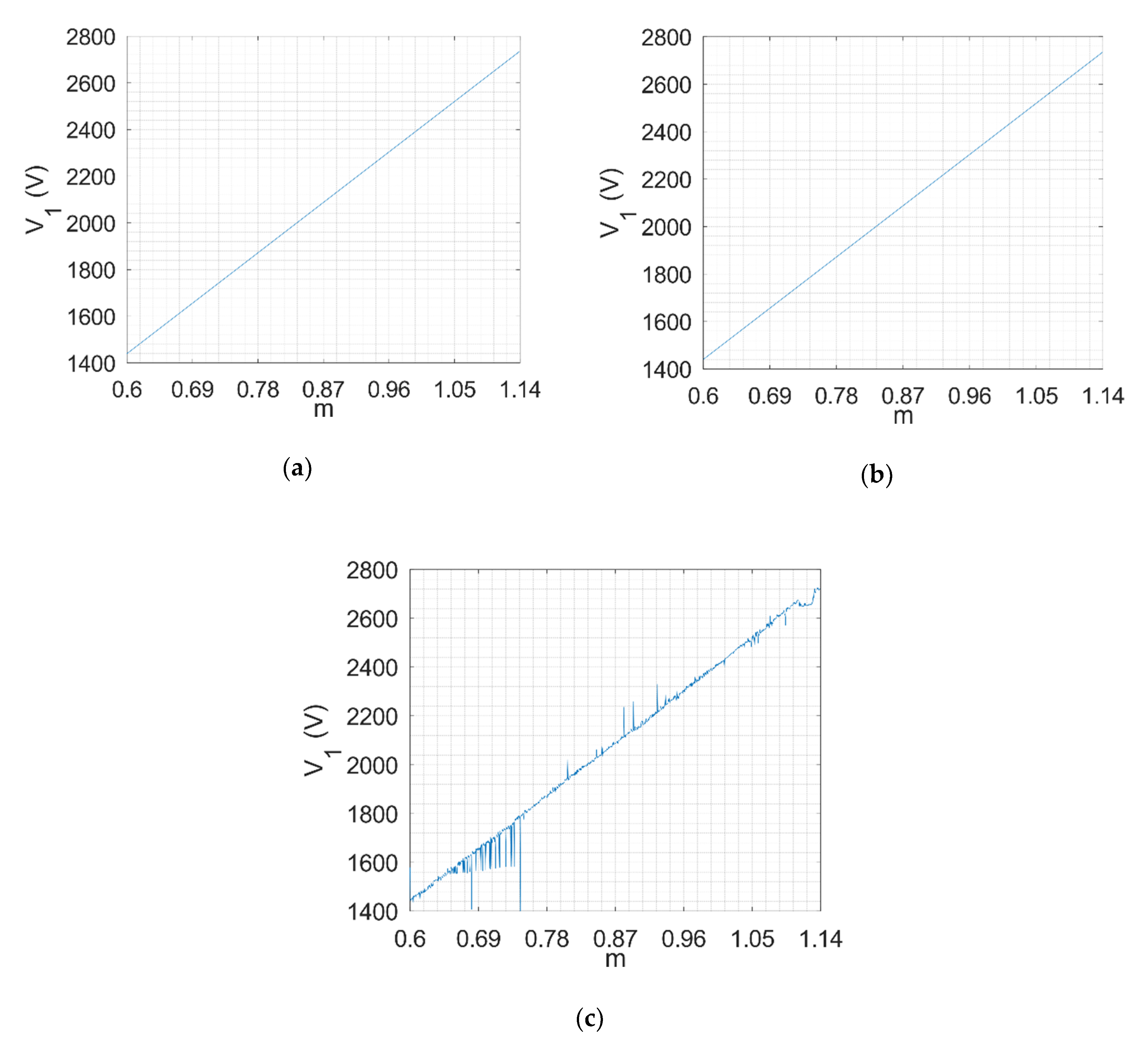
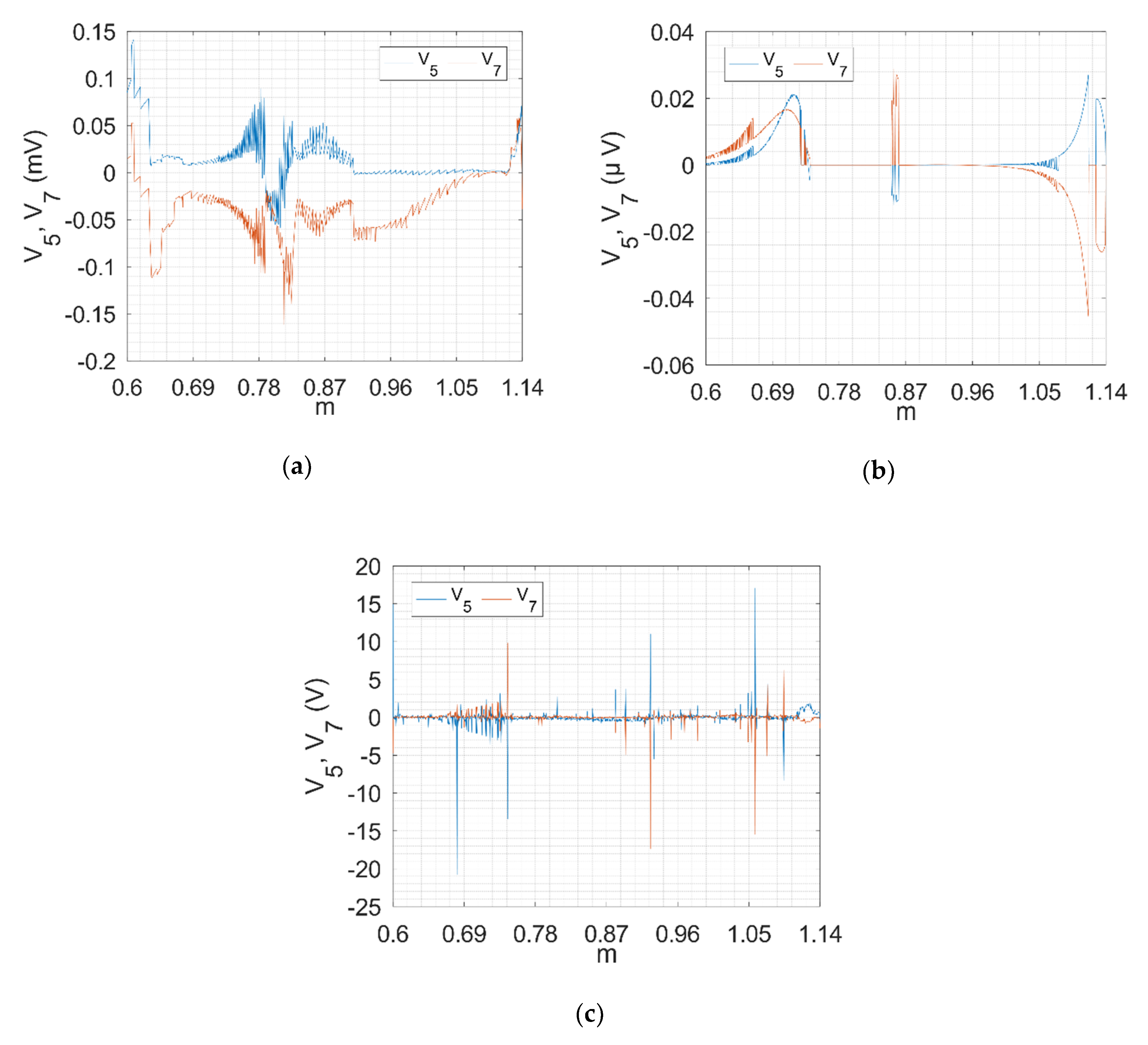
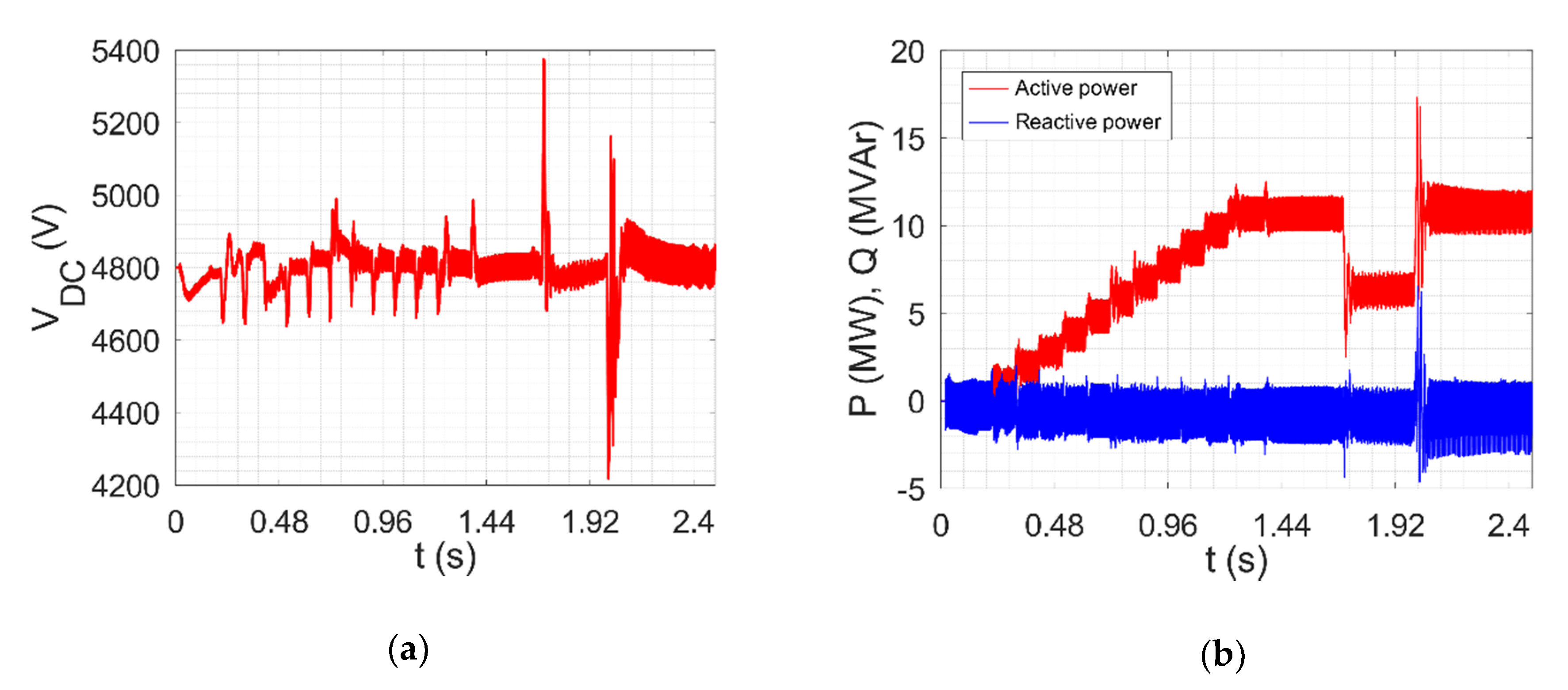
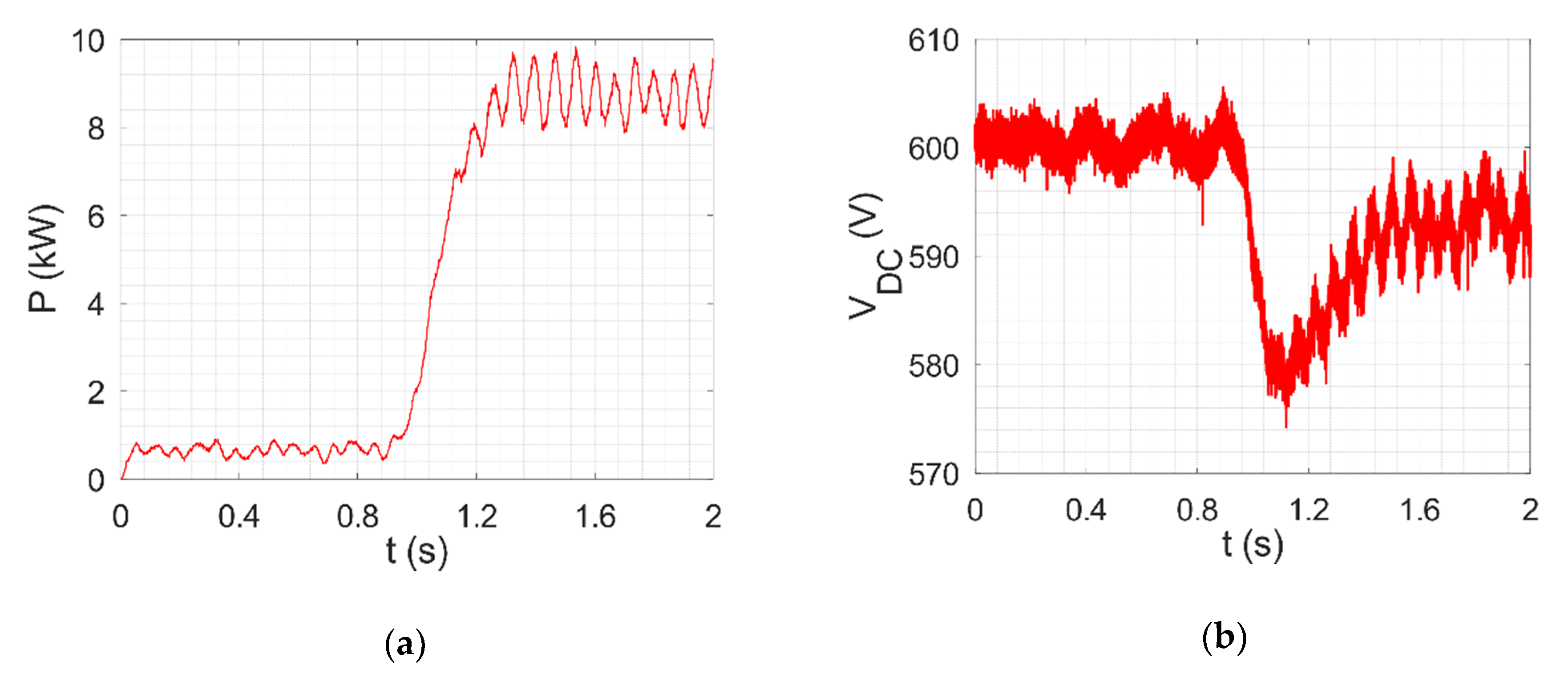
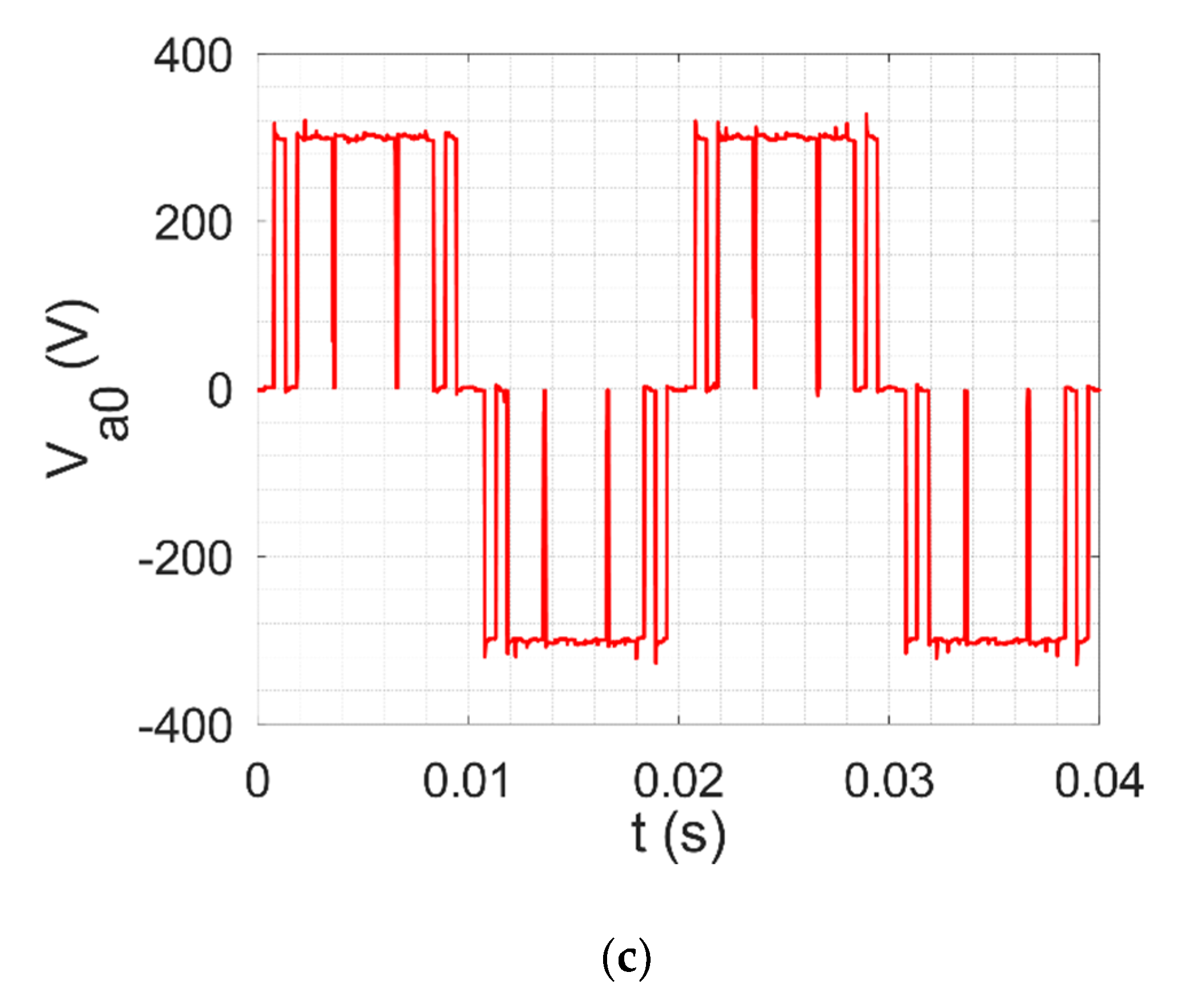
4.2. Simulation of 3LV NPC AFE with SHE-PWM in Closed Loop with Determined Pulse Patterns
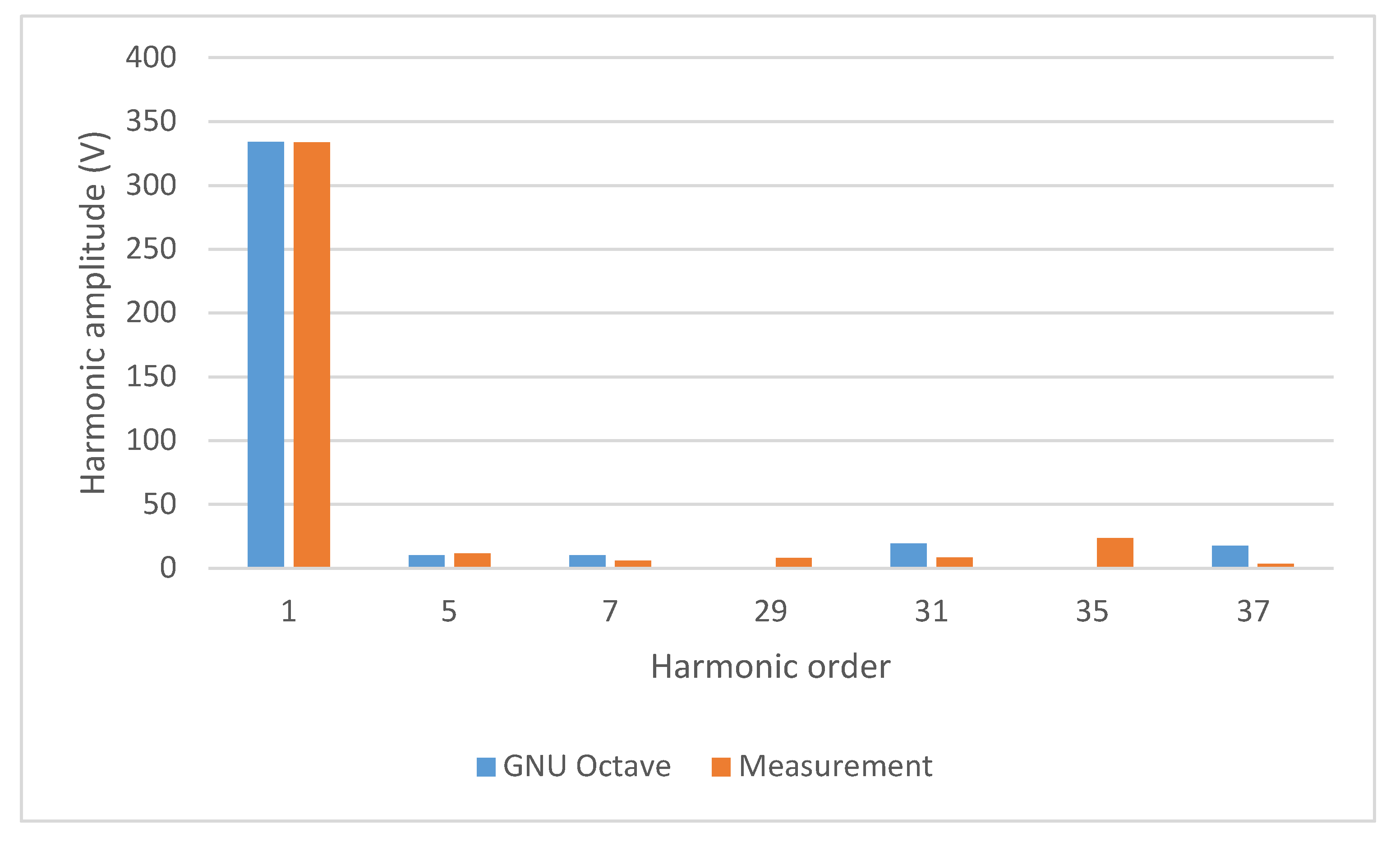
4.3. Experimental Results for 3 LV NPC AFE with SHE-PWM in Closed Loop with Determined Pulse Patterns
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol | Description | First Mentioned in |
|---|---|---|
| k-th switching angle for SHE-PWM | Equation (2) | |
| H | Highest harmonic order that can be eliminated with SHE-PWM | Equation (4) |
| m | Modulation index | Equation (5) |
| i-th solution of the brute force method | Equation (10) | |
| Small change in the five-dimensional space around solution | Equation (13) | |
| Matrix operator | Equation (18) | |
| Sine and cosine of search direction angle | Equation (20) | |
| Error compensation vector. Used for error compensation caused by linear approximation. | Equation (24) | |
| Search direction angle. Defines initial radial search directions. | Equation (28) |
Appendix B
| Parameter | Value | Unit |
|---|---|---|
| Rated current of 3 LV NPC AFE and INVERTER | 80 | A |
| Rated apparent power of 3 LV NPC AFE and INVERTER | 55.4 | kVA |
| Rated input voltage | 3 × 400 | V |
| Rated input frequency | 50 | Hz |
| Max. switching frequency | 1.5 | kHz |
References
- Ma, K.; Blaabjerg, F. The Impact of Power Switching Devices on the Thermal Performance of a 10 MW Wind Power NPC Converter. Energies 2012, 5, 2559–2577. [Google Scholar] [CrossRef]
- Luqman, M.; Yao, G.; Zhou, L.; Zhang, T.; Lamichhane, A. A Novel Hybrid Converter Proposed for Multi-MW Wind Generator for Offshore Applications. Energies 2019, 12, 4167. [Google Scholar] [CrossRef]
- He, X.; Guo, A.; Peng, X.; Zhou, Y.; Shi, Z.; Shu, Z. A Traction Three-Phase to Single-Phase Cascade Converter Substation in an Advanced Traction Power Supply System. Energies 2015, 8, 9915–9929. [Google Scholar] [CrossRef]
- Zhang, R.; Lin, F.; Yang, Z.; Cao, H.; Liu, Y. A Harmonic Resonance Suppression Strategy for a High-Speed Railway Traction Power Supply System with a SHE-PWM Four-Quadrant Converter Based on Active-Set Secondary Optimization. Energies 2017, 10, 1567. [Google Scholar] [CrossRef]
- Dai, B.; Zhang, M.; Guo, Y.; Zhang, X. Selective harmonic elimination PWM strategy for three-level NPC inverters under fault-tolerant operation. Int. J. Innovative Comput. Inf. Control 2019, 15, 1793–1805. [Google Scholar]
- Luiz, A.S.A.; Filho, B.J.C. A new design of selective harmonic elimination for adjustable speed operation of AC motors in mining industry. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017. [Google Scholar]
- Jalili, K.; Bernet, S. Design of LCL Filters of Active-Front-End Two-Level Voltage-Source Converters. IEEE Trans. Ind. Electron. 2009, 56, 1674–1689. [Google Scholar] [CrossRef]
- Beres, R.; Wang, X.; Blaabjerg, F.; Bak, C.L.; Matsumori, H.; Shimizu, T. Evaluation of core loss in magnetic materials employed in utility grid AC filters. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017. [Google Scholar]
- Kim, J.; Lai, J.S. A Hybrid Front-end for Multi-Generator Power System Harmonic Elimination. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, ML, USA, 29 September–3 October 2019. [Google Scholar]
- Pontt, J.; Rodríguez, J.; Huerta, R. Mitigation of Noneliminated Harmonics of SHEPWM Three-Level Multipulse Three-Phase Active Front End Converters With Low Switching Frequency for Meeting Standard IEEE-519-92. IEEE Trans. Power Electron. 2014, 19, 1594–1600. [Google Scholar] [CrossRef]
- Ojha, A.; Chaturvedi, P.; Mittal, A.; Jain, S. Neutral Point Potential Control for Three Phase 3-level Neutral Point Clamped Active Front End Converter. Int. J. Electr. Eng. Inf. 2017, 9, 342–363. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Holtz, J.; Rodriguez, J.; Baoming, G. Medium-Voltage Multilevel Converters–State of the Art, Challenges, and Requirements in Industrial Application. IEEE Trans. Ind. Electron. 2010, 57, 2581–2596. [Google Scholar] [CrossRef]
- Sahali, Y.; Fellah, M.K. Selective Harmonic Eliminated Pulse-Width Modulation Technique (SHE PWM) applied to Three-level Inverter/Converter. In Proceedings of the 2003 IEEE International Symposium on Industrial Electronics, Rio de Janeiro, Brazil, 9–11 June 2003. [Google Scholar]
- Pontt, J.; Rodriguez, J.; Benavides, R.; De Solminihac, R.; Müller, M. Low Switching Frequency PWM with Selective Harmonic Elimination for Three-Phase Three-Level Inverters. In Proceedings of the 10th International Power Electronics and Motion Control Conference and Exposition, Cavtat & Dubrovnik, Croatia, 9–11 September 2002. [Google Scholar]
- Ahmad, S.; Ganie, Z.A.; Ashraf, I.; Iqbal, A. Harmonics Minimization in 3-Level Inverter Waveform and its FPGA Realization. In Proceedings of the 2018 3rd International Innovative Applications of Computational Intelligence on Power, Energy and Controls with their Impact on Humanity (CIPECH), Ghaziabad, India, 1–2 November 2018. [Google Scholar]
- Al-Hitmi, M.; Ahmad, S.; Iqbal, A.; Padmanaban, S.; Ashraf, I. Selective Harmonic Elimination in a Wide Modulation Range Using Modified Newton-Raphson and Pattern Generation Methods for a Multilevel Inverter. Energies 2018, 11, 458. [Google Scholar] [CrossRef]
- Kundu, S.; Deb Burman, A.; Giri, S.A.; Mukherjee, S.; Banerjee, S. Comparative study between different optimisation techniques for finding precise switching angle for SHE-PWM of three-phase seven-level cascaded H-bridge inverter. Power Electron. IET 2018, 11, 600–609. [Google Scholar] [CrossRef]
- Luo, H.; Mao, C.; Wang, D.; Lu, J.; Wang, L. Fundamental modulation strategy with selective harmonic elimination for multilevel inverters. Power Electron. IET 2014, 7, 2173–2181. [Google Scholar]
- Sundareswaran, K.; Jayant, K.; Shanavas, T.N. Inverter Harmonic Elimination through a Colony of Continuously Exploring Ants. IEEE Trans. Power Electron. 2007, 54, 2558–2565. [Google Scholar] [CrossRef]
- Shirmohammadi, S.; Suh, Y. Cascaded Snubber Scheme Using Flyback Type Transformer for 10 kV IGCT Application. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019–ECCE Asia), Busan, Korea, 27–31 May 2019. [Google Scholar]
- Filsecker, F.; Alvarez, R.; Bernet, S. Comparison of 4.5-kV Press-Pack IGBTs and IGCTs for Medium-Voltage Converters. IEEE Trans. Ind. Electron. 2013, 60, 440–449. [Google Scholar] [CrossRef]
- Silva, C.; Oyarzún, J. High Dynamic Control of a PWM Rectifier using Harmonic Elimination. In Proceedings of the IECON 2006–32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 7–10 November 2006. [Google Scholar]
- Rodríguez, J.; Dixon, J.W.; Espinoza, J.R.; Pontt, J.; Lezana, P. PWM Regenerative Rectifiers: State of the Art. IEEE Trans. Ind. Electron. 2005, 52, 5–22. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cikač, D.; Turk, N.; Bulić, N.; Barbanti, S. Pulse Pattern Optimization Based on Brute Force Method for Medium-Voltage Three-Level NPC Converter with Active Front End. Electronics 2020, 9, 1685. https://doi.org/10.3390/electronics9101685
Cikač D, Turk N, Bulić N, Barbanti S. Pulse Pattern Optimization Based on Brute Force Method for Medium-Voltage Three-Level NPC Converter with Active Front End. Electronics. 2020; 9(10):1685. https://doi.org/10.3390/electronics9101685
Chicago/Turabian StyleCikač, Dominik, Nikola Turk, Neven Bulić, and Stefano Barbanti. 2020. "Pulse Pattern Optimization Based on Brute Force Method for Medium-Voltage Three-Level NPC Converter with Active Front End" Electronics 9, no. 10: 1685. https://doi.org/10.3390/electronics9101685
APA StyleCikač, D., Turk, N., Bulić, N., & Barbanti, S. (2020). Pulse Pattern Optimization Based on Brute Force Method for Medium-Voltage Three-Level NPC Converter with Active Front End. Electronics, 9(10), 1685. https://doi.org/10.3390/electronics9101685





