Design and VLSI Implementation of a Reduced-Complexity Sorted QR Decomposition for High-Speed MIMO Systems

Abstract

In this article, a low-complexity and high-throughput sorted QR decomposition (SQRD) for multiple-input multiple-output (MIMO) detectors is presented. To reduce the heavy hardware overhead of SQRD, we propose an efficient SQRD algorithm based on a novel modified real-value decomposition (RVD). Compared to the latest study, the proposed SQRD algorithm can save the computational complexity by more than 44.7% with similar bit error rate (BER) performance. Furthermore, a corresponding deeply pipelined hardware architecture implemented with the coordinate rotation digital computer (CORDIC)-based Givens rotation (GR) is designed. In the design, we propose a time-sharing Givens rotation structure utilizing CORDIC modules in idle state to share the concurrent GR operations of other CORDIC modules, which can further reduce hardware complexity and improve hardware efficiency. The proposed SQRD processor is implemented in SMIC 55-nm CMOS technology, which processes 62.5 M SQRD per second at a 250-MHz operating frequency with only 176.5 kilo-gates. Compared to related studies, the proposed design has the best normalized hardware efficiency and achieves a 6-Gbps MIMO data rate which can support current high-speed wireless communication systems such as IEEE 802.11ax.

1. Introduction

Multiple-input multiple-output (MIMO) is widely employed in current wireless communication systems, such as IEEE 802.11ax [1], to achieve high data throughput. A MIMO detector is used to recover the original signal from the mixed multi-dimensional data streams, which has a great impact on system performance. In the MIMO detector, QR decomposition (QRD) serves as a preprocessor dealing with a channel matrix to facilitate subsequent MIMO detection. Thus, QRD needs massive arithmetic operations and takes up a considerable part of the hardware complexity of the MIMO detector [2,3]. The sorted QRD (SQRD) can improve the bit error rate (BER) performance of detection through inserting sorting procedures into the original QRD [4]. Due to the addition of sorting modules, however, the hardware overhead further increases. In view of this, it is necessary to design an SQRD processor with high throughput and reduced complexity.

There are three well-known algorithms used for QR decomposition: Householder transformation (HT) [5], modified Gram–Schmidt (MGS) [6], and Givens rotation (GR) [7]. HT is rarely used in the QR decomposition because of its huge computational complexity. Compared with GMS, GR can be realized with a coordinate rotation digital computer (CORDIC), which can simplify the computational complexity. In addition, GR is performed row-wise and the processing of different rows can be done at the same time. Thus, GR can achieve high parallelism to improve the throughput. Given this, many studies adopt CORDIC-based GR to implement SQRD [8,9]. However, all the published studies are suffering from high computational complexity of SQRD and cost a lot of hardware overhead in hardware design. On the other hand, in the hardware design of SQRD, the iterative sorting destroys the original tight and consecutive pipelined GR process and creates a large number of “bubbles”, which are the idle states of the CORDIC-based GR structure. Therefore, the adopted CORDIC-based GR structure is underused, which makes the SQRD hardware inefficient.

In this article, we propose an efficient SQRD algorithm with a novel modified real-value decomposition (RVD), which can greatly reduce the number of CORDIC operations and simplify the computational complexity compared to previous studies. Furthermore, the corresponding deeply pipelined hardware architecture with low latency and low hardware overhead is designed and implemented. In the hardware design, we adopt a time-sharing GR structure utilizing certain CORDIC modules in idle state to perform the concurrent GR operations of other CORDIC modules, which can save hardware cost and improve hardware efficiency. The comparisons of the implementation results show that the proposed SQRD processor overmatches the other related designs in normalized hardware efficiency and achieves up to 6 Gbps MIMO data throughput. The contributions of this study are as follows:

• We propose an efficient reduced-complexity SQRD algorithm based on a novel modified RVD. Compared to the latest related study, the computational complexity of the proposed SQRD algorithm is greatly reduced by more than 44.7%. In addition, the proposed SQRD algorithm has a competitive BER performance and is implementation-friendly;
• We design a deeply pipelined SQRD hardware architecture with a time-sharing GR structure for 4 × 4 MIMO systems. The proposed time-sharing GR structure cleverly utilizes the CORDIC modules in idle state to process certain rotation operations that should have been handled by additional CORDIC module. Therefore, additional hardware is saved and the hardware efficiency of the proposed SQRD design is improved.

Notations: $\Re (\cdot )$ and $\Im (\cdot )$ denote the real and imaginary parts of the argument, respectively. $A_{i,j}$ denotes the element in the $i$th row and $j$th column of a matrix $A$. $A_{i,:}$ and $A_{:,j}$ denote the $i$th row and $j$th column of a matrix $A$, respectively. $v_i$ denotes the $i$th element of a vector $v$. ${(\cdot )}^T$ denotes the transpose of the argument. ${(\cdot )}^H$ denotes the Hermitian transpose of the argument. $a^I$ and $a^R$ denote the real and imaginary parts of a complex number $a$, respectively.

The rest of this article is organized as follows. Section 2 presents the background of this study by reviewing the MIMO detection model and related studies about SQRD. Section 3 describes the proposed SQRD algorithm based on a novel modified RVD. The proposed SQRD hardware architecture with time-sharing GR structure for 4 × 4 MIMO detectors is introduced in Section 4. In Section 5, the implementation results of the proposed SQRD processor and other related studies are discussed and compared. Finally, conclusive remarks are presented in Section 6.

2. Background

2.1. MIMO Detection Model

The MIMO system under consideration consists of $N$ transmit antennas and $N$ receive antennas. The complex-valued matrix $H$ of size $N\times N$ represents the MIMO channel; the complex-valued $N\times 1$ vector $s={\left[s_1,s_2,\cdots ,s_N\right]}^T$ and the complex-valued $N\times 1$ vector $y={\left[y_1,y_2,\cdots ,y_N\right]}^T$ denote the transmit signal and the receive signal, respectively; the $N\times 1$ vector $n={\left[n_1,n_2,\cdots ,n_N\right]}^T$ describes the zero-mean i.i.d. complex additive Gaussian noise, where $n_i\sim \mathcal{N}\left(0,{\delta }^2\right)$ and $i=1,2,\cdots ,N$. The complex-valued MIMO system model is given by

$$y=Hs+n.$$

(1)

The purpose of MIMO detection is to recover the transmit signal $s$ from the receive signal $y$. According to reference [10,11], this can be realized by the maximum likelihood (ML) principle. Therefore, the optimum solution of MIMO detection can be obtained by

$${\widehat{s}}_{ML}=\arg \underset{s\in \mathsf{\Omega }}{\min }{\Vert y-Hs\Vert }^2,$$

(2)

where $\mathsf{\Omega }$ is the solution space. The derivation process of Equation (2) is given in Appendix A. To solve the least square problem like Equation (2), QR decomposition [12] and Cholescky factorization [13] can be performed on the matrix $H$ to simplify the solution procedure. However, the detection procedure based on Cholesky factorization consists of successive forward substitution and backward substitution [14], which is incompatible with column iterative sorting. Whereas, when performed with QR decomposition, the detection procedure can be executed with only backward substitution, which is suitable for column iterative sorting. On the other hand, performing QR decomposition on $H$ can obtain a unitary matrix $Q$ and an upper triangular matrix $R$, i.e., $H=QR$ and pre-multiplying $y-Hs$ by a unitary matrix $Q^H$($Q^H=Q^T$) does not change its norm and thereby has no impact on the MIMO detection. Thus, Equation (2) can be reformulated as

$${\widehat{s}}_{ML}=\arg \underset{s\in \mathsf{\Omega }}{\min }{\Vert Q^{H}y-Rs\Vert }^2.$$

(3)

Therefore, QR decomposition is preferred in MIMO detection. With SQRD performed on the channel matrix, the columns of $R$ are rearranged by iterative sorting to try to ensure that the detection of the signals in different layers of $s$ is conducted in the order of signal-to-noise ratio (SNR) from large to small. In this way, the error propagation in the detection process is alleviated, which could improve the detection performance.

2.2. Related Studies

In recent years, there were many studies focusing on the implementation of SQRD. In reference [15,16,17,18,19,20,21], the SQRD is performed directly on the complex-valued matrix $H$ for the complex-valued MIMO detection model. However, the subsequent MIMO detection in a complex-valued model is more complicated than the one in a real-valued model [22]. Thus, many studies [3,8] develop SQRD based on conventional RVD [23], with which the complex-valued model in Equation (1) is converted into a real-valued model as follows

$$\left[\begin{array}{c}\Re \left(y\right)\\ \Im \left(y\right)\end{array}\right]=\left[\begin{array}{cc}\Re \left(H\right)& -\Im \left(H\right)\\ \Im \left(H\right)& \Re \left(H\right)\end{array}\right]\cdot \left[\begin{array}{c}\Re \left(s\right)\\ \Im \left(s\right)\end{array}\right]+\left[\begin{array}{c}\Re \left(n\right)\\ \Im \left(n\right)\end{array}\right].$$

(4)

Before performing iterative sorting and GR operations, the $N\times N$ complex channel matrix is firstly converted into its real counterpart of size $2N\times 2N$ with conventional RVD [23]. As the size of the matrix is enlarged by four times, the number of sorting procedures and operations of GR both dramatically increase, which leads to huge hardware overhead and lengthy processing latency. The design in reference [9] adopts a SQRD algorithm based on a modified RVD and utilizes the symmetry of adjacent columns of the RVD matrix to reduce the number of CORDIC operations as well as sorting procedures. However, the computational complexity of this scheme still stays at a relatively high level and thereby brings about considerable hardware cost. To alleviate this problem, we propose an efficient SQRD algorithm, which can significantly reduce the computational complexity.

3. Proposed SQRD Algorithm with a Novel Modified RVD

3.1. Proposed Modified RVD

With the proposed modified RVD, the complex-valued system model in Equation (1) can be reformulated as

$$\left[\begin{array}{c}\Re \left(y_1\right)\\ \Re \left(y_2\right)\\ \Im \left(y_1\right)\\ \Im \left(y_2\right)\\ ⋮\\ \Re \left(y_{N-1}\right)\\ \Re \left(y_N\right)\\ \Im \left(y_{N-1}\right)\\ \Im \left(y_N\right)\end{array}\right]=\left[\begin{array}{ccccc}\Re \left(\begin{array}{cc}{h}_{1,1}& h_{1,2}\\ h_{2,1}& h_{2,2}\end{array}\right)& -\Im \left(\begin{array}{cc}{h}_{1,1}& h_{1,2}\\ h_{2,1}& h_{2,2}\end{array}\right)& \cdots & \Re \left(\begin{array}{cc}{h}_{1,N-1}& h_{1,N}\\ h_{2,N-1}& h_{2,N}\end{array}\right)& -\Im \left(\begin{array}{cc}{h}_{1,N-1}& h_{1,N}\\ h_{2,N-1}& h_{2,N}\end{array}\right)\\ \Im \left(\begin{array}{cc}{h}_{1,1}& h_{1,2}\\ h_{2,1}& h_{2,2}\end{array}\right)& \Re \left(\begin{array}{cc}{h}_{1,1}& h_{1,2}\\ h_{2,1}& h_{2,2}\end{array}\right)& \cdots & \Im \left(\begin{array}{cc}{h}_{1,N-1}& h_{1,N}\\ h_{2,N-1}& h_{2,N}\end{array}\right)& \Re \left(\begin{array}{cc}{h}_{1,N-1}& h_{1,N}\\ h_{2,N-1}& h_{2,N}\end{array}\right)\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ \Re \left(\begin{array}{cc}{h}_{N-1,1}& h_{N-1,2}\\ h_{N,1}& h_{N,2}\end{array}\right)& -\Im \left(\begin{array}{cc}{h}_{N-1,1}& h_{N-1,2}\\ h_{N,1}& h_{N,2}\end{array}\right)& \cdots & \Re \left(\begin{array}{cc}{h}_{N-1,N-1}& h_{N-1,N}\\ h_{N,N-1}& h_{N,N}\end{array}\right)& -\Im \left(\begin{array}{cc}{h}_{N-1,N-1}& h_{N-1,N}\\ h_{N,N-1}& h_{N,N}\end{array}\right)\\ \Im \left(\begin{array}{cc}{h}_{N-1,1}& h_{N-1,2}\\ h_{N,1}& h_{N,2}\end{array}\right)& \Re \left(\begin{array}{cc}{h}_{N-1,1}& h_{N-1,2}\\ h_{N,1}& h_{N,2}\end{array}\right)& \cdots & \Im \left(\begin{array}{cc}{h}_{N-1,N-1}& h_{N-1,N}\\ h_{N,N-1}& h_{N,N}\end{array}\right)& \Re \left(\begin{array}{cc}{h}_{N-1,N-1}& h_{N-1,N}\\ h_{N,N-1}& h_{N,N}\end{array}\right)\end{array}\right]\left[\begin{array}{c}\Re \left(s_1\right)\\ \Re \left(s_2\right)\\ \Im \left(s_1\right)\\ \Im \left(s_2\right)\\ ⋮\\ \Re \left(s_{N-1}\right)\\ \Re \left(s_N\right)\\ \Im \left(s_{N-1}\right)\\ \Im \left(s_N\right)\end{array}\right]+\left[\begin{array}{c}\Re \left(n_1\right)\\ \Re \left(n_2\right)\\ \Im \left(n_1\right)\\ \Im \left(n_2\right)\\ ⋮\\ \Re \left(n_{N-1}\right)\\ \Re \left(n_N\right)\\ \Im \left(n_{N-1}\right)\\ \Im \left(n_N\right)\end{array}\right].$$

(5)

It can be suggested that the proposed modified RVD is a permuted version of conventional RVD and it takes 2 × 2 sub-matrices and 2 × 1 sub-vectors of original complex matrix and vectors, respectively, as basic units to perform RVD. Thus, $N$ is restricted to an even number.

3.2. The Proposed SQRD Algorithm

Based on the modified RVD introduced above, we propose a reduced-complexity SQRD algorithm with CORDIC-based GR, which is shown in Algorithm 1. The proposed SQRD algorithm basically comprises three steps. In step 1, sorted complex Givens rotation (SCGR), which contains iterative sorting, and complex Givens rotation is applied to complex channel matrix $H$ and receive signal $y$. Before the elimination process of every column, first, the sorting procedure finds the column with the smallest norm value and swaps it with the first column. Then, the reordered matrix is processed with complex Givens rotation to zero the elements below the diagonal in the first column. Repeat the two procedures until all the elements below the diagonal of $H$ are eliminated and then the complex upper triangular matrix $R^c$ is obtained. In the SCGR, the permutation matrix $P$ records the column order of the iterative sorting for subsequent MIMO detection. In step 2, $R^c$ is converted into its real counterpart $S$ with the proposed modified RVD. Figure 1 shows the diagram of the proposed modified RVD performed on $R^c$ for $N\times N$ ($N$ is even) MIMO systems, where $r^R$ and $r^I$ denote the real and imaginary part of $r$, respectively. Firstly, $R^c$ are partitioned into 2 × 2 sub-matrices $q_{i,j}^{2\times 2}$ and 2 × 1 sub-vectors $q_i^{2\times 1}$, where $i,j=1,2,\cdots ,n$ and $n=N/2$. Then, RVD is performed on all the sub-matrices $q_{i,j}^{2\times 2}$ and sub-vectors $q_i^{2\times 1}$ to obtain their corresponding extended versions $p_{i,j}^{4\times 4}$ of size 4 × 4 and $p_i^{4\times 1}$ of size 4 × 1 by Equations (6) and (7), respectively. Due to the feature of complex Givens rotation [24], the diagonal elements of the upper triangular matrix $R^c$ are all real numbers and all the elements above its diagonal are complex numbers. After the modified RVD is performed, below the diagonal of every sub-matrix $q_{i,j}^{4\times 4}$ (in red dotted box) of $S$, there is only one non-zero element. Consequently, the number of non-zero elements that need to be eliminated in $S$ is $N/2$ in total, which is quite small and does not need many elimination operations in the following real Givens rotation (RGR). It is clear that all the non-zero elements to be nullified in $S$ are located close to the diagonal but in different rows far from each other. This will facilitate the eliminating operations of the following RGR in hardware design. Finally, in step 3, these non-zero elements below the diagonal of $S$ are eliminated with RGR to get the desired upper triangular matrix $R$ and $Q^{H}y$.

$$p_{ij}^{4\times 4}=\left[\begin{array}{cc}\Re \left(q_{ij}^{2\times 2}\right)& -\Im \left(q_{ij}^{2\times 2}\right)\\ \Im \left(q_{ij}^{2\times 2}\right)& \Re \left(q_{ij}^{2\times 2}\right)\end{array}\right],$$

(6)

$$p_i^{4\times 1}=\left[\Re \left(q_i^{2\times 1}\right);\Im \left(q_i^{2\times 1}\right)\right].$$

(7)

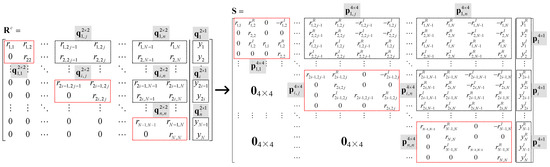
Figure 1. Schematic diagram of the expansion of $R^c$ with proposed modified real-value decomposition (RVD).

Algorithm 1 Proposed SQRD algorithm

INPUT: $H_{N\times N}$, $y_{N\times 1}$, $P=I_N$ OUTPUT: $R_{2N\times 2N}$, $Q^H{y}_{2N\times 1}$,$P$

Step 1: Sorted complex Givens rotation (SCGR) 1: $R^c=\left[H|y\right]$ 2: for $j=1:N$ 3: ${\alpha }_j={\Vert R_{:,j}^c\Vert }^2$ 4: end 5: for $i=1:N$ 6: $k_i={\underset{l=i,\dots ,N}{\mathrm{arg\; min}}}_{}{\alpha }_l$ 7: Swap $R_{:,i}^c$, $P_{:,i}$, and ${\alpha }_i$ with $R_{:,k_i}^c$, $P_{:,k_i}$, and ${\alpha }_{k_i}$, respectively 8: Perform complex Givens rotation in vectoring mode on the elements of $R_{:,i}^c$ in pairs 9: for $m=i+1:N+1$ 10: Perform complex Givens rotation in rotation mode on the elements of $R_{:,m}^c$ in pairs 11: end 12: for $j=i:N$ 13: ${\alpha }_j={\alpha }_j-{\left|R_{i,j}^c\right|}^2$ 14: end 15: end Step 2: Proposed modified RVD 16: for $i=1:N/2$ 17: for $j=1:N/2$ 18: $q_{ij}^{2\times 2}=\left[\begin{array}{cc}{R}_{2i-1,2j-1}^c& R_{2i-1:2j}^c\\ R_{2i,2j-1}^c& R_{2i,2j}^c\end{array}\right]$ 19: $S_{4i-3:4i,4j-3:4j}=\left[\begin{array}{cc}\Re \left(q_{ij}^{2\times 2}\right)& -\Im \left(q_{ij}^{2\times 2}\right)\\ \Im \left(q_{ij}^{2\times 2}\right)& \Re \left(q_{ij}^{2\times 2}\right)\end{array}\right]$ 20: end 21: $q_i^{2\times 1}=\left[R_{2i-1,N+1}^c;R_{2i,N+1}^c\right]$ 22: $S_{4i-3:4i,2N+1}=\left[\Re \left(q_i^{2\times 1}\right);\Im \left(q_i^{2\times 1}\right)\right]$ 23: end Step 3: Real Givens rotation 24: for $i=1:N/2$ 25: Perform real Givens rotation in vectoring mode on $\left(S_{4i-2,4i-2},S_{4i-1,4i-2}\right)$ 26: for $j=4i-1:2N+1$ 27: Perform real Givens rotation in rotation mode on $\left(S_{4i-2,j},S_{4i-1,j}\right)$ 28: end 29: end

3.3. Performance Evaluation of the Proposed SQRD Algorithm

For SQRD, which is implemented with CORDIC, the number of required CORDIC operations can be regarded as a measurement of the computational complexity of the SQRD algorithm. Within the proposed SQRD algorithm for $N\times N$ ($N$ is even) MIMO systems, the CORDIC operations needed in SCGR stage are given by

$${\displaystyle \sum _{k=1}^N\left(\left(N-k+1\right)\left(N-k+1\right)+\left(N-k\right)\left(1+2(N-k)\right)\right)}=N^3.$$

(8)

The detailed derivation of Equation (8) is shown in Appendix B, whereas in the following RGR, the CORDIC operations consumed are as follows:

$${\displaystyle \sum _{k=1}^{N/2}(4k-1})=\left(N^2+N\right)/2.$$

(9)

Table 1 lists the number of CORDIC operations required in the proposed SQRD algorithm as well as a latest related study. For a clear comparison, the number of CORDIC operations needed and the complexity reduction of the proposed compared to the one in reference [9] for different matrix sizes are presented in Figure 2a. It is clear that the proposed SQRD algorithm has a huge advantage over the one in reference [9] in terms of computational complexity. For 4 × 4 MIMO systems, the number of CORDIC operations of the proposed algorithm is greatly reduced by 44.7% compared to the one in reference [9]. In addition, as the size of the channel matrix increases, the reduction will be further expanded and gradually approach 50%.

Table 1. Complexity of different Givens rotation (GR)-based QR decomposition schemes.

Algorithm	Number of CORDIC Operations	$\mathbf{If} \mathit{N}=4$
[9]	$2N^3+\left(1/2\right)N^2-\left(1/2\right)N$	134
The proposed	$N^3+\left(1/2\right)N^2+\left(1/2\right)N$	74

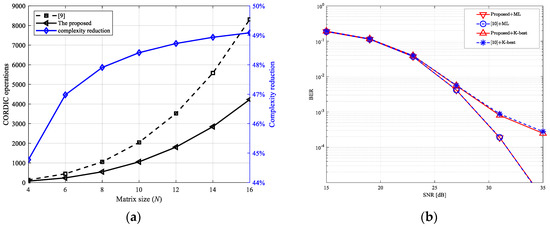
Figure 2. Performance comparisons with the design in reference [9]: (a) complexity performance for different matrix sizes; (b) uncoded bit error rate (BER) performance in 4 × 4 64-QAM multiple-input multiple-output (MIMO) system.

To evaluate the BER performance of the proposed SQRD algorithm in MIMO detection, it is simulated with a K-best detector and a maximum likelihood (ML) detector in an uncoded 4 × 4 64-QAM MIMO system along with the SQRD algorithm in reference [9]. Figure 2b shows that the proposed SQRD algorithm achieves similar BER performance with the one in reference [9].

4. Proposed SQRD VLSI Architecture

4.1. Overview of the Proposed SQRD Hardware Architecture

According to Algorithm 1, we designed the corresponding high-speed and low-complexity SQRD hardware architecture for a 4 × 4 MIMO system. To match the high throughput of current wireless communication systems, the proposed SQRD architecture is deeply pipelined and highly parallel, which can decompose one 4 × 4 channel matrix in four clock cycles and process one $Q^{H}y$ per clock cycle. In other words, the processing cycles of SQRD (clock cycles needed for decomposing one $H$) and $Q^{H}y$ (clock cycles needed for processing one $Q^{H}y$) are four clock cycles and one clock cycle, respectively, which are both decreased by 20% compared to the design of reference [9]. As $\mathrm{throughput}=\mathrm{clock} \mathrm{frequency}/\mathrm{processing} \mathrm{cycles}$, both the SQRD and $Q^{H}y$ throughput of the proposed SQRD will be improved by 25% compared to the design of reference [9]. In addition, the time-sharing GR structure is designed to take advantages of the idle state of CORDIC modules caused by iterative sorting, which can further reduce the hardware overhead and improve hardware efficiency.

The proposed SQRD hardware architecture is basically comprised of one norm calculator, three sorting modules, and four processing engines. Norm calculator and sorting modules are used for iterative sorting; processing engines with CORDIC-based Givens rotation structure are used for decomposing the channel matrix and processing $Q^{H}y$. Figure 3 presents the dataflow of the proposed SQRD design for the 4 × 4 MIMO system. Sorted complex Givens rotation (SCGR) is performed on the 4 × 4 complex channel matrix $H$ and 4 × 1 complex receive signal vector $y$ with all sorting modules and processing engines. After the iterative sorting procedure, every processing engine zeros the elements below the diagonal in the first column of the current input matrix in vectoring mode (introduced in Section 4.2) and rotates the elements of subsequent columns in rotation mode (introduced in Section 4.2). Thus, the SQRD processing cycles of SCGR are four clock cycles. After the process of all the four columns is done, the complex upper triangular matrix $R^c$ is obtained. According to Algorithm 1, next, the 4 × 4 intermediate $R^c$ is converted into its 8 × 8 real version $S$ for the following RGR, which is given by

$$\left[\begin{array}{ccccc}{r}_{1,1}& r_{1,2}& r_{1,3}& r_{1,4}& y_1\\ 0& r_{2,2}& r_{2,3}& r_{2,4}& y_2\\ 0& 0& r_{3,3}& r_{3,4}& y_3\\ 0& 0& 0& r_{4,4}& y_4\end{array}\right]\underrightarrow{\begin{array}{l}\mathrm{Modified}\\ \mathrm{RVD}\end{array}}\left[\begin{array}{ccccccccc}{r}_{1,1}& r_{1,2}^R& 0& -r_{1,2}^I& r_{1,3}^R& r_{1,4}^R& -r_{1,3}^I& -r_{1,4}^I& y_1^R\\ 0& r_{2,2}& 0& 0& r_{2,3}^R& r_{2,4}^R& -r_{2,3}^I& -r_{2,4}^I& y_2^R\\ 0& r_{1,2}^I& r_{1,1}& r_{1,2}^R& r_{1,3}^I& r_{1,4}^I& r_{1,3}^R& r_{1,4}^R& y_1^I\\ 0& 0& 0& r_{2,2}& r_{2,3}^I& r_{2,4}^I& r_{2,3}^R& r_{2,4}^R& y_2^I\\ 0& 0& 0& 0& r_{3,3}& r_{3,4}^R& 0& -r_{3,4}^I& y_3^R\\ 0& 0& 0& 0& 0& r_{4,4}& 0& 0& y_4^R\\ 0& 0& 0& 0& 0& r_{3,4}^I& r_{3,3}& r_{3,4}^R& y_3^I\\ 0& 0& 0& 0& 0& 0& 0& r_{4,4}& y_4^I\end{array}\right].$$

(10)

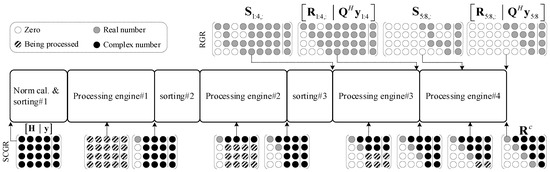
Figure 3. Dataflow diagram of the proposed sorted QR decomposition (SQRD) hardware architecture for 4 × 4 multiple-input multiple-output (MIMO) systems.

Then, RGR performed with processing engine#3–4 eliminates the two non-zero elements below the diagonal of $S$, as shown in Figure 4. It can be suggested that the elements of the upper two rows of $R^c$ are obtained after the processing in sorting#3 because the elimination of the first two columns of $\left[H | y\right]$ have been completed. As the upper four rows of $S$ are derived from the upper two rows of $R^c$ according to Equation (10), they can be obtained immediately after the process of sorting#3 is done. Therefore, the elimination processes of the non-zero element $S_{3,2}$ (i.e., $r_{1,2}^I$) in RGR and the third column of $R^c$ in SCGR are performed with processing engine#3 at the same time when the relevant elements are output from sorting#3. This will improve the parallelism of the SQRD hardware architecture and shorten the processing latency. As for the non-zero element $S_{7,6}$ (i.e., $r_{3,4}^I$), it will be zeroed with processing engine#4 when $r_{4,4}$ of $R^c$ is obtained.

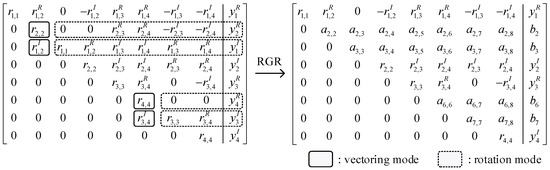
Figure 4. The processing diagram of real Givens rotation (RGR) for 4 × 4 MIMO system.

4.2. Processing Engines

Figure 5, Figure 6 and Figure 7 present the block diagram of the proposed processing engines (PEs). All these PEs comprise three kinds of CORDIC-based Givens rotation structures: processing unit a (PUa), processing unit b (PUb), and processing unit c (PUc). Figure 8 shows their architecture based on CORDIC module, all of which can work in vectoring mode (VM) and rotation mode (RM). In VM, elimination operation is applied to the leading column elements of the current input matrix; in RM, the rotation directions generated in the vectoring mode are retrieved for rotation operations of subsequent elements. PUa processes paired complex rows, zeroing the lower one and turning the upper one into a real number [25]. In vectoring mode, the upper-left three CORDIC modules are used, whereas in rotation mode, all of the four CORDIC modules are occupied. PUb is used for the paired rows of which the leading elements are real numbers and the rest are complex numbers. In vectoring mode, the upper CORDIC module processes the leading paired real elements and zeros the lower one; in rotation mode, the two CORDIC modules are used for the rotation operations of the following complex elements. PEc with only one CORDIC module processes paired real inputs. As these processing units have different processing delays (PUa has two CORDIC stages, whereas PUb and PUc have one), delay elements (DEs) are used to align the data sequences for the subsequent processing unit or sorting module. Among all these Givens rotation structures, all the processing units in PE#1 and PE#2, PUa#4 in PE#3, and PUc#2 in PE#4 are used for SCGR, whereas PUc#3 in PE#3 and PUc#4 in PE#4 are dedicated to RGR. The processing units with multiplexers (MUXs) at input and output ports, including PUb#2 and PUc#2–4, form the time-sharing Givens rotation structure, which will be introduced in the next subsection.

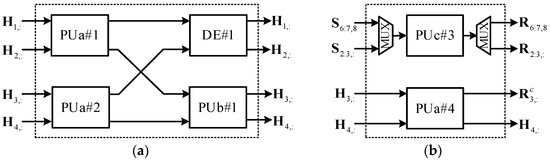
Figure 5. Block diagram of processing engines (PEs): (a) processing engine#1; (b) processing engine#3.

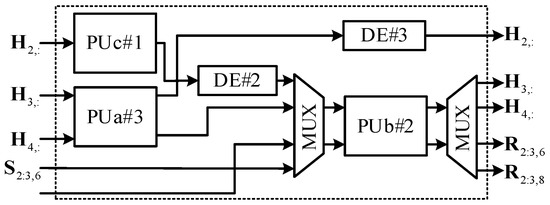
Figure 6. Block diagram of processing engine#2.

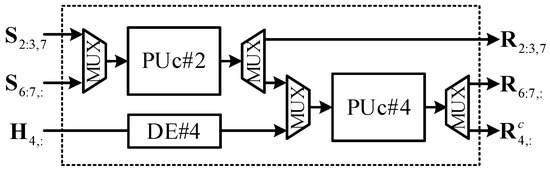
Figure 7. Block diagram of processing engine#4.

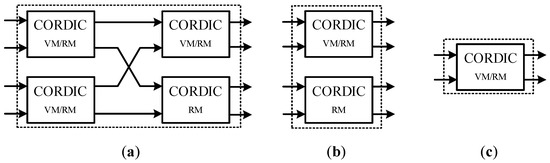
Figure 8. Architecture of coordinate rotation digital computer (CORDIC)-based processing units: (a) PUa; (b) PUb; (c) PUc.

4.3. Time-Sharing Givens Rotation Structure

During the SCGR procedure for 4 × 4 MIMO system described above, the current input matrix of PE#2 is of the size 3 × 3 after the elimination process of the first column of $H$ with PE#1. With the sorting procedures inserted in the column elimination processes, the Givens rotation structures of PE#2 process only three columns and stay in an idle state for one clock cycle within every processing cycle (four clock cycles). Similarly, the periods of idle state of PE#3 and PE#4 in every processing cycles are two and three clock cycles, respectively. As a result, quite a few processing units are operating in an unsaturated state, which causes inefficiency of the SQRD hardware architecture. On the other hand, the elimination process of non-zero elements below the diagonal of $S$ in RGR needs many Givens rotation operations which are independent of the process of SCGR. Given this, we design a time-sharing (TS) Givens rotation structure to take advantage of these idle states mentioned above to share parts of the Givens rotation operations in RGR, which can save hardware cost as well as improve hardware efficiency.

Figure 9 shows the deeply pipelined processing flow of the proposed SQRD processor with time-sharing Givens rotation structure. The index $(i,j)$ in the box denotes the element being processed in the $i$th row and $j$th column of the first $H$ during SCGR procedure or the first $S$ during RGR procedure. In the SCGR procedure, after the process of sorting#2 is done, PUc#1 and PUa#3 in PE#2 stay idle at the first clock cycle of the processing cycles and process the three columns of the current input 3 × 3 matrix in the other three clock cycles; PUa#4 in PE#3 is in an idle state for the first half of every processing cycle and processes the two columns of the current input 2 × 2 matrix in the second half; then, PUc#2 in PE#4 processes the remaining $H_{4,4}$ at the last clock cycle of the processing cycles and stays idle for the other three clock cycles. In the procedure of RGR, the elimination of $S_{3,2}$ in the first $S$ performed by PUc#3 in PE#3 in vectoring mode starts at the 41st clock cycle when $S_{3,2}$, i.e., $r_{1,2}^I$, and $S_{2,2}$, i.e., $r_{2,2}$, are obtained after the processing in sorting#3; PUc#4 in PE#4 will eliminate $S_{7,6}$ in vectoring mode at the 55th clock cycle after $S_{6,6}$, i.e., $r_{4,4}$, is obtained from the process of PUc#2. With a time-sharing Givens rotation structure, part of the rotation operations of PUc#3 and PUc#4 performed on the subsequent elements shown in Figure 4 are reasonably assigned to the suitable processing units in an idle state. As illustrated in Figure 9, the rotation operations of $(r_{2,4}^R,r_{1,4}^I)$, i.e., $(S_{2,6},S_{3,6})$, and $(-r_{2,4}^I,r_{1,4}^R)$, i.e., $(S_{2,8},S_{3,8})$, are separately assigned to the two CORDIC modules in PEb#2 because PEb#2 is just idle when $r_{1,4}$ and $r_{2,4}$ are generated. For a similar reason, the rotation operations of $(-r_{2,3}^I,r_{1,3}^R)$, i.e., $(S_{2,7},S_{3,7})$, $(0,r_{1,1})$, i.e., $(S_{2,3},S_{3,3})$, and $(0,r_{3,4}^R)$, i.e., $(S_{6,8},S_{7,8})$, are assigned to PUc#2, PUc#4, and PUc#3, respectively. If no time-sharing Givens rotation is adopted, as shown in Figure 10, an additional PUc#5 must be used for helping PUc#3 with the rotation operations to match the processing rate of SCGR because it will take seven clock cycles for PUc#3 alone to finish the Givens rotation of the seven paired elements of $S_{2:3,:}$, which exceeds the processing cycles of SCGR. Furthermore, it will cost more delay buffers (DBs) for the aligning of the relevant elements for modified RVD, because the process is extended with only three processing units (PUc#3, PUc#4, and PUc#5). Therefore, with time-sharing Givens rotation structure, one CORDIC module and eight DBs (a DB contains $N_{bw}$ bit registers; $N_{bw}$ is the adopted bit-width) are saved and the hardware efficiency of the entire SQRD is improved.

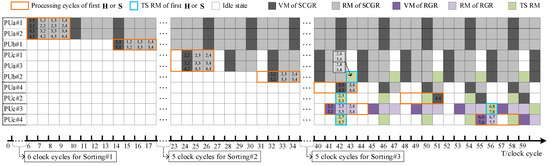
Figure 9. Deeply pipelined processing flow of the proposed SQRD processor with time-sharing Givens rotation structure.

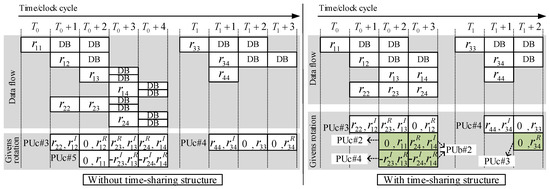
Figure 10. Processing flow of time-sharing Givens rotation structure.

4.4. CORDIC Architecture

Figure 11 and Figure 12 illustrate the detailed CORDIC architecture adopted in our design. The CORDIC module has eight micro-rotation stages and four pipelined stages. In the normal CORDIC module shown in Figure 11a, the rotation direction calculated by $y_i>0:-1:1$ is used and stored in VM; and in RM, the rotation direction is retrieved. In the CORDIC module used for the time-sharing Givens rotation structure shown in Figure 11b, a time-sharing mode (TSM) is added to process the shared rotation operation using the rotation direction from the corresponding processing unit. The scale factor of CORDIC with eight micro-rotations is ${\displaystyle {\prod }_{i=0}^7\left(1/\sqrt{1+2^{-2i}}\right)}=0.607259$. In our design, we approximate this number to $2^{-1}+2^{-3}-2^{-6}-2^{-9}=0.607421875$ and the corresponding hardware architecture is presented in Figure 12.

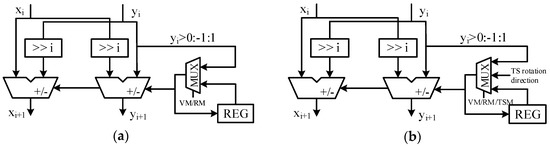
Figure 11. Architecture of micro-rotations of adopted CORDIC module: (a) micro-rotation for normal CORDIC module; (b) micro-rotation for time-sharing CORDIC module.

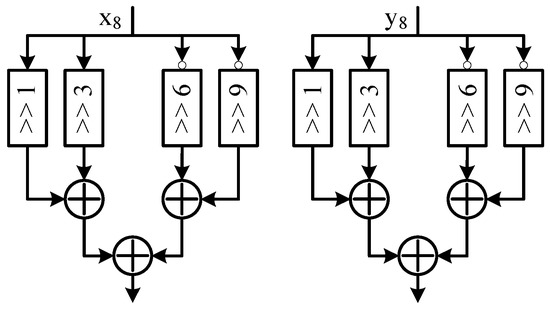
Figure 12. Architecture of scaling of adopted CORDIC module.

4.5. Sorting

The iterative sorting procedure of the proposed SQRD processor is performed with norm calculator and sorting#1–3. Figure 13 shows the architectures of these modules. The complex elements of the 4 × 4 channel matrix $H$ are delivered column by column as the input of norm calculator. First, the squares of the real part and imaginary part of the four elements in one column are calculated with SQ modules and then these squares are added up in pairs to obtain the norm value of every complex element; ultimately, all the norm values are added together with the SUM module to get the norm value of the current input column. In sorting#1, the norm update module is bypassed and the CS module compares these successive norm values until it finds the minimum one. Finally, the column with the smallest norm is swapped with the first column of the four stored in the column buffer. In a similar way, sorting#2 and sorting#3 perform the rest of the sorting procedures. However, what is different from sorting#1 is that, before the CS module, they will first update the norm values from the former sorting module according to line 13 in Algorithm 1.

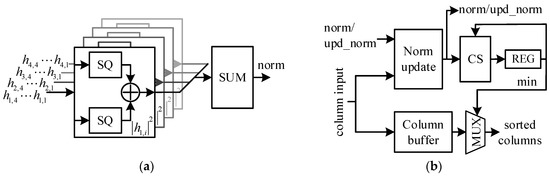
Figure 13. Architecture of the modules of the iterative sorting procedure: (a) norm calculator; (b) sorting#1–3.

5. Implementation Results and Comparisons

We designed the RTL models of the proposed SQRD processor with Verilog HDL and synthesized it by Synopsys Design Compiler with SMIC 55-nm COMS technology. The bit-width of the data pass of our design was set to 16 bits, including 5 bits for the integer part and 11 bits for the fractional part. The fixed-point design of the proposed SQRD was simulated in the same platform introduced in Section 2.1. The result shows that the BER performance has a negligible degradation compared to the floating-point one. Table 2 presents a summary of the implementation results and performance comparisons with related studies. The gate count of the proposed SQRD processor is 176.5 K which is greatly reduced compared to the other designs. This is due to the adopted low-complexity SQRD algorithm and time-sharing Givens rotation structure. Our design achieves a high throughput of 62.5 M SQRD/s and 250 M $Q^{H}y$/s, with an operating frequency of 250 MHz, which is better than most of the other studies. The design in reference [3] has the highest SQRD throughput with the best $f_{\max }$, albeit at the expense of exorbitant hardware cost and long processing latency. Therefore, we take hardware complexity and implementation technology into consideration and introduce normalized hardware efficiency (NHE) for a fair comparison of throughput. Table 2 clearly shows that our design is superior to all the other SQRD processors in terms of normalized hardware efficiency. In addition, we evaluate these designs in a 4 × 4 64QAM MIMO system and our design achieves the highest data throughput of 6 Gbps. For IEEE 802.11ax [1], the maximum uncoded data throughput in the same scenarios with a bandwidth of 160 MHz is 2.88 Gbps. Therefore, the proposed SQRD design is able to support the IEEE 802.11ax.

Table 2. Implementation results and performance comparisons.

Items	This Study	[9]	[20]	[3]	[8]	[19]
Antennas	4 × 4	4 × 4	4 × 4	4 × 4	4 × 4	4 × 4
Algorithm	GR	GR	GR	GR	GR	GR
Technology	55 nm	65 nm	0.18 µm	65 nm	0.13 µm	90 nm
$f_{\max }$ (Hz)	250 M	243.9 M	116.3 M	550 M	200 M	220 M
Gate count	176.5 K	278 K	437.5 K	468 K	299 K	375.1 K
Processing latency (ns)	236	266.5	-	625.5	685-775	654.5
SQRD Processing cycles	4	5	4	8	8	5
SQRD throughput (SQRD/s)	62.5 M	48.8 M	29 M	68.75 M	25 M	44 M
SQRD NHE 1	0.354	0.207	0.217	0.177	0.198	0.192
$Q^{H}y$ Processing cycles	1	1.25	4	-	-	5
$Q^{H}y$ throughput ($Q^{H}y$/s)	250 M	195 M	29 M	-	-	44 M
$Q^{H}y$ NHE	1.416	0.829	0.217	-	-	0.192
MIMO data throughput 2	6 Gbps	4.7 Gbps	696 Mbps	-	-	1 Gbps

¹$\mathrm{NHE}=\mathrm{throughput} \left(\mathrm{M}\right)\cdot \mathrm{Technology}/\left(55\mathrm{nm}\cdot \mathrm{Gate} \mathrm{cout} \left(\mathrm{K}\right)\right)$; ² evaluated for a 4 × 4 64QAM MIMO system [9].

6. Conclusions

In this article, we designed an SQRD processor with reduced complexity and high throughput for MIMO detectors. An efficient SQRD algorithm based on a novel modified RVD was proposed, which could significantly reduce the computational complexity compared to the latest studies. According to the proposed algorithm, we designed the corresponding SQRD hardware architecture with CORDIC-based Givens rotation. In the hardware design, a time-sharing Givens rotation structure was adopted to take advantage of the CORDIC processor in an idle state as far as possible. In this way, hardware complexity was further decreased and hardware efficiency was improved. We also implemented the SQRD processor with SMIC 55-nm COMS technology. The implementation results show that our design surpasses other related studies in normalized hardware efficiency and achieves a MIMO data throughput of 6 Gbps, which can support current high-speed wireless MIMO systems.