A Novel Calibration Method for Signal Leakage between Multiple Channels in Array Imaging
Abstract
:1. Introduction
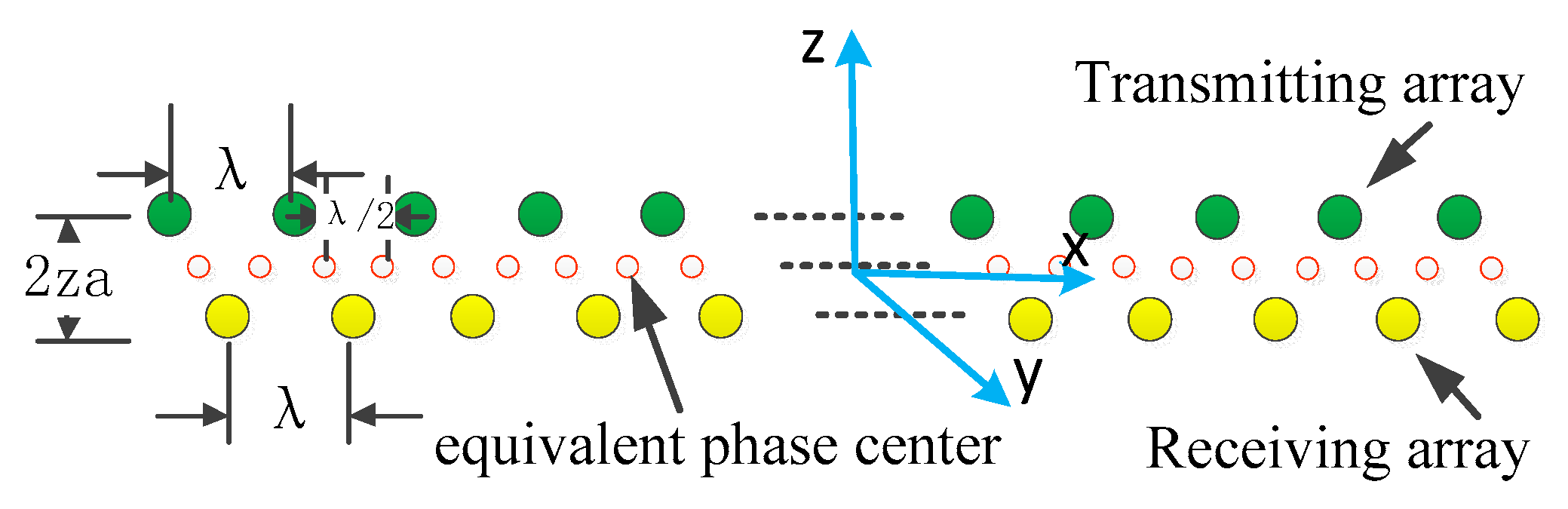
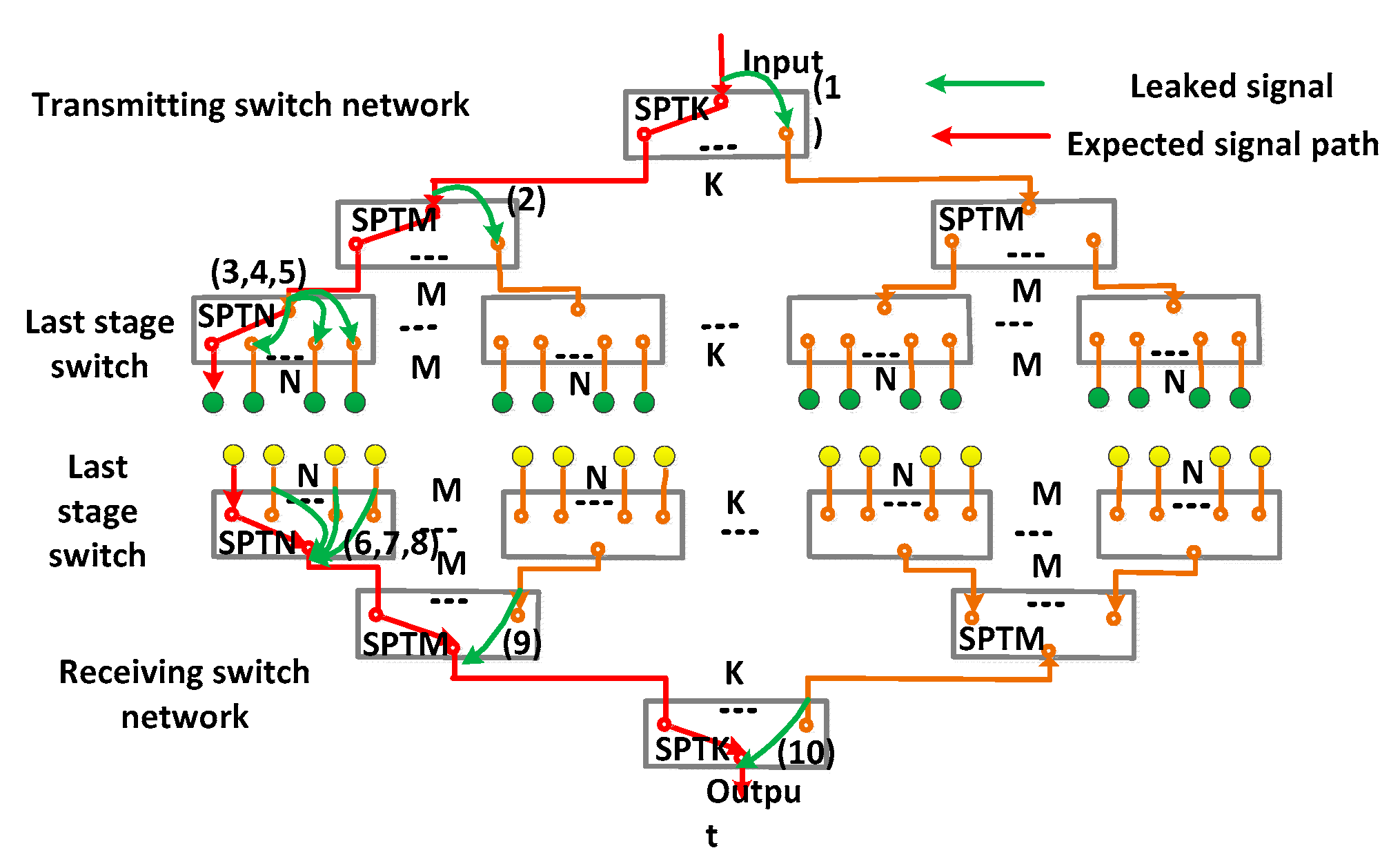
2. Array Structure and Signal Leakage Model
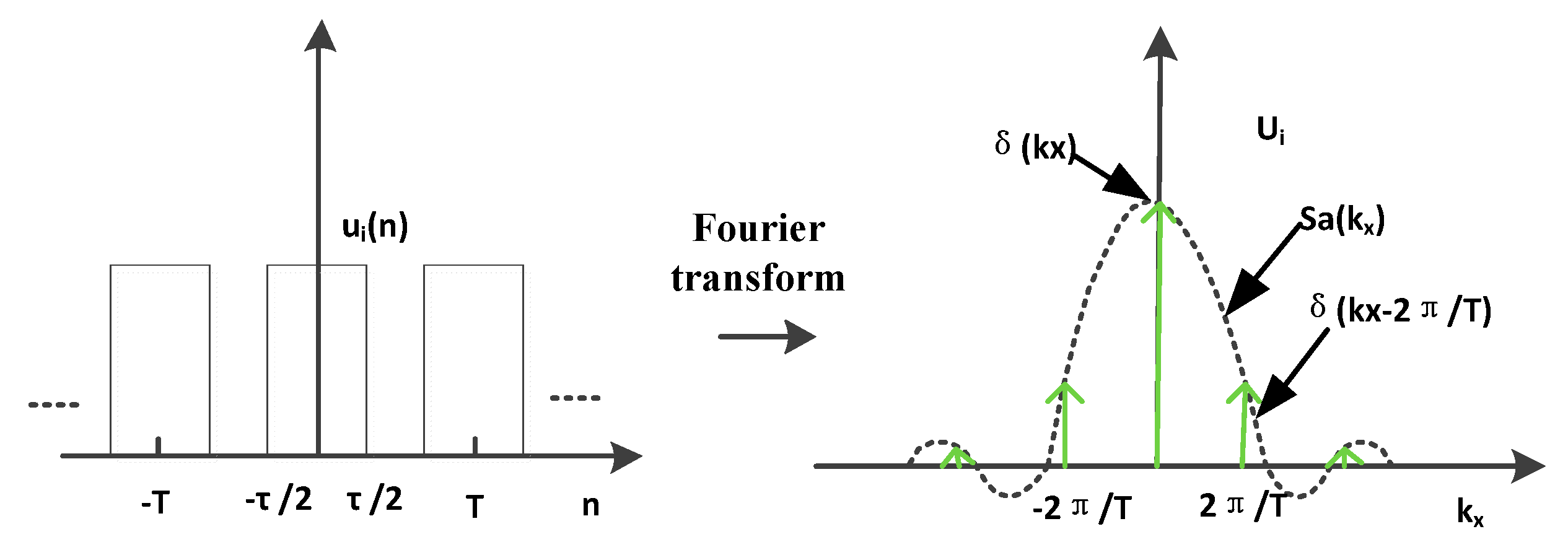
3. The Analysis of the Signal Leakage Impact on Array Imaging
4. Calibration Method of the Signal Leakage
- Step 1:
- Measure the attenuation coefficient η of the antenna array, then the coefficient ηi can be obtained.
- Step 2:
- Calculate the ratio γi according to Expression (6). It is usually difficult to obtain its analytical form; however, we can get its numerical solution through some simulation according to the application scenario of the antenna array.
- Step 3:
- Calculate the array calibration factor by using result of Step 1 and Step 2.
- Step 4:
- Calculate the calibration result P(x,y) by using Poriginal(x,y) according to Expression (11).
5. Simulation and Experiment
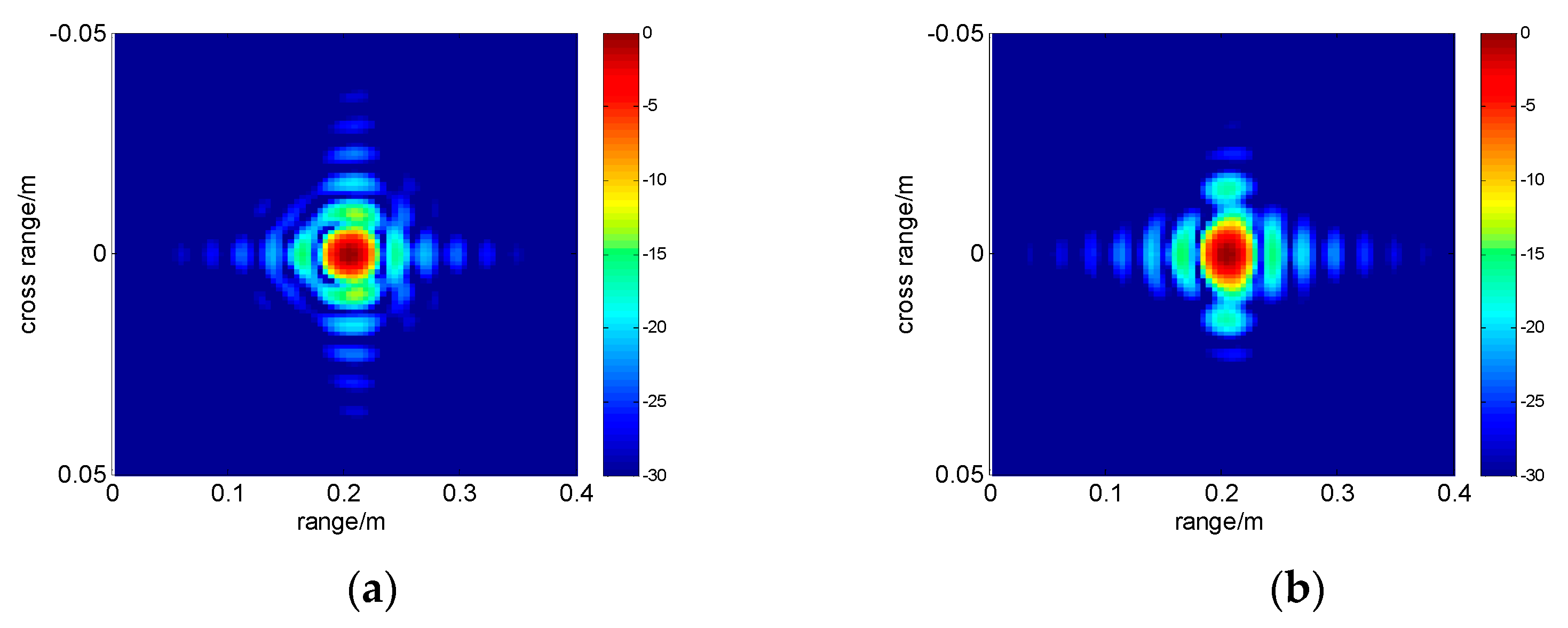
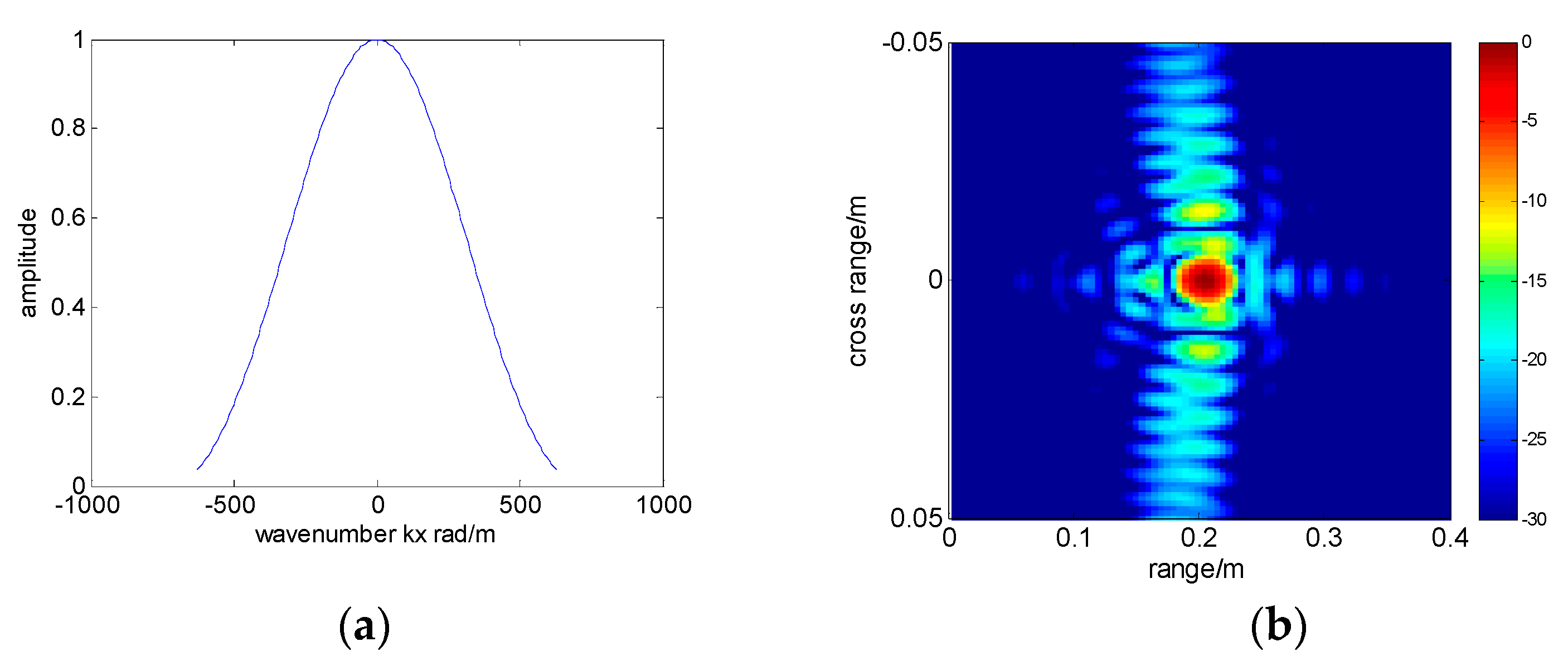
5.1. Simulation Results
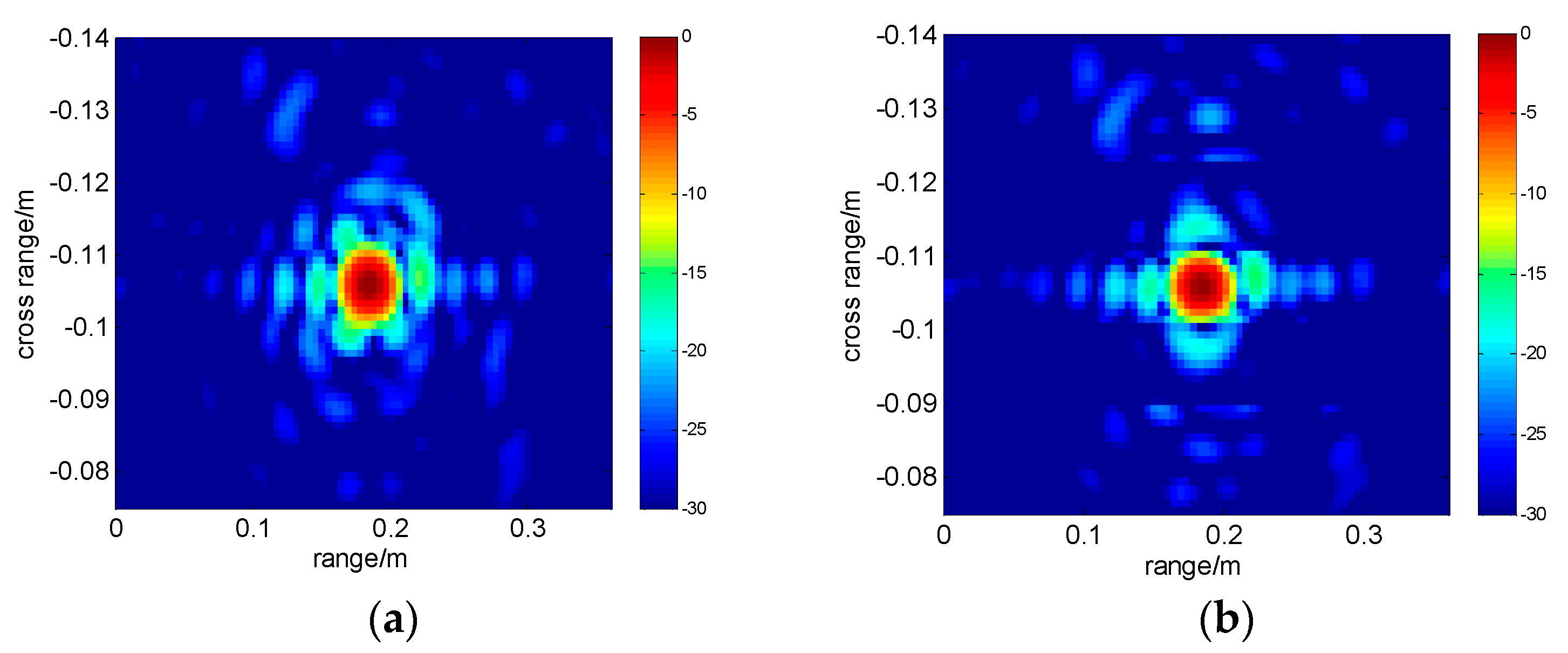
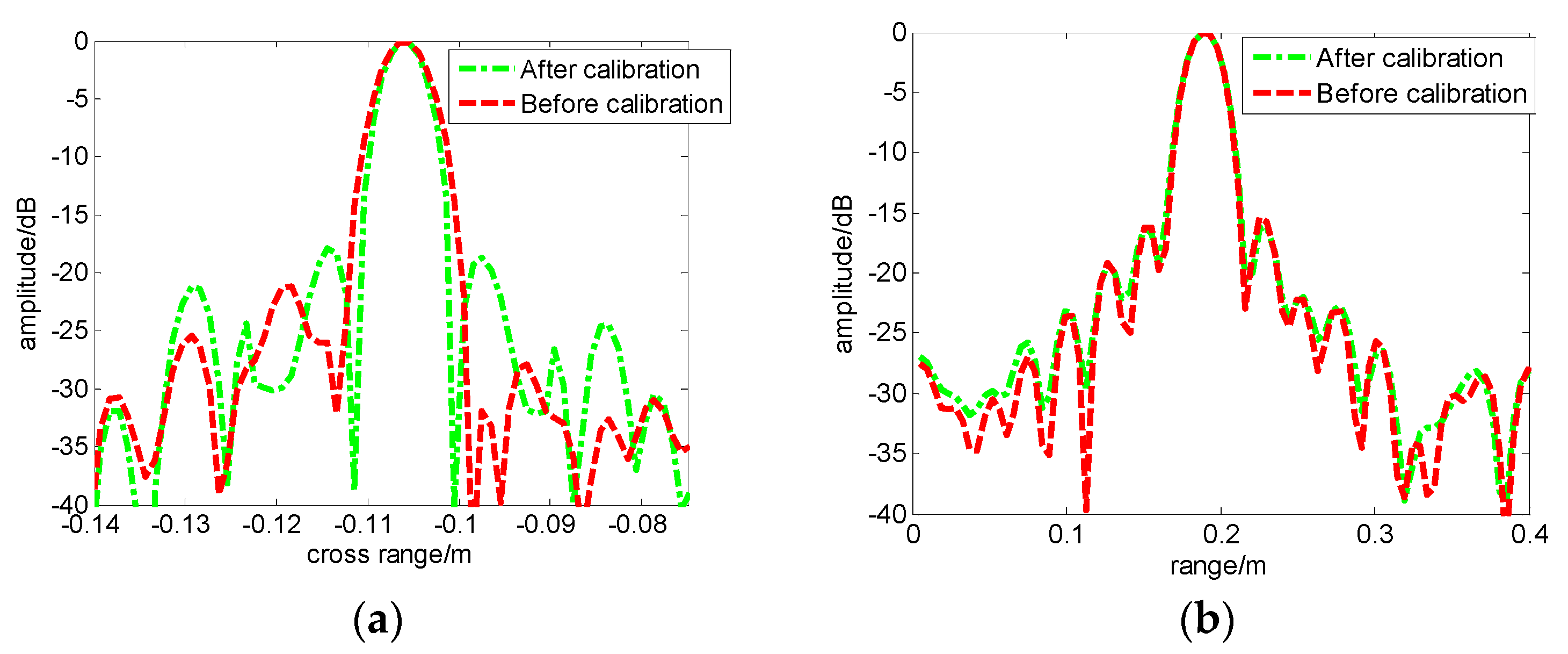
5.2. Experiment Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sheen, D.M.; Clark, R.T.; Tedeschi, J.R.; McCall, J.; Hartman, T.S.; Jones, A.M. Efficient image reconstruction method for a millimeter-wave shoe scanner. In Proceedings of the Passive and Active Millimeter-Wave Imaging XXIII, Vancouver, BC, Canada, 23 April 2020. [Google Scholar]
- Jones, M.; Sheen, D.; Tedeschi, J. Wideband archimedean spiral antenna for millimeter-wave imaging array. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–15 July 2017; pp. 845–846. [Google Scholar]
- Sheen, D.; Jones, M.; Hall, T.E. Simulation of active cylindrical and planar millimeter-wave imaging systems. In Proceedings of the Passive and Active Millimeter-Wave Imaging XXI, Orlando, FL, USA, 18–20 April 2018. [Google Scholar]
- Meng, Y.; Lin, C.; Zang, J.; Qing, A. MMW Holographic Imaging for Security Check. In Proceedings of the 2019 IEEE Asia-Pacific Microwave Conference (APMC), Singapore, 10–13 December 2019; pp. 569–571. [Google Scholar]
- Ma, Q.; Chung, H.; Rebeiz, G.M. A 4-Channel 10–40 GHz Wideband Receiver with Integrated Frequency Quadrupler for High Resolution Millimeter-Wave Imaging Systems. In Proceedings of the 2018 IEEE/MTT-S International Microwave Symposium—IMS, Philadelphia, PA, USA, 10–15 June 2018; pp. 883–886. [Google Scholar]
- Cheng, B.; Cui, Z.; Lu, B.; Qin, Y.; Liu, Q.; Chen, P.; He, Y.; Jiang, J.; He, X.; Deng, X.; et al. 340-GHz 3-D Imaging Radar With 4Tx-16Rx MIMO Array. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 509–519. [Google Scholar] [CrossRef]
- Li, S.; Zhao, G.-Q.; Sun, H.; Amin, M.G. Compressive Sensing Imaging of 3-D Object by a Holographic Algorithm. IEEE Trans. Antennas Propag. 2018, 66, 7295–7304. [Google Scholar] [CrossRef]
- Gao, J.; Qin, Y.; Beng, B.; Wang, H.; Li, X. A novel method for 3D milliter-wave holographic reconstruction based on frequency interferometry techniques. IEEE Trans. Microw. Theory Technol. 2018, 66, 1579–1596. [Google Scholar] [CrossRef]
- Gao, J.; Qin, Y.; Deng, B.; Wang, H.; Li, X. Novel Efficient 3D Short-Range Imaging Algorithms for a Scanning 1D-MIMO Array. IEEE Trans. Image Process. 2018, 27, 3631–3643. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Deng, B.; Qin, Y.; Li, X.; Wang, H. Point Cloud and 3-D Surface Reconstruction Using Cylindrical Millimeter-Wave Holography. IEEE Trans. Instrum. Meas. 2019, 68, 4765–4778. [Google Scholar] [CrossRef]
- Mirbeik-Sabzevari, A.; Oppelaar, E.; Ashinoff, R.; Tavassolian, N. High-Contrast, Low-Cost, 3-D Visualization of Skin Cancer Using Ultra-High-Resolution Millimeter-Wave Imaging. IEEE Trans. Med. Imaging 2019, 38, 2188–2197. [Google Scholar] [CrossRef] [PubMed]
- Mirbeik-Sabzevari, A.; Li, S.; Garay, E.; Nguyen, H.T.; Wang, H.; Tavassolian, N. Synthetic Ultra-High-Resolution Millimeter-Wave Imaging for Skin Cancer Detection. IEEE Trans. Biomed. Eng. 2019, 66, 61–71. [Google Scholar] [CrossRef] [PubMed]
- Mirbeik-Sabzevari, A.; Tavassoian, N.; Ashinoff, R. Ultra-High-Resolution Millimeter-Wave Imaging: A New Promising Skin Cancer Imaging Modality. In Proceedings of the 2018 IEEE Biomedical Circuits and Systems Conference (BioCAS), Cleveland, OH, USA, 17–19 October 2018; pp. 1–4. [Google Scholar]
- Wang, P.; Millar, D.; Parsons, K.; Orlik, P.V. Nonlinearity correction for range estimation in FMCW millimeter-wave automotive radar. In Proceedings of the 2018 IEEE MTT-S International Wireless Symposium (IWS), Chengdu, China, 6–10 May 2018; pp. 1–3. [Google Scholar]
- Wang, P.; Millar, D.; Parsons, K.; Ma, R.; Orlik, P.V. Range Accuracy Analysis for FMCW Systems with Source Nonlinearity. In Proceedings of the 2019 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Detroit, MI, USA, 15–16 April 2019; pp. 1–5. [Google Scholar]
- Li, Y.; Hu, W.; Zhang, X.; Zhao, Y.; Ni, J.; Ligthart, L.P. A Non-Linear Correction Method for Terahertz LFMCW Radar. IEEE Access 2020, 8, 102784–102794. [Google Scholar] [CrossRef]
- Schiessl, A.; Genghammer, A.; Ahmed, S.S.; Schmidt, L.P. Phase error sensitivity in multistatic microwave imaging systems. In Proceedings of the 43rd European Microwave Coference, Nuremberg, Germany, 7–10 October 2013; pp. 1631–1634. [Google Scholar]
- Pinel-Puyssegur, B.; Lasserre, C.; Benoit, A.; Jolivet, R.; Doin, M.; Champenois, J. A Simple Phase Unwrapping Errors Correction Algorithm Based on Phase Closure Analysis. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 23–27 July 2018; pp. 2212–2215. [Google Scholar]
- Deng, H.; Farquharson, G.; Sahr, J.; Goncharenko, Y.; Mower, J. Phase Calibration of an Along-Track Interferometric FMCW SAR. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4876–4886. [Google Scholar] [CrossRef]
- Korner, G.; Oppelt, D.; Adametz, J.; Vossiek, M. Novel Passive Calibration Method for Fully Polarimetric Near Field MIMO Imaging Radars. In Proceedings of the 2019 12th German Microwave Conference (GeMiC), Stuttgart, Germany, 25–27 March 2019. [Google Scholar]
- Zhao, Q.; Zhang, Y.; Wang, W.; Wang, P.; Wang, R.; Deng, Y.; Zhang, H.; Ye, K.; Zhou, Y. Channel Imbalance Compensation with IF Signal for China’s IDBSAR. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1112–1115. [Google Scholar]
- Shin, D.H.; Jung, D.H.; Kim, D.C.; Ham, J.W.; Park, S.O. A distributed FMCW radar system based on Fiber-Optic links for small drone decetion. IEEE Trans. Instrum. Meas. 2017, 66, 340–347. [Google Scholar] [CrossRef]
- Lee, S.J.; Jung, J.H.; Yu, J.-W. TX Leakage Canceller for Small Drone Detection Radar in 2-GHz Band. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 213–215. [Google Scholar] [CrossRef]
- Melzer, A.; Onic, A.; Huemer, M. Self-Adaptive Short-Range Leakage Canceler for Automotive FMCW Radar Transceivers. In Proceedings of the 2018 15th European Radar Conference (EuRAD), Madrid, Spain, 26–28 September 2018; pp. 26–29. [Google Scholar]
- Bauduin, M.; Bourdoux, A. Mixed-Signal Transmitter Leakage Cancellation for PMCW MIMO Radar. In Proceedings of the 2018 15th European Radar Conference (EuRAD), Madrid, Spain, 26–28 September 2018; pp. 293–297. [Google Scholar]
- Arnold, B.T.; Jensen, M.A. The Effect of Antenna Mutual Coupling on MIMO Radar System Performance. IEEE Trans. Antennas Propag. 2019, 67, 1410–1416. [Google Scholar] [CrossRef]
- Colon-Diaz, N.; McCormick, P.M.; Janning, D.; Bliss, D.W. Compensation of Mutual Coupling Effects for Co-located MIMO Radar Applications via Waveform Design. In Proceedings of the 2019 International Radar Conference (RADAR), Toulon, France, 23–27 September 2019; pp. 1–6. [Google Scholar]
- Chen, X.; Zhang, S.; Li, Q. A Review of Mutual Coupling in MIMO Systems. IEEE Access 2018, 6, 24706–24719. [Google Scholar] [CrossRef]
- Sheen, D.; McMakin, D.; Hall, T. Three-dimensional millimeter-wave imaging for concealed weapon detection. IEEE Trans. Microw. Theory Tech. 2001, 49, 1581–1592. [Google Scholar] [CrossRef]
- Kell, R. On the derivation of bistatic RCS from monostatic measurements. Proc. IEEE 1965, 53, 983–988. [Google Scholar] [CrossRef]
- Stolt, R.H. Migration by Fourier Transform. Geophysics 1978, 43, 23–48. [Google Scholar] [CrossRef]
- Jiacheng, S.; Chen, M. Research on Imaging Algorithm of Millimeter Wave Radar Based on Stolt Interpolation. In Proceedings of the 2019 IEEE MTT-S International Microwave Biomedical Conference (IMBioC), Nanjing, China, 6–8 May 2019; pp. 1–4. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data Algorithms and Implementation; Artech House: Boston, MA, USA, 2005; pp. 39–41. [Google Scholar]







| Calibration Method | IRW | PSLR (dB) |
|---|---|---|
| Array Calibration Factor Method (ACFM) | 1.008 | −13.96 |
| Window Function Calibration Method (WFCM) | 1.004 | −11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; Cheng, B.; Deng, X.; Wu, Q.; An, J.; Yu, Y. A Novel Calibration Method for Signal Leakage between Multiple Channels in Array Imaging. Electronics 2020, 9, 1628. https://doi.org/10.3390/electronics9101628
Cui Z, Cheng B, Deng X, Wu Q, An J, Yu Y. A Novel Calibration Method for Signal Leakage between Multiple Channels in Array Imaging. Electronics. 2020; 9(10):1628. https://doi.org/10.3390/electronics9101628
Chicago/Turabian StyleCui, Zhenmao, Binbin Cheng, Xianjin Deng, Qiang Wu, Jianfei An, and Yang Yu. 2020. "A Novel Calibration Method for Signal Leakage between Multiple Channels in Array Imaging" Electronics 9, no. 10: 1628. https://doi.org/10.3390/electronics9101628
APA StyleCui, Z., Cheng, B., Deng, X., Wu, Q., An, J., & Yu, Y. (2020). A Novel Calibration Method for Signal Leakage between Multiple Channels in Array Imaging. Electronics, 9(10), 1628. https://doi.org/10.3390/electronics9101628





