Voltage H∞ Control of a Vanadium Redox Flow Battery
Abstract
1. Introduction
2. System Modeling
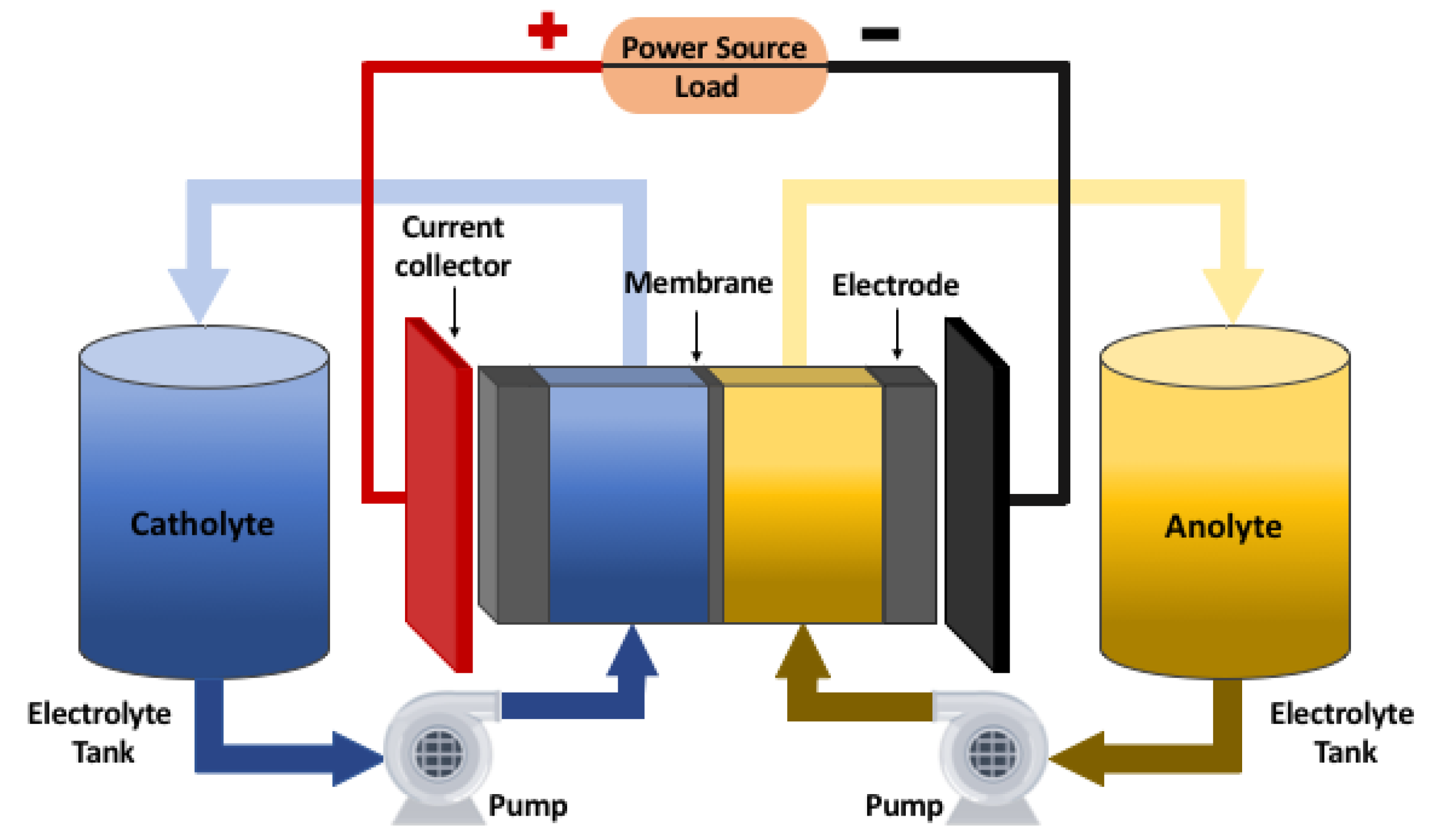
2.1. Operation of a VRFB
2.2. VRFB Electrochemical Model
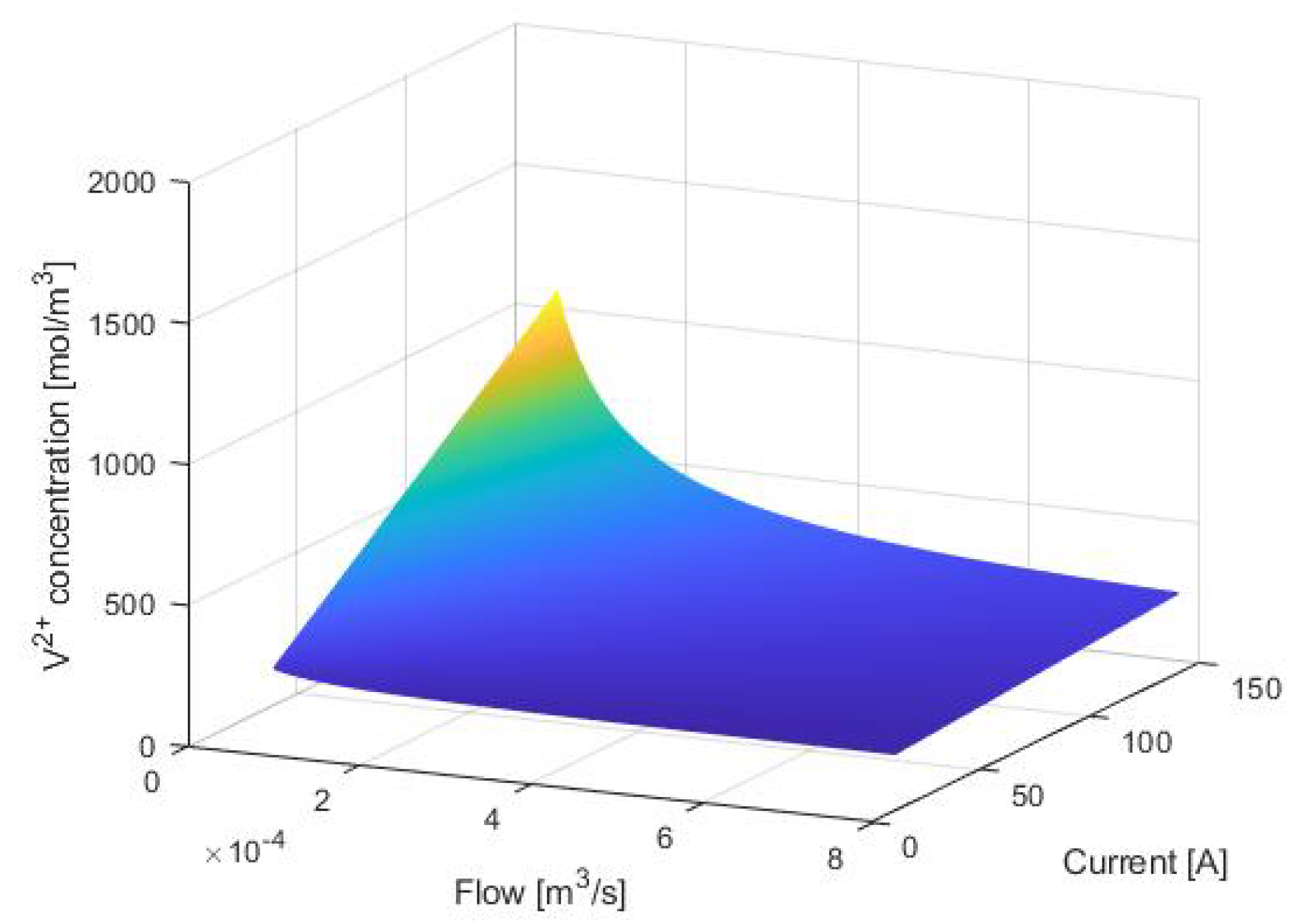
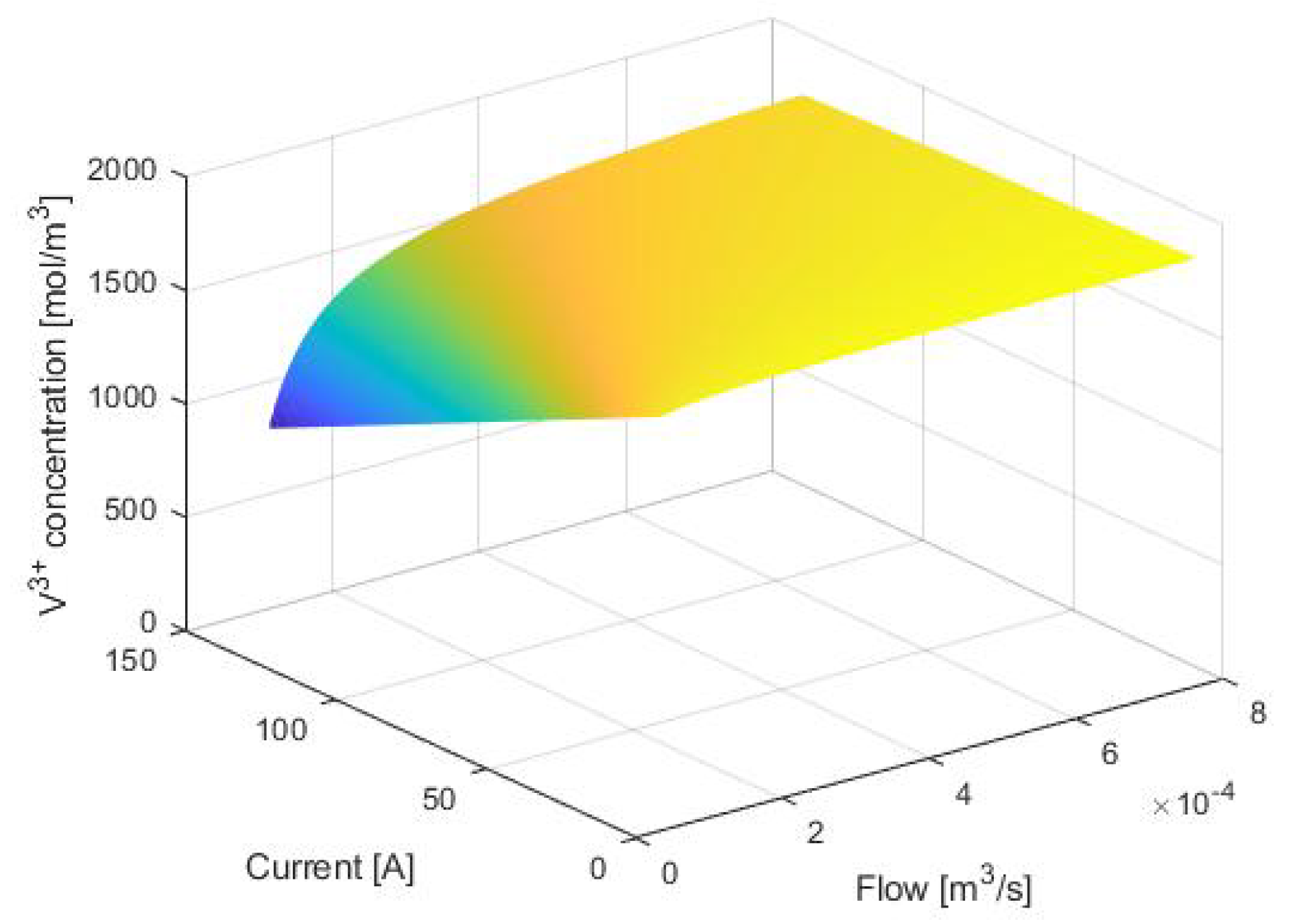
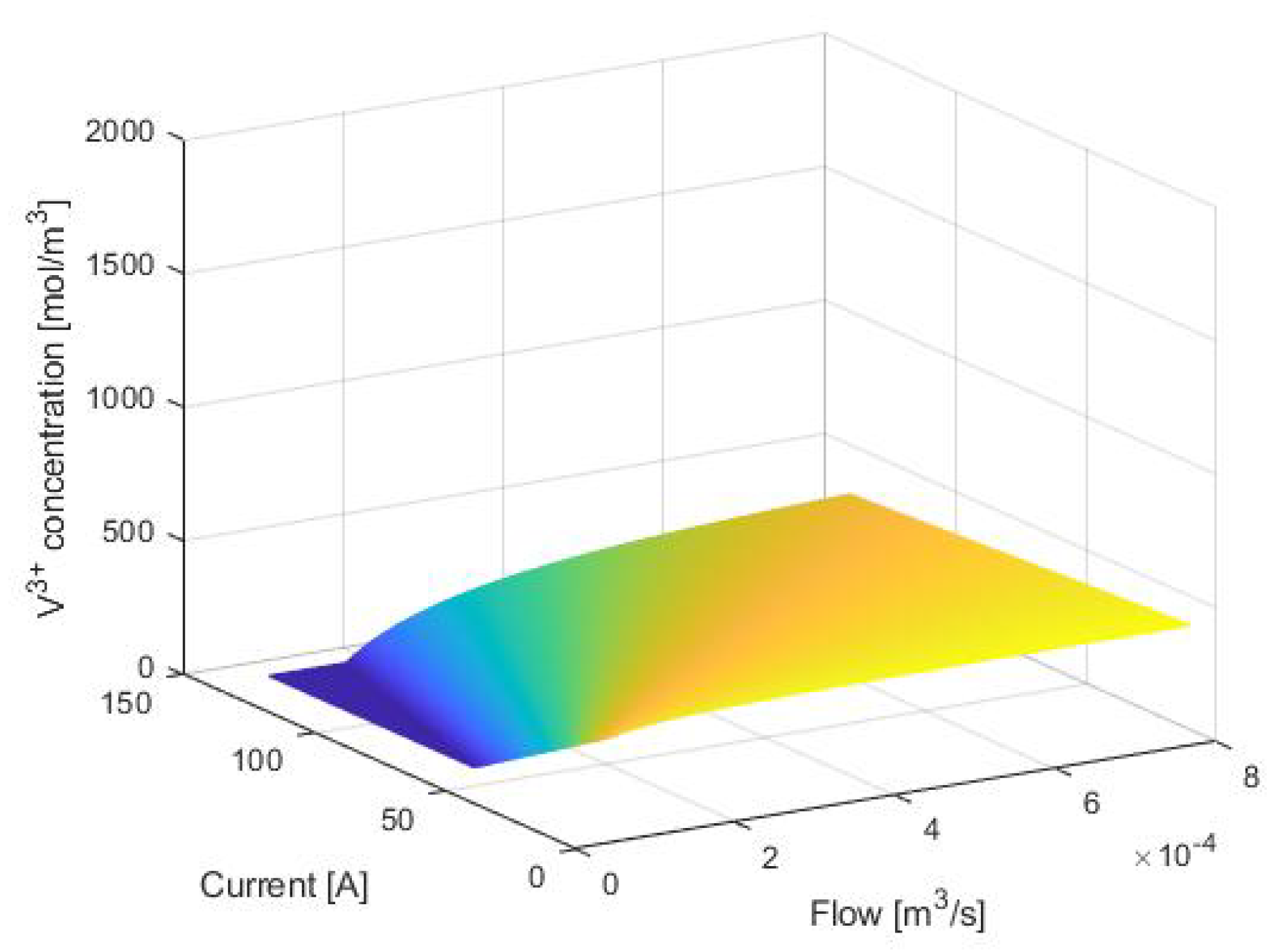
3. Equilibrium Points Analysis
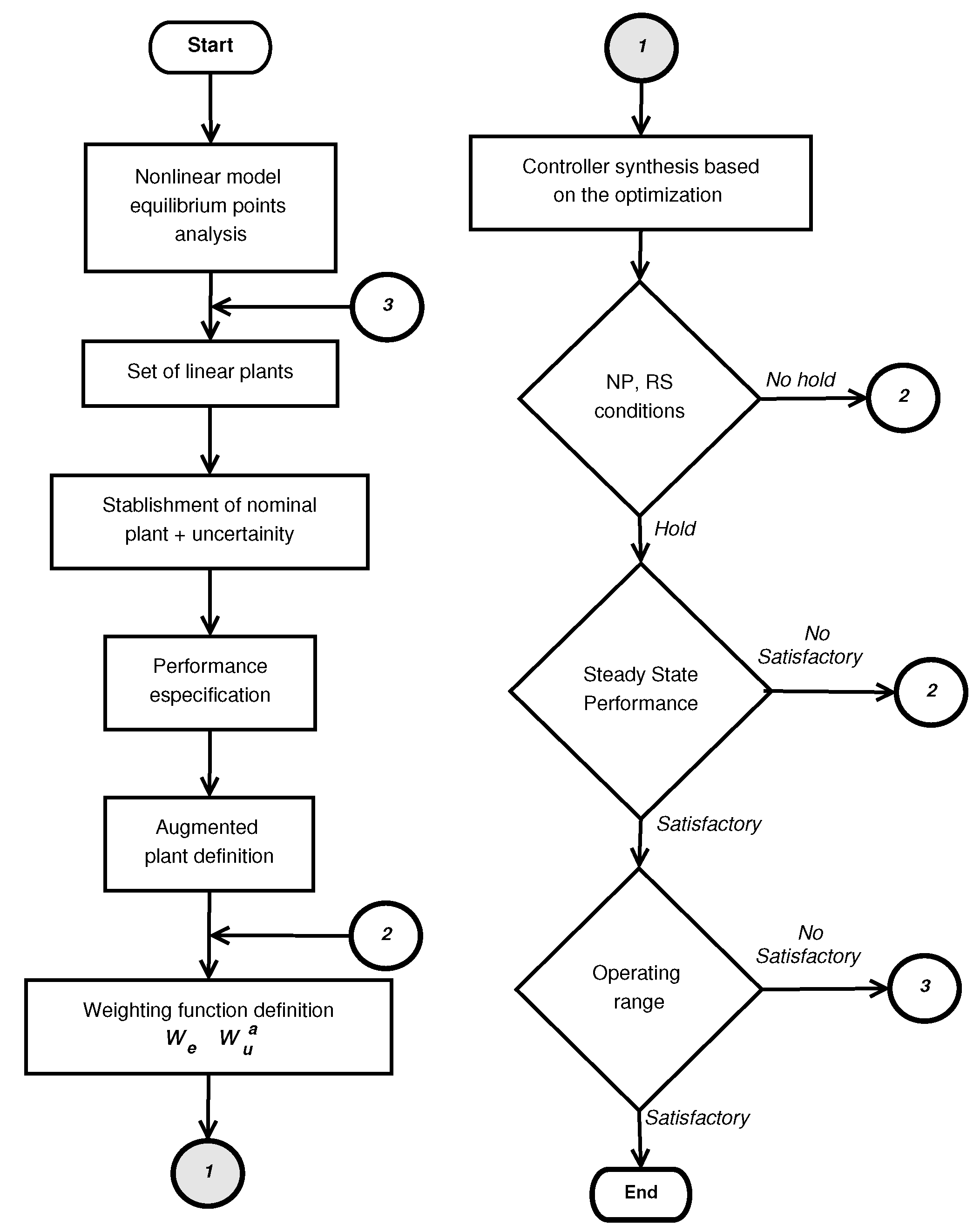
4. Controller Design
4.1. Introduction
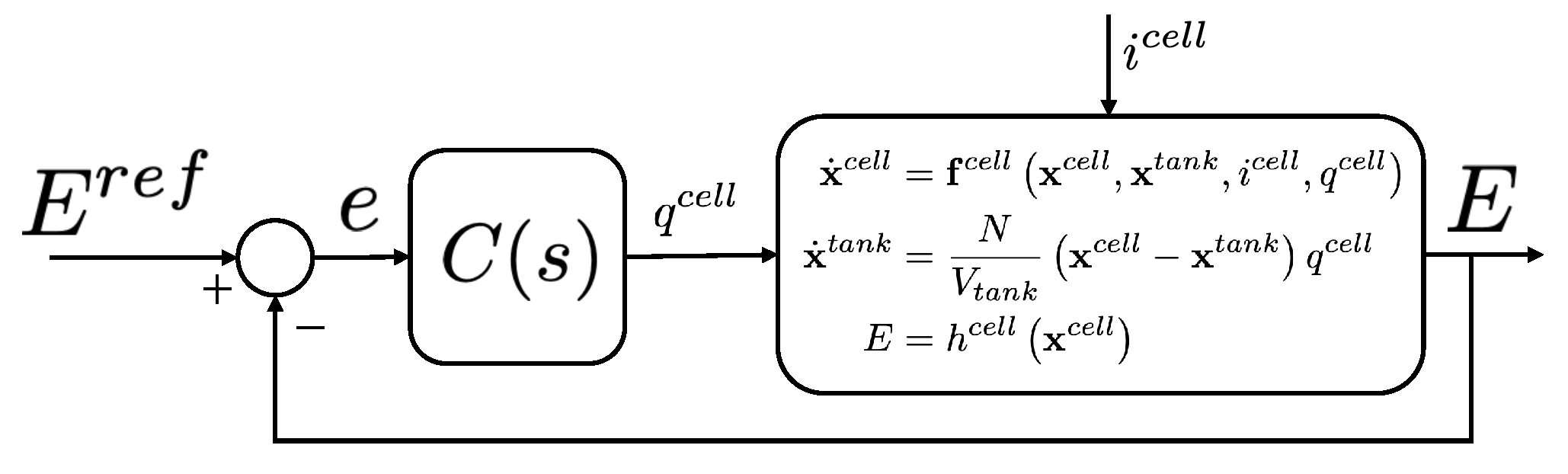
4.2. Model Simplification
- Vanadium concentrations are the same on both sides of the half cell. Therefore, it is possible to have the following correspondence:
- The tanks concentration can be expressed in terms of SOC and total vanadium concentration :
4.3. System Linearization
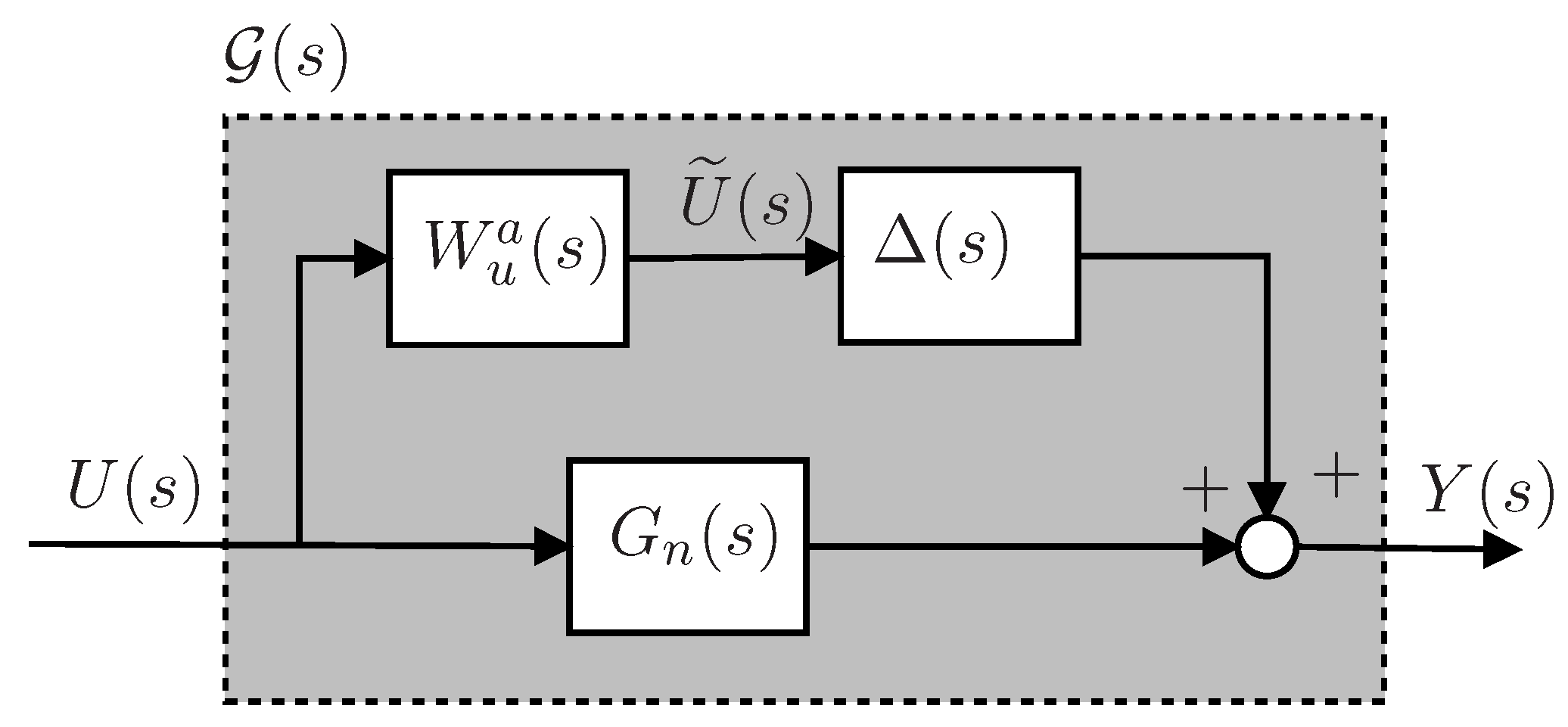
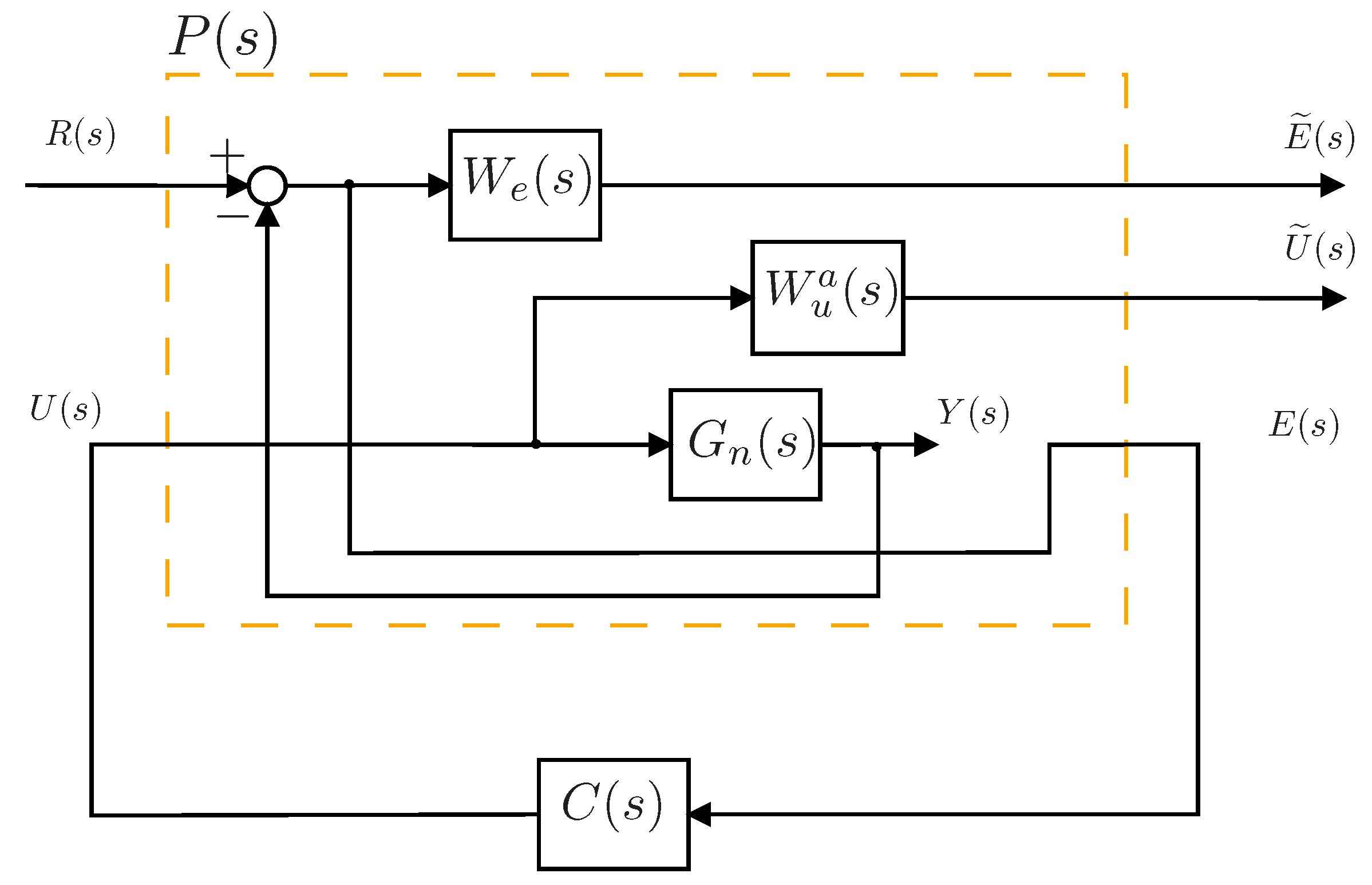
4.4. Uncertainty Modeling
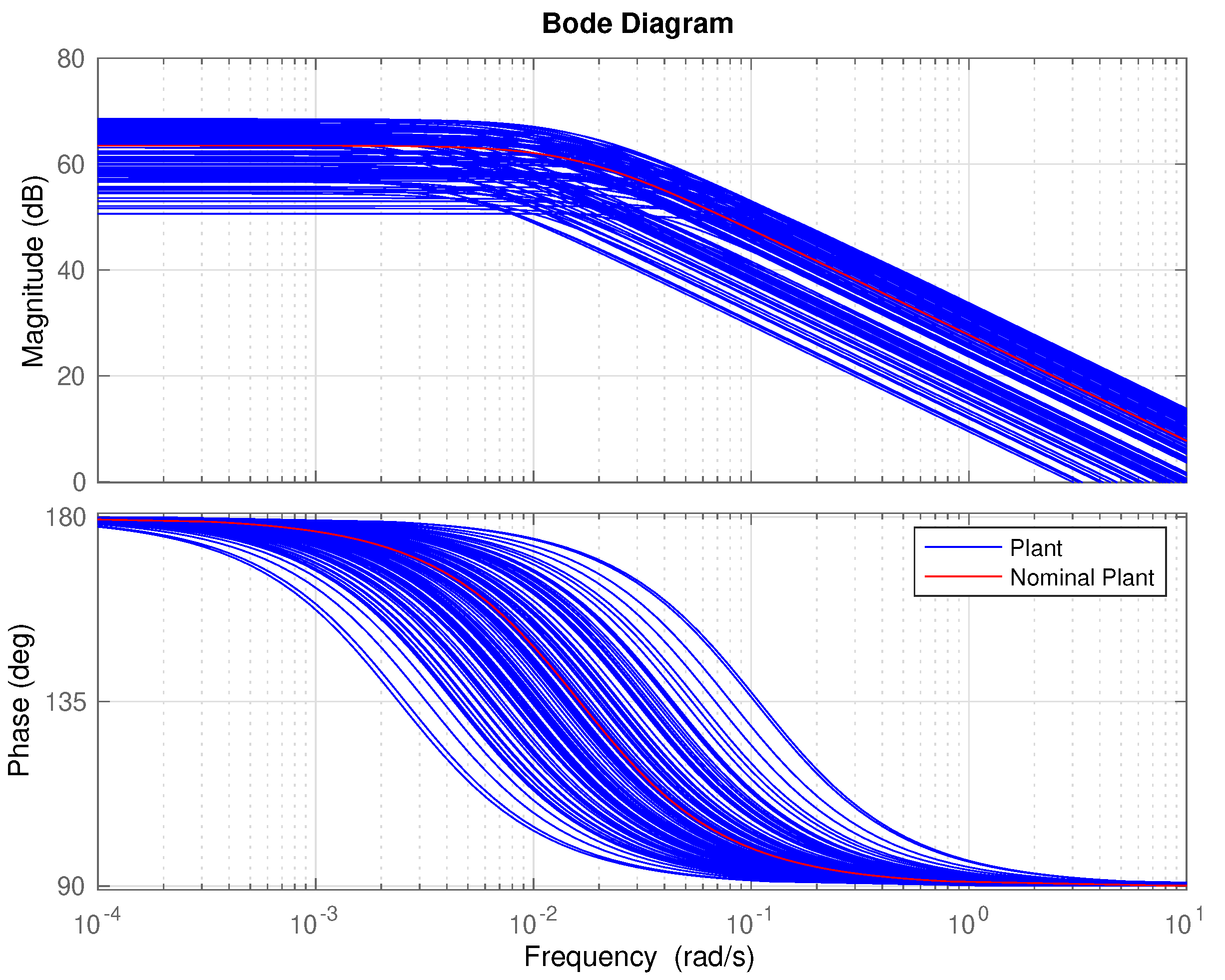
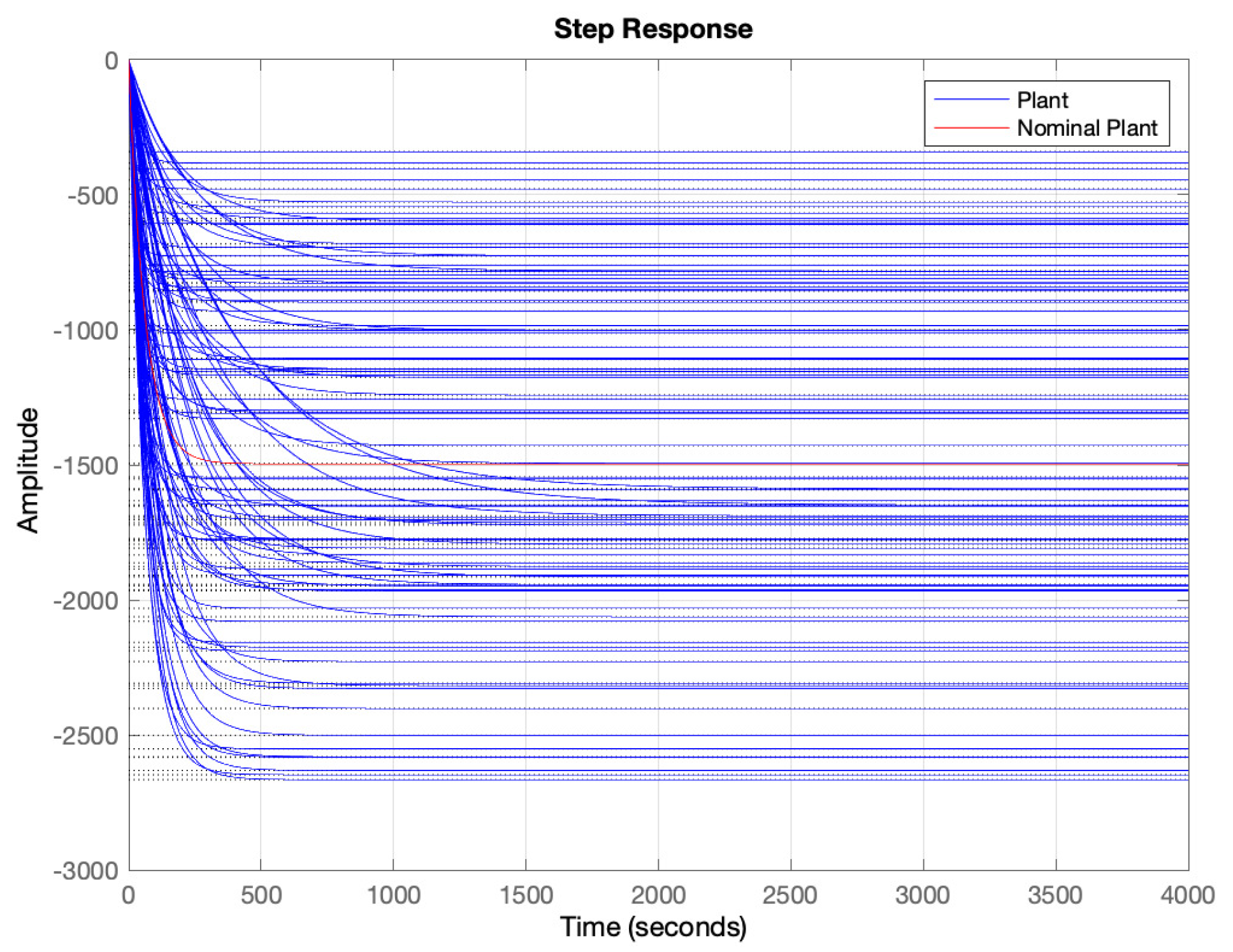
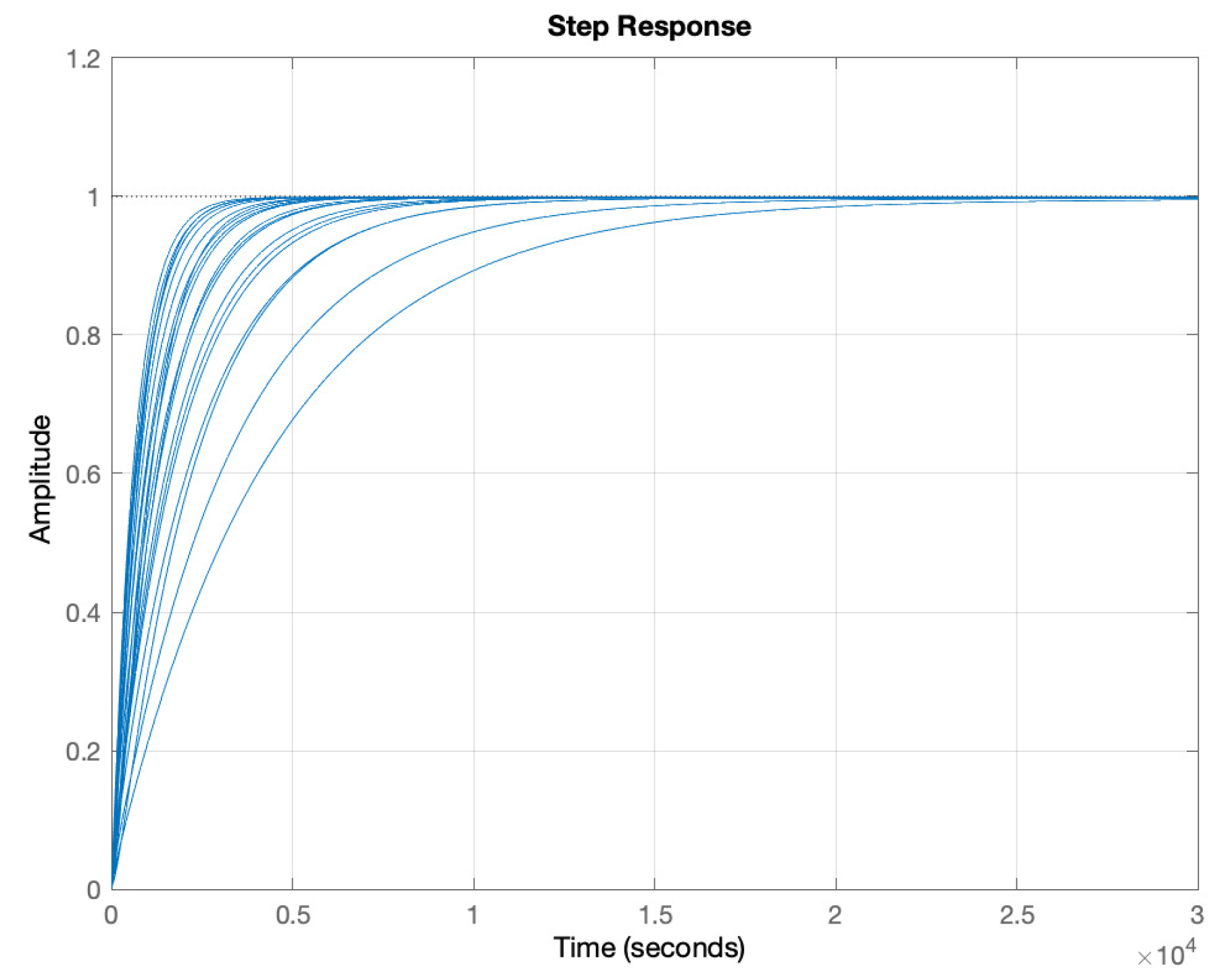
- Determine a frequency range where to model the uncertainty. In our case the, range has been selected. As can be seen in Figure 6, out of this frequency range there is almost no variability in the response. 500 points logarithmically distributed have defined in this range.
- Sample the set of plants, obtained in step 1 and the range of frequencies selected in step 2.
- Compute the error (distance) between each point with respect the nominal plant.
- Obtain stable and minimum phase rational function of polynomials that bounds all of the points obtained in step 4. The rational function order must be selected making a trade-off between the order of the function and the goodness of the fit.
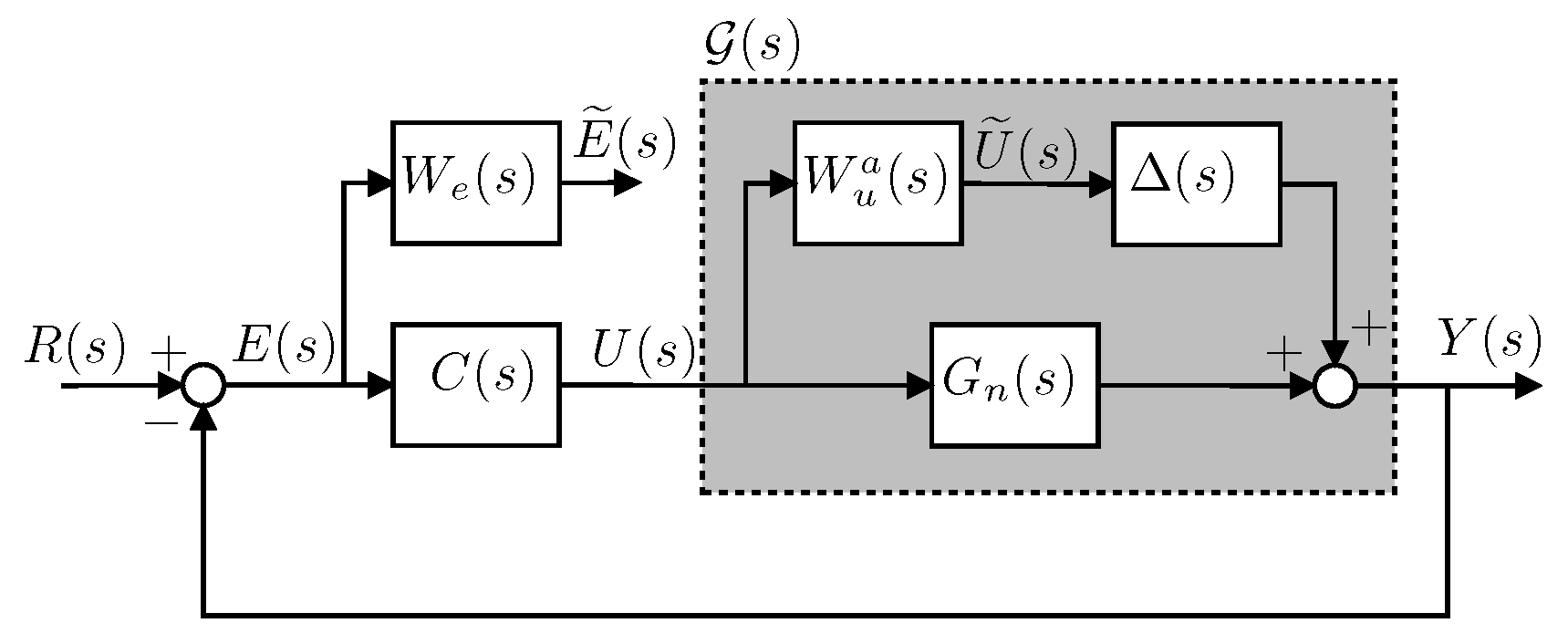
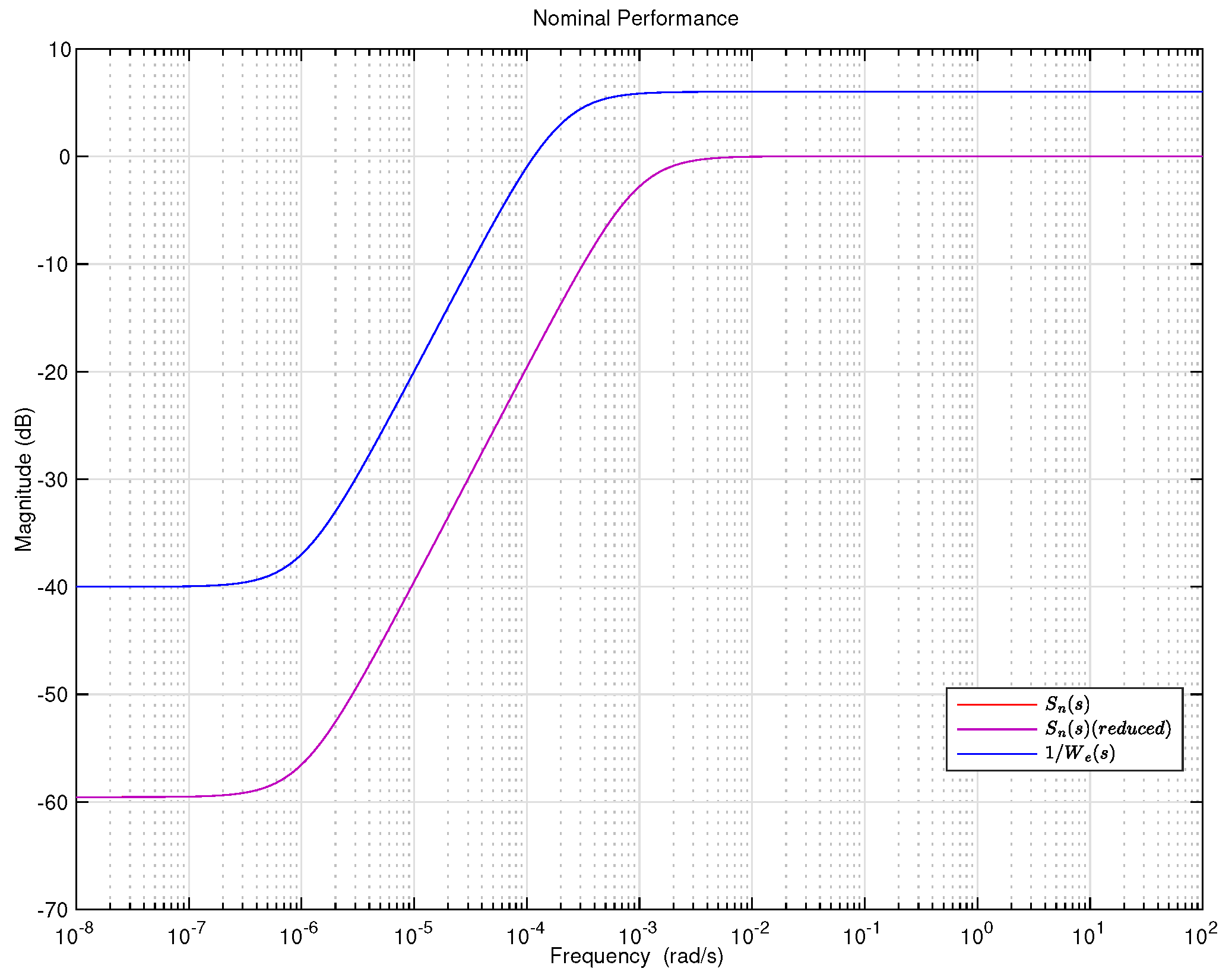
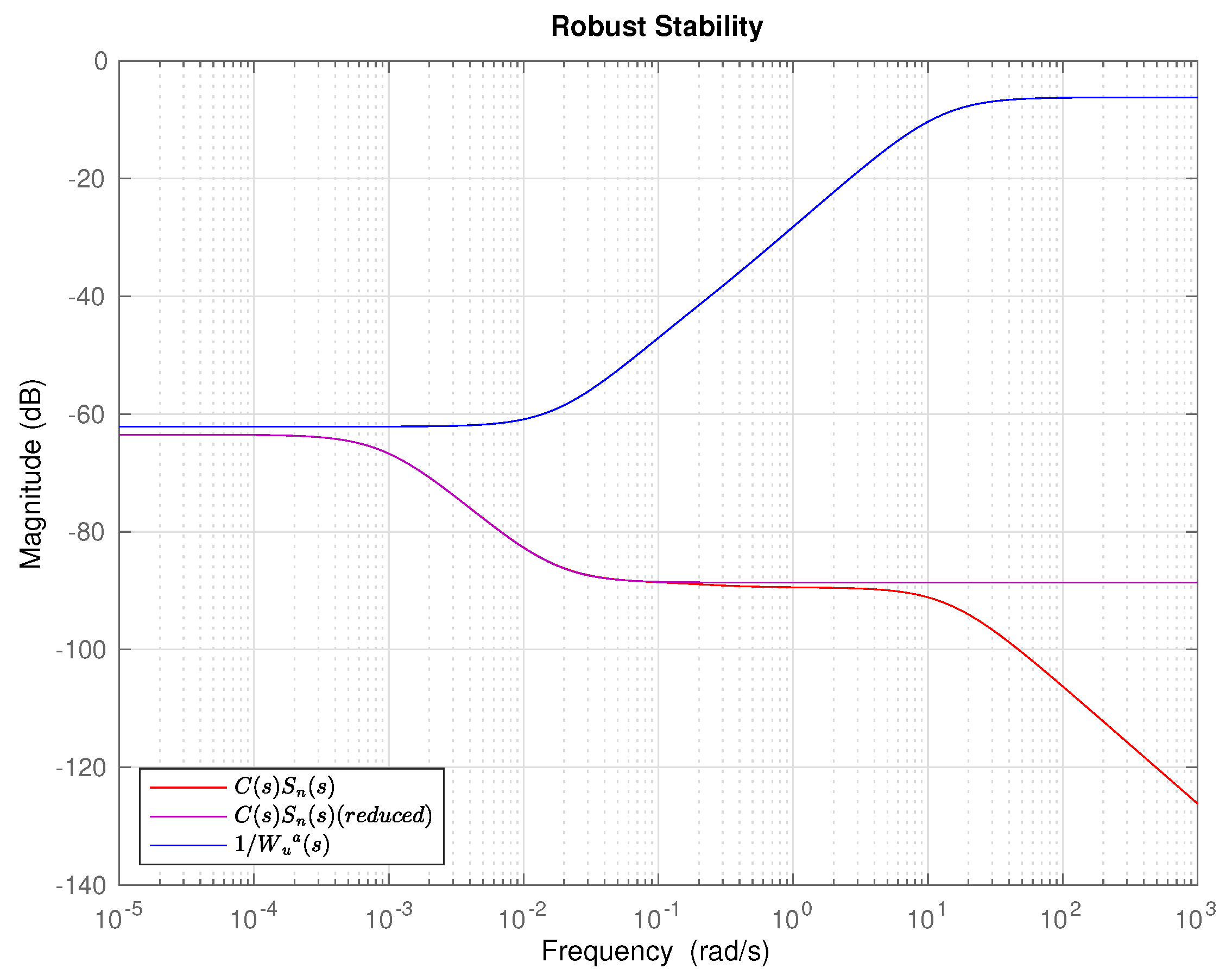
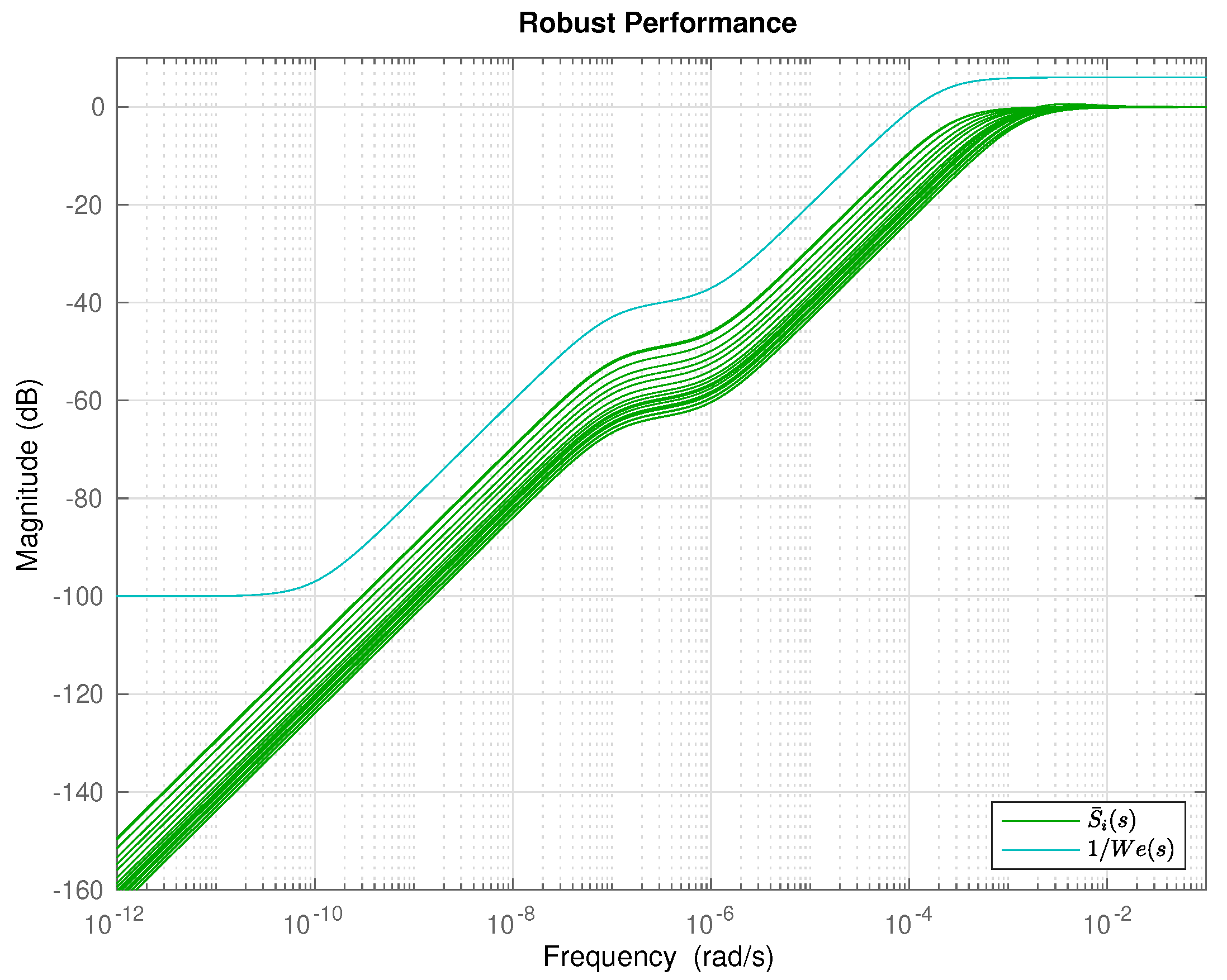
4.5. Controller Design
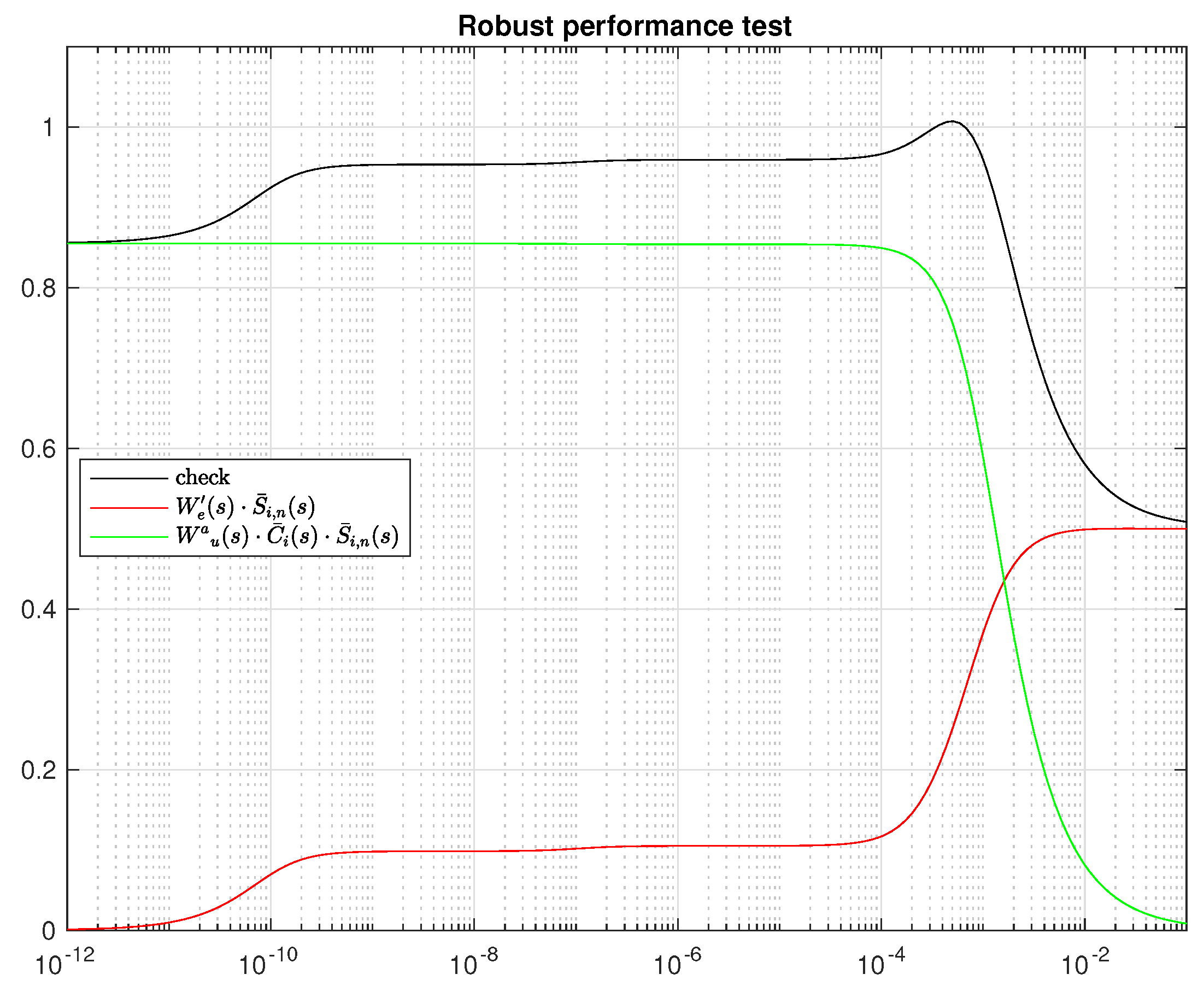
4.6. Integral Controller Design
4.7. Materials and Methods
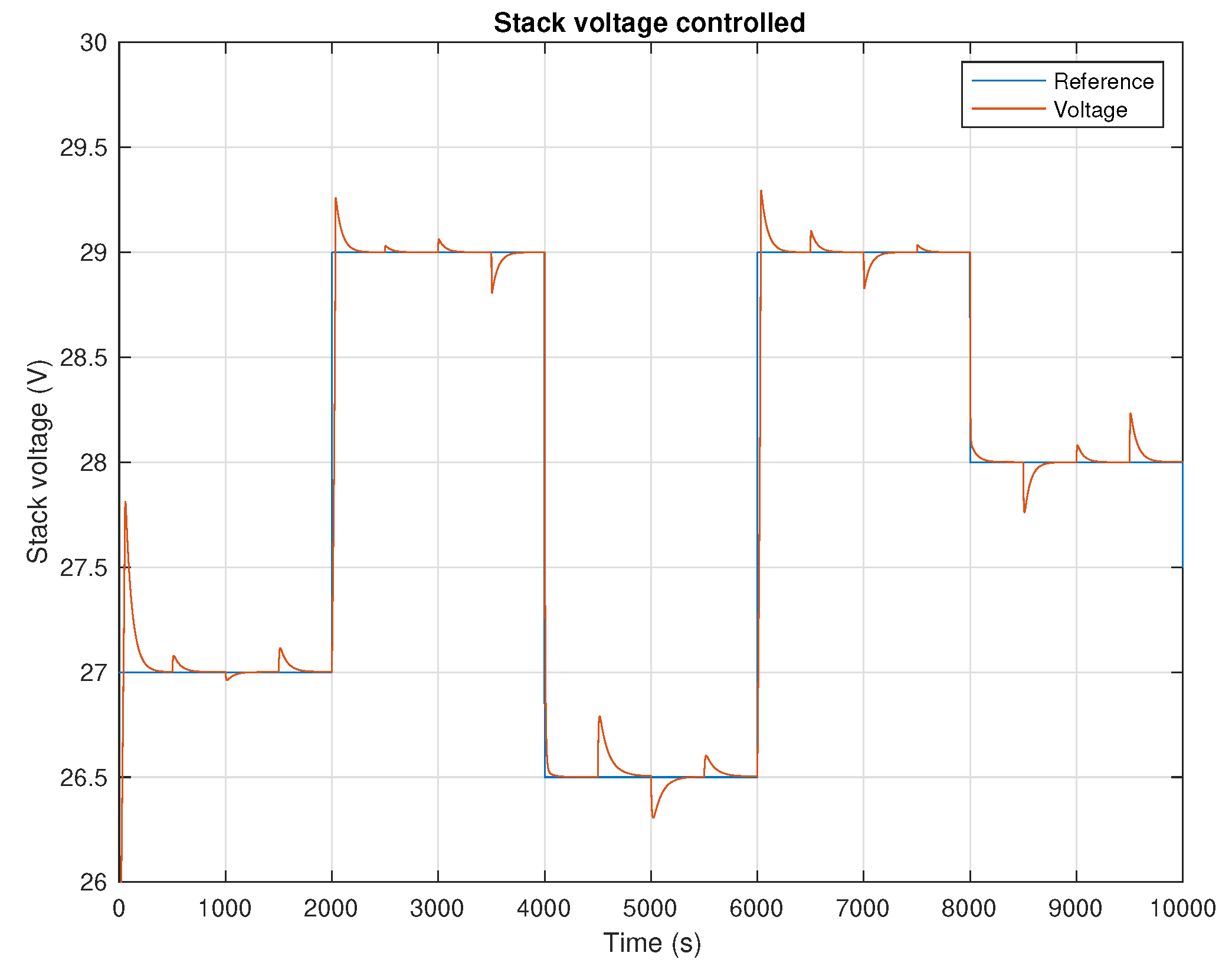
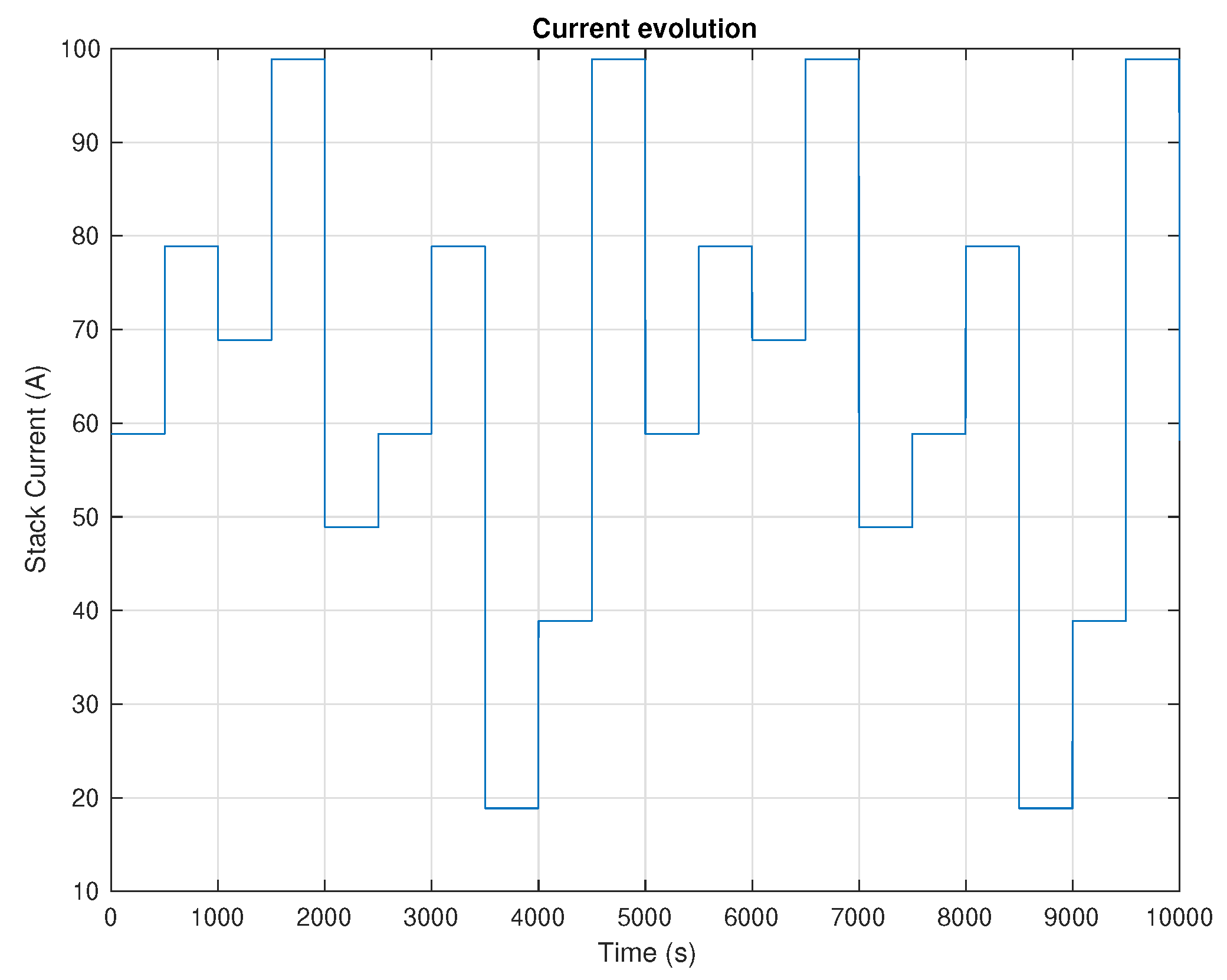
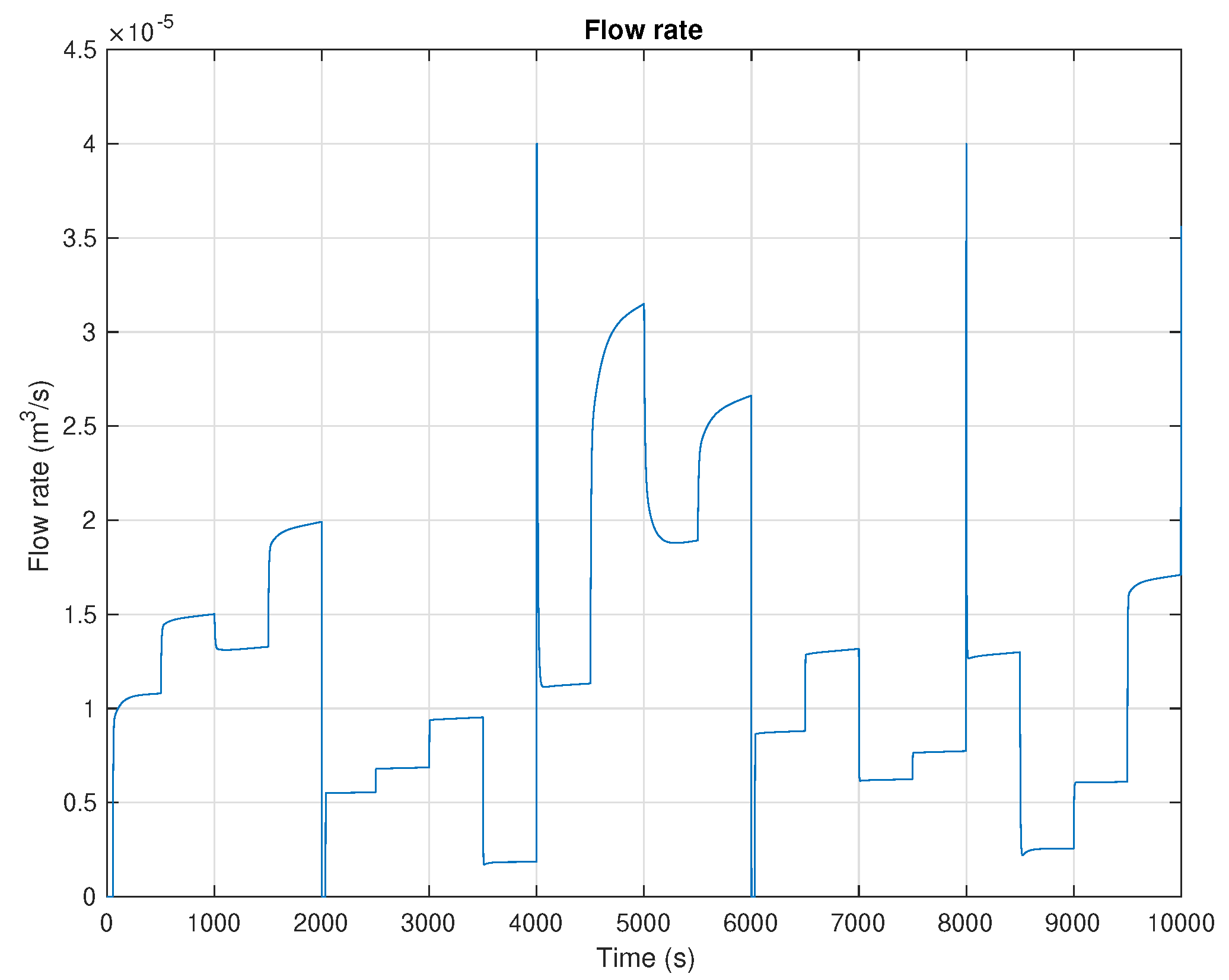
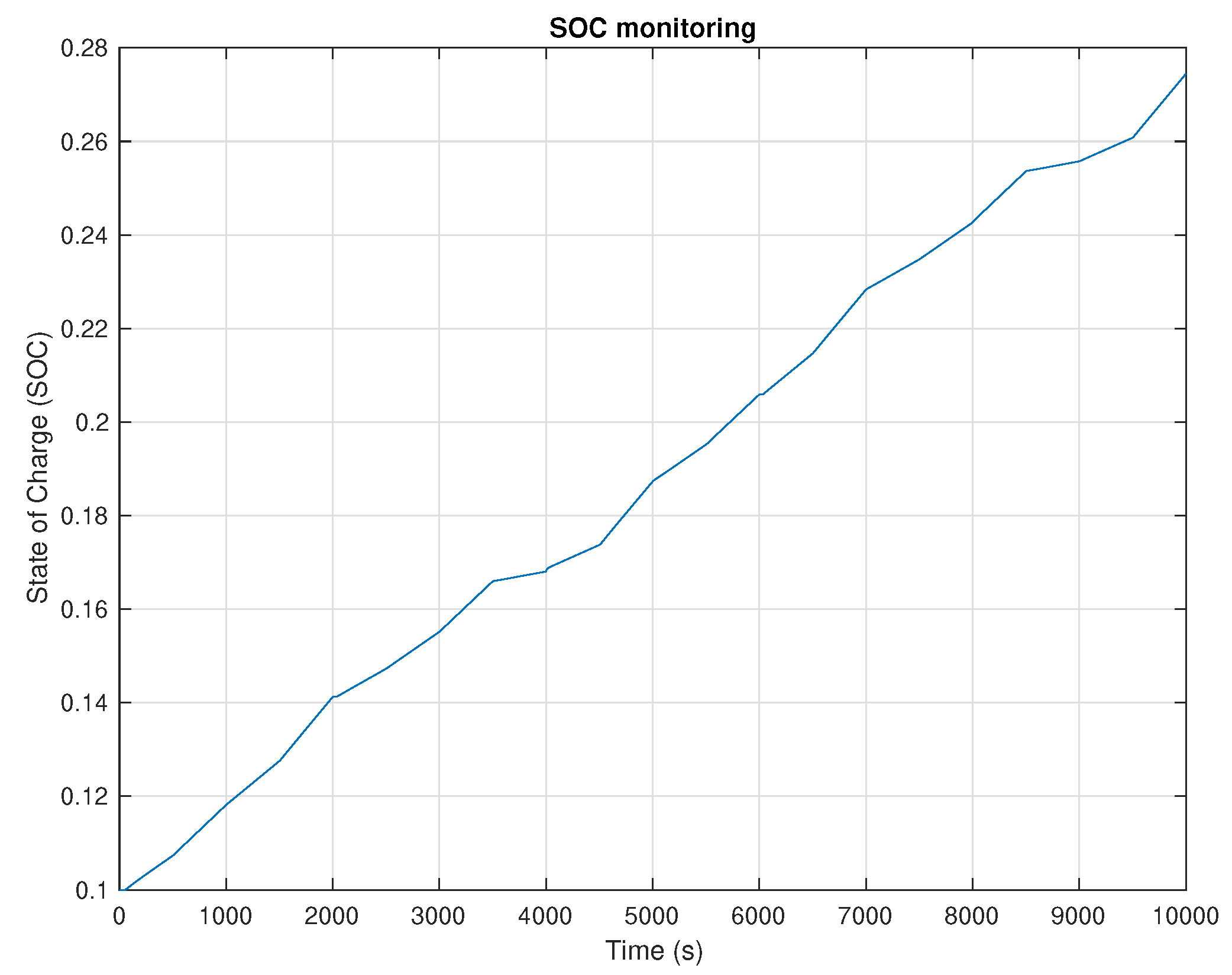
5. Results and Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ESS | Energy storage systems |
| NP | Nominal performance |
| OCV | Open circuit voltage |
| RES | Renowable energy sources |
| RFB | Redox flow battery |
| RP | Robust performance |
| RS | Robust stability |
| SOC | State of charge |
| VRFB | Vanadium redox flow battery |
References
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strateg. Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Peker, M.; Kocaman, A.S.; Kara, B.Y. Benefits of transmission switching and energy storage in power systems with high renewable energy penetration. Appl. Energies 2018, 228, 1182–1197. [Google Scholar] [CrossRef]
- Root, C.; Presume, H.; Proudfoot, D.; Willis, L.; Masiello, R. Using battery energy storage to reduce renewable resource curtailment. IEEE Power Energy ISGTC 2017, 1, 1–5. [Google Scholar] [CrossRef]
- Nair, U.R.; Costa-Castelló, R. A Model Predictive Control-Based Energy Management Scheme for Hybrid Storage System in Islanded Microgrids. IEEE Access 2020, 8, 97809–97822. [Google Scholar] [CrossRef]
- Cecilia, A.; Carroquino, J.; Roda, V.; Costa-Castelló, R.; Barreras, F. Optimal Energy Management in a Standalone Microgrid, with Photovoltaic Generation, Short-Term Storage, and Hydrogen Production. Energies 2020, 13, 1454. [Google Scholar] [CrossRef]
- Bordons, C.; Garcia-Torres, F.; Ridao, M. Model predictive control of interconnected microgrids and with electric vehicles. Rev. Iberoam. Autom. Inform. Ind. 2020, 17, 239–253. [Google Scholar] [CrossRef]
- Shigematsu, T. Redox flow battery for energy storage. SEI Tech. Rev. 2011, 73, 4–13. [Google Scholar]
- Alotto, P.; Guarnieri, M.; Moro, F.; Stella, A. Redox Flow Batteries for large scale energy storage. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; Volume 1, pp. 293–298. [Google Scholar] [CrossRef]
- Fujimoto, C.; Kim, S.; Stains, R.; Wei, X.; Li, L.; Yang, Z.G. Vanadium redox flow battery efficiency and durability studies of sulfonated Diels Alder poly(phenylene)s. Electrochem. Commun. 2012, 20, 48–51. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, Q.; Li, Y. Chapter 3—Design of flow battery. In Reactor and Process Design in Sustainable Energy Technology; Elsevier: Amsterdam, The Netherlands, 2014; pp. 61–97. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhou, X.; An, L.; Wei, L.; Zhao, T. A high-performance flow-field structured iron-chromium redox flow battery. J. Power Sources 2016, 324, 738–744. [Google Scholar] [CrossRef]
- Suresh, S.; Kesavan, T.; Yeddala, M.; Arulraj, I.; Dheenadayalan, S.; Ragupathy, P. Zinc-bromine hybrid flow battery: Effect of zinc utilization and performance characteristics. RSC Adv. 2014, 4. [Google Scholar] [CrossRef]
- Chen, R.; Kim, S.; Chang, Z. Redox Flow Batteries: Fundamentals and Applications; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef]
- Clemente, A.; Costa-Castelló, R. Redox Flow Batteries: A Literature Review Oriented to Automatic Control. Energies 2020, 13, 4514. [Google Scholar] [CrossRef]
- Messaggi, M.; Canzi, P.; Mereu, R.; Baricci, A.; Inzoli, F.; Casalegno, A.; Zago, M. Analysis of flow field design on vanadium redox flow battery performance: Development of 3D computational fluid dynamic model and experimental validation. Appl. Energy 2018, 228, 1057–1070. [Google Scholar] [CrossRef]
- Barton, J.L.; Brushett, F.R. A One-Dimensional Stack Model for Redox Flow Battery Analysis and Operation. Batteries 2019, 5, 25. [Google Scholar] [CrossRef]
- Tang, A.; McCann, J.; Bao, J.; Skyllas-Kazacos, M. Investigation of the effect of shunt current on battery efficiency and stack temperature in vanadium redox flow battery. J. Power Sources 2013, 242, 349–356. [Google Scholar] [CrossRef]
- Wei, Z.; Xiong, R.; Lim, T.M.; Meng, S.; Skyllas-Kazacos, M. Online monitoring of state of charge and capacity loss for vanadium redox flow battery based on autoregressive exogenous modeling. J. Power Sources 2018, 402, 252–262. [Google Scholar] [CrossRef]
- Challapuram, Y.R.; Quintero, G.M.; Bayne, S.B.; Subburaj, A.S.; Harral, M.A. Electrical Equivalent Model of Vanadium Redox Flow Battery. In Proceedings of the 2019 IEEE Green Technologies Conference (GreenTech), Lafayette, LA, USA, 3–6 April 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Han, D.; Yoo, K.; Lee, P.; Kim, S.; Kim, S.; Kim, J. Equivalent Circuit Model Considering Self-discharge for SOC Estimation of Vanadium Redox Flow Battery. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 7–10 October 2018; pp. 2171–2176. [Google Scholar] [CrossRef]
- Blanc, C. Modeling of a Vanadium Redox Flow Battery Electricity Storage System; EPFL: Lausanne, Switzerland, 2009. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, H.; Sun, C.; Zou, Y.; Zhang, T. An optimal strategy of electrolyte flow rate for vanadium redox flow battery. J. Power Sources 2012, 203, 153–158. [Google Scholar] [CrossRef]
- Trovò, A.; Picano, F.; Guarnieri, M. Maximizing Vanadium Redox Flow Battery Efficiency: Strategies of Flow Rate Control. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 1977–1982. [Google Scholar] [CrossRef]
- Houser, J.; Pezeshki, A.; Clement, J.T.; Aaron, D.; Mench, M.M. Architecture for improved mass transport and system performance in redox flow batteries. J. Power Sources 2017, 351, 96–105. [Google Scholar] [CrossRef]
- Tang, A.; Bao, J.; Skyllas-Kazacos, M. Studies on pressure losses and flow rate optimization in vanadium redox flow battery. J. Power Sources 2014, 248, 154–162. [Google Scholar] [CrossRef]
- Pugach, M.; Parsegov, S.; Gryazina, E.; Bischi, A. Output feedback control of electrolyte flow rate for Vanadium Redox Flow Batteries. J. Power Sources 2020, 455, 227916. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Bao, J.; Skyllas-Kazacos, M. Control of electrolyte flow rate for the vanadium redox flow battery by gain scheduling. J. Energy Storage 2017, 14, 125–133. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Saha, H. Development of an efficient thermal management system for Vanadium Redox Flow Battery under different charge-discharge conditions. Appl. Energy 2018, 230, 1182–1192. [Google Scholar] [CrossRef]
- Bueno-Contreras, H.; Ramos Fuentes, G.A.; Costa Castelló, R. Robust H∞ Design for Resonant Control in a CVCF Inverter Application over Load Uncertainties. Electronics 2020, 9, 66. [Google Scholar] [CrossRef]
- Ramos, G.A.; Ruget, R.I.; Costa Castelló, R. Robust Repetitive Control of Power Inverters for Standalone Operation in DG Systems. IEEE Trans. Energy Convers. 2020, 35, 237–247. [Google Scholar] [CrossRef]
- Knehr, K.; Kumbur, E. Open circuit voltage of vanadium redox flow batteries: Discrepancy between models and experiments. Electrochem. Commun. 2011, 13, 342–345. [Google Scholar] [CrossRef]
- Roznyatovskaya, N.; Noack, J.; Mild, H.; Fühl, M.; Fischer, P.; Pinkwart, K.; Tübke, J.; Skyllas-Kazacos, M. Vanadium Electrolyte for All-Vanadium Redox-Flow Batteries: The Effect of the Counter Ion. Batteries 2019, 5, 13. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Slotine, J.; Li, W. Applied Nonlinear Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Zhang, B.; Lei, Y.; Bai, B.; Zhao, T. A two-dimensional model for the design of flow fields in vanadium redox flow batteries. Int. J. Heat Mass Transf. 2019, 135, 460–469. [Google Scholar] [CrossRef]
- Xiong, B.; Zhao, J.; Li, J. Modeling of an all-vanadium redox flow battery and optimization of flow rates. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Sánchez-Peña, R.S.; Sznaier, M. Robust Systems Theory and Applications; Adaptive and Learning Systems for Signal Processing, Communications and Control Series; Wiley-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Balas, G.; Chiang, R.; Packard, A.; Safonov, M. Robust Control Toolbox TM User’s Guide; The MathWorks: Natick, MA, USA, 2019. [Google Scholar]






| Parameter | Meaning | Unit—Value |
|---|---|---|
| Concentration of specie i inside the cell | ||
| E | Electrode potential | V |
| Standard potential | 1.259 V | |
| T | Temperature of the cell | K |
| F | Faraday’s constant | 96,485 |
| R | Gas constant | 8.314 |
| Parameter | Meaning | Unit—Value |
|---|---|---|
| Volume of the cell | ||
| Volume of each tank | ||
| Q | Flow rate | |
| I | Current | |
| S | Surface area of the electrode | 0.15 |
| d | Membrane thickness | 1.27·10 |
| Diffusion coefficient of | ||
| Diffusion coefficient of | ||
| Diffusion coefficient of | ||
| Diffusion coefficient of | ||
| N | Number of cells of the stack | 19 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clemente, A.; Ramos, G.A.; Costa-Castelló, R. Voltage H∞ Control of a Vanadium Redox Flow Battery. Electronics 2020, 9, 1567. https://doi.org/10.3390/electronics9101567
Clemente A, Ramos GA, Costa-Castelló R. Voltage H∞ Control of a Vanadium Redox Flow Battery. Electronics. 2020; 9(10):1567. https://doi.org/10.3390/electronics9101567
Chicago/Turabian StyleClemente, Alejandro, Germán Andrés Ramos, and Ramon Costa-Castelló. 2020. "Voltage H∞ Control of a Vanadium Redox Flow Battery" Electronics 9, no. 10: 1567. https://doi.org/10.3390/electronics9101567
APA StyleClemente, A., Ramos, G. A., & Costa-Castelló, R. (2020). Voltage H∞ Control of a Vanadium Redox Flow Battery. Electronics, 9(10), 1567. https://doi.org/10.3390/electronics9101567






