Four-Level Hysteresis-Based DTC for Torque Capability Improvement of IPMSM Fed by Three-Level NPC Inverter
Abstract
1. Introduction
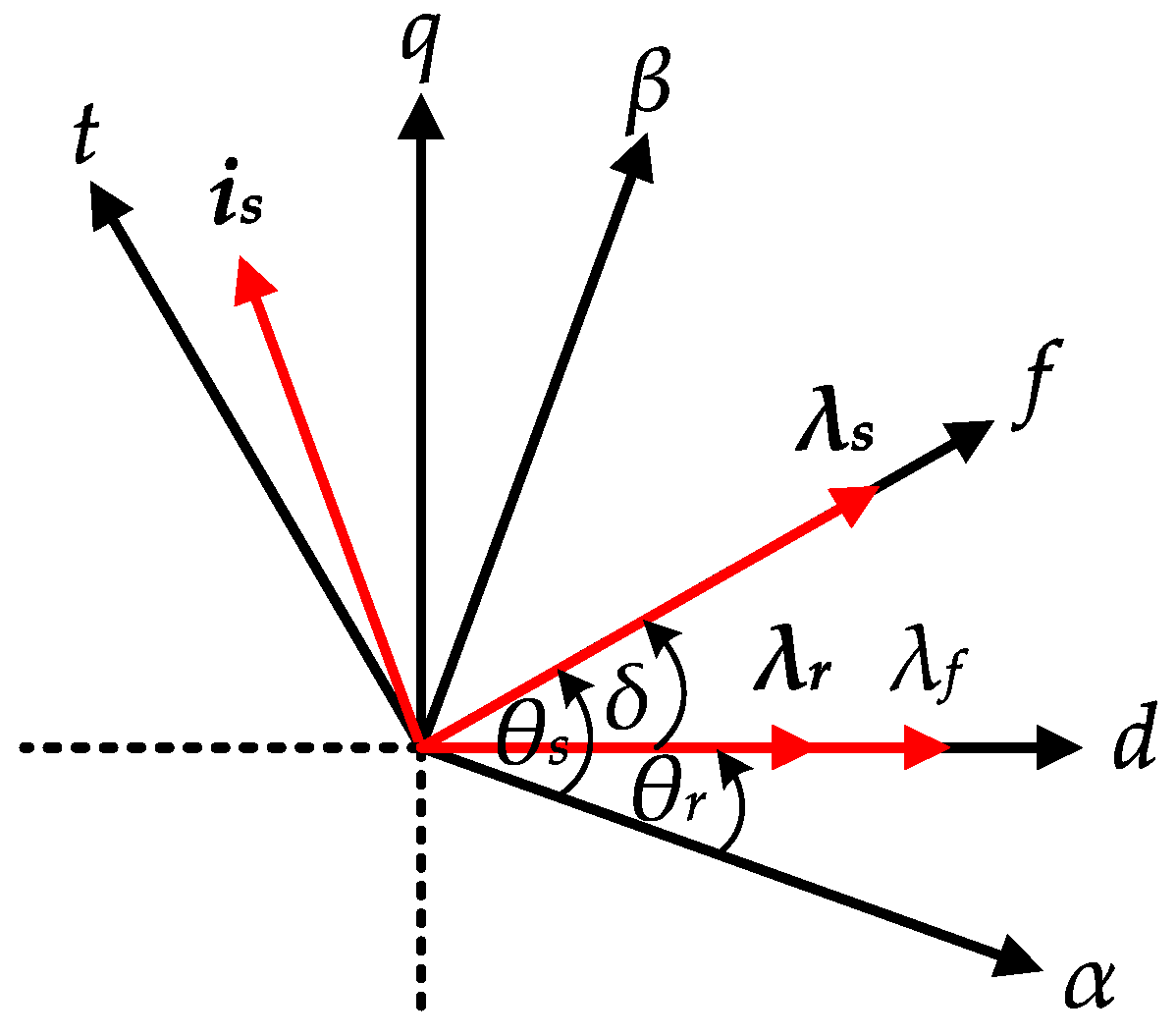
2. Mathematical Modelling of IPMSM
3. 3L-DTC for IPMSM
3.1. Torque and Stator Flux Estimation
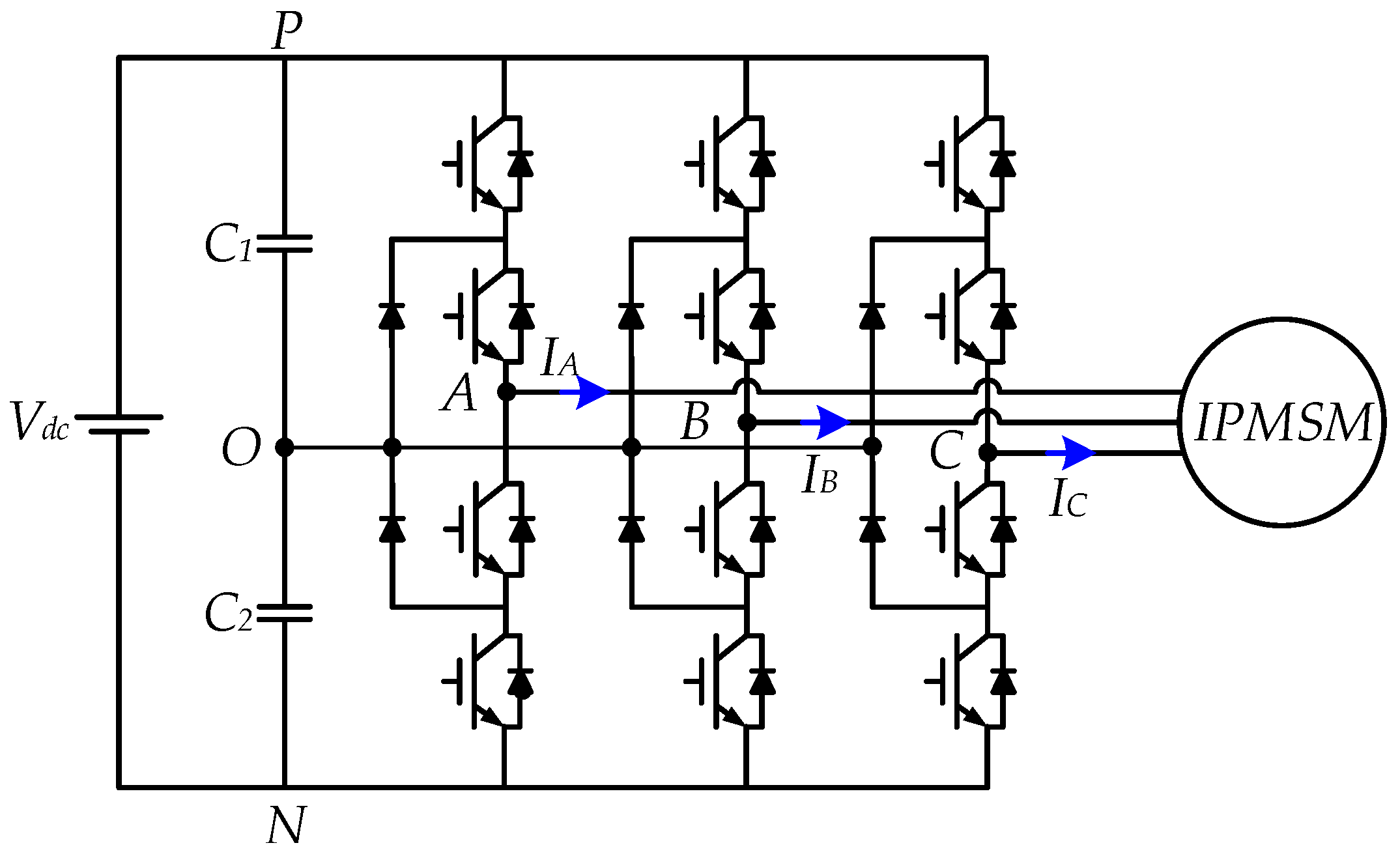
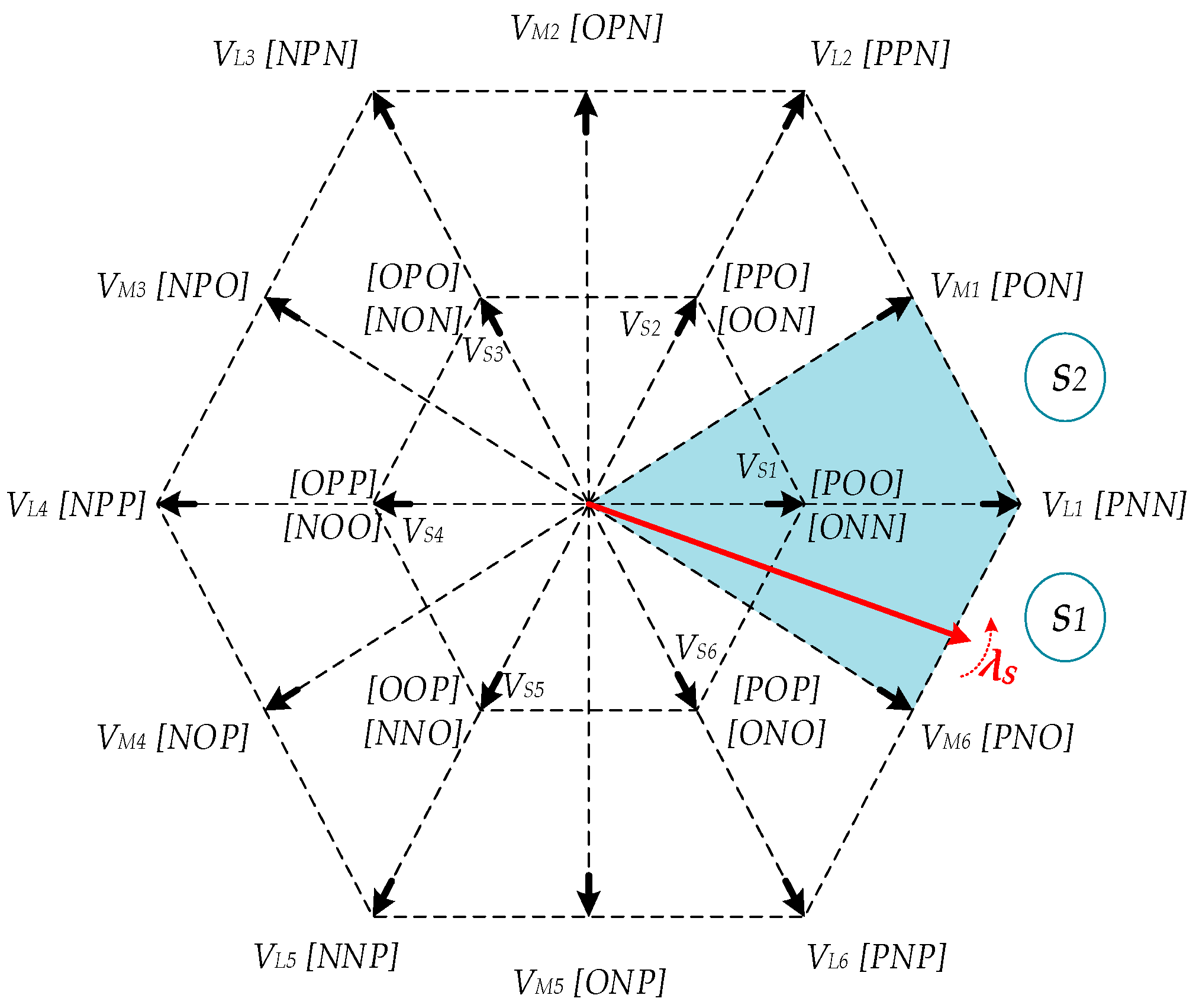
3.2. Three-Level NPC Inverter
3.3. Look-Up Table
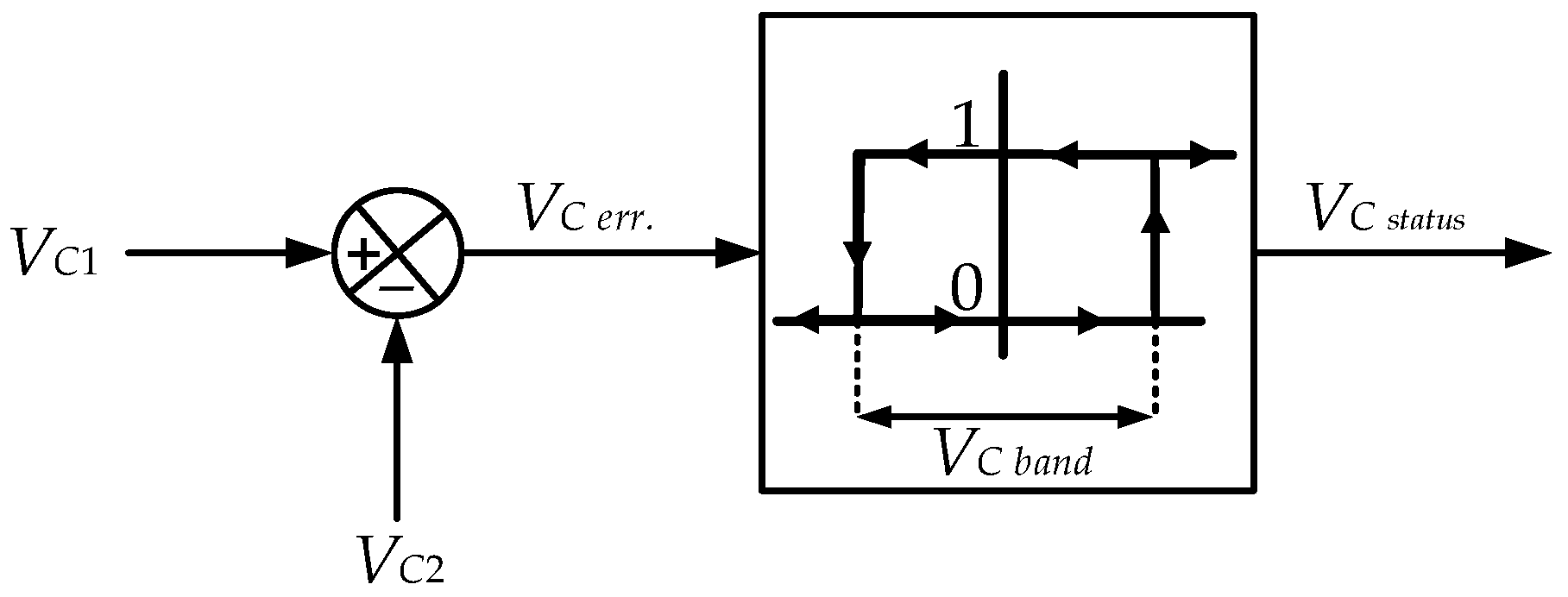
3.4. Conventional Four-Level HTC
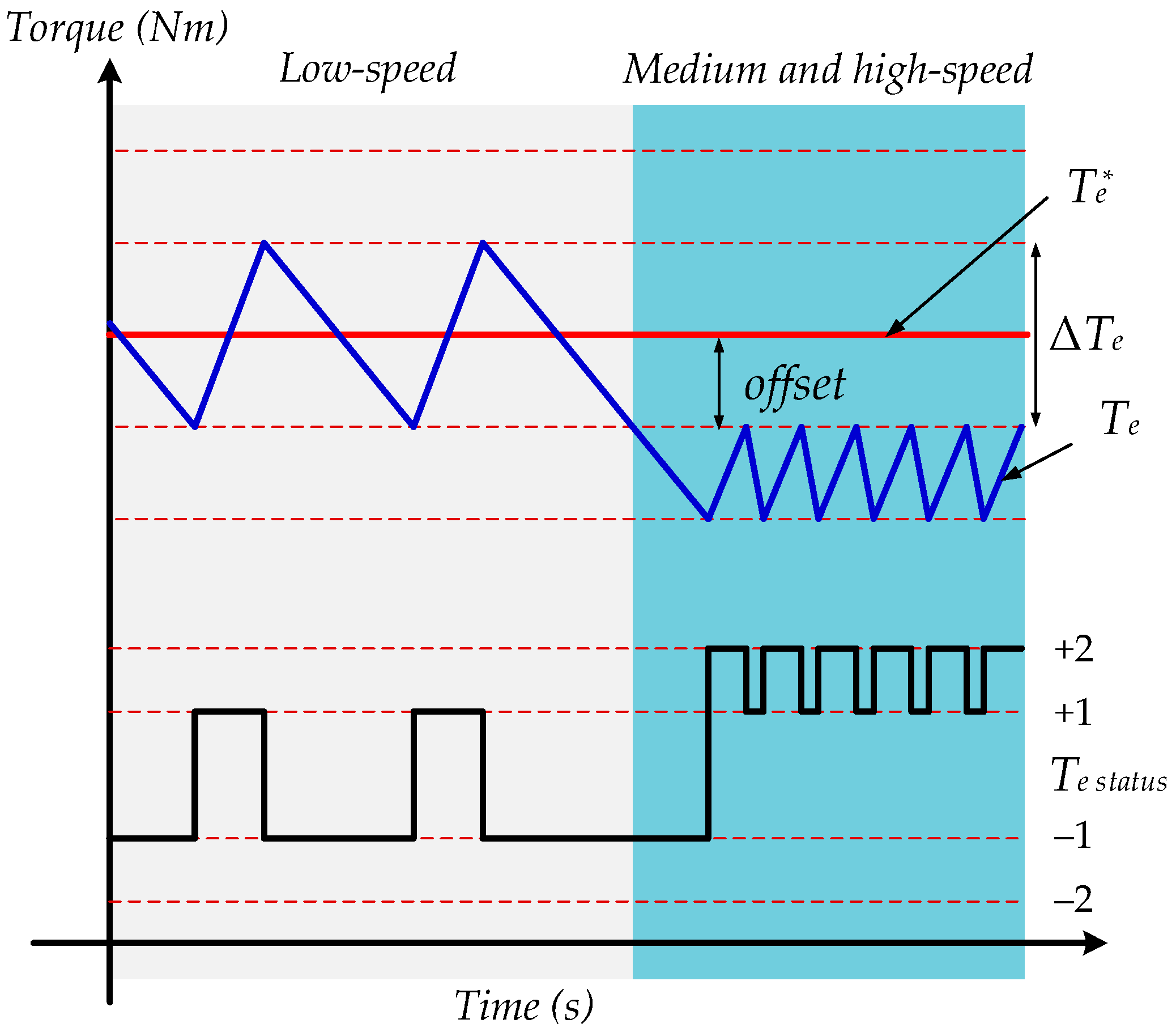
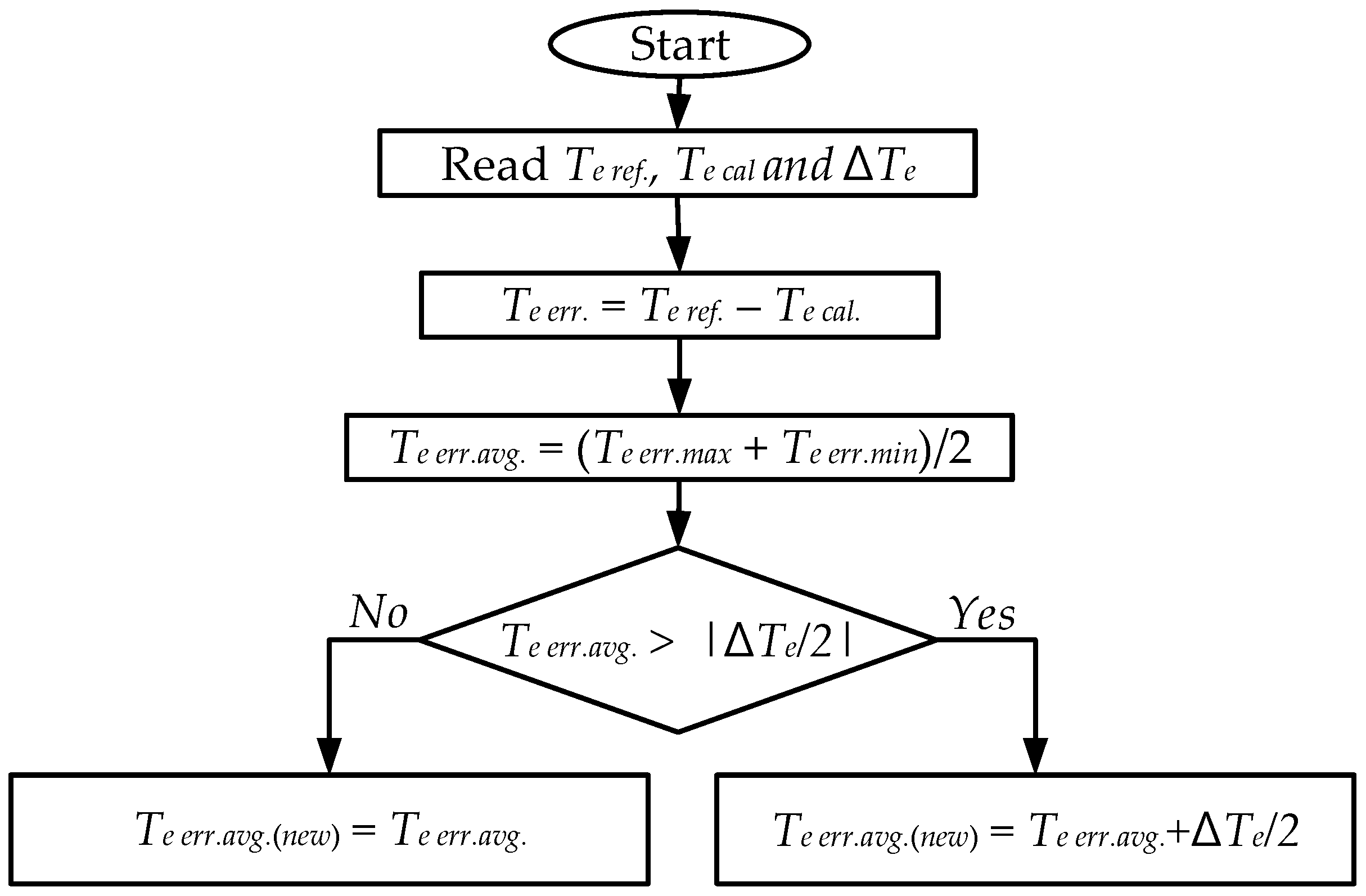
3.5. Proposed Four-Level HTC
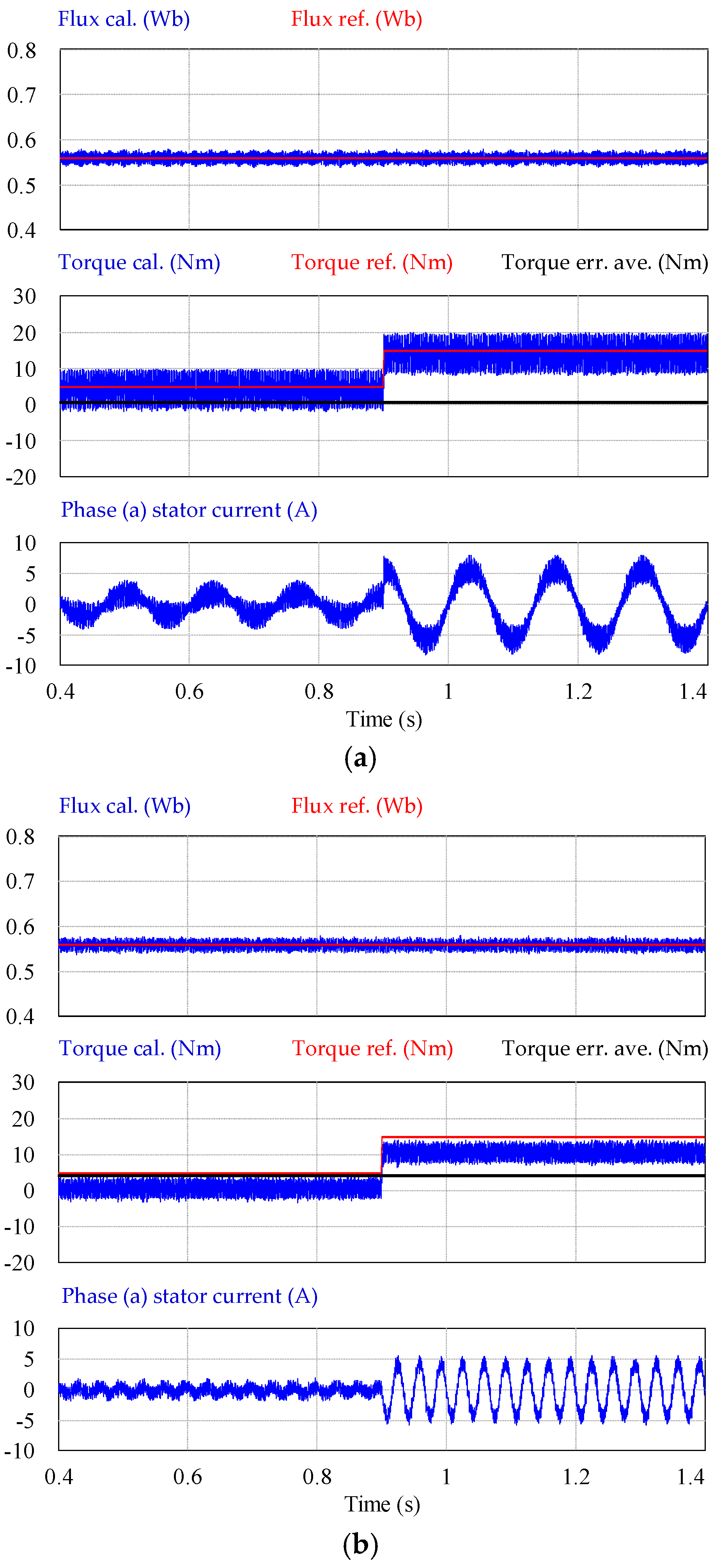
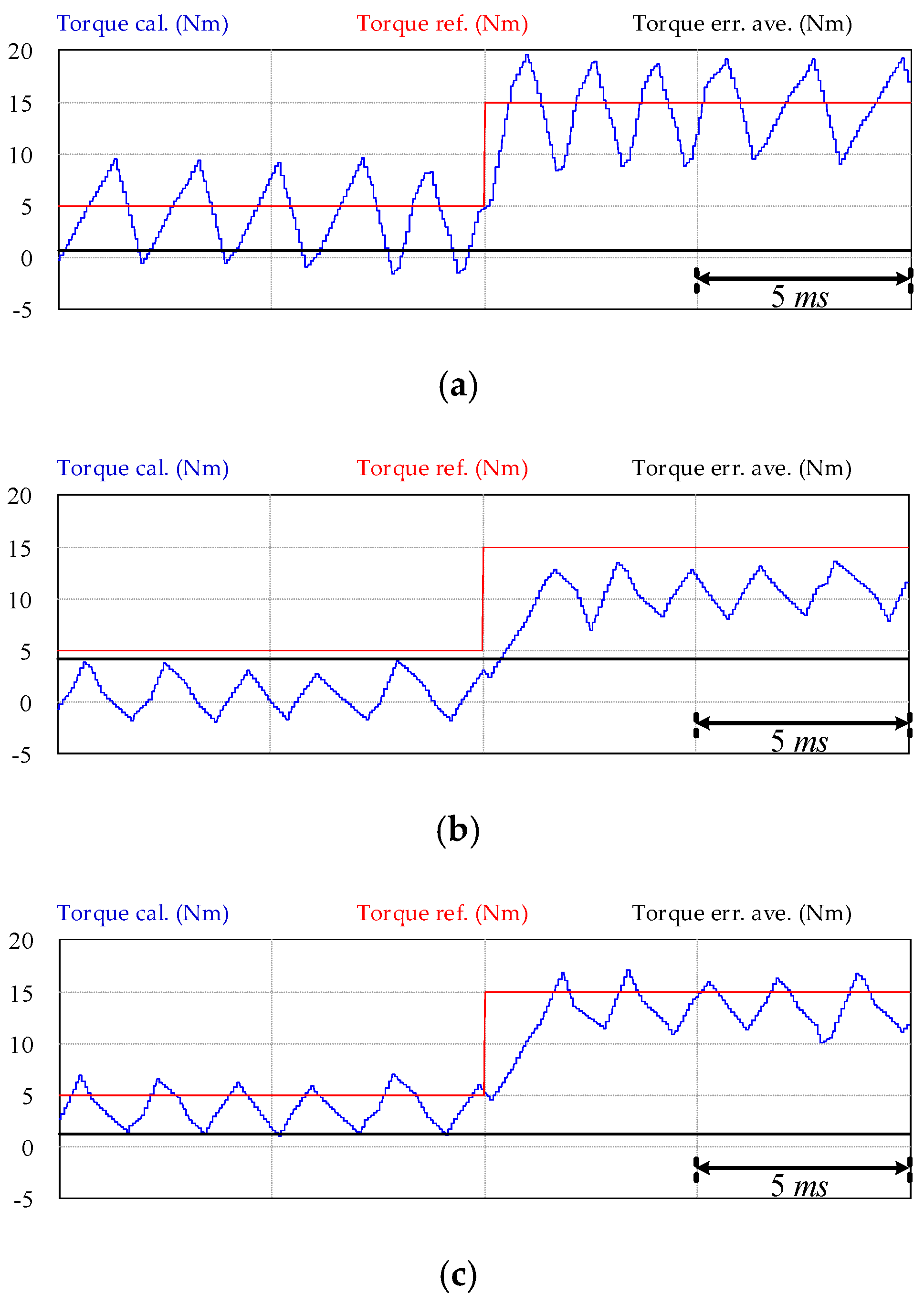
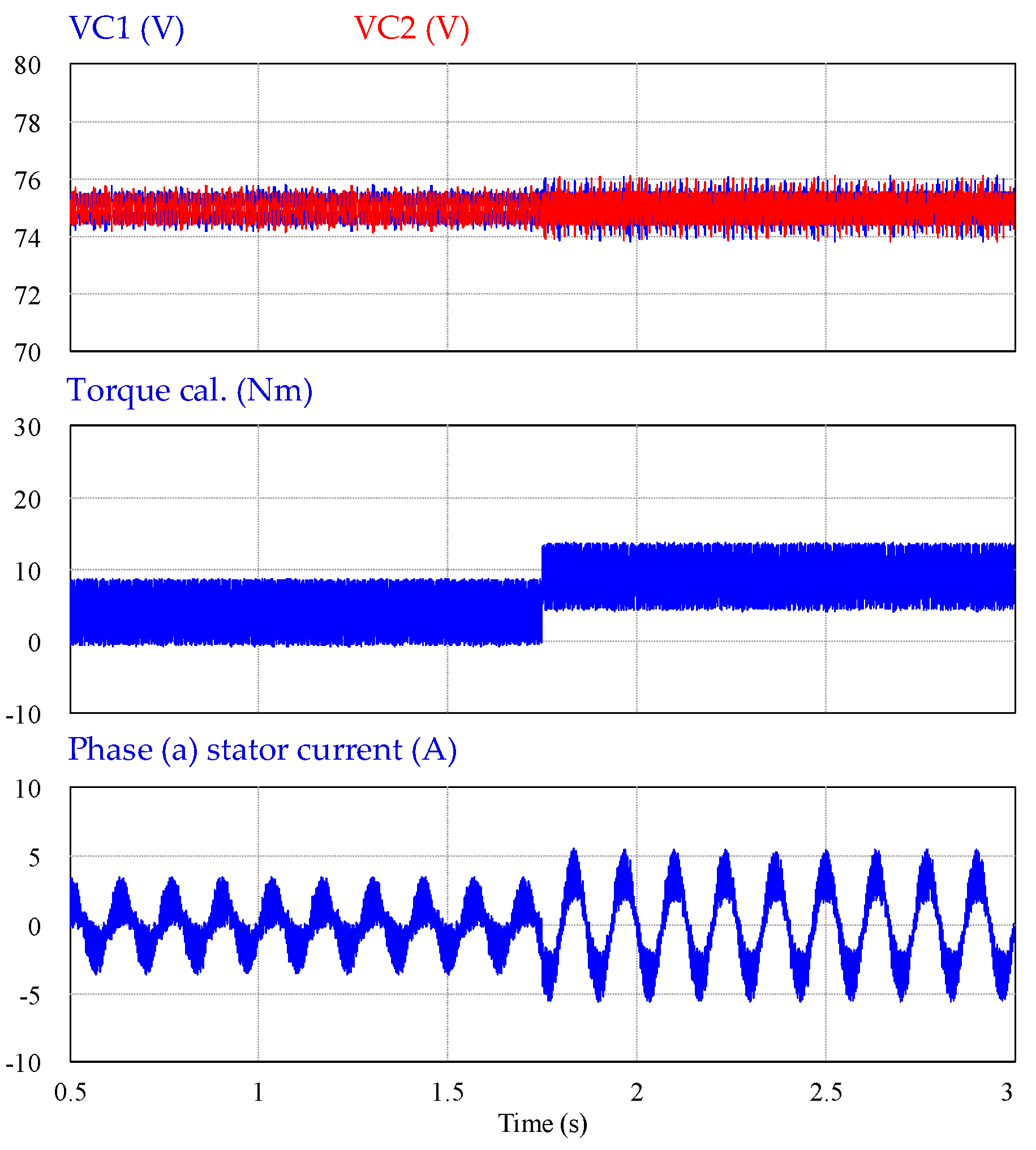
4. Simulation Results
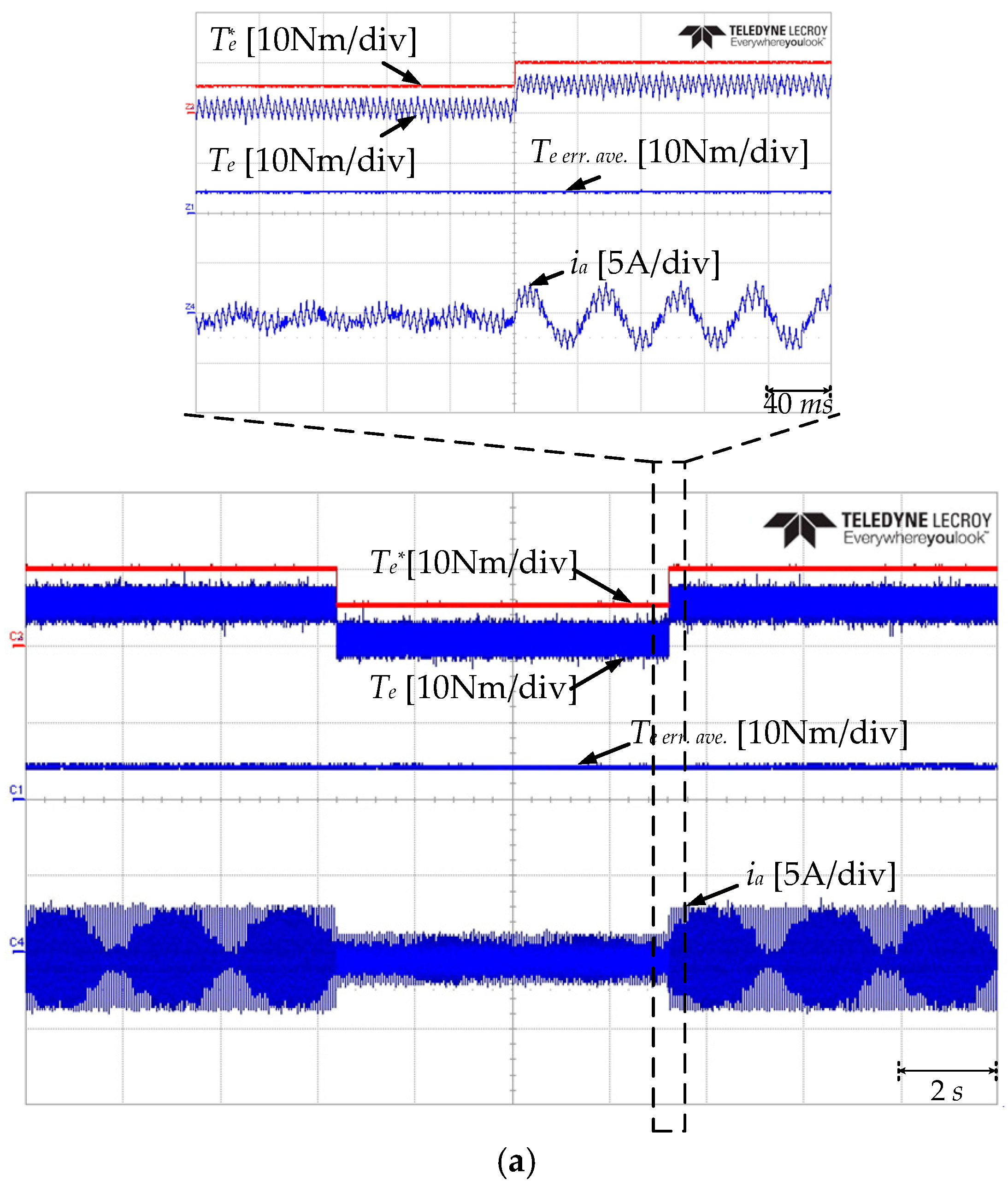
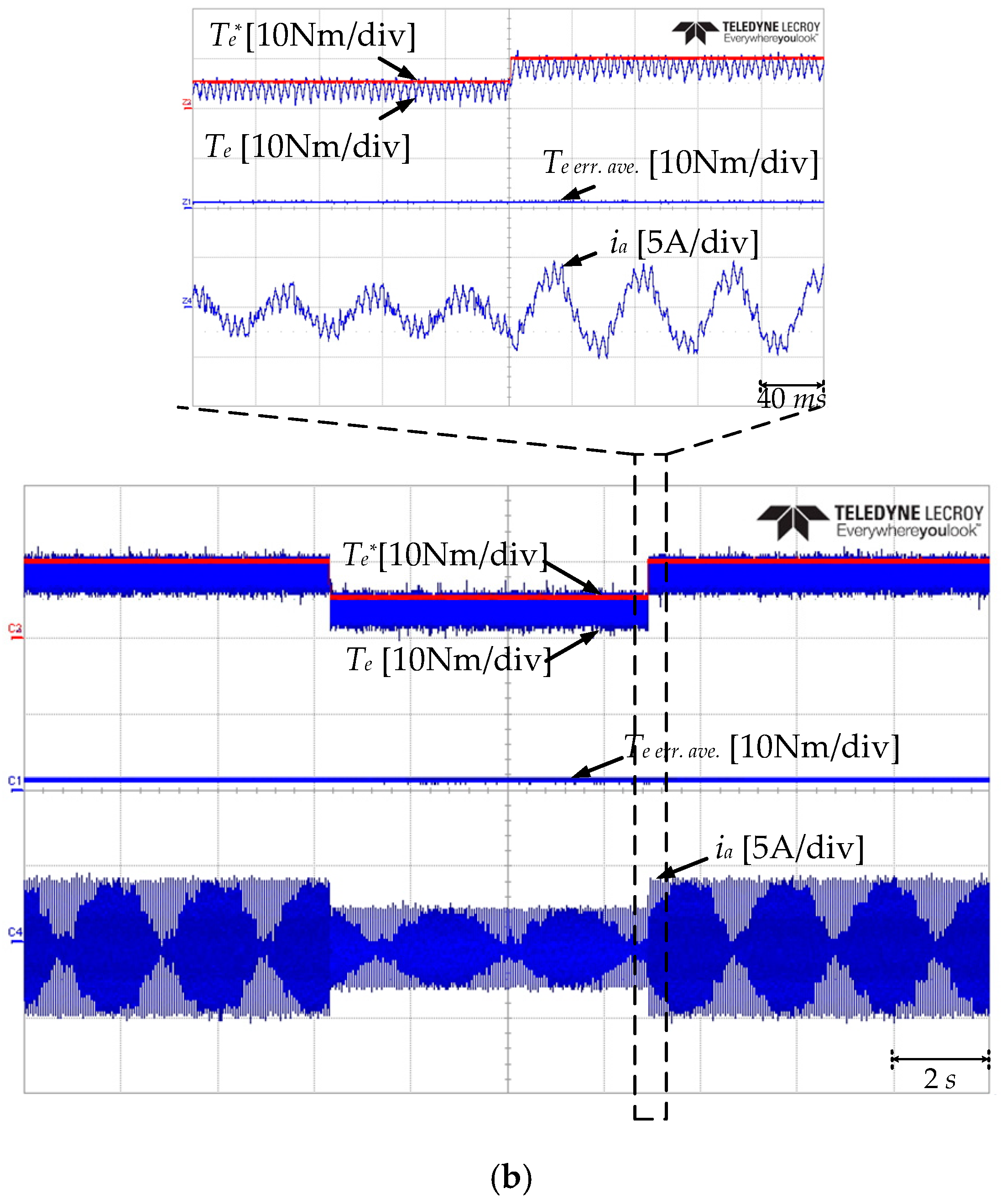
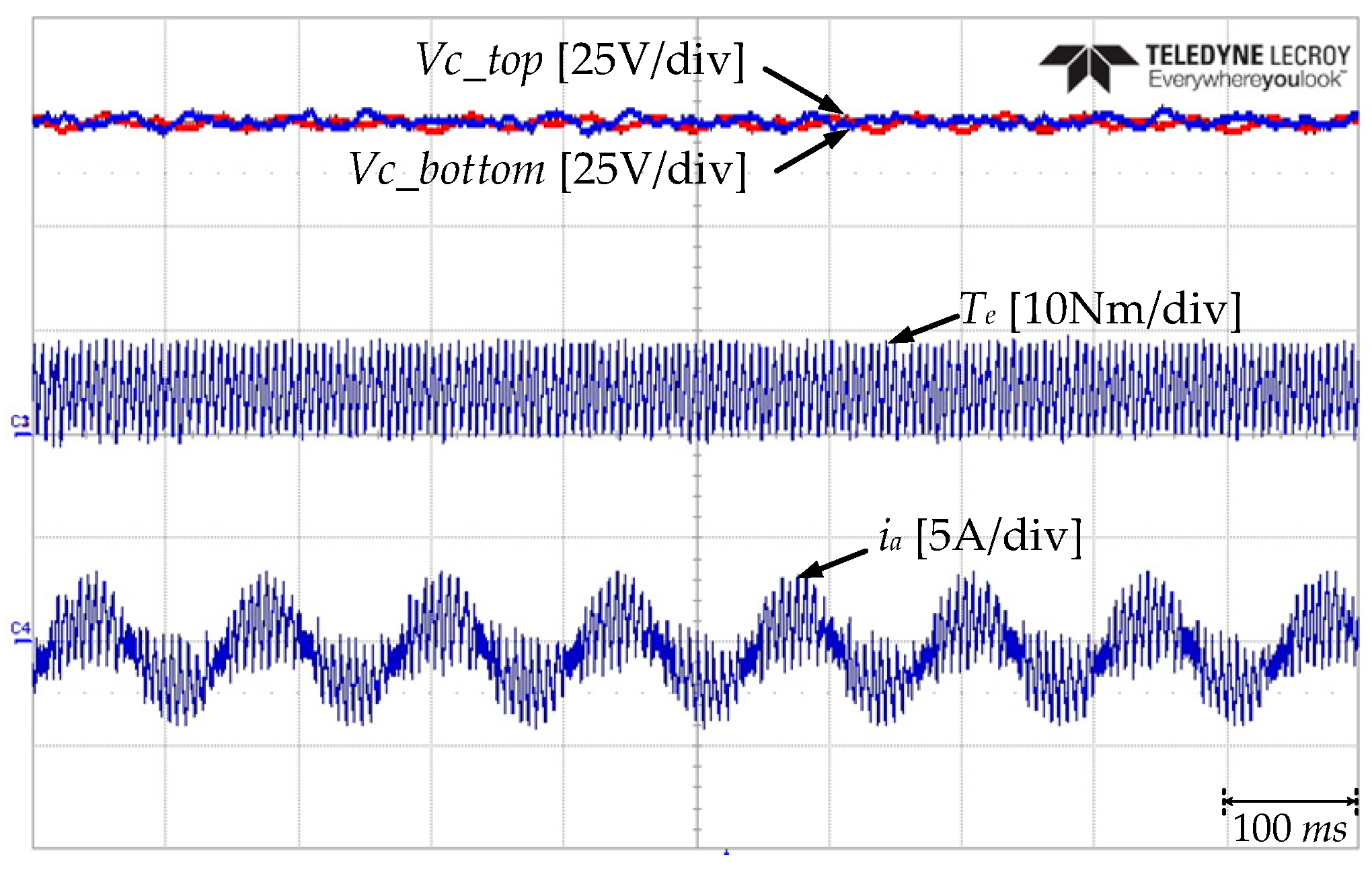
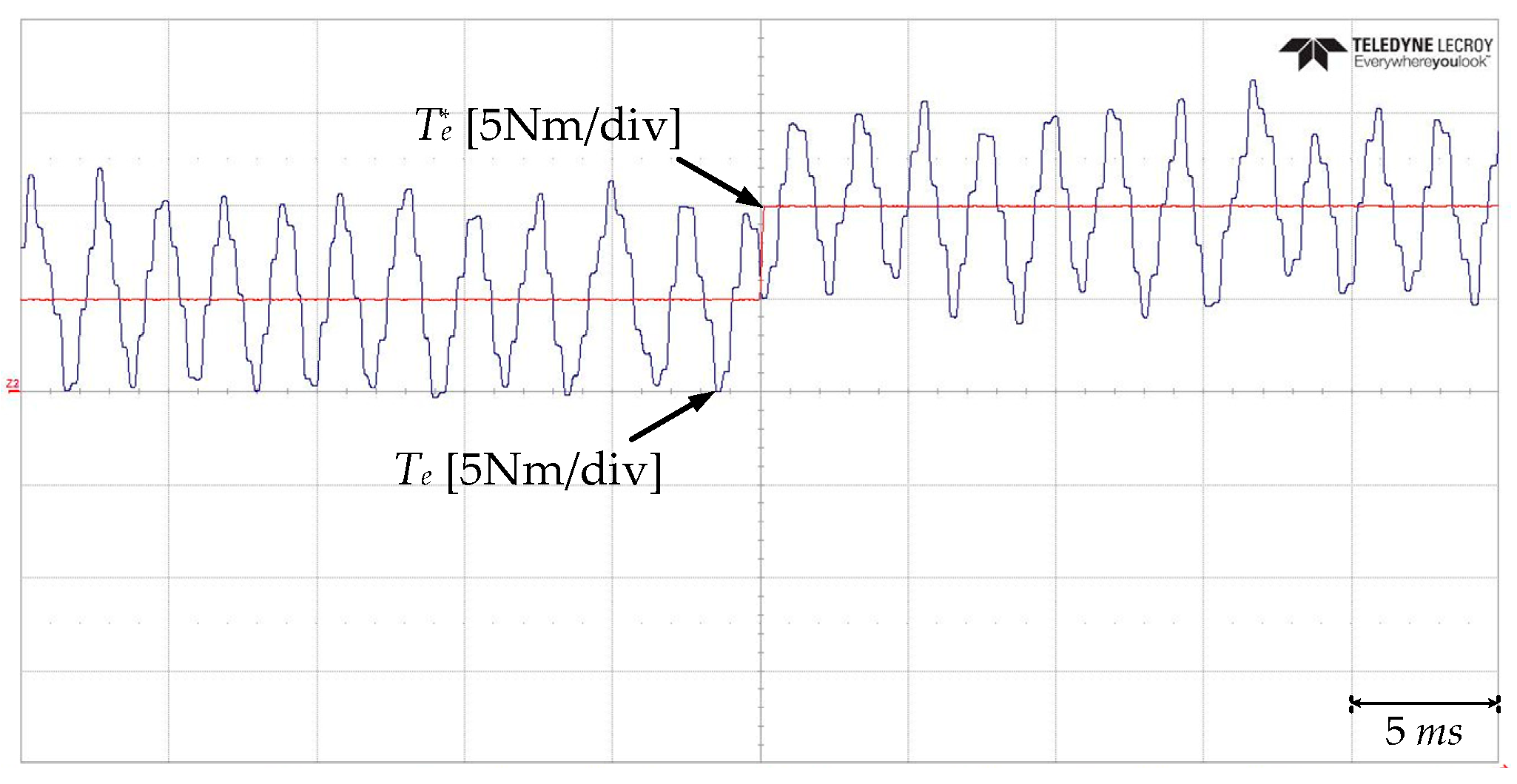
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vafaie, M.H.; Dehkordi, B.M.; Moallem, P.; Kiyoumarsi, A. A new predictive direct torque control method for improving both steady-state and transient-state operations of the PMSM. IEEE Trans. Power Electron. 2016, 31, 3738–3753. [Google Scholar] [CrossRef]
- Choi, Y.-S.; Choi, H.H.; Jung, J.-W. Feedback linearization direct torque control with reduced torque and flux ripples for IPMSM drives. IEEE Trans. Power Electron. 2016, 31, 3728–3737. [Google Scholar] [CrossRef]
- Wang, G.; Yang, L.; Yuan, B.; Wang, B.; Zhang, G.; Xu, D. Pseudo-random high-frequency square-wave voltage injection based sensorless control of IPMSM drives for audible noise reduction. IEEE Trans. Ind. Electron. 2016, 63, 7423–7433. [Google Scholar] [CrossRef]
- Ahn, H.; Park, H.; Kim, C.; Lee, H. A Review of State-of-the-art Techniques for PMSM Parameter Identification. J. Electr. Eng. Technol. 2020, 15, 1177–1187. [Google Scholar] [CrossRef]
- Zhong, L.; Rahman, M.F.; Hu, W.Y.; Lim, K.W. Analysis of direct torque control in permanent magnet synchronous motor drives. IEEE Trans. Power Electron. 1997, 12, 528–536. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Idris, N.R.N.; Lee, K.-B. Impact of Observability and Multi-objective Optimization on the Performance of Extended Kalman Filter for DTC of AC Machines. J. Electr. Eng. Technol. 2019, 14, 231–242. [Google Scholar] [CrossRef]
- Lee, K.-B.; Song, J.-H.; Choy, I.; Yoo, J.-Y. Improvement of low-speed operation performance of DTC for three-level inverter-fed induction motors. IEEE Trans. Ind. Electron. 2001, 48, 1006–1014. [Google Scholar]
- Siahbalaee, J.; Vaez-Zadeh, S.; Tahami, F. A Loss Minimization Control Strategy for Direct Torque Controlled Interior Permanent Magnet Synchronous Motors. J. Power Electron. 2009, 9, 940–948. [Google Scholar]
- Lee, K.-B.; Blaabjerg, F. Sensorless DTC-SVM for Induction Motor Driven by a Matrix Converter Using a Parameter Estimation Strategy. IEEE Trans. Ind. Electron. 2008, 55, 512–521. [Google Scholar] [CrossRef]
- Rashag, H.F.; Koh, S.P.; Abdalla, A.N.; Tan, N.M.L.; Chong, K.H. Modified Direct Torque Control using Algorithm Control of Stator Flux Estimation and Space Vector Modulation Based on Fuzzy Logic Control for Achieving High Performance from Induction Motors. J. Power Electron. 2013, 13, 369–380. [Google Scholar] [CrossRef]
- Abosh, A.H.; Zhu, Z.Q.; Ren, Y. Reduction of Torque and Flux Ripples in Space Vector Modulation-Based Direct Torque Control of Asymmetric Permanent Magnet Synchronous Machine. IEEE Trans. Power Electron. 2017, 32, 2976–2986. [Google Scholar] [CrossRef]
- Pacas, M.; Weber, J. Predictive direct torque control for the PM synchronous machine. IEEE Trans. Ind. Electron. 2005, 52, 1350–1356. [Google Scholar] [CrossRef]
- Cho, Y.; Lee, K.-B.; Song, J.-H.; Lee, Y.I. Torque-Ripple Minimization and Fast Dynamic Scheme for Torque Predictive Control of Permanent-Magnet Synchronous Motors. IEEE Trans. Power Electron. 2015, 30, 2182–2190. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, D.; Liu, J.; Gao, S.; Xu, W. Performance Improvement of Model-Predictive Current Control of Permanent Magnet Synchronous Motor Drives. IEEE Trans. Ind. Appl. 2017, 53, 3683–3695. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H.; Zhang, H.; Mao, J.; Huang, J. Model Free Deadbeat Predictive Speed Control of Surface-Mounted Permanent Magnet Synchronous Motor Drive system. J. Electr. Eng. Technol. 2019, 14, 265–274. [Google Scholar] [CrossRef]
- Bak, Y.; Jang, Y.; Lee, K.-B. Torque Predictive Control for Permanent Magnet Synchronous Motor Drives Using Indirect Matrix Converter. J. Power Electron. 2019, 19, 1536–1543. [Google Scholar]
- Zhang, T.; Chen, X.; Qi, C.; Lang, Z. Leg-By-Leg-Based Finite-Control-Set Model Predictive Control for Two-Level Voltage-Source Inverters. J. Power Electron. 2019, 19, 1162–1170. [Google Scholar]
- Xu, Y.; Li, H.; Ren, J.; Zhang, Y. Three-vector-based model predictive current control with disturbance feedforward compensation. J. Power Electron. 2020, 20, 687–697. [Google Scholar] [CrossRef]
- Feng, X.; Tao, Y.; Cui, X.; Shao, K.; Wang, Y. Sliding mode and predictive current control strategy of the three-phase Vienna rectifier. J. Power Electron. 2020, 20, 743–753. [Google Scholar] [CrossRef]
- Vafaie, M.H.; Dehkordi, B.M.; Moallem, P.; Kiyoumarsi, A. Minimizing Torque and Flux Ripples and Improving Dynamic Response of PMSM Using a Voltage Vector with Optimal Parameters. IEEE Trans. Ind. Electron. 2016, 63, 3876–3888. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, Y.; Zhou, Z.; Yan, Y.; Xia, C. Torque Ripple Reduction in Three-Level Inverter-Fed Permanent Magnet Synchronous Motor Drives by Duty-Cycle Direct Torque Control Using an Evaluation Table. J. Power Electron. 2017, 17, 368–379. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, J. A novel duty cycle control strategy to reduce both torque and flux ripples for DTC of permanent magnet synchronous motor drives with switching frequency reduction. IEEE Trans. Power Electron. 2011, 26, 3055–3067. [Google Scholar] [CrossRef]
- Zhu, H.; Xiao, X.; Li, Y. Torque ripple reduction of the torque predictive control scheme for permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2012, 59, 871–877. [Google Scholar] [CrossRef]
- Niu, F.; Li, K.; Wang, Y. Direct Torque Control for Permanent-Magnet Synchronous Machines Based on Duty Ratio Modulation. IEEE Trans. Ind. Electron. 2015, 62, 6160–6170. [Google Scholar] [CrossRef]
- Lee, K.-B.; Lee, J.S. Reliability Improvement Technology for Power Converters; Springer: Singapore, 2017. [Google Scholar]
- Abronzini, U.; Attaianese, C.; D’Arpino, M.; Di Monaco, M.; Tomasso, G. Induction Motor Drives Fed by an NPC Inverter with Unbalanced DC-Link. Electronics 2019, 8, 1379. [Google Scholar] [CrossRef]
- Li, P.; Zhang, L.; Ouyang, B.; Liu, Y. Nonlinear Effects of Three-Level Neutral-Point Clamped Inverter on Speed Sensorless Control of Induction Motor. Electronics 2019, 8, 402. [Google Scholar] [CrossRef]
- Tuyen, N.D.; Phuong, L.M.; Lee, H. SVPWM Strategies for Three-level T-type Neutral-point-clamped Indirect Matrix Converter. J. Power Electron. 2019, 19, 944–955. [Google Scholar]
- Nair, M.D.; Biswas, J.; Vivek, G.; Barai, M. Optimum Hybrid SVPWM Technique for Three-level Inverter on the Basis of Minimum RMS Flux Ripple. J. Power Electron. 2019, 19, 413–430. [Google Scholar]
- Khojakhan, Y.; Choo, K.-M.; Won, C.-Y. Stator Inductance Identification Based on Low-Speed Tests for Three-Level NPC Inverter-Fed Induction Motor Drives. Electronics 2020, 9, 183. [Google Scholar] [CrossRef]
- Hakami, S.S.; Alsofyani, I.M.; Lee, K.-B. Improved Constant Switching Frequency Torque Regulator based DTC of IM Fed by 3L-NPC Inverter for Wide Speed Region. In Proceedings of the 2019 IEEE Conference on Energy Conversion (CENCON), Yogyakarta, Indonesia, 16–17 October 2019; pp. 42–46. [Google Scholar]
- Mohan, D.; Zhang, X.; Foo, G.H.B. Three-Level Inverter-Fed Direct Torque Control of IPMSM with Constant Switching Frequency and Torque Ripple Reduction. IEEE Trans. Ind. Electron. 2016, 63, 7908–7918. [Google Scholar] [CrossRef]
- Hakami, S.S.; Alsofyani, I.M.; Lee, K.-B. Low-Speed Performance Improvement of Direct Torque Control for Induction Motor Drives Fed by Three-Level NPC Inverter. Electronics 2020, 9, 77. [Google Scholar] [CrossRef]
- Naganathan, P.; Srinivas, S.; Ittamveettil, H. Five-level torque controller-based DTC method for a cascaded three-level inverter fed induction motor drive. IET Power Electron. 2017, 10, 1223–1230. [Google Scholar] [CrossRef]
- Hakami, S.S.; Alsofyani, I.M.; Lee, K.-B. Torque Ripple Reduction and Flux-droop Minimization of DTC with Improved Interleaving CSFTC of IM Fed by Three-Level NPC Inverter. IEEE Access. 2019, 7, 184266–184275. [Google Scholar] [CrossRef]
- Arumugam, S.; Thathan, M. Novel Switching Table for Direct Torque Controlled Permanent Magnet Synchronous Motors to Reduce Torque Ripple. J. Power Electron. 2013, 13, 939–954. [Google Scholar] [CrossRef]
- Pham, K.D.; Nguyen, N.V. Pulse-Width Modulation Strategy for Common Mode Voltage Elimination with Reduced Common Mode Voltage Spikes in Multilevel Inverters with Extension to Over-Modulation Mode. J. Power Electron. 2019, 19, 727–743. [Google Scholar]
- Jung, J.-H.; Park, J.-H.; Kim, J.-M.; Son, Y.-D. DC-Link Voltage Balance Control Using Fourth-Phase for 3-Phase 3-Level NPC PWM Converters with Common-Mode Voltage Reduction Technique. J. Power Electron. 2019, 19, 108–118. [Google Scholar]
- Wang, C.; Li, Z.; Xin, H. Neutral-point Voltage Balancing Strategy for Three-level Converter based on Disassembly of Zero Level. J. Power Electron. 2019, 19, 79–88. [Google Scholar]
- Yoon, H.; Yoon, D.; Choi, D.; Cho, Y. Three-phase current balancing strategy with distributed static series compensators. J. Power Electron. 2019, 19, 803–814. [Google Scholar]
- Li, C.; Wang, G.; Li, F.; Li, H.; Xia, Z.; Liu, Z. Fault-Tolerant Control for 5L-HNPC Inverter-Fed Induction Motor Drives with Finite Control Set Model Predictive Control Based on Hierarchical Optimization. J. Power Electron. 2019, 19, 989–999. [Google Scholar]
- Han, P.; He, X.; Zhao, Z.; Yu, H.; Wang, Y.; Peng, X.; Shu, Z. DC-Link Capacitor Voltage Balanced Modulation Strategy Based on Three-Level Neutral-Point-Clamped Cascaded Rectifiers. J. Power Electron. 2019, 19, 99–107. [Google Scholar]
- Guan, B.; Doki, S. Optimal Two Degrees-of-Freedom Based Neutral Point Potential Control for Three-Level Neutral Point Clamped Converters. J. Power Electron. 2019, 19, 119–133. [Google Scholar]


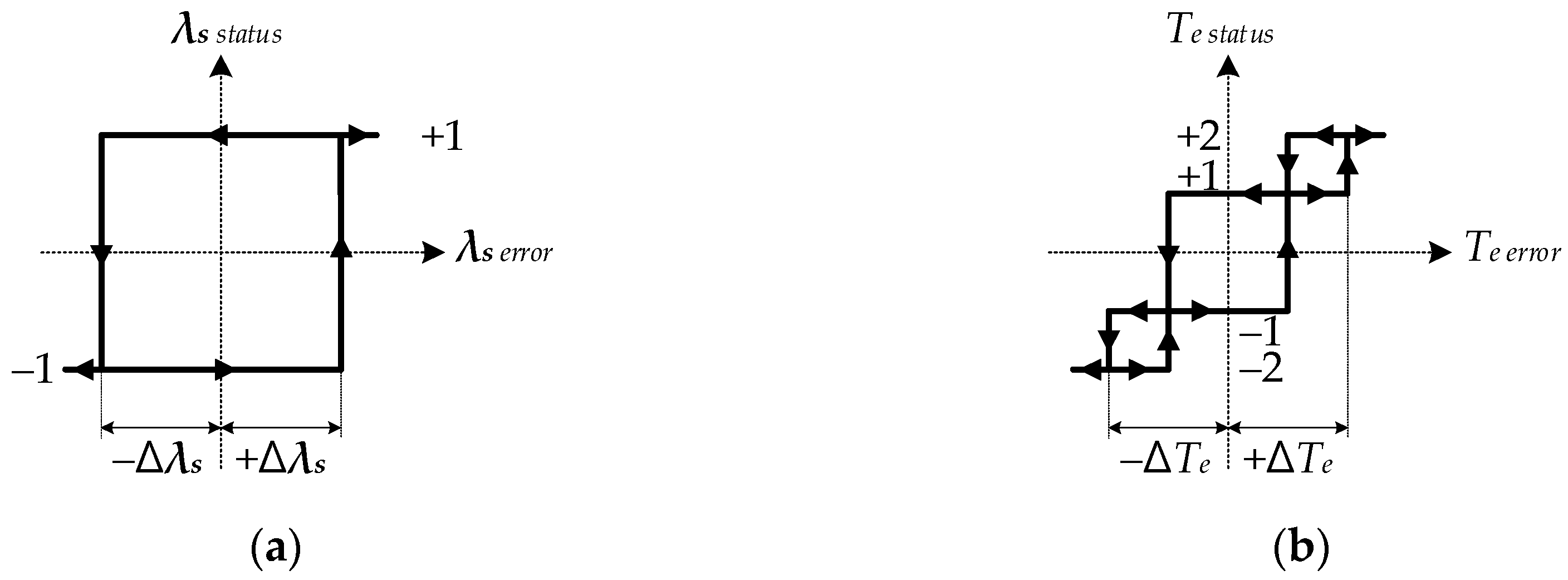



| Flux | +1 | −1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Torque | +2 | +1 | −1 | −2 | +2 | +1 | −1 | −2 | ||||
| Cap. Voltage | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | ||||
| Sector | ||||||||||||
| S1 | vM2 | vS2+ | vS2− | vS5+ | vS5− | vL5 | vM1 | vS1+ | vS1− | vS6+ | vS6− | vL6 |
| S2 | vL3 | vS2+ | vS2− | vS5+ | vS5− | vM5 | vL2 | vS1+ | vS1− | vS6+ | vS6− | vM6 |
| S3 | vM3 | vS3+ | vS3− | vS6+ | vS6− | vL6 | vM2 | vS2+ | vS2− | vS1+ | vS1− | vL1 |
| S4 | vL4 | vS3+ | vS3− | vS6+ | vS6− | vM6 | vL3 | vS2+ | vS2− | vS1+ | vS1− | vM1 |
| S5 | vM4 | vS4+ | vS4− | vS1+ | vS1− | vL1 | vM3 | vS3+ | vS3− | vS2+ | vS2− | vL2 |
| S6 | vL5 | vS4+ | vS4− | vS1+ | vS1− | vM1 | vL4 | vS3+ | vS3− | vS2+ | vS2− | vM2 |
| S7 | vM5 | vS5+ | vS5− | vS2+ | vS2− | vL2 | vM4 | vS4+ | vS4− | vS3+ | vS3− | vL3 |
| S8 | vL6 | vS5+ | vS5− | vS2+ | vS2− | vM2 | vL5 | vS4+ | vS4− | vS3+ | vS3− | vM3 |
| S9 | vM6 | vS6+ | vS6− | vS3+ | vS3− | vL3 | vM5 | vS5+ | vS5− | vS4+ | vS4− | vL4 |
| S10 | vL1 | vS6+ | vS6− | vS3+ | vS3− | vM3 | vL6 | vS5+ | vS5− | vS4+ | vS4− | vM4 |
| S11 | vM1 | vS1+ | vS1− | vS4+ | vS4− | vL4 | vM6 | vS6+ | vS6− | vS5+ | vS5− | vL5 |
| S12 | vL2 | vS1+ | vS1− | vS4+ | vS4− | vM4 | vL1 | vS6+ | vS6− | vS5+ | vS5− | vM5 |
| Quantity | Value |
|---|---|
| Rated power | 11 (kW) |
| Rated current | 19.9 (A) |
| Rated speed | 1750 (r/min) |
| Rated torque | 60 (Nm) |
| Stator resistance | 0.349 (Ω) |
| d-axis inductance | 13.17 (mH) |
| q-axis inductance | 15.60 (mH) |
| Permanent magnet flux | 0.554 (Wb) |
| Number of pole-pair | 3 |
| Moment of inertia | 0.02 (kg·m2) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hakami, S.S.; Lee, K.-B. Four-Level Hysteresis-Based DTC for Torque Capability Improvement of IPMSM Fed by Three-Level NPC Inverter. Electronics 2020, 9, 1558. https://doi.org/10.3390/electronics9101558
Hakami SS, Lee K-B. Four-Level Hysteresis-Based DTC for Torque Capability Improvement of IPMSM Fed by Three-Level NPC Inverter. Electronics. 2020; 9(10):1558. https://doi.org/10.3390/electronics9101558
Chicago/Turabian StyleHakami, Samer Saleh, and Kyo-Beum Lee. 2020. "Four-Level Hysteresis-Based DTC for Torque Capability Improvement of IPMSM Fed by Three-Level NPC Inverter" Electronics 9, no. 10: 1558. https://doi.org/10.3390/electronics9101558
APA StyleHakami, S. S., & Lee, K.-B. (2020). Four-Level Hysteresis-Based DTC for Torque Capability Improvement of IPMSM Fed by Three-Level NPC Inverter. Electronics, 9(10), 1558. https://doi.org/10.3390/electronics9101558






