Development of a High-Performance, FPGA-Based Virtual Anemometer for Model-Based MPPT of Wind Generators
Abstract
1. Introduction
- A more comprehensive analysis of past works on virtual sensors has been provided, and several new references have been added;
- The training algorithm for the GNG ANN has been described;
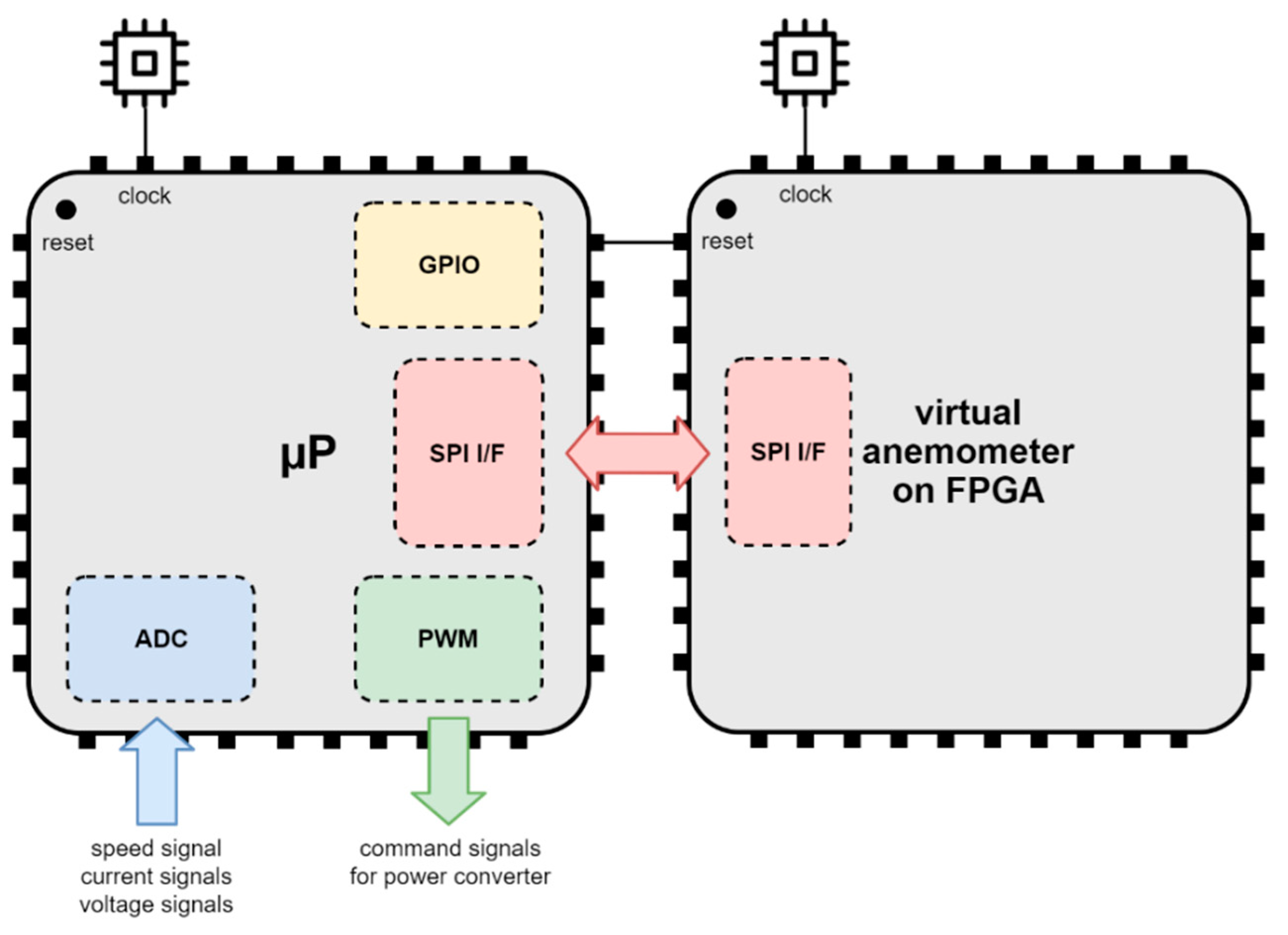
- The interaction between the main processing platform and the virtual anemometer coprocessor is better described with the help of a new figure;
- The reuse factor of VHDL components that exploit resource sharing has been explicitly stated;
- The code of the chosen parallel sorting algorithm has been added;
- The compatibility of the virtual anemometer FPGA design with application-specific integrated circuit (ASIC) and system-on-chip (SoC) implementations has been highlighted; in particular, it has been shown that even the low-end, commercial SoCs have an adequate number of resources to implement the virtual anemometer.
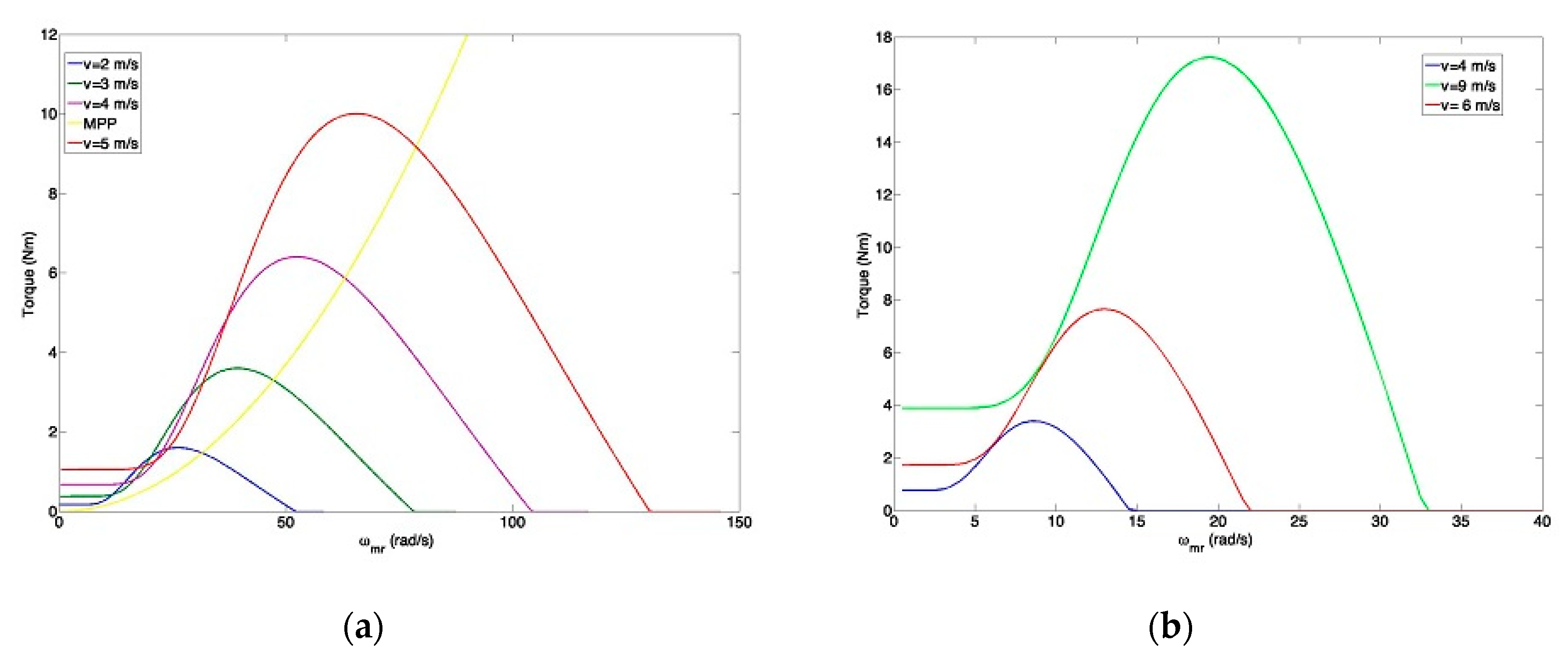
2. Models of Horizontal and Vertical Axis Wind Turbines
2.1. Horizontal Axis Wind Turbine
2.2. Vertical Axis Wind Turbine
3. The GNG Artificial Neural Network
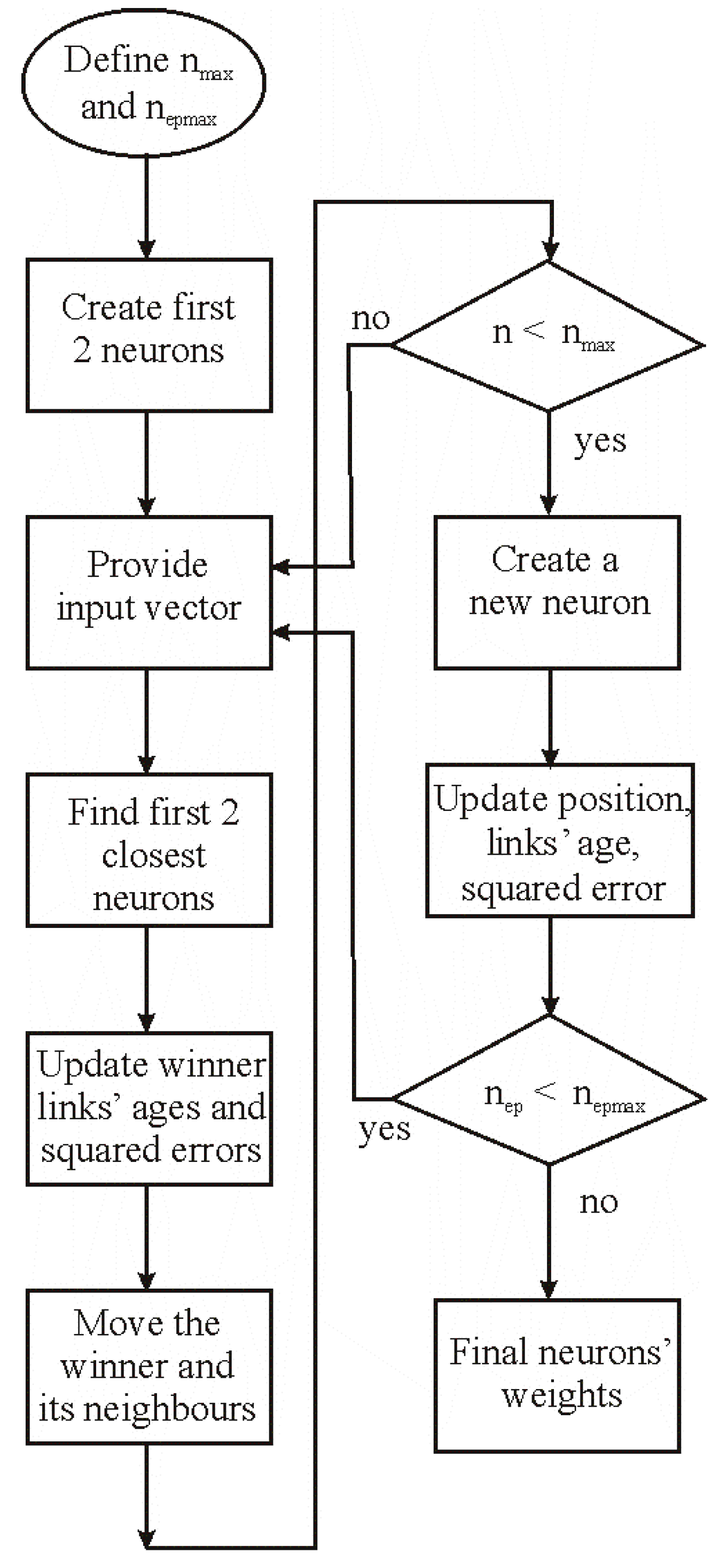
3.1. Training Phase
- Start with two neurons a and b with random weights wa and wb in ℜn;
- Present an input signal ξ belonging to the training dataset;
- Find the nearest neuron s1 and the second nearest neuron s2;
- Increment the age of all edges emanating from s1;
- Add the squared distance between the input signal and the nearest neuron in the input space to a local counter variable:
- Move s1 in its direct topological neighbors towards ξ by fractions εb and εn, respectively, of the total distance:for all direct neighbors n of s1;
- If s1 and s2 are connected by an edge, set the age of this edge to zero; if such an edge does not exist, create it;
- Remove edges with an age larger than amax; if this results in points with no emanating edges, remove them;
- If the number of input data presented so far is an integer multiple of a parameter λ, create a new neuron as follows:
- Determine the neuron q with the maximum accumulated error;
- Insert a new neuron r halfway between q and its neighbor f, and remove the original edge between q and f;
- Decrease the error variables of q and f multiplying them by a constant α; initialize the error variable of r with the new value of the error variable of q;
- Decrease all error variables multiplying them by a constant d;
- If a stopping criterion (e.g., net size or performance criterion) is not yet fulfilled, then go to step 2.
3.2. Recalling Phase
- Present the input vector ;
- Compute the K Euclidean distances Dk between the vector and the weights wi,k of the K neurons of the GNG;
- Sort the Dk’s in ascending order and consider the corresponding first P neurons;
- Compute the estimated output y by:
4. FPGA Implementation of the Virtual Anemometer
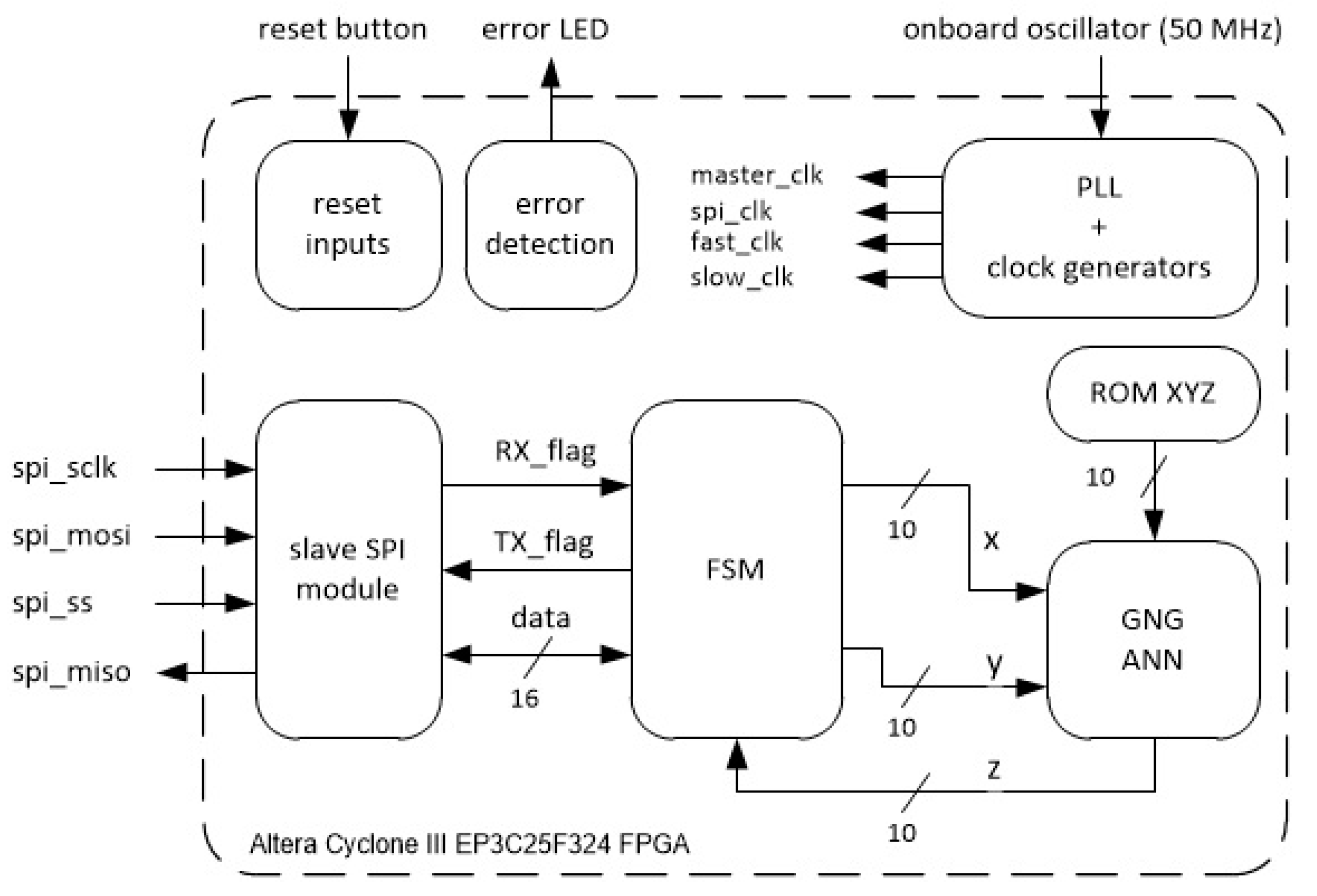
4.1. SPI Communication Interface and Protocol
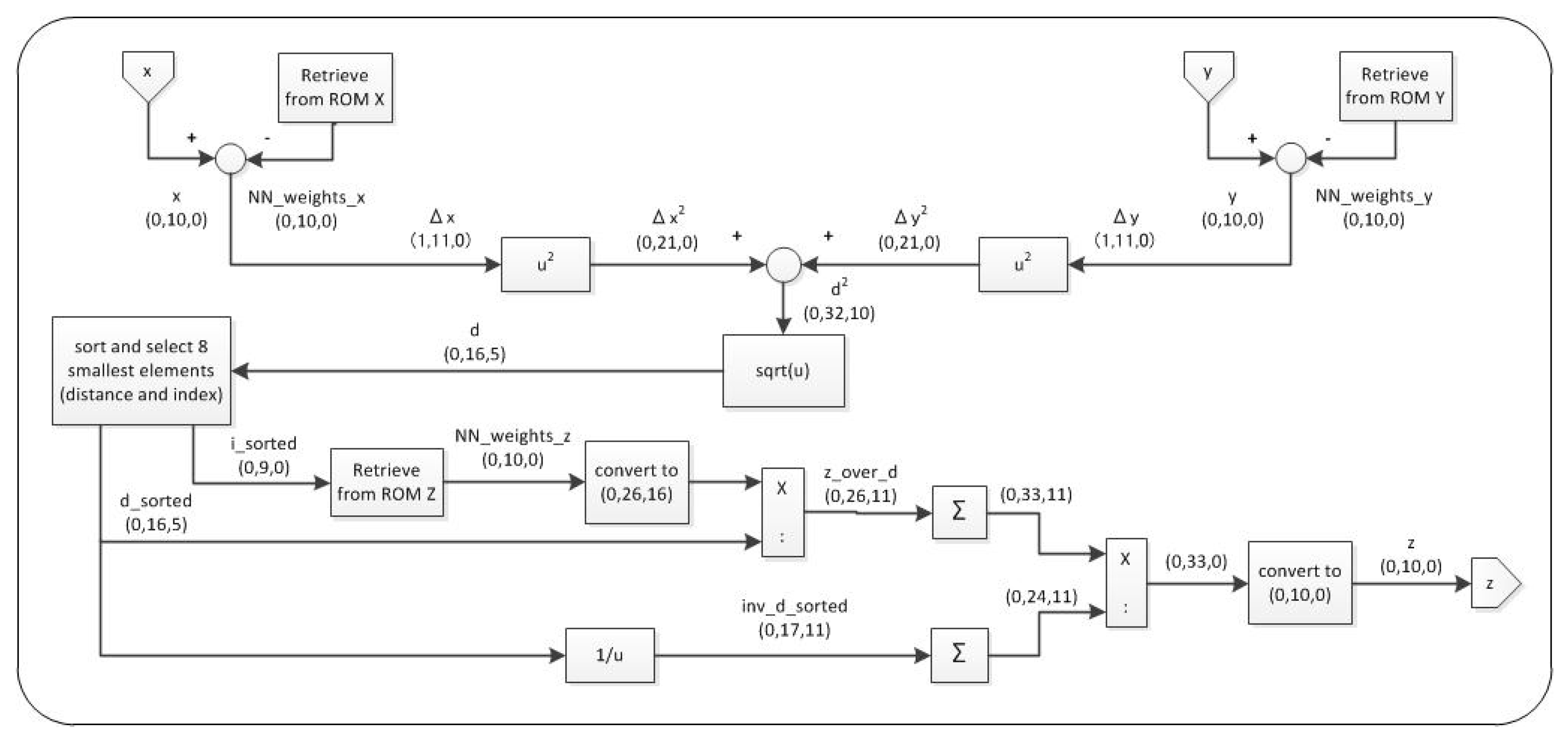
4.2. GNG ANN Implementation
- The inputs/outputs of the ANN are 10-bit integers as the data width of most ADCs commonly used within control systems;
- The weights of the ANN are also 10-bit integers, and they are stored in a ROM that is implemented using some of the dedicated memory blocks inside the FPGA chip;
- Hardware multipliers are used for computing blocks Δx2 and Δy2 of Figure 5;
- Fixed point arithmetic is used; the related precision varies from 10 bit to 32 bit; in particular, Figure 5 indicates the used datatype as a triplet (s,b,f), where s = sign bit, b = total number of bits, f = number of fractional bits;
- The final weighted sum is computed considering the eight neurons closest to the input data;
- True parallel implementation was chosen for blocks u−1, u1/u2, sqrt(u);
- Resource sharing is enforced for blocks u2 and for the sorting component with a reuse factor equal to 32;
- For this latter component a fast, parallel sorting algorithm, i.e., bitonic sort [38], has been chosen; this algorithm was implemented to select the eight smallest values among 16 input numbers; hence, the obtained VHDL component processes the distances from the input point to all neurons in blocks of 16 on several consecutive clock cycles; the bitonic sort algorithm, written as Matlab code, is shown in Algorithm 1.
| Algorithm 1. Matlab code of Bitonic Sort algorithm. |
| % this function implements bitonic sort algorithm |
| % in ascending order for 16 input elements |
| function outVec = bitonicSorter(inVec) |
| outVec = bitonicSort16(inVec); |
| end |
| function out = bitonicSort16(in) |
| out(1:8) = bitonicSort8(in(1:8), true); |
| out(9:16) = bitonicSort8(in(9:16), false); |
| out = bitonicMerge16(out, true); |
| end |
| function out = bitonicSort8(in, direction) |
| out(1:4) = bitonicSort4(in(1:4), true); |
| out(5:8) = bitonicSort4(in(5:8), false); |
| out = bitonicMerge8(out, direction); |
| end |
| function out = bitonicSort4(in, direction) |
| out(1:2) = bitonicSort2(in(1:2), true); |
| out(3:4) = bitonicSort2(in(3:4), false); |
| out = bitonicMerge4(out, direction); |
| end |
| function out = bitonicSort2(in, direction) |
| out = bitonicMerge2(in, direction); |
| end |
| function out = bitonicMerge16(in, direction) |
| for i = 1:8 |
| tmp = compare([in(i); in(i + 8)], direction); |
| out(i) = tmp(1); |
| out(i+8) = tmp(2); |
| end |
| out(1:8) = bitonicMerge8(out(1:8), direction); |
| out(9:16) = bitonicMerge8(out(9:16), direction); |
| end |
| function out = bitonicMerge8(in, direction) |
| for i = 1:4 |
| tmp = compare([in(i); in(i + 4)], direction); |
| out(i) = tmp(1); |
| out(i+4) = tmp(2); |
| end |
| out(1:4) = bitonicMerge4(out(1:4), direction); |
| out(5:8) = bitonicMerge4(out(5:8), direction); |
| end |
| function out = bitonicMerge4(in, direction) |
| for i = 1:2 |
| tmp = compare([in(i); in(i + 2)], direction); |
| out(i) = tmp(1); |
| out(i+2) = tmp(2); |
| end |
| out(1:2) = bitonicMerge2(out(1:2), direction); |
| out(3:4) = bitonicMerge2(out(3:4), direction); |
| end |
| function out = bitonicMerge2(in, direction) |
| out = compare([in(1); in(2)], direction); |
| end |
| function out = compare(in, direction) |
| if direction == (in(1) > in(2)) |
| out = [in(2); in(1)]; |
| else |
| out = in; |
| end |
| end |
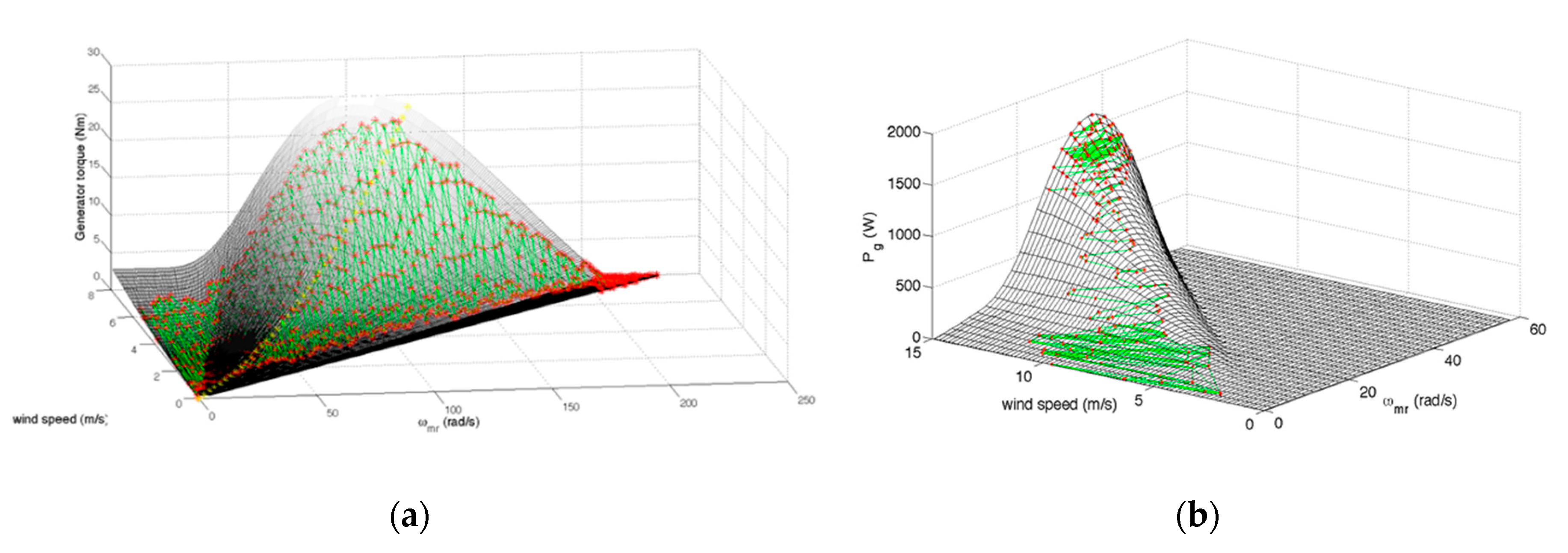
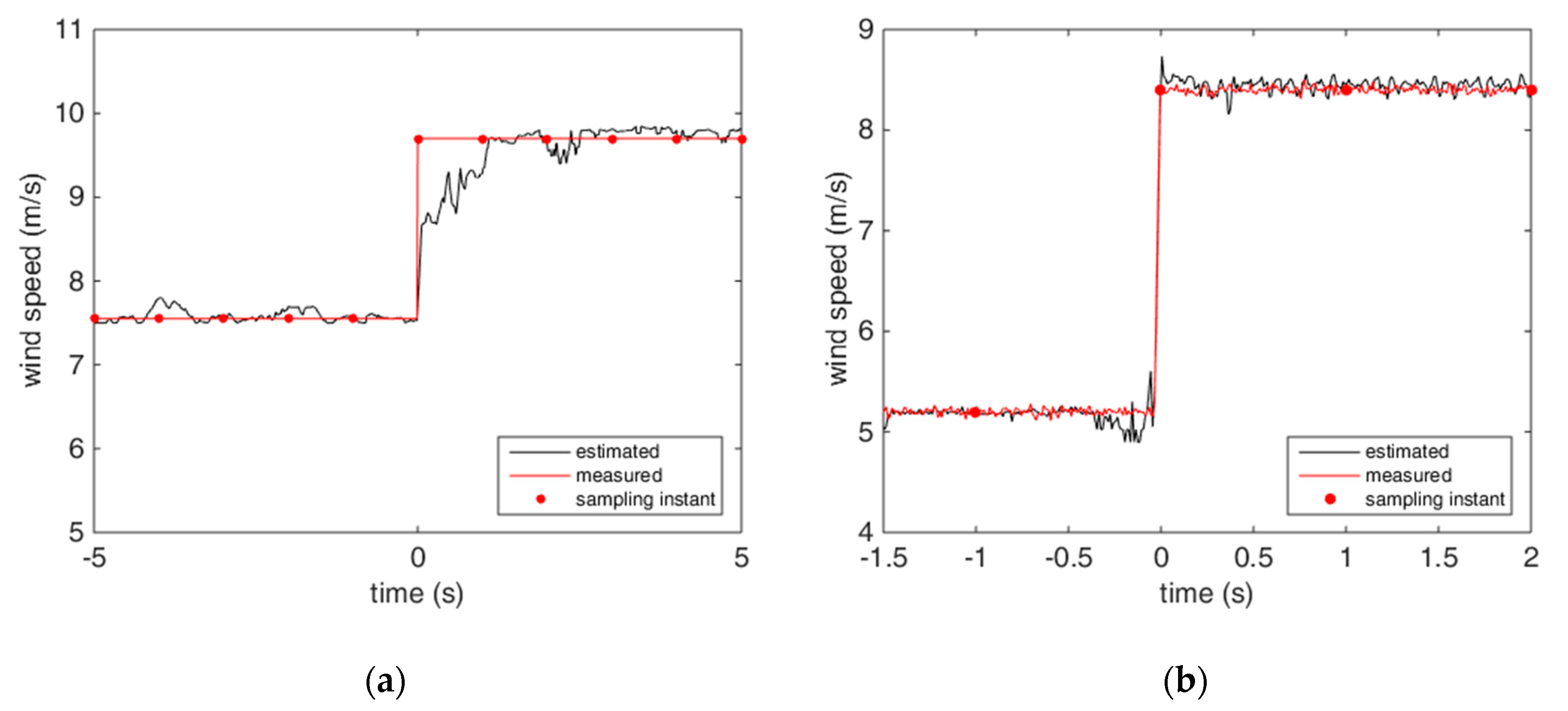
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Reisi, A.R.; Moradi, M.H.; Jamasb, S. Classification and comparison of maximum power point tracking techniques for photovoltaic system: A review. Renew. Sustain. Energy Rev. 2013, 19, 433–443. [Google Scholar] [CrossRef]
- Zhou, M.; Bao, G.; Gong, Y. Maximum Power Point Tracking Strategy for Direct Driven PMSG. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference (APPEEC), Wuhan, China, 25–28 March 2011; pp. 1–4. [Google Scholar]
- Hsieh, G.C.; Hsieh, H.I.; Tsai, C.Y.; Wang, C.H. Photovoltaic Power-Increment-Aided Incremental-Conductance MPPT with Two-Phased Tracking. IEEE Trans. Power Electron. 2013, 28, 2895–2911. [Google Scholar] [CrossRef]
- Syahputra, R.; Soesanti, I. Performance Improvement for Small-Scale Wind Turbine System Based on Maximum Power Point Tracking Control. Energies 2019, 12, 3938. [Google Scholar] [CrossRef]
- Abo-Khalil, A.G.; Lee, D.-C.; Seok, J.-K. Variable speed wind power generation system based on fuzzy logic control for maximum output power tracking. In Proceedings of the 35th Annual IEEE Power Electronics Specialists Conference (PESC 04), Aachen, Germany, 20–25 June 2004. [Google Scholar]
- Leidhold, R.; Garcia, G.; Valla, M.I. Maximum efficiency control for variable speed wind driven generators with speed and power limits. In Proceedings of the 28th Annual International Conference of the IEEE Industrial Electronics Society (IECON), Sevilla, Spain, 5–8 November 2002; pp. 57–162. [Google Scholar]
- Chedid, R.; Mrad, F.; Basma, M. Intelligent control of a class of wind energy conversion systems. IEEE Trans. Energy Convers. 1999, 14, 1597–1604. [Google Scholar] [CrossRef]
- Thongam, J.S.; Bouchard, P.; Ezzaidi, H.; Ouhrouche, M. Artificial neural network-based maximum power point tracking control for variable speed wind energy conversion systems. In Proceedings of the 2009 IEEE Control Applications, (CCA) & Intelligent Control, (ISIC), St. Petersburg, Russia, 8–10 July 2009; pp. 1667–1671. [Google Scholar]
- Gwang, H.; Seung, R.H.; Lee, K.B. An Improved Maximum Power Point Tracking Method for Wind Power Systems. Energies 2012, 5, 1339–1354. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Liu, Y. Implementation of Maximum Power Point Tracking Based on Variable Speed Forecasting for Wind Energy Systems. Processes 2019, 7, 158. [Google Scholar] [CrossRef]
- Thongam, J.S.; Bouchard, P.; Beguenane, R.; Fofana, I. Neural network based wind speed sensorless MPPT controller for variable speed wind energy conversion systems. In Proceedings of the 2010 IEEE Electric Power and Energy Conference (EPEC), Halifax, NS, Canada, 25–27 August 2010; pp. 1–6. [Google Scholar]
- Cirrincione, M.; Pucci, M.; Vitale, G. Growing Neural Gas (GNG) based Maximum Power Point Tracking for High Performance Wind Generator System with Induction Machine. IEEE Trans. Ind. Appl. 2011, 47, 861–872. [Google Scholar] [CrossRef]
- Pucci, M.; Cirrincione, M. Neural MPPT Control of Wind Generators with Induction Machines Without Speed Sensors. IEEE Trans. Ind. Electron. 2011, 58, 37–47. [Google Scholar] [CrossRef]
- Mesemanolis, A.; Mademlis, C. A Neural Network based MPPT controller for variable speed Wind Energy Conversion Systems. In Proceedings of the 8th Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (MEDPOWER 2012), Cagliari, Italy, 1–3 October 2012; pp. 1–6. [Google Scholar]
- Vitale, G.; Pucci, M.; Luna, M. Metodo e Relativo Sistema Per la Conversione di Energia Meccanica, Proveniente da un Generatore Comandato da una Turbina, in Energia Elettrica. IT Patent No. 0,001,417,881, 4 September 2015. [Google Scholar]
- Vitale, G.; Pucci, M.; Luna, M. Method and Relevant System for Converting Mechanical Energy from a Generator Actuated by a Turbine into Electric Energy. U.S. Patent No. 9,856,857 B2, 2 January 2018. [Google Scholar]
- Di Piazza, M.C.; Luna, M.; Pucci, M.; Vitale, G. PV-based Li-ion battery charger with neural MPPT for autonomous sea vehicles. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society (IECON), Vienna, Austria, 10–13 November 2013; pp. 7267–7273. [Google Scholar]
- Liu, L.; Kuo, S.M.; Zhou, M. Virtual sensing techniques and their applications. In Proceedings of the 2009 International Conference on Networking, Sensing and Control (ICNSC), Okayama, Japan, 26–29 March 2009; pp. 31–36. [Google Scholar]
- Chatterjee, A.; Keyhani, A. Neural Network Estimation of Microgrid Maximum Solar Power. IEEE Trans. Smart Grid 2012, 3, 1860–1866. [Google Scholar] [CrossRef]
- Ceylan, I.; Erkaymaz, O.; Gedik, E.; Gürel, A.E. The prediction of photovoltaic module temperature with artificial neural networks. Case Stud. Therm. Eng. 2014, 3, 11–20. [Google Scholar] [CrossRef]
- Ferreira, P.M.; Gomes, J.M.; Martins, I.A.C.; Ruano, A.E. A Neural Network Based Intelligent Predictive Sensor for Cloudiness, Solar Radiation and Air Temperature. Sensors 2012, 12, 15750–15777. [Google Scholar] [CrossRef] [PubMed]
- Karatepe, E.; Hiyama, T. Artificial neural network-polar coordinated fuzzy controller based maximum power point tracking control under partially shaded conditions. IET Renew. Power Gener. 2009, 3, 239–253. [Google Scholar]
- Mancilla-David, F.; Riganti Fulginei, F.; Laudani, A.; Salvini, A. A Neural Network-Based Low-Cost Solar Irradiance Sensor. IEEE Trans. Instrum. Meas. 2014, 63, 583–591. [Google Scholar] [CrossRef]
- Oliveri, A.; Cassottana, L.; Laudani, A.; Fulginei, F.R.; Lozito, G.M.; Salvini, A.; Storace, M. Two FPGA-Oriented High-Speed Irradiance Virtual Sensors for Photovoltaic Plants. IEEE Trans. Ind. Informat. 2017, 13, 157–165. [Google Scholar] [CrossRef]
- Hwang, Y.; Minami, Y.; Ishikawa, M. Virtual Torque Sensor for Low-Cost RC Servo Motors Based on Dynamic System Identification Utilizing Parametric Constraints. Sensors 2018, 18, 3856. [Google Scholar] [CrossRef] [PubMed]
- Guzmán, C.; Carrera, J.; Durán, H.; Berumen, J.; Ortiz, A.; Guirette, O.; Arroyo, A.; Brizuela, J.; Gómez, F.; Blanco, A.; et al. Implementation of Virtual Sensors for Monitoring Temperature in Greenhouses Using CFD and Control. Sensors 2018, 19, 60. [Google Scholar] [CrossRef] [PubMed]
- Cotton, N.J.; Wilamowski, B.M.; Dundar, G. A Neural Network Implementation on an Inexpensive Eight Bit Microcontroller. In Proceedings of the 2008 International Conference on Intelligent Engineering Systems, Miami, FL, USA, 25–29 February 2008; pp. 109–114. [Google Scholar]
- Yang, Y.R. A neural network controller for maximum power point tracking with 8-bit microcontroller. In Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 21–23 June 2011; pp. 919–924. [Google Scholar]
- Kashif, S.A.R.; Saqib, M.A.; Zia, S.; Kaleem, A. Implementation of neural network based Space Vector Pulse Width Modulation inverter-induction motor drive system. In Proceedings of the 2009 3rd International Conference on Electrical Engineering (ICEE), Lahore, Pakistan, 9–11 April 2009; pp. 1–6. [Google Scholar]
- Fratta, A.; Griffero, G.; Nieddu, S. Comparative analysis among DSP and FPGA-based control capabilities in PWM power converters. In Proceedings of the 30th Annual Conference of the IEEE Industrial Electronics Society (IECON), Busan, Korea, 2–6 November 2004; pp. 257–262. [Google Scholar]
- Economou, G.P.K.; Mariatos, E.P.; Economopoulos, N.M.; Lymberopoulos, D.; Goutis, C.E. FPGA implementation of artificial neural networks: An application on medical expert systems. In Proceedings of the 4th International Conference on Microelectronics for Neural Networks and Fuzzy Systems, Turin, Italy, 26–28 September 1994; pp. 287–293. [Google Scholar]
- Fritzke, B. A Growing Neural Gas Network Learns Topologies, Advances in Neural Information Processing Systems 7; MIT Press: Cambridge, UK, 1995. [Google Scholar]
- Accetta, A.; Di Piazza, M.C.; Tona, G.L.; Luna, M.; Pucci, M. A high-performance FPGA-based virtual anemometer for MPPT of wind energy conversion systems. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 926–933. [Google Scholar]
- Freris, L.L. Wind Energy Conversion System; Prentice Hall: New York, NY, USA, 1990. [Google Scholar]
- Fritzke, B. Growing Cell Structures—A self-organizing network for unsupervised and supervised learning. Neural Netw. 1994, 7, 1441–1460. [Google Scholar] [CrossRef]
- Fritzke, B. Incremental Learning of Linear Local Mappings. In Proceedings of the International Conference on Artificial Neural Networks (ICANN), Paris, France, 9–13 October 1995; pp. 217–222. [Google Scholar]
- Altera Cyclone III Device Handbook Volume 1. Available online: https://www.intel.com/content/dam/www/programmable/us/en/pdfs/literature/hb/cyc3/cyclone3_handbook.pdf (accessed on 30 October 2019).
- Batcher, K.E. Sorting Networks and their Applications. In Proceedings of the AFIPS Spring Joint Computer Conference, Atlantic City, NJ, USA, 30 April–2 May 1968; Volume 32, pp. 307–314. [Google Scholar]
- Zynq-7000 SoC Data Sheet: Overview. Available online: https://www.xilinx.com/support/documentation/data_sheets/ds190-Zynq-7000-Overview.pdf (accessed on 30 October 2019).

| Resource Count | Used by the Proposed Design | Available on Altera Cyclone III EP3C25F324 | Available on Xilinx Zynq Z-7007S |
|---|---|---|---|
| Logic elements/Prog. logic cells | 22,148 | 24,624 | 23,552 |
| Registers/Flip-Flops | 2265 | 24,624 | 28,800 |
| Memory bits/Block RAM | 6528 | 608,256 | 1,887,436 |
| Embedded multipliers/DSP slices | 32 | 132 | 66 |
| Parameter | Value |
|---|---|
| R [m] | 2.50 |
| λopt | 7 |
| Cpmax | 0.45 |
| n | 4.86 |
| Generator rated power [kW] | 5.5 |
| Generator rated speed [rpm] | 1500 |
| Model coefficients | c1 = 0.5176, c2 = 116, c3 = 0.4, c4 = 5, c5 = 21, c6 = 0.0068 |
| Parameter | Value |
|---|---|
| R [m] | 0.75 |
| λopt | 2 |
| Cpmax | 0.15 |
| n | 1 |
| Generator rated power [kW] | 1.0 |
| Generator rated speed [rpm] | 415 |
| Model coefficients | a1 = −25.6815, a2 = 87.6095, a3 = 8.0646, a4 = 0.048076 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
La Tona, G.; Luna, M.; Di Piazza, M.C.; Pucci, M.; Accetta, A. Development of a High-Performance, FPGA-Based Virtual Anemometer for Model-Based MPPT of Wind Generators. Electronics 2020, 9, 83. https://doi.org/10.3390/electronics9010083
La Tona G, Luna M, Di Piazza MC, Pucci M, Accetta A. Development of a High-Performance, FPGA-Based Virtual Anemometer for Model-Based MPPT of Wind Generators. Electronics. 2020; 9(1):83. https://doi.org/10.3390/electronics9010083
Chicago/Turabian StyleLa Tona, Giuseppe, Massimiliano Luna, Maria Carmela Di Piazza, Marcello Pucci, and Angelo Accetta. 2020. "Development of a High-Performance, FPGA-Based Virtual Anemometer for Model-Based MPPT of Wind Generators" Electronics 9, no. 1: 83. https://doi.org/10.3390/electronics9010083
APA StyleLa Tona, G., Luna, M., Di Piazza, M. C., Pucci, M., & Accetta, A. (2020). Development of a High-Performance, FPGA-Based Virtual Anemometer for Model-Based MPPT of Wind Generators. Electronics, 9(1), 83. https://doi.org/10.3390/electronics9010083









