Frequency Splitting and Transmission Characteristics of MCR-WPT System Considering Non-Linearities of Compensation Capacitors
Abstract
1. Introduction
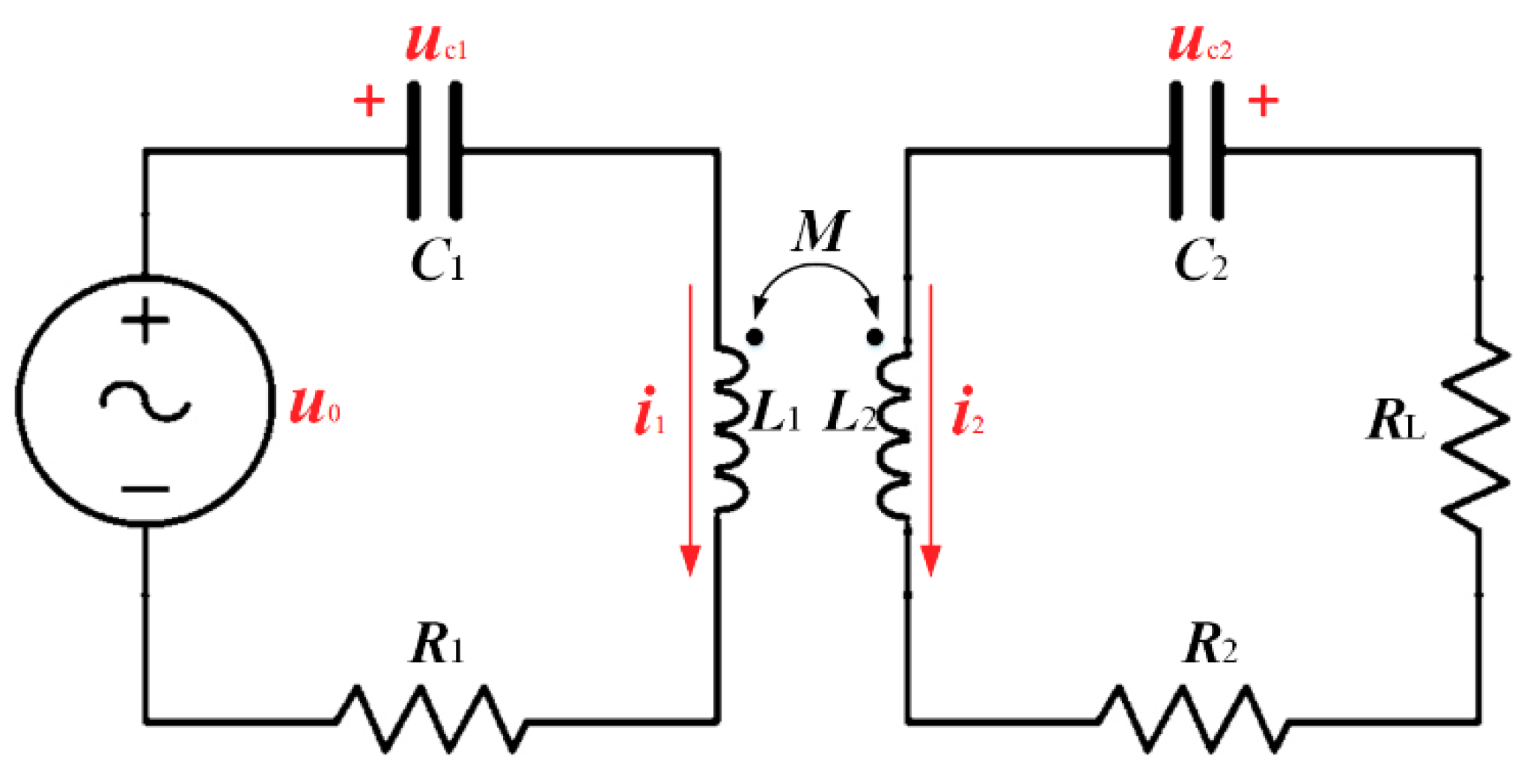
2. Circuit Model and Transmission Equations
3. Analyses of Resonance Frequency
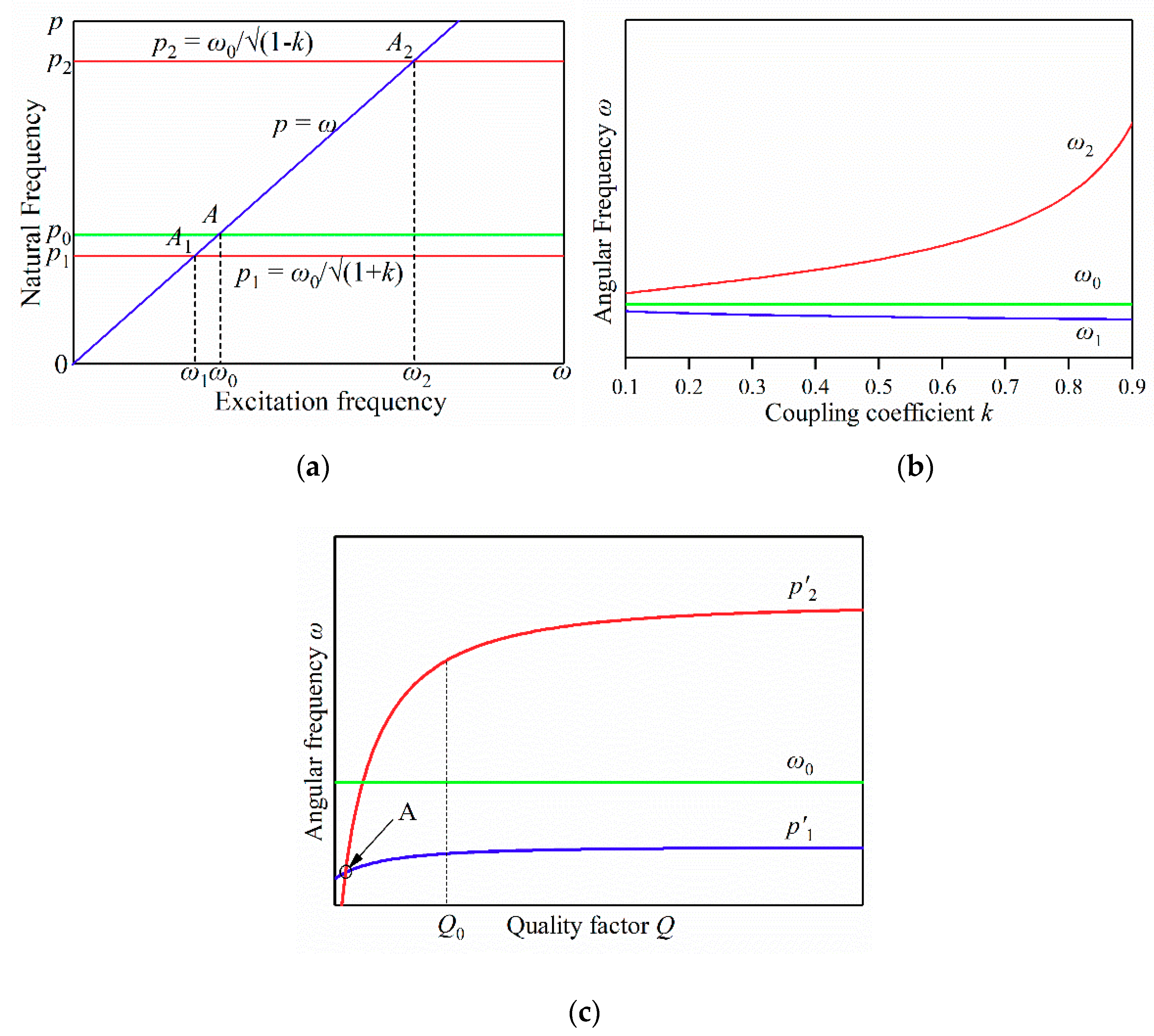
3.1. Theory Analyses
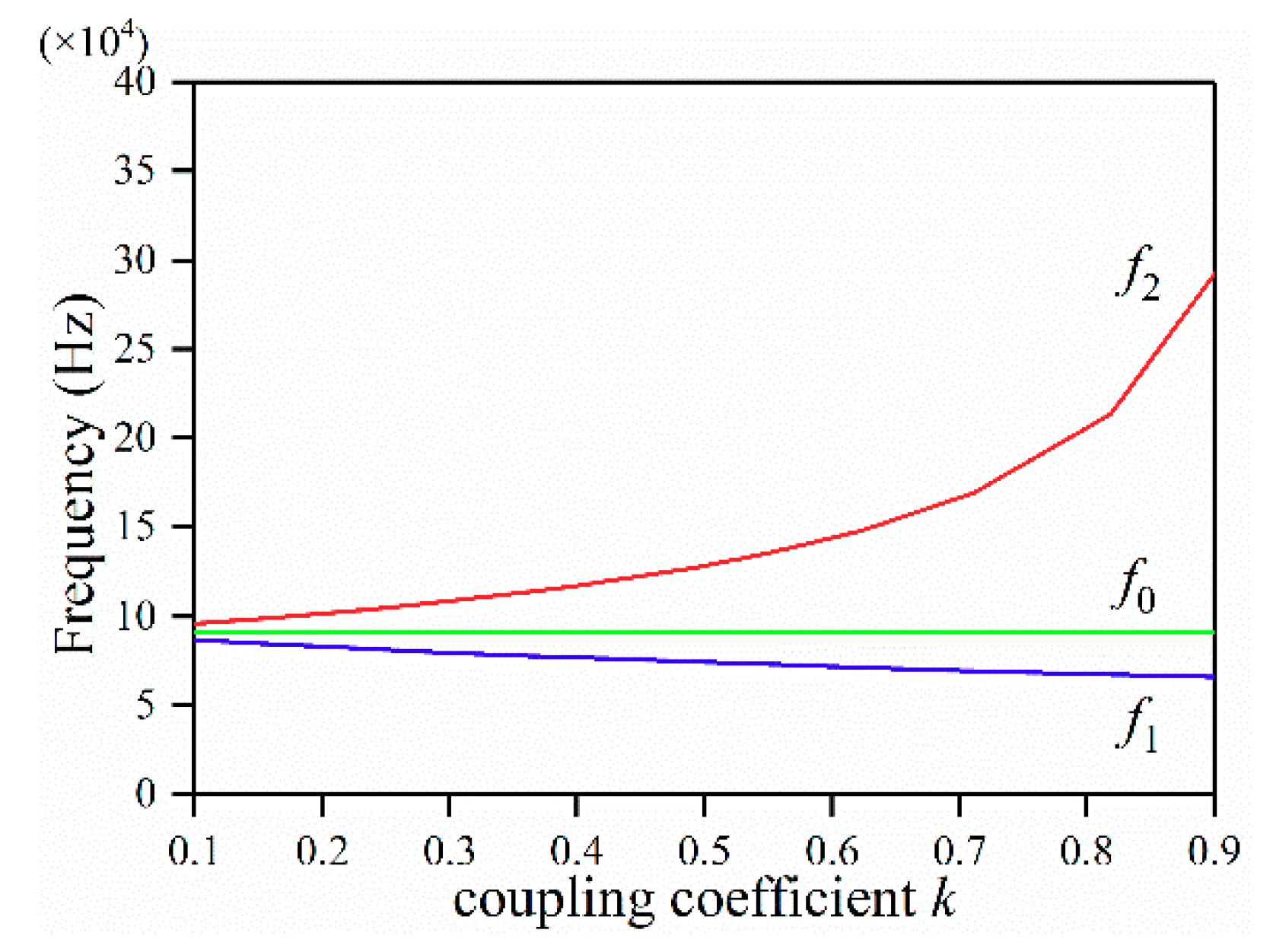
3.2. Model Validations
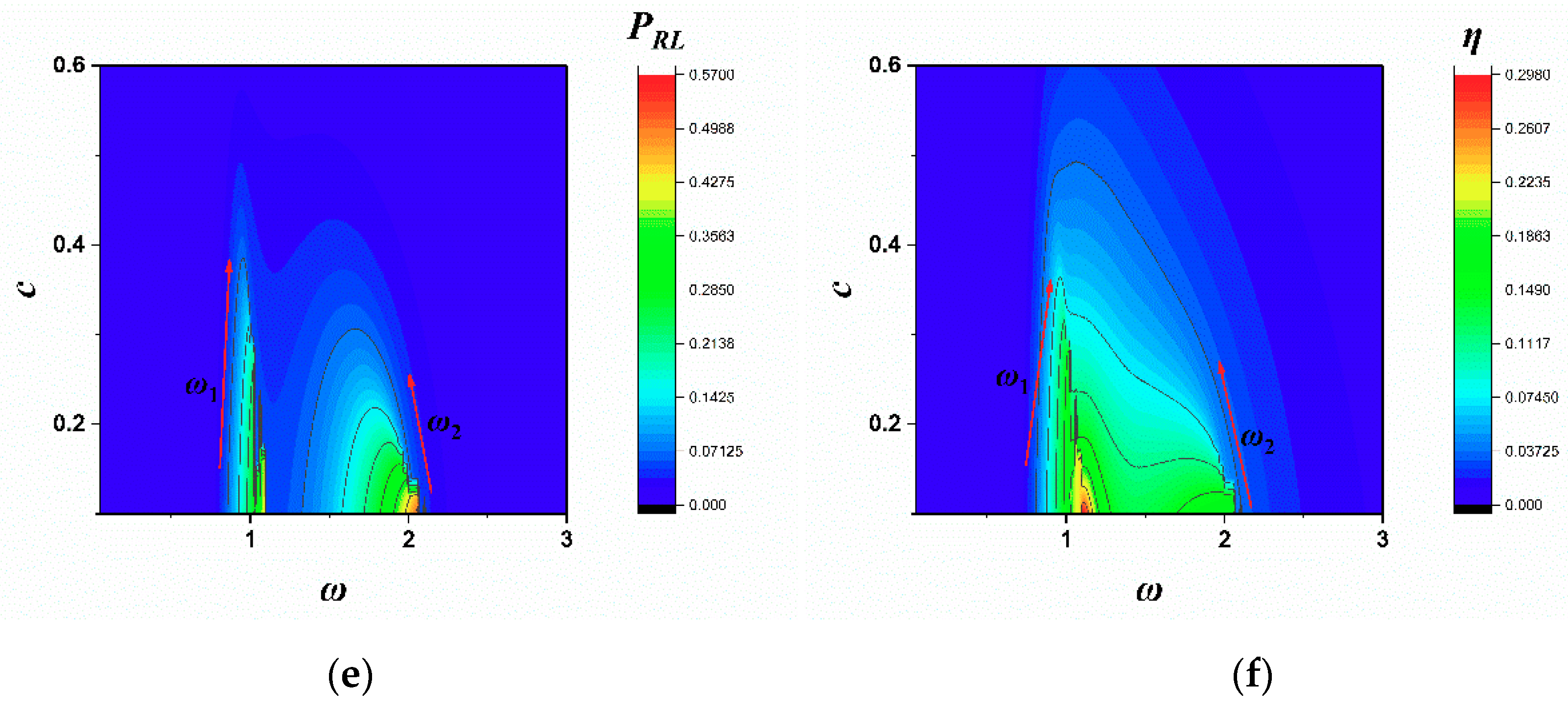
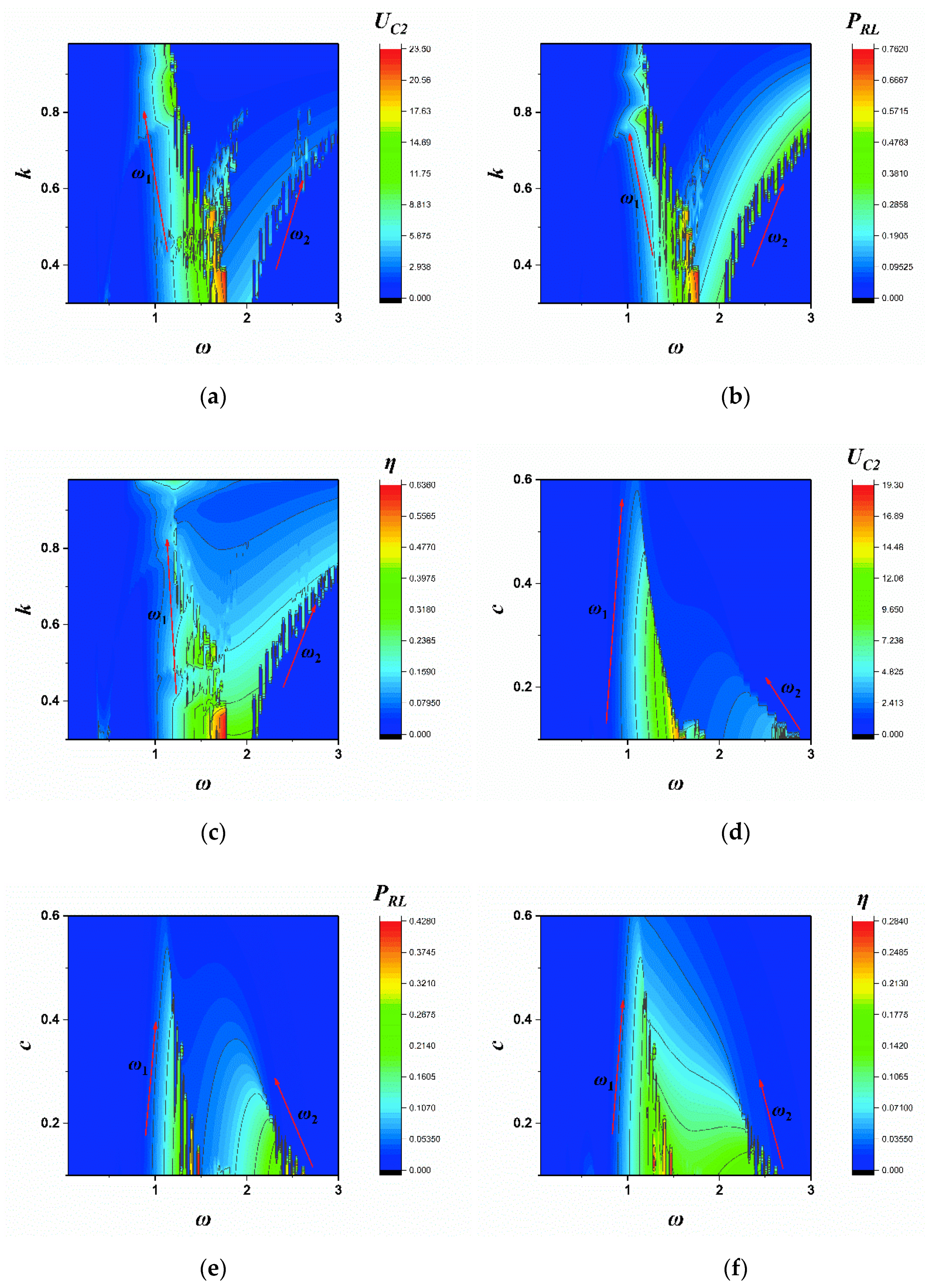
4. Transmission Characteristics of the System
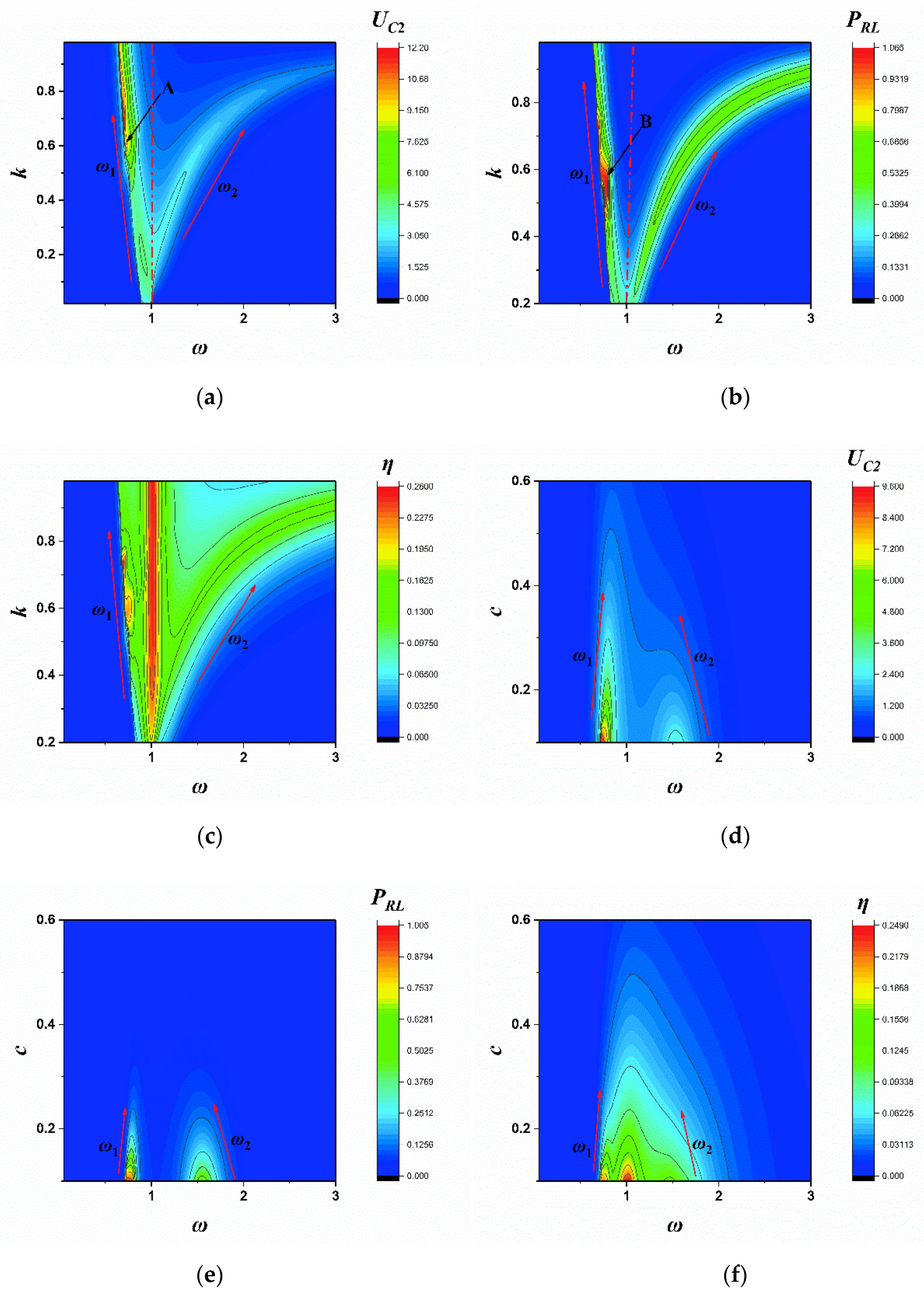
4.1. Transmission Characteristics of the Linear System
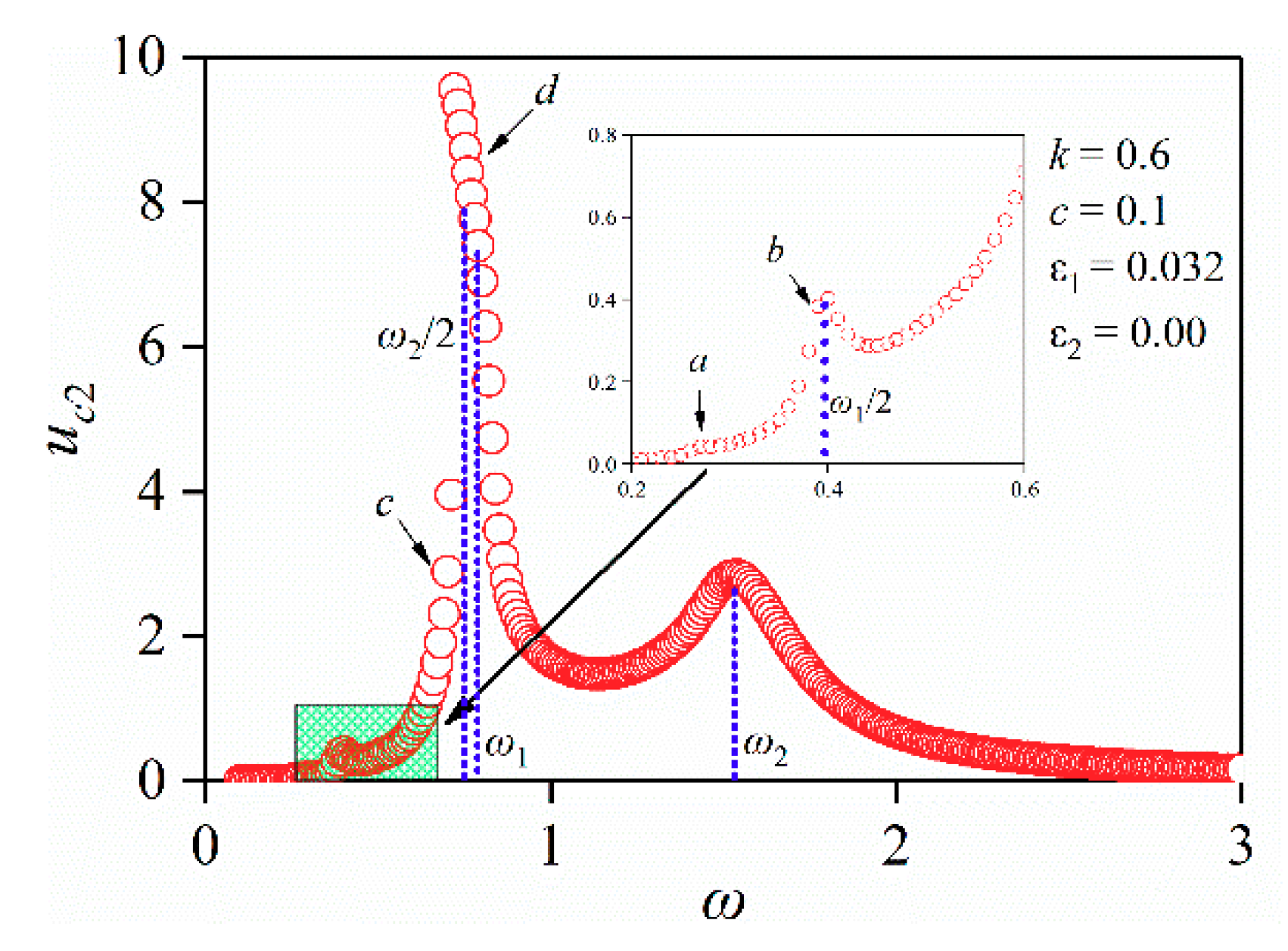
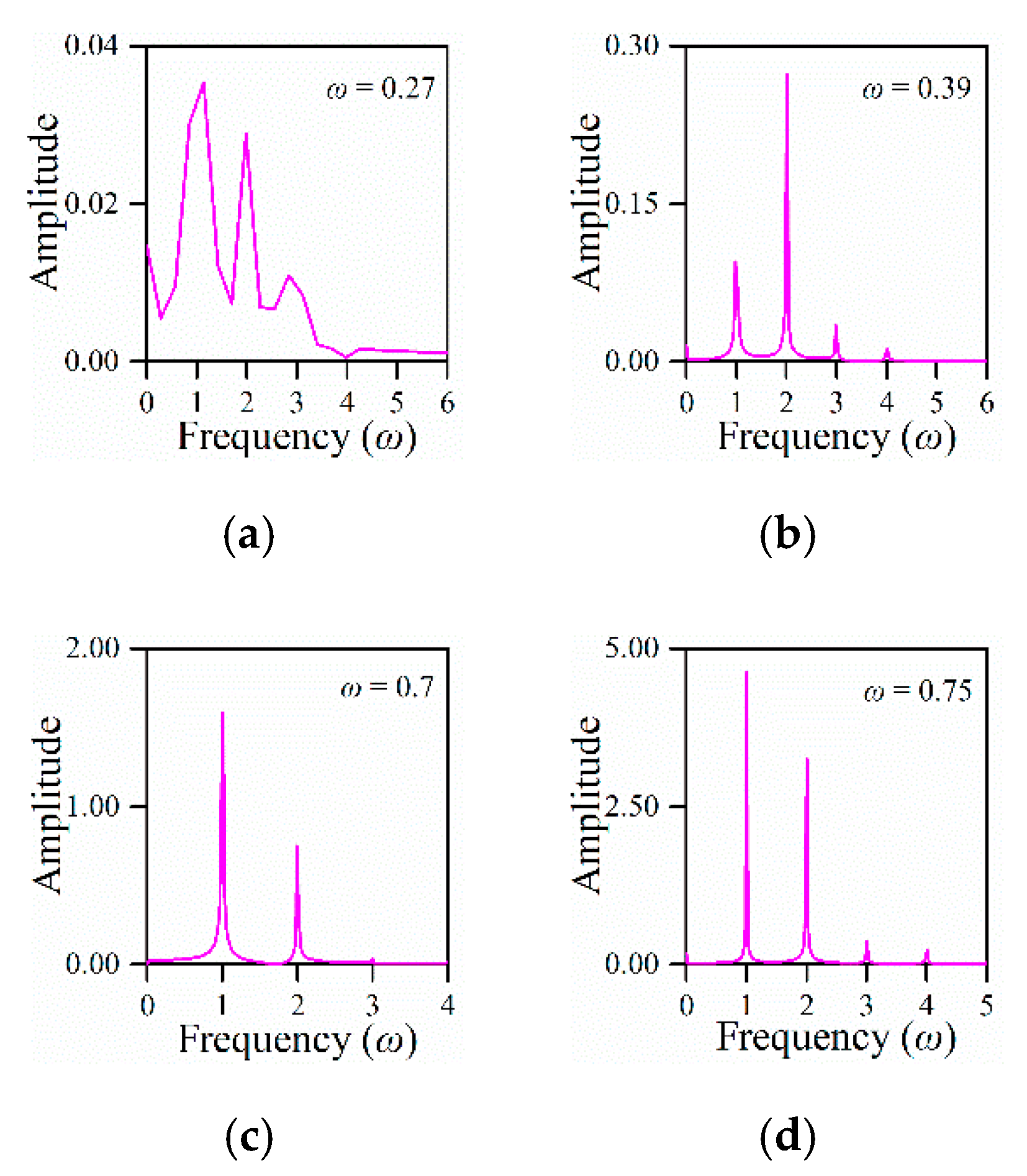
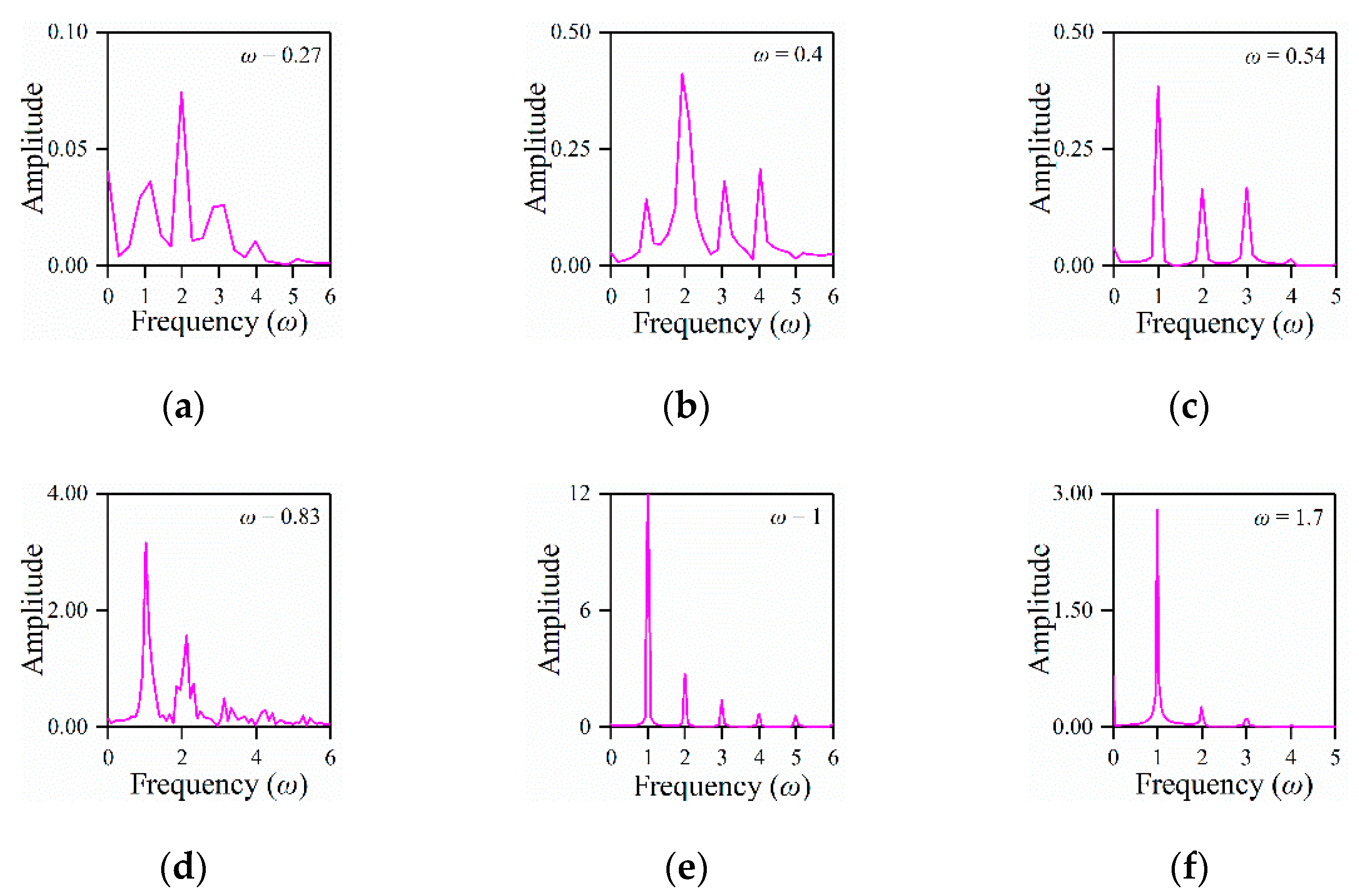
4.2. Transmission Characteristics of the Weak Non-Linear System
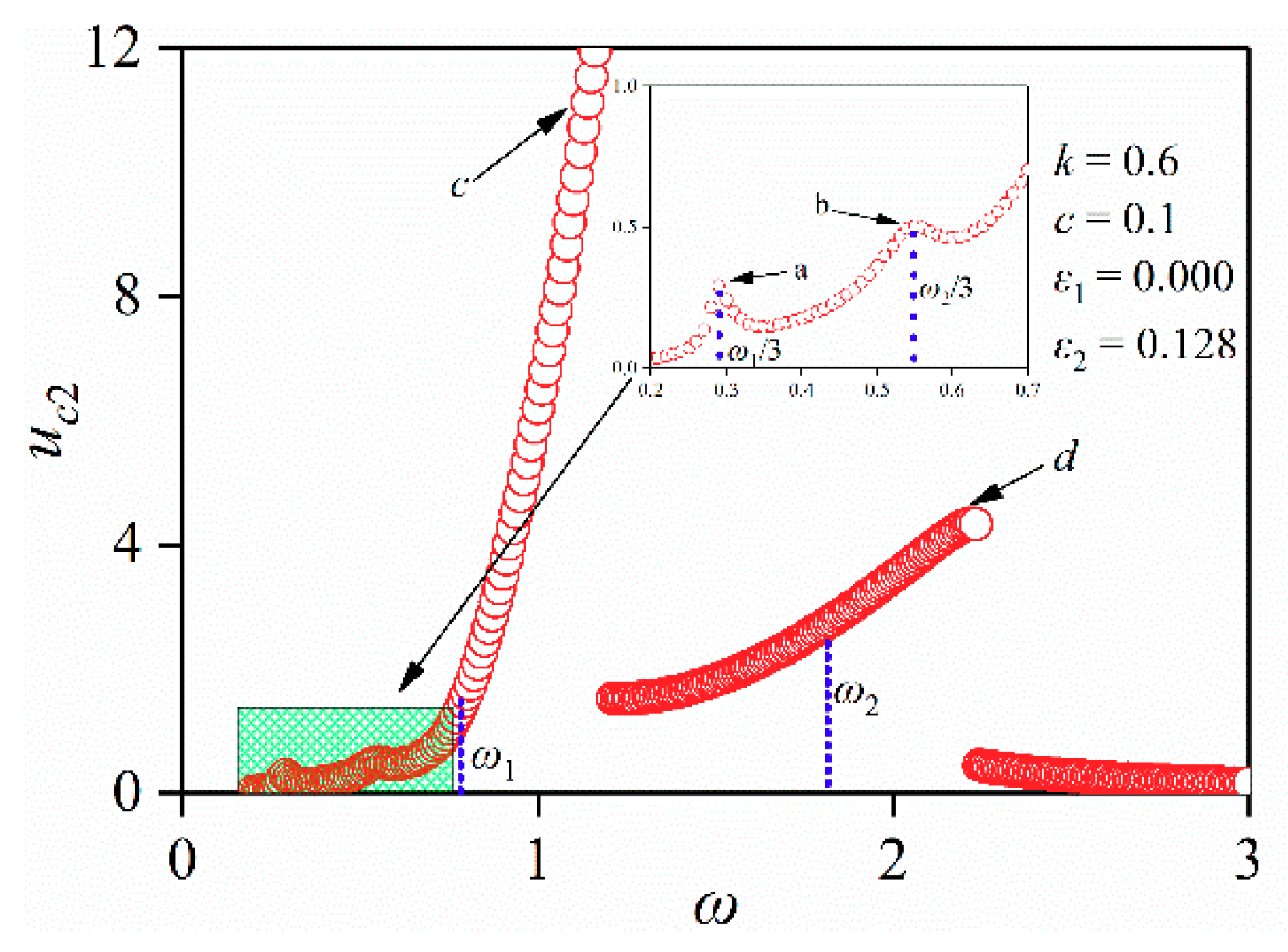
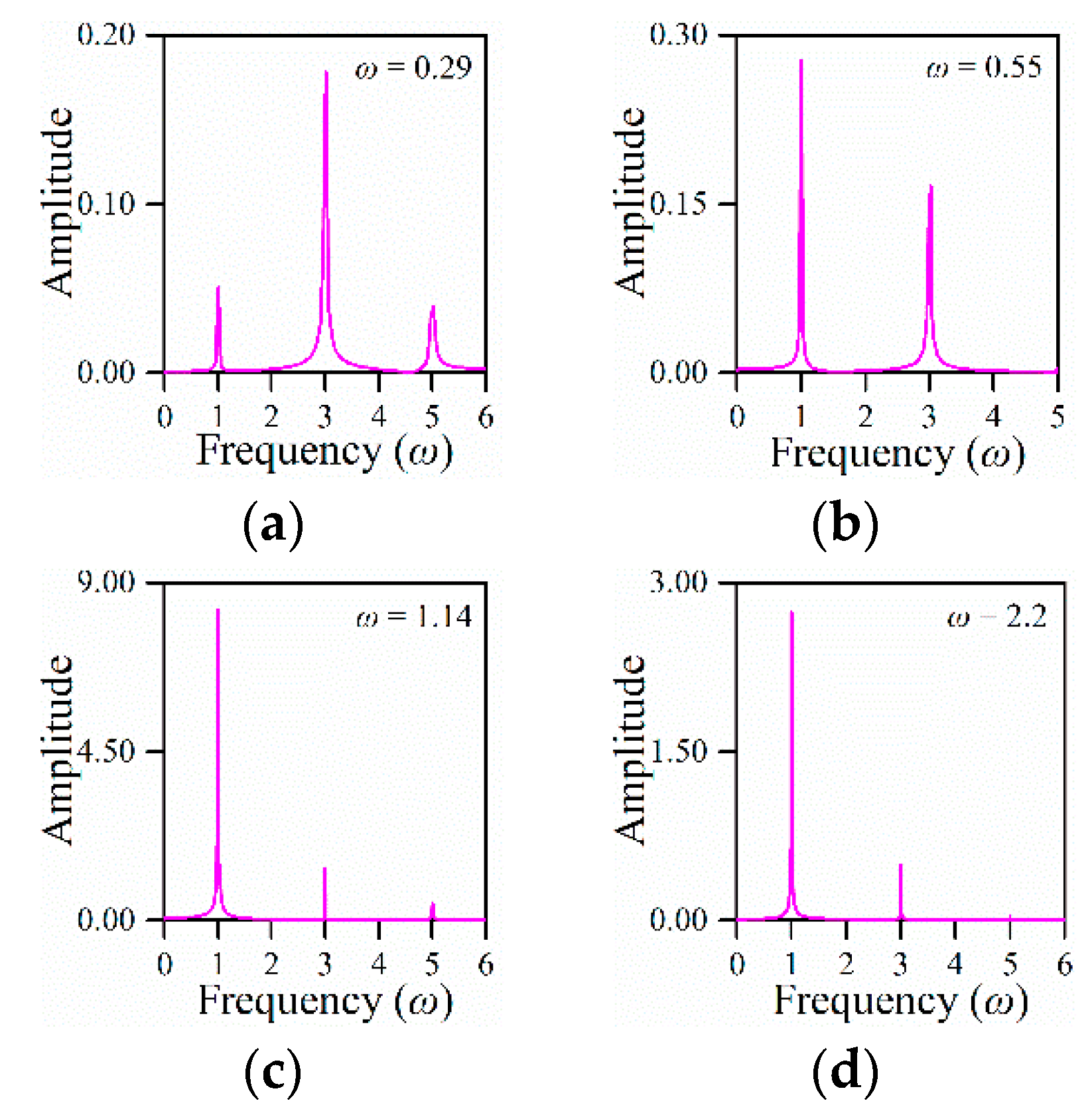
4.2.1. Considering Second Order Non-Linear Parameter ε1
4.2.2. Considering Third Order Non-Linear Parameter ε2
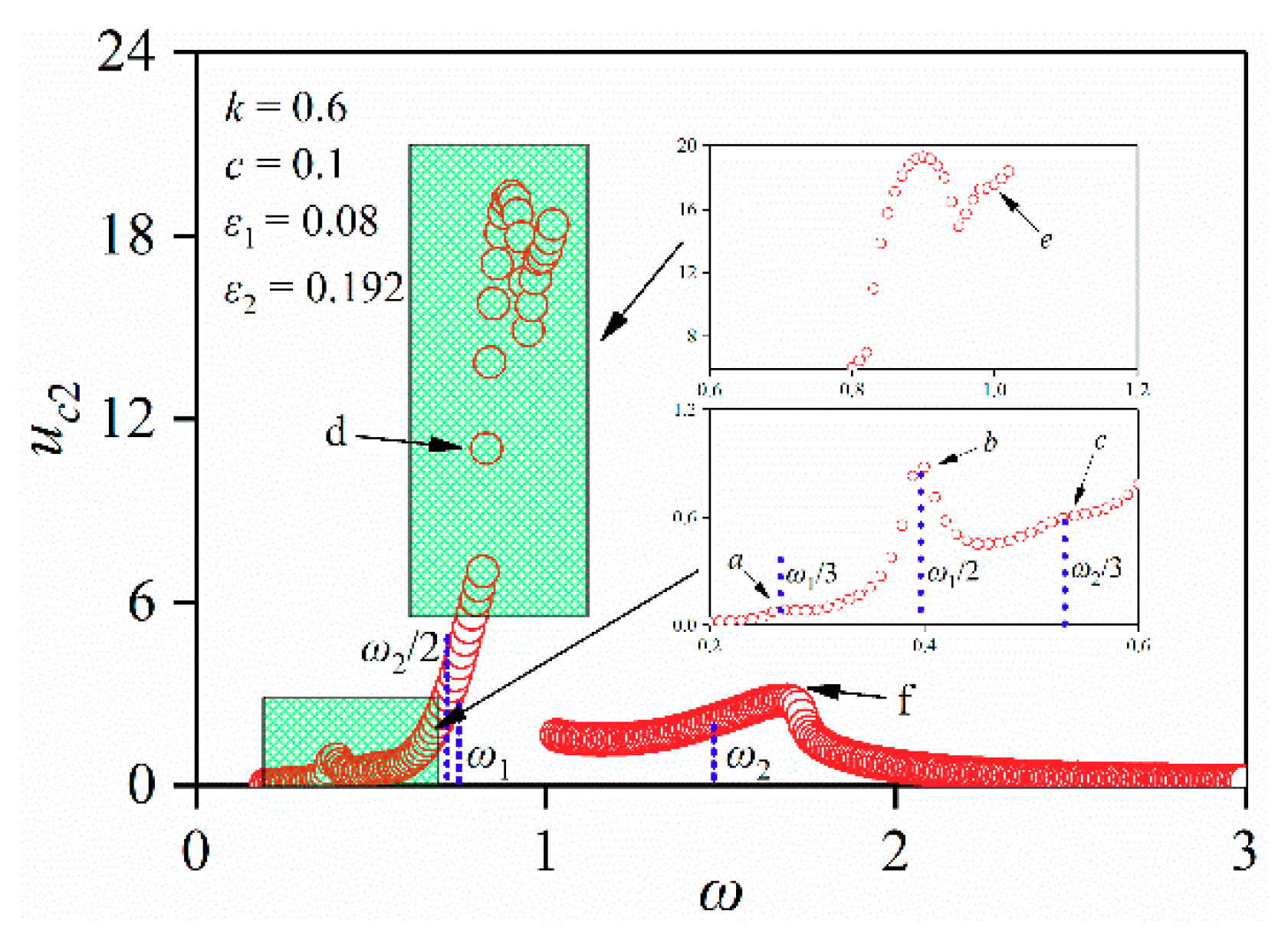
4.2.3. Considering Non-Linear Parameters ε1 and ε2
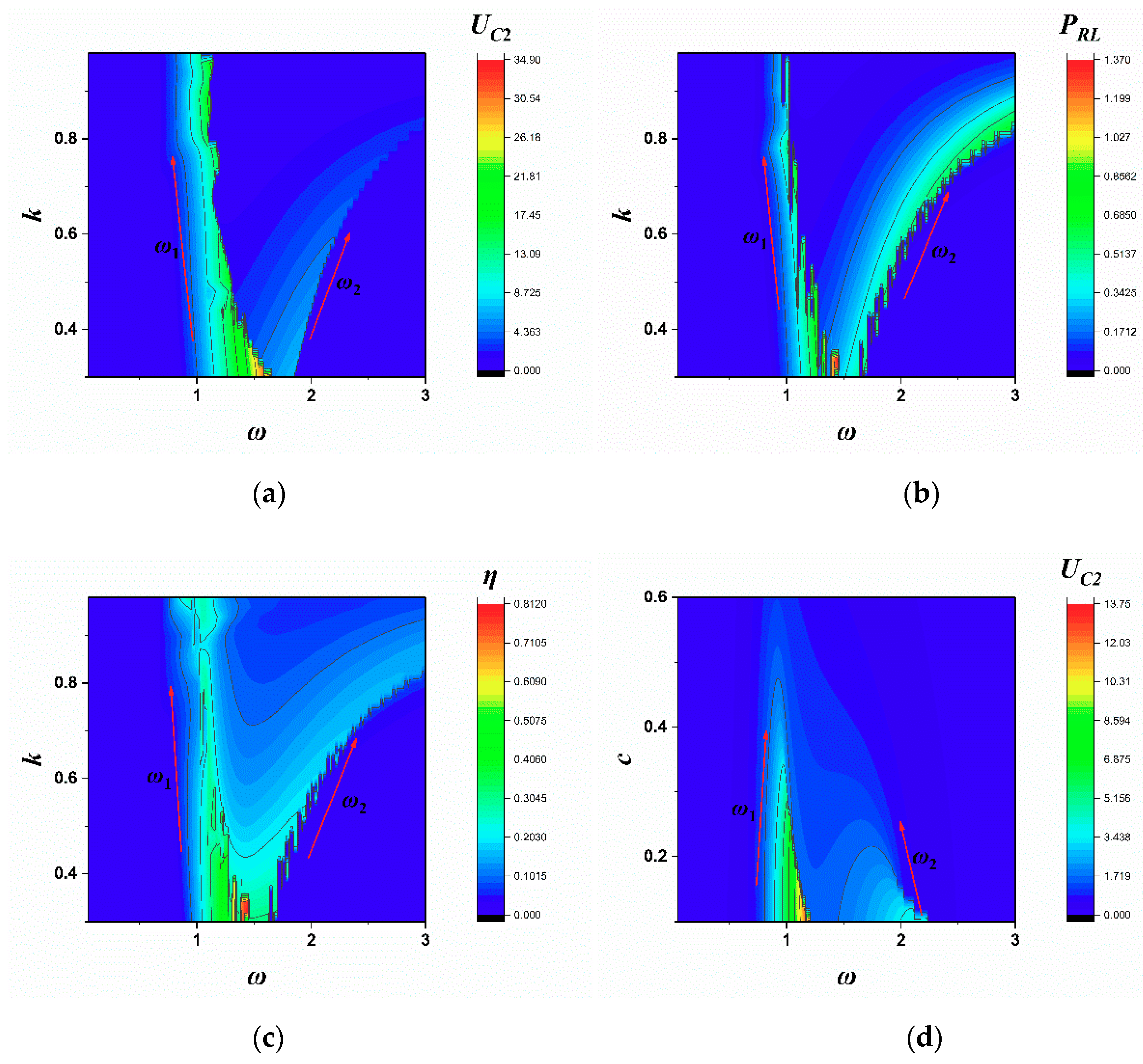
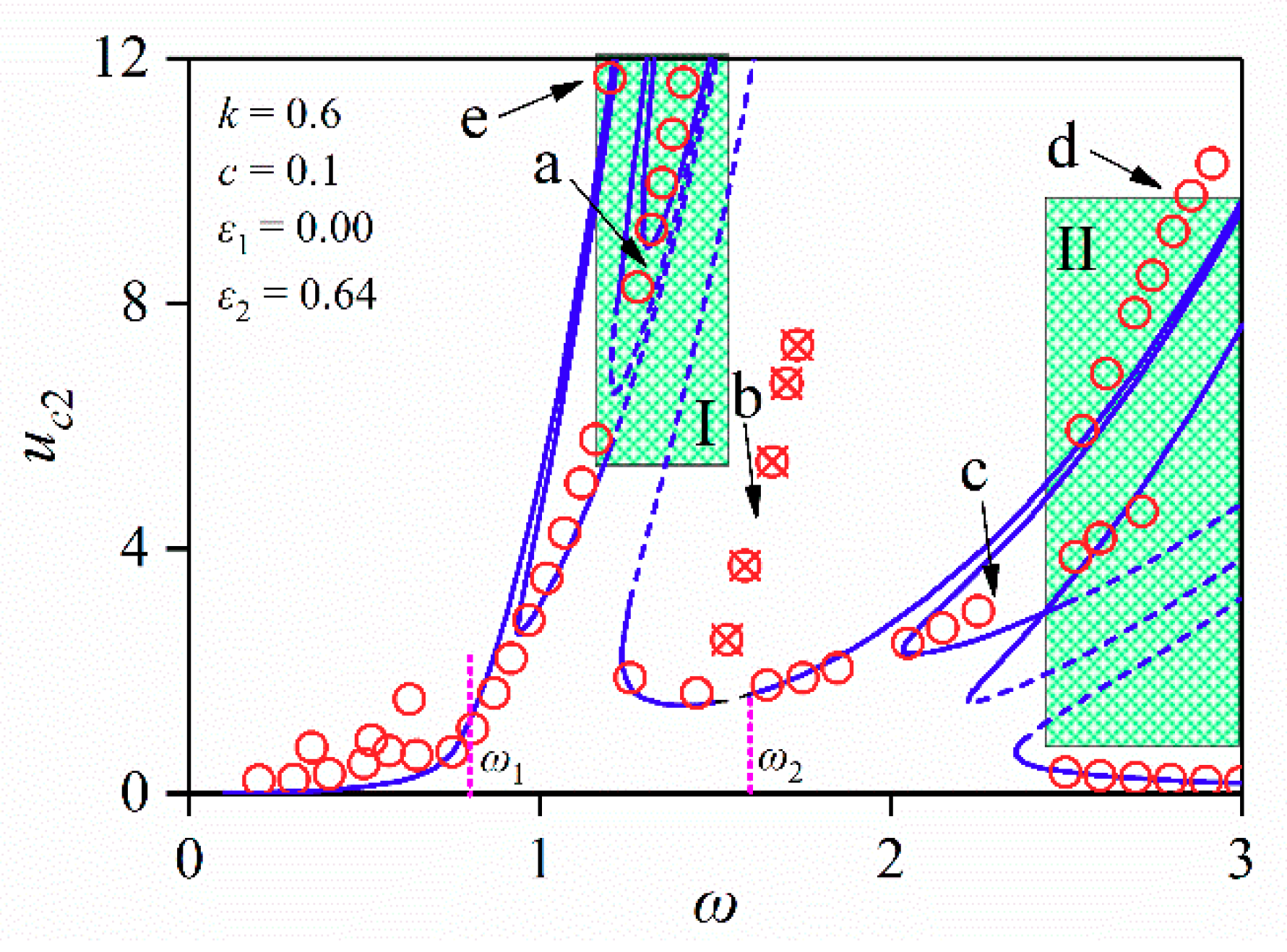
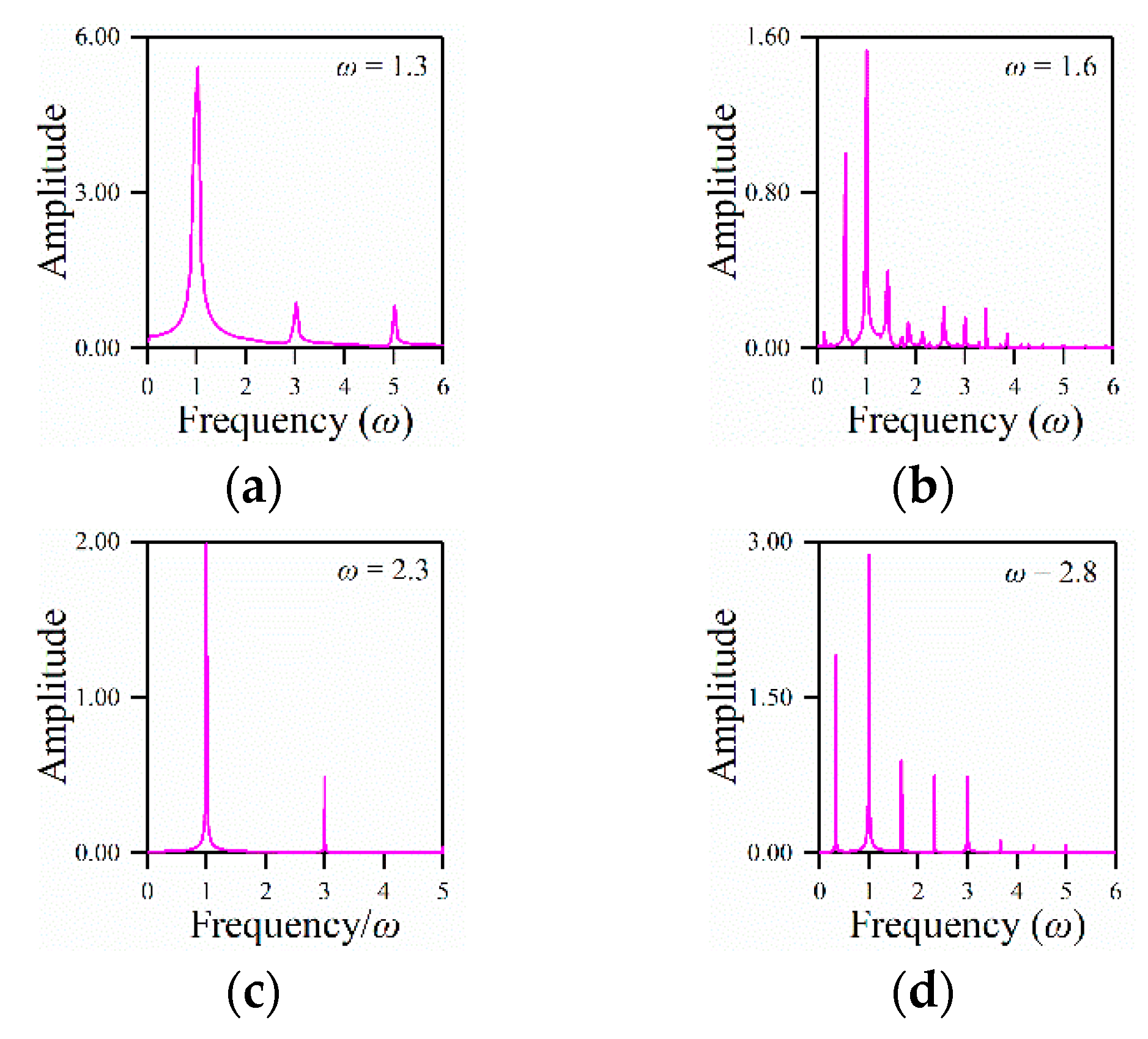
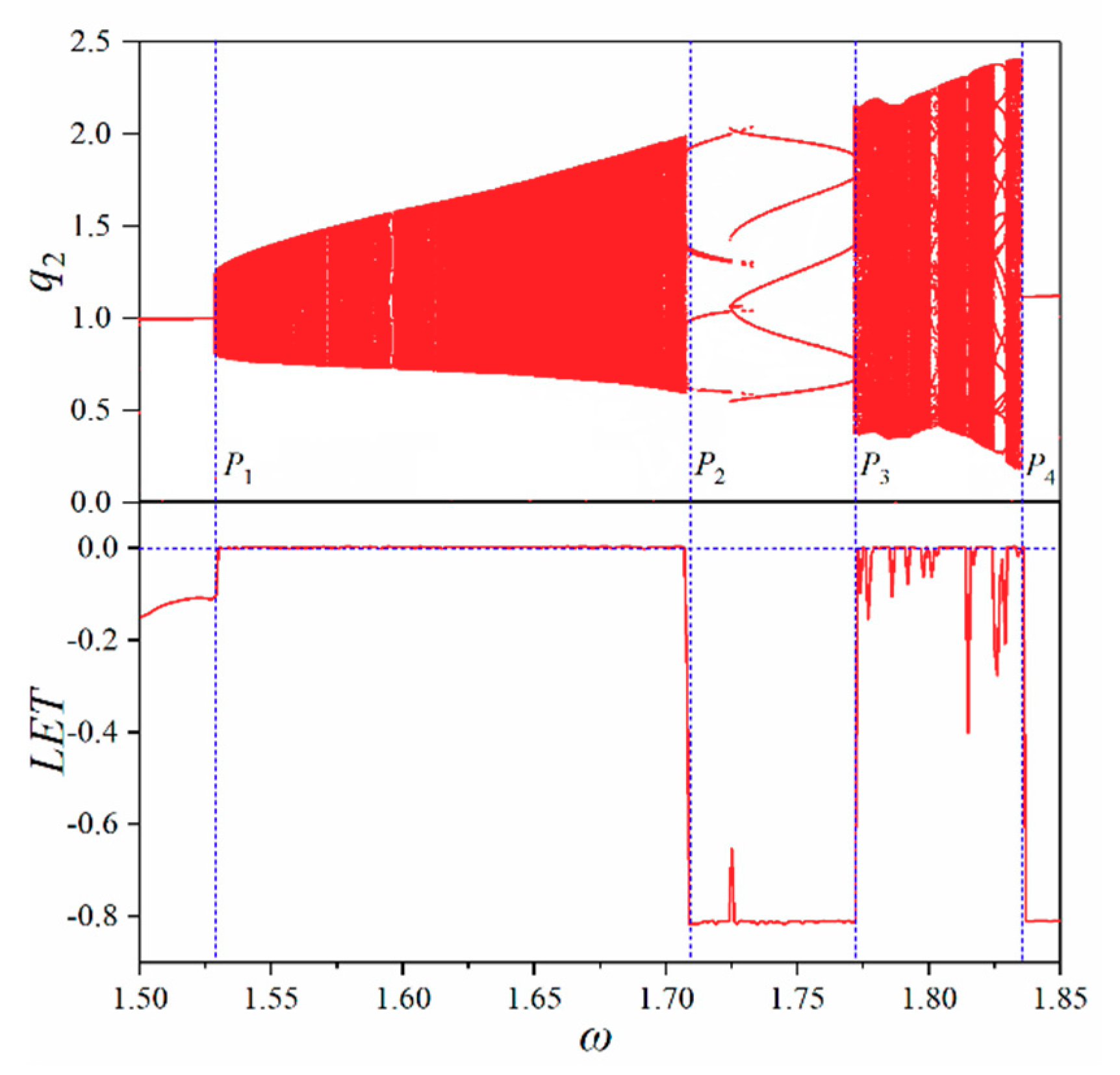
4.3. Transmission Characteristics of the Strong Non-Linear System
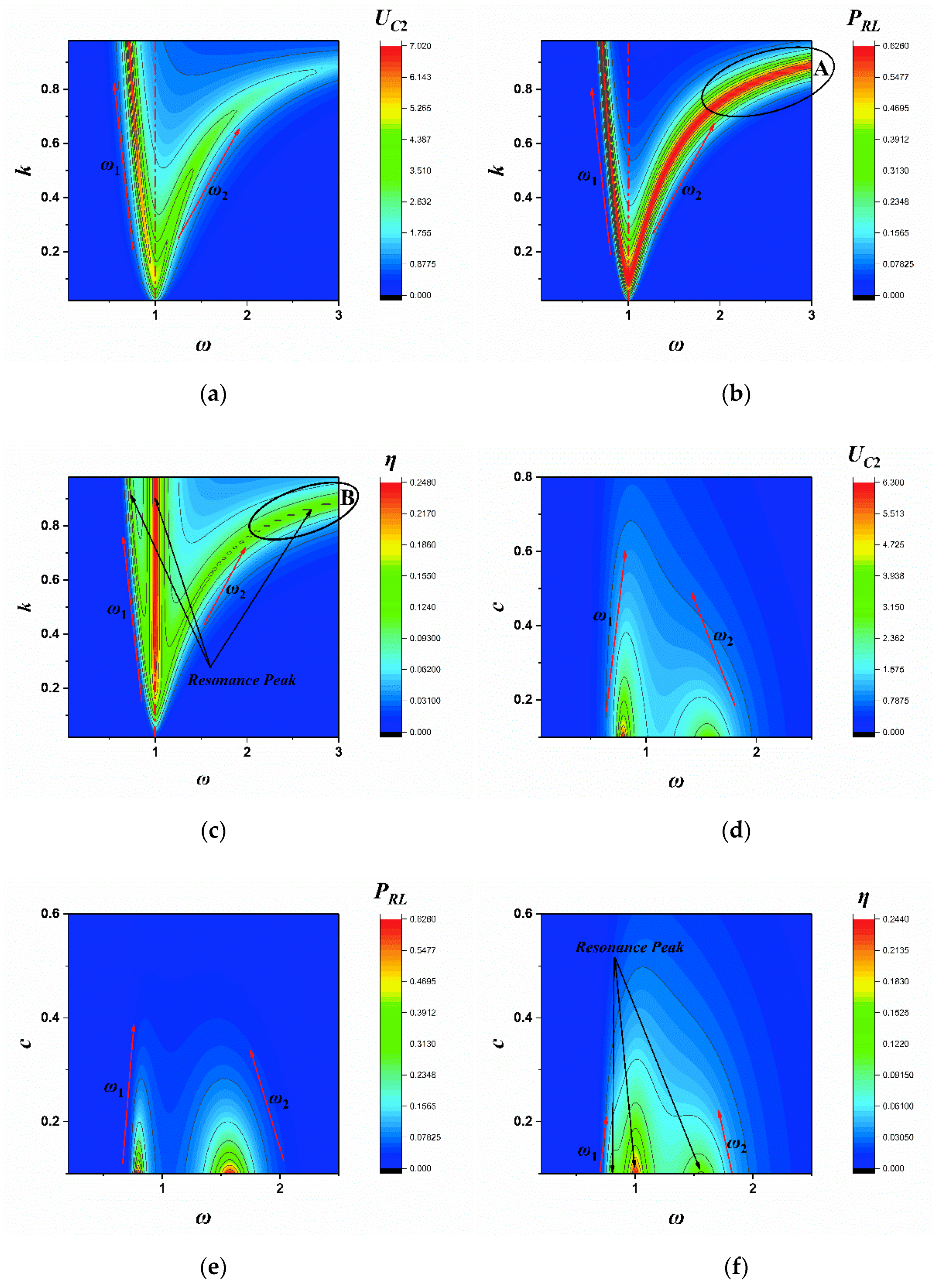
5. Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljacic, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef]
- Jiang, Y.B.; Wang, L.L.; Wang, Y.; Liu, J.W.; Li, X.; Ning, G.D. Analysis, design, and implementation o accurate zvs angle control for ev battery charging in wireless high-power transfer. IEEE Trans. Ind. Electron. 2019, 66, 4075–4085. [Google Scholar] [CrossRef]
- Zhang, Q.Q.; Wang, G.; Chen, J.; Giannakis, G.B.; Liu, Q.W. Mobile energy transfer in internet of things. IEEE Internet Things J. 2019, 6, 9012–9019. [Google Scholar] [CrossRef]
- Shaw, T.; Mitra, D. Metasurface-based radiative near-field wireless power transfer system for implantable medical devices. IET Microw. Antennas Propag. 2019, 13, 1974–1982. [Google Scholar] [CrossRef]
- Houran, M.A.; Yang, X.; Chen, W. Magnetically coupled resonance WPT: Review of compensation topologies, resonator structures with misalignment, and EMI diagnostics. Electronics 2018, 7, 296. [Google Scholar] [CrossRef]
- Barman, D.S.; Reza, A.W.; Kumar, N.; Karim, M.E.; Munir, A.B. Wireless powering by magnetic resonant coupling: Recent trends in wireless power transfer system and its applications. Renew. Sustain. Energy Rev. 2015, 51, 1525–1552. [Google Scholar] [CrossRef]
- Wei, X.; Wang, Z.; Dai, H. A critical review of wireless power transfer via strongly coupled magnetic resonances. Energies 2014, 7, 4316–4341. [Google Scholar] [CrossRef]
- Cannon, B.L.; Hoburg, J.F.; Stancil, D.D.; Goldstein, S.C. Magnetic resonant coupling as a potential means for wireless power transfer to multiple small receivers. IEEE Trans. Power Electron. 2009, 24, 1819–1825. [Google Scholar] [CrossRef]
- Imura, T.; Hori, Y. Maximizing air gap and efficiency of magnetic resonant coupling for wireless power transfer using equivalent circuit and Neumann formula. IEEE Trans. Ind. Electron. 2011, 58, 4746–4752. [Google Scholar] [CrossRef]
- Lee, H.Y.; Park, G.S. Analysis of the resonance characteristics by a variation of coil distance in magnetic resonant wireless power transmission. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Sample, A.P.; Meyer, D.T.; Smith, J.R. Analysis, experimental results, and range adaptation of magnetically coupled resonators for wireless power transfer. IEEE Trans. Ind. Electron. 2011, 58, 544–554. [Google Scholar] [CrossRef]
- Han, C.; Zhang, B.; Fang, Z.; Qiu, D.; Chen, Y.; Xiao, W. Dual-side independent switched capacitor control for wireless power transfer with coplanar coils. Energies 2018, 11, 1472. [Google Scholar] [CrossRef]
- Park, J.; Tak, Y.; Kim, Y.; Nam, S. Investigation of adaptive matching methods for near-field wireless power transfer. IEEE Trans. Antennas Propag. 2011, 59, 1769–1773. [Google Scholar] [CrossRef]
- Tan, L.; Huang, X.; Huang, H.; Zou, Y.; Li, H. Transfer efficiency optimal control of magnetic resonance coupled system of wireless power transfer based on frequency control. Sci. China Technol. Sci. 2011, 54, 1428–1434. [Google Scholar] [CrossRef]
- Anowar, T.I.; Barman, S.D.; Reza, A.W.; Kumar, N. High-efficiency resonant coupled wireless power transfer via tunable impedance matching. Int. J. Electron. 2017, 104, 1607–1625. [Google Scholar] [CrossRef]
- Dang, Z.; Cao, Y.; Abu Qahouq, J.A. Reconfigurable magnetic resonance-coupled wireless power transfer system. IEEE Trans. Power Electron. 2015, 30, 6057–6069. [Google Scholar] [CrossRef]
- Chen, L.; Liu, S.; Zhou, Y.C.; Cui, T.J. An optimizable circuit structure for high-efficiency wireless power transfer. IEEE Trans. Ind. Electron. 2013, 60, 339–349. [Google Scholar] [CrossRef]
- Ishihara, M.; Umetani, K.; Umegami, H.; Hiraki, E.; Yamamoto, M. Quasi-duality between SS and SP topologies of basic electric-field coupling wireless power transfer system. Electron. Lett. 2016, 52, 2057–2059. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Z.; Chen, K. Frequency-splitting analysis of four-coil resonant wireless power transfer. IEEE Trans. Ind. Appl. 2014, 50, 2436–2445. [Google Scholar] [CrossRef]
- Wang, S.; Hu, Z.; Rong, C.; Lu, C.; Tao, X.; Chen, J.; Liu, M. Optimisation analysis of coil configuration and circuit model for asymmetric wireless power transfer system. IET Microw. Antennas Propag. 2018, 12, 1132–1139. [Google Scholar] [CrossRef]
- Lu, Y.L.; Meng, F.Y.; Yang, G.H.; Che, B.J.; Wu, Q.; Sun, L.; Li, J.W. A method of using nonidentical resonant coils for frequency splitting elimination in wireless power transfer. IEEE Trans. Power Electron. 2015, 30, 6097–6107. [Google Scholar] [CrossRef]
- Niu, W.Q.; Chu, J.X.; Gu, W.; Shen, A.D. Exact analysis of frequency splitting phenomena of contactless power transfer systems. IEEE Trans. Circuits I 2013, 60, 1670–1677. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Wang, K.; Chen, W.; Yang, X. A maximum efficiency point tracking control scheme for wireless power transfer systems using magnetic resonant coupling. IEEE Trans. Power Electron. 2015, 30, 3998–4008. [Google Scholar] [CrossRef]
- Fan, X.M.; Mo, X.Y.; Zhang, X. Research Status and Application of Wireless Power Transmission Technology. Proc. CSEE 2015, 35, 2584–2600. [Google Scholar]
- Kim, J.; Jeong, J. Range-Adaptive Wireless Power Transfer Using Multiloop and Tunable Matching Techniques. IEEE Trans. Ind. Electron. 2015, 62, 6233–6241. [Google Scholar] [CrossRef]
- Dai, X.; Sun, Y.; Tang, C.S.; Wang, Z.H.; Su, Y.G. Wireless Power Transfer Technology, 1st ed.; Science Press: Beijing, China, 2017; pp. 22–42. [Google Scholar]
- Zhao, J.Y.; Wang, X.F.; Cui, Y.L.; Zhou, S.N. Topology Optimization and Design Realization of Magnetically-Coupled Resonant Wireless Power Transfer System with LCL-S Structure. J. Electron. Eng. Technol. 2019, 14, 1655–1664. [Google Scholar] [CrossRef]
- Li, L.; Han, J.; Zhang, Q.; Liu, C.; Guo, Z. Nonlinear dynamics and parameter identification of electrostatically coupled resonators. Int. J. Nonlinear Mech. 2019, 110, 104–114. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Farghaly, A.A.M.; Shoreh, A.A.H. A technique for studying a class of fractional-order nonlinear dynamical systems. Int. J. Bifurc. Chaos 2017, 27. [Google Scholar] [CrossRef]
- Peng, H.; He, Q. The effects of the crack location on the whirl motion of a breathing cracked rotor with rotational damping. Mech. Syst. Signal Process. 2019, 123, 626–647. [Google Scholar] [CrossRef]
- Chen, Y.F.; Xiao, W.X.; Guan, Z.P.; Zhang, B.; Qiu, D.Y.; Wu, M.Y. Nonlinear Modeling and Harmonic Analysis of Magnetic Resonant WPT System Based on Equivalent Small Parameter Method. IEEE Trans. Ind. Electron. 2019, 66, 6604–6612. [Google Scholar] [CrossRef]
- Abdelatty, O.; Wang, X.; Mortazawi, A. Position-Insensitive Wireless Power Transfer Based on Nonlinear Resonant Circuits. IEEE Trans. Microw. Theory Tech. 2019, 67, 3844–3855. [Google Scholar] [CrossRef]
| Parameters | Values |
|---|---|
| f1 | 90.79 kHz |
| f2 | 90.92 kHz |
| L1 | 66.56 μH |
| L2 | 66.49 μH |
| C1 | 46.17 nF |
| C2 | 46.09 nF |
| k | f1/Hz (×104) | f2/Hz (×104) |
|---|---|---|
| 0.011 | 9.0353 | 9.1360 |
| 0.028 | 8.9605 | 9.2153 |
| 0.06 | 8.8243 | 9.3708 |
| 0.092 | 8.6941 | 9.5344 |
| 0.127 | 8.5580 | 9.7237 |
| 0.164 | 8.4209 | 9.9365 |
| 0.179 | 8.3672 | 10.027 |
| 0.235 | 8.1753 | 10.387 |
| 0.286 | 8.0115 | 10.752 |
| 0.351 | 7.8164 | 11.275 |
| 0.391 | 7.7032 | 11.642 |
| 0.436 | 7.5816 | 12.098 |
| 0.489 | 7.4454 | 12.709 |
| 0.551 | 7.2951 | 13.559 |
| 0.624 | 7.1292 | 14.816 |
| 0.712 | 6.9436 | 16.929 |
| 0.819 | 6.7363 | 21.355 |
| 0.908 | 6.5773 | 29.953 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, C.; Wang, X.; Ge, W. Frequency Splitting and Transmission Characteristics of MCR-WPT System Considering Non-Linearities of Compensation Capacitors. Electronics 2020, 9, 141. https://doi.org/10.3390/electronics9010141
Liu J, Wang C, Wang X, Ge W. Frequency Splitting and Transmission Characteristics of MCR-WPT System Considering Non-Linearities of Compensation Capacitors. Electronics. 2020; 9(1):141. https://doi.org/10.3390/electronics9010141
Chicago/Turabian StyleLiu, Jun, Chang Wang, Xiaofeng Wang, and Weimin Ge. 2020. "Frequency Splitting and Transmission Characteristics of MCR-WPT System Considering Non-Linearities of Compensation Capacitors" Electronics 9, no. 1: 141. https://doi.org/10.3390/electronics9010141
APA StyleLiu, J., Wang, C., Wang, X., & Ge, W. (2020). Frequency Splitting and Transmission Characteristics of MCR-WPT System Considering Non-Linearities of Compensation Capacitors. Electronics, 9(1), 141. https://doi.org/10.3390/electronics9010141





