A Semidefinite Relaxation Method for Elliptical Location
Abstract
1. Introduction
- We present the negative log-likelihood (NLL) function of the elliptical location estimation problem with multiple transmitters and multiple receivers in a concise form, and then derive the Cramér–Rao bound (CRB) of the problem. This is the theoretical basis for the feasibility analysis of the problem.
- We identify the NLL function minimization as a quadratic optimization problem with multiple quadratic equality/inequality constraints and design its semidefinite relaxation.
- We find the dual problem of the primal SDP problem and give the pseudo-code of the interior-point primal-dual path-following algorithm. With these results, engineers can design customized algorithms themselves, instead of relying on codes provided by mathematicians that are not optimized for a specific problem.
- We theoretically analyze the polynomial time complexity of the algorithm and experimentally confirm that the proposed estimator attains the CRB approximately.
- We cautiously verify the deployability of the algorithm by setting the measurement noise levels far higher than what can be achieved by real systems. Simulation experiments with extreme parameter settings are alternative to the costly field tests.
2. Problem Formulation and Data Model
3. Cramér–Rao Bound
4. Design of the Estimator
4.1. Formulation of MLE as a Quadratic Optimization Problem
4.2. Some Equivalent Transformation
4.3. Semidefinite Relaxation
4.4. Semidefinite Programming Solver
| Algorithm 1 Primal-dual path-following interior-point method. |
|
4.5. Complexity Analysis
5. Results and Discussion
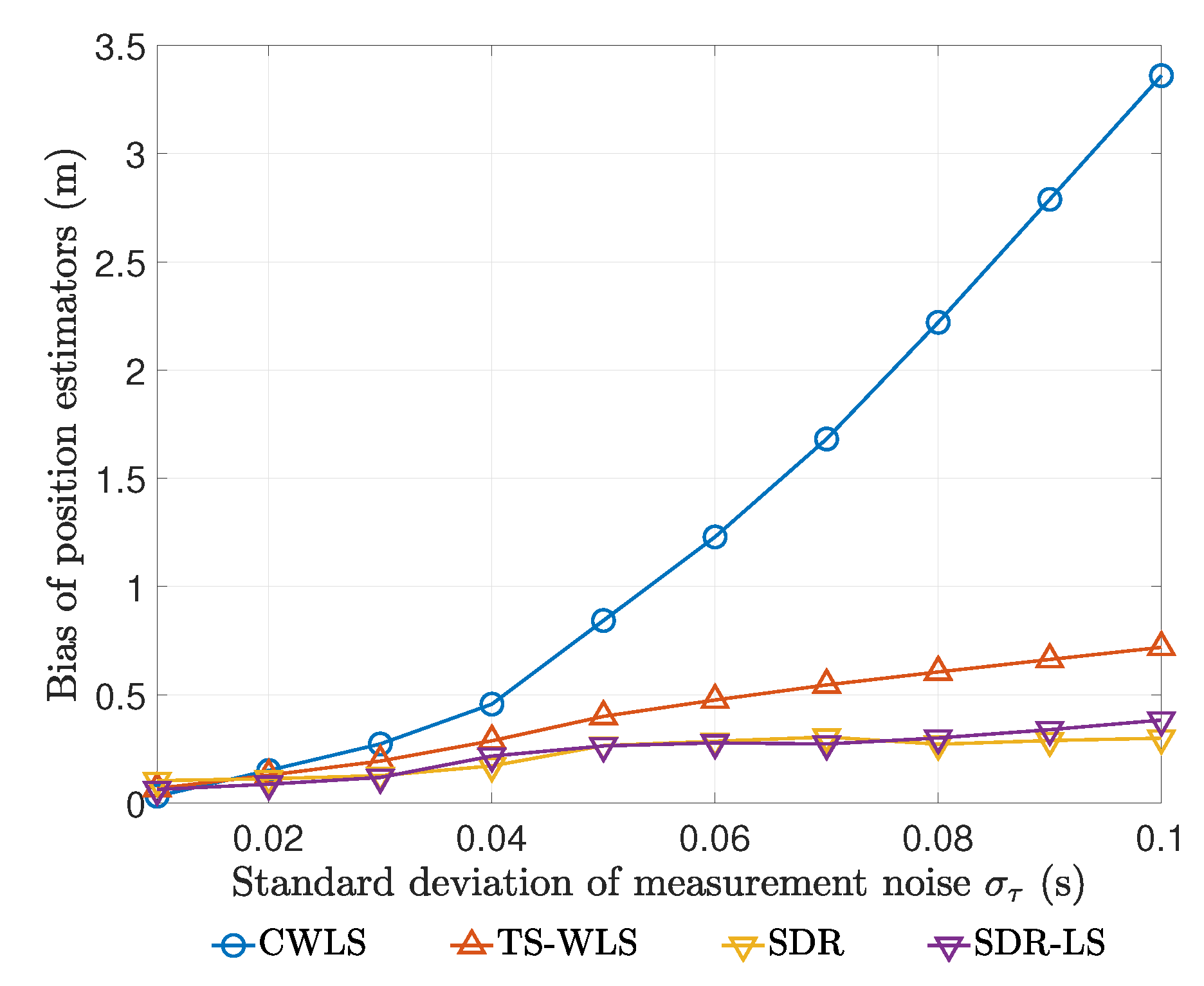
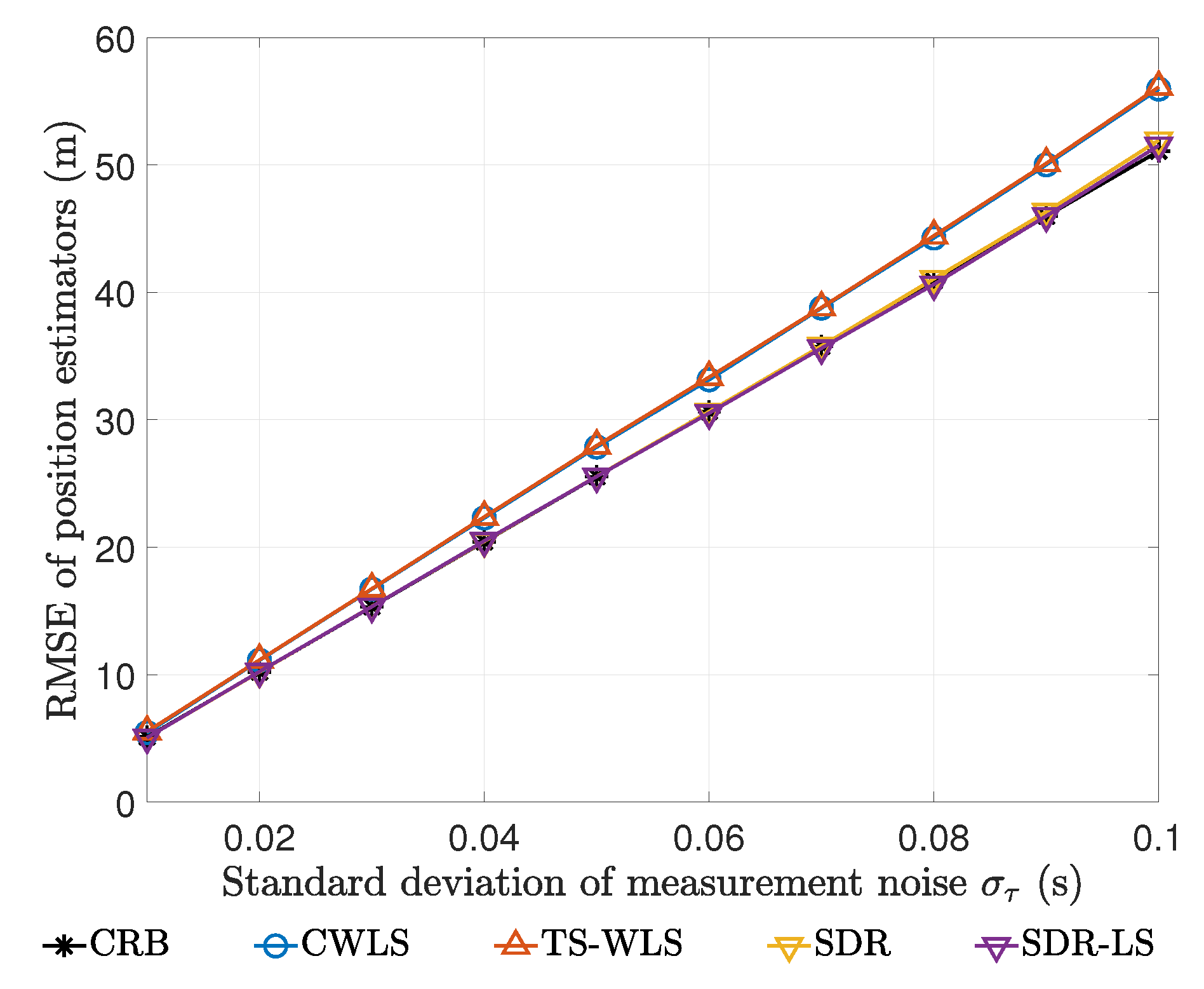
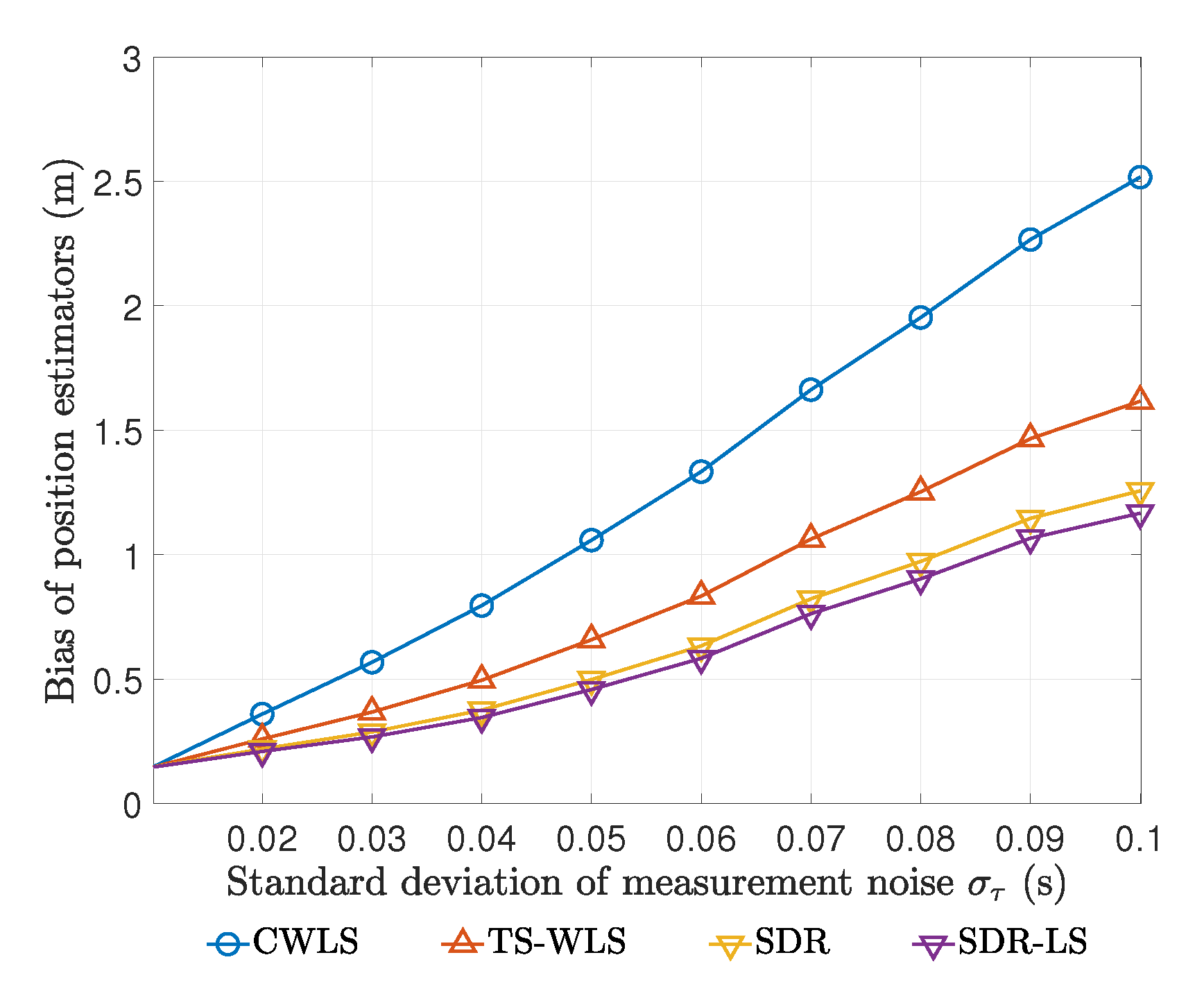
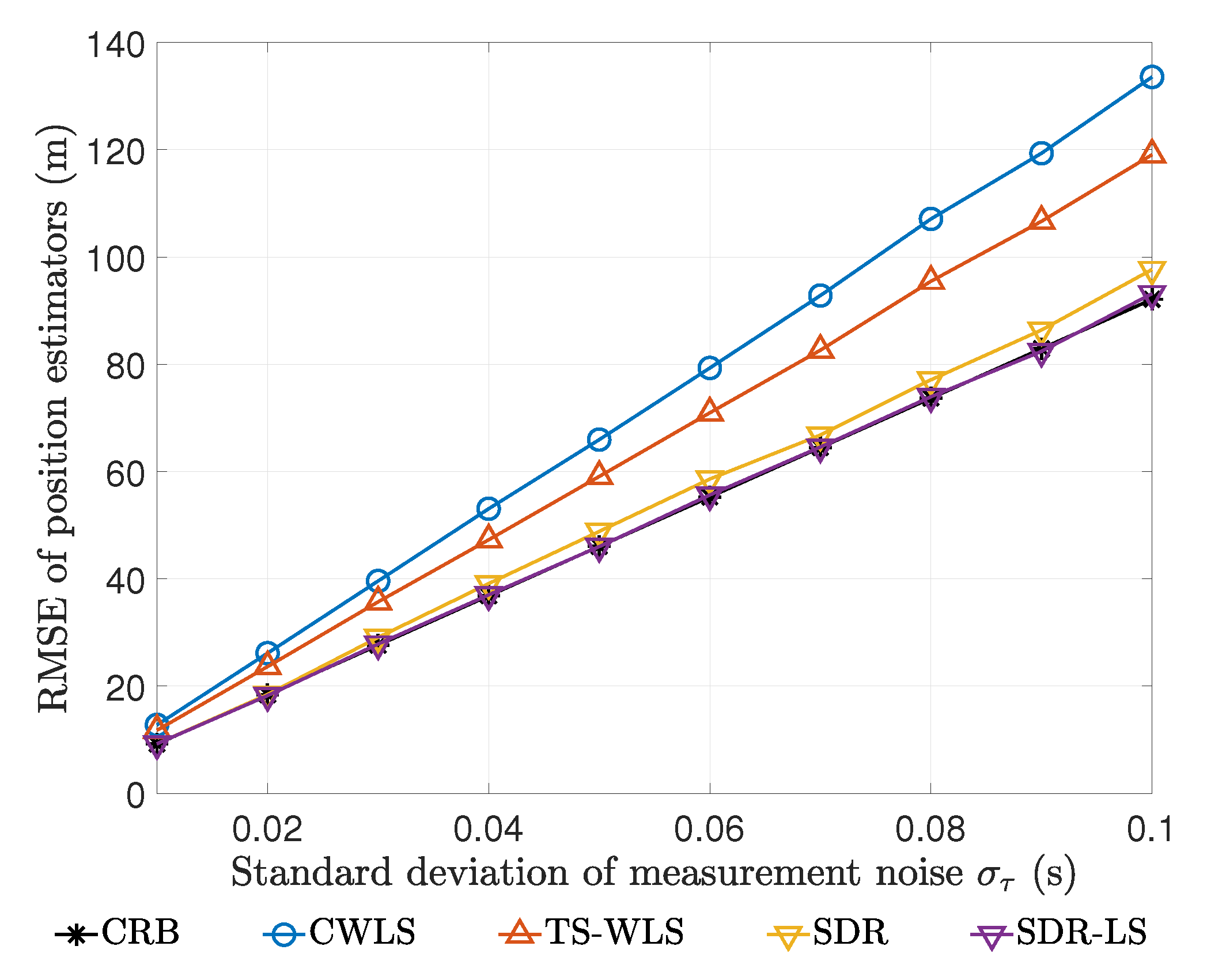
- To ascertain the statistical performance of the proposed SDR estimator, we compared it with several closed-form methods recently proposed, i.e., Yang’s TS-WLS method [21] and Amiri’s CWLS method [20]. For a given estimator of the unknown parameter , its performance is measured by the empirical bias and RMSE, which are defined as follows.where L is the number of Monte Carlo simulations and is the ℓ-th random realization of . In our following experiments, we set and compared the biases and RMSEs of all these estimators at different noise levels.
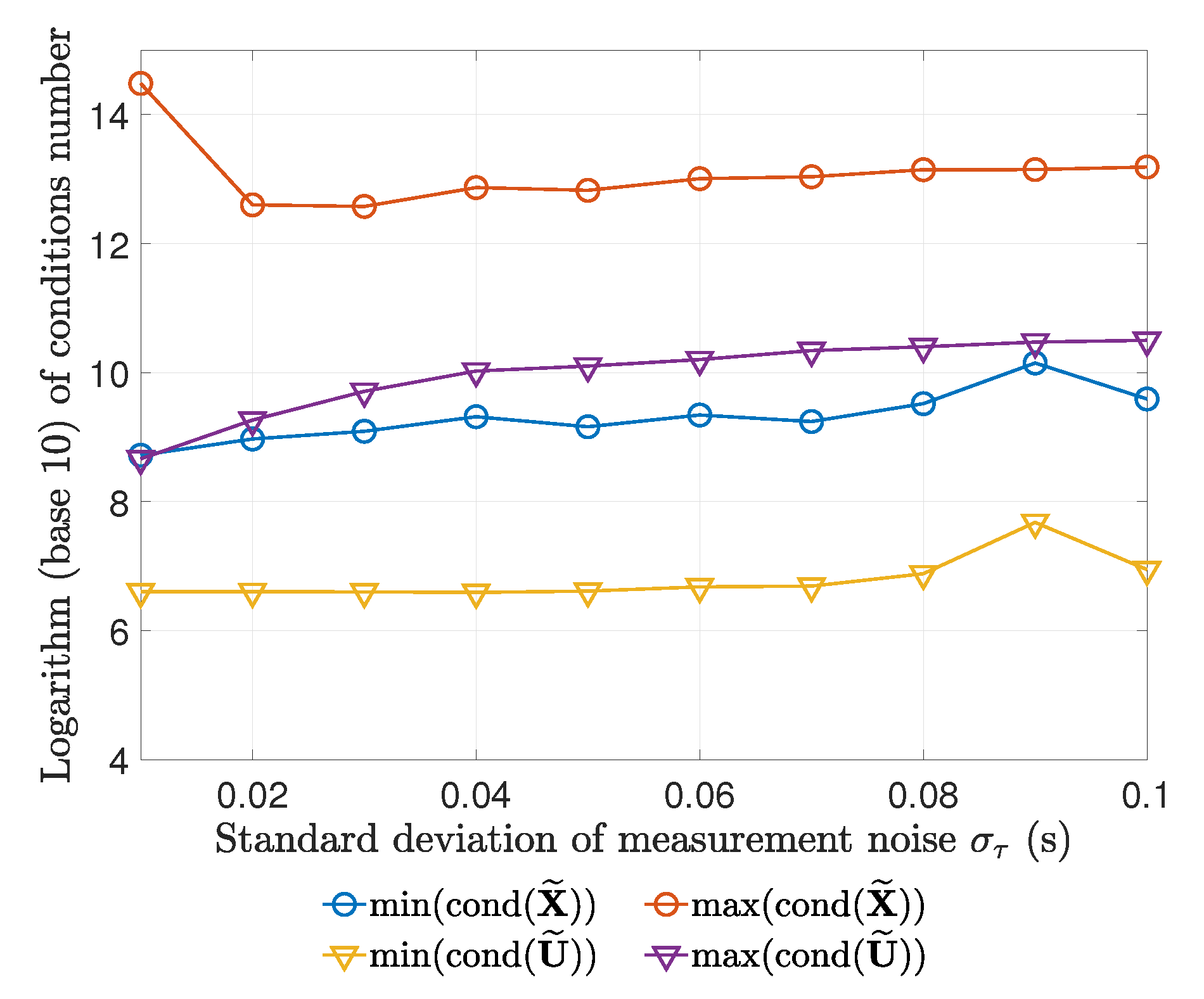
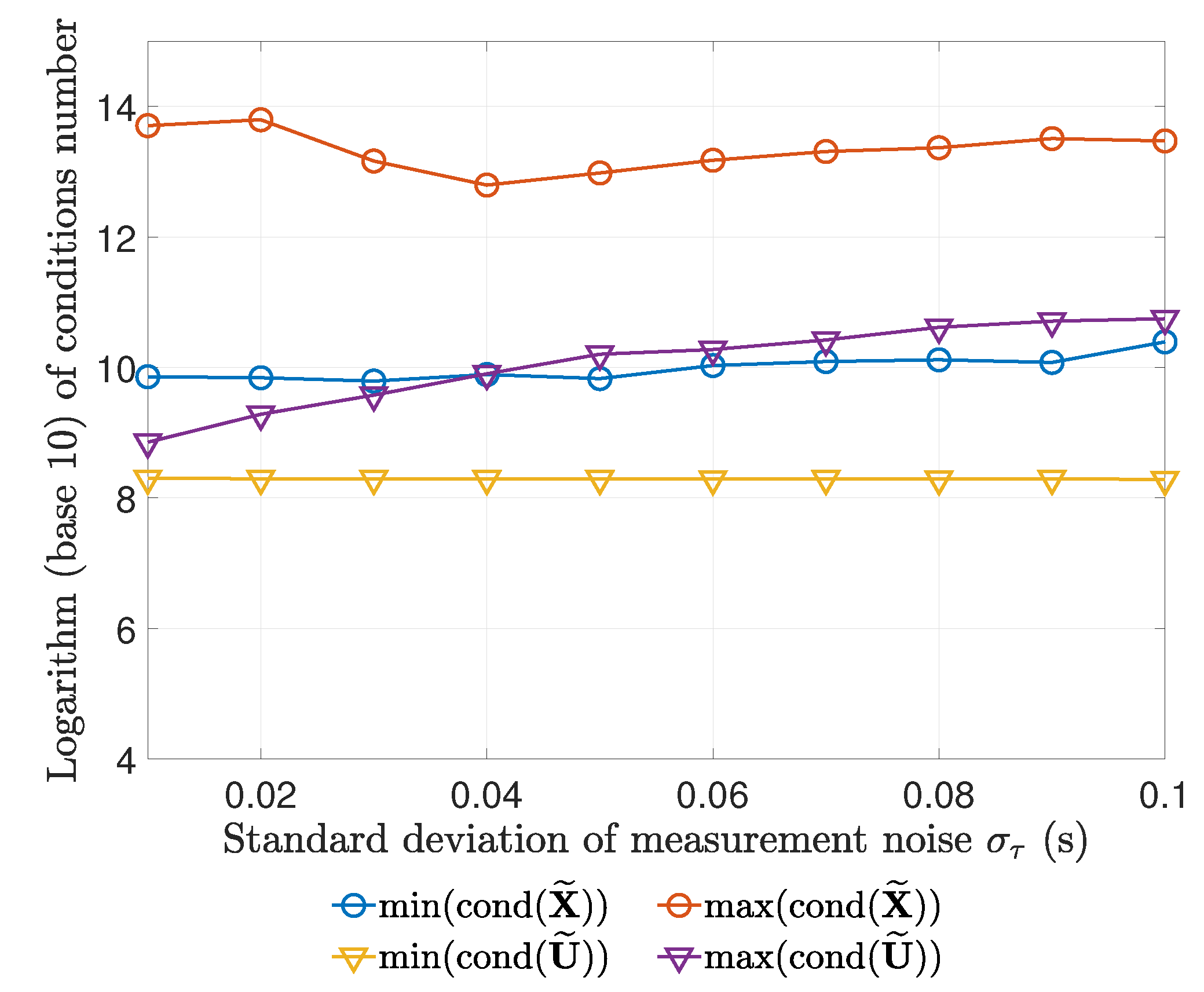
- To measure the tightness of the relaxed optimization model in (16), we recorded the condition numbers of the optimal solutions of and in (17) at different noise levels. The motivation is that if the condition number of a matrix is greater than , then it can be approximated as a rank-1 matrix [44].
- To verify whether the SDR solution needs post-processing, we checked the performance improvement gifted by post-processing using local search under different noise conditions. We used the SDR solution as the initial point for the commercial optimization solver MATLAB function lsqnonlin, and the algorithm for lsqnonlin was set as ‘trust-region-reflective‘. Our estimator with post-processing is simply referred to as SDR-LS.
5.1. Localization Scenarios
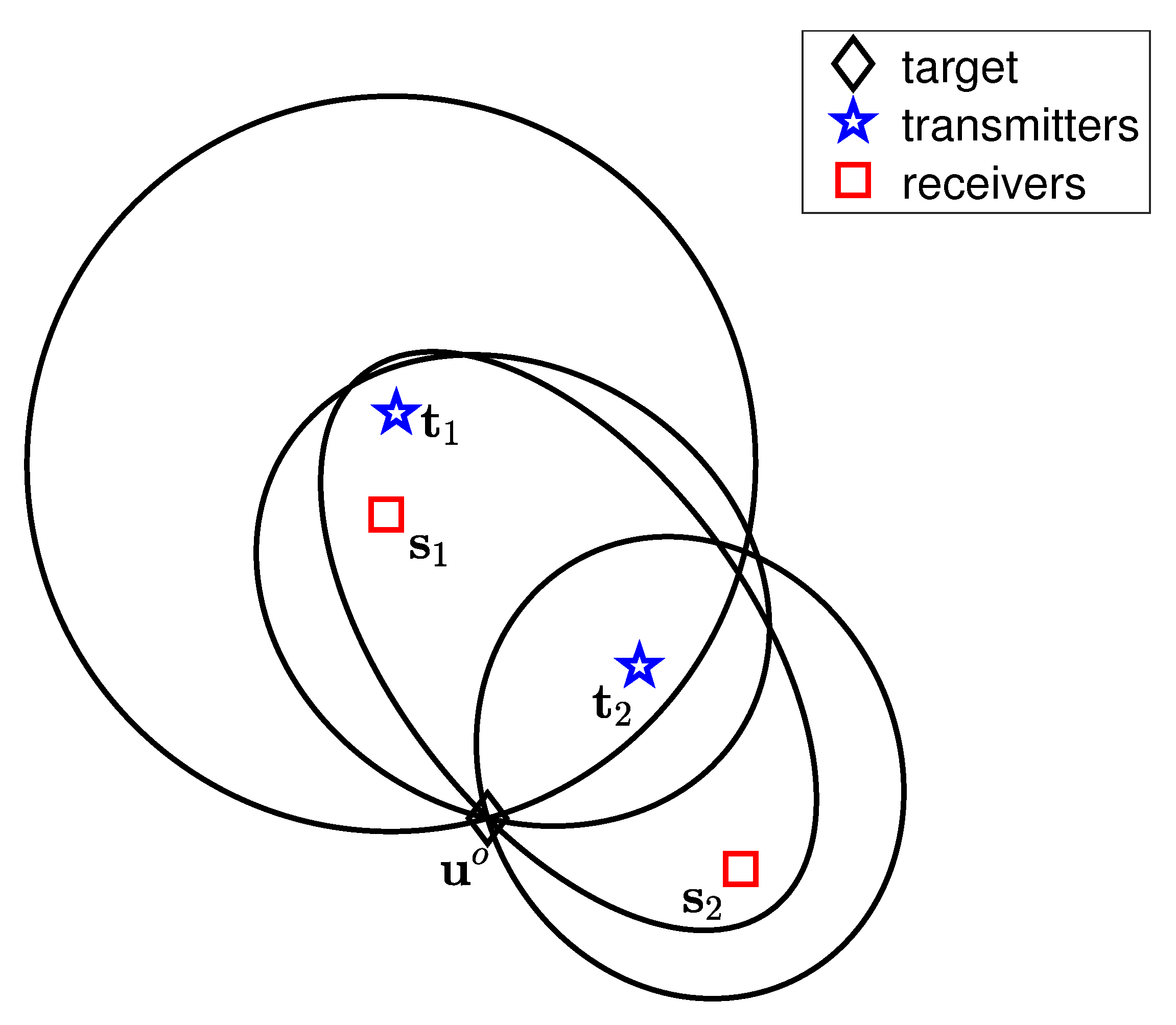
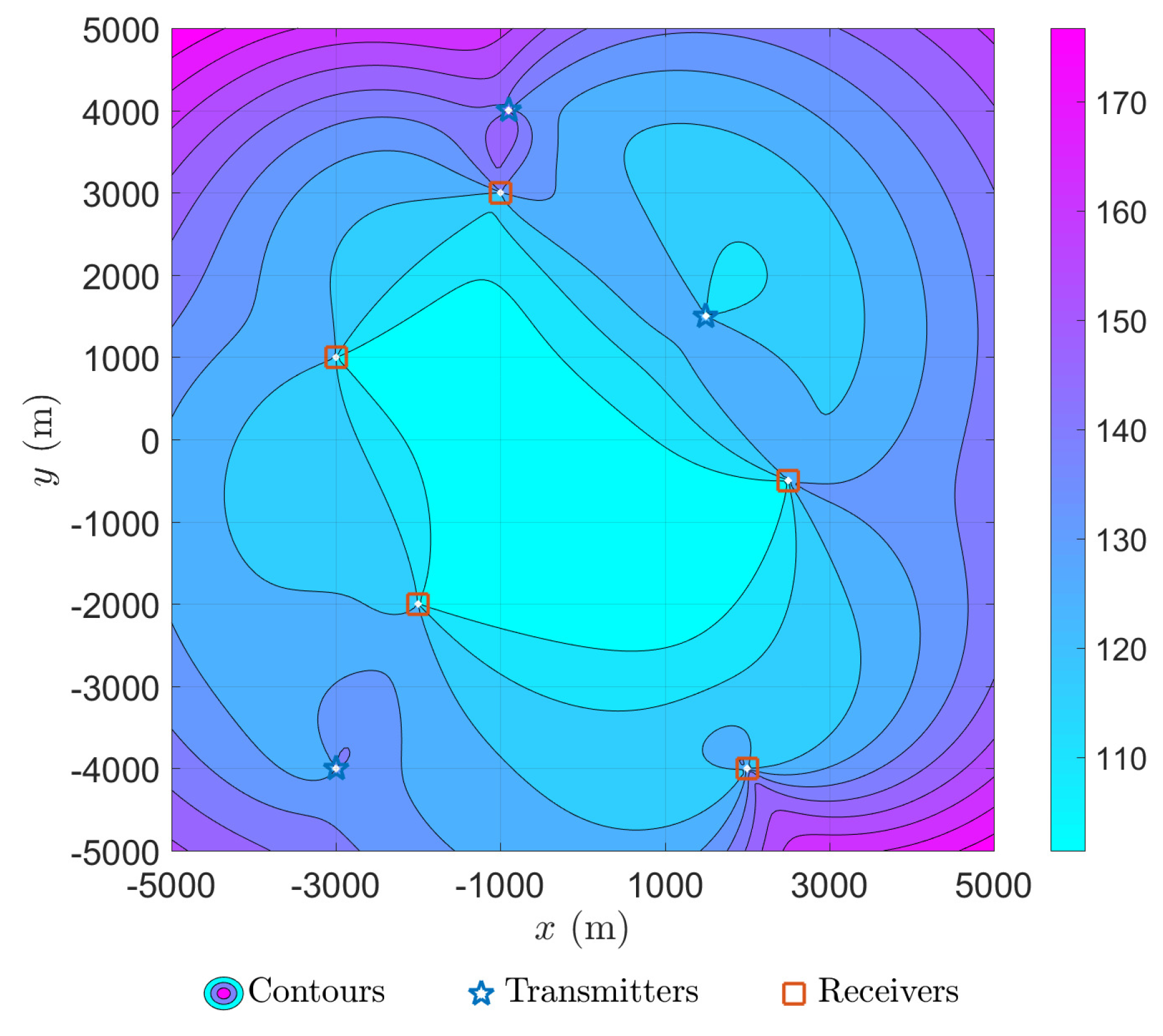
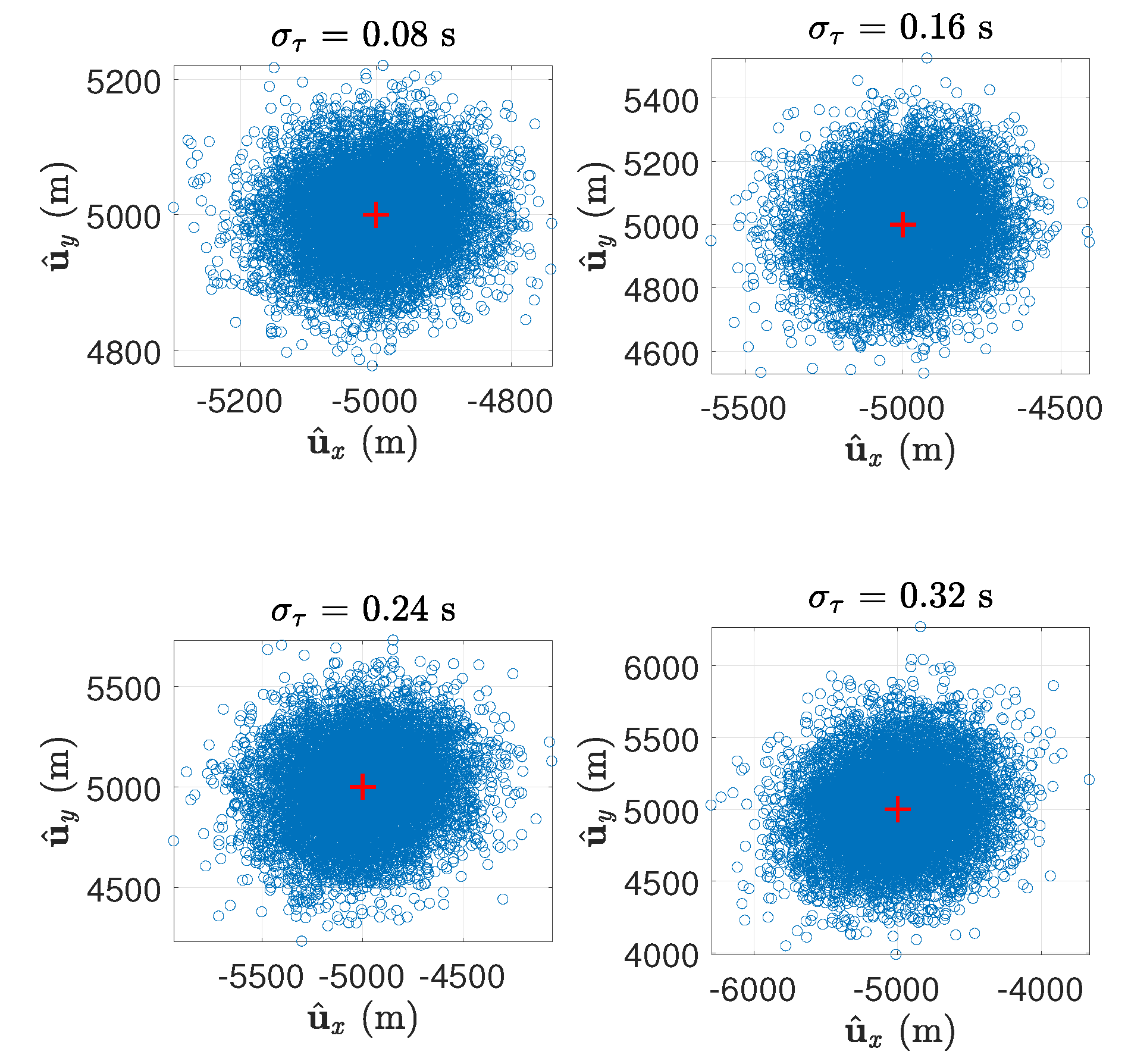
5.2. Visualization of Cramér–Rao Bound and Selection of Testing Points
5.3. Results on the Two Representative Test Points
5.3.1. Results on Easier Test Point
5.3.2. Results on Harder Test Point
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AEL | Asynchronous Elliptical Location |
| AOA | Angle of Arrival |
| CRB | Cramér–Rao Bound |
| CWLS | Constrained Weighted Least-squares |
| FDOA | Frequency Difference of Arrival |
| MLE | Maximum Likelihood Estimator |
| MSE | Mean Square Error |
| NLL | Negative Log-likelihood |
| RMSE | Root-mean-square Error |
| RSS | Received Signal Strength |
| SDP | Semidefinite Programming |
| SDR | Semidefinite Relaxation |
| SEL | Synchronous Elliptical Location |
| SI | Spherical-interpolation |
| SX | Spherical-intersection |
| TDOA | Time Difference of Arrival |
| TOA | Time of Arrival |
| TS-WLS | Two-stage Weighted least-squares |
| WLS | Weighted Least-squares |
References
- Landolsi, M.A.; Khan, H.R.; Al-Ahmari, A.S.; Muqaibel, A.H. On the performance of wireless sensor network time difference of arrival localization under realistic interference and timing estimation errors. Int. J. Distrib. Sens. Netw. 2019, 15, 1–15. [Google Scholar] [CrossRef]
- Sun, Y.; Ho, K.C.; Wan, Q. Solution and analysis of TDOA localization of a near or distant source in closed form. IEEE Trans. Signal Process. 2019, 67, 320–335. [Google Scholar] [CrossRef]
- Wang, T.; Hua, W.; Ke, W. A two-step sequential method for device-free localization using wireless sensor networks. Int. J. Distrib. Sens. Netw. 2019, 15, 1–14. [Google Scholar] [CrossRef]
- Zuo, W.; Xin, J.; Liu, W.; Zheng, N.; Ohmori, H.; Sano, A. Localization of near-field sources based on linear prediction and oblique projection operator. IEEE Trans. Signal Process. 2019, 67, 415–430. [Google Scholar] [CrossRef]
- Otim, T.; Díez, L.E.; Bahillo, A.; Lopez-Iturri, P.; Falcone, F. Effects of the body wearable sensor position on the UWB localization accuracy. Electronics 2019, 8, 1351. [Google Scholar] [CrossRef]
- Hall, D.L.; Narayanan, R.M.; Jenkins, D.M. SDR based indoor beacon localization using 3D probabilistic multipath exploitation and deep learning. Electronics 2019, 8, 1323. [Google Scholar] [CrossRef]
- Mendrzik, R.; Wymeersch, H.; Bauch, G.; Abu-Shaban, Z. Harnessing NLOS components for position and orientation estimation in 5G millimeter wave MIMO. IEEE Trans. Wirel. Commun. 2019, 18, 93–107. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Dogancay, K. Closed-form algebraic solutions for angle-of-arrival source localization with Bayesian priors. IEEE Trans. Wirel. Commun. 2019, 18, 3827–3842. [Google Scholar] [CrossRef]
- Liu, M.; Ma, L.; Wang, N.; Zhang, Y.; Yang, Y.; Wang, H. Passive multiple target indoor localization based on joint interference cancellation in an RFID system. Electronics 2019, 8, 426. [Google Scholar] [CrossRef]
- Zhou, B.; Liu, A.; Lau, V. Joint user location and orientation estimation for visible light communication systems with unknown power emission. IEEE Trans. Wirel. Commun. 2019, 18, 5181–5195. [Google Scholar] [CrossRef]
- Tran, H.Q.; Ha, C. Fingerprint-based indoor positioning system using visible light communication—A novel method for multipath reflections. Electronics 2019, 8, 63. [Google Scholar] [CrossRef]
- Sinha, R.S.; Hwang, S.H. Comparison of CNN applications for RSSI-based fingerprint indoor localization. Electronics 2019, 8, 989. [Google Scholar] [CrossRef]
- Li, J.; Gao, X.; Hu, Z.; Wang, H.; Cao, T.; Yu, L. Indoor localization method based on regional division with IFCM. Electronics 2019, 8, 559. [Google Scholar] [CrossRef]
- Haider, A.; Wei, Y.; Liu, S.; Hwang, S.H. Pre- and post-processing algorithms with deep learning classifier for Wi-Fi fingerprint-based indoor positioning. Electronics 2019, 8, 195. [Google Scholar] [CrossRef]
- Xu, C.; Ji, M.; Qi, Y.; Zhou, X. MCC-CKF: A distance constrained Kalman filter method for indoor TOA localization applications. Electronics 2019, 8, 478. [Google Scholar] [CrossRef]
- Aditya, S.; Dhillon, H.S.; Molisch, A.F.; Buehrer, R.M.; Behairy, H.M. Characterizing the impact of SNR heterogeneity on time-of-arrival-based localization outage probability. IEEE Trans. Wirel. Commun. 2019, 18, 637–649. [Google Scholar] [CrossRef]
- Wang, G.; Ho, K.C. Convex relaxation methods for unified near-field and far-field TDOA-based localization. IEEE Trans. Wirel. Commun. 2019, 18, 2346–2360. [Google Scholar] [CrossRef]
- Yan, J.; Tiberius, C.C.J.M.; Janssen, G.J.M.; Teunissen, P.J.G.; Bellusci, G. Review of range-based positioning algorithms. IEEE Aerosp. Electron. Syst. Mag. 2013, 28, 2–27. [Google Scholar] [CrossRef]
- Zhang, Y.; Ho, K.C. Multistatic localization in the absence of transmitter position. IEEE Trans. Signal Process. 2019, 67, 4745–4760. [Google Scholar] [CrossRef]
- Amiri, R.; Behnia, F.; Sadr, M.A.M. Exact solution for elliptic localization in distributed MIMO radar systems. IEEE Trans. Veh. Technol. 2018, 67, 1075–1086. [Google Scholar] [CrossRef]
- Yang, L.; Yang, L.; Ho, K.C. Moving target localization in multistatic sonar by differential delays and Doppler shifts. IEEE Signal Process. Lett. 2016, 23, 1160–1164. [Google Scholar] [CrossRef]
- Rui, L.; Ho, K.C. Efficient closed-form estimators for multistatic sonar localization. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 600–614. [Google Scholar] [CrossRef]
- Malanowski, M.; Kulpa, K. Two methods for target localization in multistatic passive radar. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 572–580. [Google Scholar] [CrossRef]
- Gogineni, S.; Nehorai, A. Target estimation using sparse modeling for distributed MIMO radar. IEEE Trans. Signal Process. 2011, 59, 5315–5325. [Google Scholar] [CrossRef]
- Zhou, Y.; Law, C.L.; Guan, Y.L.; Chin, F. Indoor elliptical localization based on asynchronous UWB range measurement. IEEE Trans. Instrum. Meas. 2011, 60, 248–257. [Google Scholar] [CrossRef]
- Simakov, S. Localization in airborne multistatic sonars. IEEE J. Ocean. Eng. 2008, 33, 278–288. [Google Scholar] [CrossRef]
- Sandys-Wunsch, M.; Hazen, M.G. Multistatic localization error due to receiver positioning errors. IEEE J. Ocean. Eng. 2002, 27, 328–334. [Google Scholar] [CrossRef]
- Rui, L.; Ho, K.C. Elliptic localization: Performance study and optimum receiver placement. IEEE Trans. Signal Process. 2014, 62, 4673–4688. [Google Scholar] [CrossRef]
- Monica, S.; Bergenti, F. Hybrid indoor localization using WiFi and UWB technologies. Electronics 2019, 8, 334. [Google Scholar] [CrossRef]
- Smith, J.O.; Abel, J.S. Closed-form least-squares source location estimation from range-difference measurements. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1661–1669. [Google Scholar] [CrossRef]
- Schau, H.; Robinson, A. Passive source localization employing intersecting spherical surfaces from time-of-arrival differences. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1223–1225. [Google Scholar] [CrossRef]
- Einemo, M.; So, H.C. Weighted least squares algorithm for target localization in distributed MIMO radar. Signal Process. 2015, 115, 144–150. [Google Scholar] [CrossRef]
- Godrich, H.; Haimovich, A.M.; Blum, R.S. Target localization accuracy gain in MIMO radar-based systems. IEEE Trans. Inf. Theory 2010, 56, 2783–2803. [Google Scholar] [CrossRef]
- Chan, Y.T.; Ho, K.C. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef]
- Wang, Q.; Li, T.; Feng, R.; Yang, C. An efficient large resource-user scale SCMA codebook design method. IEEE Commun. Lett. 2019, 23, 1787–1790. [Google Scholar] [CrossRef]
- Jiang, Y.; Zou, Y.; Guo, H.; Tsiftsis, T.A.; Bhatnagar, M.R.; de Lamare, R.C.; Yao, Y.D. Joint power and bandwidth allocation for energy-efficient heterogeneous cellular networks. IEEE Trans. Commun. 2019, 67, 6168–6178. [Google Scholar] [CrossRef]
- Zhu, F.; Gao, F.; Eldar, Y.C.; Qian, G. Robust simultaneous wireless information and power transfer in beamspace massive MIMO. IEEE Trans. Wireless Commun. 2019, 18, 4199–4212. [Google Scholar] [CrossRef]
- Luo, Z.; Ma, W.; So, A.; Ye, Y.; Zhang, S. Semidefinite relaxation of quadratic optimization problems. IEEE Signal Process. Mag. 2010, 27, 20–34. [Google Scholar] [CrossRef]
- Luo, Z. Applications of convex optimization in signal processing and digital communication. Math. Progr. 2003, 97, 177–207. [Google Scholar] [CrossRef]
- Nesterov, Y. Lectures on convex optimization. In Springer Optimization and Its Applications; Springer Nature Switzerland AG: Basel, Switzerland, 2018; Volume 137. [Google Scholar]
- Ben-Tal, A.; Nemirovski, A. Lectures on Modern Convex Optimization: Analysis, Algorithms, and Engineering Applications; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2001. [Google Scholar]
- Hernandez, M. Novel maximum likelihood approach for passive detection and localisation of multiple emitters. EURASIP J. Adv. Signal Process. 2017, 2017. [Google Scholar] [CrossRef]
- Yan, Y.; Shen, X.; Hua, F.; Zhong, X. On the semidefinite programming algorithm for energy-based acoustic source localization in sensor networks. IEEE Sens. J. 2018, 18, 8835–8846. [Google Scholar] [CrossRef]
- Wang, G.; Li, Y.; Wang, R. New semidefinite relaxation method for acoustic energy-based source localization. IEEE Sens. J. 2013, 13, 1514–1521. [Google Scholar] [CrossRef]
- Wang, G. A semidefinite relaxation method for energy-based source localization in sensor networks. IEEE Trans. Veh. Technol. 2011, 60, 2293–2301. [Google Scholar] [CrossRef]
- Chan, F.K.W.; So, H.C.; Ma, W.K.; Lui, K.W. A flexible semi-definite programming approach for source localization problems. Digit. Signal Process. 2013, 23, 601–609. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, G.; Ho, K.C. Sensor network-based rigid body localization via semi-definite relaxation using arrival time and doppler measurements. IEEE Trans. Wirel. Commun. 2019, 18, 1011–1025. [Google Scholar] [CrossRef]
- Meng, C.; Ding, Z.; Dasgupta, S. A semidefinite programming approach to source localization in wireless sensor networks. IEEE Signal Process. Lett. 2008, 15, 253–256. [Google Scholar] [CrossRef]
- Guo, X.; Chu, L.; Sun, X. Accurate localization of multiple sources using semidefinite programming based on incomplete range matrix. IEEE Sens. J. 2016, 16, 5319–5324. [Google Scholar] [CrossRef]
- Jia, C.; Yin, J.; Wang, D.; Wang, Y.; Zhang, L. Semidefinite relaxation algorithm for multisource localization using TDOA measurements with range constraints. Wirel. Commun. Mob. Comput. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, H.; Wan, Q. Joint synchronization and localization in wireless sensor networks using semidefinite programming. IEEE Internet Things J. 2018, 5, 199–205. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y. An efficient semidefinite relaxation algorithm for moving source localization using TDOA and FDOA measurements. IEEE Commun. Lett. 2017, 21, 80–83. [Google Scholar] [CrossRef]
- Wang, G.; So, A.M.C.; Li, Y. Robust convex approximation methods for TDOA-based localization under NLOS conditions. IEEE Trans. Signal Process. 2016, 64, 3281–3296. [Google Scholar] [CrossRef]
- Shi, X.; Anderson, B.D.O.; Mao, G.; Yang, Z.; Chen, J.; Lin, Z. Robust localization using time difference of arrivals. IEEE Signal Process. Lett. 2016, 23, 1320–1324. [Google Scholar] [CrossRef]
- Gholami, M.R.; Gezici, S.; Strom, E.G. A concave-convex procedure for TDOA based positioning. IEEE Commun. Lett. 2013, 17, 765–768. [Google Scholar] [CrossRef]
- Wang, G.; Li, Y.; Ansari, N. A semidefinite relaxation method for source localization using TDOA and FDOA measurements. IEEE Trans. Veh. Technol. 2013, 62, 853–862. [Google Scholar] [CrossRef]
- Xu, E.; Ding, Z.; Dasgupta, S. Reduced complexity semidefinite relaxation algorithms for source localization based on time difference of arrival. IEEE Trans. Mob. Comput. 2011, 10, 1276–1282. [Google Scholar] [CrossRef]
- Lui, K.W.K.; Chan, F.K.W.; So, H.C. Semidefinite programming approach for range-difference based source localization. IEEE Trans. Signal Process. 2009, 57, 1630–1633. [Google Scholar] [CrossRef]
- Lui, K.W.K.; Chan, F.K.W.; So, H.C. Accurate time delay estimation based passive localization. Signal Process. 2009, 89, 1835–1838. [Google Scholar] [CrossRef]
- Yang, K.; Wang, G.; Luo, Z.Q. Efficient convex relaxation methods for robust target localization by a sensor network using time differences of arrivals. IEEE Trans. Signal Process. 2009, 57, 2775–2784. [Google Scholar] [CrossRef]
- Van Trees, H.L.; Bell, K.L.; Tian, Z. Detection, Estimation, and Modulation Theory Part I: Detection, Estimation, and Filtering Theory; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Beck, A.; Stoica, P.; Li, J. Exact and approximate solutions of source localization problems. IEEE Trans. Signal Process. 2008, 56, 1770–1778. [Google Scholar] [CrossRef]
- Vandenberghe, L.; Boyd, S. Semidefinite programming. SIAM Rev. 1996, 38, 49–95. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Convex Optimization Algorithms; Athena Scientific: Nashua, NH, USA, 2015. [Google Scholar]
- Grant, M.; Boyd, S. CVX: MATLAB Software for Disciplined Convex Programming, Version 2.1. 2014. Available online: http://cvxr.com/cvx (accessed on 9 January 2020).
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
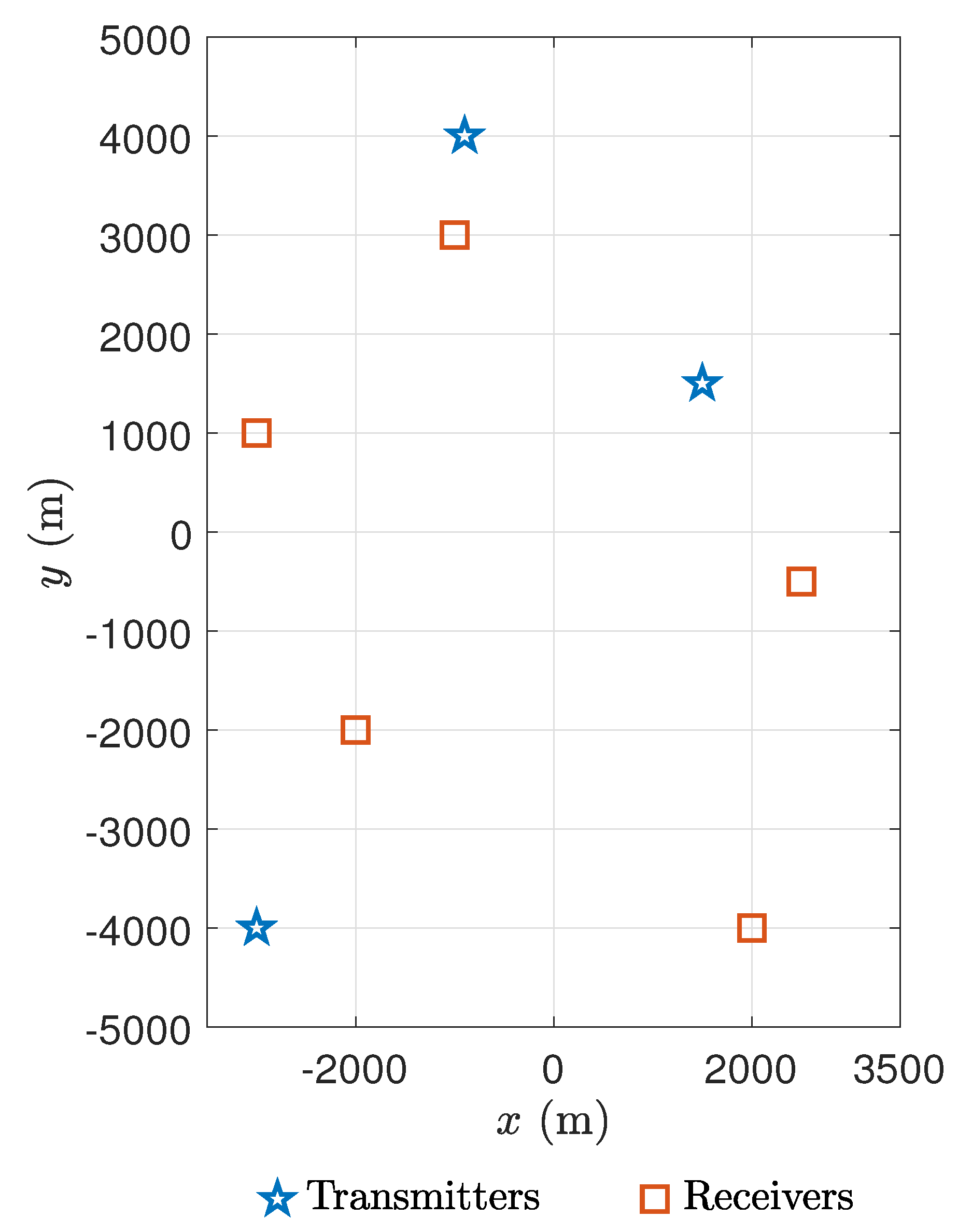
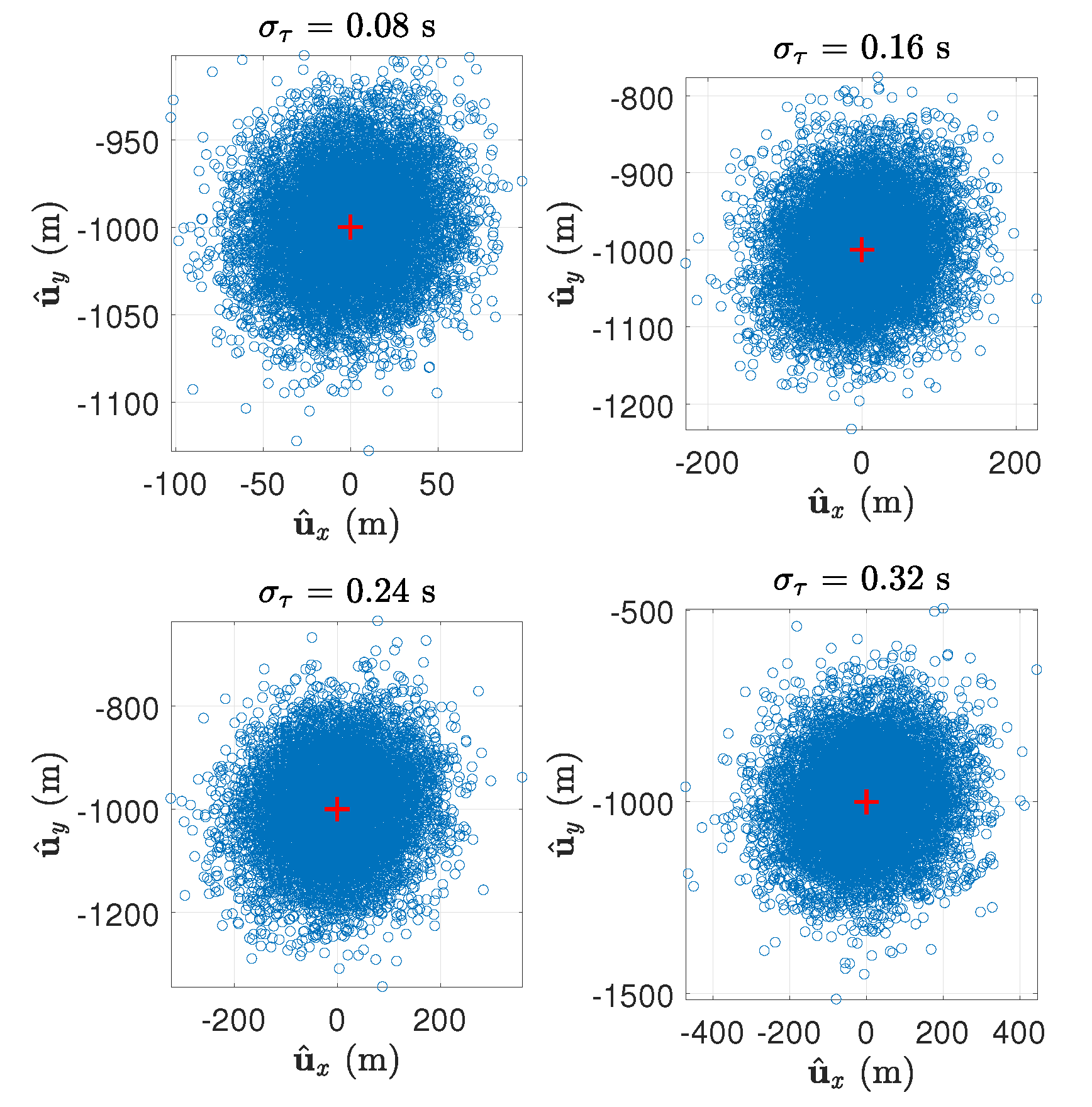
| Transmitter/Receiver No. | Position Coordinates (m) |
|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Ding, Y.; Yang, L. A Semidefinite Relaxation Method for Elliptical Location. Electronics 2020, 9, 128. https://doi.org/10.3390/electronics9010128
Wang X, Ding Y, Yang L. A Semidefinite Relaxation Method for Elliptical Location. Electronics. 2020; 9(1):128. https://doi.org/10.3390/electronics9010128
Chicago/Turabian StyleWang, Xin, Ying Ding, and Le Yang. 2020. "A Semidefinite Relaxation Method for Elliptical Location" Electronics 9, no. 1: 128. https://doi.org/10.3390/electronics9010128
APA StyleWang, X., Ding, Y., & Yang, L. (2020). A Semidefinite Relaxation Method for Elliptical Location. Electronics, 9(1), 128. https://doi.org/10.3390/electronics9010128





