Numerical Analysis on Effective Mass and Traps Density Dependence of Electrical Characteristics of a-IGZO Thin-Film Transistors

Abstract

We have investigated the effect of electron effective mass (m_e*) and tail acceptor-like edge traps density (N_TA) on the electrical characteristics of amorphous-InGaZnO (a-IGZO) thin-film transistors (TFTs) through numerical simulation. To examine the credibility of our simulation, we found that by adjusting m_e* to 0.34 of the free electron mass (m_o), we can preferentially derive the experimentally obtained electrical properties of conventional a-IGZO TFTs through our simulation. Our initial simulation considered the effect of m_e* on the electrical characteristics independent of N_TA. We varied the m_e* value while not changing the other variables related to traps density not dependent on it. As m_e* was incremented to 0.44 m_o, the field-effect mobility (µ_fe) and the on-state current (I_on) decreased due to the higher sub-gap scattering based on electron capture behavior. However, the threshold voltage (V_th) was not significantly changed due to fixed effective acceptor-like traps (N_TA). In reality, since the magnitude of N_TA was affected by the magnitude of m_e*, we controlled m_e* together with N_TA value as a secondary simulation. As the magnitude of both m_e* and N_TA increased, µ_fe and Ion deceased showing the same phenomena as the first simulation. The magnitude of V_th was higher when compared to the first simulation due to the lower conductivity in the channel. In this regard, our simulation methods showed that controlling m_e* and N_TA simultaneously would be expected to predict and optimize the electrical characteristics of a-IGZO TFTs more precisely.

1. Introduction

Metal-oxide semiconductor-based thin-film transistors (TFTs) have been highlighted as the future technology for achieving organic light-emitting diode (OLED) and micro LED backplane applications for high-resolution, flexibility, low temperature processes, commercial display, and low power consumption [1,2]. In particular, amorphous indium-gallium-zinc-oxide (a-IGZO) has been identified as a promising candidate due to the high mobility, flexibility, low-temperature processing capability, uniformity, high on-state/off-states current ratio (I_on/I_off), and easily controlled electrical characteristics by changing its chemical composition [3,4]. In order to take advantage of these properties, properties such as orbital superposition, oxygen vacancy states (V_o), peroxide states, and hydrogen complex had been demonstrated [5,6,7,8]. Among these, the effective mass (m_r*) is important for the improvement of the hall mobility in the oxide semiconductor-based TFT [9,10,11]. However, it is difficult to understand the effect of m_r* on carrier transport because of the compensating potential energy caused due to internal force in the lattice [12]. Thus, it is essential for simulation studies to analyze and understand the effect of m_r*. Simulation of a-IGZO TFTs is difficult when compared to c-Si-based metal oxide semiconductor field-effect transistors (MOSFETs) because of the need to consider many electrical parameters and chemical properties such as their amorphous phase, chemical properties, and ionic bonding properties [5,6,7,8]. Nevertheless, the simulation studies related to the electrical characteristics of a-IGZO TFTs have been studied in detail [13,14,15]. By applying these studies and theories, we could understand the effects of m_r* in a-IGZO TFTs. Therefore, it is necessary to study the change in the electrical characteristic due to the change in m_r*. Thus, further simulation-based research was required to fully identify the mechanisms that control the electrical characteristics of a-IGZO TFTs.

In this work, we have investigated the electron effective mass (m_e*) and tail acceptor-like edge traps density (N_TA) in the sub-gap density of states (DOS) using the technology computer-aided design (TCAD) simulations. At m_e* of 0.34 free electron mass (m_o) [5], we can preferentially derive the very similar simulated results as the electrical characteristics of experimental a-IGZO TFTs [3]. After optimizing the parameters utilized to model results similar to the experiment, we controlled m_e* to analyze the effects of m_e* on the electrical characteristics of the a-IGZO TFT through energy band analysis. By changing only m_e*, the effect on various electrical characteristics such as field-effect mobility (μ_fe), on–state current (I_on), and threshold voltage (V_th) changed, since the probability of electron capture also changed. Furthermore, in order to satisfy the boundary condition (BC), N_TA was varied according to m_e*. As a result, we obtained the electrical characteristics varied as a function m_e* and N_TA and analyzed the effective carrier mechanism related to acceptor-like traps. Therefore, it is expected that this work could be utilized to obtain the optimized electrical performance of a-IGZO TFTs for next-generation backplane applications.

2. Simulation Methodology and Semiconductor Mechanisms

The hall mobility property of oxide semiconductors can be explained by the orbital superposition [5,10]. These can vary depending on the oxide semiconductor material combination and chemical composition ratio [11]. In addition, it can be explained by varying the effective mass [12]. The effective mass is defined by quantum mechanics:

$${\nabla }^2\mathsf{\psi }+\frac{2{\mathrm{m}}_{\mathrm{o}}}{\hslash }\left[P-V\left(\mathrm{r}\right)\right]=0.$$

(1)

P is the momentum energy, and V(r) is the potential energy in the lattice. The potential energy is very difficult to calculate due to its relation to the internal force in the lattice. Thus, potential energy can be neglected for out simulation. We introduced a new mass concept m_r* instead of m_o for energy preservation law, with the relationship of $\frac{1}{m_{\mathrm{r}}^{*}}=\frac{1}{m_{\mathrm{e}}^{*}}+\frac{1}{m_{\mathrm{h}}^{*}}$:

$${\nabla }^2\mathsf{\psi }+\frac{2m_{\mathrm{r}}^{*}P}{\hslash }=0.$$

(2)

In the case of a-IGZO TFTs, we can approximate $\frac{1}{m_{\mathrm{r}}^{*}}\cong \frac{1}{m_{\mathrm{e}}^{*}}$ because of high values of hole effective mass (m_h*). Thus, m_e* is a very important factor to understand the electrical feature of a-IGZO TFTs. In order to fully understand the effect of m_e*, we simulated the a-IGZO TFT by controlling m_e* and analyzed it using energy band analysis.

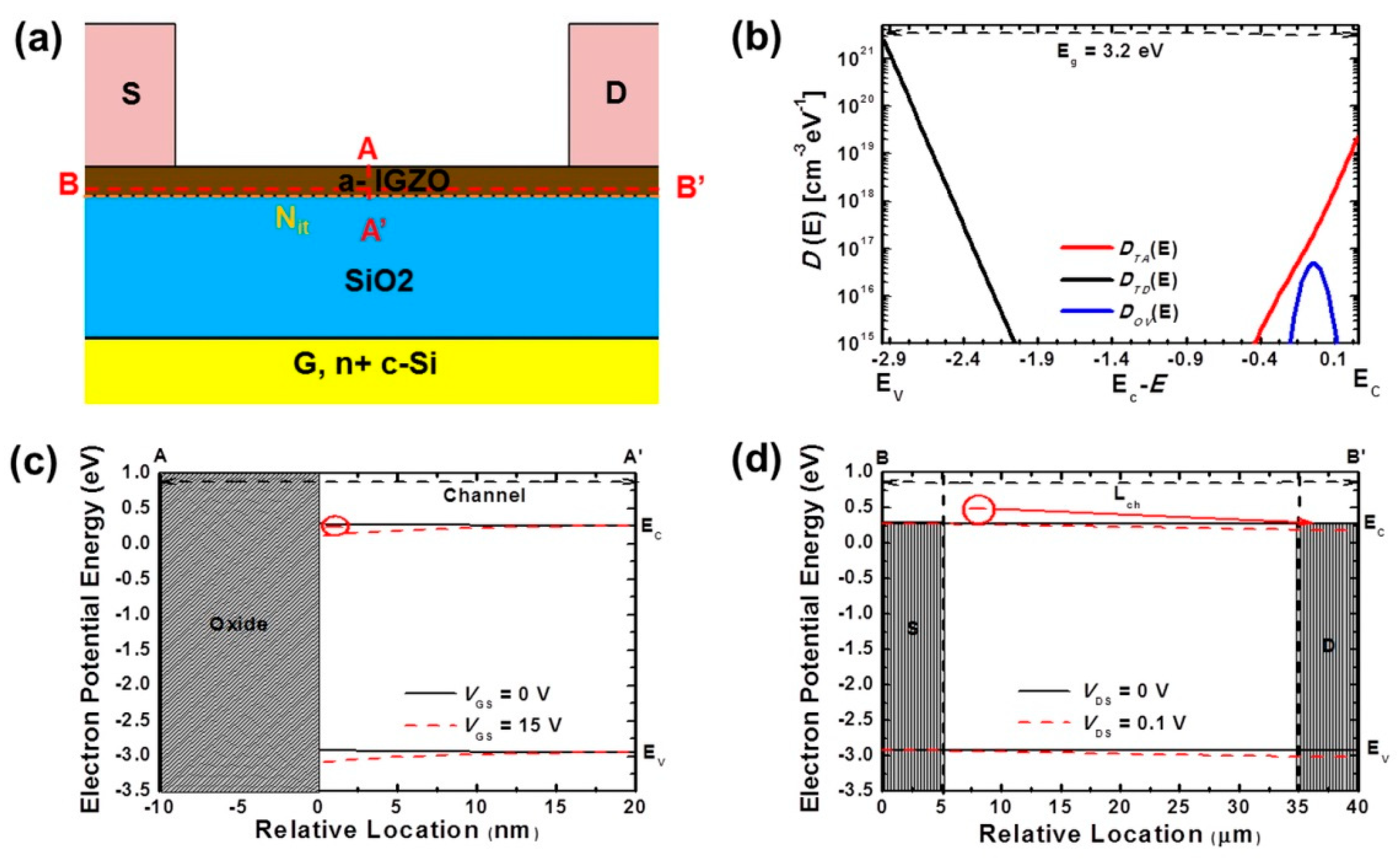
Figure 1a displays a schematic of the structure of a-IGZO-based bottom gate (BG)-top contact (TC) TFT. The gate (G), gate insulator (GI), active layer, and source (S) and drain (D) materials are n-polysilicon, SiO₂, a-IGZO, and aluminum, respectively. The GI and a-IGZO active layer have a thickness of 100 and 20 nm, respectively. The a-IGZO width (W) and length (L) are 180 and 30 µm. Figure 1b schematically illustrates the sub-gap DOS distribution in relation to m_r* in a-IGZO TFTs. Both N_TA and the conduction-band DOS (D_C (E)), and tail donor-like edge traps density (N_TD) and valence-band DOS (D_V (E)) are theoretically continuous at boundary condition (BC) [16]. In addition, the Madelung potential could lead to a metastable condition. Therefore, V_O could form near the conduction band (E_C) when the device is operated. Figure 1c presents a bonding model and the schematic of the energy band diagram in the a-IGZO TFT. When the gate voltage is applied, electrons are generated and operated to accumulation mode by V_O and oxygen interstitials (I_O⁻²) because of the Madelung potential and peroxide model [5,7].

Figure 2a shows a cross-sectional view of the a-IGZO-based BC-TG TFT. We applied the interface traps model of Heiman [17,18]. Figure 2b shows the sub-gap DOS distribution designed to match the RF-sputtered a-IGZO TFTs in terms of their electrical characteristics (RF sub-gap DOS) via sub-gap DOS engineering mechanism [13,15].

The total acceptor-like DOS (D_TA (E)), total donor-like DOS (D_TD (E)), and V_O DOS (D_OV (E)) have the properties of acceptor-like traps, donor-like traps, and D_OV (E), respectively. In practice, both N_TA and N_TD in the sub-gap DOS increase because of the presence of process stress and hydrogen defect states [5,8]. In this study, the RF sub-gap DOS design parameters were selected to match the RF-sputtered transfer characteristics of the a-IGZO TFTs as presented below in

Table 1. Simulation parameters for the a-IGZO TFT.

Parameter	Value	Unit	Description
Eg	3.2	eV	Bandgap of a-IGZO
χs	4.16	eV	Affinity of a-IGZO
εox	3.9	ε0	SiO2 dielectric constant
NOV	5 × 1016	cm−3eV−1	Gauss Donor-like edge traps density of DOV (E)
WOV	0.08	eV	Characteristic decay energy of DOV (E)
EOV	3.0	eV	Energy peak of DOV (E)
NTA	2.4 × 1019	cm−3eV−1	Tail acceptor-like edge traps density
WTA	0.06	eV	Characteristic decay energy of DTA (E)
WGA	0.28	eV	Characteristic decay energy of DGA (E)
WTD	0.08	eV	Characteristic decay energy of DTD (E)
Nit	1.1 × 1011	cm−3eV−1	Effective interface traps density
d	2	nm	Interface trap depth between semiconductor and gate insulator
cDn	1 × 10−16	cm2	Electron capture cross-section of the donor-like trap
cDp	1 × 10−14	cm2	Hole capture cross-section of the donor-like trap
cAn	1 × 10−14	cm2	Electron capture cross-section of the acceptor-like trap
cAp	1 × 10−16	cm2	Hole capture cross-section of the acceptor-like trap

.

Figure 2c,d present an energy band diagram of the a-IGZO TFT with an A to A′ vertical cutline and a B to B′ lateral cutline. This illustration can not only explain the mechanism of field-effect TFTs, but also can be used to predict the electron distribution when the device operates according to Poisson’s Equation from Labels (3) to (6):

$$\frac{dF}{dx}=\frac{q\left(D_{\mathrm{OV}}^{+2}\left(E\right)-2e-D_{\mathrm{TA}}\left(E\right)\right)}{{ϵ}_s{ϵ}_o},$$

(3)

$$\frac{dF}{dx}=\frac{q\left(2N_{\mathrm{OV}}^{+2}-N_{\mathrm{TA}}^{-}\right)}{{ϵ}_s{ϵ}_o},$$

(4)

$$F\left(x\right)=-\frac{q\left(2N_{\mathrm{OV}}^{+2}-N_{\mathrm{TA}}^{-}\right)}{{ϵ}_s{ϵ}_o}\left(W_{\mathrm{D}}-x\right),$$

(5)

$$V\left(x\right)=-\frac{q\left(2N_{\mathrm{OV}}^{+2}-N_{\mathrm{TA}}^{-}\right)}{2{ϵ}_s{ϵ}_o}{\left(W_{\mathrm{D}}-x\right)}^2,$$

(6)

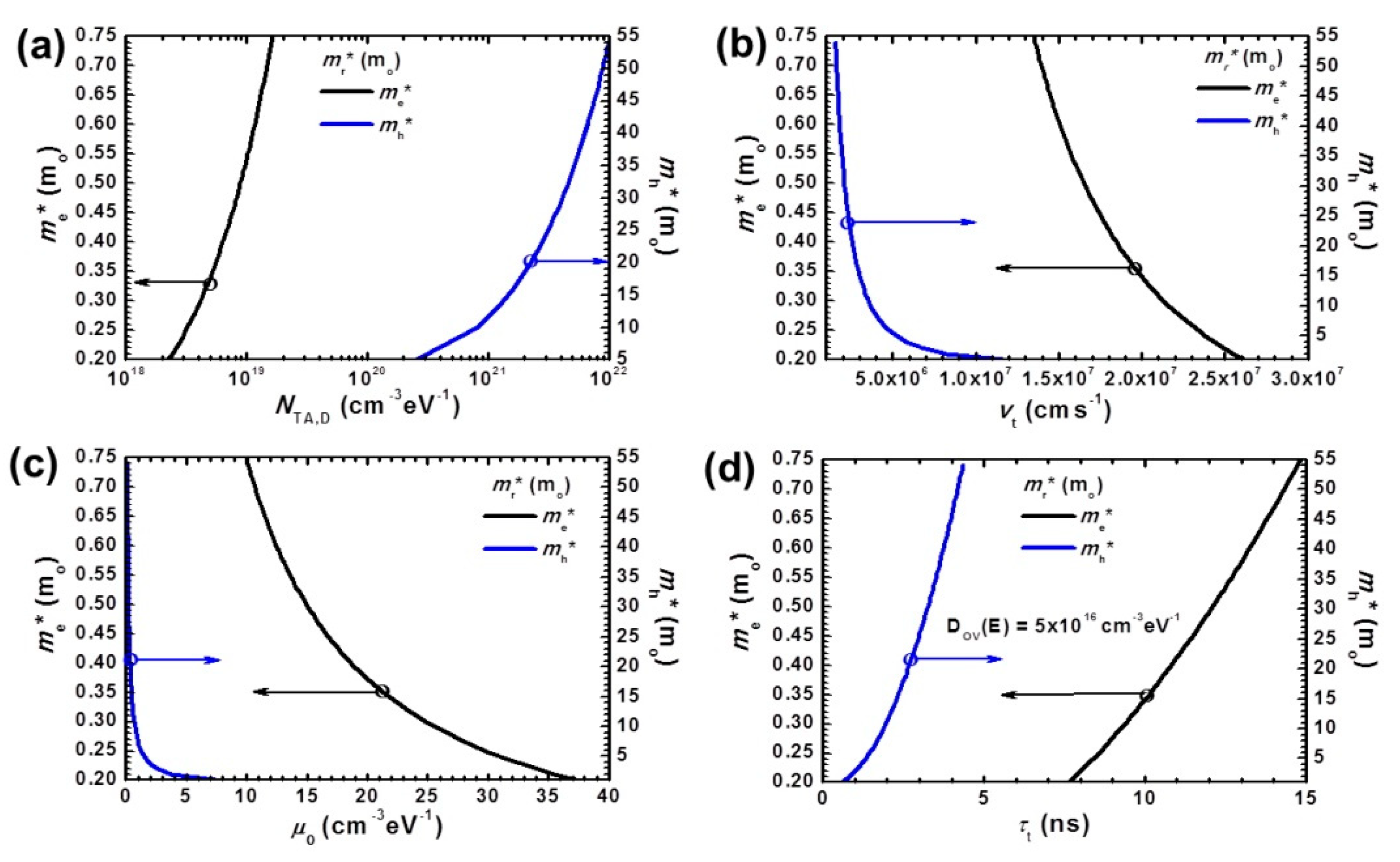
where ${ϵ}_s$ is the a-IGZO dielectric constant set at 10 in this study, ${ϵ}_o$ is the vacuum permittivity, F is the electric field, q is the elementary charge, W_D is the depletion width, and x is the relative location. The energy band analysis could observe the effect of traps through the variation of energy when an electron is working. Figure 3 shows the relationship of m_r* to the design parameters: N_TA, N_TD, thermal velocity (v_t), the lifetime related to trap site (${\tau }_{\mathrm{t}}$) at the N_OV (donor-like edge traps density of D_OV (E)), and the hall mobility (μ₀). These variables were calculated using formulas from Labels (7) to (10), respectively [18,19]. At an m_e* of 0.34 and an m_h* of 21 m_o [5,13], the following design parameters were obtained: a N_TA of 4.97 × 10¹⁸ cm⁻³eV⁻¹, a N_TD of 2.41 × 10²¹ cm⁻³eV⁻¹, a v_t of 2 × 10⁷ cms⁻¹, a ${\tau }_{\mathrm{n}}$ of 10 ns, a ${\tau }_{\mathrm{p}}$ of 2 ns, and a μ₀ of 22 cm²V⁻¹s⁻¹. As a result, we can completely obtain the transfer characteristics of the RF-sputtered a-IGZO BG-TC TFTs (

Table 2. Comparison with good transfer characteristics of a-IGZO TFTs derived from previous experimental-based work via RF-sputtering [3] and those derived numerically form this work.

Comparison	Me (mo)	µfe (cm2V−1s−1)	Vth (V)	Ion (A)
a-IGZO TFTs [3]	0.34	12.9	3.1	~10−6
This work	0.34	12.9	3.1	3 × 10−6

).

$$N_{\mathrm{C},\mathrm{V}}=2{\left(\frac{2\mathsf{\pi }{m}_{\mathrm{r}}^{*}kt}{h^2}\right)}^{\frac{3}{2}},$$

(7)

$$v_{\mathrm{t}}=\sqrt{\frac{3kt}{m_{\mathrm{r}}^{*}}},$$

(8)

$${\tau }_{\mathrm{t}}=\frac{1}{v_{\mathrm{t}}{c}_{\mathrm{n},\mathrm{h}}{N}_{\mathrm{T}}\left(E\right)},$$

(9)

$${\mu }_0=\frac{qh}{12\mathsf{\pi }{m}_{\mathrm{r}}^{*}kt},$$

(10)

in the above Equations, k is the Boltzmann constant, and t is room temperature of 300 K. c_n,p is the capture cross-section of electron and hole, N_T (E) is the trap-DOS in the active layer, and h is the Planck constant (2πђ).

We assumed that C_An, C_Ah, C_Dh, and C_Dn were 1 × 10⁻¹⁴, 1 × 10⁻¹⁶, 1 × 10⁻¹⁶, and 1 × 10⁻¹⁴ cm², respectively, since the acceptor-like traps are negatively charged when occupied by an electron, and the donor-like traps are positively charged when emptied. We also assume a fully ionized D_OV (E) at the metastable condition. Thus, the electron concentration was calculated to be 1 × 10¹⁷ cm⁻³ and (E_C − E_f) is calculated to be 0.1 eV using Equation (9):

$$(E_{\mathrm{C}}-E_{\mathrm{f}})=kt\ln \left(\frac{N_{\mathrm{C}}}{2N_{\mathrm{OV}}}\right).$$

(11)

The interface traps were modeled with the Heiman model because the electrical mechanisms between the GI and semiconductor layer are better expressed when the transient time is taken into consideration during device operation. The Heiman interface mechanism could be obtained from the following equations:

$$\frac{d{N}_{\mathrm{it}}^{-}}{dt}=N_{\mathrm{it}}[v_{\mathrm{tn}}{c}_{\mathrm{n}}\left(d\right)\left\{\mathrm{n}\left(1-f_{\mathrm{it}}\right)-f_{\mathrm{it}}{n}_{\mathrm{i}}{e}^{\frac{E_{\mathrm{t}}-E_{\mathrm{i}}}{kt}}\right\}-v_{\mathrm{th}}{c}_{\mathrm{h}}\left(\mathrm{d}\right)\left\{\mathrm{h}{f}_{\mathrm{it}}-\left(1-f_{\mathrm{it}}\right)n_{\mathrm{i}}{e}^{\frac{E_{\mathrm{i}}-E_{\mathrm{t}}}{kt}}\right\}],$$

(12)

$$c_{\mathrm{n}}\left(d\right)=c_{\mathrm{n}}{e}^{-\left\{\frac{2m_{\mathrm{e}}^{*}\left(E_{\mathrm{C}}-E_{\mathrm{it}}\right)}{{\hslash }^2}\right\}d},$$

(13)

$$c_{\mathrm{h}}\left(d\right)=c_{\mathrm{h}}{e}^{-\left\{\frac{2m_{\mathrm{h}}^{*}\left(E_{\mathrm{it}}-E_{\mathrm{V}}\right)}{{\hslash }^2}\right\}d},$$

(14)

where N_it is the effective interface traps density and d is the interface traps density depth between a-IGZO and GI. For a more accurate simulation, we used Shockley–Read–Hall (SRH) recombination with trap-assisted tunneling [18,20]:

$$R_{\mathrm{TAT}}=\frac{n_{\mathrm{i}}^2-nh}{\frac{{\tau }_{\mathrm{h}}}{1+E_{\mathrm{rh}}^2(\frac{1}{kt}-\frac{10}{3}{E}_{\mathrm{rh}}{\left(\frac{2m_{\mathrm{h}}^{*}}{qh\left|F\right|}\right)}^{\frac{1}{2}}}\left(n+n_{\mathrm{i}}{e}^{\left(\frac{E_{\mathrm{T}}-E_{\mathrm{i}}}{kt}\right)}\right)+\frac{{\tau }_{\mathrm{n}}}{1+E_{\mathrm{rn}}^2(\frac{1}{kt}-\frac{10}{3}{E}_{\mathrm{rn}}{\left(\frac{2m_{\mathrm{e}}^{*}}{qh\left|F\right|}\right)}^{\frac{1}{2}}}(h+h_{\mathrm{i}}{e}^{(\frac{E_{\mathrm{i}}-E_{\mathrm{T}}}{kt})})},$$

(15)

where E_rh is the hole tunneling range, E_rn is the electron tunneling range, and E_T is the trap energy level.

3. Results and Discussion

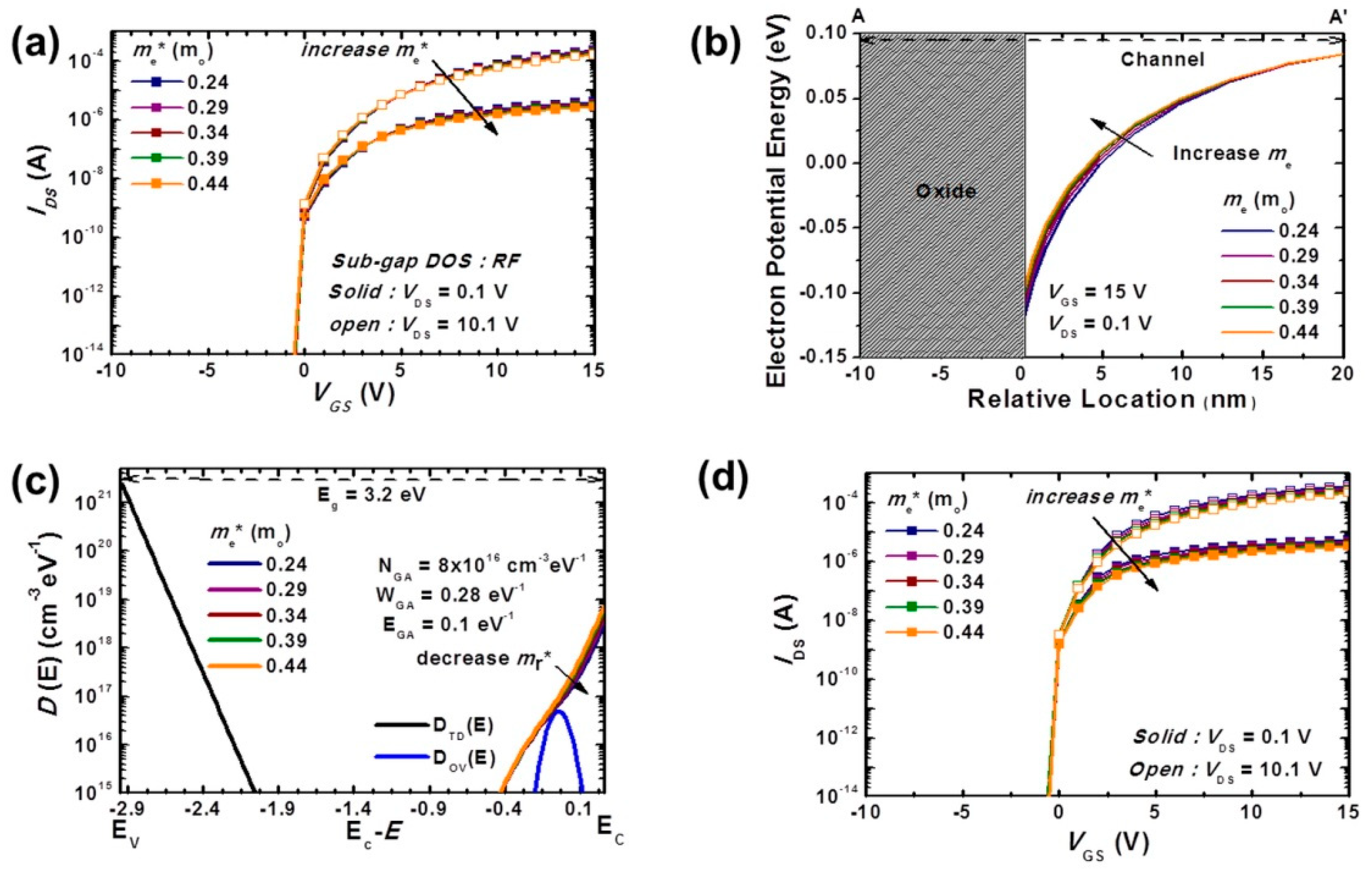
Figure 4a shows the drain current-gate voltage (I_DS − V_GS) transfer characteristics at the RF sub-gap DOS with the variation of m_e* in the linear and saturation regions. As m_e* increased up to 0.44 m_o, μ_fe and I_on in the linear region fall to 10.6 and 2.7 µA, respectively. In order to analyze the effect of only changing m_e*, we extracted a vertical energy band diagram at V_GS = 15 and V_DS = 0.1 V using the simulation tools as shown in Figure 4b. As m_e* changed from 0.24 to 0.44 m_o, the electron potential energy also increases from −0.067 to −0.049 eV. This meant that high m_e* electrons were more easily captured and hardly emitted when compared to low m_e* electrons. This was due to the negative charge of acceptor-like traps when holding the electrons, which could be explained using the Poisson’s Equation. Therefore, the relationship between m_e* and N_TA is expressed as:

$$m_{\mathrm{e}}^{*}\propto e_{\mathrm{t}}\propto \frac{1}{e_{\mathrm{e}}}.$$

(16)

The e_t defines the probability that the electrons are trapped by N_TA, and e_e defines the probability that the electrons escape N_TA. It was utilized to study the effect of m_e* through energy band analysis.

However, it is necessary for BC to consider the variation of N_TA by m_e*. as the N_TA would cause sub-gap scattering. The sub-gap scattering could be reinterpreted by the following Equations [13,18]:

$$\frac{1}{\mu }=\frac{1}{{\mu }_{\mathrm{pn}}}+\frac{1}{{\mu }_{\mathrm{sg}}}+\frac{1}{{\mu }_{\mathrm{sf}}},$$

(17)

$${\mu }_{\mathrm{sg}}=\frac{{\mu }_0}{1+\left[(D_{\mathrm{TA}}\left(E\right)+D_{\mathrm{OV}}\left(E\right)\right)/\left(cubic\right){]}^a}+\mathrm{b}.$$

(18)

In the above equations, ${\mu }_{\mathrm{pn}}$ denotes phonon scattering due to lattice vibrations, ${\mu }_{sf}$ represents surface scattering due to interface traps, ${\mu }_{\mathrm{sg}}$ shows sub-gap scattering, the cubic is D_OV (E) and D_TA (E) per cubic centimeter, and a and b are experimental coefficients. Therefore, a-IGZO TFT could reinterpret the sub-gap scattering mechanism. Figure 4c shows that, by changing m_e*, N_TA is theoretically is affected. The N_TA was increased from 2.95 × 10¹⁸ to 7.32 × 10¹⁸ cm⁻³eV⁻¹ when the m_e* changed from 0.24 to 0.44 m_o. W_TA is not related to m_r* but rather related to amorphous randomness [9,11], and N_GA (E) is not related to m_r* but rather deep traps density [4,8]. Thus, these values were maintained. Therefore, in order to accurately interpret the effect of electrical characteristics on m_r*, W_TA and N_GA (E) should maintain their values in this paper. As a result, we observed a high variation of transfer curve under the V_th region at the BC sub-gap DOS as shown in Figure 4d. In order to obtain more detailed electrical performance trends, we used the g_m extraction method as below Equation [3,5]:

$$I_{\mathrm{DS}}={\mu }_{\mathrm{fe},\mathrm{lin}}·C_{\mathrm{ox}}\left(\frac{W}{L}\right)\left(V_{\mathrm{GS}}-V_{\mathrm{th}}\right)V_{\mathrm{DS}}-\left(\frac{V_{\mathrm{DS}}^2}{2}\right)(\mathrm{at}{V}_{\mathrm{GS}}-V_{\mathrm{th}}>V_{\mathrm{DS}}),$$

(19)

$$I_{\mathrm{DS}}={\mu }_{\mathrm{fe},\mathrm{sat}}·C_{\mathrm{ox}}\left(\frac{W}{2L}\right){\left(V_{\mathrm{GS}}-V_{\mathrm{th}}\right)}^2(\mathrm{at}{V}_{\mathrm{DS}}\ge V_{\mathrm{GS}}-V_{\mathrm{th}}).$$

(20)

Thus, μ_fe and V_th can be obtained using the following g_m extraction equation:

$$g_{\mathrm{m}}=\frac{\partial I_{\mathrm{DS}}}{\partial V_{\mathrm{GS}}}={\mu }_{\mathrm{fe},\mathrm{lin}}·C_{\mathrm{ox}}\left(\frac{W}{L}\right)V_{\mathrm{DS}},$$

(21)

$${\mu }_{\mathrm{fe},\mathrm{lin}}\left(V_{\mathrm{GS}}\right)=\frac{g_{\mathrm{m}}\left(V_{\mathrm{GS}}\right)}{C_{\mathrm{ox}}·V_{\mathrm{DS}}}\left(\frac{L}{W}\right),$$

(22)

$$g_{\mathrm{m}}=\frac{\partial I_{\mathrm{DS}}^{\frac{1}{2}}}{\partial V_{\mathrm{GS}}}={({\mu }_{\mathrm{fe},\mathrm{sat}}·C_{\mathrm{ox}}\left(\frac{W}{2L}\right))}^{\frac{1}{2}},$$

(23)

$${\mu }_{\mathrm{fe},\mathrm{sat}}=\frac{{(g_{\mathrm{m}})}^2}{C_{\mathrm{ox}}}\left(\frac{2L}{W}\right).$$

(24)

The C_ox denotes the SiO₂ capacitance.

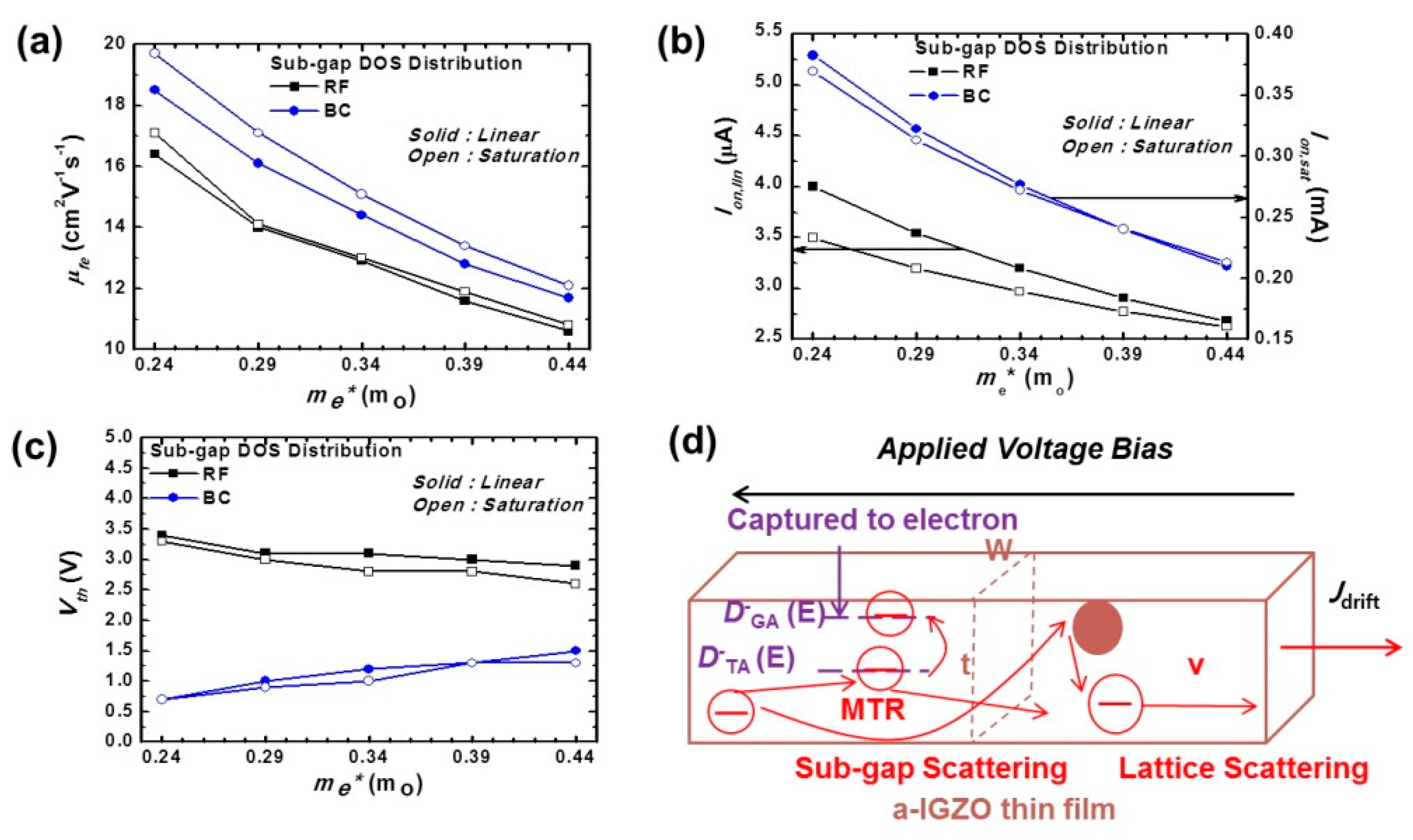
Figure 5a shows µ_fe by changing m_e* at the RF and BC sub-gap DOS distributions in the linear and saturation regions. As the m_e* increased from 0.24 to 0.44 m_o, µ_fe decreased from 16.4 to 10.6 cm²V⁻¹s⁻¹ in the linear region, and from 17.1 to 10.8 cm²V⁻¹s⁻¹ in the saturation region at the RF sub-gap DOS distribution. At the BC sub-gap DOS distribution, as the m_e* increased from 0.24 to 0.44 m_o, µ_fe also decreased from 18.5 to 11.7 cm²V⁻¹s⁻¹ in the linear region, and from 19.7 to 12.1 cm²V⁻¹s⁻¹ in the saturation region. It was found that the BC sub-gap DOS distribution exhibited higher µ_fe than the RF sub-gap DOS distribution because of relatively high N_TA. Figure 5b shows the variation of I_on with m_e* at the RF and BC sub-gap DOS distributions in the linear and saturation regions. As m_e* increased from 0.24 to 0.44 m_o, I_on decreased from 4.0 to 2.7 µA in the linear region and from 0.23 to 0.16 mA in the saturation region at the RF sub-gap DOS distribution. At the BC sub-gap DOS distribution, as m_e* increased, I_on also decreased from 5.3 to 3.2 µA in the linear region, and from 0.36 to 0.21 mA in the saturation region. It was found that the BC sub-gap DOS distribution exhibited higher I_on than RF sub-gap DOS distribution also because of the relatively high N_TA. The high N_TA distribution in the a-IGZO TFTs was caused by the increasing probability of capture electron and sub-gap scattering. Figure 5c shows the change in V_th with the variation of m_e* at the RF and BC sub-gap DOS distributions in the linear and saturation regions. As m_e* increased from 0.24 to 0.44 m_o, V_th decreased from 3.4 to 2.9 V in the linear region, and from 3.3 to 2.6 V in the saturation region at the RF sub-gap DOS distribution. Unexpectedly, the V_th decreased in the transfer curve at the RF sub-gap DOS distribution, because the x-axis intersection had negative shifted with decreasing slope, as evident from the g_m extraction equation. However, intrinsic V_th would have a slight increase as noticed through energy band analysis. At the BC sub-gap DOS distribution, as N_TA increases from 2.95 × 10¹⁸ to 7.32 × 10¹⁸ cm⁻³eV⁻¹ by varying m_e* from 0.24 to 0.44 m_o, V_th increased from 0.7 to 1.5 V in the linear region, and from 0.7 to 1.3 V in the saturation region. It was found that N_TA affected V_th more than m_e*. This could be utilized to predict the practical tendency of V_th through optimizing m_e*.

To illustrate this trend, we reinterpreted the conductivity mechanism [21]. It can be expressed to drift drain current density (J_n,drift) as

$$J_{\mathrm{n},\mathrm{drift}}=q\left(n-n_{\mathrm{t}}\right)u_{\mathrm{fe}}F.$$

(25)

Thus, the conductivity is

$$\mathsf{\sigma }=q\left(n-n_{\mathrm{t}}\right)u_{\mathrm{fe}}.$$

(26)

It is hypothesized that the observed positive shift in V_th at the BC sub-gap DOS was because of the low conductivity, which caused difficulty in channel formation through the electron capture by N_TA. To understand it in more detail, Figure 5d shows the mechanism of multiple trapping and release (MTR) [22], sub-gap scattering, and low conductivity effect of m_e*. Therefore, m_e* is a very important parameter because it affects N_TA, and has a major influence on the electrical performances in a-IGZO TFT. In addition, we would expect greater improvements in device performance to arise from appropriate m_e* design and sub-gap engineering compared with conventional a-IGZO TFTs.

4. Conclusions

In this work, the a-IGZO-based BG-TC TFT was designed through experimental-based a-IGZO TFTs using TCAD simulations. Based on the parameters optimized to mimic experimental results, we only changed m_e* from 0.24 to 0.44 m_o to study its effects. For low m_e*, μ_fe, and I_on were higher because of a lower probability of electron capture by N_TA through energy band analysis. Furthermore, we have investigated the influence of m_e* and N_TA on the BC sub-gap DOS. As a result, we had reinterpreted the effects of sub-gap scattering, low conductivity, and the relationship between m_e* and N_TA through energy band analysis and semiconductor mechanism. Thus, we were able to obtain the tendencies of μ_fe, I_on, and V_th electrical characteristics of a-IGZO TFT. In addition, our model could be utilized to predict the limit of theoretical electrical characteristics according to m_e* of a-IGZO TFT. Therefore, this study would be able to provide valuable information for the design of backplane unit devices for high-resolution applications.