Abstract
Robust chaotic systems, due to their inherent properties of mixing, ergodicity, and larger chaotic parameter space, constitute a perfect candidate for cryptography. This paper reports a novel method to generate random numbers using modified robust logistic map (MRLM). The non-smooth probability distribution function of robust logistic map (RLM) trajectories gives an un-even binary distribution in randomness test. To overcome this disadvantage in RLM, control of chaos (CoC) is proposed for smooth probability distribution function of RLM. For testing the proposed design, cryptographic random numbers generated by MRLM were vetted with National Institute of Standards and Technology statistical test suite (NIST 800-22). The results showed that proposed MRLM generates cryptographically secure random numbers (CSPRNG).
1. Introduction
Random number sequences have immense impact on numerous applications, such as signal processing [1,2], stochastic simulations [3,4], spread spectrums [5,6], gaming [7,8,9], statistics [10], captcha [11,12], machine learning [13,14], and cryptography etc. The random number generators that pertain to excellent statistical properties are considered critical for robust cryptographic applications [15]. The random numbers are categorized into two types: (1) true random number generator (TRNG), and (2) pseudorandom number generator (PRNG). TRNGs are generally based on physical and natural phenomenon and are non-deterministic, such as quantum random process, photon noise, frequency jitter in the oscillator, thermal noise, human brain signals, and free-running oscillator [16,17,18]. The generated sequences can be passed through the sampling and post-processing techniques to enhance the randomness. TRNG properties reveal that the truly generated random sequences must be non-reproducible, unpredictable, and statistically unbiased [19]. On the other hand, PRNGs are based on mathematical functions stem from initial condition to generate deterministic sequences over a long period. These PRNGs possess good statistical properties, such as repeatability, reproducibility, and fast execution time. A special type of PRNG, desirable for cryptography, is cryptographically secure PRNG (CSPRNG). A CSPRNG is unpredictable and computationally infeasible to generate the prior data bits. CSPRNGs are used in cryptographic mechanisms to provide cryptographic services of encryption, digital signature, hashing algorithms, and key generation.
Shannon, in his famous secrecy theory [20], stated that a source to design primitive cryptography must have the properties like sensitive dependence on initial condition, mixing and ergodicity to change, iteratively, position, and value of plaintext known as confusion and diffusion, respectively. Over the last decade, the use of the chaos in cryptography has gained increased attention due to the properties of mixing, ergodicity, sensitive dependence on initial condition, and deterministic dynamics. Chaotic maps are simple mathematical functions that exhibit chaotic behavior. Chaotic maps are iterated using an initial seed that gives nonlinear trajectories, which are mapped to binary sequences in order to generate highly unpredictable random numbers that are employed in cryptography [21,22,23,24,25,26].
In recent years, researchers have implemented PRNGs based on chaotic maps in both hardware and software form. There are several drawbacks when these maps are used in cryptographic systems such as the discontinuity of ranges, non-uniform distribution, periodicity in chaotic range, and a small key space [27]. Ahmed et al. [28] proposed a reconfigurable hardware-based chaotic PRNG. In their proposed system, Lorenz [29] and Lü [30] used chaotic systems, which generated four three-dimensional chaotic attractors with the distribution of one and three attractors respectively. Hereby, multiplexing and shifting schemes are used for reconfiguration in real-time. The proposed method is synthesized on a field-programmable array (FPGA) and tested successfully using the National Institute of Standard and Technology (NIST) 800-22 test suite. Only 1.4% of the FPGA’s slices were utilized with the operating frequency of 78 MHz Random robustness strongly depends upon the data type, fixed-point, and floating-point notation. Floating-point notation has a lower data rate and inefficient resource utilization. Rania and Ehab [31] proposed a hardware-based PRNG using single skew tent map [32], coupled skew tent map [33], and cross-coupled skew tent map [34]. They examined the fixed-point notation and its consequence on the periodicity and statistical possessions of the random sequences. The authors reduced the fixed-point fraction length and expand the dependency on control parameters. The generated sequences required randomness for cryptography, by passing the NIST 800-22 tests. Koyuncu and Özcerit [35], presented the implementation of Sundarapandian—Pehlivan chaotic system [36] to design on Xilinx Virtex-6 with 58.76 Mbit/s data rate. NIST 800-22 and FIPS 140-1 tests were successful for the generated sequences. Avaroğlu et al. [37] presented a hybrid scheme to generate pseudo-random numbers. Sprott 94 G chaotic system is used as an additional input to improve the security of raw PRNG, which is generated from the proposed system. This additional input element is implemented on Virtex-6 FPGA. A seed value is randomly selected, and the Sprott 94 G is used to generate the key and fed to AES to generate the state values, which are XORed with the additional input to increase unpredictability. NIST 800-22 generated the successful result in the generated sequence. Murrilo-Escobar et al. [38] proposed a novel method to generate random numbers by modifying the logistic map. They presented successful statistical tests such as NIST 800-22 and TestU01. Moreover, the authors presented 2128 possible secret keys for a seed value to verify the sensitivity of key at bit-level. Wang et al. [39] proposed a piecewise logistic method to generate random numbers by modifying the logistic map and enhance the range of control parameters with successful statistical test NIST 800-22. Avaroğlu et al. [40] proposed a novel technique for generating TRNG. The ring oscillator is used as an entropy source and the logistic map is used to generate high-quality random numbers at the post-processing stage. Altera FPGA board is used to implement the proposed scheme. Successful results are presented using TESTU01 and NIST 800-22. François et al. [41], proposed a method to generate random numbers by mixing three chaotic maps with the initial vectors. The positions and indexes are calculated using chaotic function and linear congruence, which is used for the permutation. NIST 800-22 verified that the generated sequences are cryptographically secure.
Robust chaotic map [1] possesses positive Lyapunov exponent however they might result in cryptographically unsecure random numbers. Thus, CoC might represent a valid solution to generate CSPRNG. The larger parameter space of robust chaotic maps can be beneficial to fulfill cryptographic mechanisms. In this paper, we used a robust chaotic map with positive Lyapunov exponent, however the distribution of this map is non-uniform. The non-uniform distribution of the opted map is the cause of the failure of NIST 800-22 tests that require equal probability of ‘0’ and ‘1’ in a binary sequence. Hence, the control of chaos is proposed which styles the probability of 0’s and 1’s equally likely. The uniform region of output is selected to produce CSPRNG by applying the scaling operation followed by modulo shifting operation. The threshold value is chosen carefully and considered critical in mapping the output value to either zero or one. The probability for the occurrence of each value of the set {0,1} remains equally likely. To validate the proposed PRNG design, we apply the NIST 800-22 test suite, which passes all the tests successfully. Hence, the proposed CSPRNG can be used effectively in different cryptographic applications including key generation, image encryption, and watermarking.
This paper is organized into following sections. Section 2 discusses the robust logistic map’s bifurcation diagram, Lyapunov exponent, and ergodic behavior. The proposed scheme of PRNG design using RLM and NIST 800-22 tests evaluation is presented in Section 3. In Section 4, the performance analysis of proposed CSPRNG is explained for correlation, key-space and key sensitivity analysis. Finally, the conclusion of this paper is provided in Section 5.
2. The Robust Chaotic Logistic Map
The chaotic logistic map is one-dimensional. One-dimensional maps are considered simple because they are based on single mathematical equation. The chaotic logistic map, due to its simple structure, is generally studied to generate a PRNG for cryptographic services [42,43,44,45]. Equation (1) defines the one-dimensional logistic map.
where γ is a control parameter γ ∈ [0,4] while ∈ (0,1) is initial value. The map is chaotic when control parameter γ ∈ [3.57,4]. When γ = 4, the map’s output ∈ (0,1) covers the complete phase, which is evident in Figure 1. The chaotic logistic map has positive Lyapunov for the region γ ∈ [3.57,4] in Figure 2 that represents the chaotic behavior. The Lyapunov exponent measures the quantitative divergence of orbits which confirms the chaotic behavior.

Figure 1.
Bifurcation diagram for the Logistic Map.
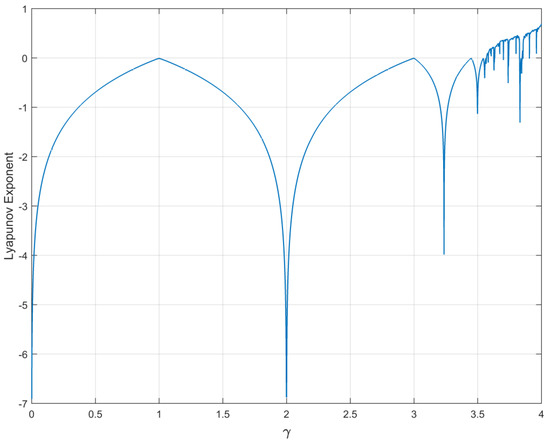
Figure 2.
Lyapunov Exponent of Logistic Map.
Chen et al. [1], proposed an RLM which is an improved form of the logistic map, they enhanced the control parameter space for γ ∈ [0,4]→γ ∈ [0,31]. Equation (2) defines the modified map.
In Equation (2) above, ∈ (0,1)\, where ∈ [,], = 1/2−√(1/4−⌊γ/4⌋/γ) and = 1/2+√(1/4−⌊γ/4⌋/γ). Figure 3 measures the correlation between trajectories that are generated using the logistic map and RLM with an arbitrary initial condition. The x-axis shows input and y-axis shows the map’s output . Based on the comparison, RLM and logistic map generates completely different trajectories at various values of γ. We have changed the initial conditions and results became same and maps are highly de-correlated. The inherent chaotic behavior of the RLM is discussed below:

Figure 3.
Correlation between trajectories of robust chaotic logistic map and chaotic logistic map.
2.1. Ergodicity
Ergodicity is an essential and closely related to the mixing property of chaotic system. In an ergodic system, orbit of every initial point from its definition interval leads to cover the complete phase space after a large number of iterations. For example, if one picks arbitrary initial condition and another number in phase space then trajectory of eventually visit during the course of iterations sometime or the other. The orbits having nature of visiting complete phase are called ergodic. Hence when iterated, the ergodic orbits are mixed throughout the whole interval.
By iterating Equation (2), the orbits of different arbitrary chosen inputs provide ergodic behavior and cover the complete phase space (0,1) when γ ≥ 4 (Figure 4). It has good mixing properties when γ ∈ [3.9,31] (Figure 5).
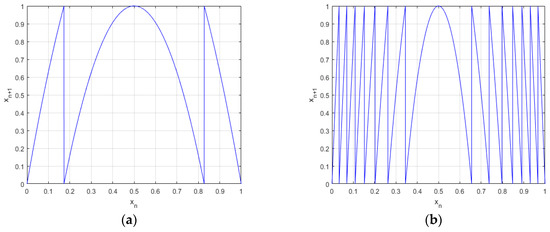
Figure 4.
Mapping of xn vs. xn+1 (a) γ = 7 (b) γ = 31.

Figure 5.
State Distribution of RLM (a) γ = 5 (b) γ = 11.5 (c) γ = 16 (d) γ = 31.
2.2. Bifurcation Diagram
The bifurcation diagram shows the mapping of orbits. It gives an inherent behavior of the chaotic system with the change of control parameters. The logistic map and its variants demonstrate period doubling bifurcation as shown in Figure 1 and Figure 6. With the change in control parameter, chaotic obits switch their behavior to stable/unstable that results in period doubling bifurcation. All stable orbits mean they are covering the complete phase space, and hence the system is chaotic. The bifurcation diagram of RLM in Figure 6 shows chaotic behavior at γ ≥ 4 and this range keep growing till γ = 31.
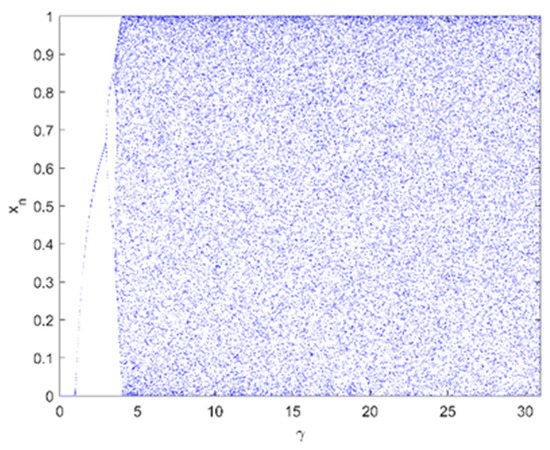
Figure 6.
Bifurcation diagram of robust logistic map.
2.3. Lyapunov Exponent
The Lyapunov exponent is a quantitative measure of chaos and orbital divergence, by which the chaotic orbit of the logistic map is verified. A positive value of Lyapunov exponent indicates chaotic behavior and orbital divergence. The Lyapunov exponents of RLM for γ = 0 to 16 is shown in Figure 7. The Lyapunov exponent for RLM is positive for γ ≥ 4.
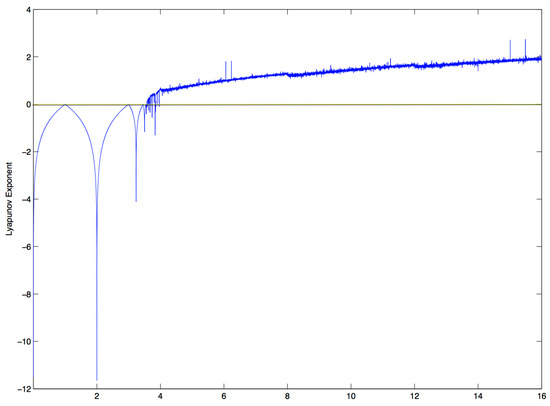
Figure 7.
Lyapunov Exponent of robust logistic map.
3. Proposed Methodology
The objective of this study is to investigate RLM for CSPRNG. Initially, we show that NIST 800-22 test suite PRNG for RLM is unsecure. Therefore, in this study, the design of CSPRNG is presented. The NIST 800-22 test of PRNG using CSPRNG validates the effectiveness of proposed methodology. The next subsection will cover both methodologies in detail.
3.1. Parameter Selection
The initial conditions and control parameters are chosen arbitrarily for the maps. Small perturbation on initial conditions and control parameters gives us completely different trajectories that are used to measure the key sensitivity and key space analysis. Small perturbations on control value investigate the behavior of bifurcations of the maps as shown in Figure 6. The logistic map bifurcations diagram in Figure 1 show that all trajectories are stable and covers complete phase space when γ = 4. Based on the results in Figure 6, RLM is chaotic and covers the complete phase space, and all trajectories are stable for γ ∈ [4,31].
3.2. PRNG Using RLM
In this study, PRNs generated using RLM are verified using NIST test suit. The PRNGs are crucially important, because the achieved randomness directly affects the security of encrypted applications. PRNGs having uniform probability distribution of binary sequences are desirable in cryptography. The chaotic trajectories generated using RLM having infinite real number values in range . However, Figure 8 validated the non-uniform distribution of RLM trajectories. Therefore, efficient mapping is required from real to binary domain that gives random bits stream of ‘0’ and ‘1’ with uniform probability distribution. One of the methods is to threshold the real domain to generate binary sequence. We choose a median value as a threshold Ʈ = 0.5. The performance of the proposed RNG is evaluated with NIST-800-22 statistical test suite [46], which includes 15 different tests. A bit stream of length 1 million (1M) is required for NIST-800-22 statistical tests. The flow graph of unsecure random bit generator (RBG) is shown in Figure 9, and the steps for generating a random bit stream using RLM PRNG are as follows:
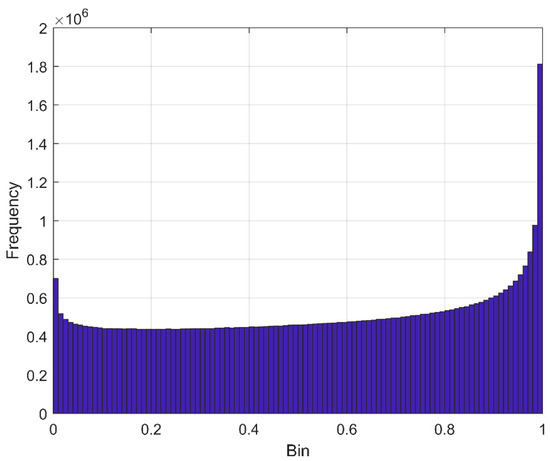
Figure 8.
Histogram of RLM.
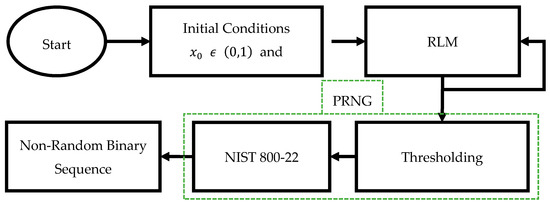
Figure 9.
Unsecure RBG using RLM.
- Step-1:
- Choose an arbitrary chosen initial condition ∈ (0,1) and control parameter γ ∈ [4,31] as an input to iterate RLM for generating output ∈ [0,1].
- Step-2:
- The RLM is iterated 1M times for generating N random floating-point values ∈ [0,1].
- Step-3:
- For real to binary domain mapping, thresholding is applied to the floating-point numbers. Threshold value of Ʈ = 0.5 is chosen.
- Step-4:
- Each generated output of RLM is checked where it falls. The binary value of ‘1’ is chosen if ≥ Ʈ or ‘0’ otherwise.
- Step-5:
- Stop iterating RLM once the bit stream of 1M is generated.
The generated bit stream using above mention steps is tested using NIST 800-22 test. Based on the results in Table 1, standard NIST test on RLM’s PRNG is failed. This is because the non-uniform probability distribution nature of RLM trajectories. Thus, PRNGs using RLM are not suitable to be used in cryptography. The next subsection presents the proposed CSPRNG design using modified RLM.

Table 1.
Randomness test of robust logistic map using national institute of standards and technology (NIST) 800-22 test suit.
3.3. Modified RLM (MRLM) Aided by CoC
PRNG to be used in any cryptographic application requires passing all the NIST tests. The Lyapunov exponent of RLM is positive but NIST test is failed. During mapping from real to decimal domain, maybe the inherent randomness of chaotic map is reduced. Therefore, in this study CoC is proposed where small perturbations are applied to the input parameters to generate RLM chaotic trajectories with uniform probability distribution function. For the CoC of RLM, the output region is desirable where the output of RLM is uniform as shown in Figure 10. The flow graph of proposed CSPRNG using Modified RLM (MRLM) is give in Figure 11 and Figure 12. The pseudocode of the proposed method is also presented in Algorithm 1.
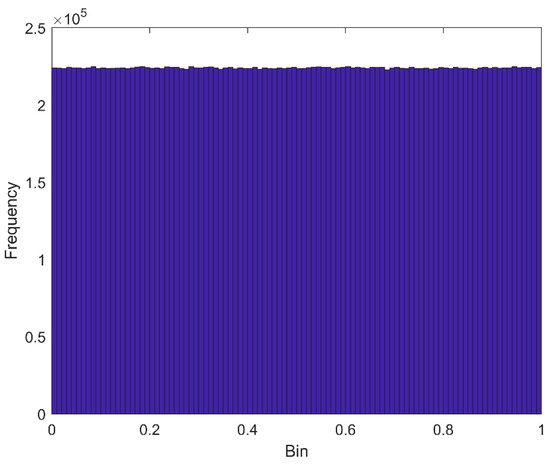
Figure 10.
Histogram of modified robust chaotic logistic map aided CoC.

Figure 11.
Controlling of Chaos (CoC) in RLM.
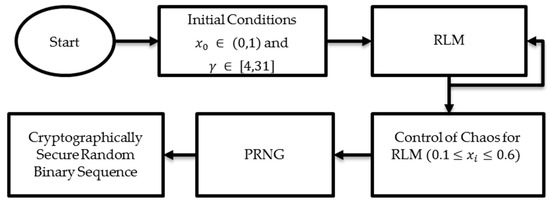
Figure 12.
Secure RBG by CoC.
| Algorithm 1: Generation of CSPRNG. |
| Pseudocode: Generation of Optimized Pseudo-random binary Sequence |
| Output: Pseudo-random binary sequence |
| Procedure: |
| initial seed value of and . |
| fordo |
| if |
| else |
| if and |
| else |
| end if |
| end if |
| if and |
| if |
| else |
| end if |
| else |
| discard |
| end if |
| end for |
| is the resultant binary sequence |
The detail of steps involved in generating CSPRNG using proposed MRLM is given below:
- Step-1:
- Choose an arbitrary initial condition and control parameter .
- Step-2:
- Calculate , where and .
- Step-3:
- Iterate RLM using (2) N times, and generate N floating-point numbers in the range .
- Step-4:
- Apply CoC to choose the output region within the range by carefully small perturbations are applied to the input to filter out the desired output sequence.
- Step-5:
- Scale the output region by a factor of 1010.
- Step-6:
- Apply modulo 1 operation on scaled region to generate output value .
- Step-7:
- Apply threshold to the resultant floating values such that each random value is mapped to ‘1’ if , else it is mapped to ‘0’. In this regard, choose a threshold value such that the probability distribution of 0’s and 1’s is almost equal. In our case, we choose for CoC to generate cryptographically secure pseudorandom numbers.
- Step-8:
- Stop iterating the map when 1M bits stream is generated.
The generated bits stream is then tested using NIST suit. Based on the results in Table 2, the proposed MRLM passed all the NIST tests with chosen and .

Table 2.
Randomness NIST test for MRLM.
4. Performance Analysis
The proposed method is tested for the well-established performance parameters of correlation, key space and key sensitivity analysis. The details of these properties are explained in the next subsection.
4.1. Key Space Analysis
The key space of secret keys or seed values must be larger than 2100 to resist against the brute force attack [47]. The proposed CSPRNG using MRLM is based on the two parameters of initial condition and control parameter of . The precision of double floating-point is 10−16 stated in the IEEE floating-point standard [48]. Therefore, can be any of 1016 values. Similarly, can be any value in the range . Therefore, the key-space of proposed PRNG is . The given range is used to compare the key space of proposed method with recently proposed methods is given in Table 3. Based on the results, the proposed scheme has a larger key space compared to recently proposed schemes. The proposed method satisfies the key space requirement and resists the brute force attack.

Table 3.
Comparison analysis of key space.
4.2. Correlation Analysis
The correlation coefficient is used to measure the dependence and statistical relationship among random variables. The correlation coefficient between the two sequences is given as:
where and are two random variable sequences , . The MRLM is iterated 1000 times by ignoring initial transient. To measure correlation using (2) and (3), small perturbations of are applied to control parameter to generate MRLM trajectories. The chosen value of is required that generate uncorrelated MRLM trajectories. The correlation coefficient falls in the range [−0.0875,0.0915] as shown in Figure 13. In other words, there is no correlation between the generated sequences.
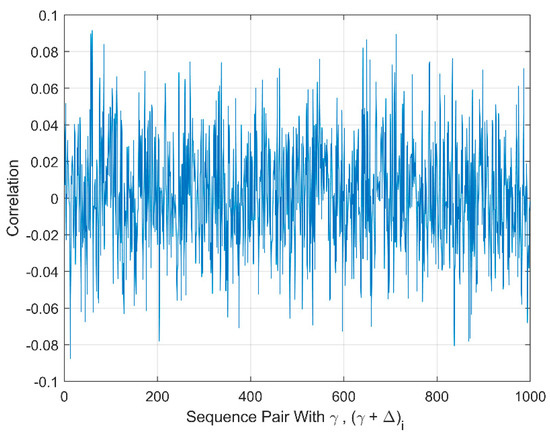
Figure 13.
Correlation analysis of MRLM trajectories with the slight change in control parameter.
4.3. Key Sensitivity Analysis
Essentially, a cryptographic algorithm is required to be highly sensitive to small change in the key [47]. In this study, to measure key sensitivity between the keys, arbitrary keys of length 128-bits are generated with the change of one bit at least significant bit positions. A method for initial condition mapping to generate CSPRNG is given in Figure 14. Key sensitivity analysis measures small change in keys can generate highly uncorrelated CSPRNGs. The steps involved for initial condition mapping is given below:
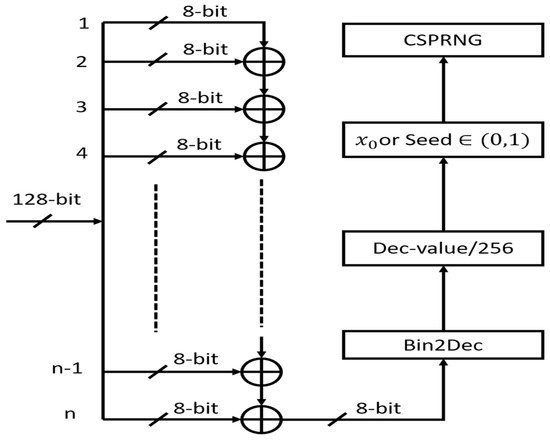
Figure 14.
Initial Condition mapping for MRLM.
- Step-1:
- Choose an arbitrary 128-bit hexadecimal key
- Step-2:
- Split the key into sixteen bytes. To spread the effect of small change at least significant bit over complete key and CSPRNGs, sixteen bytes are XORed together to generate an 8-bit number.
- Step-3:
- Convert the 8-bit binary number into decimal.
- Step-4:
- Divide the decimal value by 256 to generate real value .
CSPRNGs are generated by iterating MRLM with varying mapped and arbitrary chosen fixed control parameter . Arbitrary chosen keys with Single bit change at least significant bit are given in Table 4, generate highly CSPRNGs of 1000 bits are given in. Based on results in Figure 15, CSPRNGs are apparently uncorrelated and highly sensitive to small change in the key. The correlation between the generated sequences falls in the range (−0.0245, 0.0138).

Table 4.
Arbitrary Keys involved in sensitivity analysis.

Figure 15.
Correlation analysis between trajectories using proposed method.
4.4. CoC on Chaotic Map
Essentially, the probability distribution function of any given chaotic map describes its behavior. Smooth probability distribution function is required in chaotic map to generate CSPRNG. Therefore, in Table 5 four different chaotic maps such as circle [51], iterative [52], tent [53], and singer [54] maps are chosen with non-smooth probability distribution function. NIST STS test is performed on these maps with and without applying proposed CoC. It is apparent in Table 4 that typical chaotic maps used for comparison pass all NIST STS tests using the proposed CoC.

Table 5.
Comparison with different Chaotic Maps.
In any given chaotic map, changing the control parameters beyond the given limit move the fix points to infinity hence chaotic behavior is vanished. Therefore, modifications are proposed in maps to keep the chaotic fix points stable and within the range [1,53]. Chaotic maps are based on mathematical equations. Modified chaotic maps for larger parameter space having variable internal region that is shrink and expand with the change in control parameters. The change in internal region is described mathematically based on chaotic map’s equation aided scaling and modulo operations. In [53] author modified chaotic tent map (MCTM) that enlarge the parameter space. The internal region is mathematically derived and aided by modulo and scaling operations. In [1] chaotic logistic map’s parameter space is expanded with derived internal region. The internal region required deriving carefully for chaotic behavior and entirely based on map’s equation. To analyze internal region selection, two different use cases are presented. Case 1 is measuring the NIST STS of MCTM and RLM with their respective internal region equations. Case 2 is measuring NIST STS by swapping the internal region equations. Based on the results in Table 6, it is evident that the wrongly derived internal region entails a failed NIST STS test.

Table 6.
Comparison with region equations.
5. Conclusions
In this study, modifying RLM using the proposed CoC generates cryptographically secure pseudorandom numbers. The RLM has large chaotic parameter space and possesses a positive Lyapunov exponent, but it has a non-uniform probability distribution of trajectories that makes it undesirable for cryptography. Hence, CoC in RLM gives a uniform distribution of the output sequence. The CSPRNG proposed design is vetted using NIST 800-22 tests. The correlation, key-sensitivity and key-space statistical analysis show that large parameter space of RLM gives sufficiently large key length and key space to resist all known attacks. The proposed modified RLM (MRLM) has the potential to be used in various cryptographic applications including image, telemedicine, electronic payment, computation, text source, personal information, biometrics, and military among others.
Author Contributions
All authors contributed in the design problem and the proposed methodology. Simulations were performed by M.I. and M.E.-u.-H. Initial draft was written by A.A., M.E.-u.-H. The simulations were verified by M.A.K. The conceptualization and supervised by M.A.K. and S.N.M.S. Final Draft was proofread and edited by M.A.K., W.A. and A.S. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
I would like to thank department of computer engineering, university of engineering and technology, Taxila, Pakistan for their support and facilitation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, S.-L.; Chang, S.-M.; Lin, W.-W.; Hwang, T. Digital secure-communication using robust hyper-chaotic systems. Int. J. Bifurc. Chaos 2008, 18, 3325–3339. [Google Scholar] [CrossRef]
- Eisencraft, M.; Evangelista, J.V.C.; Costa, R.A.; Fontes, R.T.; Candido, R.; Chaves, D.P.B.; Pimentel, C.; Silva, M.T.M. New Trends in Chaos-Based Communications and Signal Processing; Springer: Berlin, Germany, 2019. [Google Scholar]
- Ghauch, Z.G.; Aitharaju, V.; Rodgers, W.R.; Pasupuletti, P.; Dereims, A.; Ghanem, R.G. Integrated stochastic analysis of fiber composites manufacturing using adapted polynomial chaos expansions. Compos. Part A Appl. Sci. Manuf. 2019. [Google Scholar] [CrossRef]
- Waqas, A.; Melati, D.; Manfredi, P.; Melloni, A. Stochastic process design kits for photonic circuits based on polynomial chaos augmented macro-modelling. Opt. Express 2018. [Google Scholar] [CrossRef]
- Bai, C.; Ren, H.P.; Baptista, M.S.; Grebogi, C. Digital underwater communication with chaos. Commun. Nonlinear Sci. Numer. Simul. 2019. [Google Scholar] [CrossRef]
- Soujeri, E.; Kaddoum, G.; Herceg, M. Design of an initial condition-index chaos shift keying modulation. Electron. Lett. 2018. [Google Scholar] [CrossRef]
- Nomura, H.; Temsiririrkkul, S.; Ikeda, K. Generation of “Natural” Pseudorandom Numbers from the Standard Player’s View. Available online: https://ci.nii.ac.jp/naid/120006675914/en (accessed on 1 November 2019).
- Berg, D.A.; Luciano, R.A., Jr.; Saffari, A. Central Random Number Generation for Gaming System. U.S. Patent 5,779,545, 14 July 1998. [Google Scholar]
- Meoni, F. Casino Random Number Card Covering Game. U.S. Patent 5,700,009, 23 December 1997. [Google Scholar]
- Hull, T.E.; Dobell, A.R. Random number generators. SIAM Rev. 1962, 4, 230–254. [Google Scholar] [CrossRef]
- Singh, V.; Pal, P. Survey of different types of CAPTCHA. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 2242–2245. [Google Scholar]
- Pawar, T.S.; Sawant, R.G.; Bothe, P.S.; Chopade, S.A. A Survey on Login Authentication System using Captcha as Graphical Password Technquies. Int. J. Innov. Res. Comput. Commun. Eng. 2015. [Google Scholar] [CrossRef]
- Tiwari, A.K. Introduction to machine learning. In Ubiquitous Machine Learning and Its Applications; IGI Global: Dehradun, India, 2017. [Google Scholar]
- Seeger, M. Gaussian processes for machine learning. Int. J. Neural Syst. 2004, 14, 69–106. [Google Scholar] [CrossRef]
- Corrigan-Gibbs, H.; Mu, W.; Boneh, D.; Ford, B. Ensuring high-quality randomness in cryptographic key generation. In Proceedings of the ACM Conference on Computer and Communications Security, Berlin, Germany, 4–8 November 2013; pp. 685–696. [Google Scholar]
- Bucci, M.; Germani, L.; Luzzi, R.; Tommasino, P.; Triftlettv, A.; Varanonuov, M. A high speed truly IC random number source for Smart Card microcontrollers. In Proceedings of the IEEE International Conference on Electronics, Circuits, and Systems, Rodos, Greece, 6 August 2002. [Google Scholar]
- Pétrie, C.S.; Alvin Connelly, J. A noise-based ic random number generator for applications in Cryptography. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000. [Google Scholar] [CrossRef]
- Qi, B.; Chi, Y.-M.; Lo, H.-K.; Qian, L. High-speed quantum random number generation by measuring phase noise of a single-mode laser. Opt. Lett. 2010. [Google Scholar] [CrossRef] [PubMed]
- Schindler, W.; Killmann, W. Evaluation criteria for true (Physical) random number generators used in cryptographic applications. In Proceedings of the 4th International Workshop, Redwood Shores, CA, USA, 13–15 August 2002. [Google Scholar]
- Shannon, C.E. Communication Theory of Secrecy Systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Patidar, V.R.; Sud, K.K. A novel pseudo random bit generator based on chaotic standard map and its testing. Electron. J. Theor. Phys. 2009, 6, 327–344. [Google Scholar]
- Pellicer-Lostao, C.; López-Ruiz, R. Pseudo-random bit generation based on 2D chaotic maps of logistic type and its applications in chaotic cryptography. In Proceedings of the Computational Science and Its Applications—ICCSA 2008, Perugia, Italy, 30 June–3 July 2008. [Google Scholar]
- Shatheesh Sam, I.; Devaraj, P.; Bhuvaneswaran, R.S. Transformed logistic block cipher scheme for image encryption. In Communications in Computer and Information Science; Springer: Berlin, Germany, 2011. [Google Scholar]
- Kocarev, L.; Jakimoski, G. Logistic map as a block encryption algorithm. Phys. Lett. Sect. A Gen. Solid State Phys. 2001. [Google Scholar] [CrossRef]
- Yang, H.; Wong, K.W.; Liao, X.; Wang, Y.; Yang, D. One-way hash function construction based on chaotic map network. Chaos Solitons Fractals 2009. [Google Scholar] [CrossRef]
- Jhansi Rani, P.; Rao, M.S.; Durga Bhavani, S. Design of secure chaotic hash function based on logistic and tent maps. In Communications in Computer and Information Science; Springer: Berlin, Germany, 2011. [Google Scholar]
- Arroyo, D.; Amigó, J.M.; Alvarez, G.; Aplicada, F. On the inadequacy of unimodal maps for cryptographic applications. In XI Reunión Española Sobre Criptología y Seguridad de la Información (XI RECSI); Available online: https://pdfs.semanticscholar.org/7b96/a768e2eeaf86bbe789cfc14f7ece29b97d96.pdf (accessed on 1 November 2019).
- Rezk, A.A.; Madian, A.H.; Radwan, A.G.; Soliman, A.M. Reconfigurable chaotic pseudo random number generator based on FPGA. AEU-Int. J. Electron. Commun. 2019, 98, 174–180. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. In Universality in Chaos, 2nd ed.; Taylor and Francis: New York, NY, USA, 2017; pp. 367–378. [Google Scholar]
- Lü, J.; Chen, G. A new chaotic attractor coined. Int. J. Bifurc. Chaos 2002. [Google Scholar] [CrossRef]
- Elmanfaloty, R.A.; Abou-Bakr, E. Random property enhancement of a 1D chaotic PRNG with finite precision implementation. Chaos Solitons Fractals 2019. [Google Scholar] [CrossRef]
- Kadir, A.; Hamdulla, A.; Guo, W.Q. Color image encryption using skew tent map and hyper chaotic system of 6th-order CNN. Optik (Stuttg) 2014. [Google Scholar] [CrossRef]
- Hasler, M.; Maistrenko, Y.L. An introduction to the synchronization of chaotic systems: Coupled skew tent maps. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 856–866. [Google Scholar] [CrossRef]
- Tan, Z.; Wu, Q. Study of linearly cross-coupled chaotic systems for a random bit generator. In Proceedings of the 2008 International Conference on Computational Intelligence and Security, CIS 2008, Suzhou, China, 13–17 December 2008. [Google Scholar]
- Koyuncu, İ.; Turan Özcerit, A. The design and realization of a new high speed FPGA-based chaotic true random number generator. Comput. Electr. Eng. 2017, 58, 203–214. [Google Scholar] [CrossRef]
- Sundarapandian, V.; Pehlivan, I. Analysis, control, synchronization, and circuit design of a novel chaotic system. Math. Comput. Model. 2012, 55, 1904–1915. [Google Scholar] [CrossRef]
- Avaroğlu, E.; Tuncer, T.; Özer, A.B.; Türk, M. A new method for hybrid pseudo random number generator. Inf. MIDEM 2014, 44, 303–311. [Google Scholar]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Cardoza-Avendaño, L.; Méndez-Ramírez, R. A novel pseudorandom number generator based on pseudorandomly enhanced logistic map. Nonlinear Dyn. 2017, 87, 407–425. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Ma, J.; He, H. A pseudorandom number generator based on piecewise logistic map. Nonlinear Dyn. 2016, 83, 2373–2391. [Google Scholar] [CrossRef]
- Avaroğlu, E.; Tuncer, T.; Özer, A.B.; Ergen, B.; Türk, M. A novel chaos-based post-processing for TRNG. Nonlinear Dyn. 2015, 81, 189–199. [Google Scholar] [CrossRef]
- François, M.; Defour, D.; Negre, C. A fast chaos-based pseudo-random bit generator using binary64 floating-point arithmetic. Informatica 2014, 38, 115–124. [Google Scholar]
- Rostami, M.J.; Shahba, A.; Saryazdi, S.; Nezamabadi-pour, H. A novel parallel image encryption with chaotic windows based on logistic map. Comput. Electr. Eng. 2017, 62, 384–400. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image Vis. Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Patidar, V.; Pareek, N.K.; Sud, K.K. A new substitution-diffusion based image cipher using chaotic standard and logistic maps. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3056–3075. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Abundiz-Pérez, F.; López-Gutiérrez, R.M.; Acosta Del Campo, O.R. A RGB image encryption algorithm based on total plain image characteristics and chaos. Signal Process. 2015, 109, 119–131. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications—Special Pub. 800-22—Rev. 1; NIST Spec. Publ. 800-22; Natl. Inst. Stand. Technol. (NIST): Gaithersburg, MD, USA, 2010.
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Kahan, W. IEEE Standard 754 for Binary Floating-Point Arithmetic. Lect. Notes Status IEEE 1996, 754, 11. [Google Scholar]
- Wang, L.; Cheng, H. Pseudo-Random Number Generator Based on Logistic Chaotic System. Entropy 2019, 21, 960. [Google Scholar] [CrossRef]
- Behnia, S.; Akhavan, A.; Akhshani, A.; Samsudin, A. A novel dynamic model of pseudo random number generator. J. Comput. Appl. Math. 2011, 235, 3455–3463. [Google Scholar] [CrossRef][Green Version]
- Li-Jiang, Y.; Tian-Lun, C. Application of chaos in genetic algorithms. Commun. Theor. Phys. 2002, 38, 168. [Google Scholar] [CrossRef]
- Guo, Z.; Cheng, B.; Ye, M.; Cao, B. Self-adaptive chaos differential evolution. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin, Germany, 2006. [Google Scholar]
- Khan, M.A.; Jeoti, V. On the enlargement of robust region of chaotic tent map for the use in key based substitution-box (S-Box). J. Comput. Sci. 2015, 11, 517–525. [Google Scholar] [CrossRef][Green Version]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).