Abstract
We consider a robust design problem for achieving max-min fairness amongst users in an uplink non-orthogonal multiple access system under imperfect channel state information. Contrary to the conventional approach adopted in the literature, we propose an optimal decoding order-based successive interference cancellation technique by introducing new binary variables, which results in a difficult class of mixed-integer nonconvex optimization problem. For a practical application, we devise an efficient suboptimal solution based on the inner convex approximation framework, which solves a second-order-cone program at each iteration. Simulation results are provided to demonstrate its performance gain over state-of-the-art designs. The proposed design also yields data rates close to those obtained by an exhaustive search method.
1. Introduction
Power domain non-orthogonal multiple access (NOMA) has recently been recognized as a promising solution for next generation of mobile communications, due to its capability of delivering higher throughput, improved reliability and increased spectral efficiency [1,2]. Contrary to the well-known water-filling method, NOMA aims at concurrently allocating different power levels to the users over the same spectrum. In particular, NOMA tends to allocate more power to the users with poorer channel conditions to guarantee the user fairness, while users in better channel conditions benefit from canceling the strong interference by using a successive interference cancellation (SIC) technique [3].
In downlink NOMA systems, SIC technique should be performed at users who have high processing power, especially in the case that the number of users in one resource block is large. However, the probability of successful implementation of SIC may decrease gradually when the number of users increases [4]. Therefore, a popular technique used in downlink NOMA systems is either to pair two users or to group a few users into one cluster with distinct channel conditions.
Compared to downlink NOMA, there has been less attention on uplink (UL) NOMA (see [2] and references therein). In a typical scenario of two-user uplink NOMA (i.e., users i and j), SIC is carried out at the base station (BS) to detect the signal of user i first by treating user j’s signal as interference. By using the SIC technique, it re-encodes the recovered signal and subtracts the interference imposed by user i before decoding the user j’s signal. It is evident that the SIC decoding order has a strong impact on the individual rate. The works in [5,6] considered a random decoding order with respect to the users’ indices, leading to a suboptimal solution. Recently, the users’ descending channel gain-based decoding order has been widely investigated in [7,8,9,10,11], which has the advantage in terms of fairness. In this scheme, the signal of user with the strongest channel gain is decoded first and the signal of user with the weakest channel gain is decoded last. For the case of perfect channel state information (CSI), the strongest user can transmit with full power, while the throughput of the weakest user is clearly improved due to no multiuser interference (MUI). However, these results do not hold true when imperfect CSI is taken into account. The reason is that the strongest user may not be able to transmit with full power due to the additional term appearing in the denominator of the signal-to-interference-plus-noise ratio (SINR) function caused by the channel estimation error. To the authors’ best knowledge, optimization of individual rates of UL-NOMA systems taking the imperfect CSI into account has not been investigated.
In this paper, we formulate a novel optimization problem to maximize the minimum data rate among all users in the UL-NOMA system. Unlike the aforementioned works, the problem of interest considers the following completely new issues: (i) a joint uplink users’ decoding order and power control is investigated to better exploit different channel conditions, which is done by introducing binary association variables; and () imperfect channel state information (CSI) due to estimation inaccuracies is taken into account. In addition, the MUI cannot be completely removed by SIC, and thus a robust receiver together with an efficient power control method is crucial to guarantee user fairness. Even for a fixed decoding order, the resulting problem is known to be NP-hard, and, thus, is nonconvex. We first derive an optimal decoder based on the minimum mean-square error and SIC (MMSE-SIC) at the BS to arrive at the robust design problem. To approximately solve this problem, we relax binary association variables to be continuous and develop a low-complexity iterative algorithm based on the inner approximation (IA) framework [12,13], which can be transformed into a second-order cone programming (SOCP) at each iteration. The proposed algorithm is proved to converge monotonically to at least locally optimal solution of the continuous relaxation problem. Finally, extensive numerical results are provided to confirm that our proposed approach is efficient in terms of the rate fairness and robustness against the estimation error under imperfect CSI.
Notation: , and are the transpose, Hermitian transpose and trace of a matrix , respectively. denotes the Euclidean norm of a matrix or vector, while stands for the absolute value of a complex scalar. and denote the statistical expectation and the real part of the argument, respectively. represents a random vector following a complex circularly symmetric Gaussian distribution with mean and covariance matrix . denotes the matrix of all ones.
2. System Model
This section describes UL-NOMA system model and formulates an optimization problem for achieving max-min fairness among all users.
2.1. Signal Model
In a UL system, as illustrated in Figure 1, we consider a BS equipped with N antennas serving a set of K single-antenna UL users, denoted by . Assuming a frequency-flat fading channel, the received signal at the BS is
where is the channel vector from the kth UL user, denoted by , to the BS; and with are the transmission power coefficient and the transmit data symbol of , respectively; and is the additive white Gaussian noise at the BS.
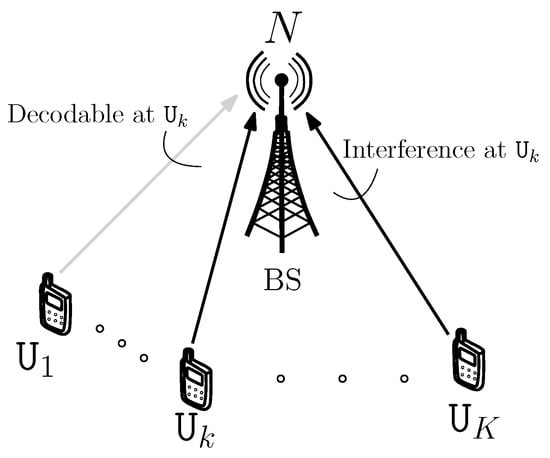
Figure 1.
Illustration of a UL-NOMA system with assumption that the decoding order is from to . A BS with N antennas serves K single-antenna users.
Let us introduce binary association variables to represent the SIC decoding order at the BS as
By following the NOMA principle, the following constraints must be satisfied:
where . From Equation (2) and by applying MMSE-SIC receiver [14], the data rate of can be written as
where the SINR is defined by
with , , and . It is worth mentioning that the interference-plus-noise matrix experienced by is simplified to if the SIC decoding order is assumed to be from 1 to K [14].
2.2. CSI Model
For imperfect CSI, each channel vector is modeled as , where is the channel estimate and is the CSI error due to estimation inaccuracies. In this paper, we assume that is independent of and distributed as , where is the variance of the CSI error and assumed to be known a priori [15]. Since is unbounded, the actual rate cannot be considered as a design metric. Toward a robust design, we consider the following worst-case achievable rate of :
where .
3. Problem Formulation
3.1. Optimization Problem Formulation
We are interested in the robust optimization problem for achieving rate fairness, which can be mathematically expressed as
where is the transmit power budget of . Herein, Equation (7b) represents the power constraint at each user while the constraints in Equations (7c)–(7f) guarantee the SIC-based decoding order for K users. The constraint in Equation (7e) is a direct result from Equation (2). In addition, the constraint in Equation (7f) is sufficient condition to ensure that the BS will decode a single signal at each iteration, which can be explained intuitively as follows. Assuming that BS decodes the signals following the order from to . The optimal values of should have the following form:
It can be seen that the object in Equation (7a) is a non-concave and non-smooth function and Equation (7f) is also a non-convex constraint, which result in the mixed-integer non-convex optimization problem in Equation (7).
3.2. Relations to Exhaustive Search and Random SIC
Exhaustive Search
With K users, there are possible cases of decoding order, in which the following subproblem for given :
corresponds to one possible case. In other words, it requires to solve subproblems of Equation (8), and the final optimal solution corresponds to the solution of the subproblem having the highest objective value. It is clear that the exhaustive search method can provide the global optimal solution, but its computational complexity is extremely high, especially when K increases. Thus, the solution of Equation (8) is considered the benchmark (an upper bound) for our considered problem.
On the other hand, the random decoding order at the BS, so-called random SIC, is widely used in [14,16] due to its low complexity. Clearly, the optimization problem based on random SIC is a subproblem of Equation (8), which can be stated as:
where is derived from for a random value of .
It can be foreseen that the two problems in Equations (8) and (9) are also non-convex due to their non-concave objective functions. However, the solutions for these two problems can be found by applying the proposed algorithm for solving Equation (7) presented shortly, after some slight modifications.
4. Proposed Method for Solving Equation (7)
In this section, we derive an optimal MMSE-SIC receiver to further simplify the worst-case achievable rate in Equation (6) and then propose an IA-based algorithm to solve the resulting nonconvex problem.
4.1. Robust MMSE-SIC Receiver
We first derive an optimal MMSE-SIC receiver to further simplify Equation (6). Let and be the post-SIC signal and the output of the optimal MMSE-SIC receiver corresponding to under imperfect CSI, respectively.
Lemma 1.
The optimal MMSE-SIC receiver can be obtained by solving
which is given as
where . By treating CSI errors as noise, the worst-case achievable rate of in Equation (6) can be re-expressed as
where
Proof.
The proof of Lemma 1 is given in Appendix A. □
4.2. Proposed IA-Based Algorithm
To tackle the discrete part of Equation (7), we first relax binary variables to be continuous, which is a standard step in solving a mixed-integer problem. To this end, we consider the following continuous relaxation of Equation (7):
which can be rewritten equivalently as
where is a newly introduced variable. It can be easily foreseen that Equation (15b) must hold with equality at optimum, leading to the equivalence between Equations (14) and (15). Since the objective is monotonic in its argument, we now focus on convexifying the nonconvex constraints in Equations (15b) and (15g).
Convex approximation of the constraint in Equation (15b): Let be a feasible point found at iteration i of the proposed IA algorithm presented shortly. By customizing the inequality [16] (Equation (20)) a global lower bound of is given by
where
with
We note that and are constant, while is a nonconvex function due to the product of , leading to a non-concavity of the right-hand side of Equation (16). We now introduce new variables to iteratively replace Equation (15b) by
where
From [17] (Equation (B.1)) we make use of inequality
to convexify Equation (17a) as
where
Note that is concave and satisfies .
Convex approximation of constraint in Equation (15g): We note that Equation (15g) is a nonconvex constraint due to the quasi-convexity of the left-hand side. Herein, we define and to rewrite Equation (15g) equivalently as
To overcome the nonsmooth function , we consider the following lower bound:
which is done by using the smooth approximation via the log-sum-exp function with being a predefined positive large number. In Equation (22), is a convex function with respect to , which can be easily proved by checking its Hessian matrix. By using the IA method, we iteratively replace Equation (21) by the following convex constraint:
where
is the lower bound concave function of at the feasible point .
Summing up, the approximate convex program of Equation (14) solved at iteration is given by
We note that the problem in Equation (25) can be cast as an SOCP since all the constraints are linear and quadratic.
Convergence and complexity analysis: After solving the problem in Equation (25) at each iteration, the involved variables are updated for the next iteration until convergence. Since the approximate functions in Equations (19) and (23) satisfy the IA properties presented in [13], the non-decreasing sequence of the objective values in Equation (25a) is not difficult to see (i.e., ). In addition, the proposed iterative algorithm is guaranteed to converge due to the limited transmit power. Following the same convergence analysis in [13], we can prove that the optimal solution obtained from Equation (25) satisfies the Karush–Kuhn–Tucker (KKT) conditions of Equation (14). The problem in Equation (25) has real variables and conic constraints. Then, the worst-case per-iteration complexity for solving Equation (25) is .
Recovering binary solution from continuous relaxation: We have numerically observed that some relaxed association variables obtained from solving Equation (25) do not take binary values. To guarantee the feasibility of Equation (7), we further consider a post-processing. We first introduce the rounding process, i.e., , to obtain exact binary values of the association variables, and then re-run the algorithm with fixed to find the optimal solution of by solving the following convex program:
The proposed method for solving Equation (7) is summarized in Algorithm 1.
| Algorithm 1 Proposed IA-based Algorithm for Solving Equation (7) |
|
5. Numerical Results
In this section, we demonstrate the effectiveness of the proposed method by using SeDuMi solver in MATLAB environment. We consider a small-cell network with a centered-BS serving users, which are randomly and uniformly distributed in the area from 10 m to 100 m. The path loss (in dB) from a user to BS is modeled as , where d is the distance in meters. The signal bandwidth and noise power spectral density are set to 10 MHz and dBm/Hz, respectively. All the users are assumed to use the same power budget, i.e., . The variance of the CSI errors is modeled as , where capture a variety of CSI acquisition schemes and denotes the SNR of the kth link [15]. For performance comparison, “Exhaustive search” and “Random SIC” schemes (i.e., (8) and (9)) are considered. In addition, the SIC decoding order based on the descending channel gains, called “SIC-channel gain” for short, is also investigated [18].
We evaluate the effect of imperfect CSI on different resource allocation schemes as a function of for in Figure 2a and in Figure 2b. As expected, Algorithm 1 yields the max-min rate very close to the exhaustive search method, especially for a small . However, we note that the exhaustive search method requires solving subproblems of the power control, which is computationally expensive even for networks of small-to-medium size, and thus it only acts as a benchmark. As can be seen, the proposed algorithm significantly outperforms the random SIC and SIC-channel gain schemes. For corresponding to the case of perfect CSI, the SIC-channel gain offers better user fairness compared to the random SIC, and performs close to the proposed algorithm when . However, the performance of this scheme drops quickly in the case of imperfect CSI (i.e., ) and tends to worse than that of other schemes. This also supports our statement given in Section 1. Another observation is that the post-processing procedure (i.e., Step 8 in Algorithm 1) is needed to refine the optimal solution.
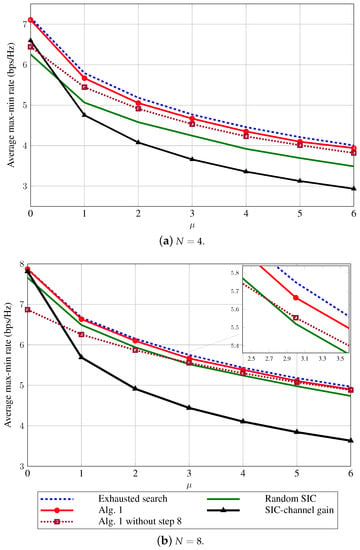
Figure 2.
Comparison of different schemes in terms of average max-min rate dBm and .
In Figure 3, we demonstrate the robustness of Algorithm 1. Herein, “Non-Robust” refers to the problem in Equation (7), where we use the presumed CSIs (rather than the true ones) to compute the solutions and then evaluate the resultant worst-case achievable rate. We can see that the proposed algorithm achieves much better max-min rate performance compared to the non-robust design. Moreover, the performance gap is found to rapidly increase as increases.
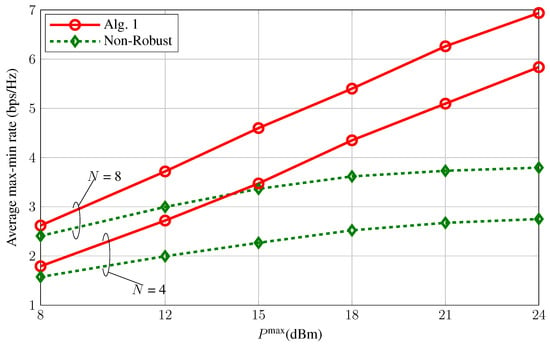
Figure 3.
Improvement of average max-min rate based on robust design ( and ).
In Figure 4, we show the impact of the number of users on the system performance. We have numerically observed that the exhaustive search method may be infeasible in terms of the computational complexity when due to the requirement of solving subproblems of the power control. It can be seen that the average max-min rates of all the considered schemes are dramatically degraded as K increases. Again, our proposed algorithm provides better performance compared to random SIC and SIC-channel gain, and its performance gains are even more higher when K is relatively large. This result further confirms the importance of jointly optimizing SIC decoding order.
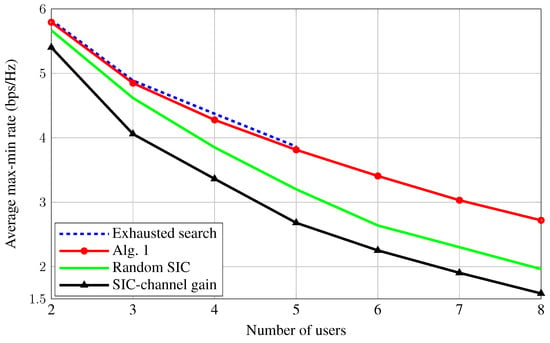
Figure 4.
Average max-min rate versus the number of users dBm, , and .
Figure 5 illustrates the average max-min rate versus . We note that increasing also results in a strong severe interference situation. Thus, when becomes larger, the performance gain of the proposed scheme over the random SIC one is more remarkable, thanks to the optimal SIC decoding order. Figure 6 plots the cumulative distribution functions (CDFs) of the max-min rate. Again, the proposed scheme tends to outperform the random SIC scheme when the number of receive antennas is relatively small.
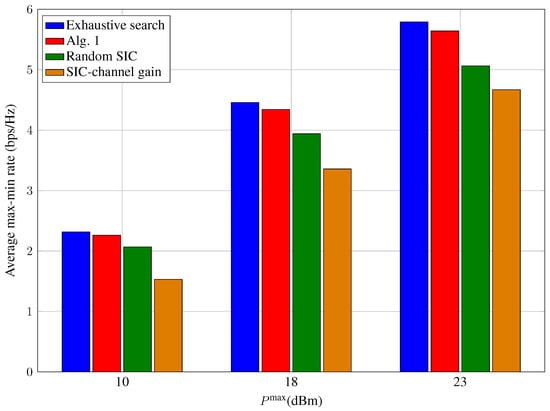
Figure 5.
Average max-min rate versus with different schemes ( and ).
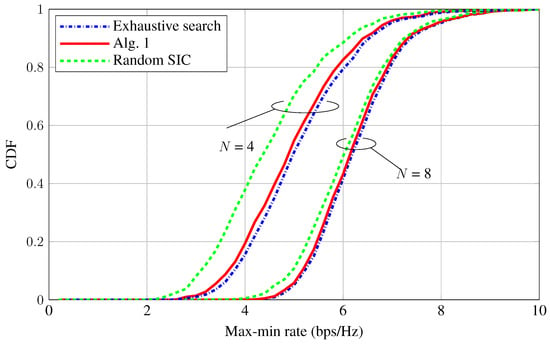
Figure 6.
CDF of max-min rate performance ( and ).
6. Conclusions
We propose a novel optimization problem of maximizing the minimum rate among all users by jointly considering users’ decoding order and transmit power in a UL-NOMA system. The IA-based algorithm has been developed to solve the nonconvex optimization problem, which can be cast as an SOCP. Numerical results reveal that the proposed algorithm is very efficient in the scenario of strong network interference. In addition, the robustness of the proposed design against CSI errors was confirmed.
Author Contributions
Conceptualization, V.-P.B., H.V.N. and V.-D.N.; methodology, V.-P.B. and V.-D.N.; software, V.-P.B. and H.V.N.; validation, V.-P.B., H.V.N., V.-D.N. and O.-S.S.; formal analysis, V.-P.B., H.V.N. and V.-D.N.; investigation, V.-P.B., H.V.N. and V.-D.N.; resources, O.-S.S.; data curation, V.-P.B., H.V.N. and V.-D.N.; writing—original draft preparation, V.-P.B.; writing—review and editing, H.V.N., V.-D.N. and O.-S.S.; visualization, V.-P.B. and V.-D.N.; supervision, O.-S.S.; project administration, V.-D.N. and O.-S.S.; and funding acquisition, O.-S.S.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. 2017R1D1A1B03030436).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ICMC | Information Communication, Materials, and Chemistry Convergence |
| NOMA | Non-orthogonal multiple access |
| SIC | Successive interference cancellation |
| UL | Uplink |
| BS | Base station |
| NP-Hard | Non-deterministic polynomial-time hard |
| MMSE | Minimum mean-square error |
| IA | Inner approximation |
| SOCP | Second-order cone programming |
| SINR | Signal-to-interference-plus-noise ratio |
| KKT | Karush–Kuhn–Tucker |
| CSI | Channel state information |
| CDF | Cumulative distribution function |
Appendix A
We note that a detailed analysis for Lemma 1 with similar structure can be found, e.g., in Appendix C of [19]. However, to be self-contained, we follow the same steps as those in [19] but customize them to our considered problem. It follows from that
where . Then, in Equation (11) is easily found by solving
which is achieved at , as shown in Equation (11). Next, by treating CSI errors as noise, the SINR of can be expressed as
As a result, we can further simplify as
Making use of the Woodbury matrix identity to have
we arrive at the compact form of SINR in Equation (13).
References
- Ding, Z.; Liu, Y.; Choi, J.; Sun, Q.; Elkashlan, M.I.C.; Poor, H. Application of Non-Orthogonal Multiple Access in LTE and 5G Networks. IEEE Commun. Mag. 2017, 55, 185–191. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Ding, Z.; Nallanathan, A.; Hanzo, L. Nonorthogonal Multiple Access for 5G and Beyond. Proc. IEEE 2017, 105, 2347–2381. [Google Scholar] [CrossRef]
- Nguyen, V.N.; Tuan, H.; Duong, T.; Poor, H.; Shin, O. Precoder Design for Signal Superposition in MIMO-NOMA Multicell Networks. IEEE J. Sel. Areas Commun. 2017, 35, 2681–2695. [Google Scholar] [CrossRef]
- Muller, R. Power and Bandwidth Efficiency of Multiuser Systems with Random Spreading; Shaker: Aachen, Germany, 1999. [Google Scholar]
- Ding, Z.; Schober, R.; Poor, H. A General MIMO Framework for NOMA Downlink and Uplink Transmission Based on Signal Alignment. IEEE Trans. Wirel. Commun. 2016, 15, 4438–4454. [Google Scholar] [CrossRef]
- Wang, H.; Leung, S.; Song, R. Precoding Design for Two-Cell MIMO-NOMA Uplink with CoMP Reception. IEEE Commun. Lett. 2018, 22, 2607–2610. [Google Scholar] [CrossRef]
- Gao, Y.; Xia, B.; Xiao, K.; Chen, Z.; Li, X.; Zhang, S. Theoretical Analysis of the Dynamic Decode Ordering SIC Receiver for Uplink NOMA Systems. IEEE Commun. Lett. 2017, 21, 2246–2249. [Google Scholar] [CrossRef]
- Pischella, M.; Le Ruyet, D. NOMA-Relevant Clustering and Resource Allocation for Proportional Fair Uplink Communications. IEEE Wirel. Commun. Lett. 2019, 8, 873–876. [Google Scholar] [CrossRef]
- Salehi, M.; Tabassum, H.; Hossain, E. Meta Distribution of SIR in Large-Scale Uplink and Downlink NOMA Networks. IEEE Trans. Commun. 2019, 67, 3009–3025. [Google Scholar] [CrossRef]
- Ali, M.; Tabassum, H.; Hossain, E. Dynamic User Clustering and Power Allocation for Uplink and Downlink Non-Orthogonal Multiple Access (NOMA) Systems. IEEE Access 2016, 4, 6325–6343. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, R.; Song, R.; Leung, S. A Novel Power Minimization Precoding Scheme for MIMO-NOMA Uplink Systems. IEEE Commun. Lett. 2018, 22, 1106–1109. [Google Scholar] [CrossRef]
- Marks, B.; Wright, G. Technical Note—A General Inner Approximation Algorithm for Nonconvex Mathematical Programs. Oper. Res. 1978, 26, 681–683. [Google Scholar] [CrossRef]
- Beck, A.; Ben-Tal, A.; Tetruashvili, L. A sequential parametric convex approximation method with applications to nonconvex truss topology design problems. J. Glob. Optim. 2009, 47, 29–51. [Google Scholar] [CrossRef]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Maurer, J.; Jalden, J.; Seethaler, D.; Matz, G. Vector Perturbation Precoding Revisited. IEEE Trans. Signal Proc. 2011, 59, 315–328. [Google Scholar] [CrossRef]
- Nguyen, V.; Duong, T.; Tuan, H.; Shin, O.; Poor, H. Spectral and Energy Efficiencies in Full-Duplex Wireless Information and Power Transfer. IEEE Trans. Commun. 2017, 65, 2220–2233. [Google Scholar] [CrossRef]
- Nguyen, V.; Nguyen, H.; Dobre, O.; Shin, O. A New Design Paradigm for Secure Full-Duplex Multiuser Systems. IEEE J. Sel. Areas Commun. 2018, 36, 1480–1498. [Google Scholar] [CrossRef]
- Islam, S.; Durrani, S.; Sadeghi, P. A novel user pairing scheme for functional decode-and-forward multi-way relay network. Phys. Commun. 2015, 17, 128–148. [Google Scholar] [CrossRef]
- Nguyen, H.; Nguyen, V.; Dobre, O.; Wu, Y.; Shin, O. Joint Antenna Array Mode Selection and User Assignment for Full-Duplex MU-MISO Systems. IEEE Trans. Wirel. Commun. 2019, 18, 2946–2963. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).