A Review of Impedance Matching Techniques in Power Line Communications
Abstract
:1. Introduction
2. The Tradeoffs Considered Before Designing an Effective Impedance Matching Network
2.1. The Tradeoff Between Gain and Insertion Loss
2.2. The Tradeoff Between Efficiency and Cost
2.3. The Tradeoff Between Bandwidth and Attenuation
2.4. The Tradeoff Between Matching Region and Structure
3. The Impedance Matching Approaches in PLC
3.1. Based on Matching Methods
3.2. Based on Fixed or Variable Components / Structures
3.3. Based on the Implementation Cost
3.4. Based on Bandwidth
3.5. Based on Impedance Types
3.6. Based on Component Types
3.7. Based on Voltage Levels
3.8. Based on Channel Types
3.9. Based on Transmittal Modes
3.10. Classification of the Impedance Matching Solutions in PLC
4. Future Trends and Works
- In PLC, lumped matching elements, e.g., capacitors and inductors, are usually assumed lossless. In practice, the gain obtained from an impedance matching network can be partly undone by the insertion loss of the matching network in the presence of non-ideal elements. If the matching elements are lossy, traditional impedance matching approaches, such as conjugate matching, do not guarantee maximum power transfer to the receiver. Furthermore, any additional losses to the matching network may be particularly severe at a specific frequency, which will severely degrade efficiency [43]. In PLC, few works have investigated the impedance matching problems when non-ideal matching elements are considered. Therefore, characterizing and minimizing insertion losses of matching networks are important issues to resolve.
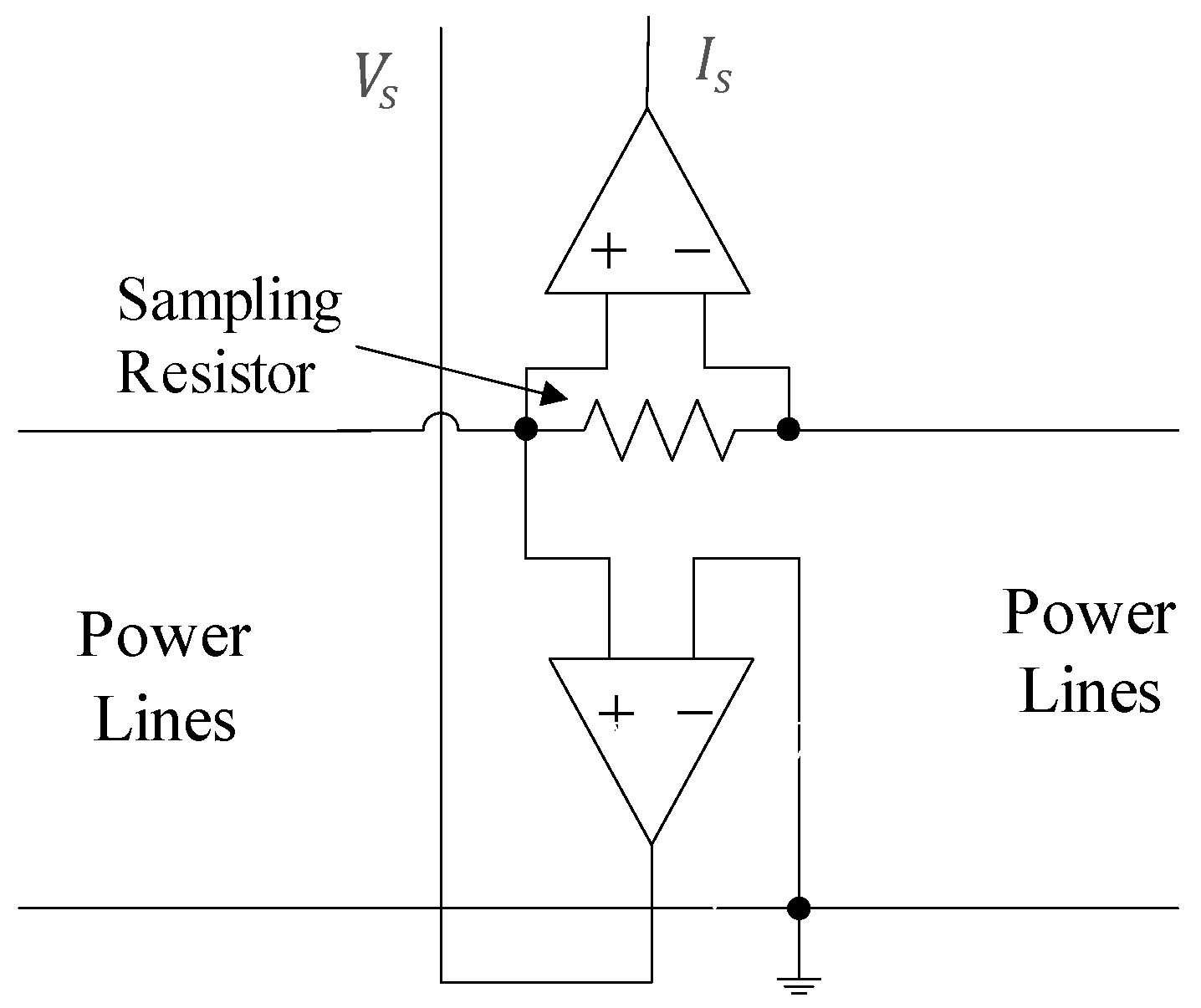
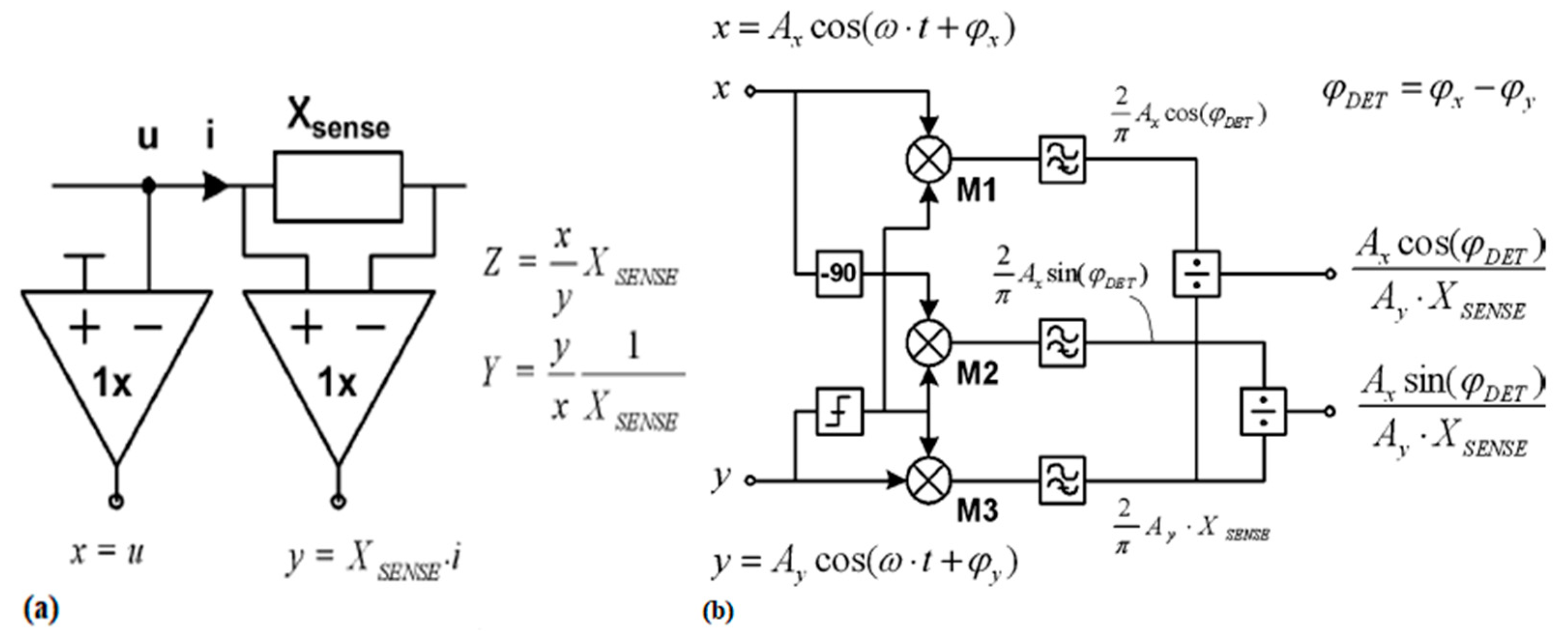
- Inaccurate impedance measurements have a negative impact on the performance of impedance matching solutions. The average power line impedance used in some work, produces poor quality impedance matching circuits. However, the network access impedance that varies with time, frequency and location, leads to impedance measurement challenges. Therefore, designing an accurate and effective impedance measurement circuit is of particular importance.
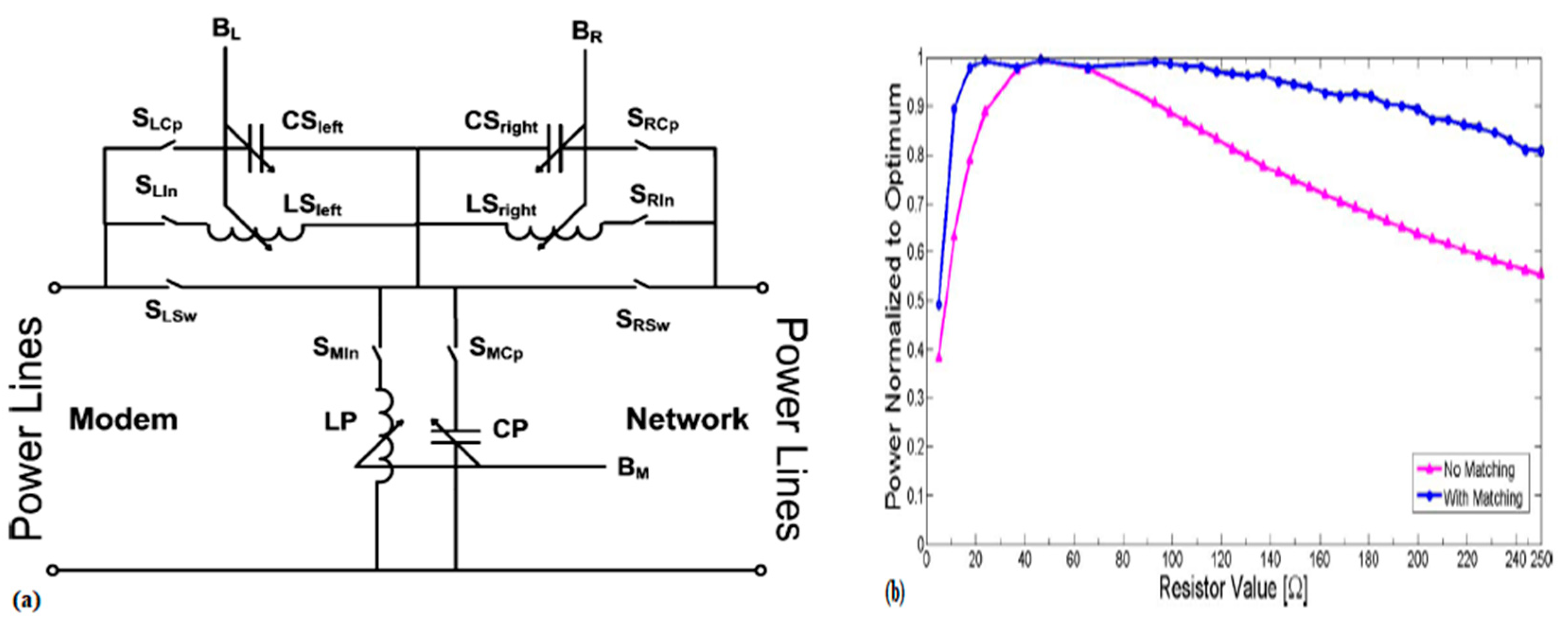
- In practice, matching networks with fewer components are preferred. For PLC, two-element, L-shaped matching networks have been investigated. However, three-element matching networks, which consist of three variable reactance components, facilitate better impedance matching capabilities (because they have a larger matching region than L-shaped networks). For PLC, few researchers have studied three-element matching network solutions required for real-to-complex impedance matching in PLCs, e.g., П-shaped networks and T-shaped networks.
- A large number of passive capacitors and inductors increase the structural complexity and size of the system; these components also impose an extra burden on the control logic for adaptive impedance matching. An ideal adaptive impedance matching system can be implemented by a matching network of tunable capacitors (voltage-controlled) and tunable inductors. However, there are no available tunable inductors. Therefore, implementing a tunable or active inductor with large variable values is an important issue to be addressed.
- More recently, IBFD has been introduced to the PLC context. In IBFD-PLC, the main task to solve is to enhance SI reduction or echo cancellation when designing a PLC-IBFD system. The SI or echo that influences communication reliability will emerge when there is an impedance mismatch between the hybrid coupler and the power line channel. Therefore, designing an effective hybrid coupler with impedance matching is an important issue to be solved.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ferreira, H.C.; Lampe, L.; Newbury, J.; Swart, T.G. Power Line Communications: Theory and Applications for Narrowband and Broad-band Communications over Power Lines; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Schwartz, M. Carrier-wave telephony over power lines: Early history [History of Communications]. IEEE Commun. Mag. 2009, 47, 14–18. [Google Scholar] [CrossRef]
- Costa, L.G.S.; Queirz, A.C.M.; Adebisi, B.; Ribeiro, M.V. Coupling for power line communication: A Survey. J. Commun Inf. Syst. 2017, 32, 8–22. [Google Scholar] [CrossRef]
- Sanchez-Pacheco, F.J.; Sotorrio-Ruiz, P.J.; Heredia-Larrubia, J.R.; Perez-Hidalgo, F.; Cardona, M.S. PLC-Based PV Plants Smart Monitoring System: Field Measurements and Uncertainty Estimation. IEEE Trans. Instrum. Meas. 2014, 63, 2215–2222. [Google Scholar] [CrossRef]
- Choi, M.; Ju, S.; Lim, Y. Design of integrated meter reading system based on power-line communication. In Proceedings of the 2008 IEEE International Symposium on power line communications and its applications, Jeju City, Korea, 2–4 April 2008. [Google Scholar]
- Li, M.; Lin, H. Design and Implementation of Smart Home Control Systems Based on Wireless Sensor Networks and Power Line Communications. IEEE Trans. Ind. Electron. 2015, 62, 4430–4442. [Google Scholar] [CrossRef]
- Vitale, G. Characterization of a DC grid for Power Line Communications in smart grids. In Proceedings of the Control and Modeling for Power Electronics (COMPEL), Santander, Spain, 22–25 June 2014. [Google Scholar]
- Sirinamaratana, P.; Leelarasmee, E.; Pora, W. A Series DC Power Line Communication and its application to monitoring photo-voltaic strings. J. Circuits Syst. Comput. 2013, 22, 1340010. [Google Scholar] [CrossRef]
- Mao, W.; Zhang, X.; Cao, R.; Wang, F.; Zhao, T.; Xu, L. A Research on Power Line Communication Based on Parallel Resonant Coupling Technology in PV Module Monitoring. IEEE Trans. Ind. Electron. 2018, 65, 2653–2662. [Google Scholar] [CrossRef]
- Napoli, F.D.; Guerriero, P.; D’Alessandro, V.; Daliento, S. A power line communication on DC bus with photovoltaic strings. In Proceedings of the 3rd Renewable Power Generation Conference, Naples, Italy, 24–25 September 2014. [Google Scholar]
- Sirinamaratana, P.; Leelarasmee, E. Circuits for data communication through DC power line in solar farm. In Proceedings of the IEEE International Conference of Electron Devices and Solid-state Circuits (EDSSC), Hong Kong, China, 3–5 June 2013. [Google Scholar]
- Shukla, A.; Dahiya, R. 8-PSK Power Line Communication Analysis and Modeling for Renewable Smart Grids. In Proceedings of the 2015 International Conference on Signal Processing and Communication (ICS), Noida, India, 16–18 March 2015. [Google Scholar]
- Degauque, P.; Stievano, I.; Pignari, S.; Degardin, V.; Canavero, F. Power-Line Communication: Channel Characterization and Modeling for Transportation Systems. IEEE IEEE Veh. Technol. Mag. 2015, 10, 28–37. [Google Scholar] [CrossRef] [Green Version]
- Takanashi, M.; Takahashi, A.; Tanaka, H.; Hayashi, H. High-Voltage Power Line Communication in a Hybrid Vehicle. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2017, 100, 1705–1713. [Google Scholar] [CrossRef]
- Barmada, S.; Bellanti, L.; Raugi, M.; Tucci, M. Analysis of Power-Line Communication Channels in Ships. IEEE Trans. Veh. Technol. 2010, 59, 3161–3170. [Google Scholar] [CrossRef]
- Antoniali, M.; Tonello, A.M.; Lenardon, M.; Qualizza, A. Measurements and analysis of PLC channels in a cruise ship. In Proceedings of the IEEE International Symposium Power Line Communications Applications, Udine, Italy, 3–6 April 2011. [Google Scholar]
- Degardin, V.; Junqua, I.; Lienard, M.; Degauque, P.; Bertuol, S. Theoretical Approach to the Feasibility of Power-Line Communication in Aircrafts. IEEE Trans. Veh. Technol. 2013, 62, 1362–1366. [Google Scholar] [CrossRef]
- Chedid, M.; Belov, I.; Leisner, P. Low Power High Bandwidth Power-Line Communication Network for Wearable Applications. In Proceedings of the Fifth International Conference on Body Area Networks, New York, NY, USA, 10–12 September 2010. [Google Scholar]
- Lin, H.; Hu, J.; Zhou, X.; Lu, Z. New DC Grid Power Line Communication Technology Used in Networked LED Driver. Energies 2018, 11, 3531. [Google Scholar] [CrossRef]
- Rensburg, P.A.J.V.; Snyders, A.J.; Ferreira, H.C. Modeling of Coupling Diversity for Extra-Low-Voltage Power-Line Communication Networked LED Lighting in Smart Buildings. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 224–1234. [Google Scholar]
- Héla, G.; Bali, M.C.; Duval, F. Coupling interface circuit design for experimental characterization of the narrowband power line communication channel. In Proceedings of the 2012 IEEE International Symposium on Electromagnetic Compatibility, Pittsburgh, PA, USA, 6–10 August 2012. [Google Scholar]
- Ferreira, H.C.; Grove, H.M.; Hooijen, O. Power line communications: An overview. In Proceedings of the IEEE. AFRICON’96, Stellenbosch, South Africa, 27–27 September 1996. [Google Scholar]
- Tang, L.T.; So, P.L.; Gunawan, E. Characterization of power distribution lines for high-speed data transmission. In Proceedings of the 2000 International Conference on Power System Technology, Perth, Australia, 4–7 December 2000. [Google Scholar]
- Rasool, B.; Rasool, A.; Khan, I. Impedance Characterization of Power Line Communication Networks. Arab. J. Sci. Eng. 2014, 39, 6255–6267. [Google Scholar] [CrossRef]
- Esmailian, T.; Kschischang, F.R.; Gulak, P.G. In-building power lines as high-speed communication channels: Channel characterization and a test channel ensemble. Int. J. Commun. Syst. 2003, 16, 381–400. [Google Scholar] [CrossRef]
- Bausch, J.; Kistner, T.; Babic, M. Characteristics of Indoor Power Line Channels in the Frequency Range 50-500 kHz. In Proceedings of the 2006 IEEE International Symposium on Power Line Communications and Its Applications, Orlando, FL, USA, 30 October 2006. [Google Scholar]
- Joshi, R.P.; Bhosale, S.; Patil, P.H. Analysis and Simulation of Noise in Power Line Communication Systems. In Proceedings of the First International Conference on Emerging Trends in Engineering and Technology, Washington, DC, USA, 16–18 July 2008. [Google Scholar]
- Katayama, M.; Yamazato, T.; Okada, H. A mathematical model of noise in narrowband power line communication systems. IEEE J. Sel. Areas Commun. 2006, 24, 1267–1276. [Google Scholar] [CrossRef]
- Huck, T.; Schirmer, J.; Hogenmuller, T. Tutorial about the implementation of a vehicular high speed communication system. In Proceedings of the International Symposium on Power Line Communications and Its Applications, Vancouver, BC, Canada, 6–8 April 2005. [Google Scholar]
- Lin, J.; Zhao, T.; Liu, G.Q. The design of active power filter based on power line carrier communication. Adv. Mater. Res. 2013, 614, 1587–1590. [Google Scholar]
- Rastogi, M.; Mitra, D.K.; Bhattacharya, A. A Novel Implementation of Bidirectional Coupling Circuit for Broadband, High-Voltage, Power-Line Communications. In Proceedings of the 2005 Asia-Pacific Conference on Communications, Perth, Australia, 3–5 October 2005. [Google Scholar]
- Zhu, Q.; Chen, Z.; He, X. Resource Allocation for Relay-Based OFDMA Power Line Communication System. Electronics 2019, 8, 125. [Google Scholar] [CrossRef]
- Antoniali, M.; Piante, M.D.; Tonello, A.M. PLC noise and channel characterization in a compact electrical car. In Proceedings of the IEEE 17th International Symposium on Power Line Communications and Its Applications, Johannesburg, South Africa, 24–27 March 2013. [Google Scholar]
- Degardin, V.; Lienard, M.; Degauque, P. Impulsive Noise Characterization of In-Vehicle Power Line. IEEE Trans. Electromagn. Compat. 2008, 50, 861–868. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Petit, P.; Sawicki, J.P. DC Power-line Communication based Network Architecture for HVDC Distribution of a Renewable Energy System. Energy Procedia 2014, 50, 147–154. [Google Scholar] [CrossRef] [Green Version]
- Marrocco, G.; Statovci, D.; Trautmann, S. A PLC broadband channel simulator for indoor communications. In Proceedings of the 17th IEEE International Symposium on Power Line Communications and Its Applications, Johannesburg, South Africa, 24–27 March 2013. [Google Scholar]
- Tonello, A.M.; Versolatto, F.; Pittolo, A. In-Home Power Line Communication Channel: Statistical Characterization. IEEE Trans. Commun. 2014, 62, 2096–2106. [Google Scholar] [CrossRef]
- Mohammadi, M.; Lampe, L.; Lok, M. Measurement study and transmission for in-vehicle power line communication. In Proceedings of the 2009 IEEE International Symposium on Power Line Communications and Its Applications, Dresden, Germany, 29 March–1 April 2009. [Google Scholar]
- Barmada, S.; Raugi, M.; Tucci, M. Power line communication in a full electric vehicle: Measurements, modelling and analysis. In Proceedings of the 2010 IEEE International Symposium on Power Line Communications and Its Applications, Rio de Janeiro, Brazil, 28–31 March 2010. [Google Scholar]
- Stievano, I.S.; Canavero, F.G.; Garcia, V.W.R. Multipath modeling of automotive power line communication channels. IEEE Trans. Ind. Inf. 2014, 10, 1381–1391. [Google Scholar] [CrossRef]
- Gu, Q.; Luis, J.R.D.; Morris, A.S.I. An Analytical Algorithm for Pi-Network Impedance Tuners. IEEE Trans. Circuits Syst. Regul. Pap. 2011, 58-I, 2894–2905. [Google Scholar] [CrossRef]
- Gu, Q. RF Tunable Devices and Subsystems: Methods of Modeling, Analysis and Applications; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Chen, Y.; Chiu, C. Insertion Loss Characterization of Impedance Matching Networks for Low-Power Rectennas. IEEE Trans Compon. Packag. Manuf. Technol. 2018, 8, 1632–1641. [Google Scholar] [CrossRef]
- Van Bezooijen, A.; De Jongh, M.A.; Van Straten, F.; Mahmoudi, R.; Van Roermund, A.H. Adaptive Impedance-Matching Techniques for Controlling L Networks. IEEE Trans. Circuits Syst. Regul. Pap. 2010, 57, 495–505. [Google Scholar] [CrossRef]
- Freitas, V.; Arnould, J.D.; Ferrari, P. General expression for tunable matching network efficiency in the case of complex impedances. Microw. Opt. Technol. Lett. 2015, 57, 1160–1166. [Google Scholar] [CrossRef]
- Han, Y.; Perreault, D.J. Analysis and Design of High Efficiency Matching Networks. IEEE Trans. Power Electron. 2006, 21, 1484–1491. [Google Scholar] [CrossRef]
- Martins, G.C.; Serdijn, W.A. Multistage Complex-Impedance Matching Network Analysis and Optimization. IEEE Trans. Circuits Syst. Express Br. 2016, 63, 833–837. [Google Scholar] [CrossRef] [Green Version]
- Chappidi, C.K.R.; Sengupta, K. Globally Optimal Matching Networks with Lossy Passives and Efficiency Bounds. IEEE Trans. Circuits Syst. Regul. Pap. 2018, 65, 257–269. [Google Scholar] [CrossRef]
- Chappidi, C.K.R.; Sengupta, K. Methods for finding globally maximum-efficiency impedance matching networks with lossy passives. In Proceedings of the 2015 IEEE Custom Integrated Circuits Conference (CICC), San Jose, CA, USA, 28–30 September 2015. [Google Scholar]
- Stiri, S.; Chaoub, A.; Maliki, T.E. Realization of a low-cost impedance matching circuit for stable power line communications: From testbeds to practical implementation. In Proceedings of the 19th IEEE Mediterranean Electrotechnical Conference (MELECON), Marrakech, Morocco, 2–7 May 2018. [Google Scholar]
- Farias, L.D.R.; Monteiro, L.F.; Leme, M.O. Empirical Analysis of the Communication in Industrial Environment Based on G3-Power Line Communication and Influences from Electrical Grid. Electronics 2018, 7, 1–17. [Google Scholar]
- Cortés, J.A.; Sanz, A.; Estopinán, P. Analysis of narrowband power line communication channels for advanced metering infrastructure. EURASIP J. Adv. Signal Process. 2015, 27, 1–13. [Google Scholar] [CrossRef]
- Pukale, R.S.; Bavache, S.V.; Kashid, S.N. Automatic meter reading of electricity by using power line communication. In Proceedings of the 2017 International Conference on Innovations in Green Energy and Healthcare Technologies (IGEHT), Coimbatore, India, 16–18 March 2017. [Google Scholar]
- Božanić, M.; Sinha, S. Power Amplifiers for the S-, C-, X- and Ku bands: An EDA Perspective; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Thompson, M.; Fidler, J.K. Determination of the impedance matching domain of impedance matching networks. IEEE Trans. Circuits Syst. Regul. Pap. 2004, 51, 2098–2106. [Google Scholar] [CrossRef]
- Chung, B.K. Q-based design method for T network impedance matching. Microelectron. J. 2006, 37, 1007–1011. [Google Scholar] [CrossRef]
- Sun, Y.; Fidler, J.K. Design of impedance matching networks. In Proceedings of the IEEE International Symposium on Circuits and Systems, London, UK, 30 May–2 June 1994. [Google Scholar]
- Schmidt, M.; Lourandakis, E.; Leidl, A. A comparison of tunable ferroelectric П- and T-matching networks. In Proceedings of the 2007 European Microwave Conference, Munich, Germany, 9–12 October 2007. [Google Scholar]
- De Piante, M.; Tonello, A.M. On Impedance Matching in a Power Line Communication System. IEEE Trans. Circuits Syst. Express Br. 2016, 63, 653–657. [Google Scholar] [CrossRef]
- De Piante, M.; Tonello, A.M. Impedance Matching and Channel Capacity in Power Line Communication Systems. In Proceedings of the 2017 IEEE International Symposium on Power Line Communications and its Applications (ISPLC), Madrid, Spain, 3–5 April 2017. [Google Scholar]
- Antoniali, M.; Tonello, A.M.; Versolatto, F. A Study on the optimal receiver impedance for SNR maximization in broadband PLC. J. Electr. Comput Eng. 2013, 2013, 1–11. [Google Scholar] [CrossRef]
- Sibanda, M.P.; Rensburg, P.A.J.V.; Ferreira, H.C. Passive, transformerless coupling circuitry for narrow-band power-line communications. In Proceedings of the 2009 IEEE International Symposium on Power Line Communications and Its Applications, Dresden, Germany, 29 March–1 April 2009. [Google Scholar]
- Sibanda, M.P.; Rensburg, P.A.J.V.; Ferreira, H.C. Impedance matching with low-cost, passive components for narrowband PLC. In Proceedings of the 2011 IEEE International Symposium on Power Line Communications and Its Applications, Udine, Italy, 3–6 April 2011. [Google Scholar]
- Wang, B.; Cao, Z.; Luan, Z. Design and Evaluation of Band-Pass Matching Coupler for Narrow-Band DC Power Line Communications. J. Circuits Syst. Comput. 2019, 28, 1–19. [Google Scholar] [CrossRef]
- Sibanda, M.P.; Rensburg, P.A.J.V.; Ferreira, H.C. A compact economical PLC band-pass coupler with impedance matching. In Proceedings of the IEEE 17th International Symposium on Power Line Communications and Its Applications, Johannesburg, South Africa, 24–27 March 2013. [Google Scholar]
- Rensburg, P.A.J.V.; Sibanda, M.P.; Ferreira, H.C. Integrated Impedance-Matching Coupler for Smart Building and Other Power-Line Communications Applications. IEEE Trans. Power Deliv. 2015, 30, 949–956. [Google Scholar] [CrossRef]
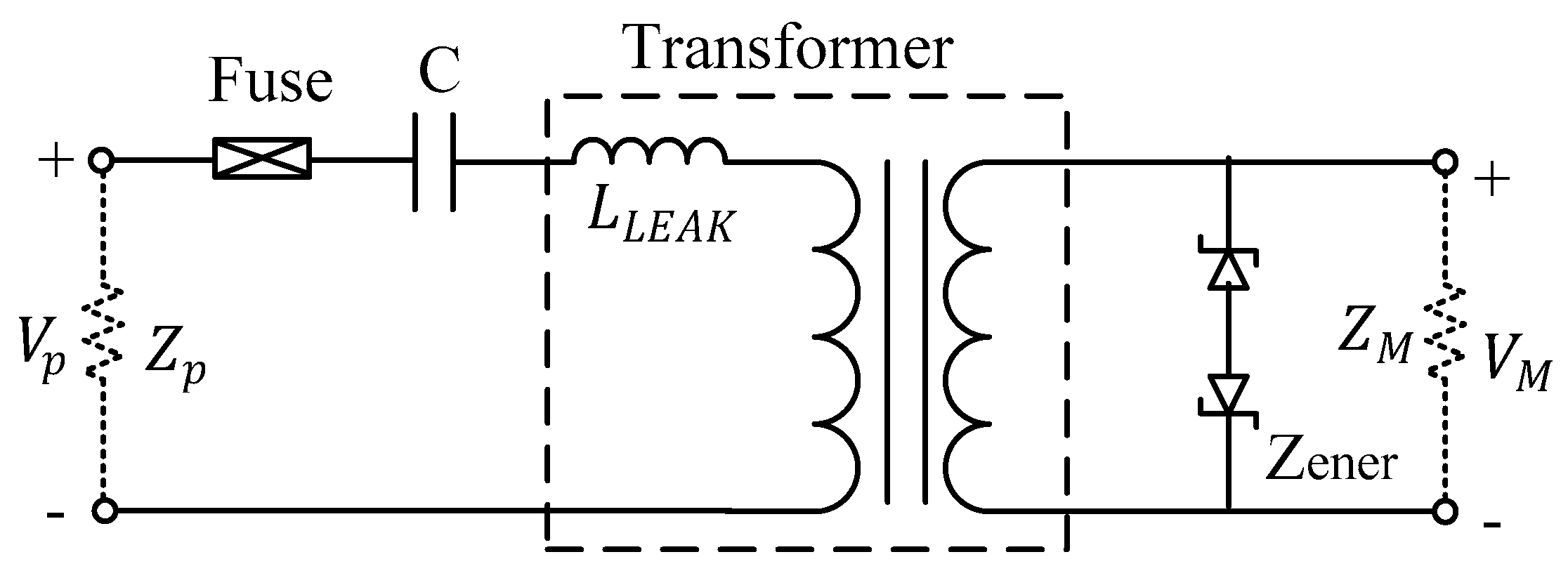
- Brison, M.; Bensetti, M.; Lacerda, R.D. Optimised PLC power transfer on avionic DC Power Lines: Coupling circuit and lightning protection. In Proceedings of the 2017 IEEE International Symposium on Power Line Communications and Its Applications, Madrid, Spain, 3–5 April 2017. [Google Scholar]
- Rahola, J. Power Waves and Conjugate Matching. IEEE Trans. Circuits Syst-II Express Br. 2008, 55, 92–96. [Google Scholar] [CrossRef]
- Araneo, R.; Celozzi, S.; Lovat, G. Design of impedance matching couplers for power line communications. In Proceedings of the 2009 IEEE International Symposium on Electromagnetic Compatibility, Austrin, TX, USA, 17–21 August 2009. [Google Scholar]
- Araneo, R.; Celozzi, S.; Lovat, G. Multi-port impedance matching technique for power line communications. In Proceedings of the 2011 IEEE International Symposium on Power Line Communications and Its Applications, Udine, Italy, 3–6 April 2011. [Google Scholar]
- Yang, S.; Li, H.; Goldberg, M. Broadband Impedance matching circuit design and using Numerical optimization techniques and field Measurements. In Proceedings of the 2007 IEEE International Symposium on Power Line Communications and Its Applications, Pisa, Italy, 26–28 March 2007. [Google Scholar]
- Munoz, F.; Carvajal, R.G.; Torralba, A. ADAPT: Mixed-signal ASIC for impedance adaptation in power line communications using fuzzy logic. In Proceedings of the 25th Annual Conference of the IEEE Industrial Electronics Society, San Jose, CA, USA, 29 November–30 3 December 1999. [Google Scholar]
- Choi, W.H.; Park, C.Y. A simple line coupler with adaptive impedance matching for Power line communication. In Proceedings of the 2007 IEEE International Symposium on Power Line Communications and Its Applications, Pisa, Italy, 26–28 March 2007. [Google Scholar]
- Park, C.Y.; Jung, K.H.; Choi, W.H. Coupling circuitary for impedance adaptation in power line communications using VCGIC. In Proceedings of the 2008 IEEE International Symposium on Power Line Communications and Its Applications, Jeju City, Korea, 2–4 April 2008. [Google Scholar]
- Rui, C.P.; Barsoum, N.N.; Ming, A.W.K. Adaptive impedance matching network with digital capacitor in narrowband power line communication. In Proceedings of the 2013 IEEE International Symposium on Industrial Electronics, Taipei, Taiwan, 28–31 May 2013. [Google Scholar]
- Chin, P.R.; Wong, A.K.M.; Wong, K.I. Modelling of LCRC adaptive impedance matching circuit in narrowband power line communication. In Proceedings of the IEEE 11th International Conference on Power Electronics & Drive Systems, Sydney, Australia, 9–12 June 2015. [Google Scholar]
- Taherinejad, N.; Lampe, L.; Mirabbasi, S. Adaptive impedance matching for Vehicular Power Line Communication systems. In Proceedings of the 18th IEEE International Symposium on Power Line Communications and Its Applications, Glasgow, UK, 30 March–2 April 2014. [Google Scholar]
- Taherinejad, N.; Lampe, L.; Mirabbasi, S. An Adaptive Impedance-Matching System for Vehicular Power Line Communication. IEEE Trans. Veh. Technol. 2017, 66, 927–940. [Google Scholar] [CrossRef]
- Rensburg, P.A.J.V.; Ferreira, H.C. The role of magnetizing and leakage inductance in transformer coupling circuitry. In Proceedings of the 8th International Symposium on Power-Line Communications and Its Applications, Zaragoza, Spain, 31 March–2 April 2004. [Google Scholar]
- Rensburg, P.A.J.V.; Ferreira, H.C. Coupling circuitry: Understanding the functions of different components. In Proceedings of the 7th International Symposium on Power-Line Communications and Its Applications, Kyoto, Japan, 26–28 March 2003. [Google Scholar]
- Rensburg, P.A.J.V.; Ferreira, H.C. Design of a bidirectional impedance adapting transformer coupling circuit for low-voltage power-line communications. IEEE Trans. Power Deliv. 2005, 20, 64–70. [Google Scholar]
- Rensburg, P.A.J.V.; Ferreira, H.C. Step-by step design of a coupling circuit with bi-directional transmission capabilities. In Proceedings of the 8th IEEE International Symposium on Power Line Communications and Its Applications, Zaragoza, Spain, 31 March–2 April 2004. [Google Scholar]
- Rensburg, P.A.J.V.; Ferreira, H.C. Coupler winding ratio selection for effective narrowband power-line communications. IEEE Trans. Power Deliv. 2008, 23, 140–149. [Google Scholar] [CrossRef]
- Rensburg, P.A.J.V.; Ferreira, H.C. Design and evaluation of a dual impedance-adapting power-line communications coupler. IEEE Trans. Power Deliv. 2010, 25, 667–673. [Google Scholar] [CrossRef]
- European Committee for Electrotechnical Standardization (CENELEC). Signalling on low-voltage electrical installations in the frequency range 3 kHz to 148.5 kHz—part 1: General requirements, frequency bands and electromagnetic disturbances. European Standard EN 50065–1. Available online: http://www.doc88.com/p-1048982237653.html (accessed on 10 September 2019).
- Martinez, B.; Cante, N.; Limas, M. Design of a T-coupling circuit for PLC on broadband. In Proceedings of the 2014 IEEE Colombian Conference on Communications and Computing, Bogota, Colombia, 4–6 June 2014. [Google Scholar]
- Pittolo, A.; Piante, M.D.; Versolatto, F. In-Vehicle Power Line Communication: Differences and Similarities Among the In-Car and the In-Ship Scenarios. IEEE Veh. Technol. Mag. 2017, 11, 43–51. [Google Scholar] [CrossRef]
- Malack, J.A.; Engstrom, J.R. RF Impedance of United states and European Power Lines. IEEE Trans. Electromag. Compat. 1976, 18, 36–38. [Google Scholar] [CrossRef]
- Vines, R.M.; Trussell, H.J.; Shuey, K.C. Impedance of Residential Power-Distribution Circuit. IEEE Trans. Electromag. Compat. 1985, 27, 6–12. [Google Scholar] [CrossRef]
- Cavdar, H.; Karadeniz, E. Measurements of Impedance and Attenuation at CENELEC Bands for Power Line Communications Systems. Sensors 2008, 8, 8027–8036. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pasdar, A.M.; Cavdar, I.H.; Sozer, Y. Power-Line Impedance Estimation at FCC Band Based on Intelligent Home Appliances Status Detection Algorithm Through Their Individual Energy and Impedance Signatures. IEEE Trans. Power Deliv. 2014, 29, 1407–1416. [Google Scholar] [CrossRef]
- Lienard, M.; Carrion, M.O.; Degardin, V. Modeling and Analysis of In-Vehicle Power Line Communication Channels. IEEE Trans. Veh. Technol. 2008, 57, 670–679. [Google Scholar] [CrossRef]
- Taherinejad, N.; Rosales, R.; Lampe, L. Channel characterization for power line communication in a hybrid electric vehicle. In Proceedings of the 2012 IEEE International Symposium on Power Line Communications and Its Applications, Beijing, China, 27–30 March 2012. [Google Scholar]
- Yarman, B.S.; Şengül, M.; Trabert, J. Design of wideband matching networks for wireless communication systems. In Proceedings of the Second International Symposium on Communications, Control and Signal Processing, Marrakech, Morocco, 13–15 March 2006. [Google Scholar]
- Antoniou, A. Gyrator using operational amplifier. Electron. Lett. 1967, 3, 350–352. [Google Scholar] [CrossRef]
- Antoniou, A. Realisation of gyrators using operational amplifiers, and their use in RC-active-network synthesis. Proc. Inst. Electr. Eng. 1969, 116, 1838–1850. [Google Scholar]
- Sun, Y.; Amaratunga, G.A.J. High-current adaptive impedance matching in narrowband power-line communication systems. In Proceedings of the 2011 IEEE International Symposium on Power Line Communications and Its Applications, Udine, Italy, 3–6 April 2011. [Google Scholar]
- Nisbet, P.; He, M.; Zhao, L. Transformerless impedance matching networks for automotive power line communication. J. Electr. Electron. Eng. Res. 2014, 6, 13–20. [Google Scholar]
- Chedid, M.; Nilsson, H.; Johansson, A. Realization of an active inductance for a low power high bandwidth DC power line communication network transceiver. AEU Int. J. Electron. Commun. 2010, 64, 947–952. [Google Scholar] [CrossRef]
- Shima, T. Application of the inductor multiplier. In Proceedings of the 13th IEEE international conference on electronics, circuits and systems, Nice, France, 10–13 December 2006. [Google Scholar]
- Milioudis, A.N.; Syranidis, K.N.; Andreou, G.T.; Labridis, D.P. Modeling of Medium-Voltage Power-Line Communication Systems Noise Levels. IEEE Trans. Power Deliv. 2013, 28, 2004–2013. [Google Scholar] [CrossRef]
- Milioudis, A.; Andreou, G.; Labridis, D. Optimum transmitted power spectral distribution for broadband power line communication systems considering electromagnetic emissions. Electr. Power Syst. Res. 2016, 140, 958–964. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, W.; Wang, Y. Characteristic Impedance Analysis of Medium-Voltage Underground Cables with Grounded Shields and Armors for Power Line Communication. Electronics 2019, 8, 571. [Google Scholar] [CrossRef]
- Nkom, B.; Taylor, A.P.R.; Baguley, C. Narrowband Modeling of Single-Wire Earth Return Distribution Lines. IEEE Trans. Power Deliv. 2018, 33, 1565–1575. [Google Scholar] [CrossRef]
- Artale, G.; Cataliotti, A.; Cosentino, V.; Guaiana, S.; Care, D.D.; Tinè, G. Development of a coupling system for medium voltage power line communication in the CENELEC A frequency band. In Proceedings of the 2016 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 28–30 September 2016. [Google Scholar]
- Artale, G.; Cataliotti, A.; Cosentino, V.; Di Cara, D.; Fiorelli, R.; Guaiana, S.; Tine, G. A New Low Cost Coupling System for Power Line Communication on Medium Voltage Smart Grids. IEEE Trans. Smart Grid 2018, 9, 3324–3329. [Google Scholar] [CrossRef]
- Artale, G.; Cataliotti, A.; Cosentino, V.; Di Cara, D.; Fiorelli, R.; Guaiana, S.; Panzavecchia, N.; Tinè, G. A new PLC-based smart metering architecture for medium/low voltage grids: Feasibility and experimental characterization. Measurement 2018, 129, 479–488. [Google Scholar] [CrossRef]
- Nkom, B.; Taylor, A.P.R.; Baguley, C. The Impact of Transformer Energization Levels on Powerline Communication Signal Integrity. IEEE Trans. Power Deliv. 2018, 33, 1668–1678. [Google Scholar] [CrossRef]
- Lefort, R.; Vauzelle, R.; Courtecuisse, V.; Idir, N.; Poussard, A.M. Influence of the MV/LV transformer impedance on the propagation of the PLC signal in the power grid. IEEE Trans. Power Deliv. 2017, 32, 1339–1349. [Google Scholar] [CrossRef]
- Oh, H.M.; Choi, S.; Lee, J.J.; Shon, S.; Kim, H.S.; In, D.S.; Bae, J. Coupler with transformer for impedance matching on mv power distribution line for BPL. In Proceedings of the IEEE International Symposium on Power Line Communications and Its Applicationse, Jeju City, Korea, 2–4 April 2008. [Google Scholar]
- Lee, D.E.; In, D.S.; Lee, J.J.; Park, Y.J.; Kim, K.H.; Kim, J.T.; Shon, S.G. A field trial of medium voltage power line communication system for AMR and DAS. In Proceedings of the 2009 Transmission & Distribution Conference & Exposition: Asia & Pacific, Seoul, Korea, 26–30 October 2009. [Google Scholar]
- Berger, L.T.; Pagani, A.S.P.; Schneider, D.M. MIMO Power Line Communications. IEEE Commun. Surv. Tutor. 2015, 17, 106–124. [Google Scholar] [CrossRef]
- Schneider, D.; Speidel, J.; Stadelmeier, L.; Schill, D. Precoded spatial multiplexing MIMO for inhome power line communications. In Proceedings of the IEEE Global Telecommunication. Conference, New Orleans, LO, USA, 30 November–4 December 2008. [Google Scholar]
- Hashmat, R.; Pagani, P.; Zeddam, A. MIMO communications for inhome PLC networks: Measurements and results up to 100 MHz. In Proceedings of the IEEE International Symposium on Power Line Communications and Its Applications, Rio de Janeiro, Brazil, 28–31 March 2010. [Google Scholar]
- Versolatto, F.; Tonello, A. A MIMO PLC random channel generator and capacity analysis. In Proceedings of the 2011 IEEE International Symposium on Power Line Communications and Its Applications, Udine, Italy, 3–6 April 2011. [Google Scholar]
- Nikfar, B.; Vinck, A.J.H. Combining Techniques Performance Analysis in Spatially Correlated MIMO-PLC Systems. In Proceedings of the 2013 IEEE 17th International Symposium on Power Line Communications and Its Applications, Johannesburg, South Africa, 24–27 March 2013. [Google Scholar]
- Gazalet, K.K.M.G.; Coudoux, P.C.F.X.; Gharbi, M. An MIMO Random Channel Generator for Indoor Power-Line Communication. IEEE Trans. Power Deliv. 2014, 9, 1561–1568. [Google Scholar]
- Schwager, A.; Schneider, D.; Baschlin, W. MIMO PLC: Theory, Measurements and System Setup. In Proceedings of the 2011 IEEE International Symposium on Power Line Communications and Its Applications, Udine, Italy, 3–6 April 2011. [Google Scholar]
- Nikfar, B.; Akbudak, T.; Vinck, A.J. MIMO Capacity of Class A Impulsive Noise Channel for Different Levels of Information Availability at Transmitter. In Proceedings of the 2014 18th IEEE International Symposium on Power Line Communications and Its Applications, Glasgow, UK, 30 March–2 April 2014. [Google Scholar]
- Alberto, P.; Andrea, T. A synthetic Statistical MIMO PLC channel Model Applied to an In-Home Scenario. IEEE Trans. Commun. 2017, 65, 2543–2553. [Google Scholar]
- Chen, W.Y.; Dixon, J.L.; Waring, D.L. High bit rate digital subscriber line echo cancellation. IEEE J. Sel. Areas Commun. 1991, 9, 848–860. [Google Scholar] [CrossRef]
- Su, W.K.; Chen, Y.R.; Lin, D.W. Optimization of hybrid circuits for echo cancellation in high-rate digital subscriber line transmission. In Proceedings of the 1994 IEEE Asia-Pacific Conference on Circuit and Systems, Taipei, Taiwan, 5–8 December 1994. [Google Scholar]
- Duarte, M.; Dick, C.; Sabharwal, A. Experiment-driven characterization of full-duplex wireless systems. IEEE Trans. Wireless Commun. 2012, 11, 4296–4307. [Google Scholar] [CrossRef]
- Sabharwal, A.; Schniter, P.; Guo, D.; Bliss, D.W. In-band full-duplex wireless: Challenges and opportunities. IEEE J. Sel. Areas Commun. 2013, 32, 1637–1652. [Google Scholar] [CrossRef]
- Prasad, G.; Lampe, L. Introducing in-band full duplexing for broadband power line communication. In Proceedings of the Workshop on Power Line Communications (WSPLC), Klagenfurt, Austria, 21–22 September 2015. [Google Scholar]
- Passerini, F.; Tonello, A.M. In Band Full Duplex PLC: The Role of the Hybrid Coupler. In Proceedings of the 2016 International Symposium on Power Line Communications and its Applications, Bottrop, Germany, 20–23 March 2016. [Google Scholar]
- Prasad, G.; Lampe, L.; Shekhar, S. In-Band Full Duplex Broadband Power Line Communications. IEEE Trans. Commun. 2016, 64, 3915–3931. [Google Scholar] [CrossRef]
- Prasad, G.; Lampe, L.; Shekhar, S. Digitally Controlled Analog Cancellation for Full Duplex Broadband Power Line Communications. IEEE Trans. Commun. 2017, 65, 4419–4432. [Google Scholar] [CrossRef]
- Passerini, F.; Tonello, A.M. Adaptive Hybrid Circuit for Enhanced Echo Cancellation in Full Duplex PLC. In Proceedings of the 2018 IEEE International Symposium on Power Line Communications and its Applications, Manchester, UK, 8–11 April 2018. [Google Scholar]
- Passerini, F.; Tonello, A.M. Analog Full-Duplex Amplify-and-Forward Relay for Power Line Communication Networks. IEEE Commun. Lett. 2019, 23, 676–679. [Google Scholar] [CrossRef]
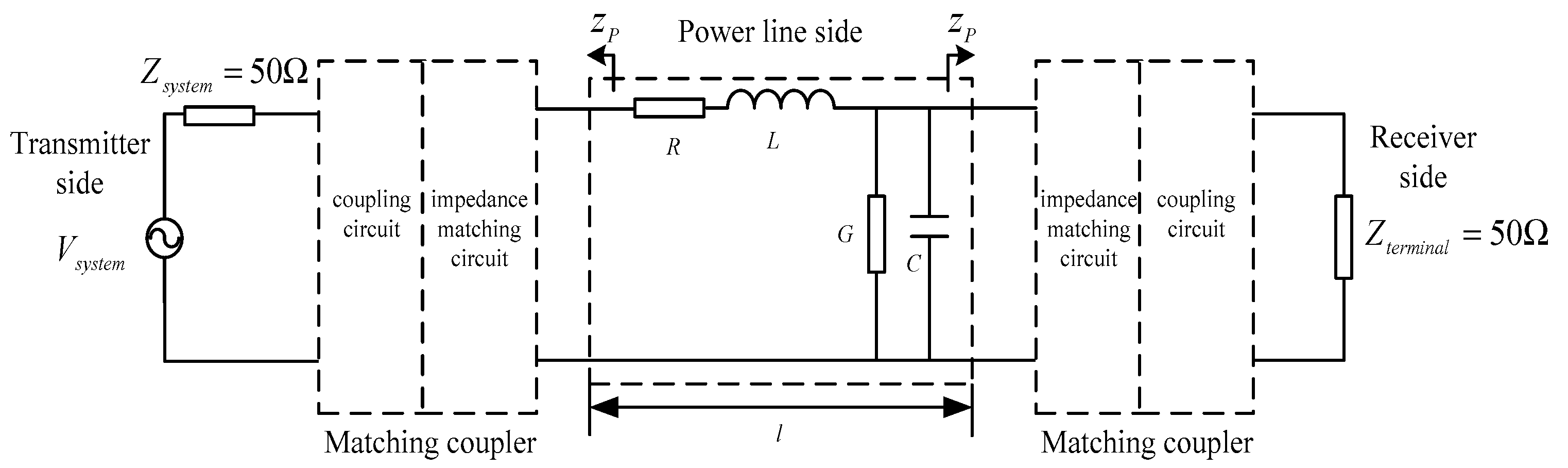
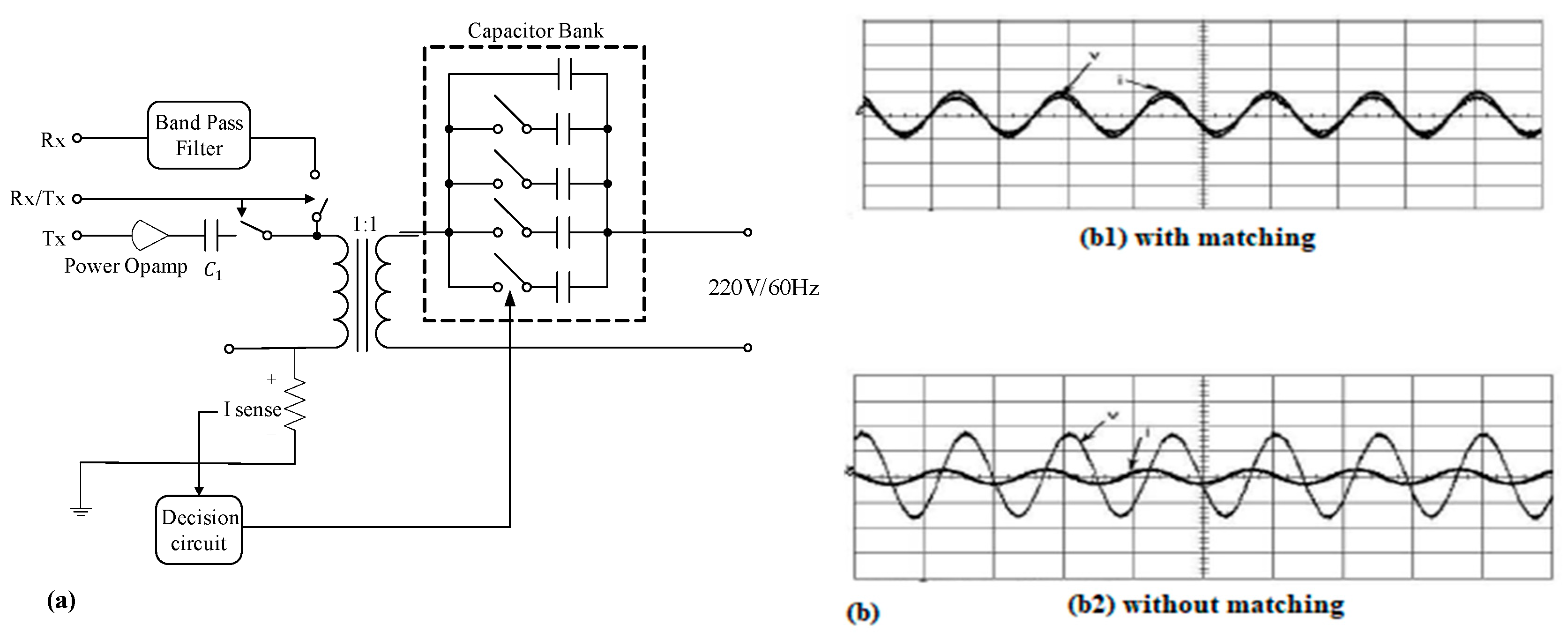
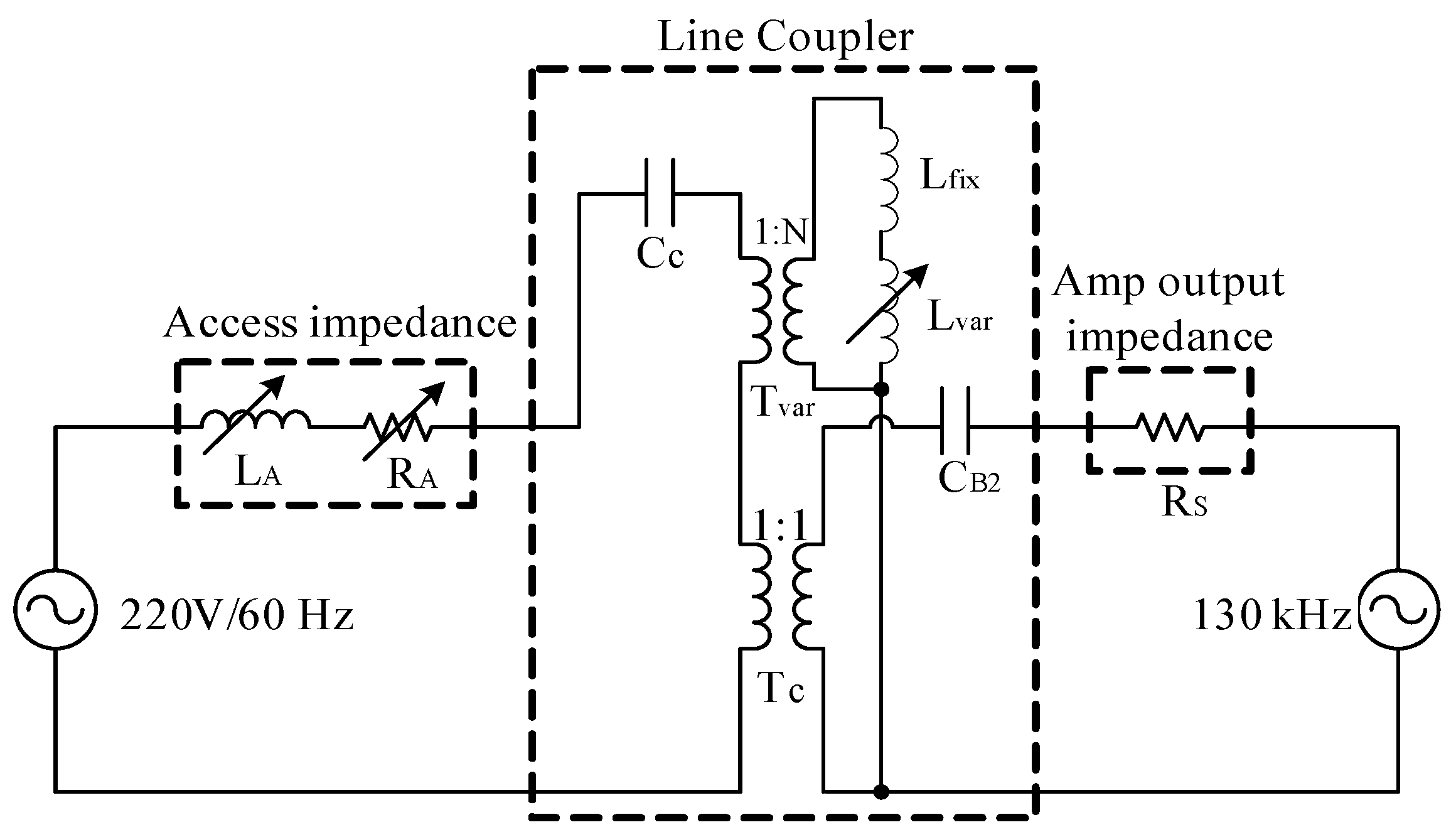
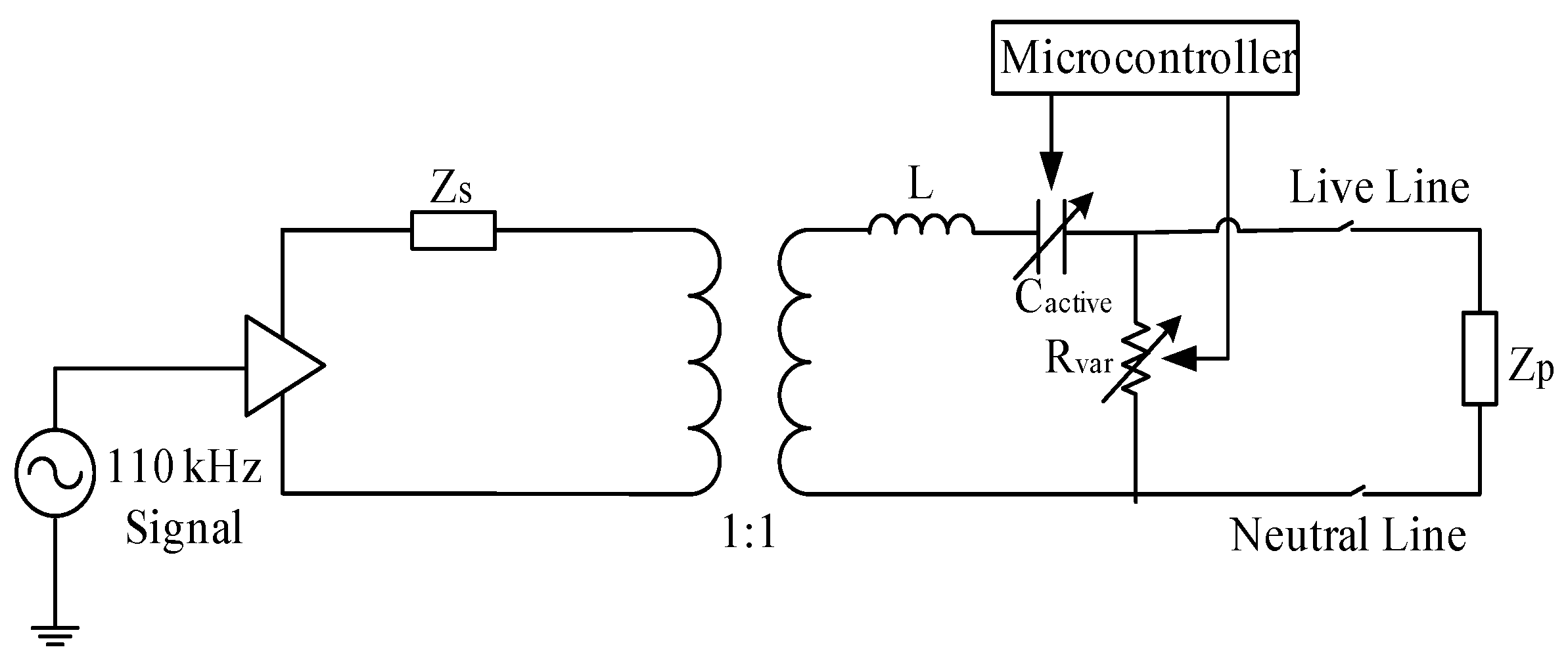
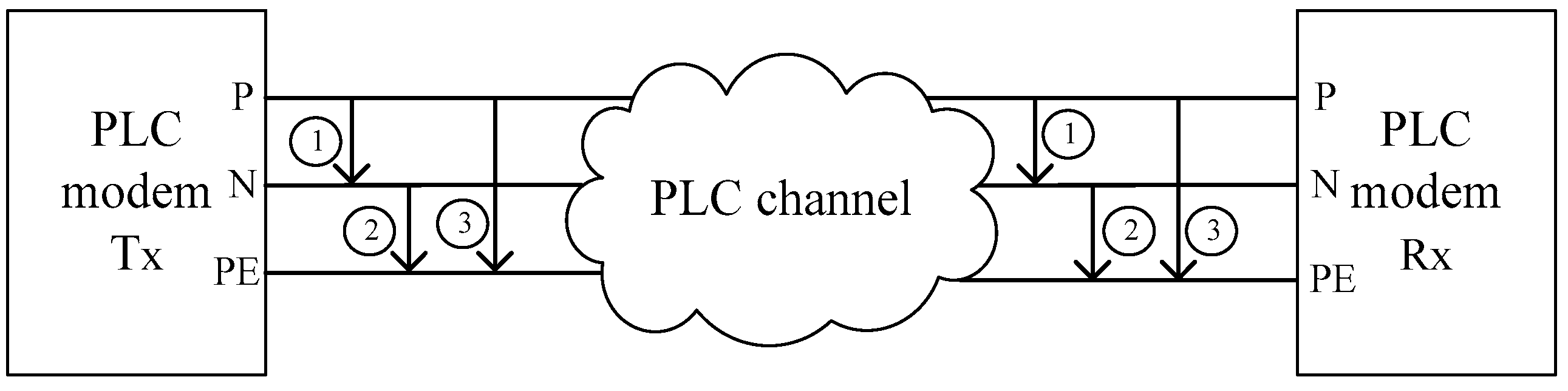
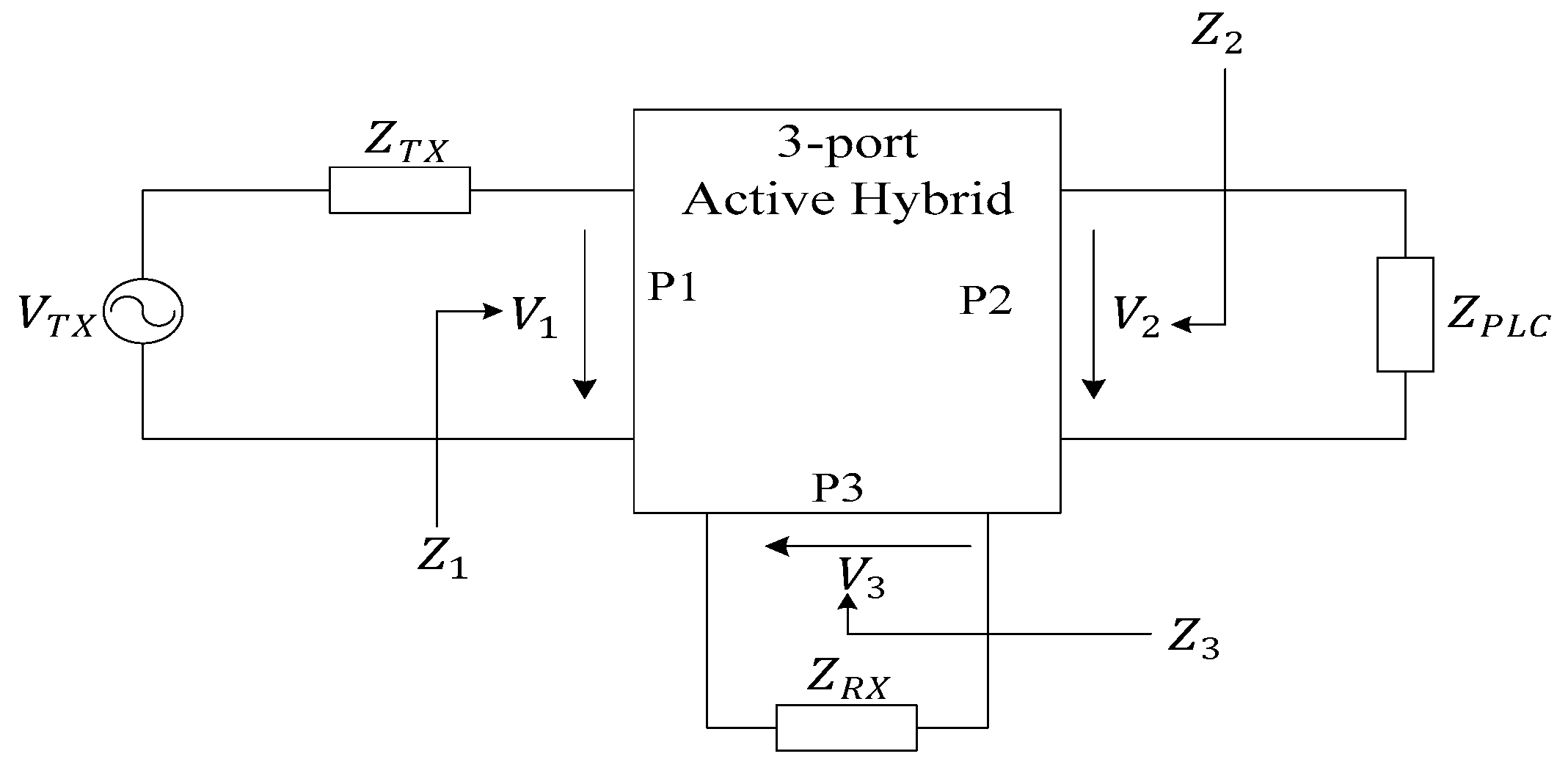
| Quantity | Equal Impedance Matching | Complex Conjugate Matching | Voltage Maximization Matching |
|---|---|---|---|
| Frequency Bands | Related Works | Frequencies | |
|---|---|---|---|
| Narrowband | [89] | 5–20 kHz | , |
| [90] | 10–170 kHz | for rural; for urban; for industrial | |
| [91] | 0–500 kHz | ||
| Broadband | [88] | 20 kHz–30 MHz | ; , |
| [78] | 1–100 MHz | , |
| Criterion | Classes | Description |
| Methods | Equal impedance matching | Minimize voltage reflection coefficient |
| Complex conjugate matching | Minimize power reflection coefficient | |
| Voltage maximization matching | Maximum voltage amplitude/SNR | |
| Structure/ Component | Both fixed | BPF circuit |
| Variable component | Adaptive matching system | |
| Both variable | L-shaped adaptive matching system | |
| Cost | High | With transformer |
| Low | Without transformer | |
| Impedance types | Real-to-real | Equal impedance matching |
| Real-to-complex | Complex conjugate matching | |
| Complex-to-complex | Voltage maximization matching | |
| Bandwidth | Narrowband | CENELEC bands or FCC band |
| Broadband | Smart home and VPLC applications | |
| Component types | Passive | Lumped components |
| Active | Active components | |
| Voltage levels | LV | Smart grid; Smart home |
| MV/HV | Communication between MV/HV and LV | |
| Channel types | SISO | configuration |
| MIMO | , or configurations | |
| Transmittal modes | HD | PLC coupler |
| IBFD | Hybrid coupler or circulator |
| Related Works | Methods | Structure/Component | Cost | Impedance Types | Bandwidth | Component Types | Voltage Levels | Channel Types | Transmittal Modes |
|---|---|---|---|---|---|---|---|---|---|
| [62,64] | Equal impedance matching | Both fixed | Low | Real-to-real | Narrowband | Passive | LV | SISO | HD |
| [86] | Equal impedance matching | Both fixed | Low | Real-to-real | Broadband | Passive | LV | SISO | HD |
| [81,82,83,84] | Equal impedance matching | Both fixed | High (with transformer) | Real-to-real | Narrowband | Passive | LV | SISO | HD |
| [72,73,74,75,76] | Complex conjugate matching | Variable component | High (with transformer) | Real/complex-to-complex | Narrowband | Passive/active | LV | SISO | HD |
| [77,78] | Complex conjugate matching | Both variable | Low | Real-to-complex | Broadband | Passive | LV | SISO | HD |
| [97,98] | Complex conjugate matching | Variable component | Low | Real-to-complex | Broadband | Active | LV | SISO | HD |
| [59] | Voltage maximization matching | Complex-to-complex | Broadband | LV | SISO | HD | |||
| [105,106,110,111] | Equal impedance matching | Both fixed | High (with transformer) | Real-to-real | Narrowband/Broadband | Active/Passive | MV | SISO | HD |
| [127,128] | Equal impedance matching | Both fixed | Low | Real-to-real | Broadband | Active | LV | MIMO | IBFD |
| [129,130] | Equal impedance matching | Variable component | Low | Real-to-real | Broadband | Active | LV | SISO | IBFD |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Cao, Z. A Review of Impedance Matching Techniques in Power Line Communications. Electronics 2019, 8, 1022. https://doi.org/10.3390/electronics8091022
Wang B, Cao Z. A Review of Impedance Matching Techniques in Power Line Communications. Electronics. 2019; 8(9):1022. https://doi.org/10.3390/electronics8091022
Chicago/Turabian StyleWang, Bingting, and Ziping Cao. 2019. "A Review of Impedance Matching Techniques in Power Line Communications" Electronics 8, no. 9: 1022. https://doi.org/10.3390/electronics8091022
APA StyleWang, B., & Cao, Z. (2019). A Review of Impedance Matching Techniques in Power Line Communications. Electronics, 8(9), 1022. https://doi.org/10.3390/electronics8091022





