State of Charge Estimation for Lithium-Ion Batteries Based on Temperature-Dependent Second-Order RC Model
Abstract
1. Introduction
2. Temperature-Dependent Second-Order RC Model
2.1. Characteristics of Lithium-Ion Batteries
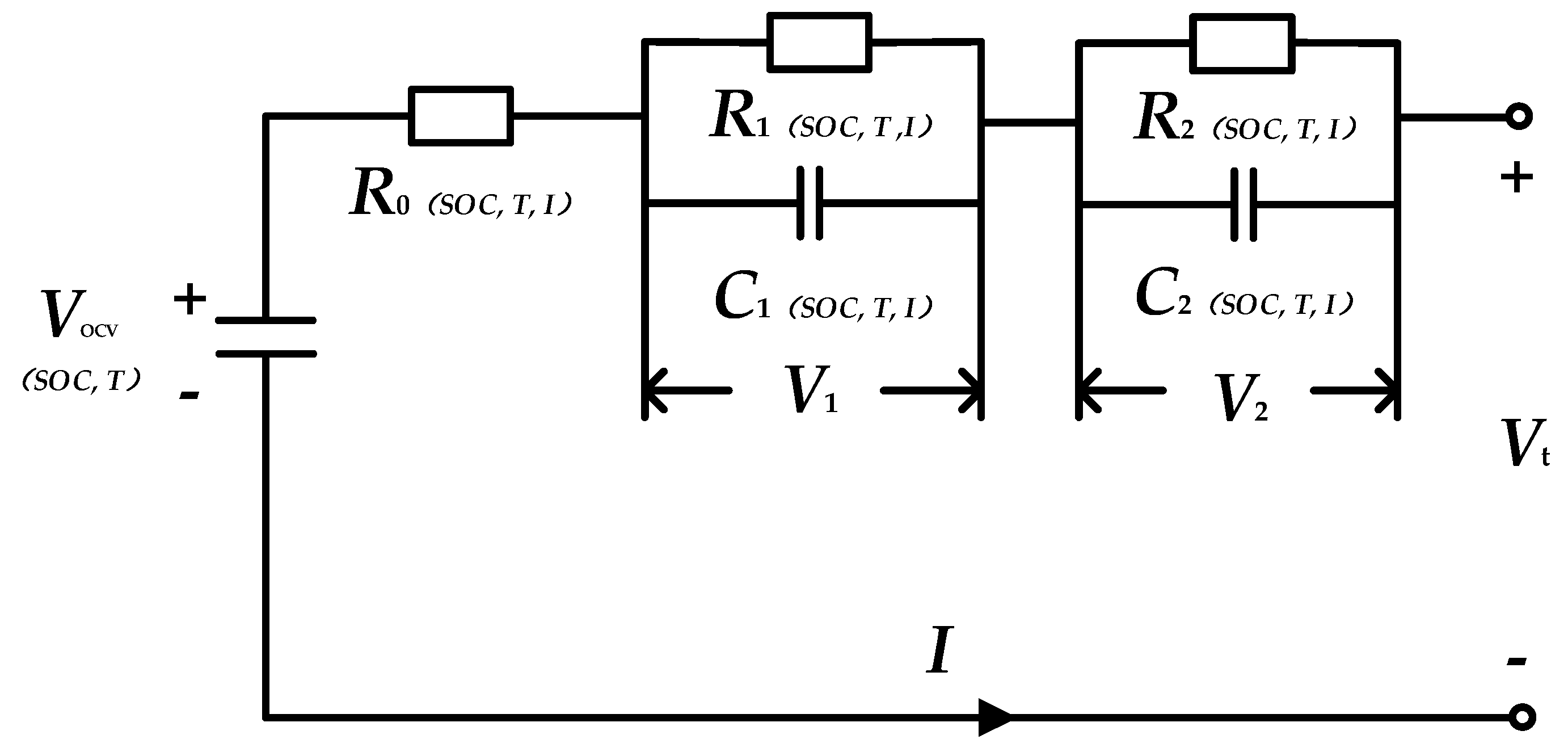
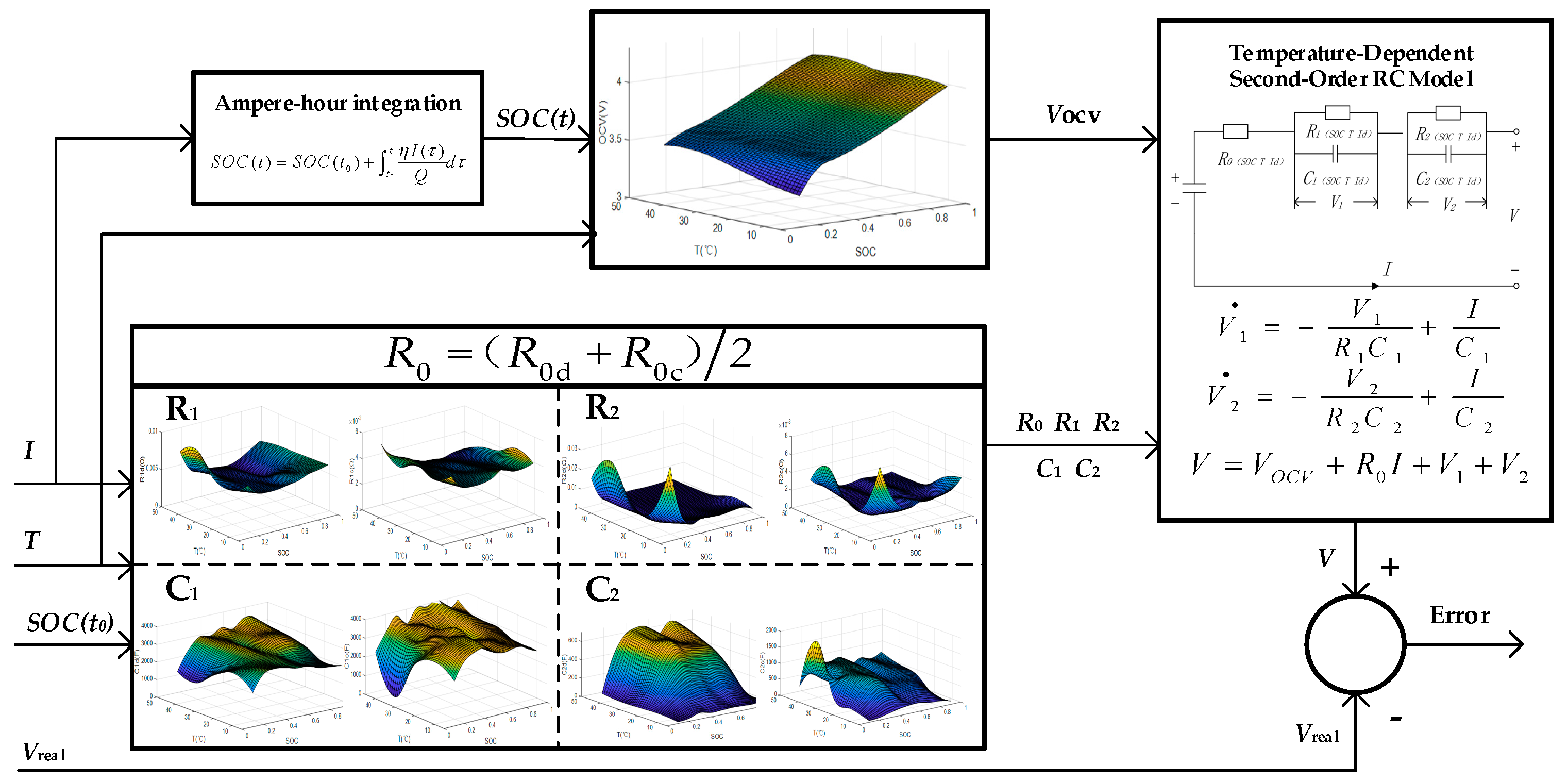
2.2. Battery Modeling
3. Model Parameter Identification
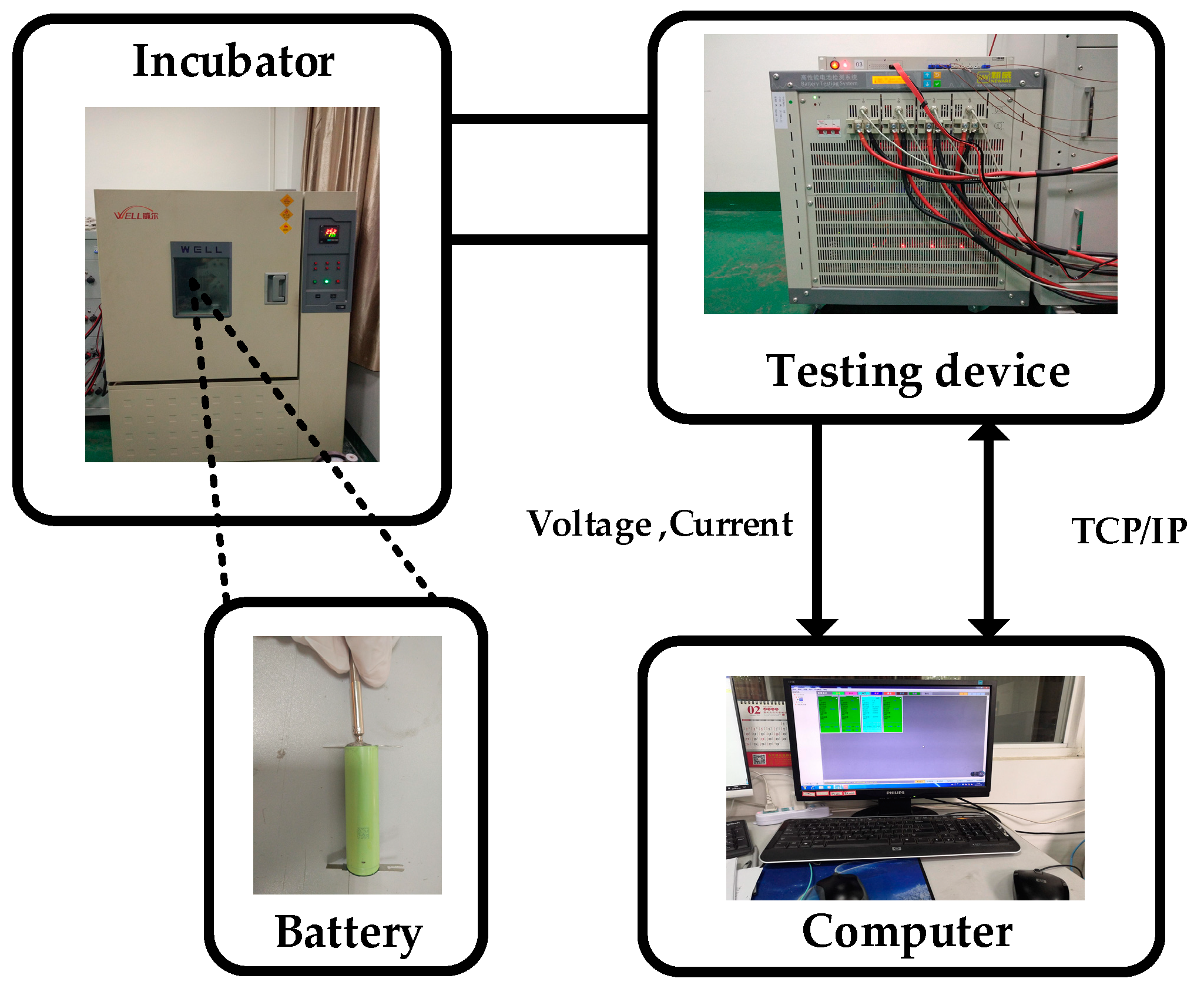
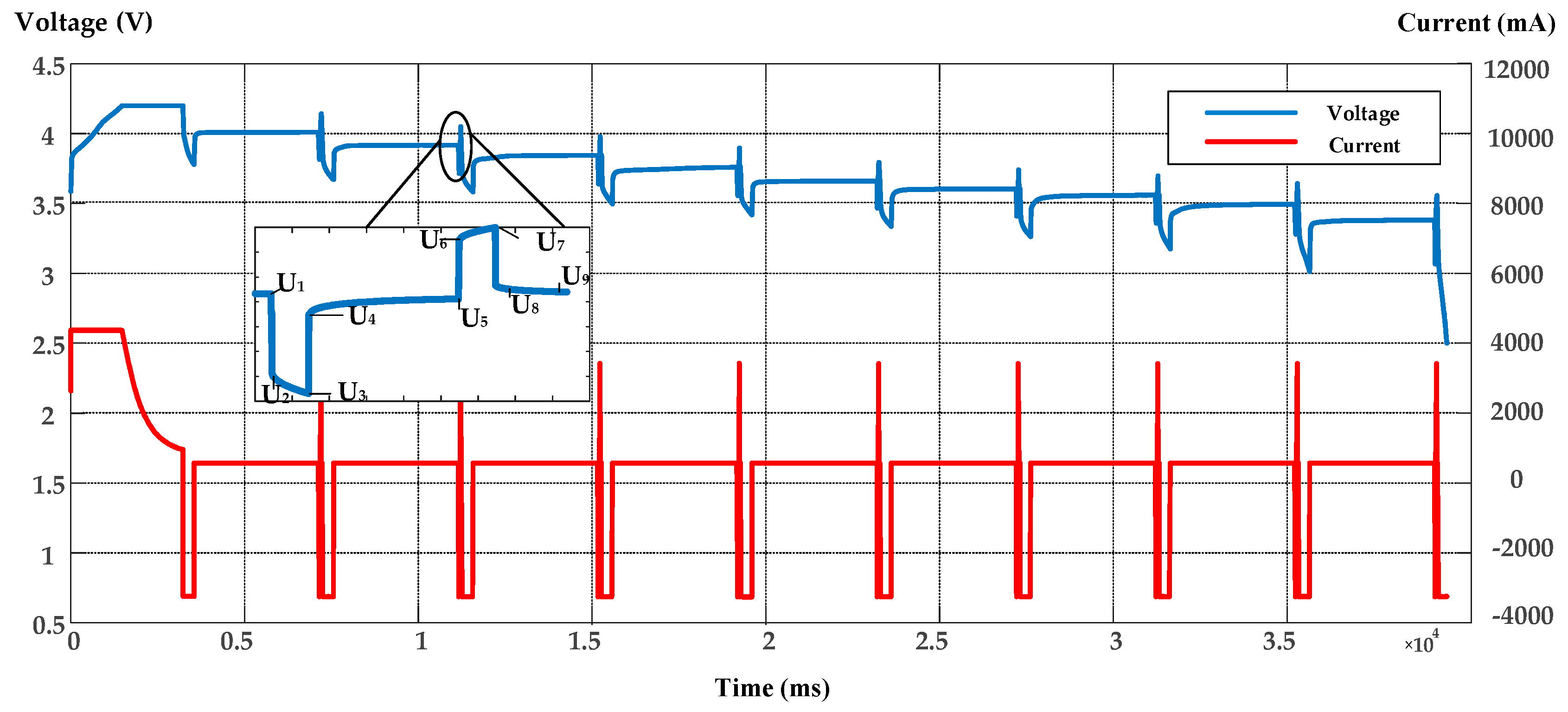
3.1. Experiment Specifications
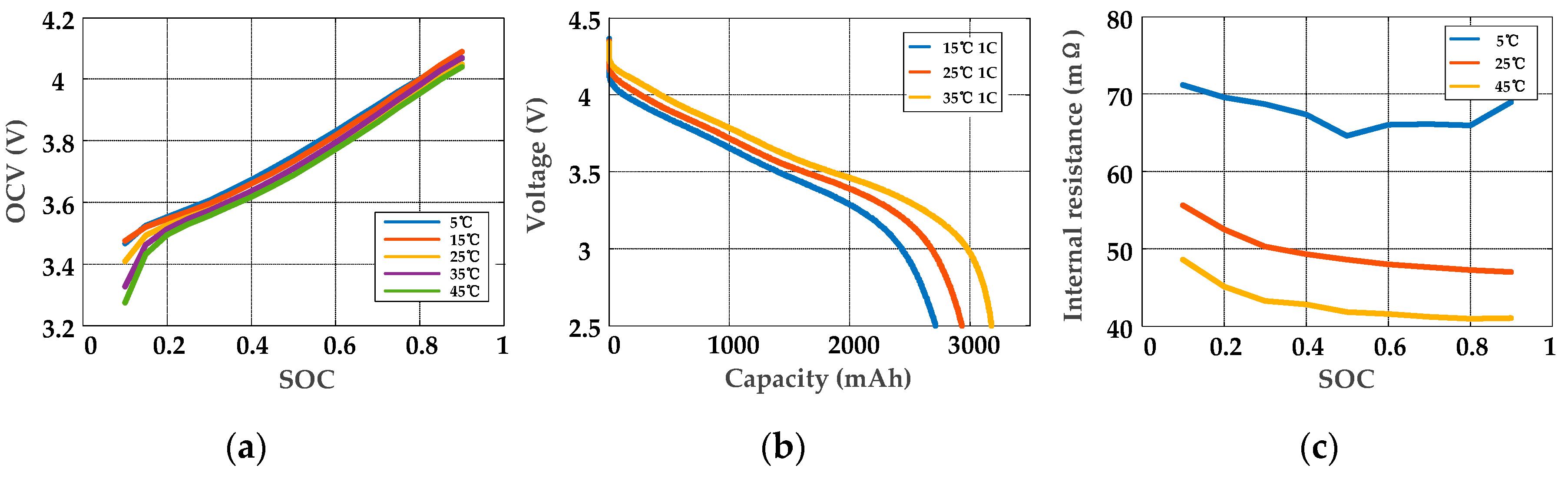
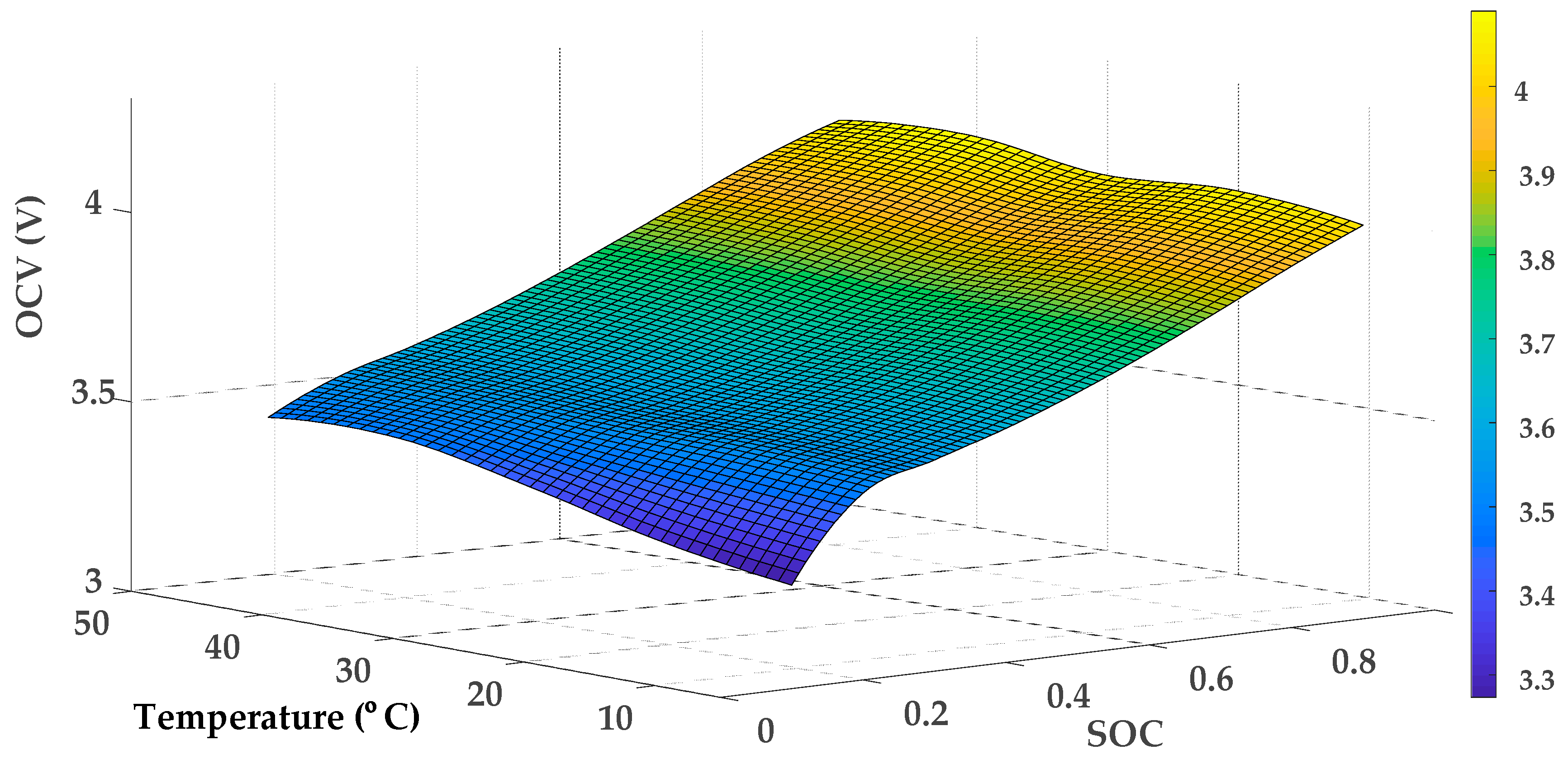
3.2. Identification of OCV
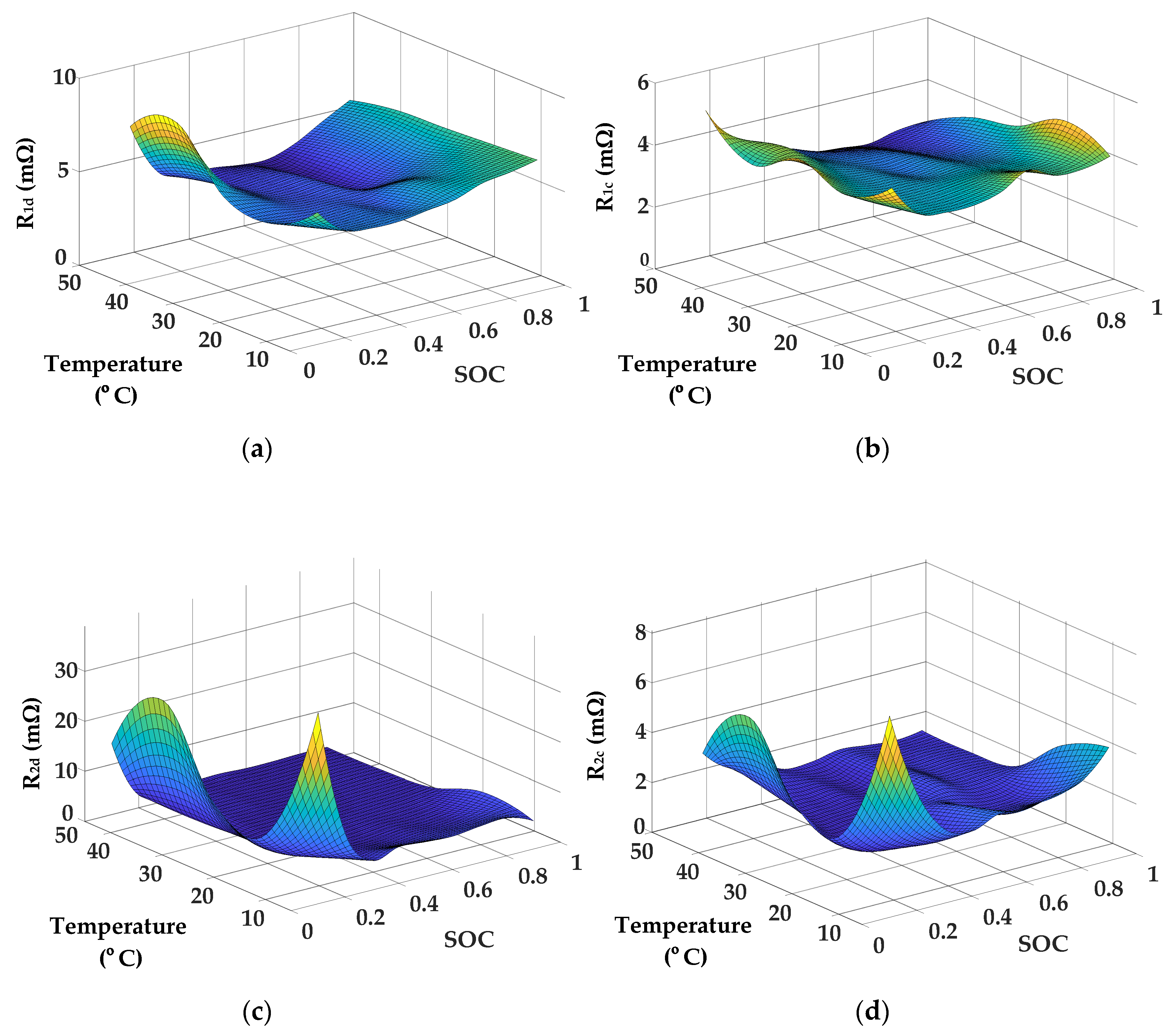
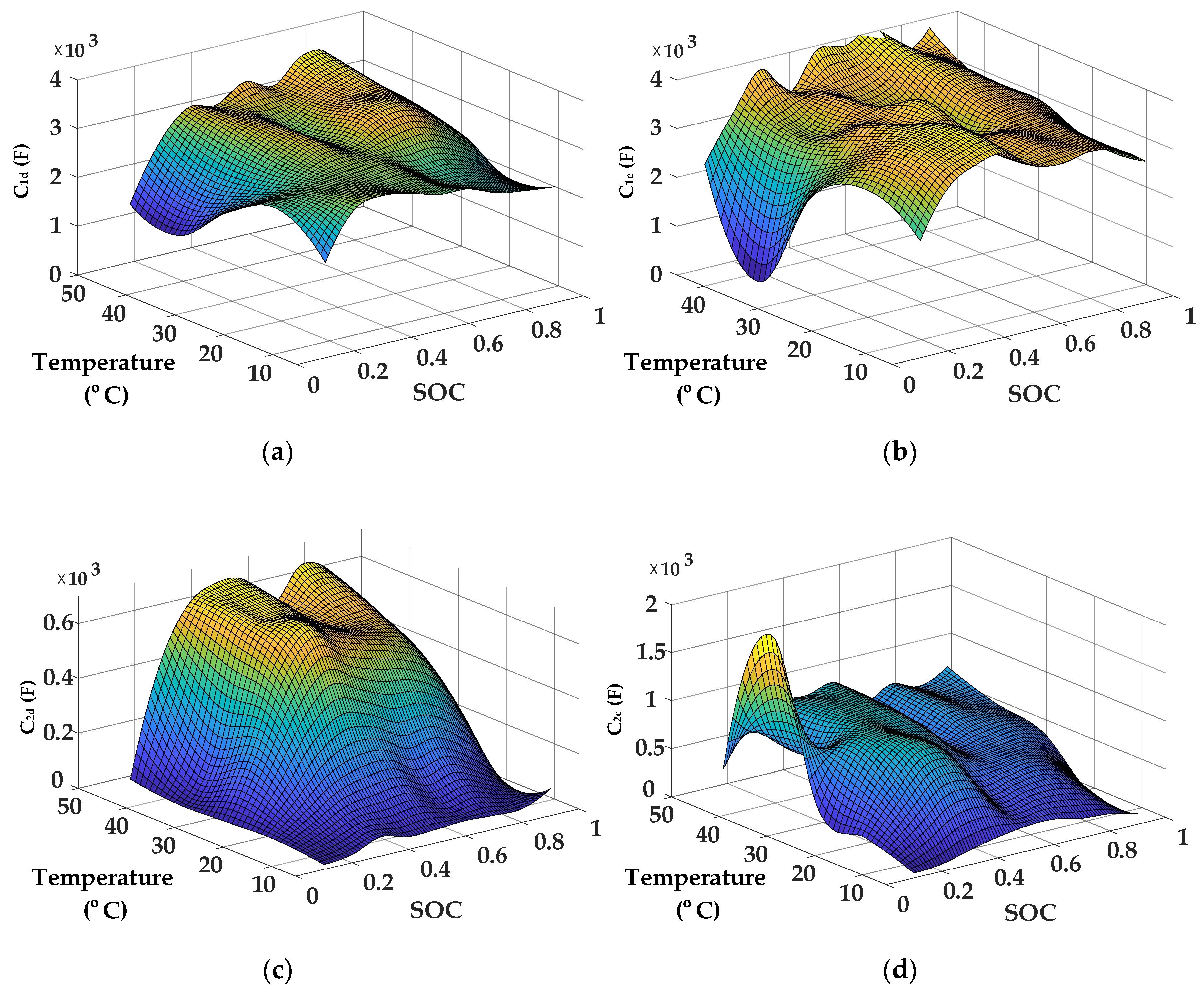
3.3. Identification of Internal Resistances and Capacitances
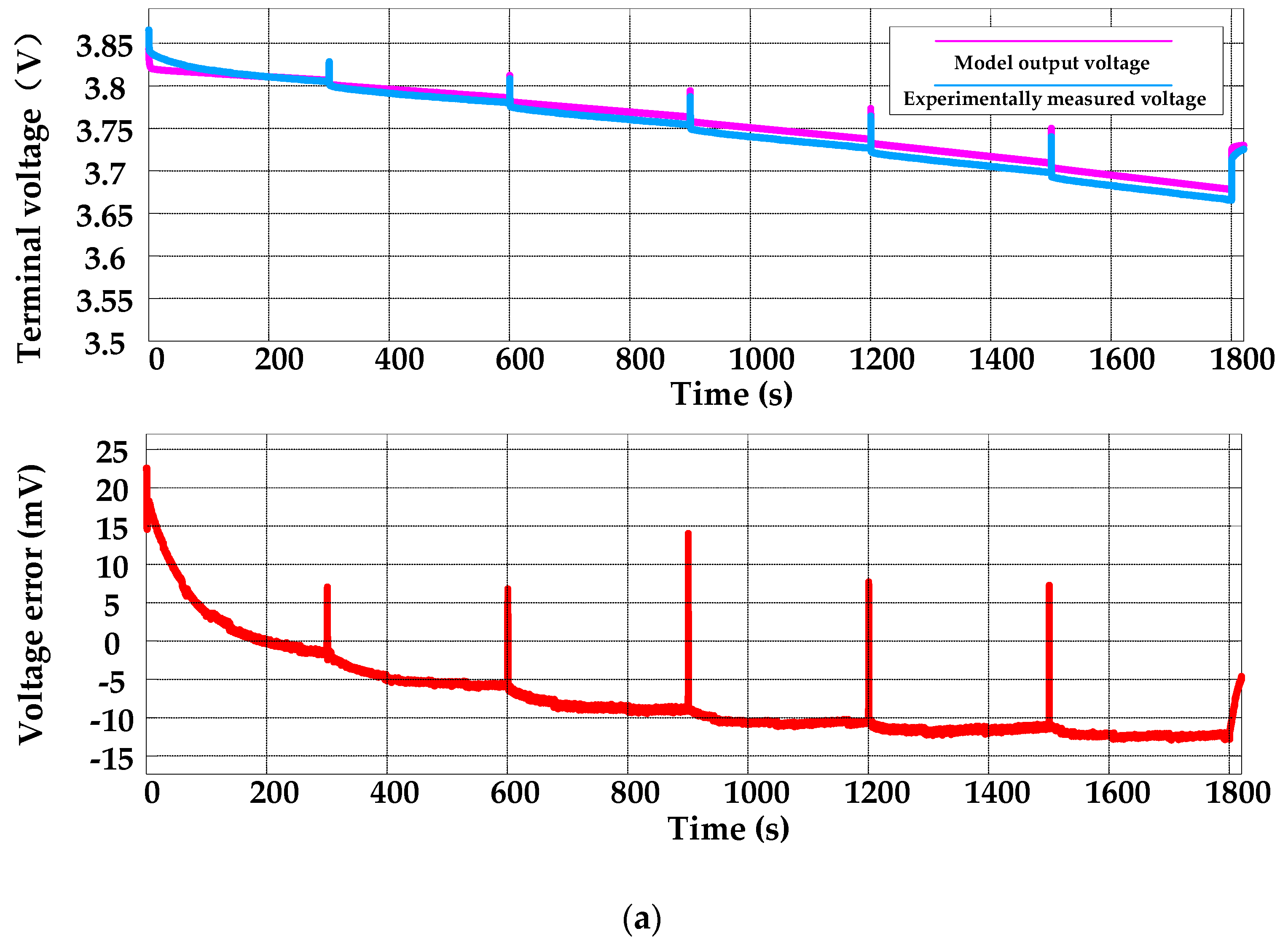
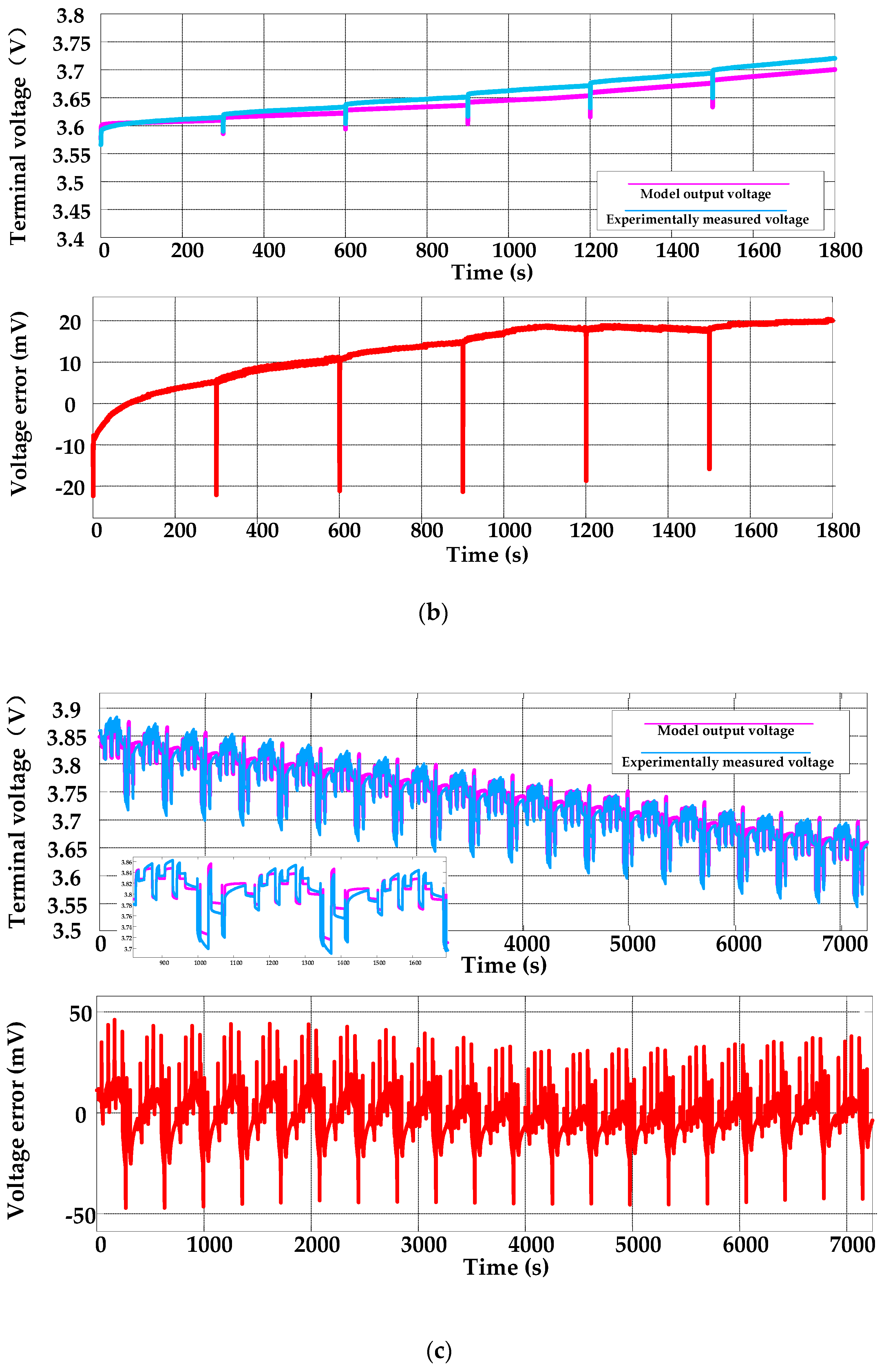
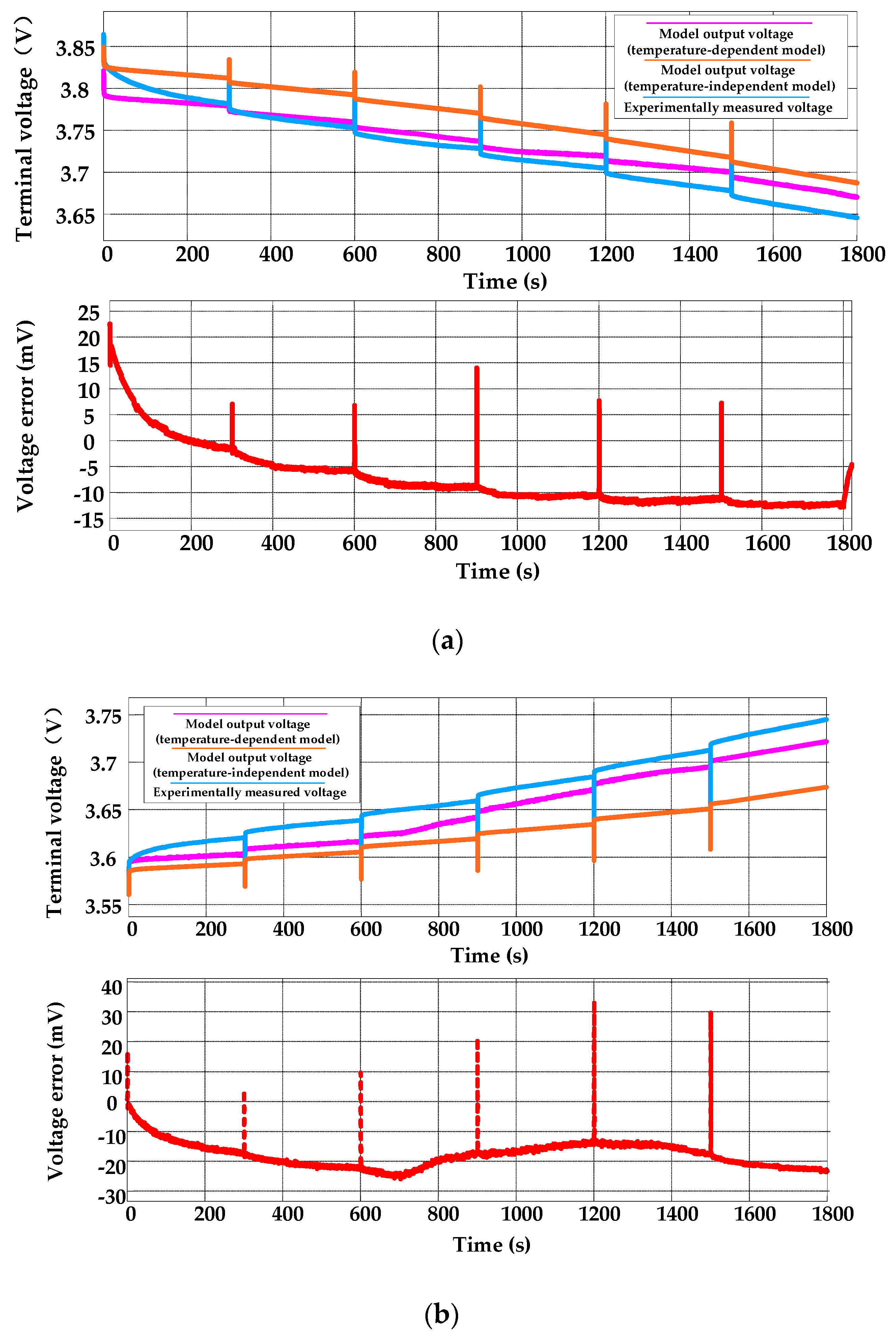
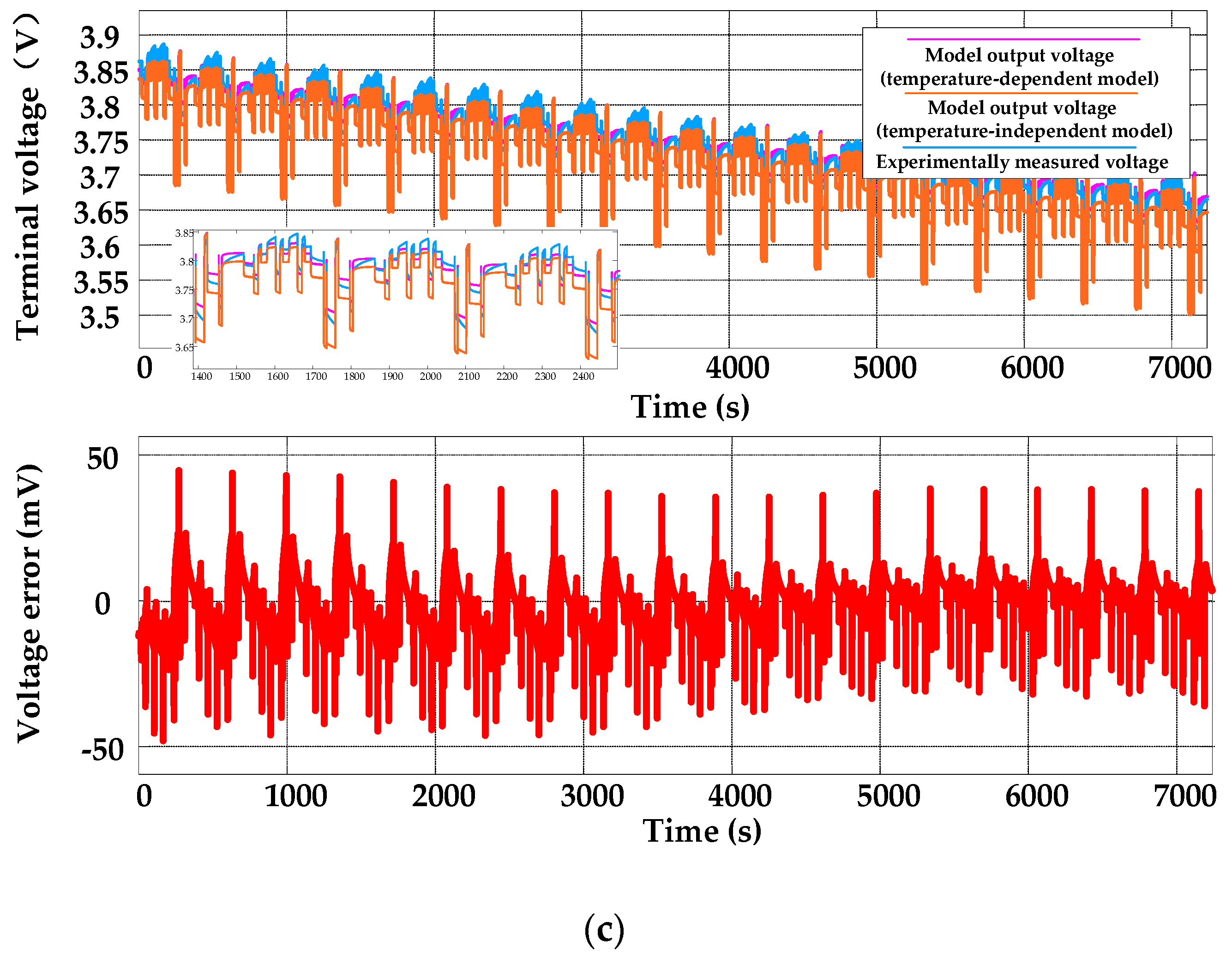
4. Model Verification and Discussion
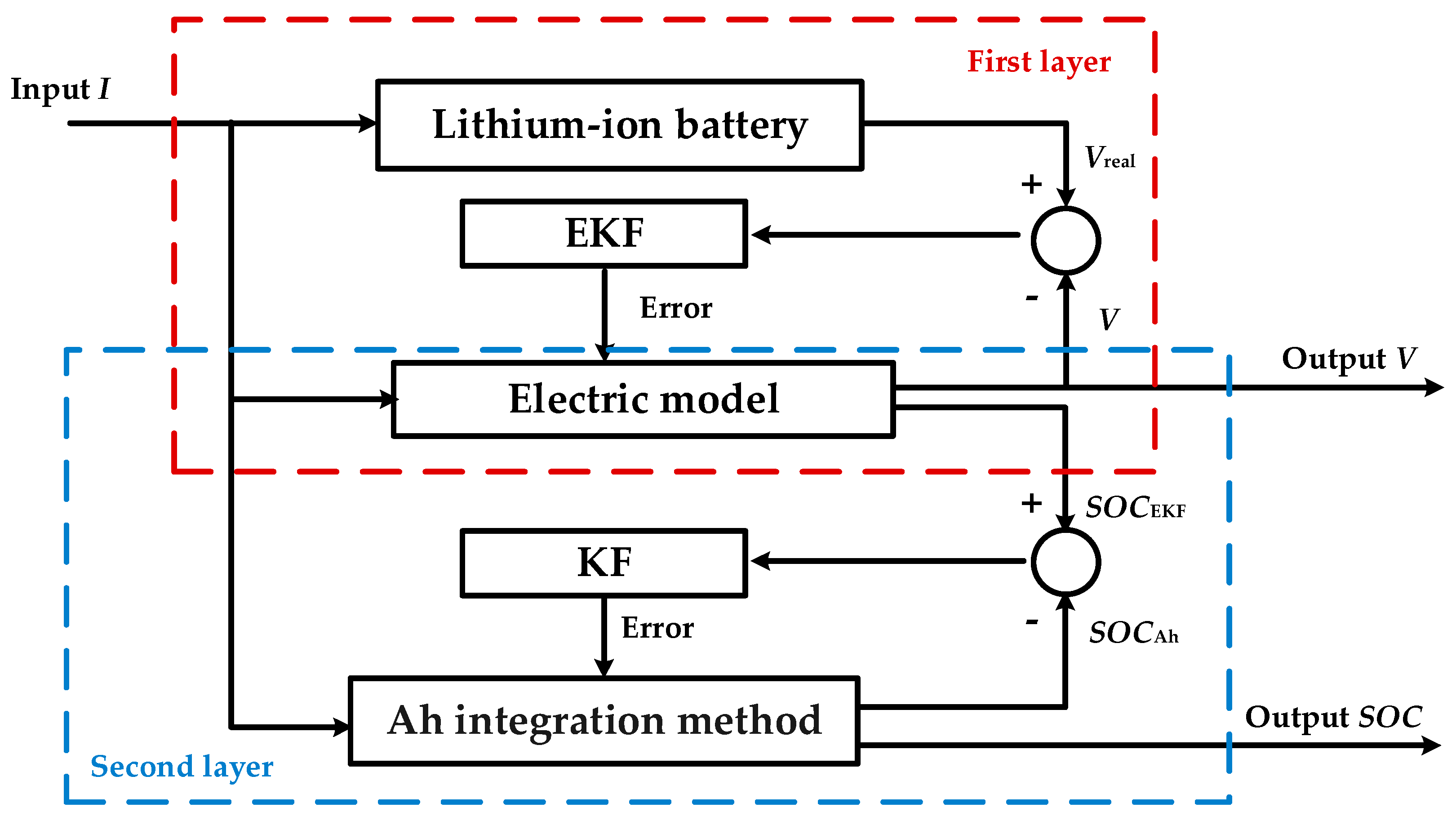
5. SOC Estimation Based on Double Kalman Filter Algorithm
5.1. DKF Algorithm
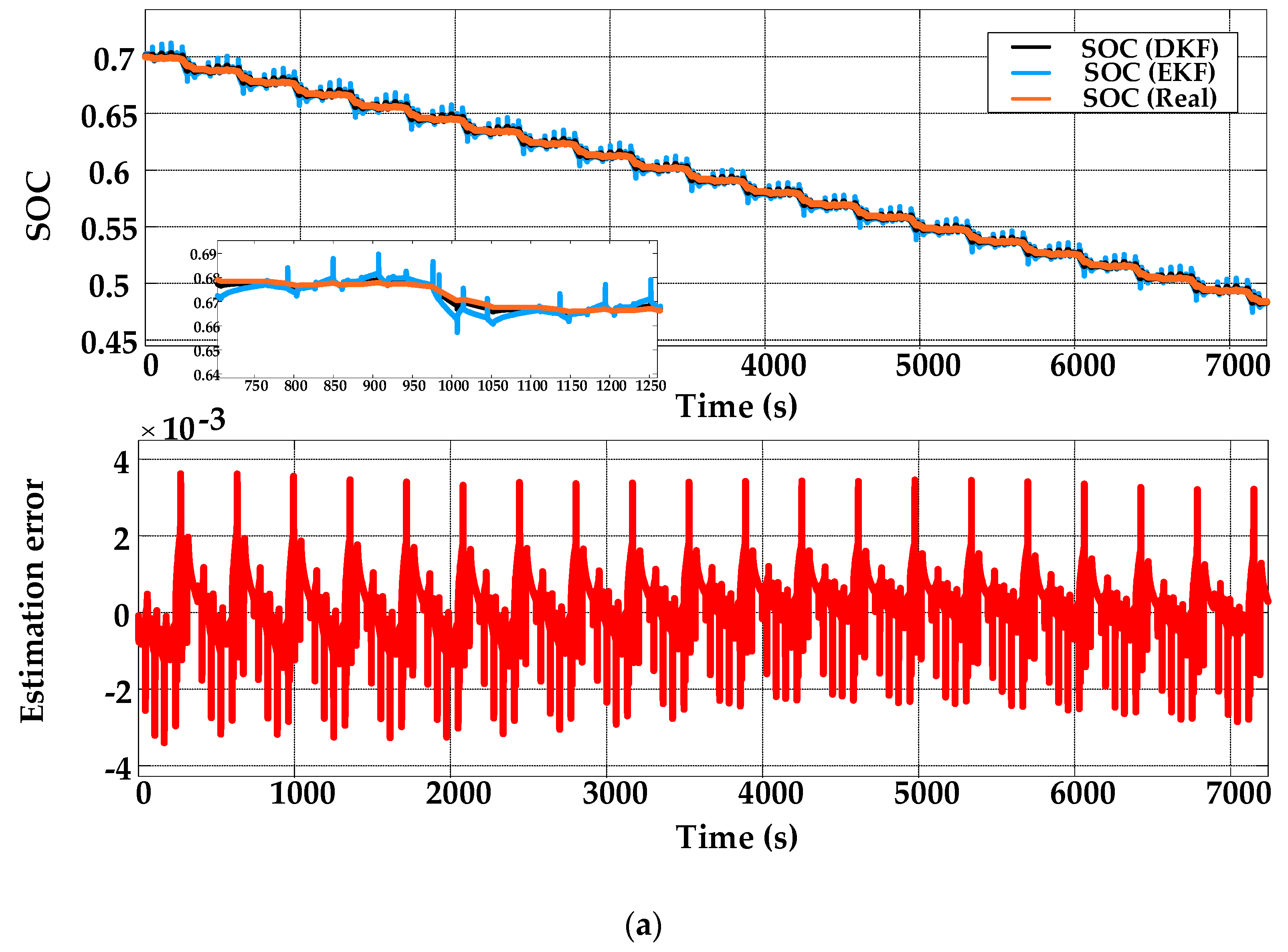
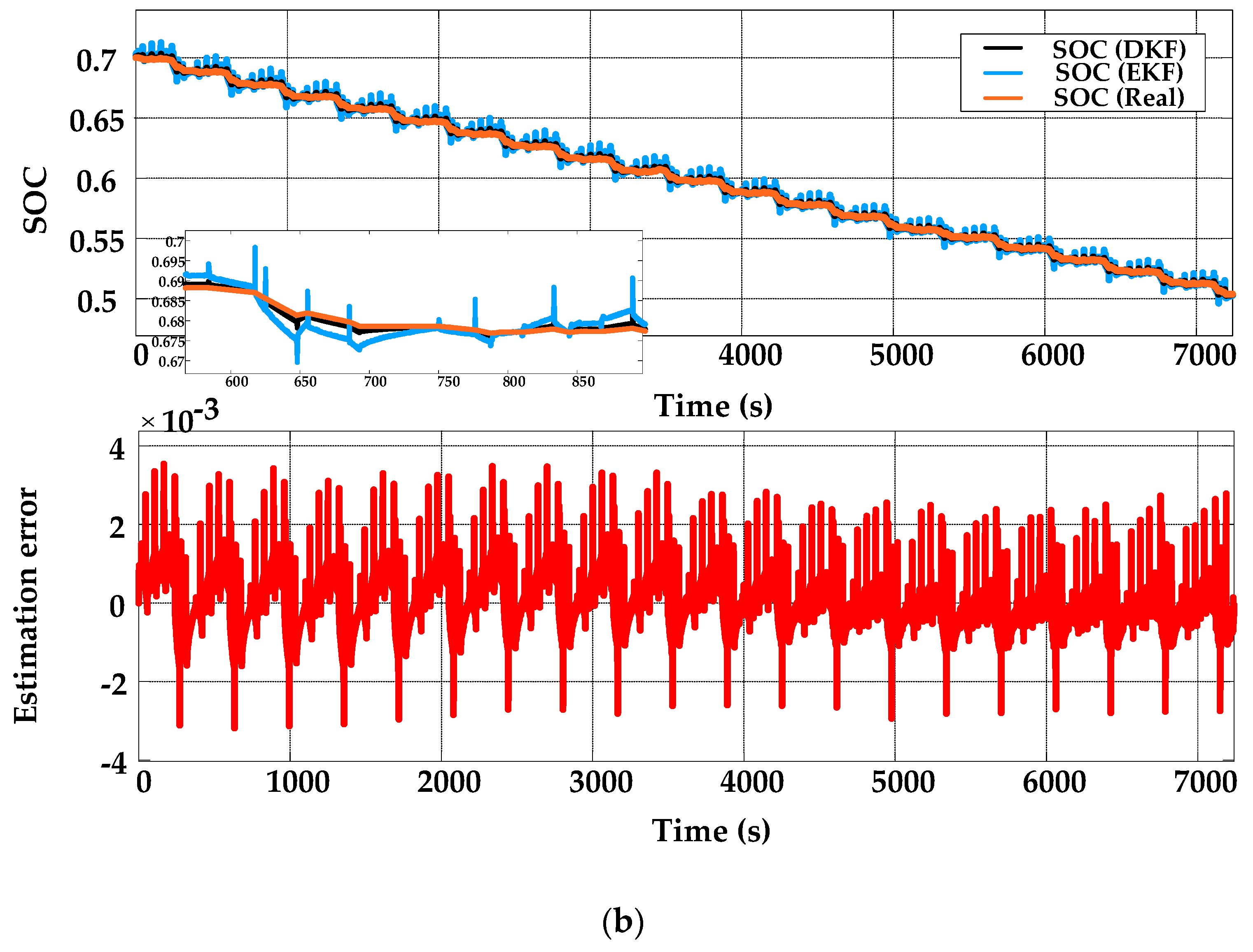
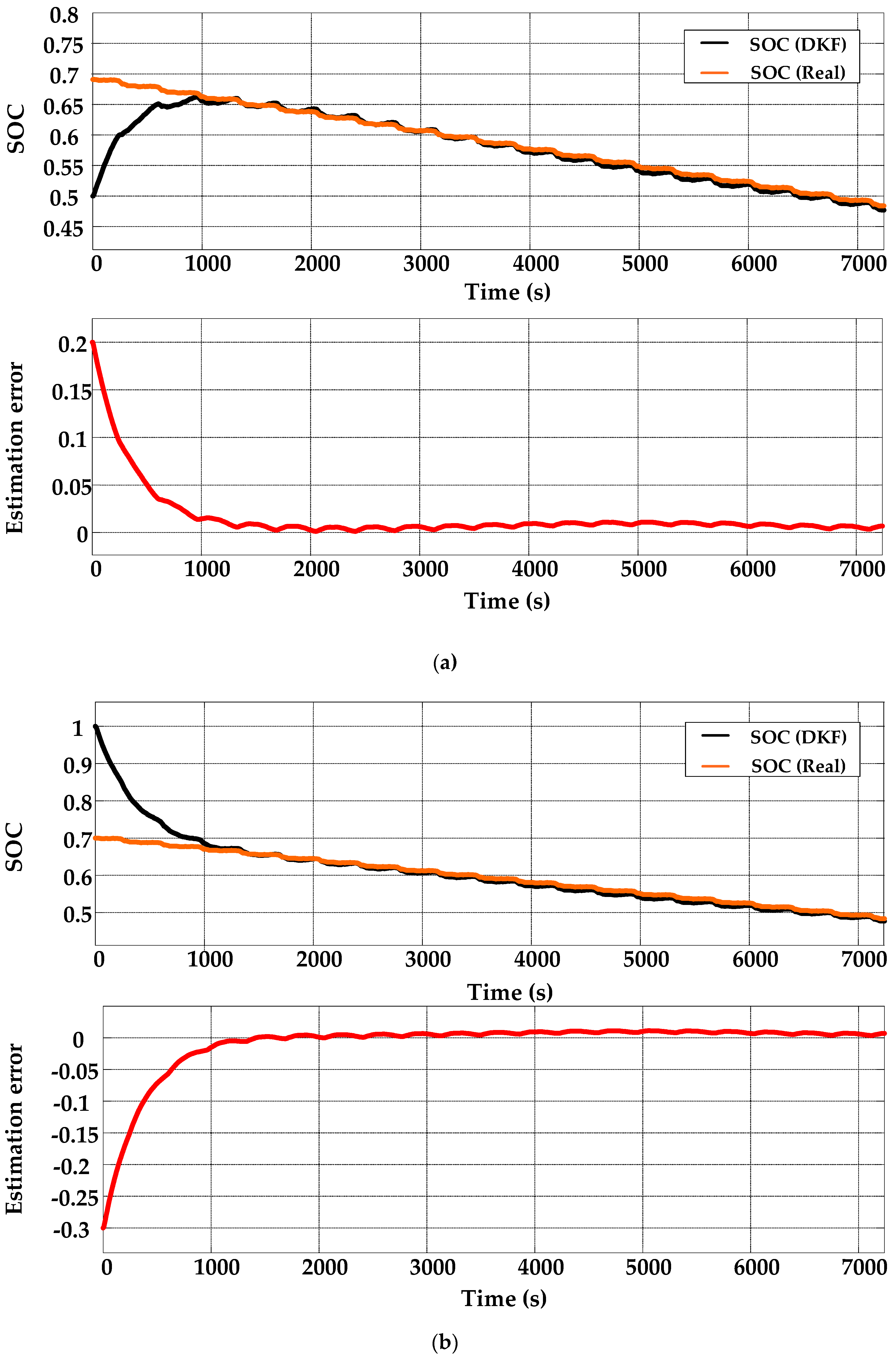
5.2. Algorithm Verification and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chaoui, H.; Ibe-Ekeocha, C.C. State of Charge and State of Health Estimation for Lithium Batteries Using Recurrent Neural Networks. IEEE Trans. Veh. Technol. 2017, 66, 8773–8783. [Google Scholar] [CrossRef]
- Ng, K.S.; Moo, C.S.; Chen, Y.P.; Hsieh, Y.C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Stan, A.I.; Swierczynski, M.; Stroe, D.I.; Teodorescu, R.; Andreasen, S.J. Lithium Ion Battery Chemistries from Renewable Energy Storage to Automotive and Back-up Power Applications—An Overview. In Proceedings of the 2014 International Conference on Optimization of Electrical and Electronic Equipment (Optim), Bran, Romania, 22–24 May 2014; pp. 713–720. [Google Scholar]
- Xiong, R.; Cao, J.Y.; Yu, Q.Q.; He, H.W.; Sun, F.C. Critical Review on the Battery State of Charge Estimation Methods for Electric Vehicles. IEEE Access 2018, 6, 1832–1843. [Google Scholar] [CrossRef]
- Yang, N.X.; Zhang, X.W.; Shang, B.B.; Li, G.J. Unbalanced discharging and aging due to temperature differences among the cells in a lithium-ion battery pack with parallel combination. J. Power Sources 2016, 306, 733–741. [Google Scholar] [CrossRef]
- Deng, Y.; Hu, Y.L.; Cao, Y. An Improved Algorithm of SOC Testing Based on Open-Circuit Voltage-Ampere Hour Method. Intell. Comput. Smart Grid Electr. Veh. 2014, 463, 258–267. [Google Scholar]
- Lee, S.; Kim, J.; Lee, J.; Cho, B.H. State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge. J. Power Sources 2008, 185, 1367–1373. [Google Scholar] [CrossRef]
- Orchard, M.E.; Hevia-Koch, P.; Zhang, B.; Tang, L. Risk Measures for Particle-Filtering-Based State-of-Charge Prognosis in Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2013, 60, 5260–5269. [Google Scholar] [CrossRef]
- Piller, S.; Perrin, M.; Jossen, A. Methods for state-of-charge determination and their applications. J. Power Sources 2001, 96, 113–120. [Google Scholar] [CrossRef]
- Tulsyan, A.; Tsai, Y.; Gopaluni, R.B.; Braatz, R.D. State-of-charge estimation in lithium-ion batteries: A particle filter approach. J. Power Sources 2016, 331, 208–223. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs. Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 2: Simultaneous state and parameter estimation. J. Power Sources 2006, 161, 1369–1384. [Google Scholar] [CrossRef]
- Sun, F.C.; Xiong, R.; He, H.W. A systematic state-of-charge estimation framework for multi-cell battery pack in electric vehicles using bias correction technique. Appl. Energy 2016, 162, 1399–1409. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Zheng, Y.J.; Ouyang, M.G.; Han, X.B.; Lu, L.G.; Li, J.Q. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles. J. Power Sources 2018, 377, 161–188. [Google Scholar] [CrossRef]
- Cai, C.H.; Du, D.; Liu, Z.Y.; Zhang, H. Artificial neural network in estimation of battery state-of-charge (SOC) with nonconventional input variables selected by correlation analysis. In Proceedings of the 2002 International Conference on Machine Learning and Cybernetics, Beijing, China, 4–5 November 2002; Volume 3, pp. 1619–1625. [Google Scholar]
- He, H.W.; Zhang, X.W.; Xiong, R.; Xu, Y.L.; Guo, H.Q. Online model-based estimation of state-of-charge and open-circuit voltage of lithium-ion batteries in electric vehicles. Energy 2012, 39, 310–318. [Google Scholar] [CrossRef]
- Shi, Q.-S.; Zhang, C.-H.; Cui, N.-X. Estimation of battery state-of-charge using ν-support vector regression algorithm. Int. J. Automot. Technol. 2008, 9, 759–764. [Google Scholar] [CrossRef]
- Schwunk, S.; Armbruster, N.; Straub, S.; Kehl, J.; Vetter, M. Particle filter for state of charge and state of health estimation for lithium–iron phosphate batteries. J. Power Sources 2013, 239, 705–710. [Google Scholar] [CrossRef]
- Khumprom, P.; Yodo, N. A data-driven predictive prognostic model for lithium-ion batteries based on a deep learning algorithm. Energies 2019, 12, 660. [Google Scholar] [CrossRef]
- Li, C.; Xiao, F.; Fan, Y. An approach to state of charge estimation of lithium-ion batteries based on recurrent neural networks with gated recurrent unit. Energies 2019, 12, 1592. [Google Scholar] [CrossRef]
- Zenati, A.; Desprez, P.; Razik, H. Estimation of the SOC and the SOH of Li-ion Batteries, by combining Impedance Measurements with the Fuzzy Logic Inference. In Proceedings of the 36th Annual Conference on IEEE Industrial Electronics Society (IECON 2010), Glendale, AZ, USA, 7–10 November 2010; pp. 1773–1778. [Google Scholar]
- Bhangu, B.S.; Bentley, P.; Stone, D.A.; Bingham, C.M. Nonlinear Observers for Predicting State-of-Charge and State-of-Health of Lead-Acid Batteries for Hybrid-Electric Vehicles. IEEE Trans. Veh. Technol. 2005, 54, 783–794. [Google Scholar] [CrossRef]
- Chen, Z.; Fu, Y.H.; Mi, C.C. State of Charge Estimation of Lithium-Ion Batteries in Electric Drive Vehicles Using Extended Kalman Filtering. IEEE Trans. Veh. Technol. 2013, 62, 1020–1030. [Google Scholar] [CrossRef]
- Li, S.X.; Hu, M.H.; Li, Y.X.; Gong, C.C. Fractional-order modeling and SOC estimation of lithium-ion battery considering capacity loss. Int. J. Energy Res. 2019, 43, 417–429. [Google Scholar] [CrossRef]
- Duong, V.H.; Bastawrous, H.A.; Lim, K.; See, K.W.; Zhang, P.; Dou, S.X. Online state of charge and model parameters estimation of the LiFePO4 battery in electric vehicles using multiple adaptive forgetting factors recursive least-squares. J. Power Sources 2015, 296, 215–224. [Google Scholar] [CrossRef]
- Yang, F.F.; Xing, Y.J.; Wang, D.; Tsui, K.L. A comparative study of three model-based algorithms for estimating state-of-charge of lithium-ion batteries under a new combined dynamic loading profile. Appl. Energy 2016, 164, 387–399. [Google Scholar] [CrossRef]
- Rooij, D.M.R.D. Electrochemical Methods: Fundamentals and Applications. Anti Corros. Methods Mater. 2003, 50, 414–421. [Google Scholar] [CrossRef]
- Yatsui, M.W.; Bai, H. Kalman filter based state-of-charge estimation for lithium-ion batteries in hybrid electric vehicles using pulse charging. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011. [Google Scholar]
- Hu, M.H.; Li, Y.X.; Li, S.X.; Fu, C.Y.; Qin, D.T.; Li, Z.H. Lithium-ion battery modeling and parameter identification based on fractional theory. Energy 2018, 165, 153–163. [Google Scholar] [CrossRef]
- Idaho National Engineering and Environmental Laboratory. FreedomCAR Battery Test Manual for Power-Assist Hybrid Electric Vehicles; INEEL (DOE/ID-11069): Cuernavaca, Mexico, 2003. [Google Scholar]
- Zhu, Q.; Xiong, N.; Yang, M.L.; Huang, R.S.; Hu, G.D. State of Charge Estimation for Lithium-Ion Battery Based on Nonlinear Observer: An H-infinity Method. Energies 2017, 10, 679. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, L.; Hu, X.S.; Xiong, N.; Hu, G.D. H-infinity-Based Nonlinear Observer Design for State of Charge Estimation of Lithium-Ion Battery with Polynomial Parameters. IEEE Trans. Veh. Technol. 2017, 66, 10853–10865. [Google Scholar] [CrossRef]
- Idaho National Engineering Laboratory. USABC Electric Vehicle Battery Test Procedures Manual–Revision 2; INEEL (DOE/ID-10479): Cuernavaca, Mexico, 1996. [Google Scholar]
| Battery Model | Nominal Capacity | Rated Voltage | Charge Cutoff Voltage | Discharge Cutoff Voltage |
|---|---|---|---|---|
| 18,650 | 3350 mAh | 3.6 V | 4.2 V | 2.5 V |
| Test Name | Test Steps |
|---|---|
| SCT Test |
|
| HPPC Test |
|
| Double Pulse Test |
|
| Coefficient | 5 °C | 15 °C | 25 °C | 35 °C |
|---|---|---|---|---|
| K1 | 2.7758 | 2.81055 | 2.58785 | 2.4553 |
| K2 | 1.6295 | 1.48735 | 1.78815 | 1.96495 |
| K3 | −0.04675 | −0.04095 | −0.07095 | −0.1013 |
| K4 | −0.43585 | −0.4026 | −0.5894 | −0.7354 |
| K5 | 0.07365 | 0.02485 | 0.05735 | 0.05175 |
| Parameter | 5 °C | 15 °C | 25 °C | 35 °C | 45 °C |
|---|---|---|---|---|---|
| R0 | 0.067551 | 0.056435 | 0.048624 | 0.046138 | 0.043975 |
| Working Conditions | EKF | DKF | ||||
|---|---|---|---|---|---|---|
| Constant temperature | R2 | Maximum error | Average error | R2 | Maximum error | Average error |
| 0.9978 | 0.0134 | 0.0024 | 0.9998 | 0.0036 | 0.0006 | |
| Varying temperature | R2 | Maximum error | Average error | R2 | Maximum error | Average error |
| 0.9984 | 0.131 | 0.0018 | 0.9999 | 0.0035 | 0.0005 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Hu, M.; Fu, C.; Cao, K.; Su, Z.; Yang, Z. State of Charge Estimation for Lithium-Ion Batteries Based on Temperature-Dependent Second-Order RC Model. Electronics 2019, 8, 1012. https://doi.org/10.3390/electronics8091012
Xu Y, Hu M, Fu C, Cao K, Su Z, Yang Z. State of Charge Estimation for Lithium-Ion Batteries Based on Temperature-Dependent Second-Order RC Model. Electronics. 2019; 8(9):1012. https://doi.org/10.3390/electronics8091012
Chicago/Turabian StyleXu, Yidan, Minghui Hu, Chunyun Fu, Kaibin Cao, Zhong Su, and Zhong Yang. 2019. "State of Charge Estimation for Lithium-Ion Batteries Based on Temperature-Dependent Second-Order RC Model" Electronics 8, no. 9: 1012. https://doi.org/10.3390/electronics8091012
APA StyleXu, Y., Hu, M., Fu, C., Cao, K., Su, Z., & Yang, Z. (2019). State of Charge Estimation for Lithium-Ion Batteries Based on Temperature-Dependent Second-Order RC Model. Electronics, 8(9), 1012. https://doi.org/10.3390/electronics8091012







