Control Design of LCL Type Grid-Connected Inverter Based on State Feedback Linearization
Abstract
:1. Introduction
2. Single Closed-Loop Controller Design Based on State Feedback Linearization
2.1. Model of the Three-Phase Three-Leg Grid-Connected Inverter
2.2. Single Closed-Loop Control Strategy Based on State Feedback Linearization
- for all 0 ≤ j ≤ m, for all k ≤ ri − 1, for all 0 ≤ i≤ m and for all x in a neighborhood of x0.
- the m × m matrix E(X) is nonsingular at .
2.3. Parameters Design of Current Single Closed Loop Controller
- Stability conditions of the system
- 2.
- Restrictive conditions of dipoles parameters
- 3.
- Cut-off frequency of the closed loop system
- 4.
- Closed loop amplitude frequency characteristic at zero frequency
3. Design of Double Closed Loop Controller Based on Reduced Order State Feedback Linearization
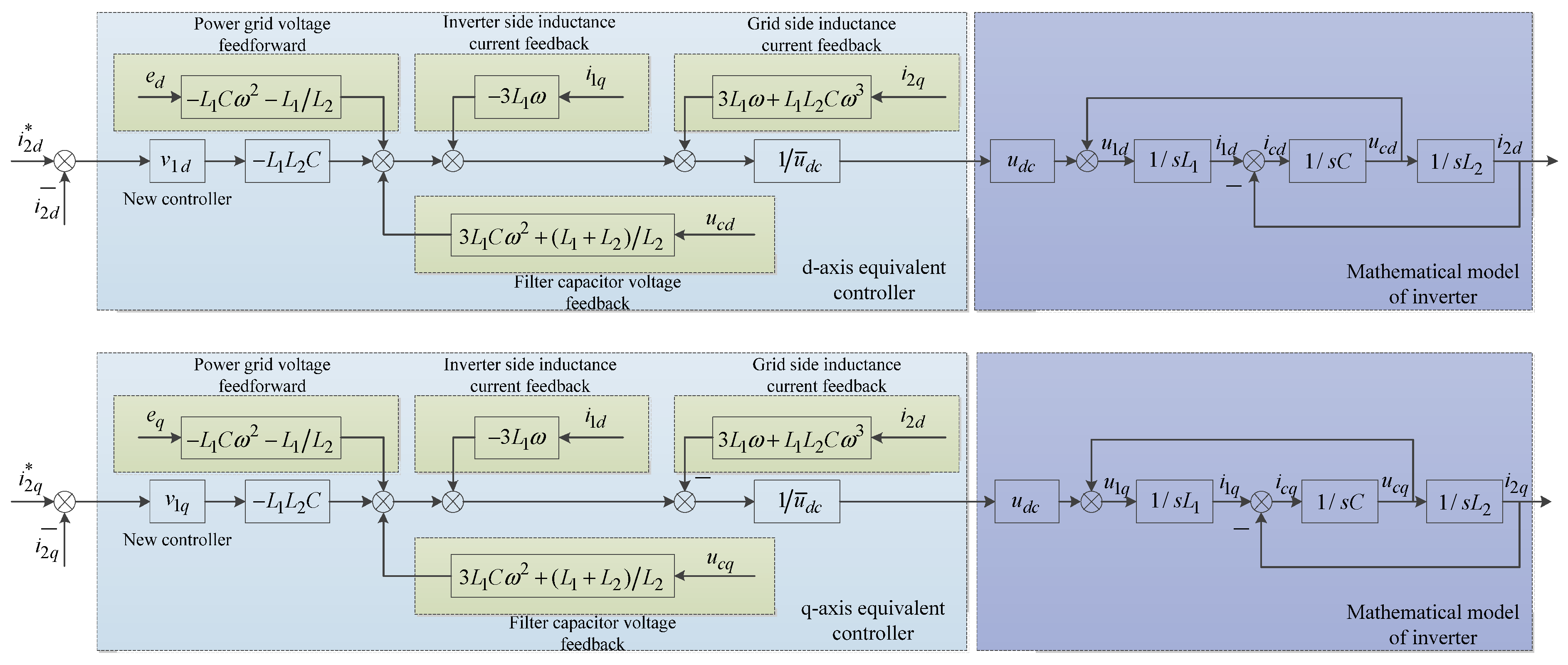
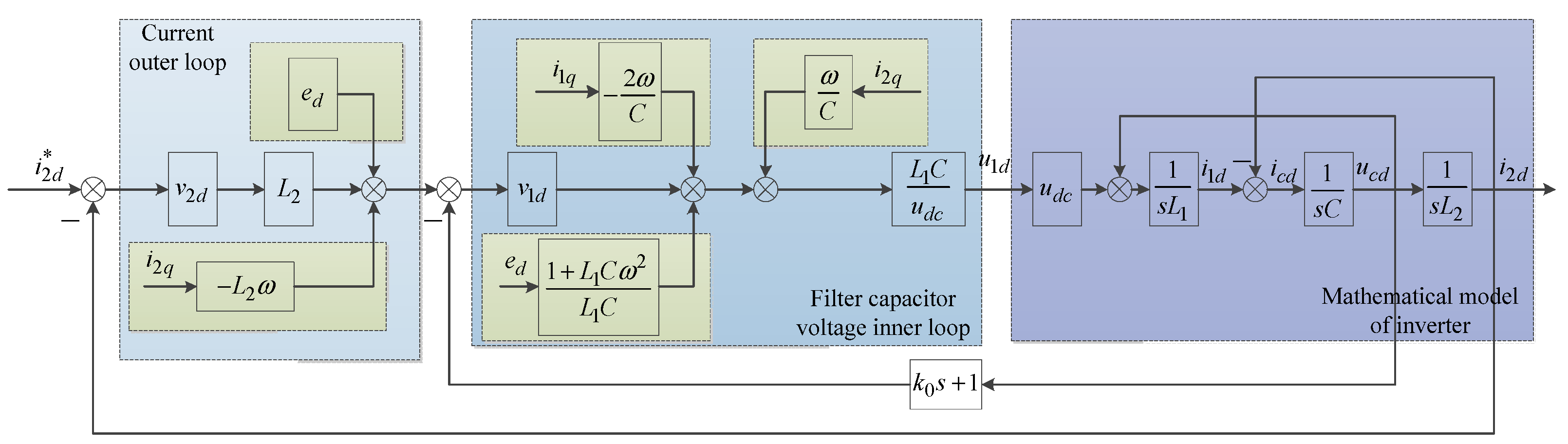
3.1. State Feedback of Inverter Side Inductance and Filter Capacitor Subsystem
3.2. State Feedback of Grid-Side Inductance Subsystem
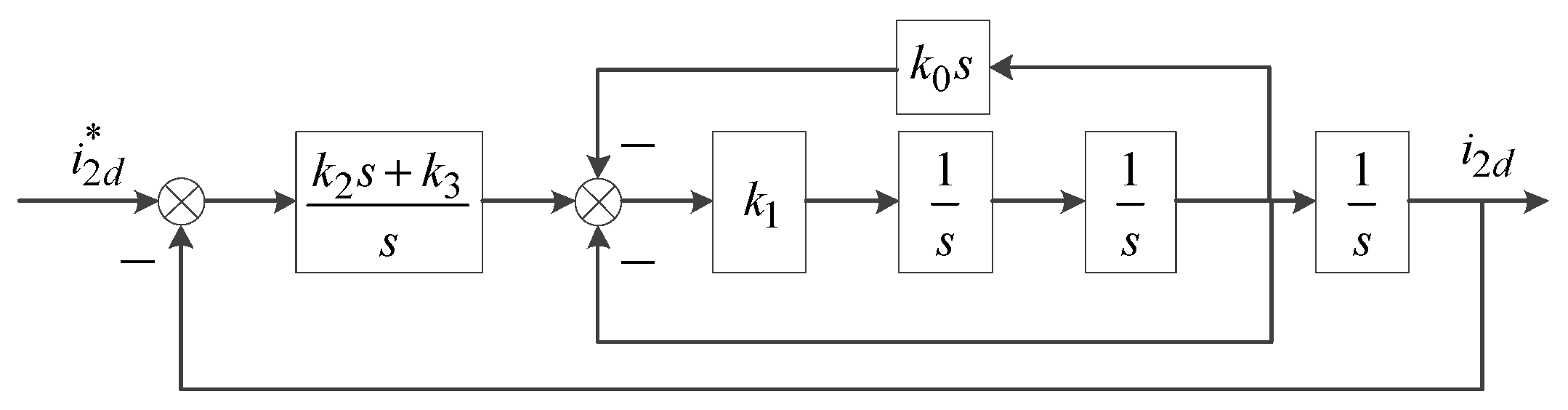
3.3. Parameters Design of Double Closed Loop Controller
4. Simulations and Experiments
4.1. Simulation and Experimental Environment
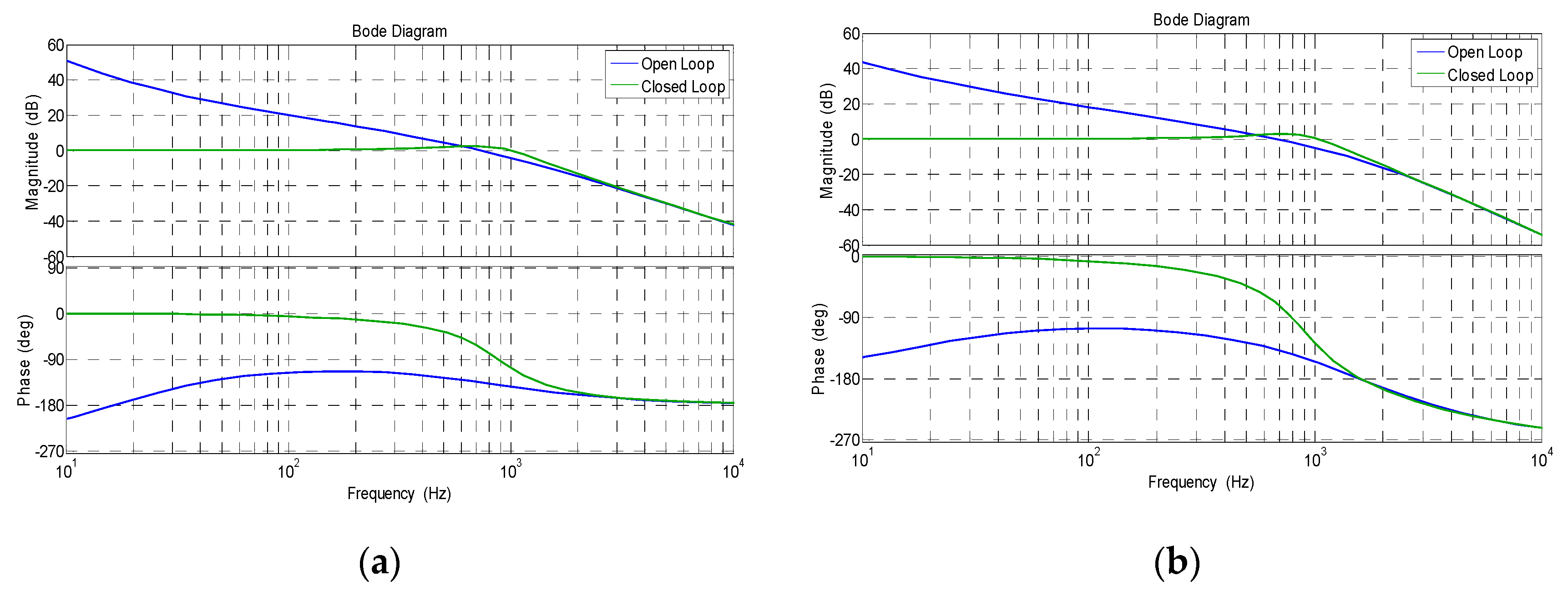
- Based on Equations (17)–(20), selecting the cut-off frequency of the open-loop transfer function as 750 Hz, the single closed-loop control system parameters can be designed as: k3 = 5000, k2 = 107π, k1 = 200k2, k0 = 104k2. At this time, the corresponding phase margin is Pm = 45°, and the closed-loop bandwidth is 1 kHz.
- Similarly, the parameters of the double closed loop control system can be designed as: k0 = 2 × 10−4, k1 = 108, k2 = 5 × 103, k3 = 102k3. Then, the corresponding open loop cut-off frequency is 680 Hz, phase margin is Pm = 43°, and closed-loop bandwidth is 1 kHz.
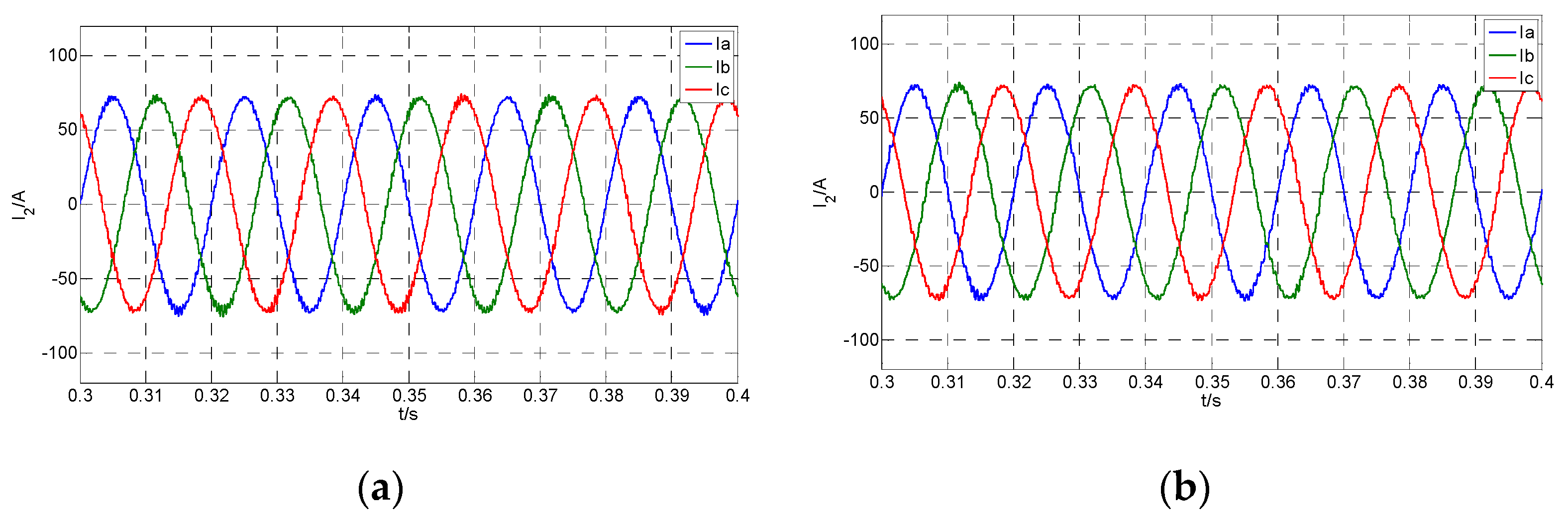
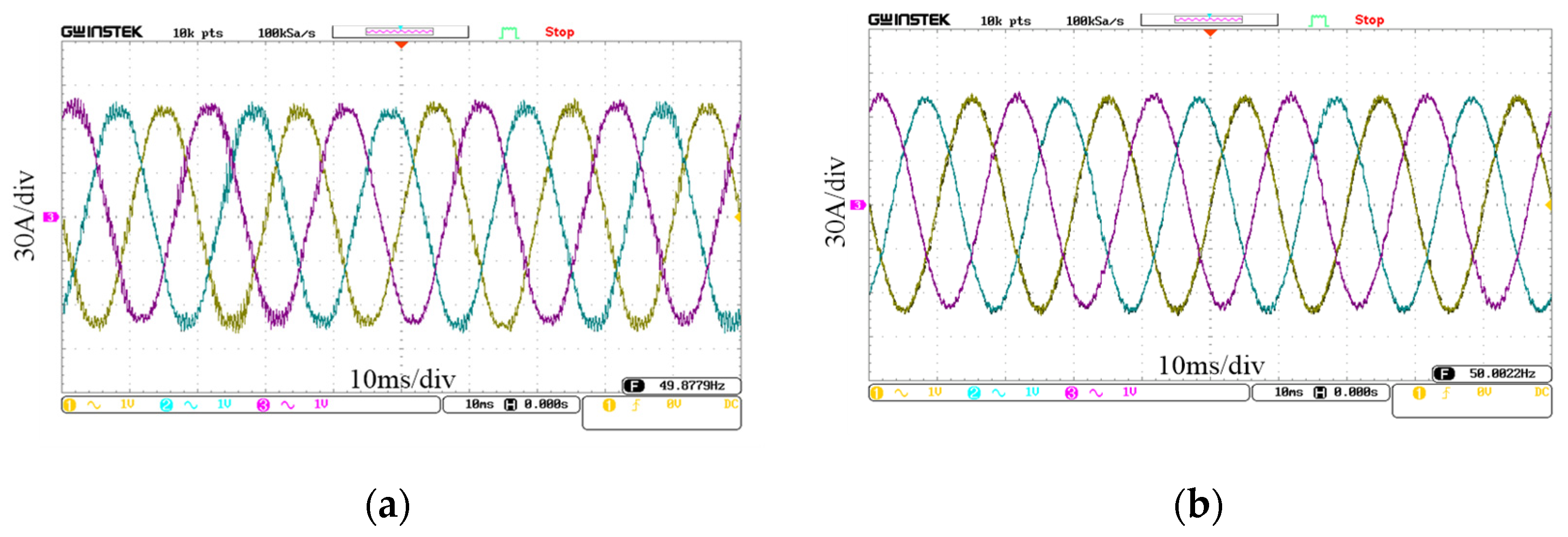
4.2. Steady State Control Performance
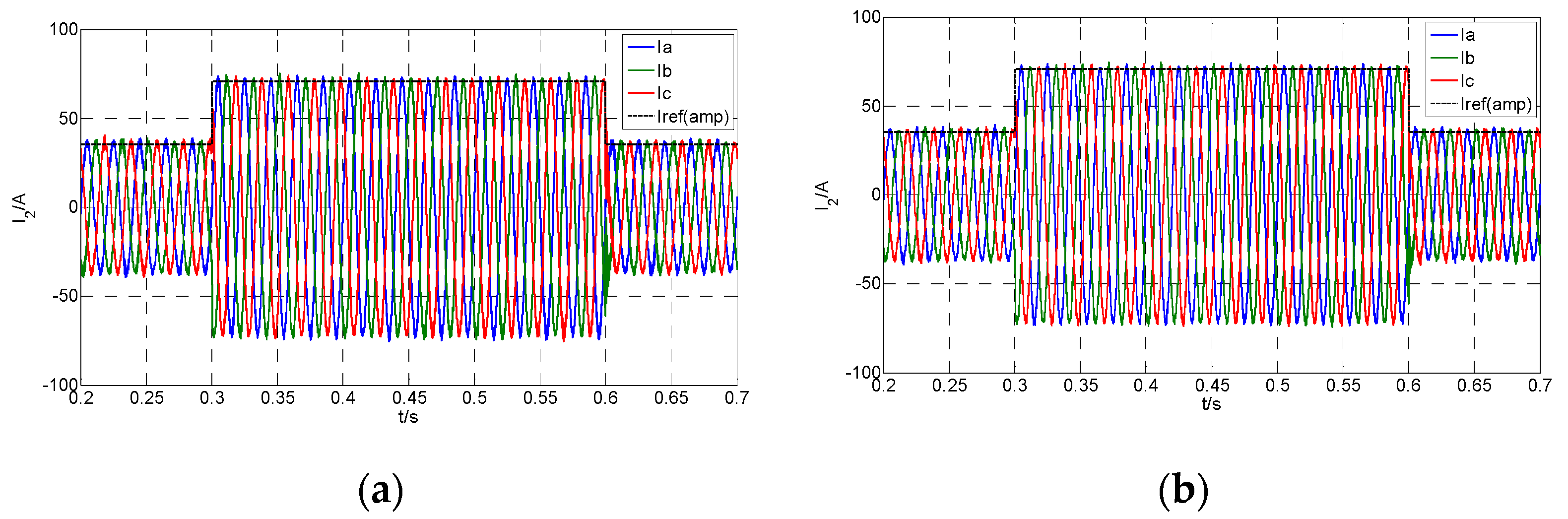
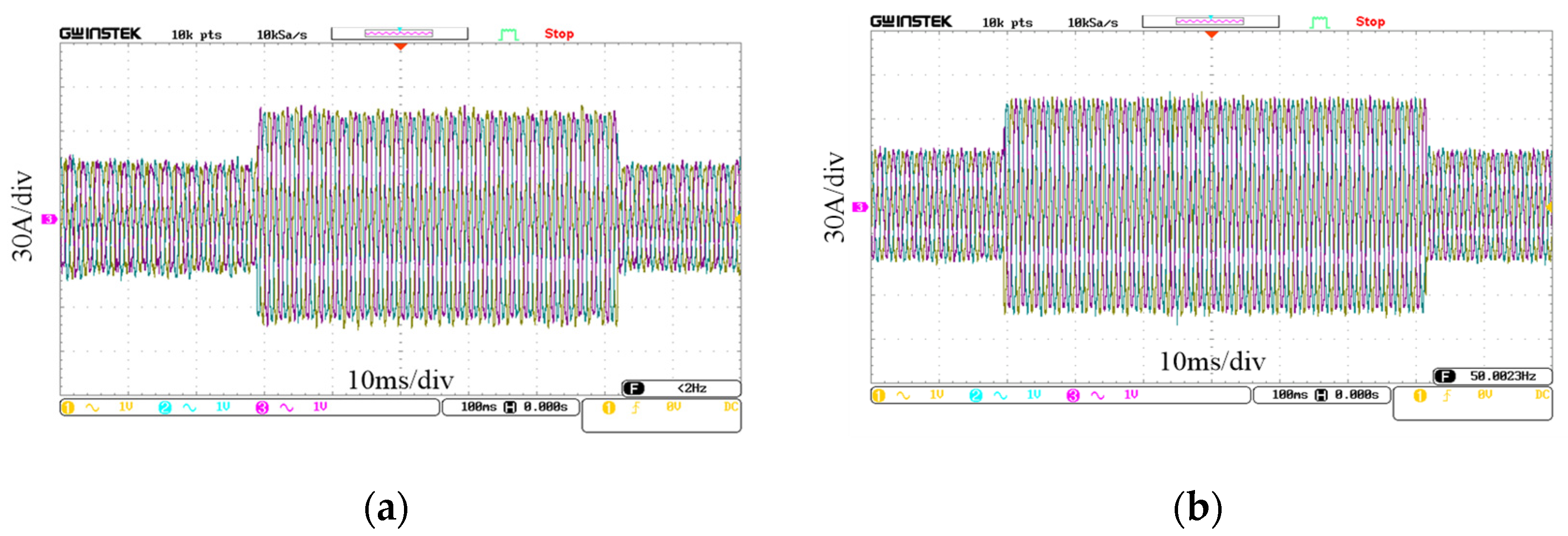
4.3. Dynamic Control Performance
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Farokhian, F.M.; Roosta, A.; Gitizadeh, M. Stability analysis and decentralized control of inverter-based ac microgrid. Prot. Control Mod. Power Syst. 2019, 4, 65–86. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Liang, J.; Gao, J.; Walker, P.; Zhang, N. Sliding-mode observer based voltage-sensorless model predictive power control of pwm rectifier under unbalanced grid condition. IEEE Trans. Ind. Electron. 2018, 65, 5550–5560. [Google Scholar] [CrossRef]
- Xu, X.; Casale, E.; Bishop, M. Application guidelines for a new master controller model for statcom control in dynamic analysis. IEEE Trans. Power Deliv. 2017, 32, 2555–2564. [Google Scholar] [CrossRef]
- Bosch, S.; Staiger, J.; Steinhart, H. Predictive current control for an active power filter with lcl-filter. IEEE Trans. Ind. Electron. 2018, 65, 4943–4952. [Google Scholar] [CrossRef]
- Liu, B.; Wei, Q.; Zou, C.; Duan, S. Stability analysis of lcl-type grid-connected inverter under single-loop inverter-side current control with capacitor voltage feedforward. IEEE Trans. Ind. Inform. 2017, 14, 691–702. [Google Scholar] [CrossRef]
- Jamshidifar, A.; Jovcic, D. Small-signal dynamic dq model of modular multilevel converter for system studies. IEEE Trans. Power Deliv. 2016, 31, 191–199. [Google Scholar] [CrossRef]
- Bao, X.; Zhuo, F.; Tian, Y.; Tan, P. Simplified feedback linearization control of three-phase photovoltaic inverter with an lcl filter. IEEE Trans. Power Electron. 2013, 28, 2739–2752. [Google Scholar] [CrossRef]
- Lamperski, A.; Ames, A.D. Lyapunov theory for zeno stability. IEEE Trans. Autom. Control 2012, 58, 100–112. [Google Scholar] [CrossRef]
- Hwang, C.L.; Fang, W.L. Global fuzzy adaptive hierarchical path tracking control of a mobile robot with experimental validation. IEEE Trans. Fuzzy Syst. 2016, 24, 724–740. [Google Scholar] [CrossRef]
- Kim, D.E.; Lee, D.C. Feedback linearization control of three-phase ups inverter systems. IEEE Trans. Ind. Electron. 2010, 57, 963–968. [Google Scholar]
- Akhtar, A.; Nielsen, C.; Waslander, S.L. Path following using dynamic transverse feedback linearization for car-like robots. IEEE Trans. Robot. 2017, 31, 269–279. [Google Scholar] [CrossRef]
- Choi, Y.S.; Han, H.C.; Jung, J.W. Feedback linearization direct torque control with reduced torque and flux ripples for ipmsm drives. IEEE Trans. Power Electron. 2015, 31, 3728–3737. [Google Scholar] [CrossRef]
- Yang, L.Y.; Liu, J.H.; Wang, C.L.; Du, G.F. Sliding mode control of three-phase four-leg inverters via state feedback. J. Power Electron. 2014, 14, 1028–1037. [Google Scholar] [CrossRef]
- Lascu, C.; Jafarzadeh, S.; Fadali, S.M.; Blaabjerg, F. Direct torque control with feedback linearization for induction motor drives. IEEE Trans. Power Electron. 2016, 32, 2072–2080. [Google Scholar] [CrossRef]
- Yang, S.; Wang, P.; Tang, Y. Feedback linearization based current control strategy for modular multilevel converters. IEEE Trans. Power Electron. 2017, 33, 161–174. [Google Scholar]
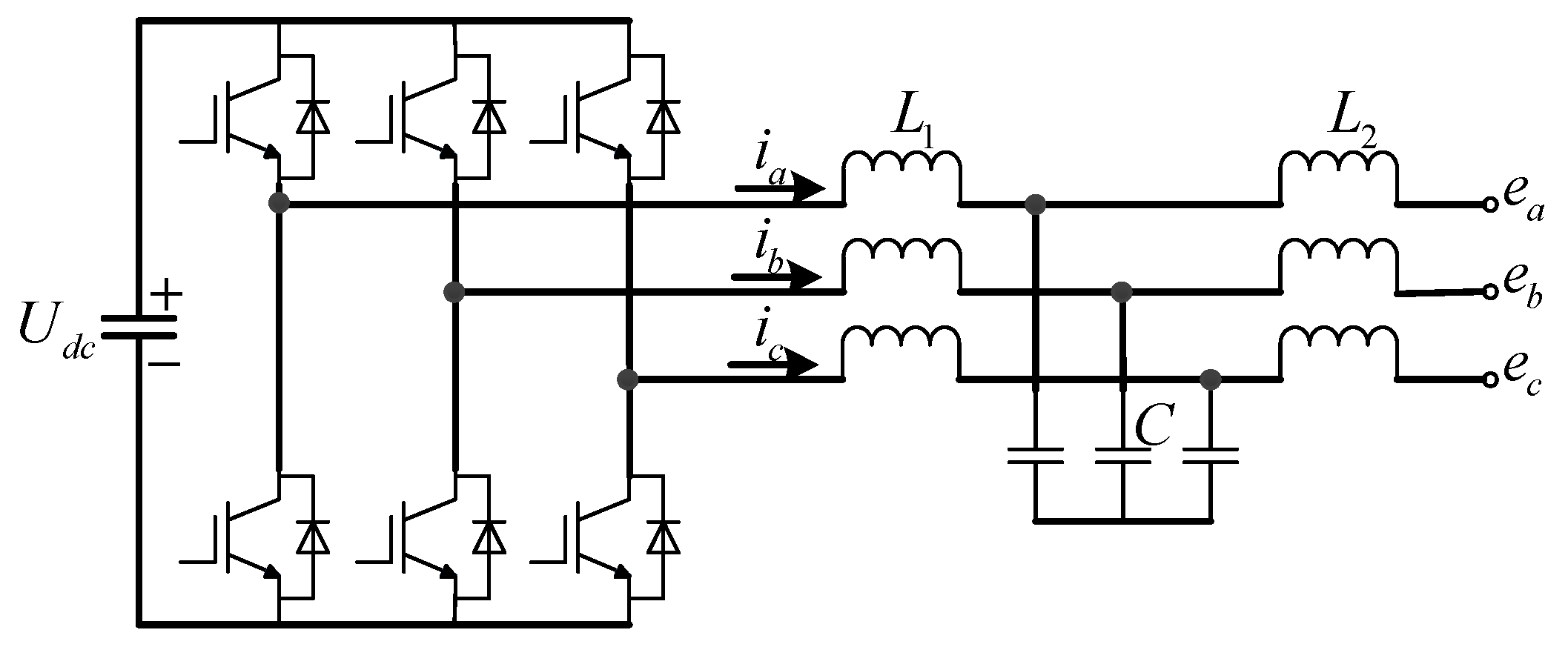


| Variables | Symbols | Value |
|---|---|---|
| DC Bus Voltage | udc | 650 V |
| Grid Voltage | ug | 380 V |
| Grid-side inductor | L2 | 0.2 mH |
| Inverter side inductor | L1 | 0.3 mH |
| Filter capacitor | C | 20 uF |
| Switching frequency | f | 10 kHz |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Feng, C.; Liu, J. Control Design of LCL Type Grid-Connected Inverter Based on State Feedback Linearization. Electronics 2019, 8, 877. https://doi.org/10.3390/electronics8080877
Yang L, Feng C, Liu J. Control Design of LCL Type Grid-Connected Inverter Based on State Feedback Linearization. Electronics. 2019; 8(8):877. https://doi.org/10.3390/electronics8080877
Chicago/Turabian StyleYang, Longyue, Chunchun Feng, and Jianhua Liu. 2019. "Control Design of LCL Type Grid-Connected Inverter Based on State Feedback Linearization" Electronics 8, no. 8: 877. https://doi.org/10.3390/electronics8080877




