Real-Time Monte Carlo Optimization on FPGA for the Efficient and Reliable Message Chain Structure
Abstract
:1. Introduction
2. Problem Description
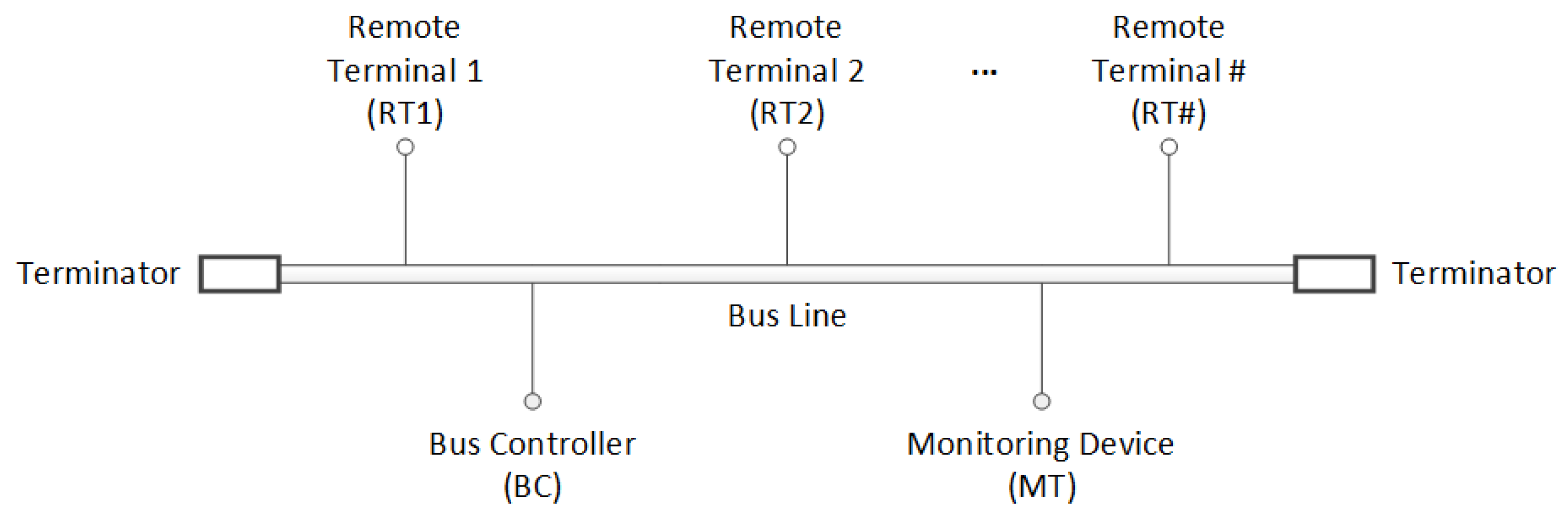
2.1. MIL-STD-1553B Communications
2.2. Problem of Real-Time Optimization
3. Proposed Method
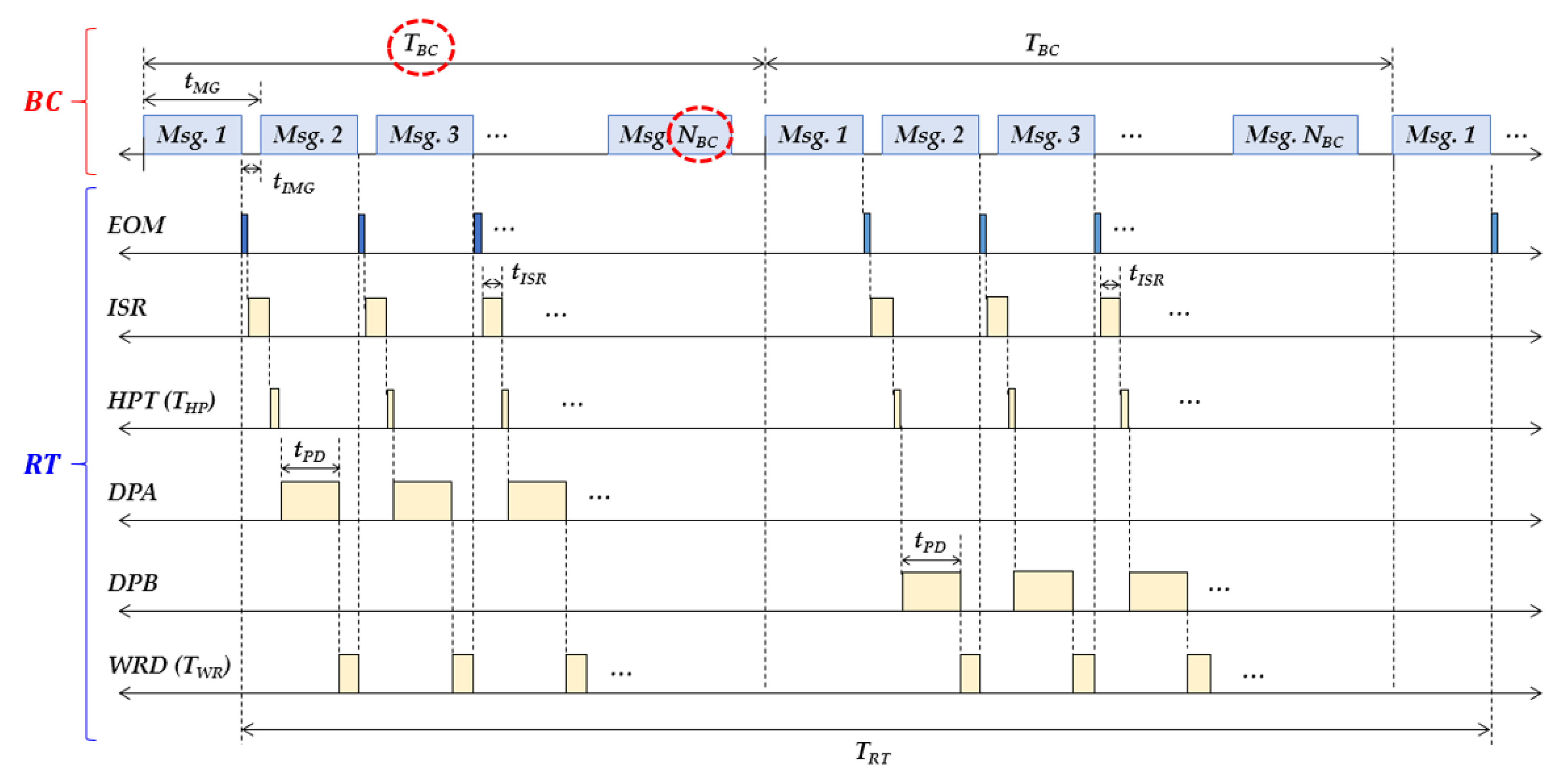
3.1. Formulation of System Constraints
3.2. Monte Carlo Optimization
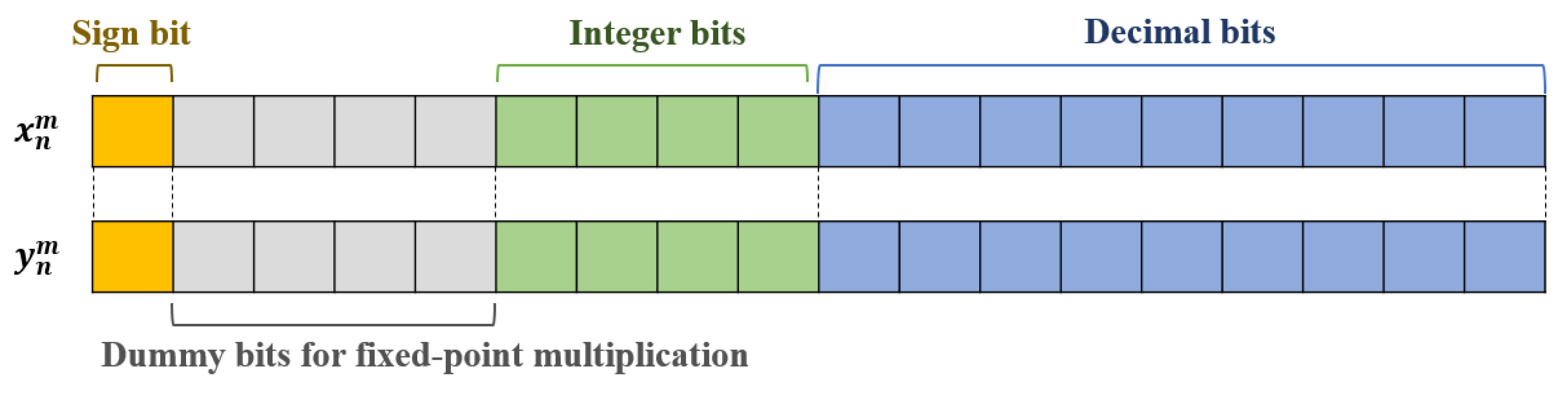
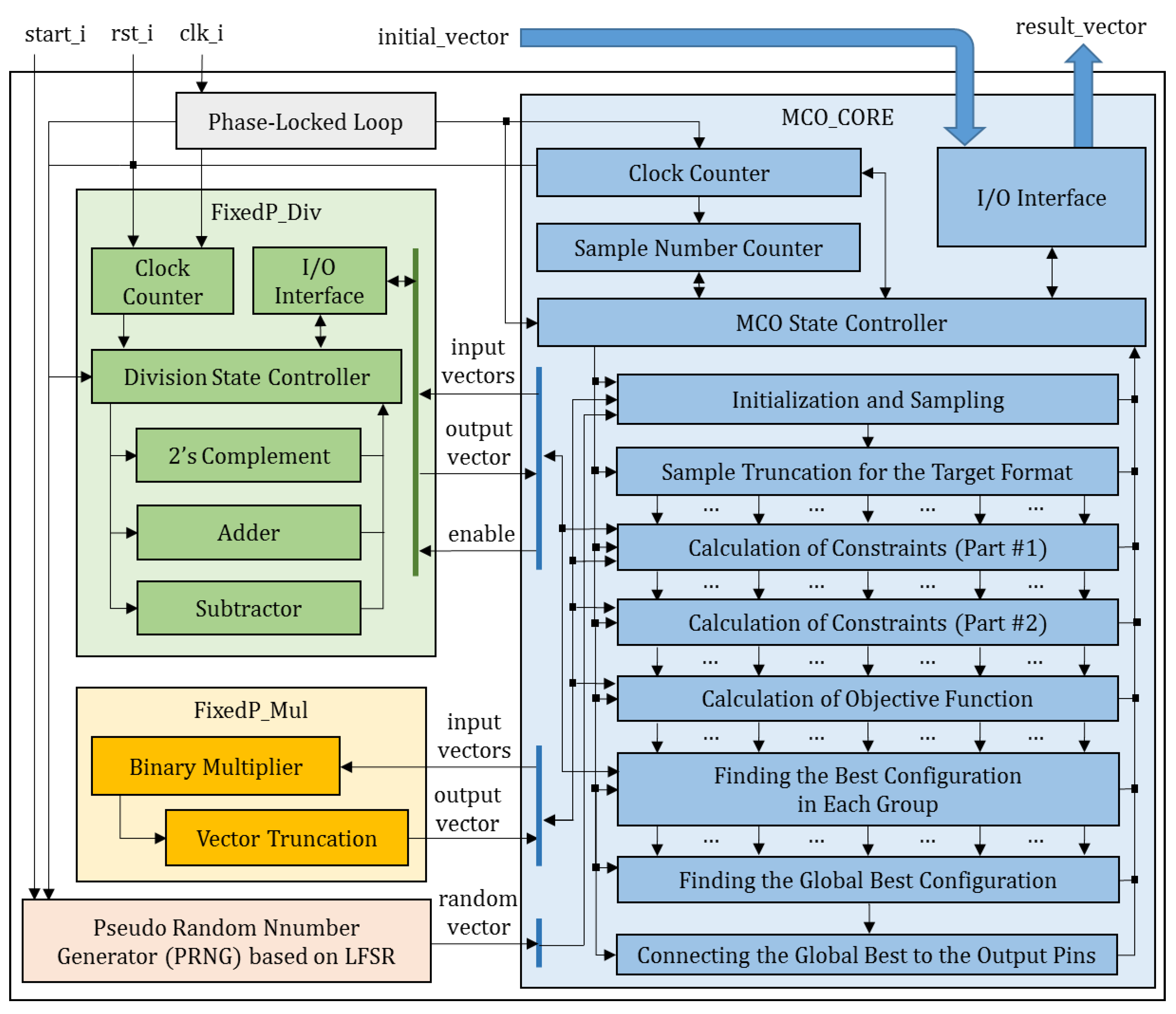
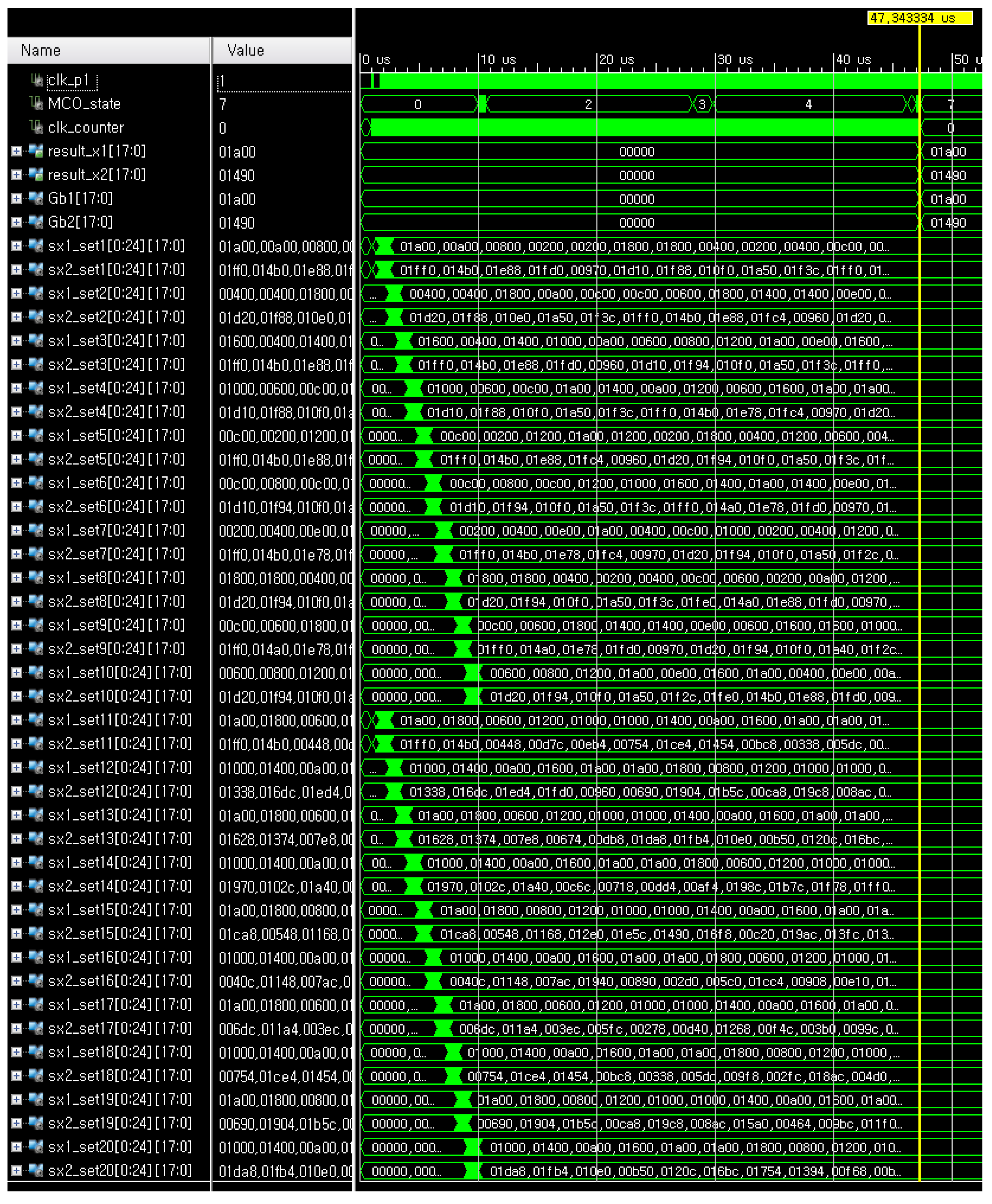
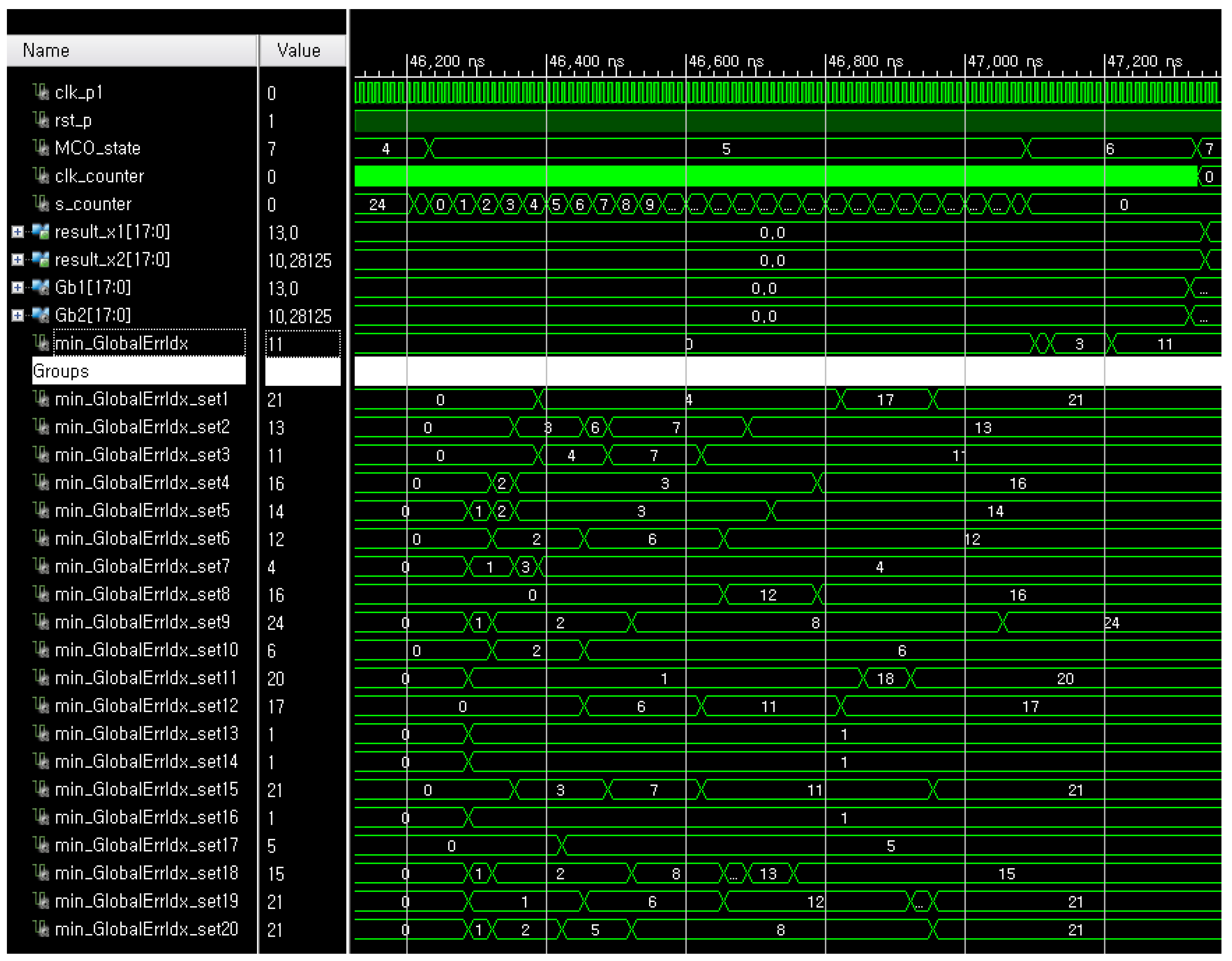
3.3. FPGA-Based Real-Time MCO
| Algorithm: | FPGA-based Real-Time Monte Carlo Optimization (FRMCO) |
| Input: | Initial vector, clock (clk_i), reset signal (rst_i), PRNG start signal (start_i) |
| Output: | Result vector |
| 1: | Start the phase-locked loop block with clk_i and generate clk_p |
| 2: | Start the PRNG block with start_i |
| 3: | Initialize the FixedP_Mul and the Fixed_Div blocks with clk_p and rst_i |
| 4: | Initialize the signals and variables in the MCO_CORE block with clk_p and rst_i |
| 5: | Process for the MCO_CORE block |
| 6: | Initialize the MCO state, clock counter (CC), sample number counter (SNC) |
| 7: | Iterate the loop controlled by CC and SNC |
| 8: | Sample particles using the PRNG block from the given search space |
| 9: | Truncate the sampled particles for the target format |
| 10: | Calculate a part of the time constraint in Equation (6) |
| 11: | Calculate the constraints by Equations (6) and (7) |
| 12: | Calculate the objective function by Equation (8) |
| 13: | Connect the global best configuration to the assigned output pins |
| 14: | End loop |
| 15: | Find the best configuration in each group |
| 16: | Find the global best configuration as the optimal value |
| 17: | End process |
4. Implementation and Evaluations
4.1. Implementation
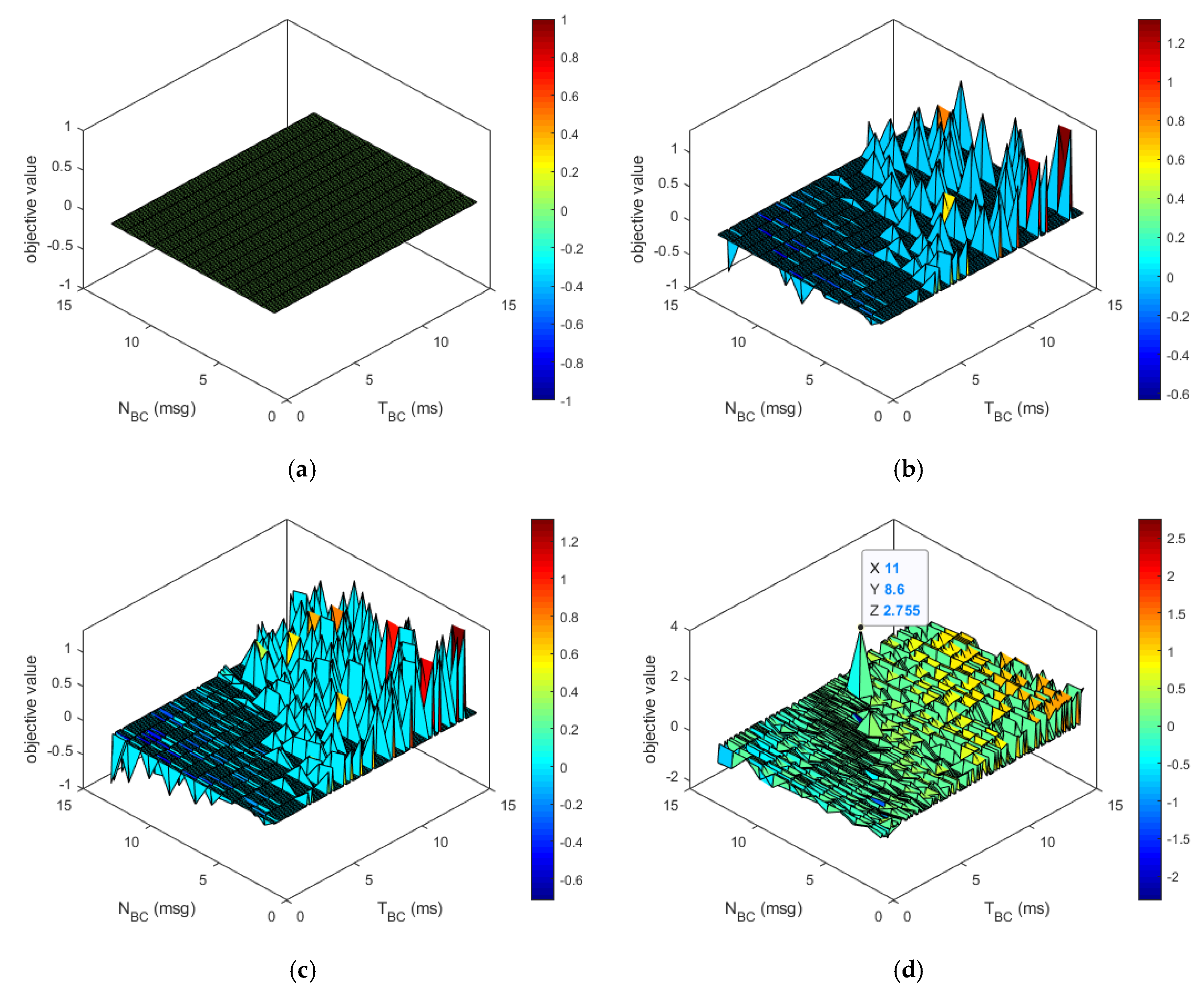
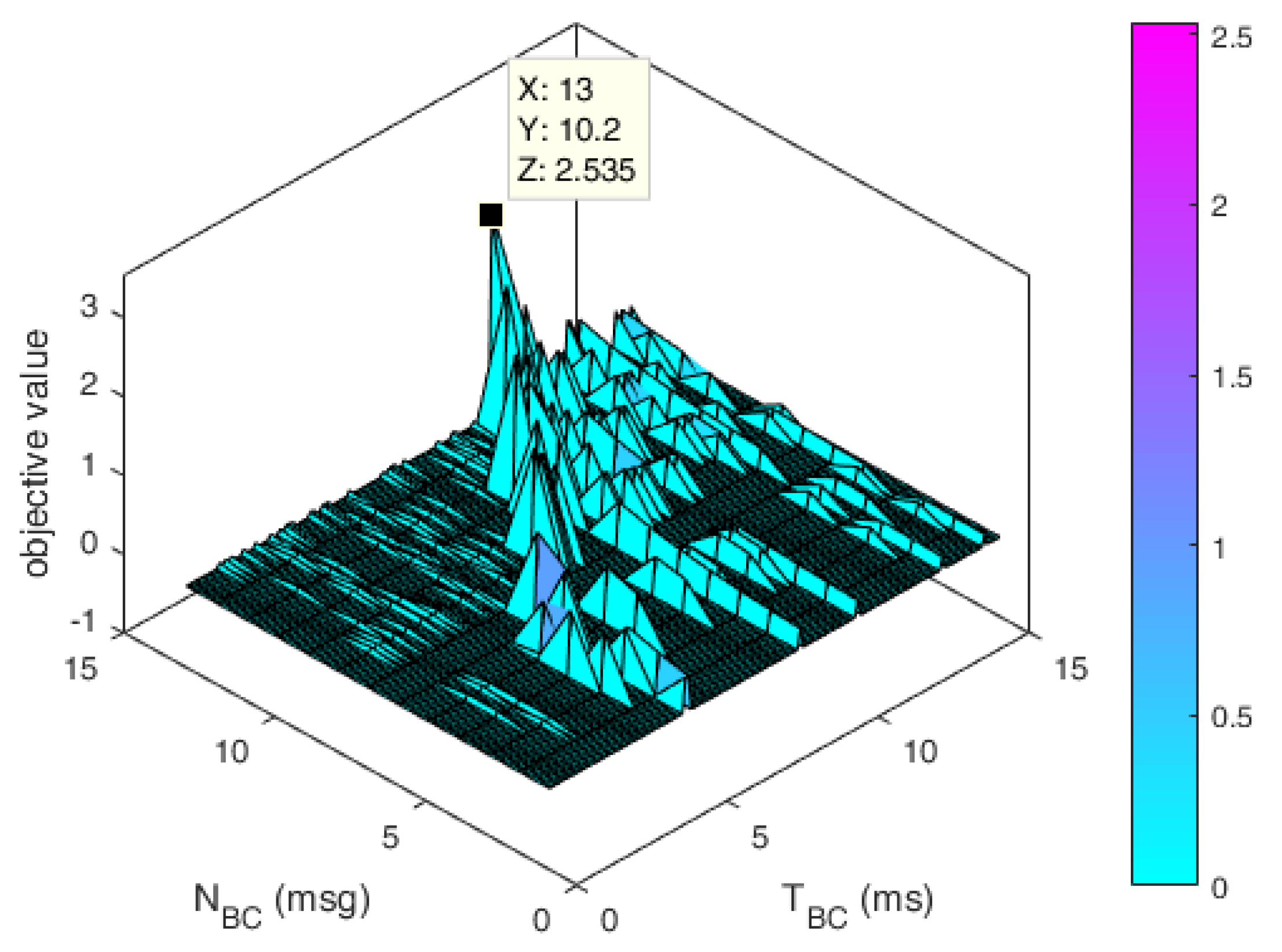
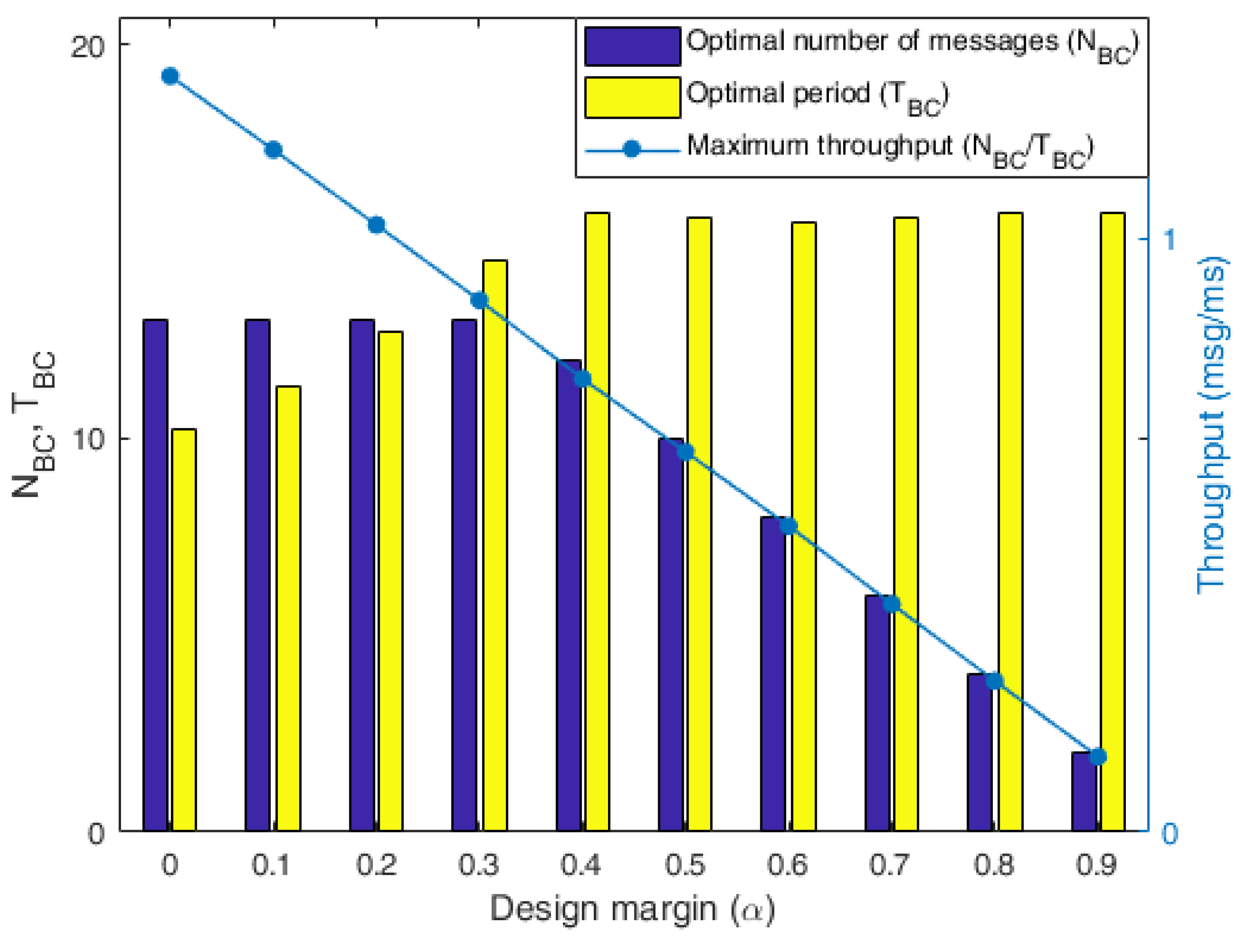
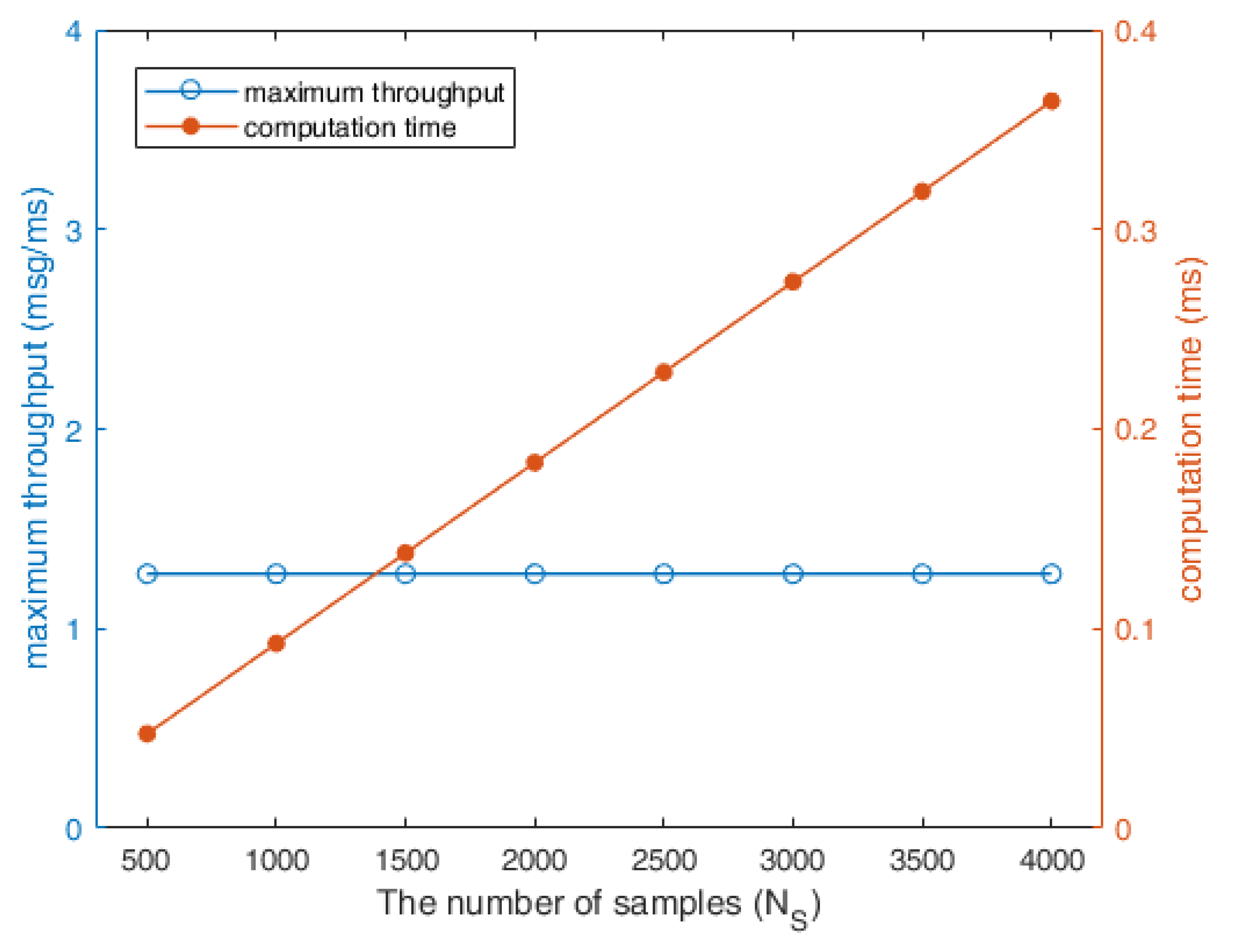
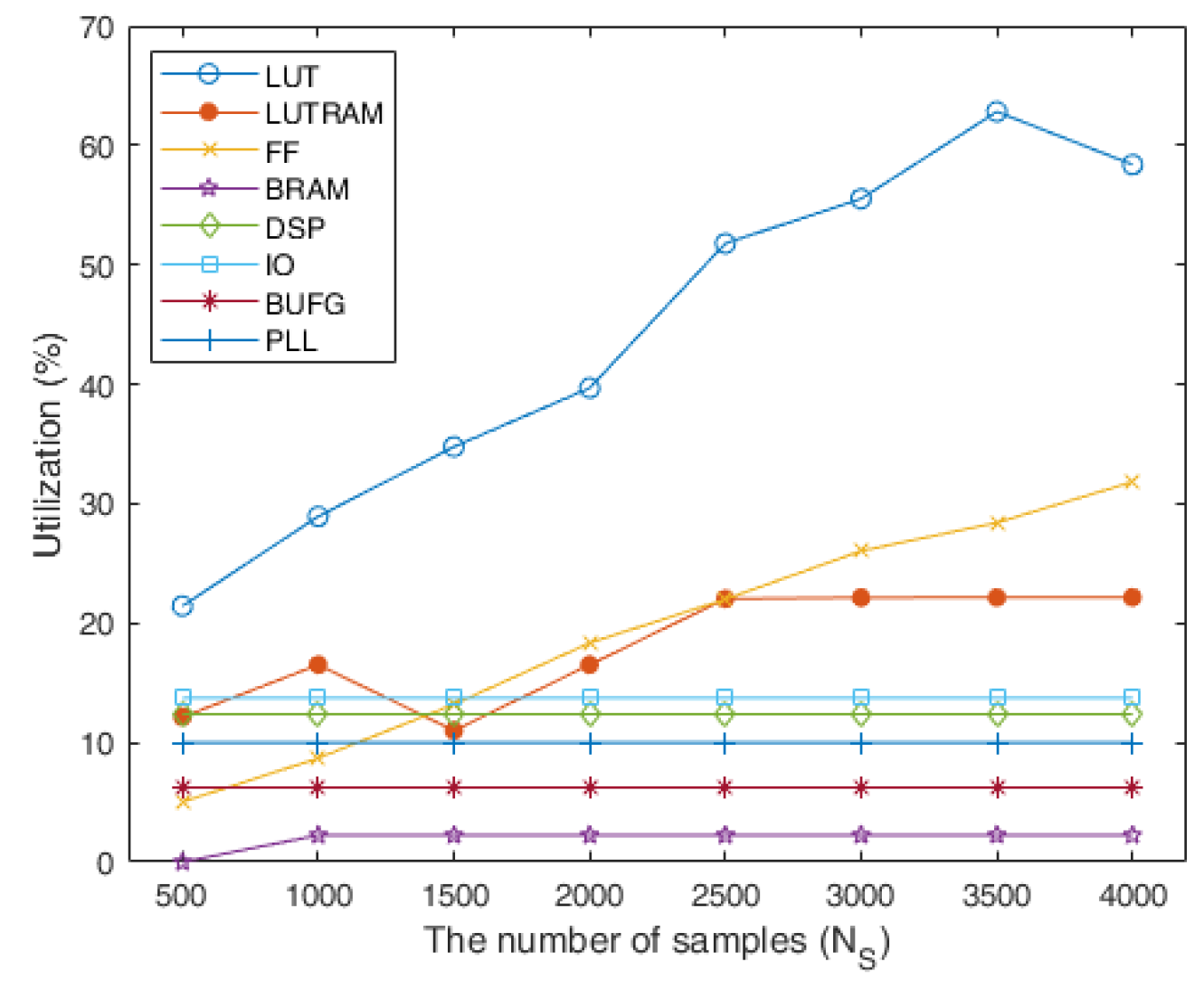
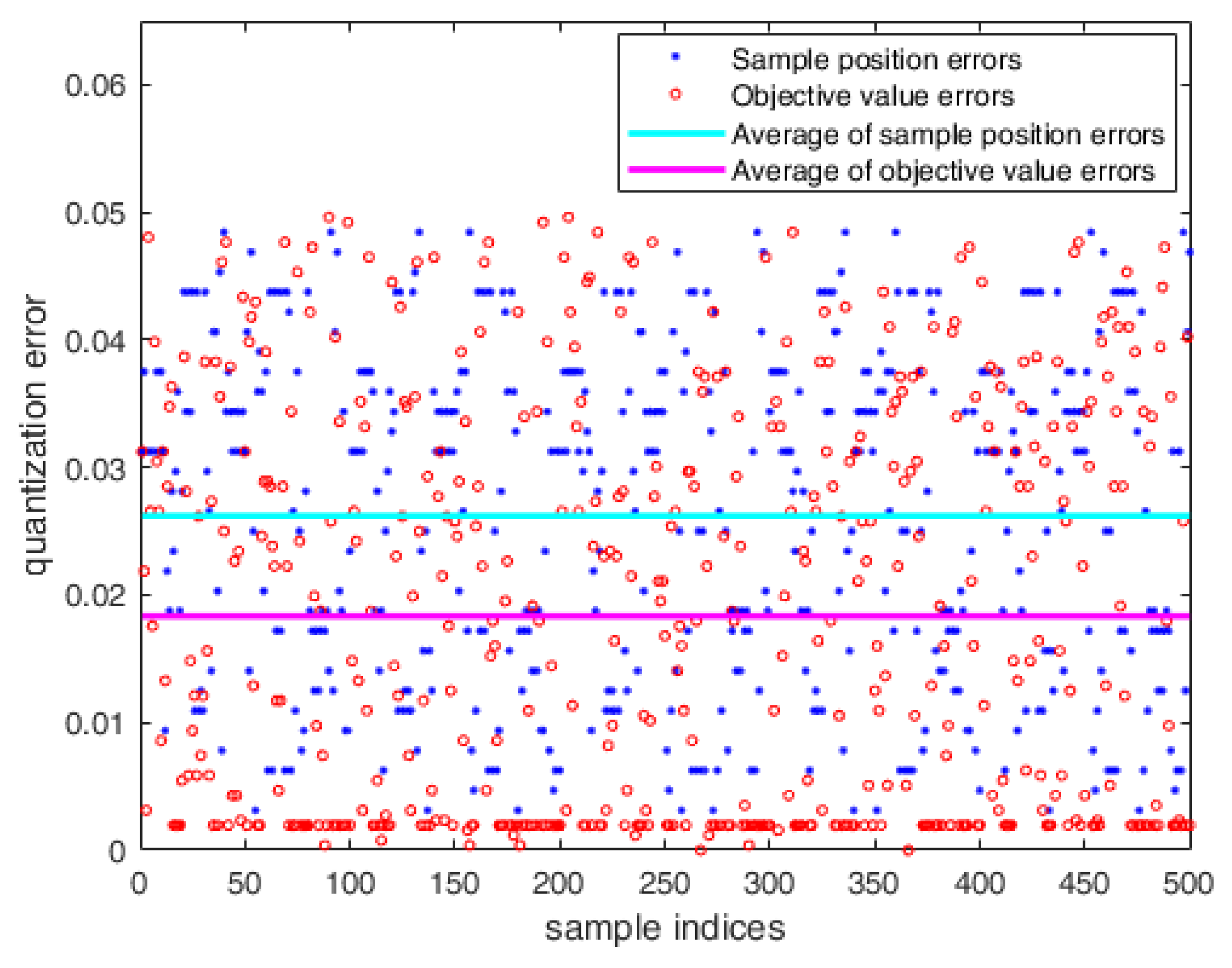
4.2. Evaluations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- MIL-STD-1553B NOTICE II; Department of Defense: Washington, DC, USA, 1986.
- MIL-STD-1553B Designer’s Guide; Data Device Corporation: Bohemia, NY, USA, 1998.
- MIL-STD-1553B Evolves with the Times; White Paper; Data Device Corporation: Bohemia, NY, USA, 2010.
- Zhang, J.; Liu, M.; Shi, G.; Pan, W. A MIL-STD-1553B bus command optimization algorithm based on load balance. Appl. Mech. Mater. 2012, 130, 3839–3842. [Google Scholar] [CrossRef]
- Liang, Y.; Xing, X.; Li, Y. A GPU-based large-scale Monte Carlo simulation method for systems with long-range interactions. J. Comput. Phys. 2018, 338, 252–268. [Google Scholar] [CrossRef]
- Luu, J.; Redmond, K.; Lo, W.C.Y.; Chow, P.; Lilge, L.; Rose, J. FPGA-based Monte Carlo Computation of Light Absorption for Photodynamic Cancer Therapy. In Proceedings of the IEEE Symposium on Field Programmable Custom Computing Machines, Napa, CA, USA, 5–7 April 2009. [Google Scholar]
- Ortega-Zamorano, F.; Montemurro, M.A.; Cannas, S.A.; Jerez, J.M.; Franco, L. FPGA Hardware Acceleration of Monte Carlo Simulations for the Ising Model. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 2618–2627. [Google Scholar] [CrossRef]
- Aliee, H.; Zarandi, H.R. Fast and accurate fault tree analysis based on stochastic logic implemented on field-programmable gate arrays. IEEE Trans. Reliab. 2013, 62, 13–22. [Google Scholar] [CrossRef]
- Lee, H.; Kim, K.; Kwon, Y.; Hong, E. Real-Time Particle Swarm Optimization on FPGA for the Optimal Message-Chain Structure. Electronic 2018, 7, 274. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Kim, K.; Ahn, K.; Kwon, Y.; Yun, S.; Lee, S. Analysis and implementation of high speed data processing technology using multi-message chain and double buffering method with MIL-STD-1553B. J. Korea Inst. Mil. Sci. Technol. 2013, 16, 422–429. [Google Scholar] [CrossRef]
- Design Guide—Dealing with DDR2/DDR3 Clock Jitter; Technical Note TN-04-56; Micron Technology, Inc.: Boise County, ID, USA, 2008.
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Doucet, A.; Logothetis, A.; Krishnamurthy, V. Stochastic sampling algorithms for state estimation in jump Markov linear systems. IEEE Trans. Autom. Control 2000, 45, 188–202. [Google Scholar] [CrossRef]
- Spall, J.C. Estimation via Markov chain Monte Carlo. IEEE Control. Syst. Mag. 2003, 23, 34–45. [Google Scholar]
- Fishman, G.S. Monte Carlo: Concepts, Algorithms and Applications; Springer: New York, NY, USA, 1996. [Google Scholar]
- Kroese, D.P.; Taimre, T.; Botev, Z.I. Handbook of Monte Carlo Methods; John Wiley & Sons: Hoboken, NJ, USA, September 2011. [Google Scholar]
- Rubinstein, R.Y.; Ridder, A.; Vaisman, R. Fast Sequential Monte Carlo methods for counting and optimization; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Press, W.; Teukolsky, S.; Vetterling, W.; Flannery, B. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007; p. 386. [Google Scholar]
- Tutueva, A.V.; Butusov, D.N.; Pesterev, D.O.; Belkin, D.A.; Ryzhov, N.G. Novel Normalization Technique for Chaotic Pseudo-Random Number Generators Based on Semi-Implicit ODE Solvers. In Proceedings of the International Conference Quality Management, Transport and Information Security, Information Technologies, St. Petersburg, Russia, 21–23 September 2017; pp. 292–295. [Google Scholar]
- Torres-Perez, E.; Fraga, L.G.; Tlelo-Cuautle, E.; Leon-Salas, W.D. On the FPGA implementation of random number generators from chaotic maps. In Proceedings of the IEEE International Conference Electronics, Electrical Engineering and Computing, Cusco, Peru, 15–18 August 2017; pp. 1–4. [Google Scholar]
- Nepomuceno, E.G.; Nardo, L.G.; Arias-Garcia, J.; Butusov, D.N.; Tutueva, A. Image encryption based on the pseudo-orbits from 1D chaotic map. Chaos 2019, 29, 061101. [Google Scholar] [CrossRef] [PubMed]

| Notation | Description |
|---|---|
| The number of messages in a message chain in the BC | |
| The transmission period of a message chain in the BC | |
| The whole required time in the RT | |
| Total writing time for responding messages in the RT | |
| Total processing time for the high-priority tasks in the RT | |
| Message gap time in the BC | |
| Processing time for the received message in the RT | |
| Processing time for an interrupt service routine in the RT | |
| The n-th sampled configuration in the m-th group | |
| The time constraint for the n-th sampled configuration in the m-th group | |
| The design margin constraint for the n-th sampled configuration in the m-th group | |
| The objective value for the n-th sampled configuration in the m-th group |
| Type | Conventional MCO | FRMCO |
|---|---|---|
| Implementation | On CPU with C/C++ | On FPGA with HDL |
| Time step | Logical (OS-depend.) | Real system clock |
| Num. of states | Four | Eight |
| Operation | Generally sequential | Sequential and Parallel |
| Parallelizability | Depends on CPU cores | Depends on LUTs |
| Resource | Available | Utilization | Utilization (%) |
|---|---|---|---|
| LUT | 203,800 | 43,697 | 21.44 |
| LUTRAM | 64,000 | 7768 | 12.14 |
| FF | 407,600 | 20,521 | 5.03 |
| DSP | 840 | 104 | 12.38 |
| IO | 400 | 55 | 13.75 |
| BUFG | 32 | 2 | 6.25 |
| PLL | 10 | 1 | 10.00 |
| Type | Value |
|---|---|
| Total number of endpoints | 89,621 |
| The number of failing endpoints | 0 |
| Worst negative slack (WNS) | 1.085 ns |
| Total negative slack (TNS) | 0.000 ns |
| Worst hold slack (WHS) | 0.091 ns |
| Total hold slack (THS) | 0.000 ns |
| Total pulse width negative slack (TPWS) | 0.000 ns |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Kim, K. Real-Time Monte Carlo Optimization on FPGA for the Efficient and Reliable Message Chain Structure. Electronics 2019, 8, 866. https://doi.org/10.3390/electronics8080866
Lee H, Kim K. Real-Time Monte Carlo Optimization on FPGA for the Efficient and Reliable Message Chain Structure. Electronics. 2019; 8(8):866. https://doi.org/10.3390/electronics8080866
Chicago/Turabian StyleLee, Heoncheol, and Kipyo Kim. 2019. "Real-Time Monte Carlo Optimization on FPGA for the Efficient and Reliable Message Chain Structure" Electronics 8, no. 8: 866. https://doi.org/10.3390/electronics8080866
APA StyleLee, H., & Kim, K. (2019). Real-Time Monte Carlo Optimization on FPGA for the Efficient and Reliable Message Chain Structure. Electronics, 8(8), 866. https://doi.org/10.3390/electronics8080866





