Energy Efficiency Optimization for Massive MIMO Non-Orthogonal Unicast and Multicast Transmission with Statistical CSI
Abstract
:1. Introduction
- With statistical CSI, we formulate the EE maximization problem for NOUM transmission in the massive MIMO scenario.
- We determine the optimal transmit directions of the multicast and unicast transmission in closed-form, respectively, and then simplify the large-scale complex-matrix-valued precoding design problem into a real-vector-valued power allocation problem in the beam domain.
- We reduce the computational complexity of the EE optimization problem significantly by replacing the objective function with its deterministic equivalent (DE).
- With guaranteed convergence, we propose an algorithm on beam domain power allocation using the minorize maximize (MM) algorithm and Dinkelbach’s transform. We deal with the EE optimization problem by iteratively solving a series of related convex optimization problems.
- We adopt to represent real-valued vector space and to denote complex-valued vector space.
- represents the identity matrix of size .
- indicates that matrix is positive semidefinite.
- represents the expectation operation.
- ⊙ denotes the Hadamard product.
- Denote as the trace operation, as the transpose operation, as the conjugate operation, as the conjugate-transpose operation, and as the determinant operation.
- ∼ stands for “be distributed as”, and ≜ stands for “be defined as”.
2. System Model
3. NOUM Transmission in Massive MIMO
3.1. Problem Formulation
3.2. Optimal Transmit Directions
3.3. Energy-Efficient Power Allocation for NOUM Transmission
| Algorithm 1 Energy-Efficient Power Allocation Algorithm in the Beam Domain for Massive MIMO NOUM Transmission |
| Input: Beam domain channel statistics , initial power allocation matrix , outer iteration threshold and inner iteration threshold Output: Power allocation matrix in the beam domain 1: Initialization: 2: Calculate 3: while do 4: Initialization: , let , calculate with (38) 5: while do 6: Let 7: Calculate via solving problem (37) with 8: Calculate using (38) 9: end while 10: Let 11: Let 12: Calculate with (39) 13: end while 14: return |
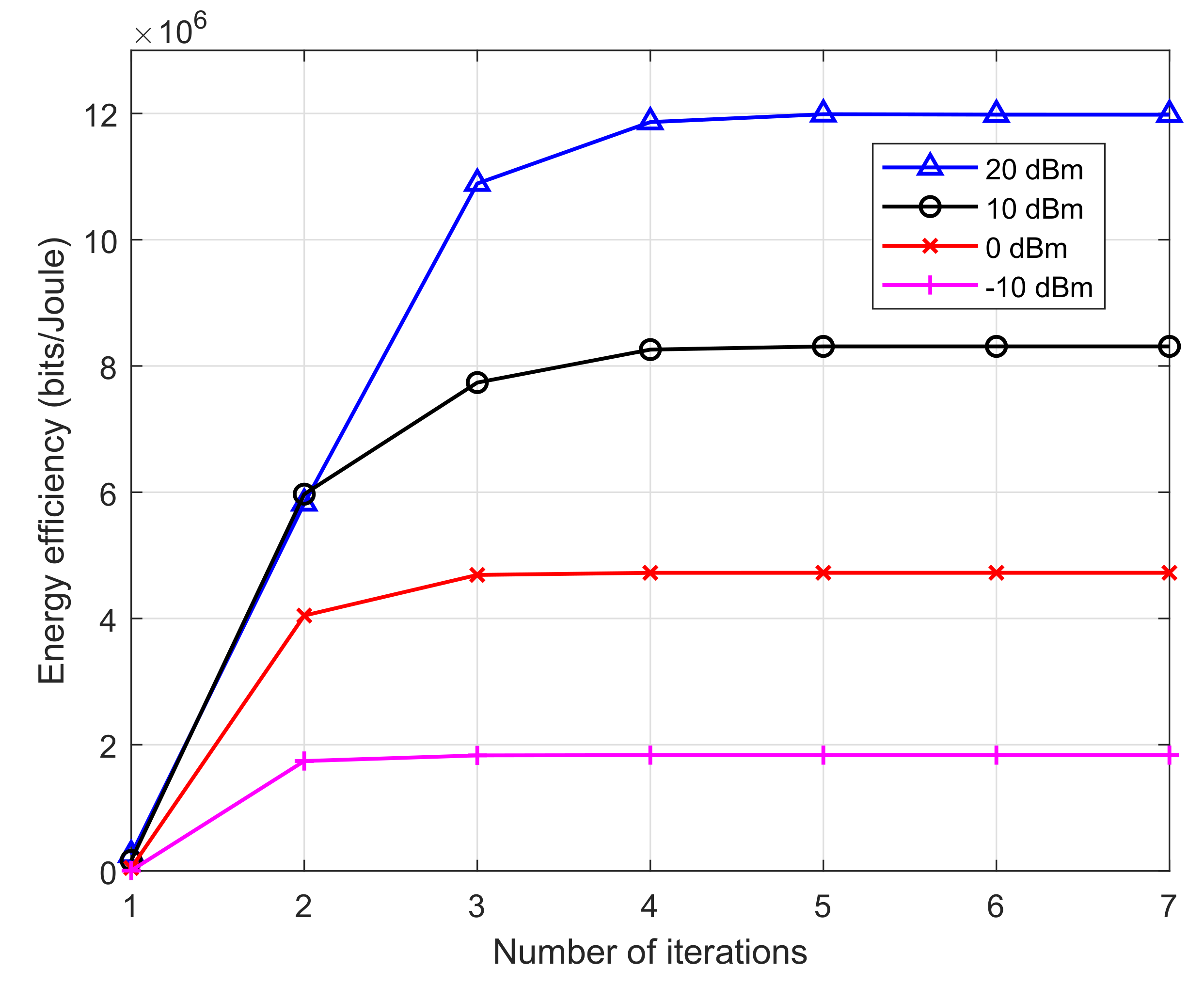
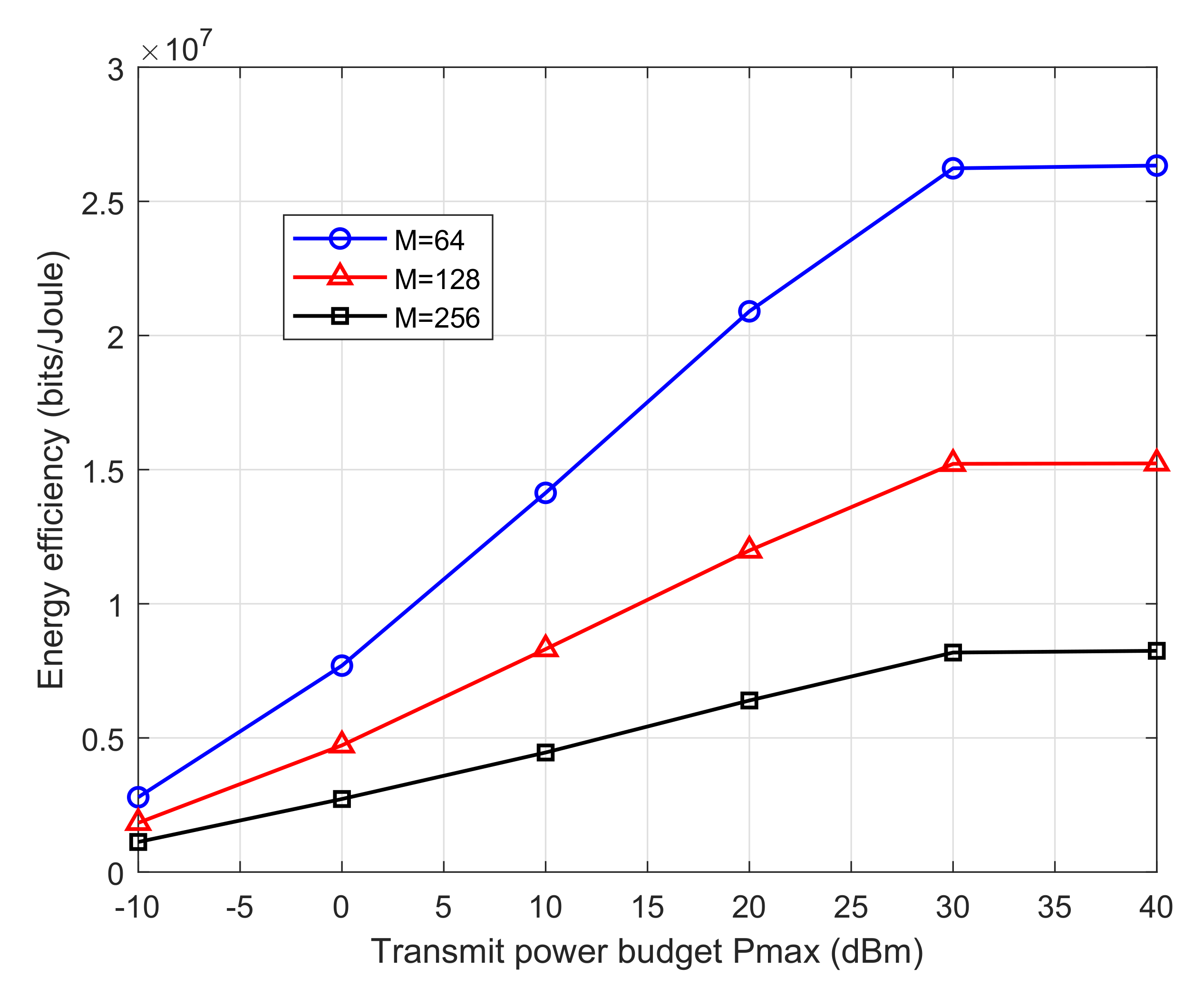
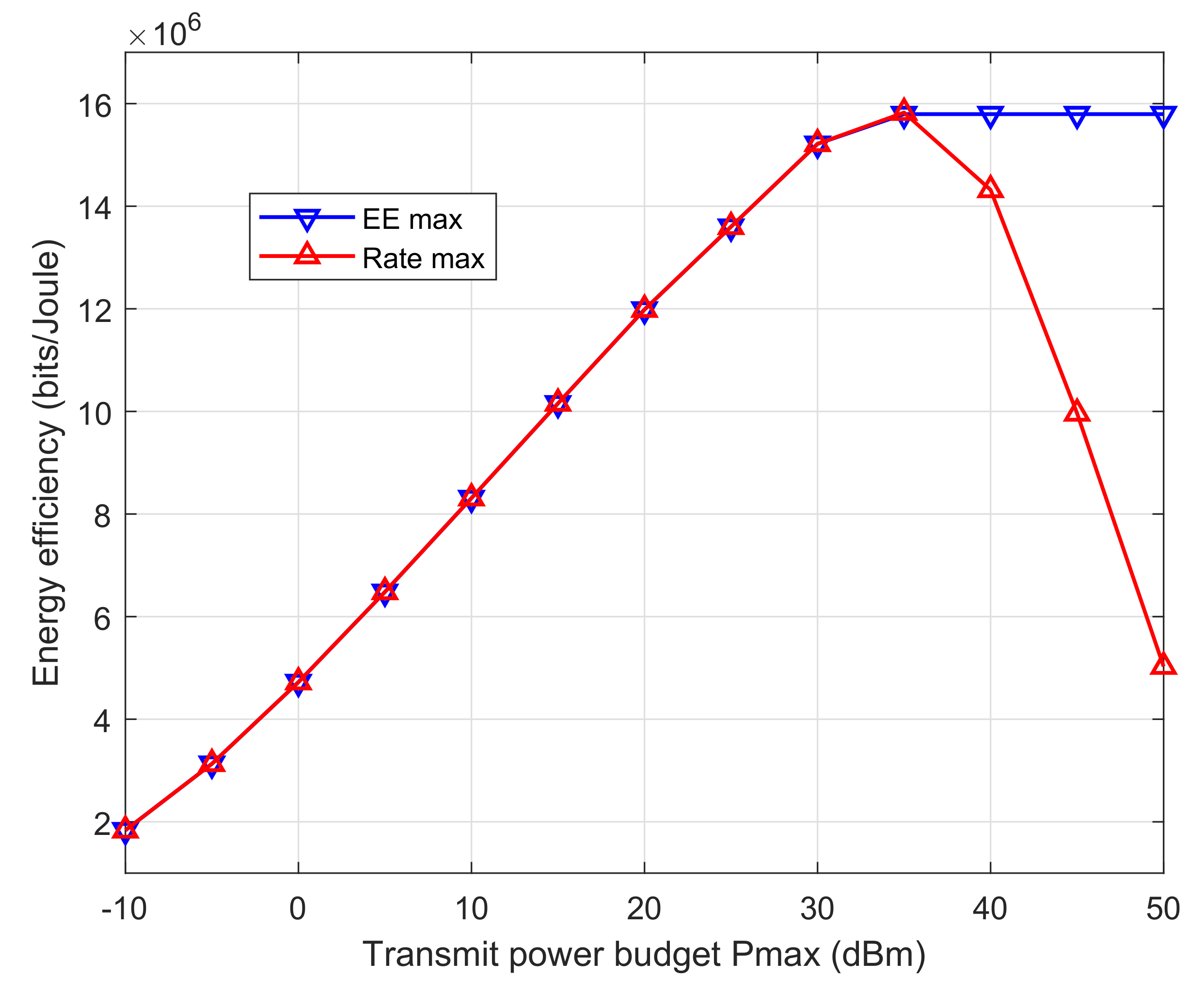
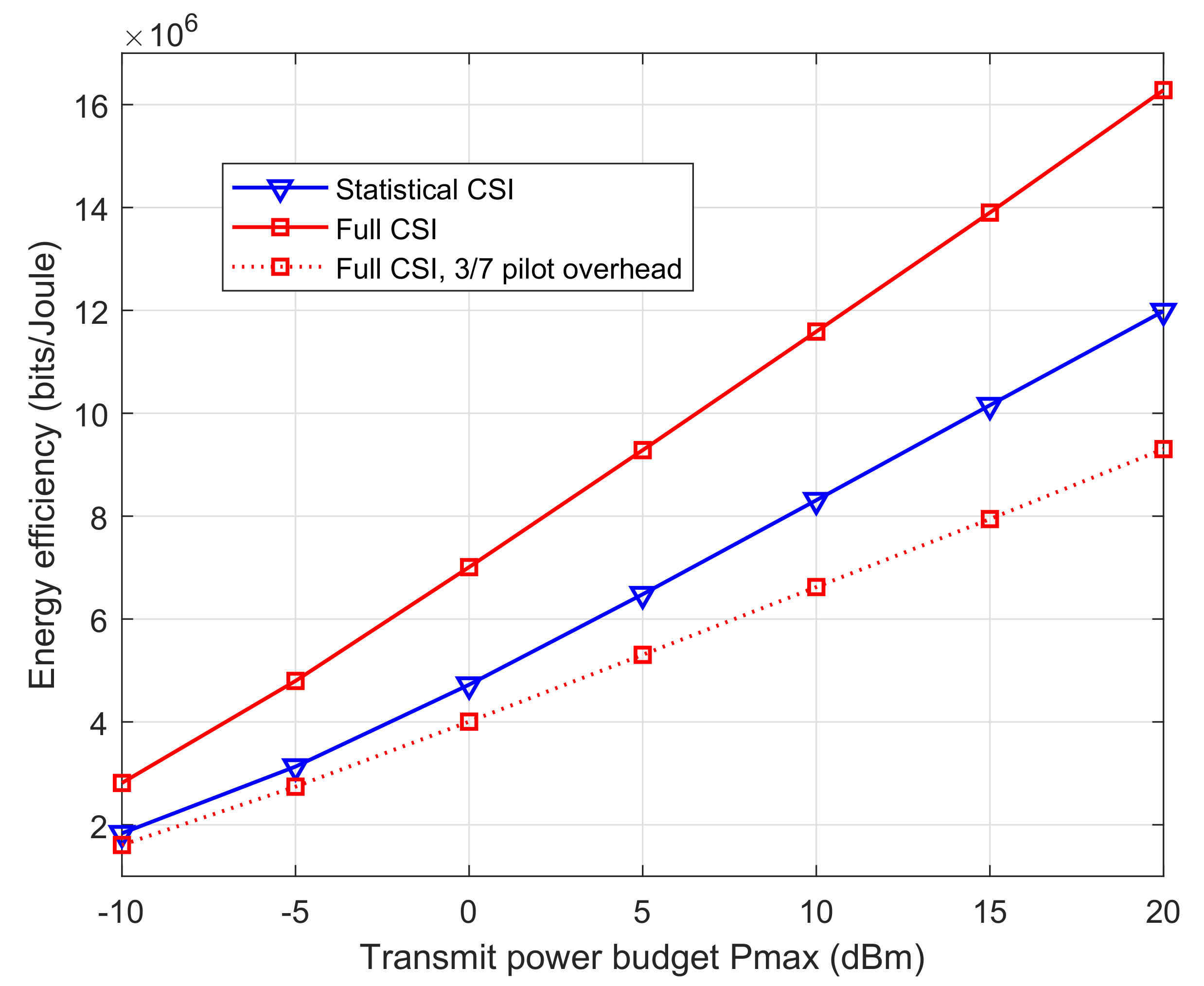
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
References
- Lecompte, D.; Gabin, F. Evolved multimedia broadcast/multicast service (eMBMS) in LTE-advanced: Overview and Rel-11 enhancements. IEEE Commun. Mag. 2012, 50, 68–74. [Google Scholar] [CrossRef]
- Wang, W.; Liu, A.; Zhang, Q.; You, L.; Gao, X.; Zheng, G. Robust multigroup multicast transmission for frame-based multi-beam satellite systems. IEEE Access 2018, 6, 46074–46083. [Google Scholar] [CrossRef]
- You, L.; Liu, A.; Wang, W.; Gao, X. Outage constrained robust multigroup multicast beamforming for multi-beam satellite communication systems. IEEE Wirel. Commun. Lett. 2019, 8, 352–355. [Google Scholar] [CrossRef]
- You, L.; Wang, J.; Wang, W.; Gao, X. Secure multicast transmission for massive MIMO with statistical channel state information. IEEE Signal Process. Lett. 2019, 26, 803–807. [Google Scholar] [CrossRef]
- Chen, E.; Tao, M.; Liu, Y. Joint base station clustering and beamforming for non-orthogonal multicast and unicast transmission with backhaul constraints. IEEE Trans. Wirel. Commun. 2018, 17, 6265–6279. [Google Scholar] [CrossRef]
- Sadeghi, M.; Björnson, E.; Larsson, E.G.; Yuen, C.; Marzetta, T. Joint unicast and multi-group multicast transmission in massive MIMO systems. IEEE Trans. Wirel. Commun. 2018, 17, 6375–6388. [Google Scholar] [CrossRef]
- Wang, J.; Xu, H.; Zhu, B.; Fan, L.; Zhou, A. Hybrid beamforming design for mmWave joint unicast and multicast transmission. IEEE Commun. Lett. 2018, 22, 2012–2015. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Larsson, E.G.; Marzetta, T.L. Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun. 2013, 61, 1436–1449. [Google Scholar]
- Hoydis, J.; ten Brink, S.; Debbah, M. Massive MIMO in the UL/DL of cellular networks: How many antennas do we need? IEEE J. Sel. Areas Commun. 2013, 31, 160–171. [Google Scholar] [CrossRef]
- Sadeghi, M.; Björnson, E.; Larsson, E.G.; Yuen, C.; Marzetta, T.L. Max–min fair transmit precoding for multi-group multicasting in massive MIMO. IEEE Trans. Wirel. Commun. 2018, 17, 1358–1373. [Google Scholar] [CrossRef]
- You, L.; Xiong, J.; Li, K.; Wang, W.; Gao, X. Non-orthogonal unicast and multicast transmission for massive MIMO with statistical channel state information. IEEE Access 2018, 6, 66841–66849. [Google Scholar] [CrossRef]
- Alibakhshikenari, M.; Virdee, B.S.; See, C.H.; Abd-Alhameed, R.A.; Falcone, F.; Limiti, E. High-isolation leaky-wave array antenna based on CRLH-metamaterial implemented on SIW with 30o frequency beam-scanning capability at millimetre-waves. Electronics 2019, 8, 642. [Google Scholar] [CrossRef]
- Song, Y.J.; Sarabandi, K. Equivalent circuit model for metamaterial-based electromagnetic band-gap isolator. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1366–1369. [Google Scholar] [CrossRef]
- Alibakhshikenari, M.; Khalily, M.; Virdee, B.S.; See, C.H.; Abd-Alhameed, R.A.; Limiti, E. Mutual-coupling isolation using embedded metamaterial EM bandgap decoupling slab for densely packed array antennas. IEEE Access 2019, 7, 51827–51840. [Google Scholar] [CrossRef]
- Farsi, S.; Aliakbarian, H.; Schreurs, D.; Nauwelaers, B.; Vandenbosch, G.A.E. Mutual coupling reduction between planar antennas by using a simple microstrip U-section. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1501–1503. [Google Scholar] [CrossRef]
- Alibakhshikenari, M.; Khalily, M.; Virdee, B.S.; See, C.H.; Abd-Alhameed, R.A.; Limiti, E. Mutual coupling suppression between two closely placed microstrip patches using EM-bandgap metamaterial fractal loading. IEEE Access 2019, 7, 23606–23614. [Google Scholar] [CrossRef]
- Singh, K.; Gupta, A.; Ratnarajah, T. QoS-driven energy-efficient resource allocation in multiuser amplify-and-forward relay networks. IEEE Trans. Signal Inf. Process. Over Netw. 2017, 3, 771–786. [Google Scholar] [CrossRef]
- Singh, K.; Gupta, A.; Ratnarajah, T. QoS-driven resource allocation and EE-balancing for multiuser two-way amplify-and-forward relay networks. IEEE Trans. Wirel. Commun. 2017, 16, 3189–3204. [Google Scholar] [CrossRef]
- Singh, K.; Gupta, A.; Ratnarajah, T. A utility-based joint subcarrier and power allocation for green communications in multi-user two-way regenerative relay networks. IEEE Trans. Commun. 2017, 65, 3705–3722. [Google Scholar] [CrossRef]
- Li, G.Y.; Xu, Z.; Xiong, C.; Yang, C.; Zhang, S.; Chen, Y.; Xu, S. Energy-efficient wireless communications: Tutorial, survey, and open issues. IEEE Wirel. Commun. 2011, 18, 28–35. [Google Scholar] [CrossRef]
- Khan, T.A.; Yazdan, A.; Heath, R.W. Optimization of power transfer efficiency and energy efficiency for wireless-powered systems with massive MIMO. IEEE Trans. Wirel. Commun. 2018, 17, 7159–7172. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L.; Hoydis, J.; Debbah, M. Optimal design of energy-efficient multi-user MIMO systems: Is massive MIMO the answer? IEEE Trans. Wirel. Commun. 2015, 14, 3059–3075. [Google Scholar] [CrossRef]
- Tervo, O.; Tran, L.; Chatzinotas, S.; Juntti, M.; Ottersten, B. Energy-efficient joint unicast and multicast beamforming with multi-antenna user terminals. In Proceedings of the 2017 IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Sapporo, Japan, 3–6 July 2017; pp. 1–5. [Google Scholar]
- He, S.; Huang, Y.; Jin, S.; Yang, L. Energy efficient coordinated beamforming design in multi-cell multicast networks. IEEE Commun. Lett. 2015, 19, 985–988. [Google Scholar] [CrossRef]
- Tervo, O.; Tran, L.; Pennanen, H.; Chatzinotas, S.; Ottersten, B.; Juntti, M. Energy-efficient multicell multigroup multicasting with joint beamforming and antenna selection. IEEE Trans. Signal Process. 2018, 66, 4904–4919. [Google Scholar] [CrossRef]
- You, L.; Gao, X.; Xia, X.; Ma, N.; Peng, Y. Pilot reuse for massive MIMO transmission over spatially correlated rayleigh fading channels. IEEE Trans. Wirel. Commun. 2015, 14, 3352–3366. [Google Scholar] [CrossRef]
- You, L.; Gao, X.; Swindlehurst, A.L.; Zhong, W. Channel acquisition for massive MIMO-OFDM with adjustable phase shift pilots. IEEE Trans. Signal Process. 2016, 64, 1461–1476. [Google Scholar] [CrossRef]
- You, L.; Chen, X.; Wang, W.; Gao, X. Coordinated multicast precoding for multi-cell massive MIMO transmission exploiting statistical channel state information. Electronics 2018, 7, 338. [Google Scholar] [CrossRef]
- You, L.; Wang, W.; Gao, X. Energy-efficient multicast precoding for massive MIMO transmission with statistical CSI. Energies 2018, 11, 3175. [Google Scholar] [CrossRef]
- Weichselberger, W.; Herdin, M.; Ozcelik, H.; Bonek, E. A stochastic MIMO channel model with joint correlation of both link ends. IEEE Trans. Wirel. Commun. 2006, 5, 90–100. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.; Jiang, B.; Li, X.; Gershman, A.B.; McKay, M.R. Statistical eigenmode transmission over jointly correlated MIMO channels. IEEE Trans. Inf. Theory 2009, 55, 3735–3750. [Google Scholar] [CrossRef]
- You, L.; Gao, X.; Li, G.Y.; Xia, X.; Ma, N. BDMA for millimeter-wave/terahertz massive MIMO transmission with per-beam synchronization. IEEE J. Sel. Areas Commun. 2017, 35, 1550–1563. [Google Scholar] [CrossRef]
- Sun, C.; Gao, X.; Jin, S.; Matthaiou, M.; Ding, Z.; Xiao, C. Beam division multiple access transmission for massive MIMO communications. IEEE Trans. Commun. 2015, 63, 2170–2184. [Google Scholar] [CrossRef]
- Wen, C.; Jin, S.; Wong, K.; Chen, J.; Ting, P. Channel estimation for massive MIMO using Gaussian-mixture Bayesian learning. IEEE Trans. Wirel. Commun. 2015, 14, 1356–1368. [Google Scholar] [CrossRef]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Energy-efficient resource allocation in OFDMA systems with large numbers of base station antennas. IEEE Trans. Wirel. Commun. 2012, 11, 3292–3304. [Google Scholar] [CrossRef]
- Lu, A.; Gao, X.; Xiao, C. Free deterministic equivalents for the analysis of MIMO multiple access channel. IEEE Trans. Inf. Theory 2016, 62, 4604–4629. [Google Scholar] [CrossRef]
- Couillet, R.; Debbah, M. Random Matrix Methods for Wireless Communications; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Dinkelbach, W. On nonlinear fractional programming. Manag. Sci. 1967, 13, 492–498. [Google Scholar] [CrossRef]
- Lipp, T.; Boyd, S. Variations and extension of the convex-concave procedure. Optim. Eng. 2016, 17, 263–287. [Google Scholar] [CrossRef]
- Yuille, A.L.; Rangarajan, A. The concave-convex procedure. Neural Comput. 2003, 15, 915–936. [Google Scholar] [CrossRef]
- Hunter, D.R.; Lange, K. A tutorial on MM algorithms. Am. Stat. 2004, 58, 30–37. [Google Scholar] [CrossRef]
- Zappone, A.; Jorswieck, E. Energy efficiency in wireless networks via fractional programming theory. Found. Trends® Commun. Inf. Theory 2015, 11, 185–396. [Google Scholar] [CrossRef]
- Marzetta, T.L. Noncooperative Cellular Wireless with Unlimited Numbers of Base Station Antennas. IEEE Trans. Wirel. Commun. 2010, 9, 3590–3600. [Google Scholar] [CrossRef]
- Tulino, A.M.; Lozano, A.; Verdú, S. Capacity-achieving input covariance for single-user multi-antenna channels. IEEE Trans. Wirel. Commun. 2006, 5, 662–671. [Google Scholar] [CrossRef] [Green Version]
| Parameter | Value |
|---|---|
| Scenario | Suburban macro |
| Channel model | 3GPP SCM |
| Pathloss | −120 dB |
| Array topology | ULA with antenna spacing half wavelength |
| Noise variance | dBm |
| Number of UTs | |
| Number of BS antennas | |
| Number of UT antennas | |
| Transmission bandwidth | W= 10 MHz |
| Amplifier drain efficiency | |
| Circuit power consumption per antenna | dBm |
| Static power consumption | dBm |
| Weights |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Huang, Y.; You, L.; Xiong, J.; Li, J.; Gao, X. Energy Efficiency Optimization for Massive MIMO Non-Orthogonal Unicast and Multicast Transmission with Statistical CSI. Electronics 2019, 8, 857. https://doi.org/10.3390/electronics8080857
Wang W, Huang Y, You L, Xiong J, Li J, Gao X. Energy Efficiency Optimization for Massive MIMO Non-Orthogonal Unicast and Multicast Transmission with Statistical CSI. Electronics. 2019; 8(8):857. https://doi.org/10.3390/electronics8080857
Chicago/Turabian StyleWang, Wenjin, Yufei Huang, Li You, Jiayuan Xiong, Jiamin Li, and Xiqi Gao. 2019. "Energy Efficiency Optimization for Massive MIMO Non-Orthogonal Unicast and Multicast Transmission with Statistical CSI" Electronics 8, no. 8: 857. https://doi.org/10.3390/electronics8080857






