Fine Frequency Acquisition Scheme in Weak Signal Environment for a Communication and Navigation Fusion System
Abstract
:1. Introduction
2. System Model
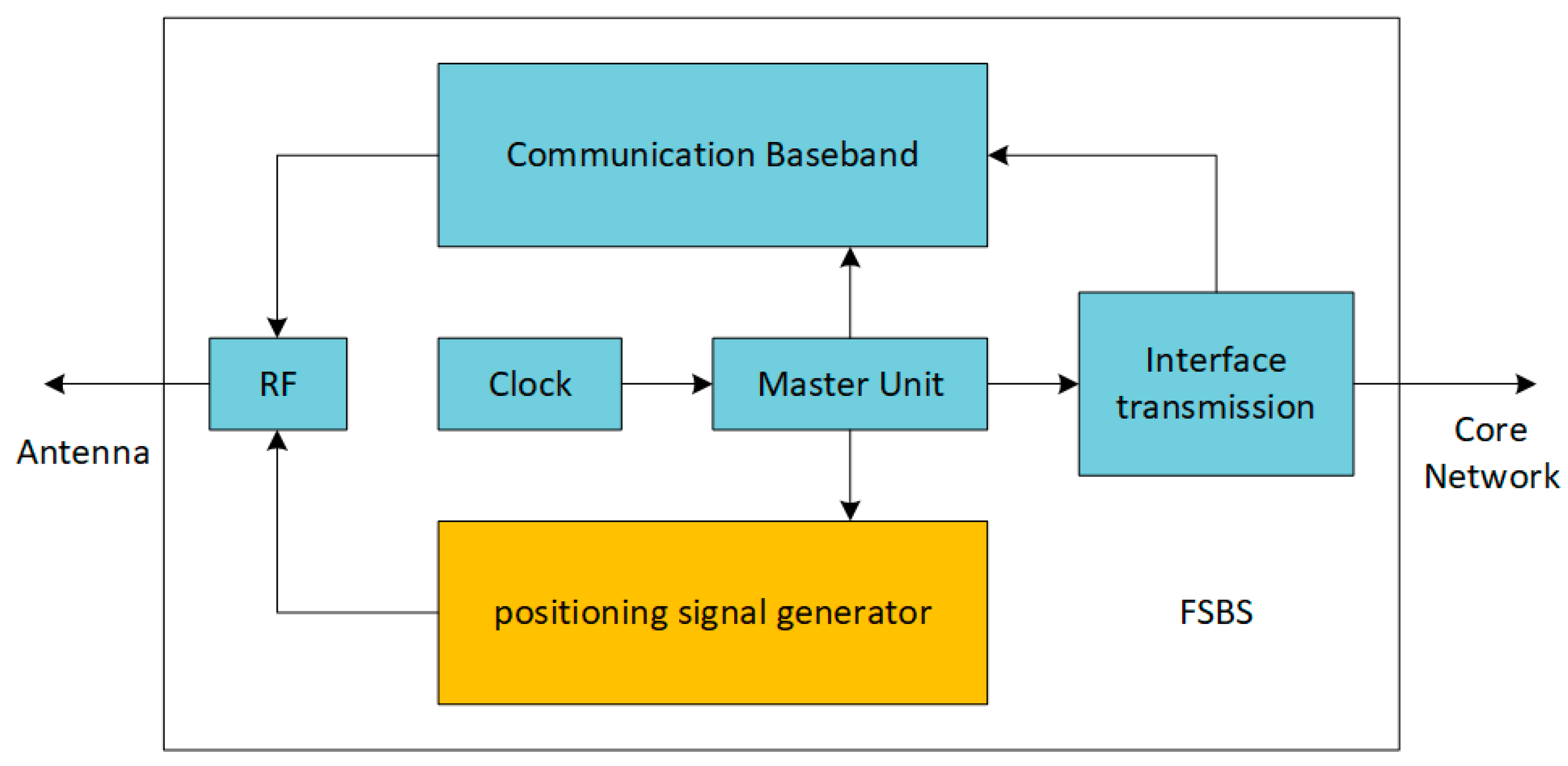
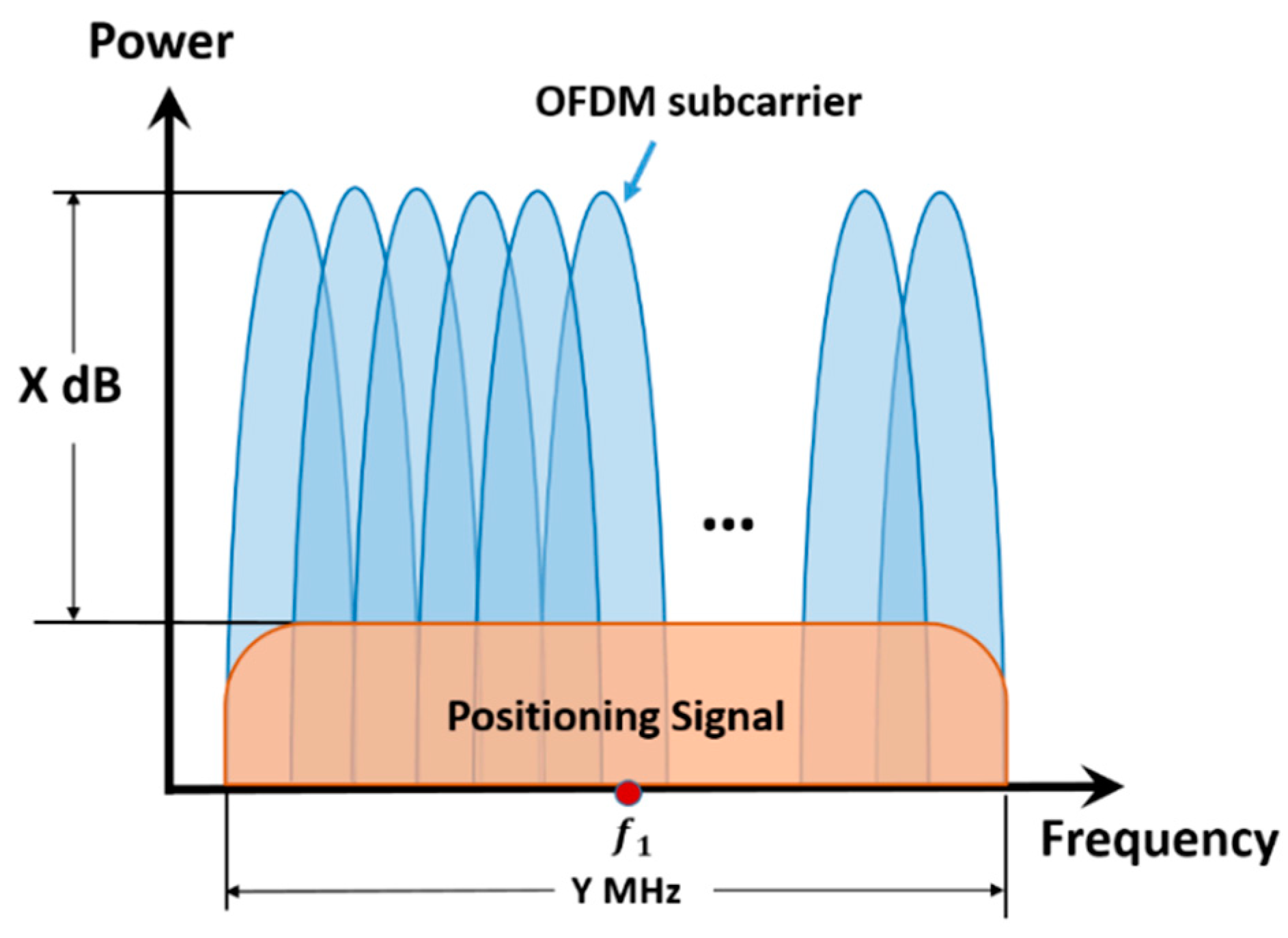
2.1. System Model
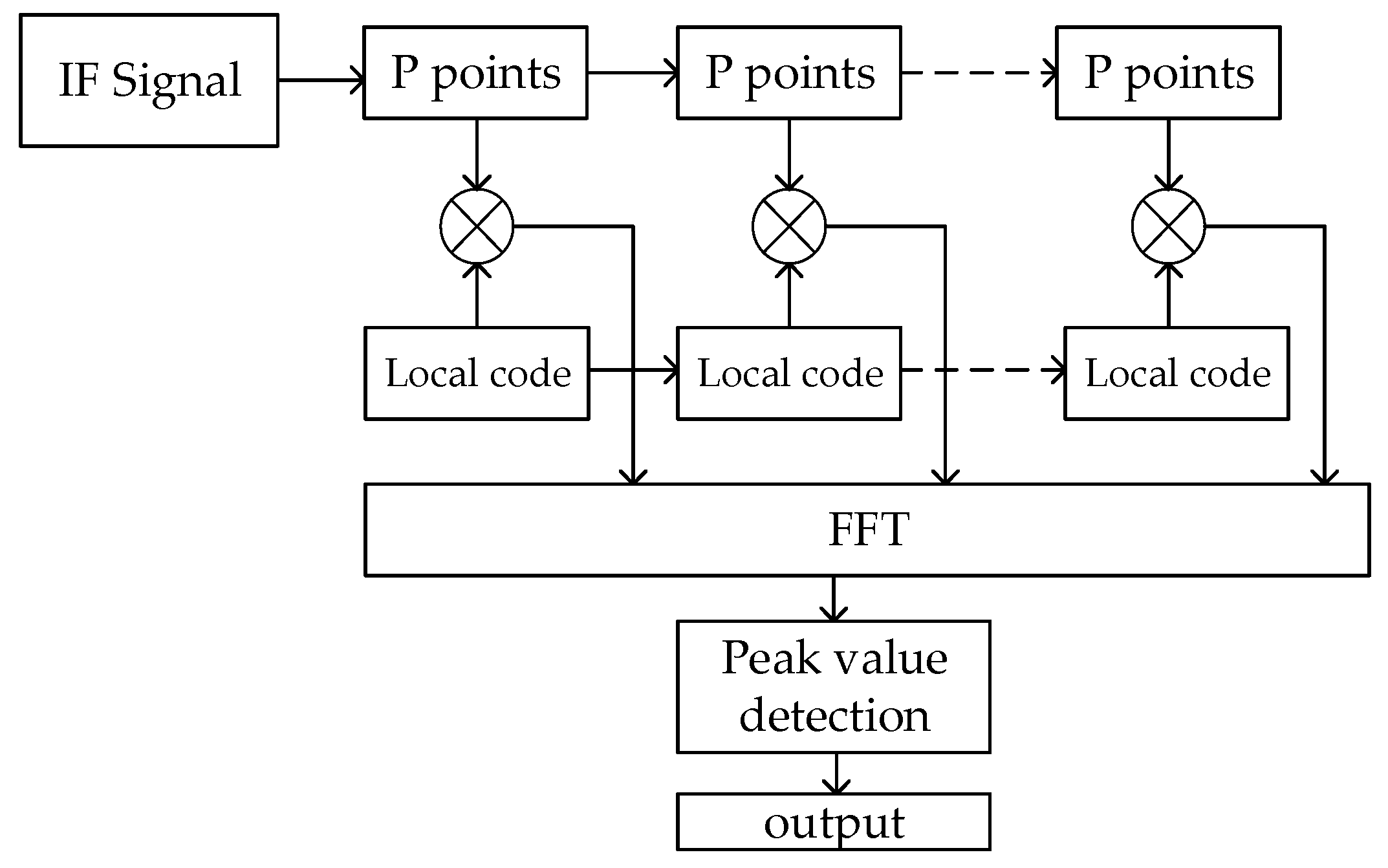
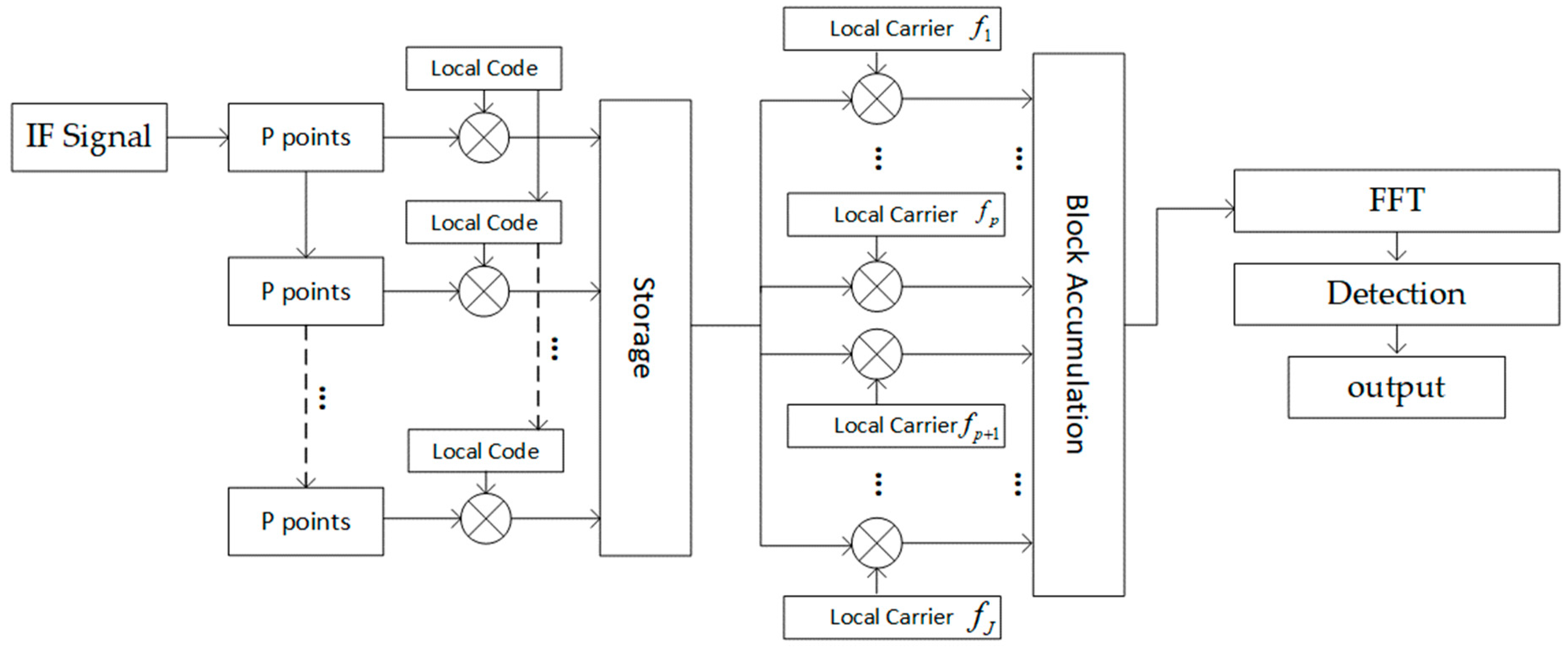
2.2. FFT Acquisition Based on Partial Matched Filter
3. Proposed Algorithm
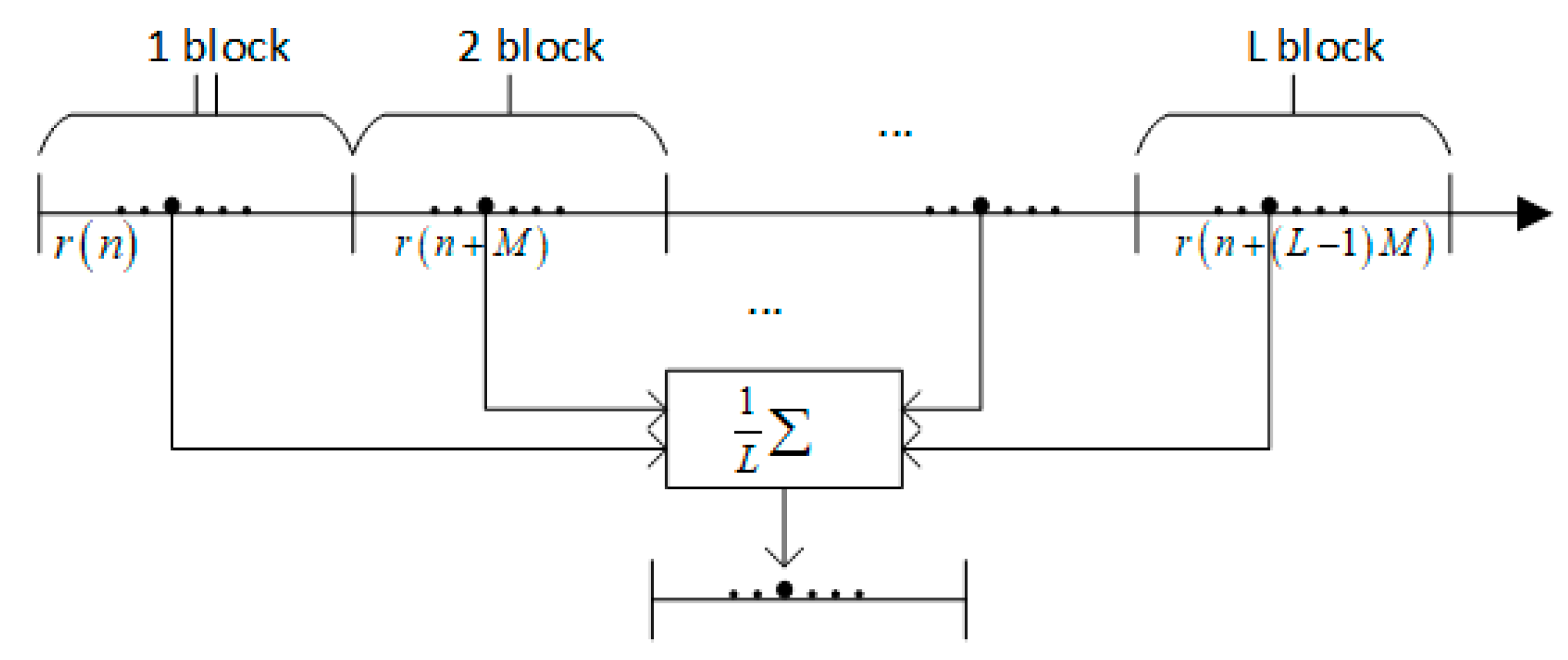
3.1. PMF-FC-BA-FFT Acquisition Method
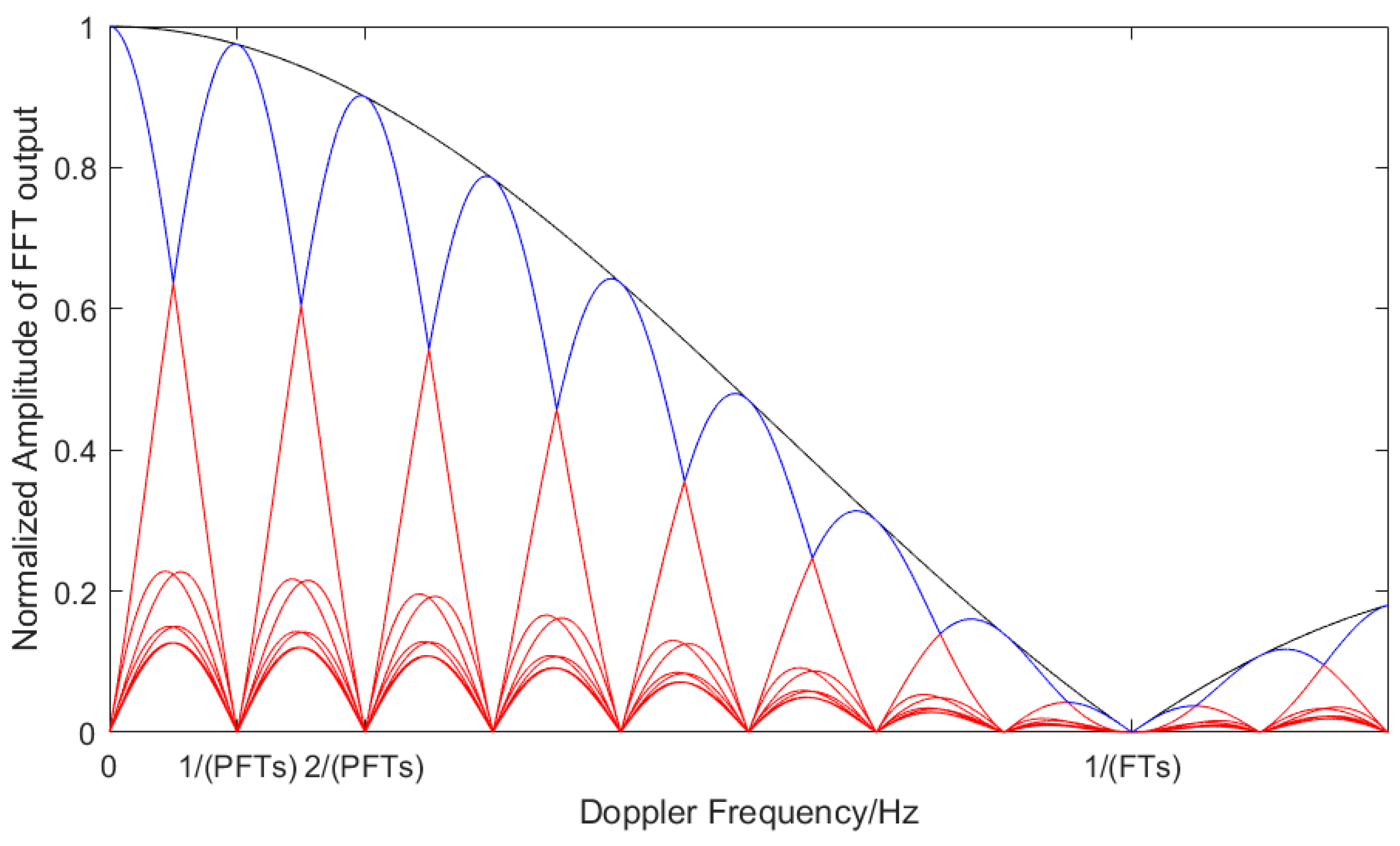
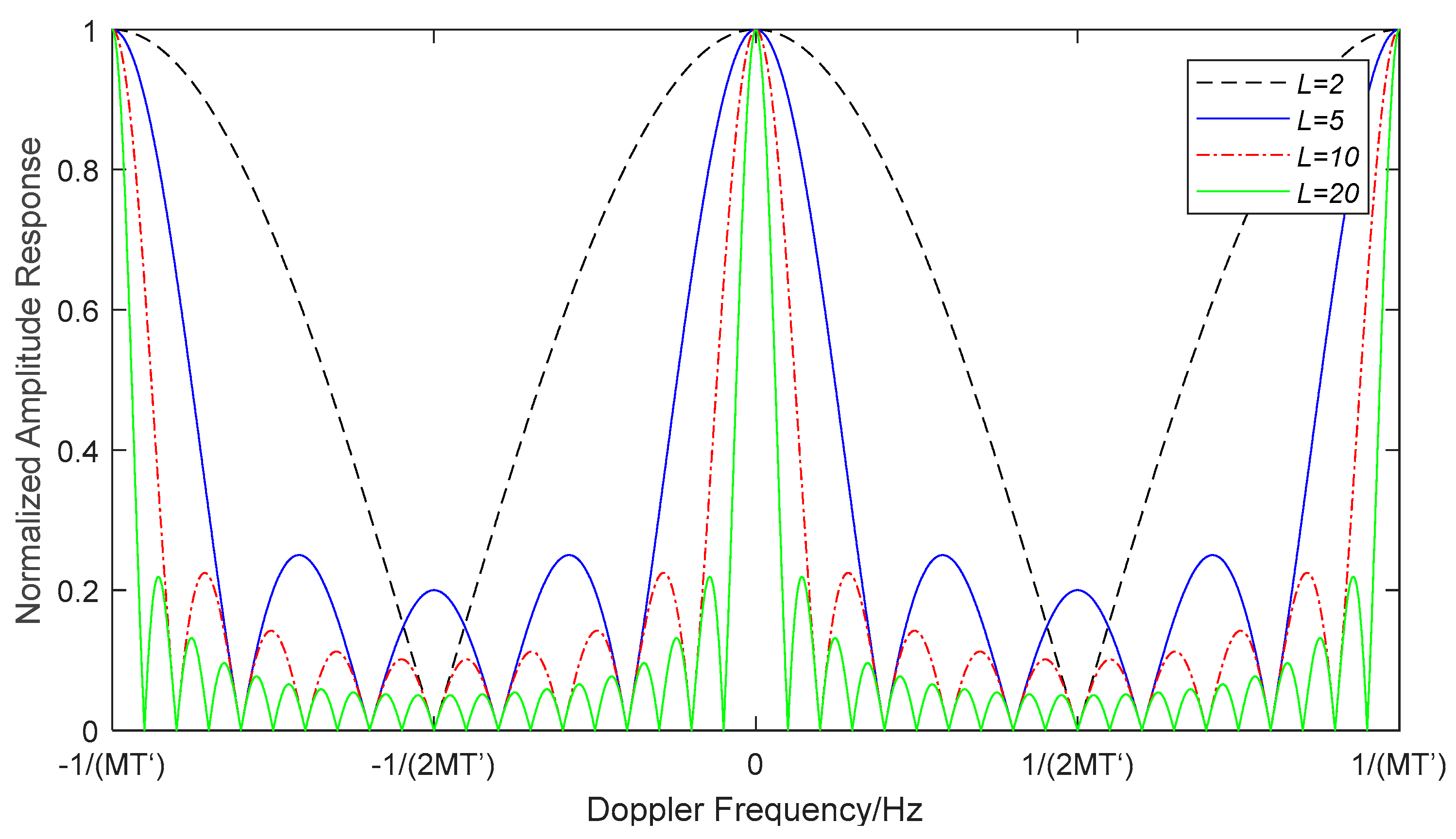
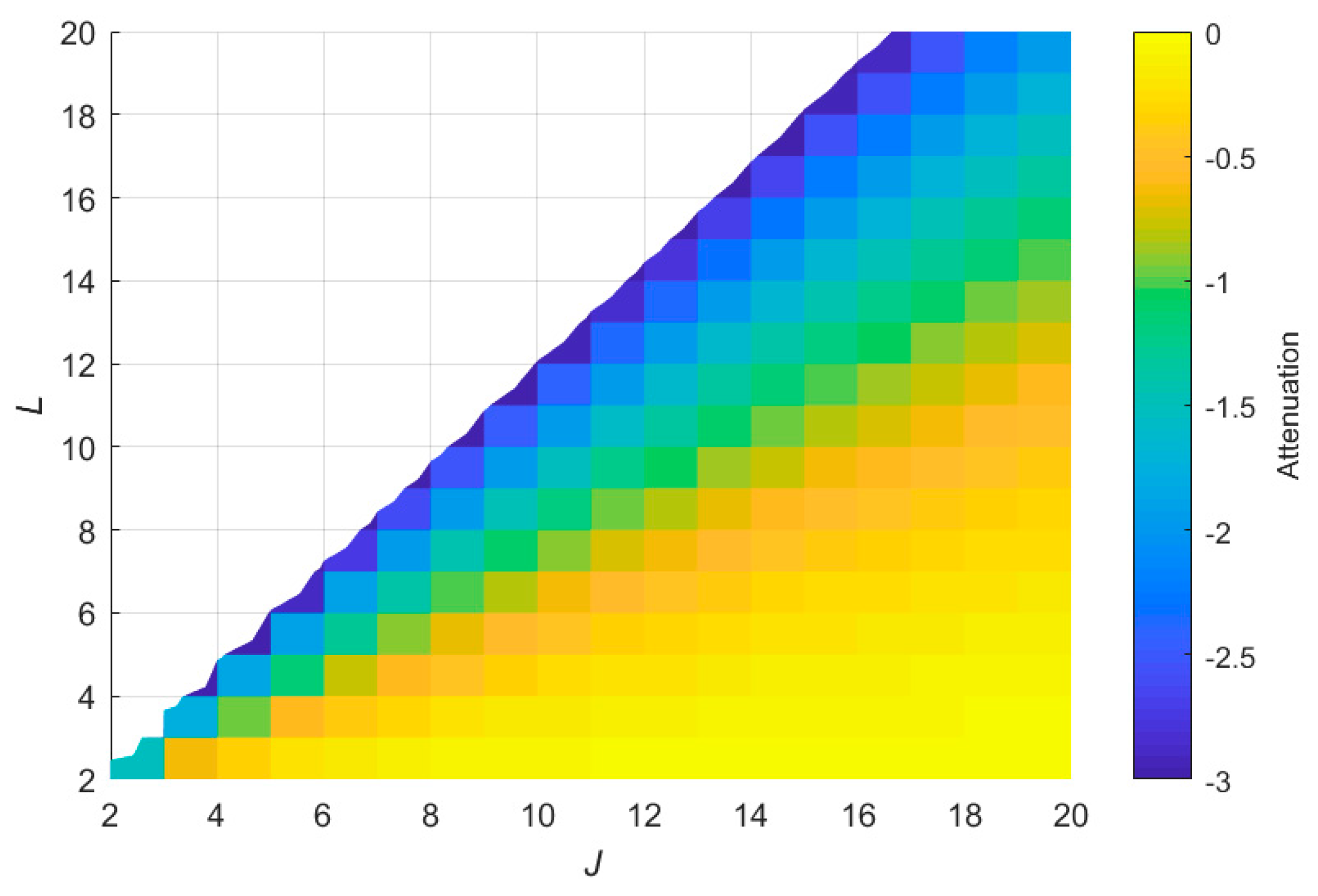
3.2. Frequency Acquisition Accuracy
3.3. Effect of Proposed Algorithm on SNR
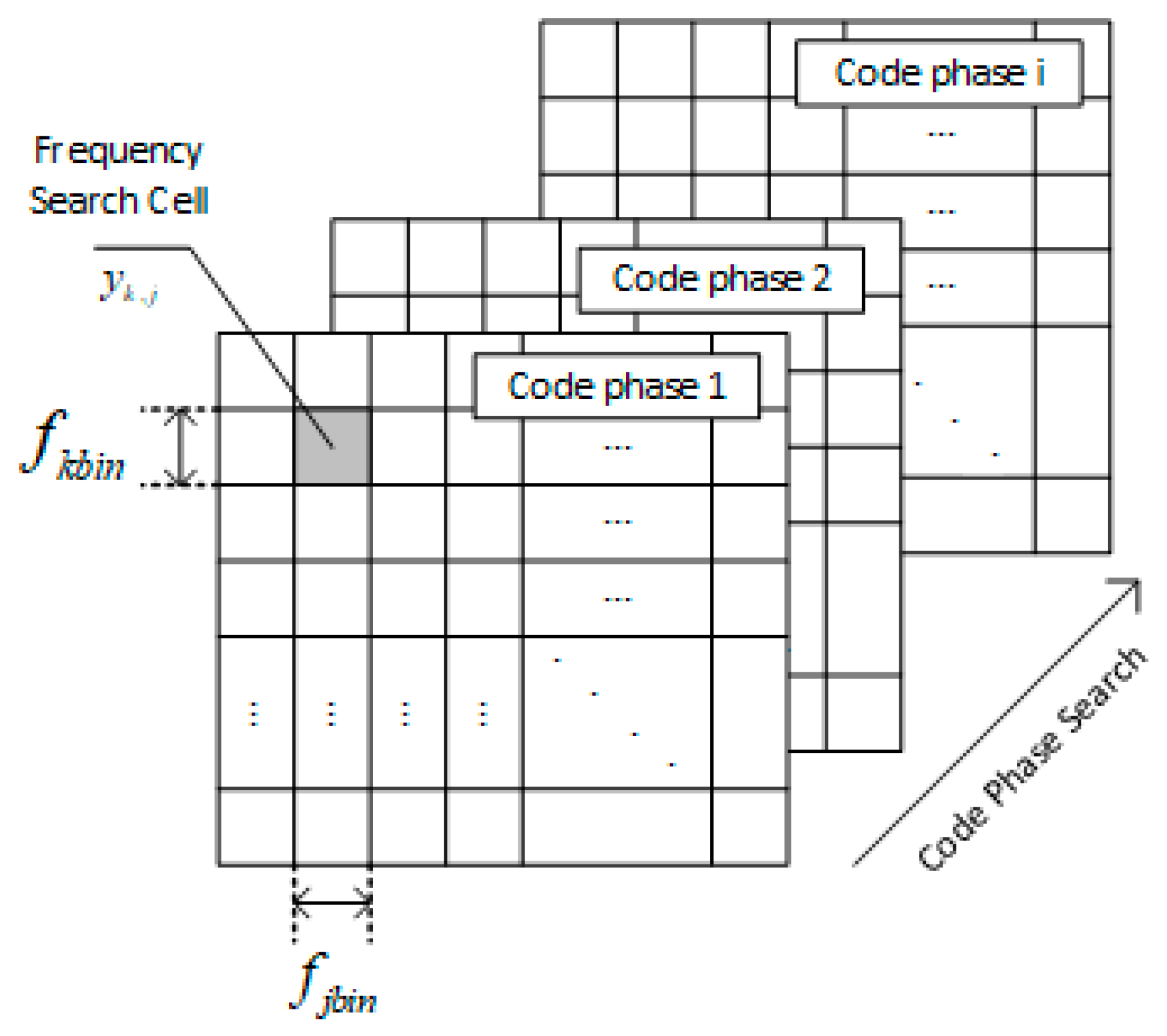
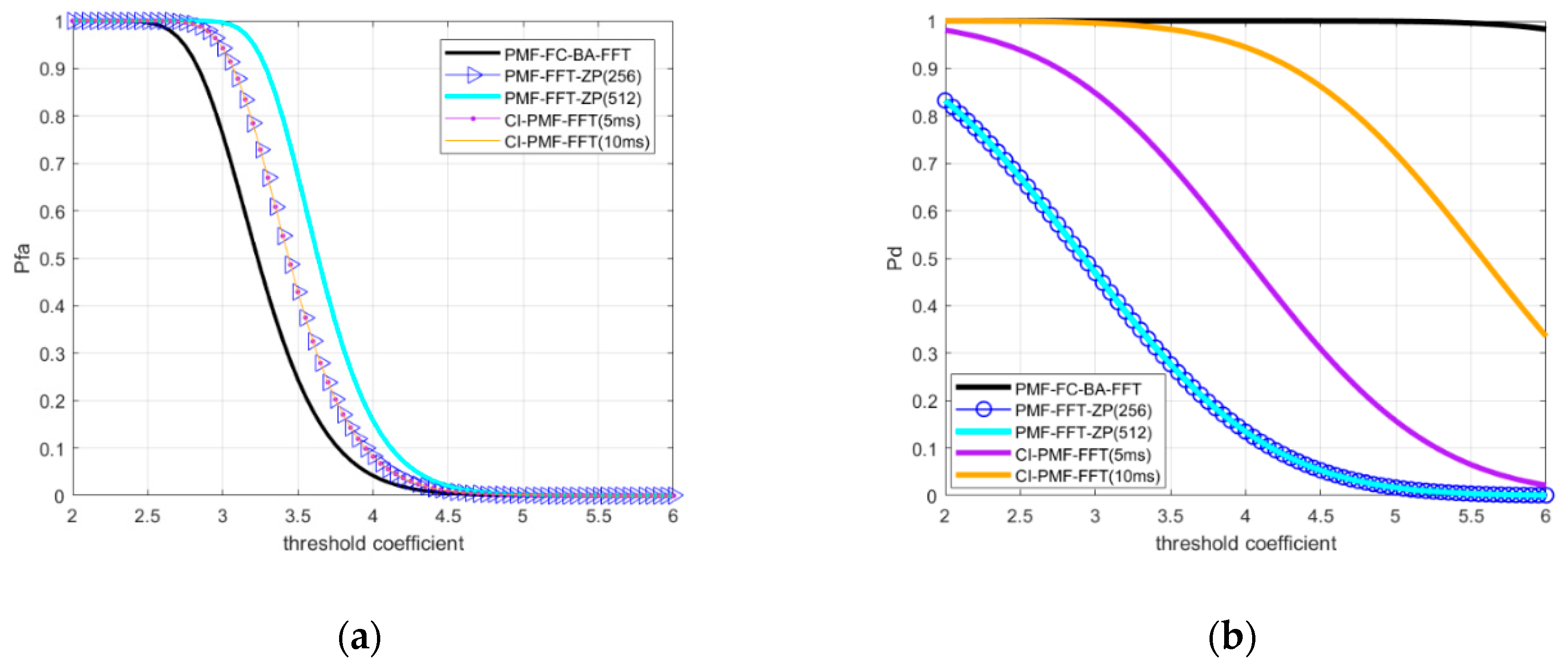
3.4. Probability of False Alarm and the Probability of Detection
4. Simulation and Test Result
4.1. Simulation Conditions
4.2. Computational Load
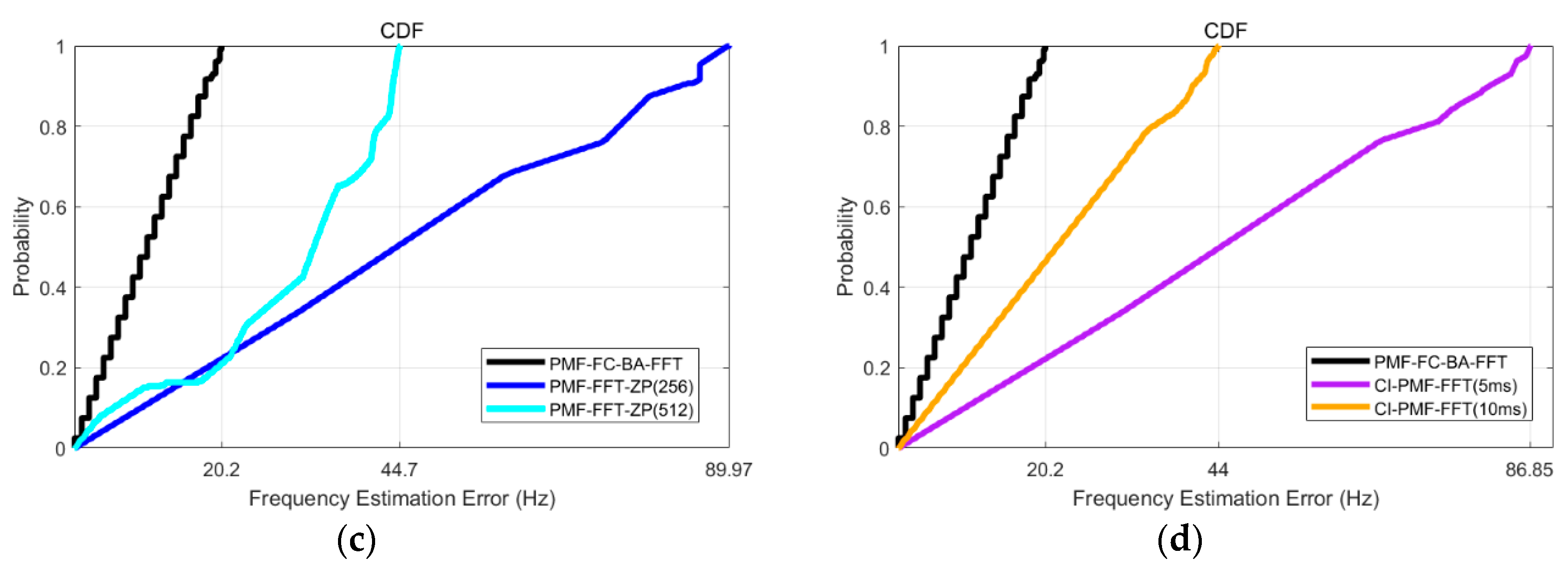
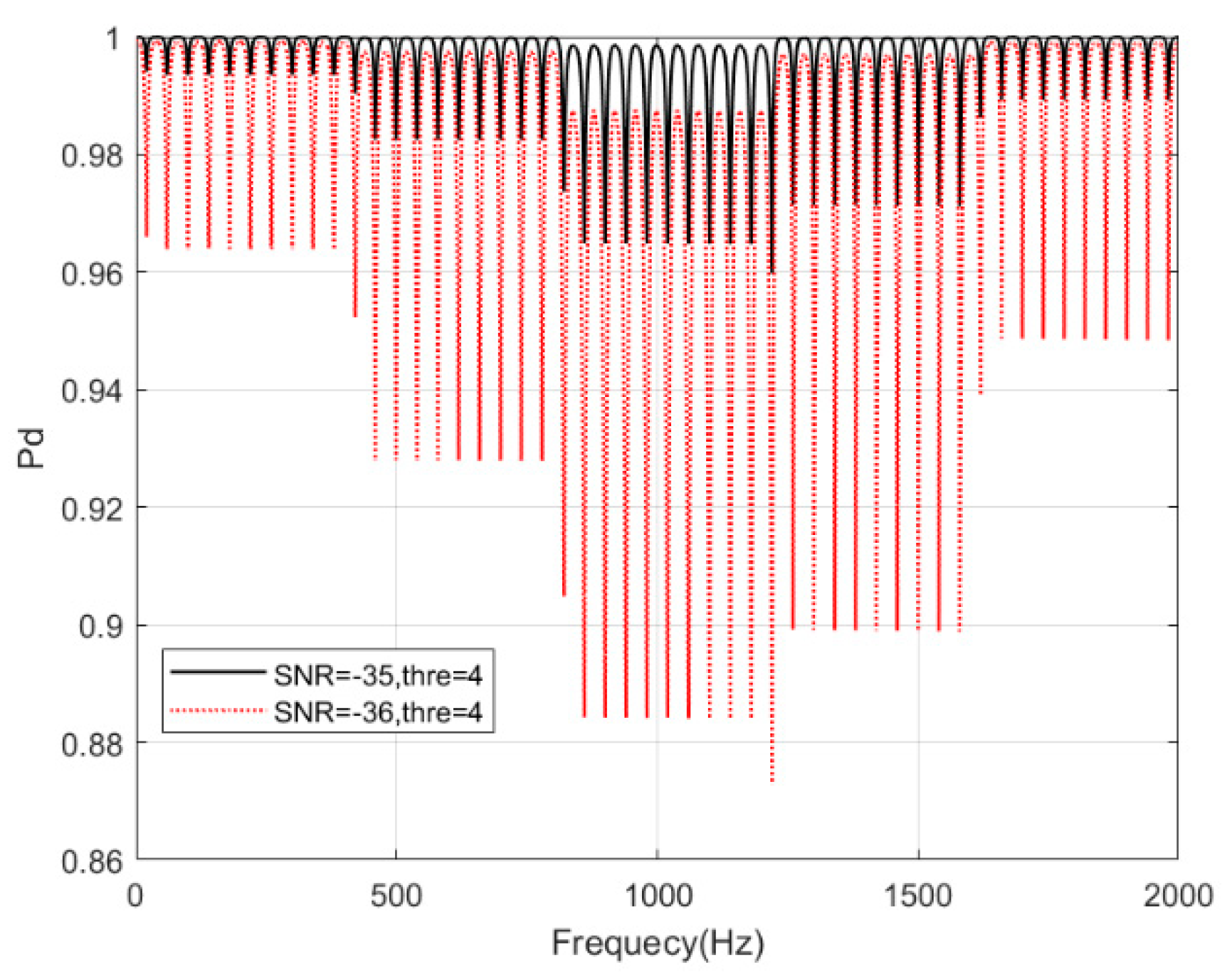
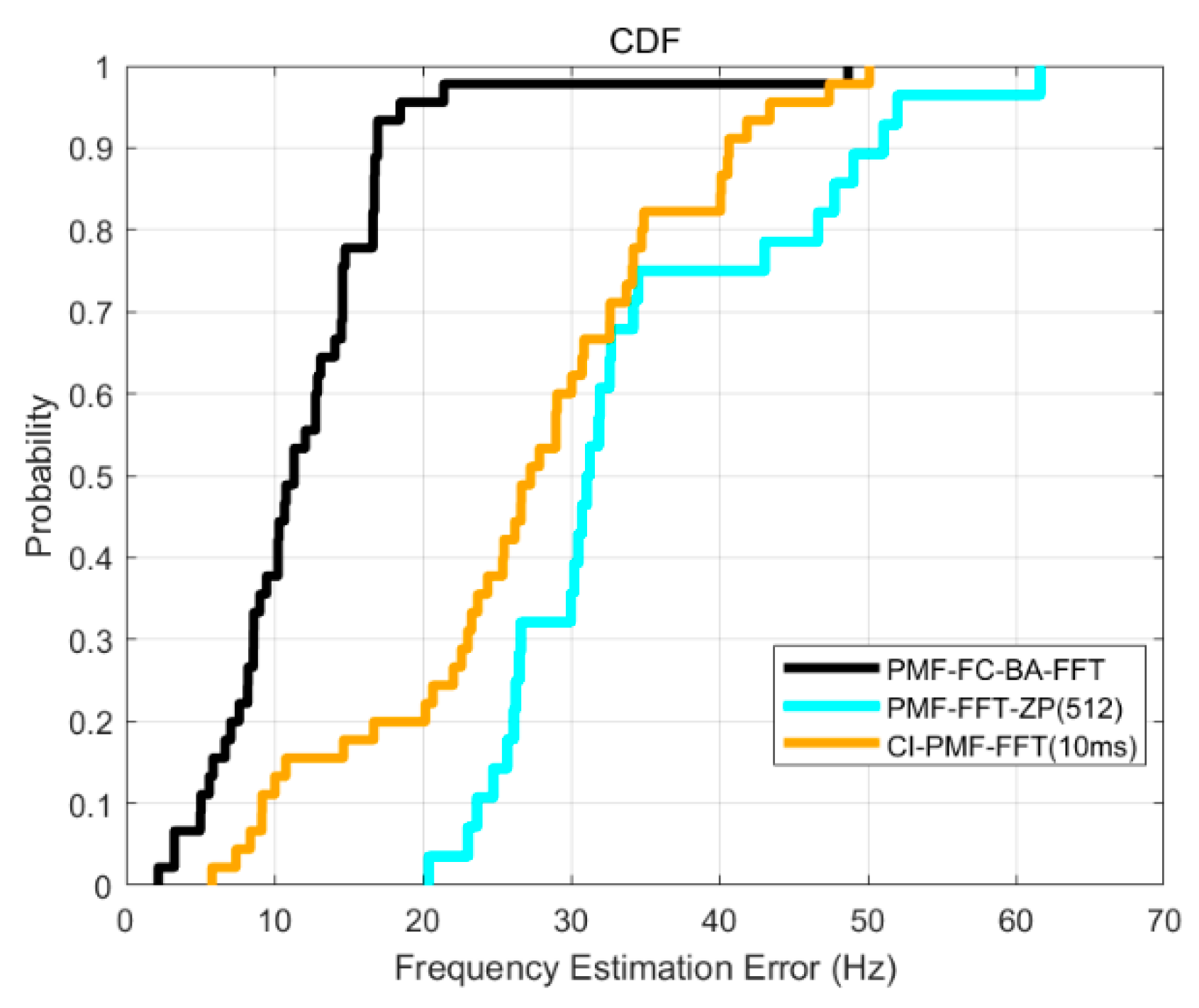
4.3. Frequency Acquisition Accuracy
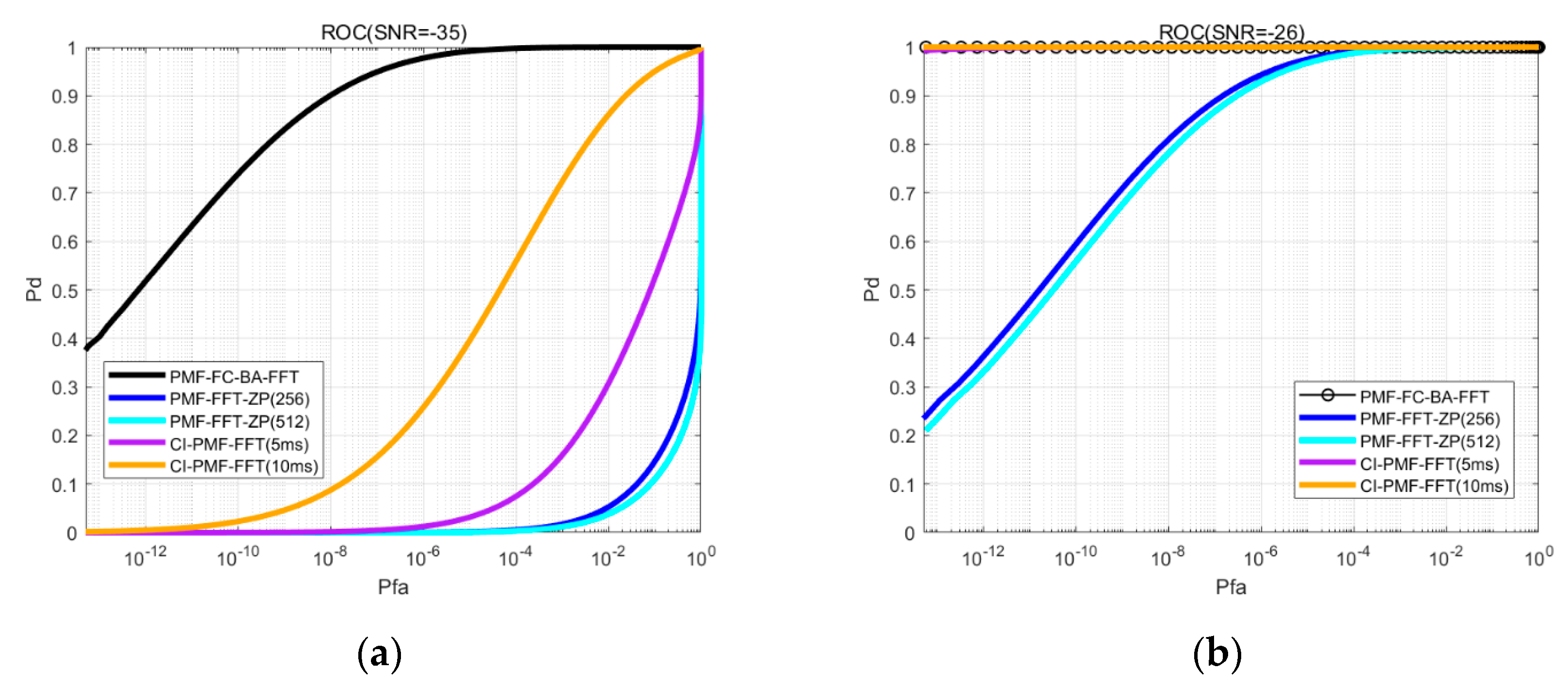
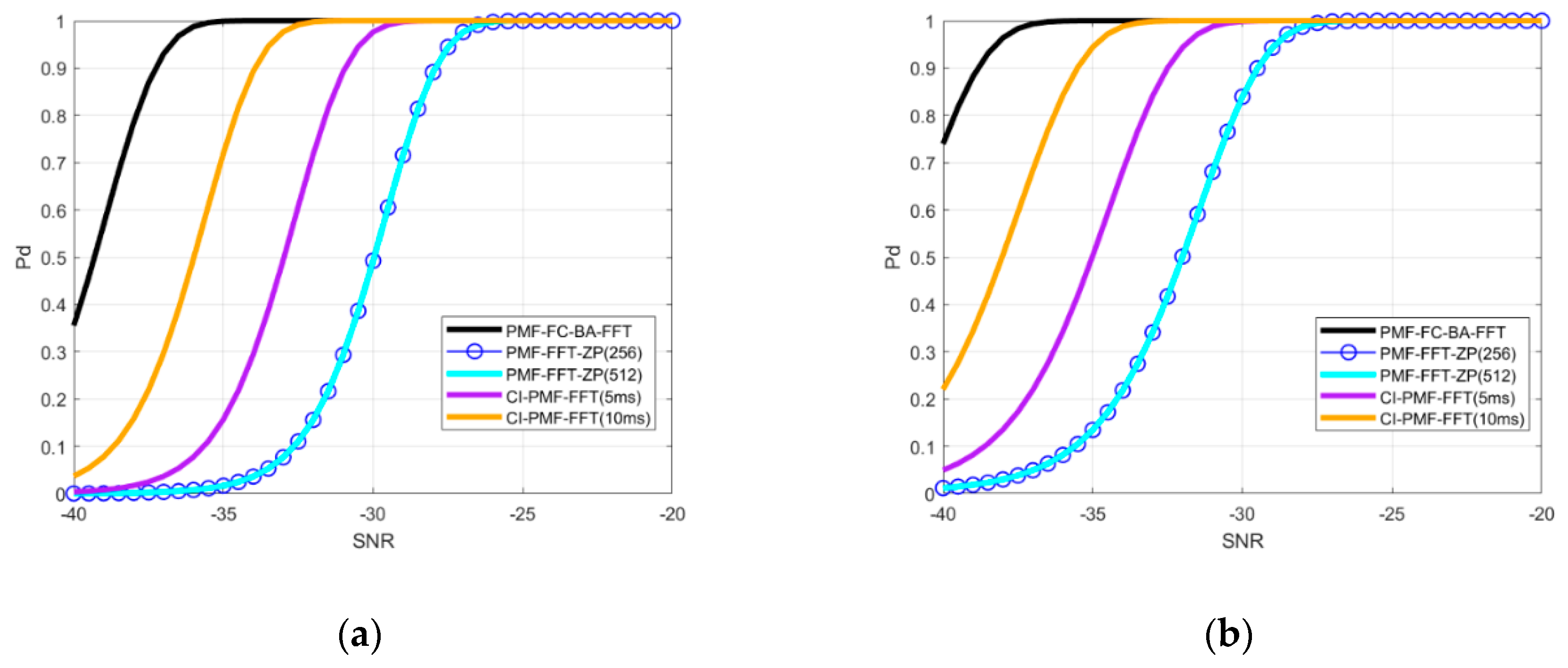
4.4. Acquisition Sensitivity
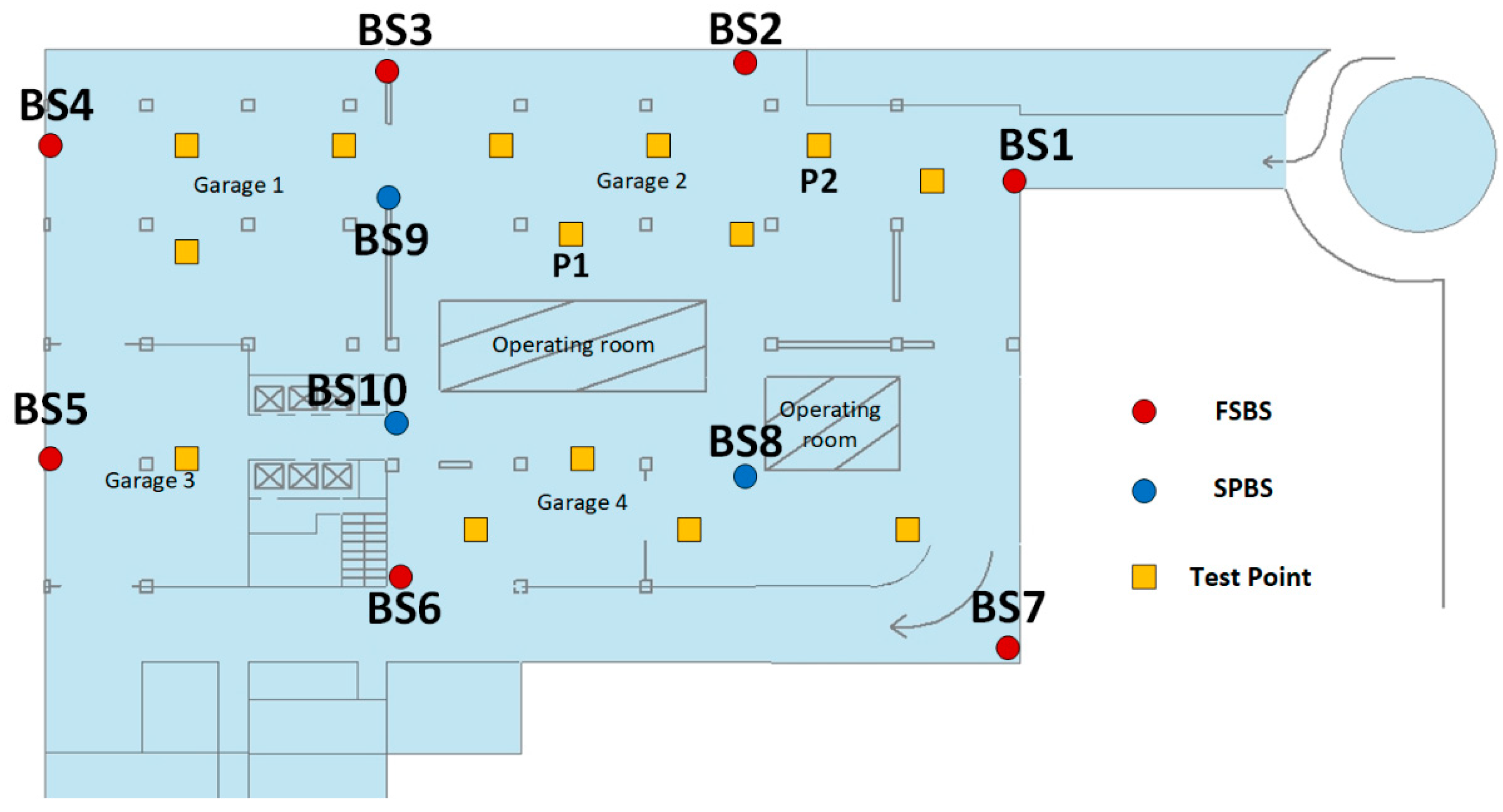
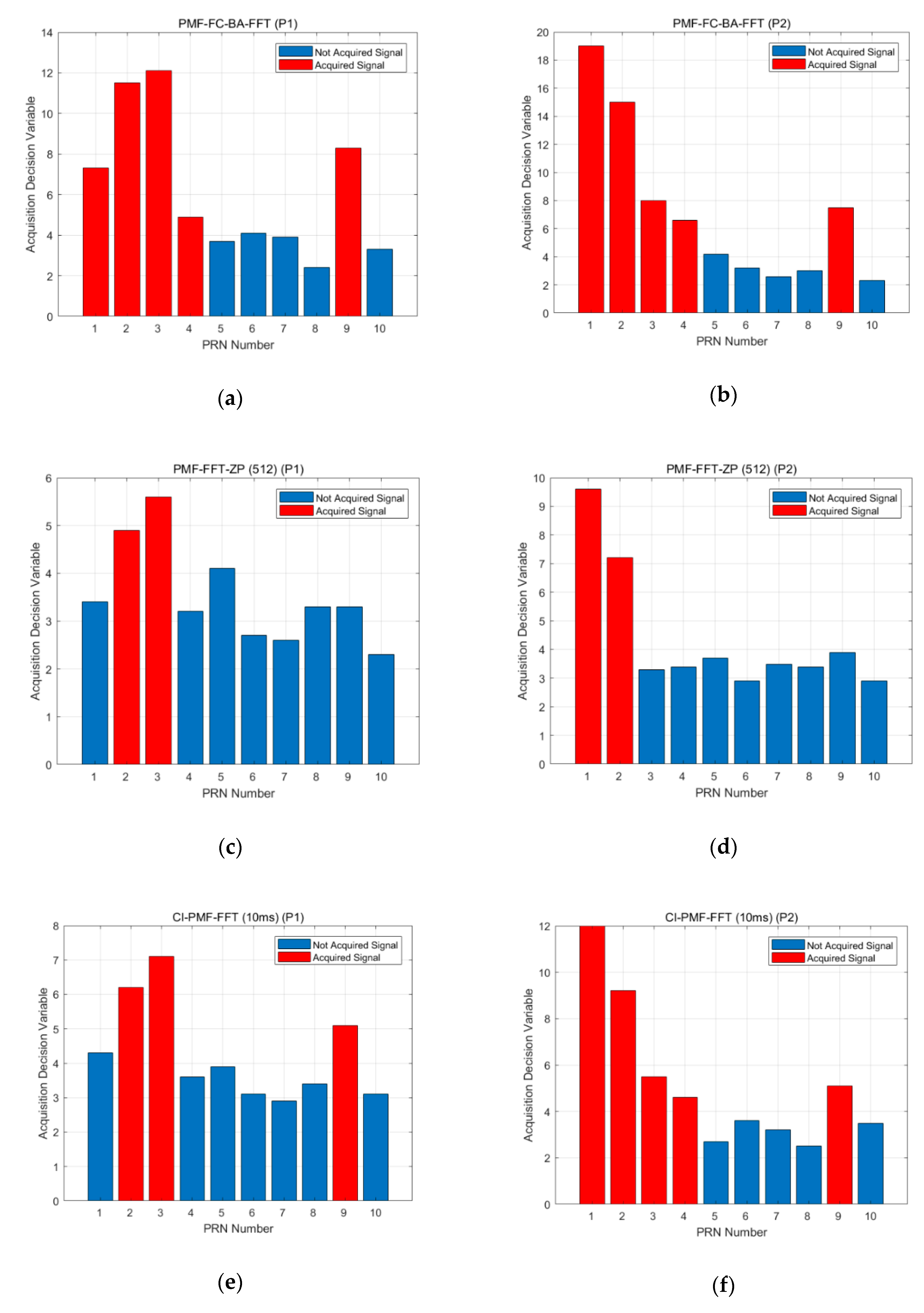
4.5. Experimental Tests
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shamaei, K.; Khalife, J.; Kassas, Z.M. Exploiting LTE Signals for Navigation: Theory to Implementation. IEEE Trans. Wirel. Commun. 2018, 17, 2173–2189. [Google Scholar] [CrossRef] [Green Version]
- Mautz, R. Overview of current indoor positioning systems. Geod. Kartogr. 2009, 35, 18–22. [Google Scholar] [CrossRef]
- Peral-Rosado, J.A.D.; Raulefs, R.; López-Salcedo, J.A.; Seco-Granados, G. Survey of Cellular Mobile Radio Localization Methods: From 1G to 5G. IEEE Commun. Surv. Tutor. 2018, 20, 1124–1148. [Google Scholar] [CrossRef]
- Commission, F.C. FCC Wireless 911 Requirements. Available online: https://transition.fcc.gov/pshs/services/911-services/enhanced911/archives/factsheet_requirements_012001.pdf (accessed on 20 May 2019).
- Laoudias, C.; Moreira, A.; Kim, S.; Lee, S.; Wirola, L.; Fischione, C. A Survey of Enabling Technologies for Network Localization, Tracking, and Navigation. IEEE Commun. Surv. Tutor. 2018, 20, 3607–3644. [Google Scholar] [CrossRef] [Green Version]
- Peral-Rosado, J.A.D.; López-Salcedo, J.A.; Kim, S.; Seco-Granados, G. Feasibility study of 5G-based localization for assisted driving. In Proceedings of the 2016 International Conference on Localization and GNSS (ICL-GNSS), Barcelona, Spain, 28–30 June 2016; pp. 1–6. [Google Scholar]
- Otsason, V.; Varshavsky, A.; LaMarca, A.; de Lara, E. Accurate GSM Indoor Localization. In Proceedings of the UbiComp 2005: Ubiquitous Computing, Berlin, Heidelberg, 11–14 September 2005; pp. 141–158. [Google Scholar]
- Zang, H.; Baccelli, F.; Bolot, J. Bayesian Inference for Localization in Cellular Networks. In Proceedings of the 2010 Proceedings IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1–9. [Google Scholar]
- Bravo, A.M.; Moreno, J.I.; Soto, I. Advanced positioning and location based services in 4G mobile-IP radio access networks. In Proceedings of the 2004 IEEE 15th International Symposium on Personal, Indoor and Mobile Radio Communications (IEEE Cat. No.04TH8754), Barcelona, Spain, 5–8 September 2004; Volume 1082, pp. 1085–1089. [Google Scholar]
- Ericsson. Mobile Positioning System. Available online: https://www.ericsson.com/en/portfolio/digital-services/automated-network-operations/analytics-and-assurance/mobile-positioning-system (accessed on 20 May 2019).
- Paek, J.; Kim, K.-H.; Singh, J.P.; Govindan, R. Energy-efficient positioning for smartphones using Cell-ID sequence matching. In Proceedings of the 9th international conference on Mobile systems, applications, and services, Bethesda, MD, USA, 28 June–1 July 2011; pp. 293–306. [Google Scholar]
- Ibrahim, M.; Youssef, M. CellSense: An Accurate Energy-Efficient GSM Positioning System. IEEE Trans. Veh. Technol. 2012, 61, 286–296. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, X.F.; He, S.B.; Shi, Z.G. Prospective Positioning Architecture and Technologies in 5G Networks. IEEE Netw. 2017, 31, 115–121. [Google Scholar] [CrossRef]
- Chen, C.Y.; Wu, W.R. Three-Dimensional Positioning for LTE Systems. IEEE Trans. Veh. Technol. 2017, 66, 3220–3234. [Google Scholar] [CrossRef]
- Fischer, S. Observed Time Difference of Arrival (OTDOA) Positioning in 3GPP LTE; Qualcomm: San Diego, CA, USA, 2014. [Google Scholar]
- Deng, Z.L.; Mo, J.; Jia, B.Y.; Bian, X.M. An Acquisition Scheme Based on a Matched Filter for Novel Communication and Navigation Fusion Signals. Sensors 2017, 17, 18. [Google Scholar] [CrossRef]
- Mo, J.; Deng, Z.L.; Jia, B.Y.; Jiang, H.J.; Bian, X.M. A Novel FLL-Assisted PLL With Fuzzy Control for TC-OFDM Carrier Signal Tracking. IEEE Access 2018, 6, 52447–52459. [Google Scholar] [CrossRef]
- Liu, W.; Bian, X.M.; Deng, Z.L.; Mo, J.; Jia, B.Y. A Novel Carrier Loop Algorithm Based on Maximum Likelihood Estimation (MLE) and Kalman Filter (KF) for Weak TC-OFDM Signals. Sensors 2018, 18, 22. [Google Scholar] [CrossRef]
- Yu, S.C.; Deng, Z.L.; Jiao, J.C.; Jiang, S.; Mo, J.; Xu, F.H. The Multipath Fading Channel Simulation for Indoor Positioning. In China Satellite Navigation Conference; Sun, J., Liu, J., Fan, S., Wang, F., Eds.; Springer: New York, NY, USA, 2016; Volume 389, pp. 341–347. [Google Scholar]
- Deng, Z.; Yu, Y.; Yuan, X.; Wan, N.; Yang, L. Situation and development tendency of indoor positioning. Chin. Commun. 2013, 10, 42–55. [Google Scholar] [CrossRef]
- Boudreau, G.; Panicker, J.; Guo, N.; Chang, R.; Wang, N.; Vrzic, S. Interference coordination and cancellation for 4G networks. IEEE Commun. Mag. 2009, 47, 74–81. [Google Scholar] [CrossRef]
- Suman, P.; Baenke, J.; Harmon, A.; Irizarry, M.S.; Jakubek, R.; Leiterman, J.J.; Osman, A. Impact of Dirty Devices on CDMA Network Coverage and Capacity. IEEE Access 2015, 3, 752–758. [Google Scholar] [CrossRef]
- Cho, S.H.; Yeo, S.R.; Choi, H.H.; Park, C.; Lee, S.J. A design of synchronization method for TDOA-based positioning system. In Proceedings of the 2012 12th International Conference on Control, Automation and Systems, Jeju Island, Korea, 17–21 October 2012; pp. 1373–1375. [Google Scholar]
- Deng, Z.; Mo, J.; Jia, B.; Bian, X. A Fine Frequency Estimation Algorithm Based on Fast Orthogonal Search (FOS) for Base Station Positioning Receivers. Electronics 2018, 7, 376. [Google Scholar] [CrossRef]
- Wu, J.; Hu, Y. The Study on GPS Signal Acquisition Algorithm in Time Domain. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–14 October 2008; pp. 1–3. [Google Scholar]
- Wen, H.; Meng, Z.; Teng, Z.S.; Guo, S.Y.; Yang, Y.X. Comparative Study of Influence of Noise on Power Frequency Estimation of Sine wave Using Interpolation FFT. Fluct. Noise Lett. 2014, 13, 11. [Google Scholar] [CrossRef]
- Wang, K.; Jiang, R.; Li, Y.; Zhang, N. A new algorithm for fine acquisition of GPS carrier frequency. GPS Solut. 2014, 18, 581–592. [Google Scholar] [CrossRef]
- Ren, T.; Petovello, M.G. A Stand-Alone Approach for High-Sensitivity GNSS Receivers in Signal-Challenged Environment. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2438–2448. [Google Scholar] [CrossRef]
- Chang, L.; Jun, Z.; Zhu, Y.; Qingge, P. Analysis and optimization of PMF-FFT acquisition algorithm for high-dynamic GPS signal. In Proceedings of the 2011 IEEE 5th International Conference on Cybernetics and Intelligent Systems (CIS), Qingdao, China, 17–19 September 2011; pp. 185–189. [Google Scholar]
- Guo, W.F.; Niu, X.J.; Guo, C.; Cui, J.S. A new FFT acquisition scheme based on partial matched filter in GNSS receivers for harsh environments. Aerosp. Sci. Technol. 2017, 61, 66–72. [Google Scholar] [CrossRef]
- Zhang, H.L.; Ba, X.; Chen, J.; Zhou, H. FFT-based fine frequency estimation for weak GPS signal. J. Electron. Inf. Technol. 2015, 37, 2132–2137. [Google Scholar] [CrossRef]
- Tamazin, M.; Noureldin, A.; Korenberg, M.J.; Massoud, A. Navigation and Instrumentation Research Group. Robust fine acquisition algorithm for GPS receiver with limited resources. GPS Solut. 2016, 20, 77–88. [Google Scholar] [CrossRef]
- Borre, K.; Akos, D.M.; Bertelsen, N.; Rinder, P.; Jensen, S.H. A Software-Defined GPS and Galileo Receiver: A Single-Frequency Approach; Springer: Berlin, Germany, 2007. [Google Scholar]
- Tang, X.; Falletti, E.; Presti, L.L. Fine Doppler frequency estimation in GNSS signal acquisition process. In Proceedings of the 2012 6th ESA Workshop on Satellite Navigation Technologies (Navitec 2012) & European Workshop on GNSS Signals and Signal Processing, Noordwijk, The Netherlands, 5–7 December 2012; pp. 1–6. [Google Scholar]
- Pang, H.-S.; Lim, J.-S.; Kwon, O.-J.; Shin, B.J. Iterative Frequency Estimation for Accuracy Improvement of Three DFT Phase-Based Methods. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2012, E95-A, 969–973. [Google Scholar] [CrossRef]
- Miller, M.; Nguyen, T.; Yang, C.; Blasch, E. Comparative study of coherent, non-coherent, and semi-coherent integration schemes for GNSS receivers. In Proceedings of the 63rd Annual Meeting of the Institute of Navigation 2007, Cambridge, MA, USA, 23–25 April 2007; pp. 572–588. [Google Scholar]
- Gao, F.Q.; Xia, H.X. Fast GNSS signal acquisition with Doppler frequency estimation algorithm. GPS Solut. 2018, 22, 13. [Google Scholar] [CrossRef]
- Corazza, G.E. On the MAX/TC criterion for code acquisition and its application to DS-SSMA systems. IEEE Trans. Commun. 1996, 44, 1173–1182. [Google Scholar] [CrossRef]
- Lu, W.J.; Zhang, Y.B.; Lei, D.Y.; Yu, D.S. Efficient Weak Signals Acquisition Strategy for GNSS Receivers. IEICE Trans. Commun. 2016, 99, 288–295. [Google Scholar] [CrossRef]
- Kim, B.; Kong, S.H. Determination of Detection Parameters on TDCC Performance. IEEE Trans. Wirel. Commun. 2014, 13, 2422–2431. [Google Scholar] [CrossRef]
- Kong, S.H.; Kim, B. Two-Dimensional Compressed Correlator for Fast PN Code Acquisition. IEEE Trans. Wirel. Commun. 2013, 12, 5859–5867. [Google Scholar] [CrossRef]
- Spangenberg, S.M.; Scott, I.; McLaughlin, S.; Povey, G.J.R.; Cruickshank, D.G.M.; Grant, P.M. An FFT-based approach for fast acquisition in spread spectrum communication systems. Wirel. Pers. Commun. 2000, 13, 27–56. [Google Scholar] [CrossRef]
- Tahir, M.; Lo Presti, L.; Fantino, M. A Novel Acquisition Strategy for Weak GNSS Signals Based on MAP Criterion. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1913–1928. [Google Scholar] [CrossRef]
- Svaton, J.; Vejrazka, F. Pre- and Post-Correlation Method for Acquisition of New GNSS Signals with Secondary Code. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 23–26 April 2018; IEEE: New York, NY, USA, 2018; pp. 1422–1427. [Google Scholar]
- Benachenhou, K.; Hamadouche, M.; Taleb-Ahmed, A. New formulation of GNSS acquisition with CFAR detection. Int. J. Satell. Commun. Netw. 2017, 35, 215–230. [Google Scholar] [CrossRef]
- Oh, H.S.; Han, D.S. An adaptive double-dwell PN code acquisition system in DS-CDMA communications. Signal Process. 2005, 85, 2327–2337. [Google Scholar] [CrossRef]




| Parameters | Value |
|---|---|
| Length of Match Filter | 186 |
| Number of Match Filter | 110 |
| Length of FFT | 128 |
| Block Number | 10 |
| Frequency Compensation step (Hz) | 40 |
| Parameters | Value |
|---|---|
| Length of Match Filter | 186 |
| Number of Match Filter | 110 |
| Length of FFT | 256,512 |
| Parameters | Value |
|---|---|
| Integration Time | 5 ms, 10 ms |
| Length of Match Filter | 186,372 |
| Number of Match Filter | 110 |
| Length of FFT | 256 |
| Resources | PMF-FC-BA-FFT | PMF-FFT-ZP (256) | PMF-FFT-ZP (512) | CI-PMF-FFT (5 ms) | CI-PMF-FFT (10 ms) |
|---|---|---|---|---|---|
| Multiplier | 220 | 2304 | 7424 | 2304 | 2676 |
| Adder | 220 | 3456 | 11,136 | 3456 | 3828 |
| Memory | 1100 | 192 | 576 | 192 | 192 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Z.; Jia, B.; Tang, S.; Fu, X.; Mo, J. Fine Frequency Acquisition Scheme in Weak Signal Environment for a Communication and Navigation Fusion System. Electronics 2019, 8, 829. https://doi.org/10.3390/electronics8080829
Deng Z, Jia B, Tang S, Fu X, Mo J. Fine Frequency Acquisition Scheme in Weak Signal Environment for a Communication and Navigation Fusion System. Electronics. 2019; 8(8):829. https://doi.org/10.3390/electronics8080829
Chicago/Turabian StyleDeng, Zhongliang, Buyun Jia, Shihao Tang, Xiao Fu, and Jun Mo. 2019. "Fine Frequency Acquisition Scheme in Weak Signal Environment for a Communication and Navigation Fusion System" Electronics 8, no. 8: 829. https://doi.org/10.3390/electronics8080829





