A n-out-of-n Sharing Digital Image Scheme by Using Color Palette
Abstract
1. Introduction
2. Preliminaries
3. Motivation and Design Concept
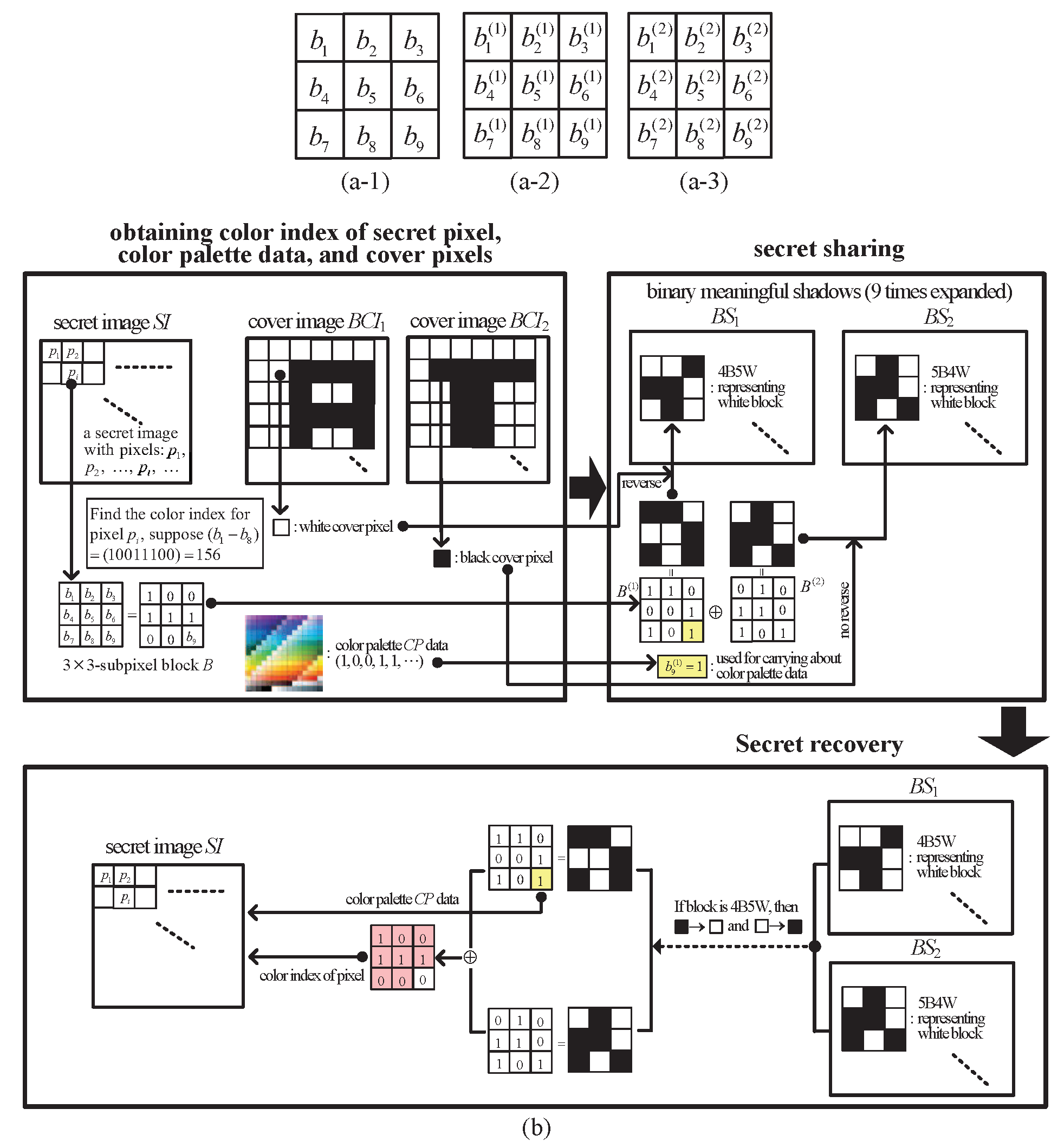
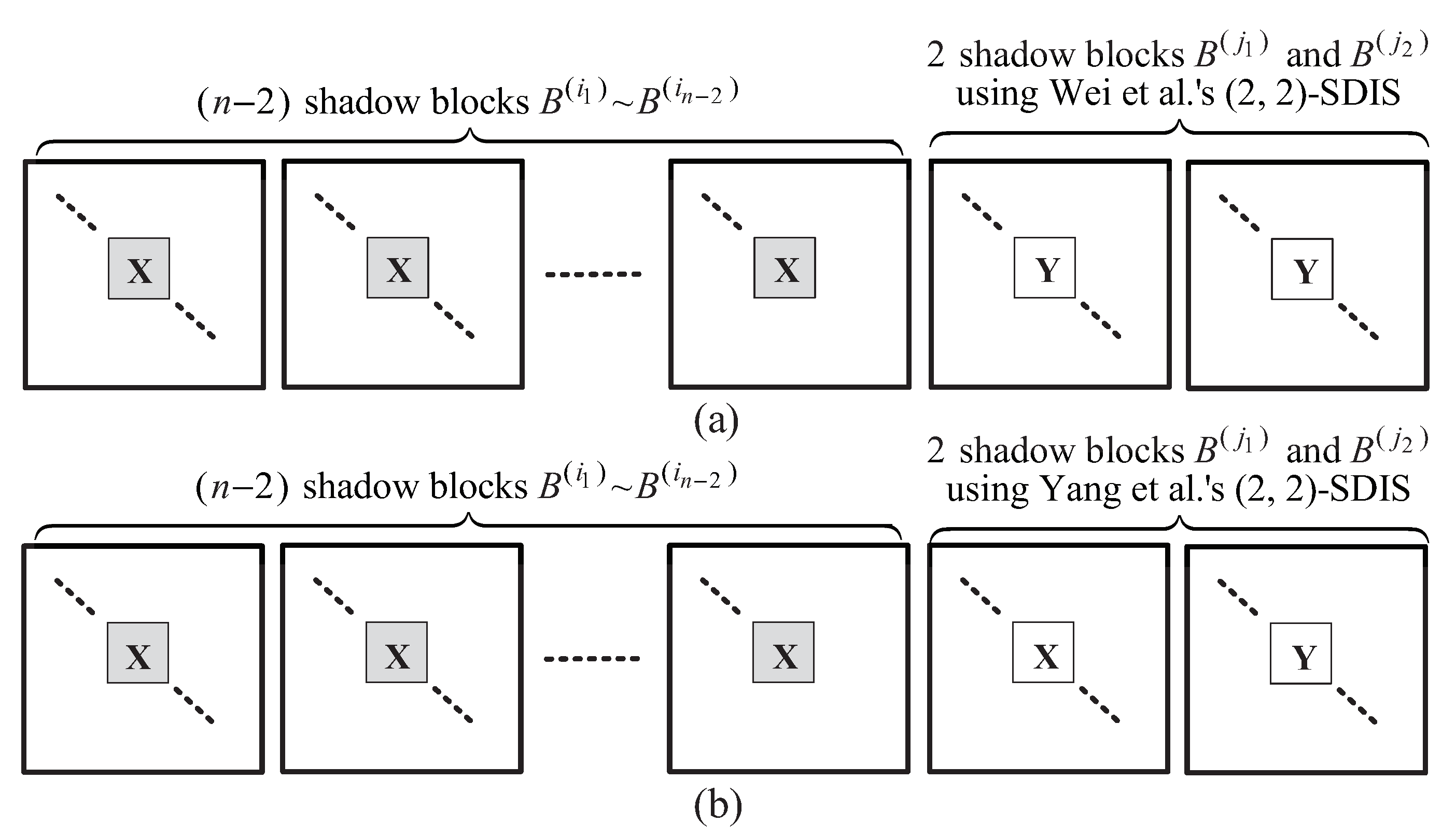
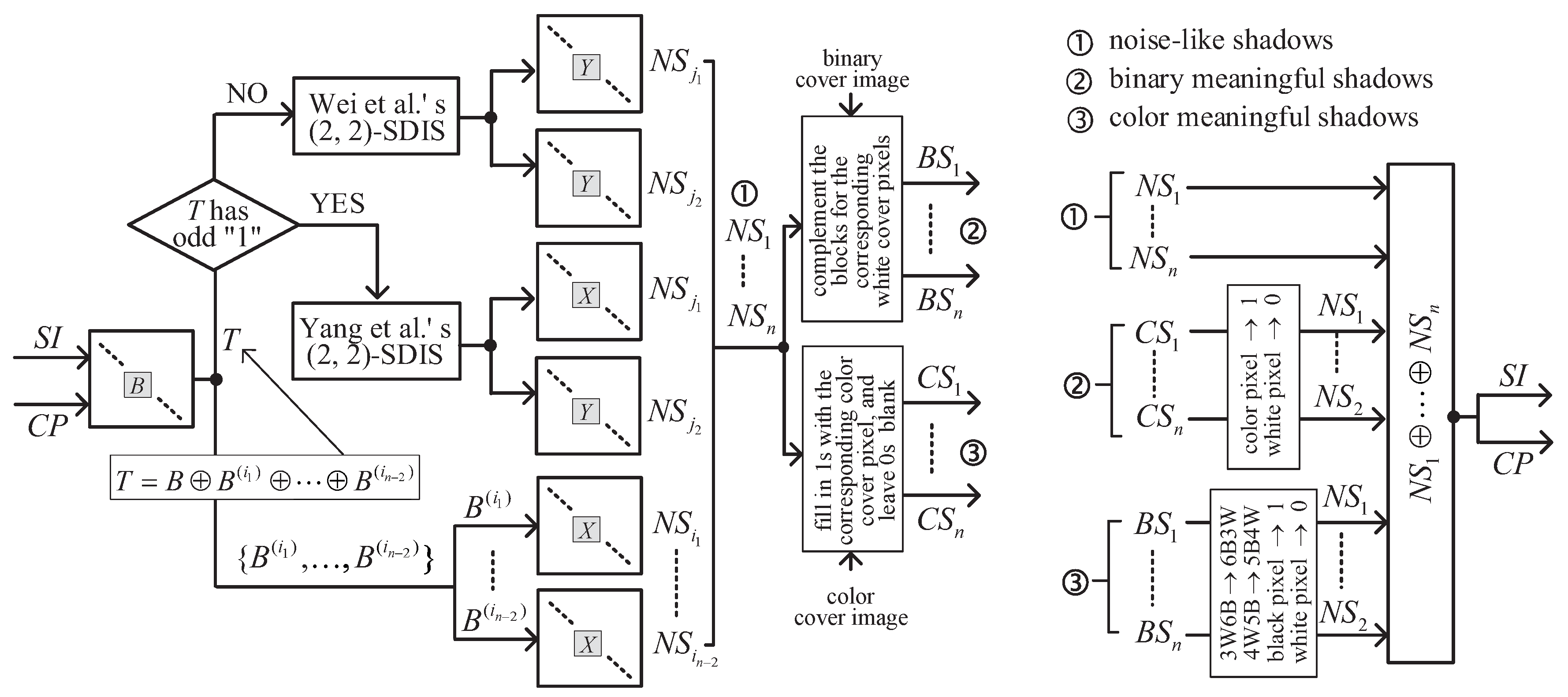
4. The Proposed -SDIS
4.1. Sharing and Recovering Algorithms
- (S-1)
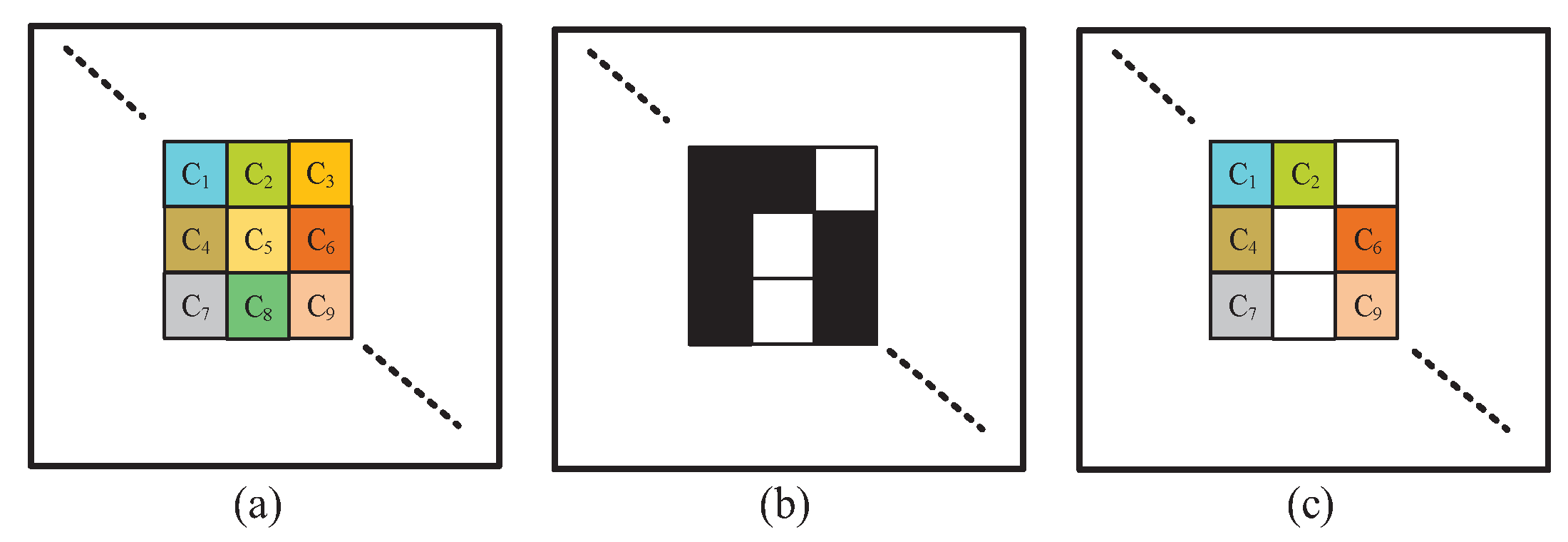
- Obtain the block from the secret image and the color palate .
- (S-2)
- Randomly generate blocks .
- (S-3)
- By random blocks and the block B, calculate the temporary block T via .
- (S-4)
- If is 9, we reduce its Hamming weight to via modifying any one shadow block of ./* (1) In Lemma 1, we prove that the reduction of Hamming weight can always be accomplished (2) After step (S-4), the Hamming weight distribution is */.
- (S-5)
- If is odd () then construct two other shadows by ; else by , where ./* In Lemma 2, we prove that can be obtained from for odd , and from for even . */
- (S-6)
- Process all the blocks, and output shadow blocks on n noise-like shadows , respectively.
- (S-1)
- Obtain B by XOR-ing via from n noise-like shadows ./* Theorem 1, demonstrates that we can obtain the original block from */
- (S-2)
- Recover the color index and the data of color palette , respectively, from B.
- (S-3)
- Repeat the above until all blocks in are processed, and finally and can be recovered.
4.2. Extension of -SDIS to Share True Color Secret Image
- (S-1)
- Obtain 24-bit true color , , and from the secret image , and random generate a bit to form a 25-bit block , as shown in Figure 4a./* Parity bit is not used to covey any information, and thus it can be randomly generated */
- (S-2)
- Subdivide the true color block to red, green, and blue shadow blocks .
- (S-3)
- Using as 9-bit block B in (S-1), respectively, to generate n shadow blocks , where , through (S-1) (S-6).
- (S-4)
- Collect every first 8 bits in , and append a black subpixel in the 25-th subpixel to generate a 25-bit shadow block , where ./* Because we do not use the 25-th bit in the XOR-ed result to convey any information, we can use black subpixel in 25-th subpixel for all shadow blocks to enhance the number of black subpixels. */
- (S-5)
- Process all the blocks, and output blocks on n noise-like shadows , respectively.
- (R-1)
- Obtain every 25-bit block by XOR-ing via XOR-ing n noise-like shadows .
- (R-2)
- Recover a true color from the first 24 bits in , i.e., , , and .
- (R-3)
- Repeat the above until all blocks in are processed, and finally a true color is obtained.
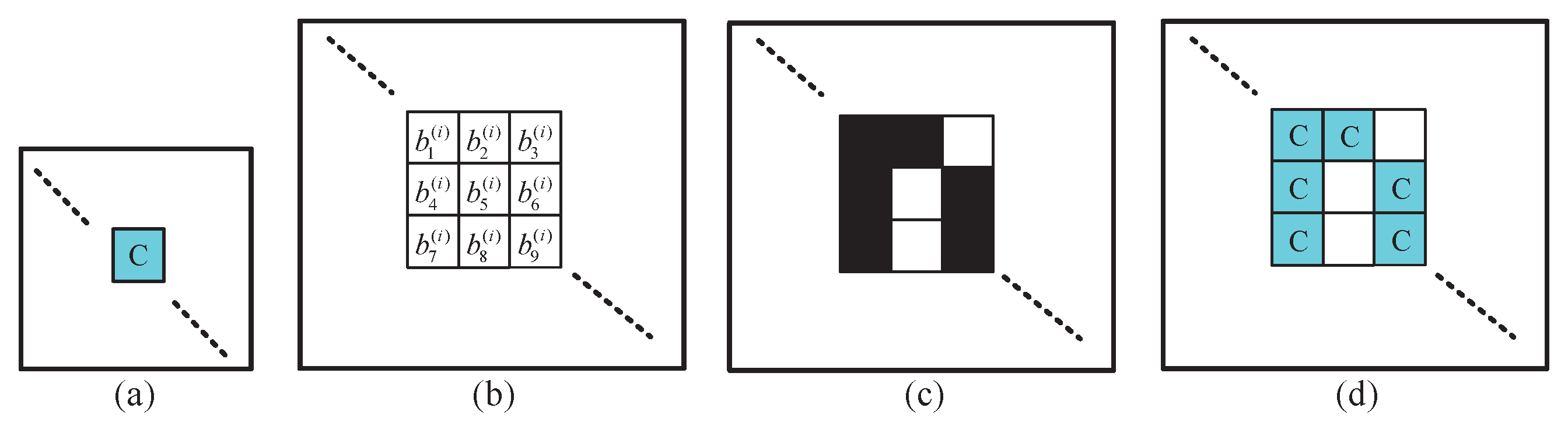
4.3. Enhancing Visual Quality of Color Meaningful Shadow
5. Theorem and Security Analysis
5.1. Main Theorems and Examples
5.2. Security Analysis: The -Colluder Attack
6. Evaluation and Comparisons
6.1. Experimental Results
6.2. Discussion and Comparison
6.2.1. Enhancing
6.2.2. Comparison
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Naor, M.; Shamir, A. Visual cryptography. In Advances in Cryptology-EUROCRYPT’94; LNCS 950; Springer: Berlin/Heidelberg, Germany, 1995; pp. 1–12. [Google Scholar]
- Shyu, S.J.; Jiang, H.W. General constructions for threshold multiple-secret visual cryptography Schemes. IEEE Trans. Inf. Forensics Secur. 2013, 8, 733–743. [Google Scholar] [CrossRef]
- Yang, C.N.; Wu, C.C.; Lin, Y.C. k out of n region-based progressive visual cryptography. IEEE Trans. Circuits Syst. Video Technol. 2017. [Google Scholar] [CrossRef]
- Karolin, M.; Meyyappan, T.; Thamarai, S.M. Encryption and decryption of color images using visual cryptography. Int. J. Pure Appl. Math. 2018, 118, 277–281. [Google Scholar]
- Kansal, I.; Kasana, S.S. Sharing two true colour images using (3,3)-extended visual cryptography technique. J. Mod. Opt. 2018, 65, 1949–1959. [Google Scholar]
- Yang, C.N.; Wu, F.H.; Peng, S.L. Enhancing multi-factor cheating prevention in visual cryptography based minimum (k, n)-connected graph. J. Vis. Commun. Image Represent. 2018, 55, 660–676. [Google Scholar] [CrossRef]
- Shamir, A. How to share a secret. Commun. Assoc. Comput. Mach. 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Thien, C.C.; Lin, J.C. Secret image sharing. Comput. Graph. 2002, 26, 765–770. [Google Scholar] [CrossRef]
- Liu, Y.X.; Yang, C.N.; Wu, C.M.; Sun, Q.D.; Bi, W. Threshold changeable secret image sharing scheme based on interpolation polynomial. Multimed. Tools Appl. 2019, 78, 18653–18667. [Google Scholar] [CrossRef]
- Yang, C.N.; Chen, T.S.; Yu, K.H.; Wang, C.C. Improvements of image sharing with steganography and authentication. J. Syst. Softw. 2007, 80, 1070–1076. [Google Scholar] [CrossRef]
- Pakniat, N.; Noroozi, M.; Eslami, Z. Secret image sharing scheme with hierarchical threshold access structure. J. Vis. Commun. Image Represent. 2014, 25, 1093–1101. [Google Scholar] [CrossRef]
- Liu, Y.X.; Zhang, Y.Z.; Yang, C.N. Reducing file size and time complexity in secret sharing based document protection. Math. Biosci. Eng. 2019, 16, 4802–4817. [Google Scholar] [CrossRef]
- Kanso, A.; Ghebleh, M. An efficient lossless secret sharing scheme for medical images. J. Vis. Commun. Image Represent. 2018, 56, 245–255. [Google Scholar] [CrossRef]
- Li, P.; Liu, Z.; Yang, C.N. A construction method of (t, k, n)-essential secret image sharing scheme. Signal Process. Image Commun. 2018, 65, 210–220. [Google Scholar] [CrossRef]
- Wu, X.; Yang, C.N.; Zhuang, Y.T.; Hsu, S.C. Improving recovered image quality in secret Image sharing by simple modular arithmetic. Signal Process. Image Commun. 2018, 66, 42–49. [Google Scholar] [CrossRef]
- Lukac, R.; Plataniotis, K.N. Bit-level based secret sharing for image encryption. Pattern Recognit. 2005, 38, 767–772. [Google Scholar] [CrossRef]
- Wei, S.C.; Hou, Y.C.; Lu, Y.C. A technique for sharing a digital image. Comput. Stand. Interfaces 2015, 40, 53–61. [Google Scholar] [CrossRef]
- Yang, C.N.; Chen, C.H.; Cai, S.R. Enhanced Boolean-based multi secret image sharing scheme. J. Syst. Softw. 2016, 116, 22–34. [Google Scholar] [CrossRef]
- Yang, C.N.; Wu, C.H.; Yeh, Z.X.; Wang, D.; Kim, C. A new sharing digital image scheme with clearer shadow images. Comput. Stand. Interfaces 2017, 51, 118–131. [Google Scholar] [CrossRef]
- Liu, Y.X.; Yang, C.N.; Wu, S.Y.; Chou, Y.S. Progressive (k, n) secret image sharing schemes based on Boolean operations and covering codes. Signal Process. Image Commun. 2018, 66, 77–86. [Google Scholar] [CrossRef]












| Notation | Description |
|---|---|
| a 256-color color palette | |
| a secret image with the size with the size pixels | |
| binary (black-and-white) over image and color cover image with the size pixels | |
| n noise-like shadows with the size (respectively, ) subpixels for 256-color (respectively, true color) secret image, where | |
| binary meaningful shadows with the size (respectively, ) subpixels for 256-color (respectively, true color) secret image | |
| color meaningful shadows with the size (respectively, ) subpixels for 256-color (respectively, true color) secret image | |
| B | a -subpixel block B including 8-bit color index and one bit (Note: the bit in B is collected to covey the information for the proposed -SDIS) |
| a -subpixel block including the first three 8-tuples, , , and , are used to represent and B color planes, and the other one bit in is . | |
| a -pixel block on shadow i, where , including 8-bit and one bit . (Note: the ninth bit in every block (i.e., ) of is collected to covey the information for Wei et al.’s -SDIS and Yang et al.’s -SDIS) | |
| x black subpixels and y white subpixels in a block | |
| , | and blocks have and subpixels, respectively |
| Hamming weight function, the number of in a binary vector | |
| Operation of Wei et al.’s -SDIS, i.e., where both are blocks | |
| Operation of Yang et al.’s -SDIS, i.e., where one is block and the other is block |
| Wei et al.’s -SDIS | Yang et al.’s -SDIS | The Proposed -SDIS | ||
|---|---|---|---|---|
| number of shadows | 2 | 2 | ||
| structure of block | block | and blocks | and blocks | |
| percentage of block | : | :, : | :,: | |
| region in color shadows revealing cover image | ||||
| contrast of binary meaningful shadows | ||||
| enhancement of | No | No | Yes | |
| embedding the data of color palette data | having a problem for the color index 255 | using partitioned sets for some color indices | using a simple approach by reducing Hamming weight | |
| where to embed color palette data | the bit in | the bit in | the bit in the XOR-ed B | |
| enhancing visual quality of color meaningful shadows | No | No | Yes | |
| encoding/decoding complexity | XOR operation | XOR operation; lookup table | XOR operation | |
| security | probability to recover B under -colluder | |||
| probability to obtain under -colluder | can be obtained from only one shadow | can be obtained from only one shadow | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.-N.; Sun, Q.-D.; Liu, Y.-X.; Wu, C.-M. A n-out-of-n Sharing Digital Image Scheme by Using Color Palette. Electronics 2019, 8, 802. https://doi.org/10.3390/electronics8070802
Yang C-N, Sun Q-D, Liu Y-X, Wu C-M. A n-out-of-n Sharing Digital Image Scheme by Using Color Palette. Electronics. 2019; 8(7):802. https://doi.org/10.3390/electronics8070802
Chicago/Turabian StyleYang, Ching-Nung, Qin-Dong Sun, Yan-Xiao Liu, and Ci-Ming Wu. 2019. "A n-out-of-n Sharing Digital Image Scheme by Using Color Palette" Electronics 8, no. 7: 802. https://doi.org/10.3390/electronics8070802
APA StyleYang, C.-N., Sun, Q.-D., Liu, Y.-X., & Wu, C.-M. (2019). A n-out-of-n Sharing Digital Image Scheme by Using Color Palette. Electronics, 8(7), 802. https://doi.org/10.3390/electronics8070802






