Embedded Flight Control Based on Adaptive Sliding Mode Strategy for a Quadrotor Micro Air Vehicle
Abstract
:1. Introduction
Contribution
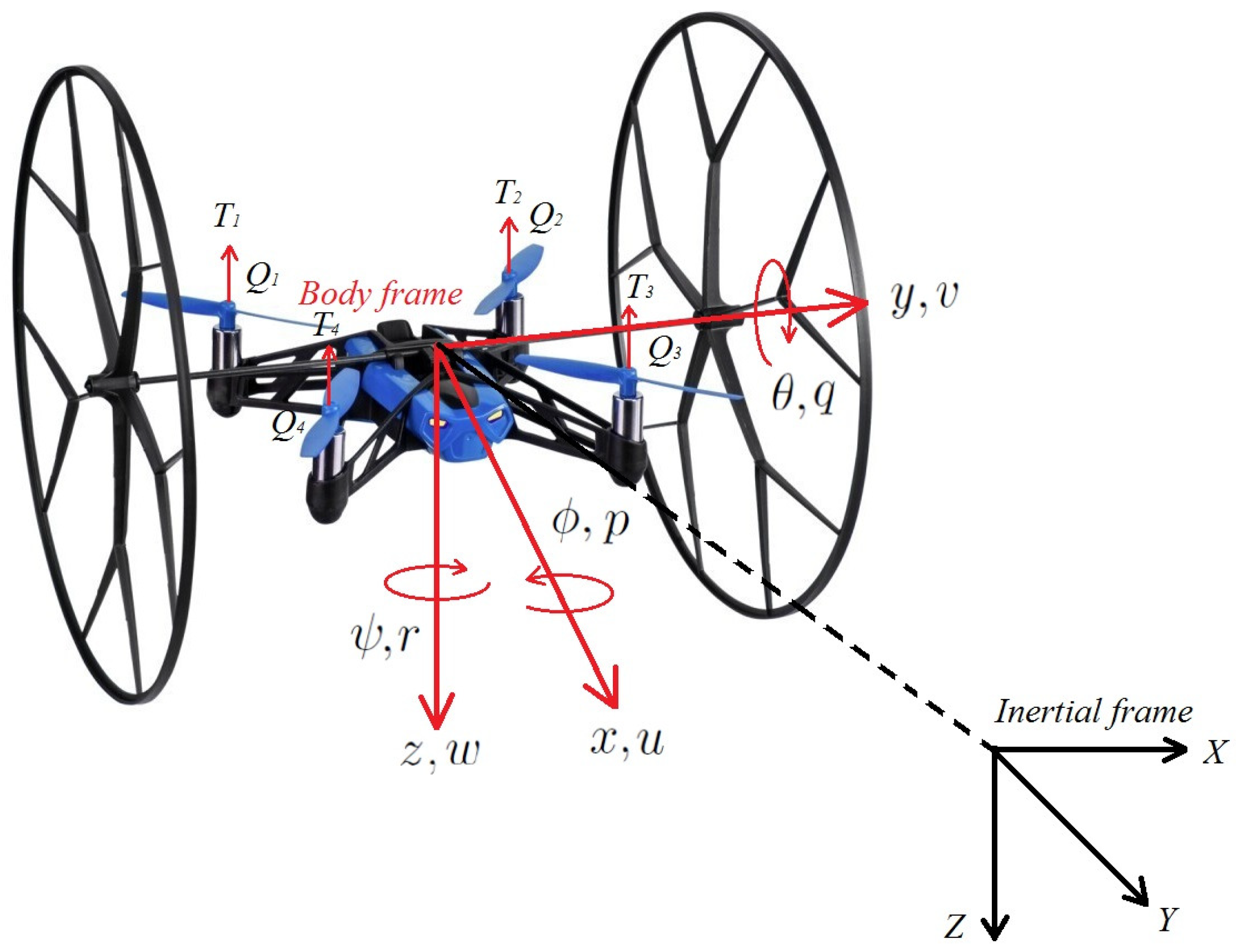
2. Mathematical Model
3. Embedded Flight Control Design
3.1. Actuated System
3.2. Underactuated System
3.3. Closed-Loop Stability
4. Simulation and Experimental Results
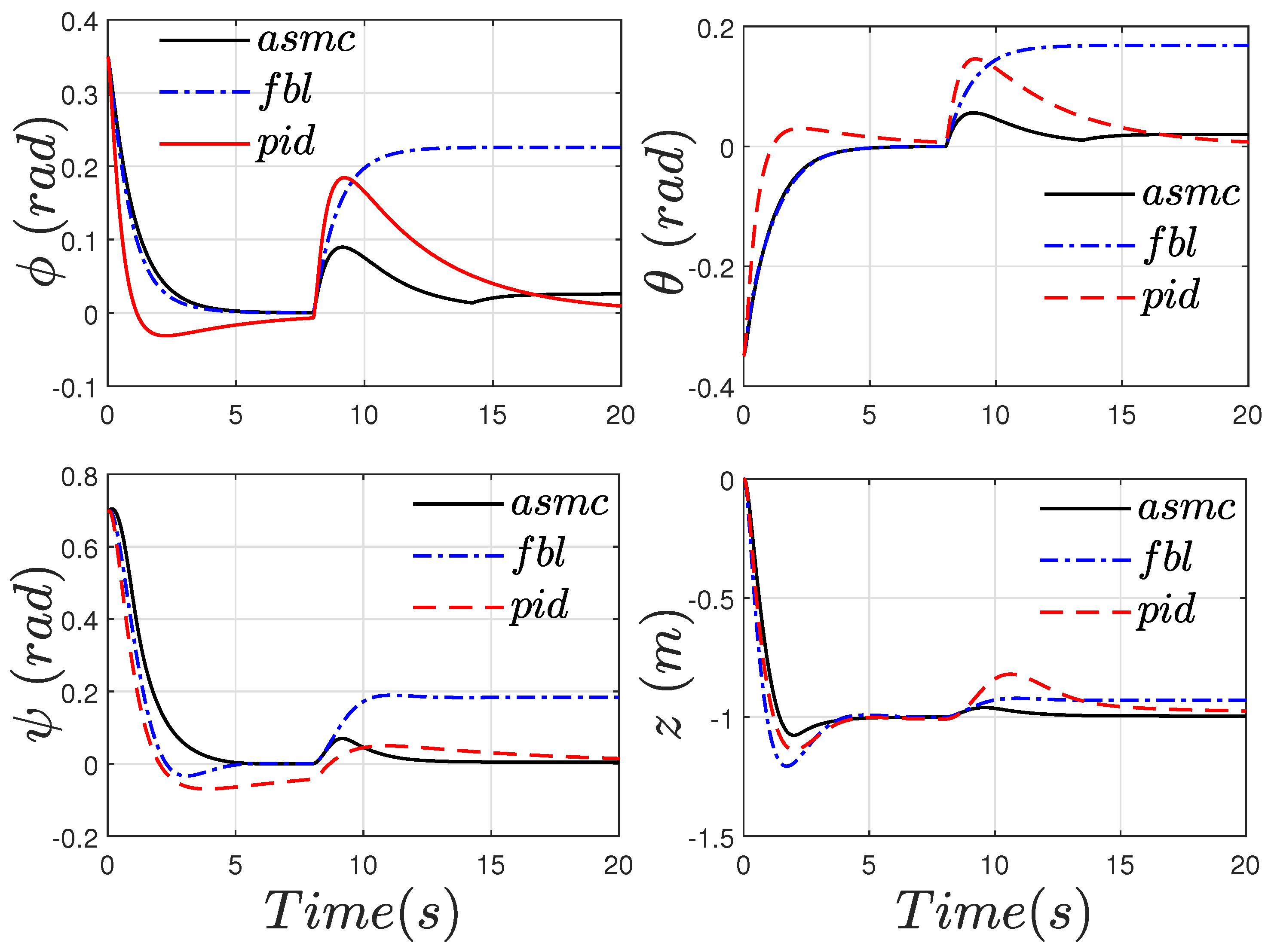
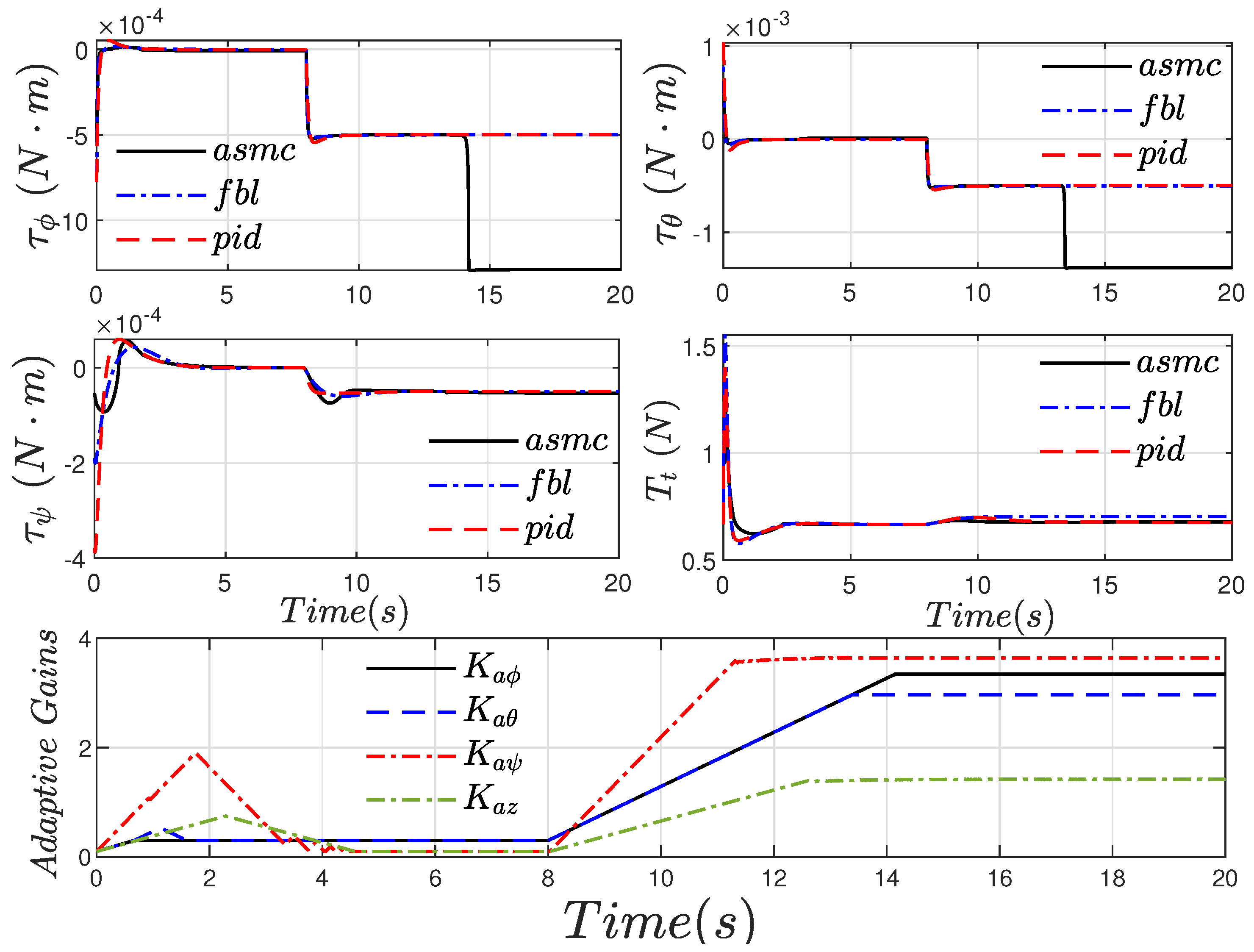
4.1. Simulation Results
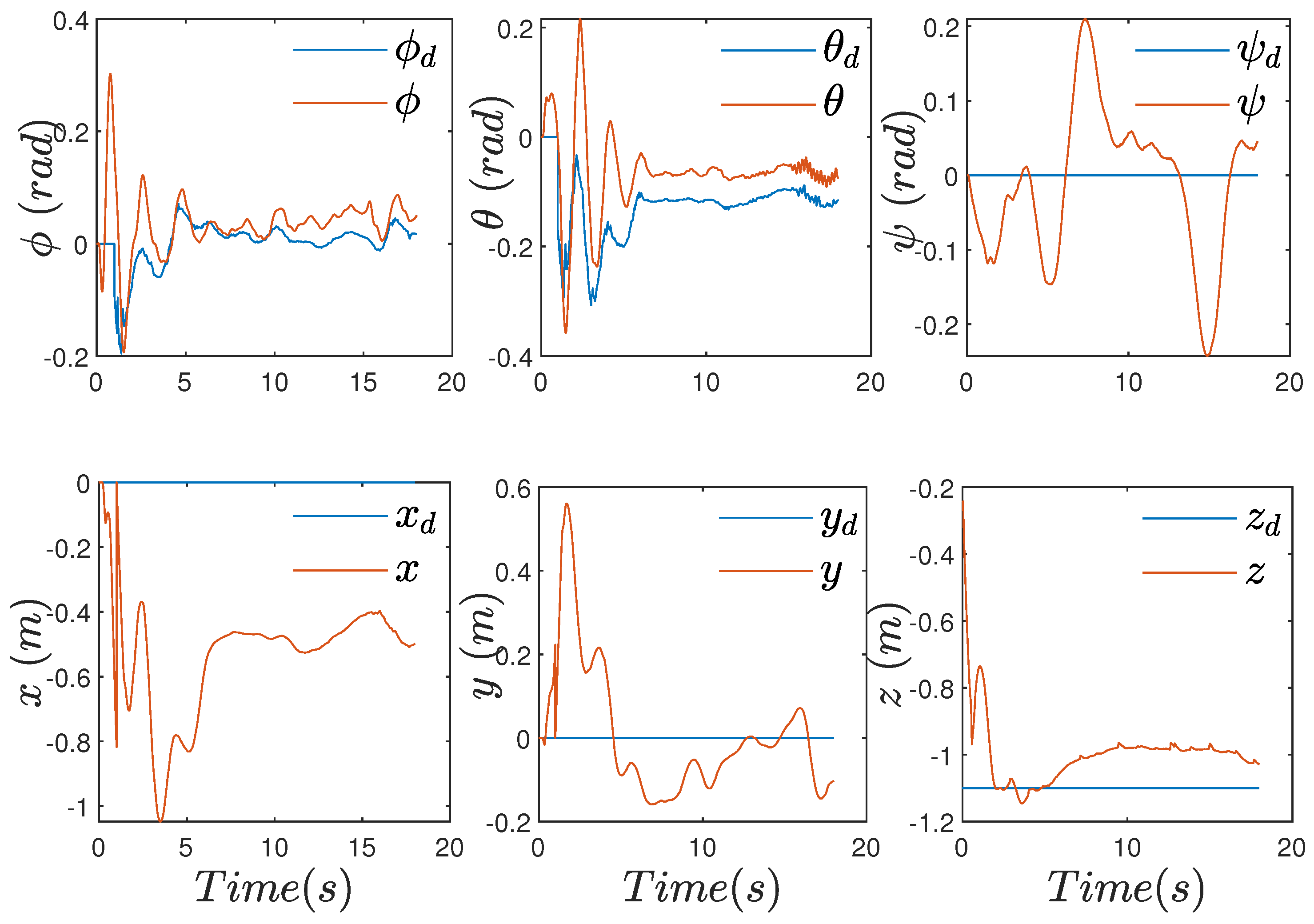
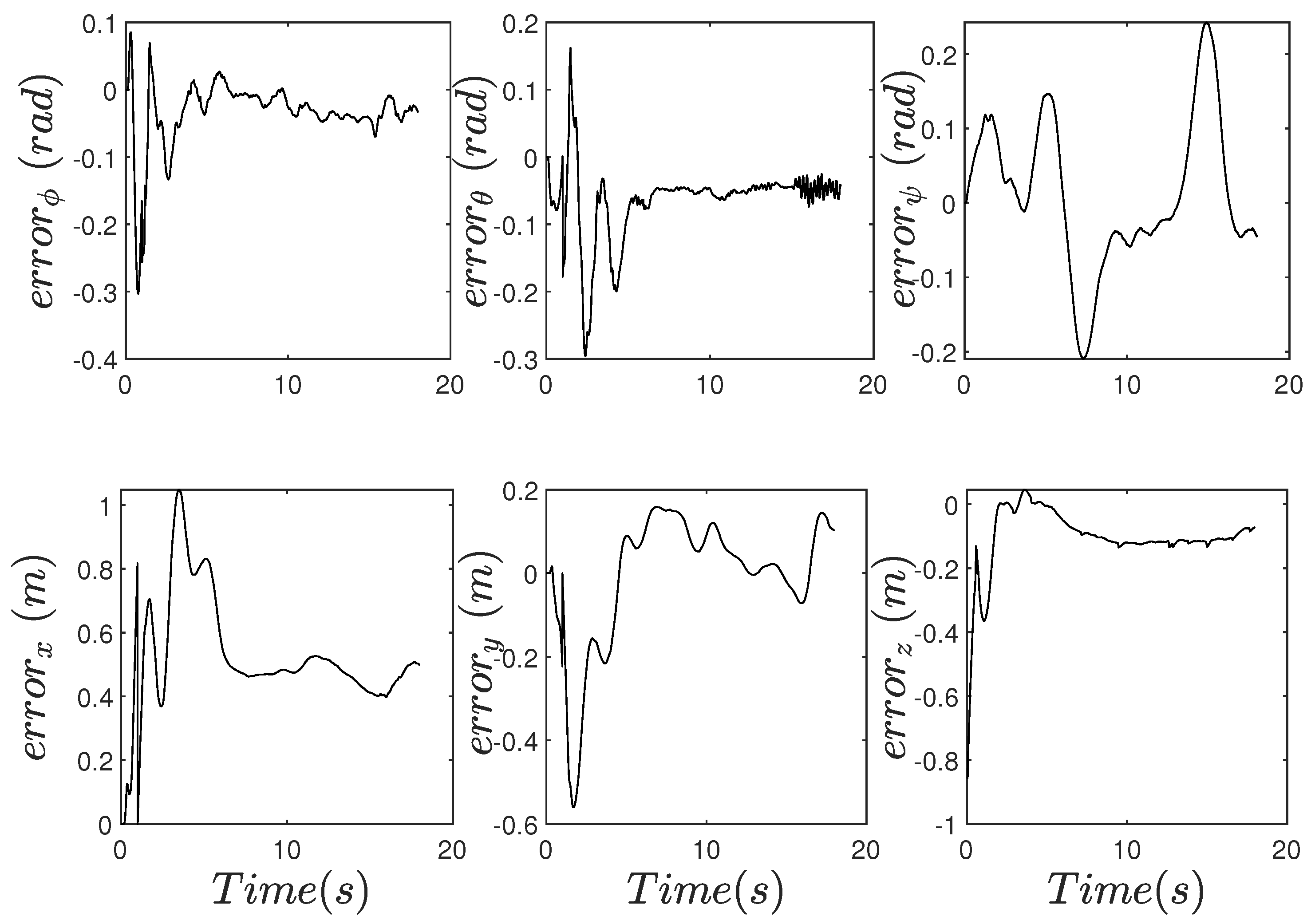
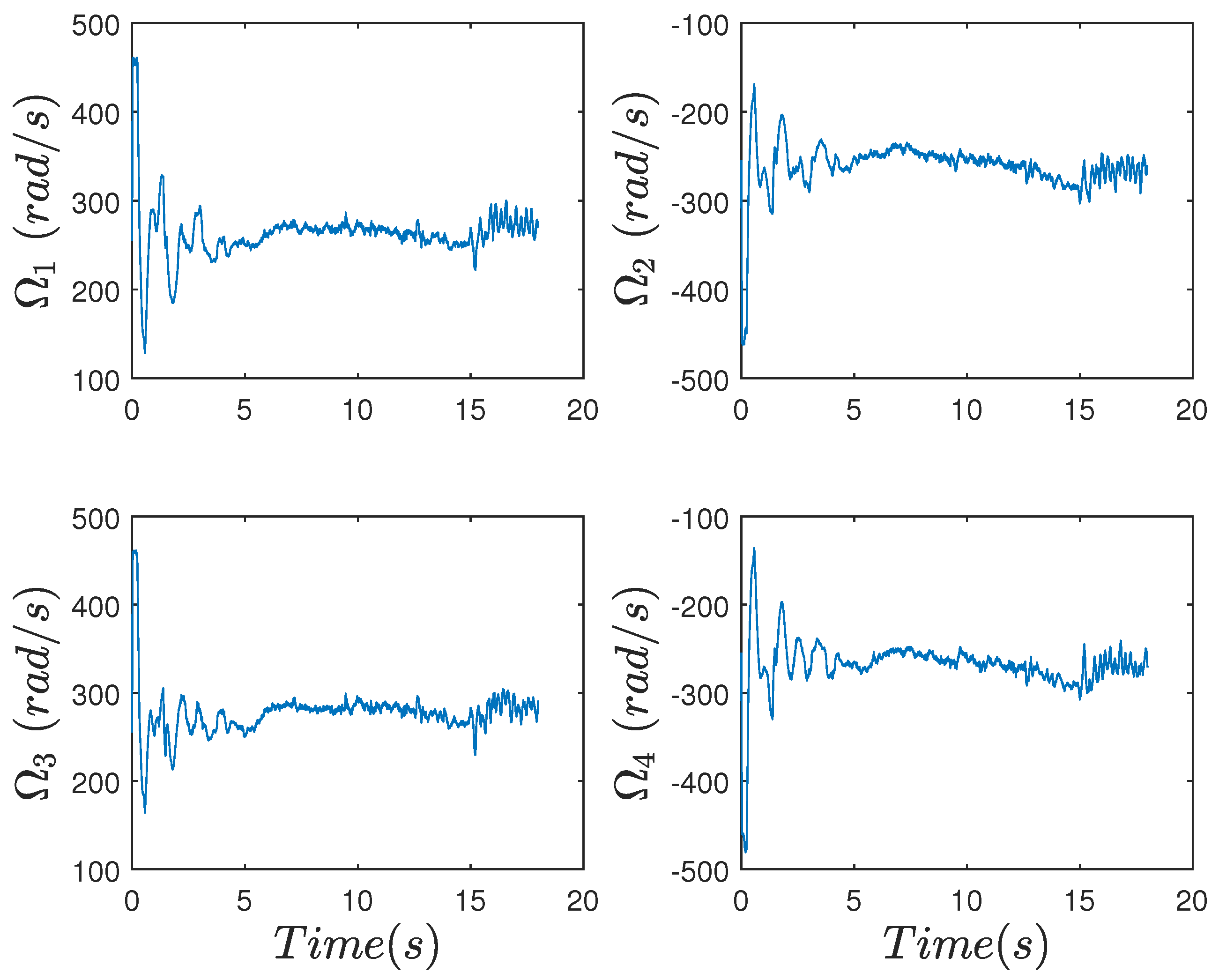
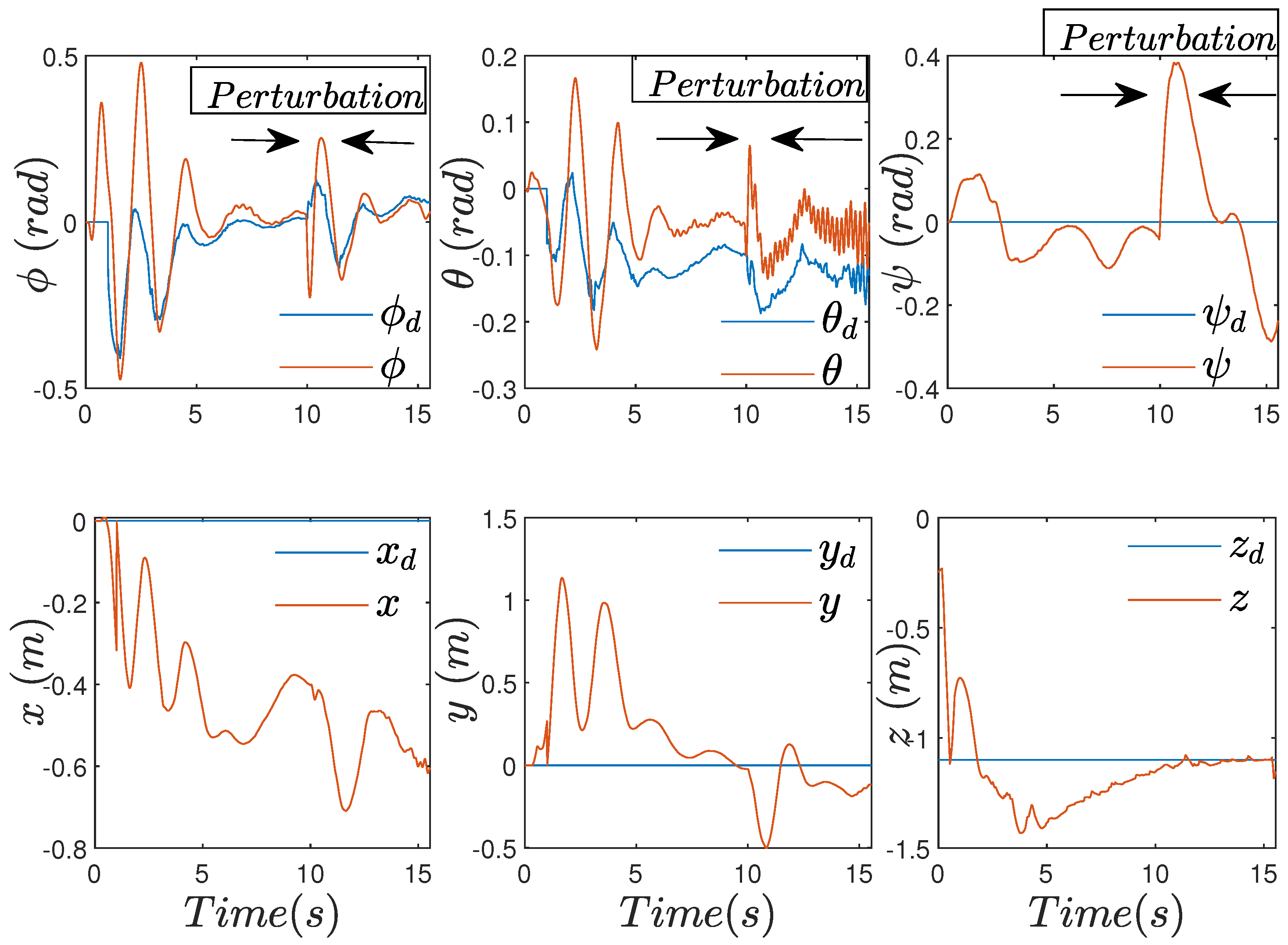
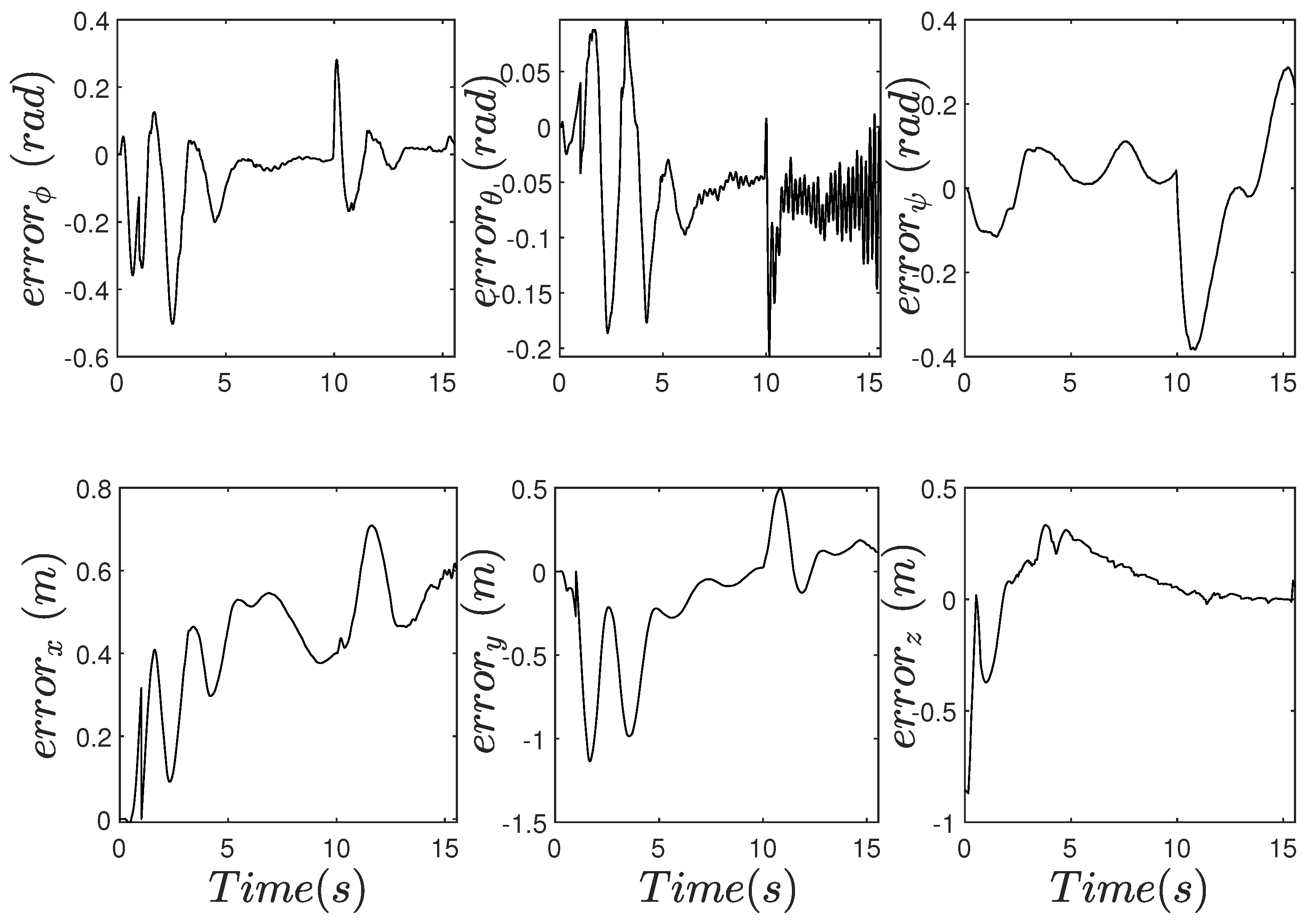
4.2. Experimental Results
4.2.1. Case without Perturbations
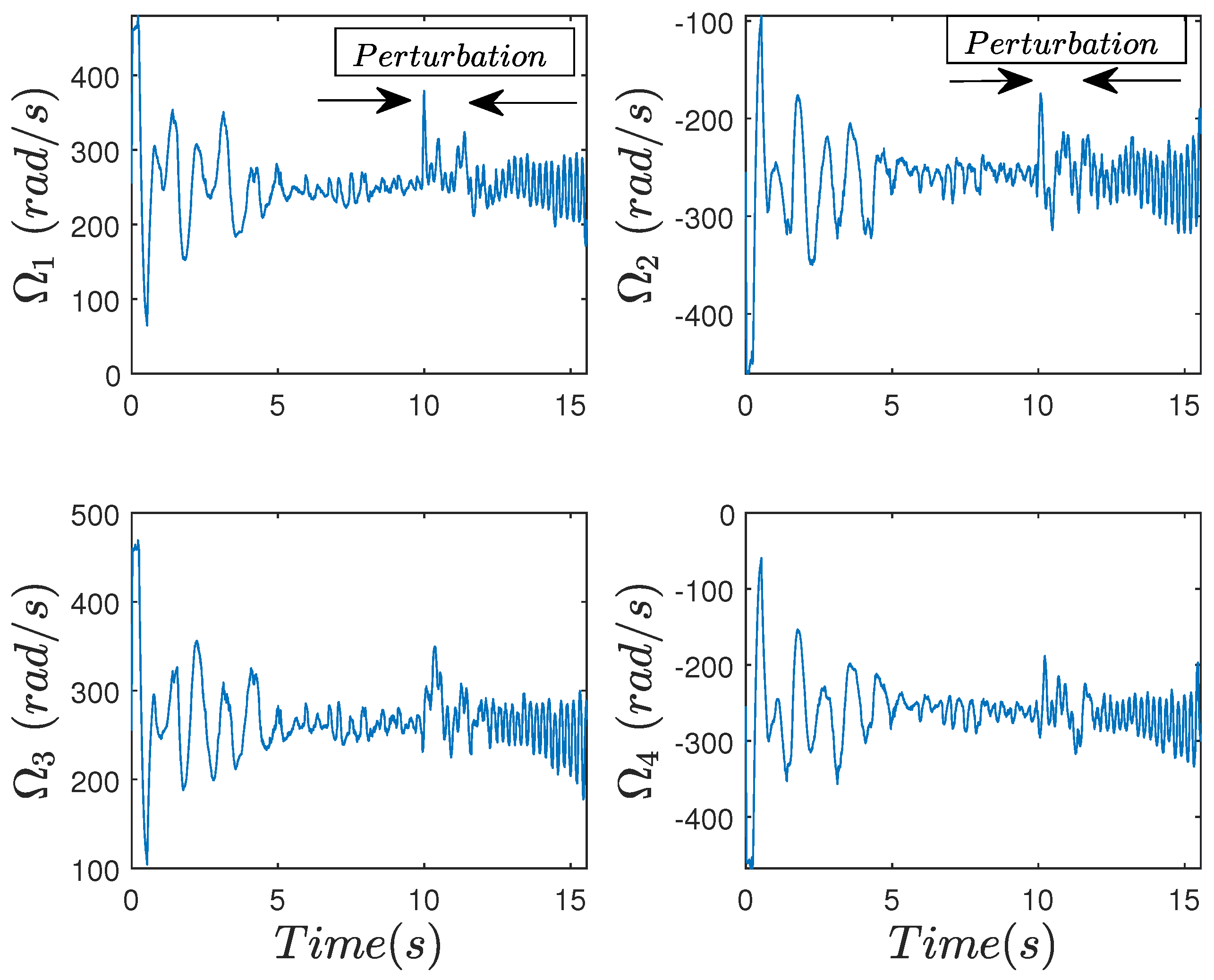
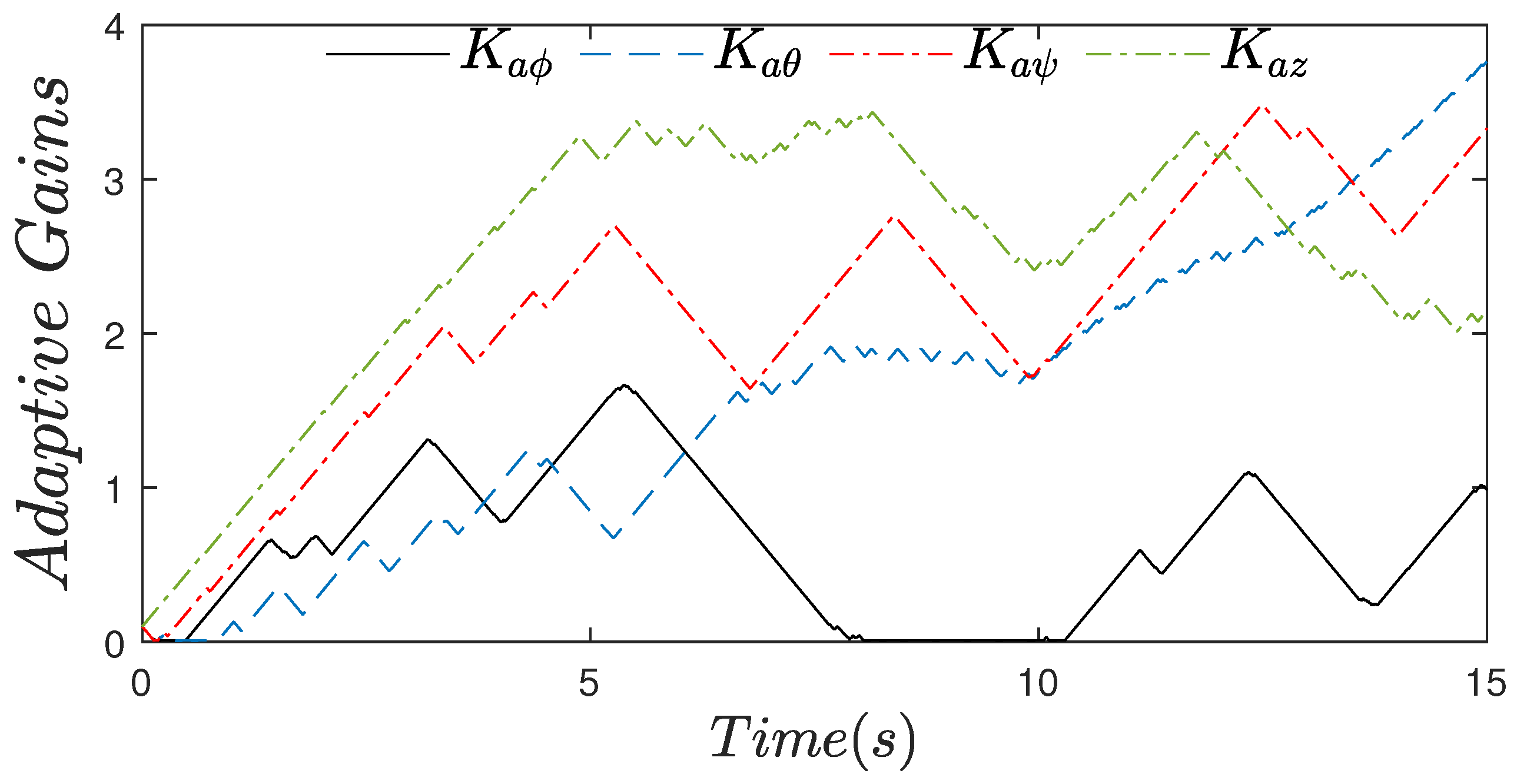
4.2.2. Case with Perturbations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MAV | Micro Air Vehicle |
| UAV | Unmanned Aerial Vehicle |
| IMU | Inertial Measurement Unit |
References
- Cai, G.; Dias, J.; Seneviratne, L. Survey of Small-Scale Unmanned Aerial Vehicles: Recent Advances and Future Development Trends. Unmanned Syst. 2014, 2, 175–199. [Google Scholar] [CrossRef]
- Mathworks. Parrot Minidrones Support from Simulink. Available online: https://la.mathworks.com/hardware-support/parrot-minidrones.html (accessed on 14 June 2019).
- Available online: https://github.com/Parrot-Developers/RollingSpiderEdu (accessed on 14 June 2019).
- Dydek, Z.T.; Annaswamy, M.A.; Lavretsky, E. Adaptive Control of Quadrotor UAVs: A Design Trade Study With Flight Evaluations. IEEE Trans. Control Syst. Technol. 2013, 4, 1400–1406. [Google Scholar] [CrossRef]
- Mohd Basri, M.A.; Husain, A.R.; Danapalasingam, K.A. Enhanced Backstepping Controller Design with Application to Autonomous Quadrotor Unmanned Aerial Vehicle. J. Intell. Robot. Syst. 2015, 79, 295–321. [Google Scholar] [CrossRef]
- Satici, A.C.; Poonawala, H.; Spong, M.W. Robust Optimal Control of Quadrotor UAVs. IEEE Access 2013, 1, 79–93. [Google Scholar] [CrossRef]
- Gautam, D.; Ha, C. Control of a quadrotor using a smart self-tuning fuzzy PID controller. Int. J. Adv. Robot. Syst. 2013, 10, 1–9. [Google Scholar] [CrossRef]
- Guo, Y.; Jiang, B.; Zhang, Y. A novel robuts attitude control for quadrotor aircraft subject to actuator faults and wind gusts. IEEE/CAA J. Autom. Sin. 2018, 1, 292–300. [Google Scholar] [CrossRef]
- Xiong, J.; Zhang, G. Global fast dynamical terminal sliding mode control for a quadrotor UAV. ISA Trans. 2017, 66, 233–240. [Google Scholar] [CrossRef]
- Xiong, J.; Zheng, E. Position and attitude tracking control for a quadrotor UAV. ISA Trans. 2014, 53, 725–731. [Google Scholar] [CrossRef]
- Zheng, E.; Xiong, J.; Luo, J. Second order sliding mode control for a quadrotor UAV. ISA Trans. 2014, 53, 1350–1356. [Google Scholar] [CrossRef]
- Besnard, L.; Shtessel, Y.; Landrum, B. Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer. J. Frankl. Inst. 2012, 349, 658–684. [Google Scholar] [CrossRef]
- Luque-Vega, L.; Castillo-Toledo, B.; Loukianov, A. Robust block second order sliding mode control for a quadrotor. J. Frankl. Inst. 2012, 349, 719–739. [Google Scholar] [CrossRef]
- Rida, M.; Cherki, B. A new robust control for minirotorcraft unmanned aerial vehicles. ISA Trans. 2014, 56, 86–101. [Google Scholar] [CrossRef]
- Ramirez-Rodriguez, H.; Parra-Vega, V.; Sanchez-Orta, A.; Garcia-Salazar, O. Robust Backstepping Control Based on Integral Sliding Modes for Tracking of Quadrotors. J. Intell. Robot. Syst. 2014, 73, 51–66. [Google Scholar] [CrossRef]
- Sumantri, B.; Uchiyama, N.; Sano, S. Generalized super-twisting sliding mode control with a nonlinear sliding surface for robust and energy-efficient controller of a quad-rotor helicopter. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 2042–2053. [Google Scholar] [CrossRef]
- Villanueva, A.; Castillo-Toledo, B.; Bayro-Corrochano, E.; Luque-Vega, L.; González-Jiménez, L.E. Multi-mode flight sliding mode control system for a Quadrotor. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015. [Google Scholar]
- Derafa, L.; Benallegue, A.; Fridman, L. Super twisting control algorithm for the attitude tracking of a four rotors UAV. J. Frankl. Inst. 2012, 349, 685–689. [Google Scholar] [CrossRef]
- Rajappa, S.; Masone, C.; Bulthoff, H.H.; Stegagno, P. Adaptive Super Twisting Controller for a Quadrotor UAV. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016. [Google Scholar]
- Castañeda, H.; Gordillo, J.L. Spatial Modeling and Robust Flight Control Based on Adaptive Sliding Mode Approach for a Quadrotor MAV. Int. J. Intell. Robot. Syst. 2019, 93, 101–111. [Google Scholar] [CrossRef]
- Valavanis, K.P.; Vachtsevanos, G.V. Handbook of Unmanned Aerial Vehicles, 1st ed.; Springer: Dordrecht, The Netherlands, 2015. [Google Scholar]
- Haifeng, L. Multivariable Control of a Rolling Spider Drone. Master’s Thesis, University of Rhode Island, Kingston, RI, USA, 2017. Paper 1064. Available online: http://digitalcommons.uri.edu/theses/1064 (accessed on 14 June 2019).

| Parameter | Value | Unit |
|---|---|---|
| Weight m | kg | |
| Arm length l | m | |
| Gravity g | m/s | |
| Inertia moment | kgm | |
| Inertia moment | kgm | |
| Inertia moment | kgm | |
| Thrust coefficient | N/(rad/s) | |
| Torque coefficient | Nm/(rad/s) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castañeda, H.; Gordillo, J.L. Embedded Flight Control Based on Adaptive Sliding Mode Strategy for a Quadrotor Micro Air Vehicle. Electronics 2019, 8, 793. https://doi.org/10.3390/electronics8070793
Castañeda H, Gordillo JL. Embedded Flight Control Based on Adaptive Sliding Mode Strategy for a Quadrotor Micro Air Vehicle. Electronics. 2019; 8(7):793. https://doi.org/10.3390/electronics8070793
Chicago/Turabian StyleCastañeda, Herman, and J.L. Gordillo. 2019. "Embedded Flight Control Based on Adaptive Sliding Mode Strategy for a Quadrotor Micro Air Vehicle" Electronics 8, no. 7: 793. https://doi.org/10.3390/electronics8070793
APA StyleCastañeda, H., & Gordillo, J. L. (2019). Embedded Flight Control Based on Adaptive Sliding Mode Strategy for a Quadrotor Micro Air Vehicle. Electronics, 8(7), 793. https://doi.org/10.3390/electronics8070793





