A Surface-Potential-Based Analytical I-V Model of Full-Depletion Single-Gate SOI MOSFETs
Abstract
:1. Introduction
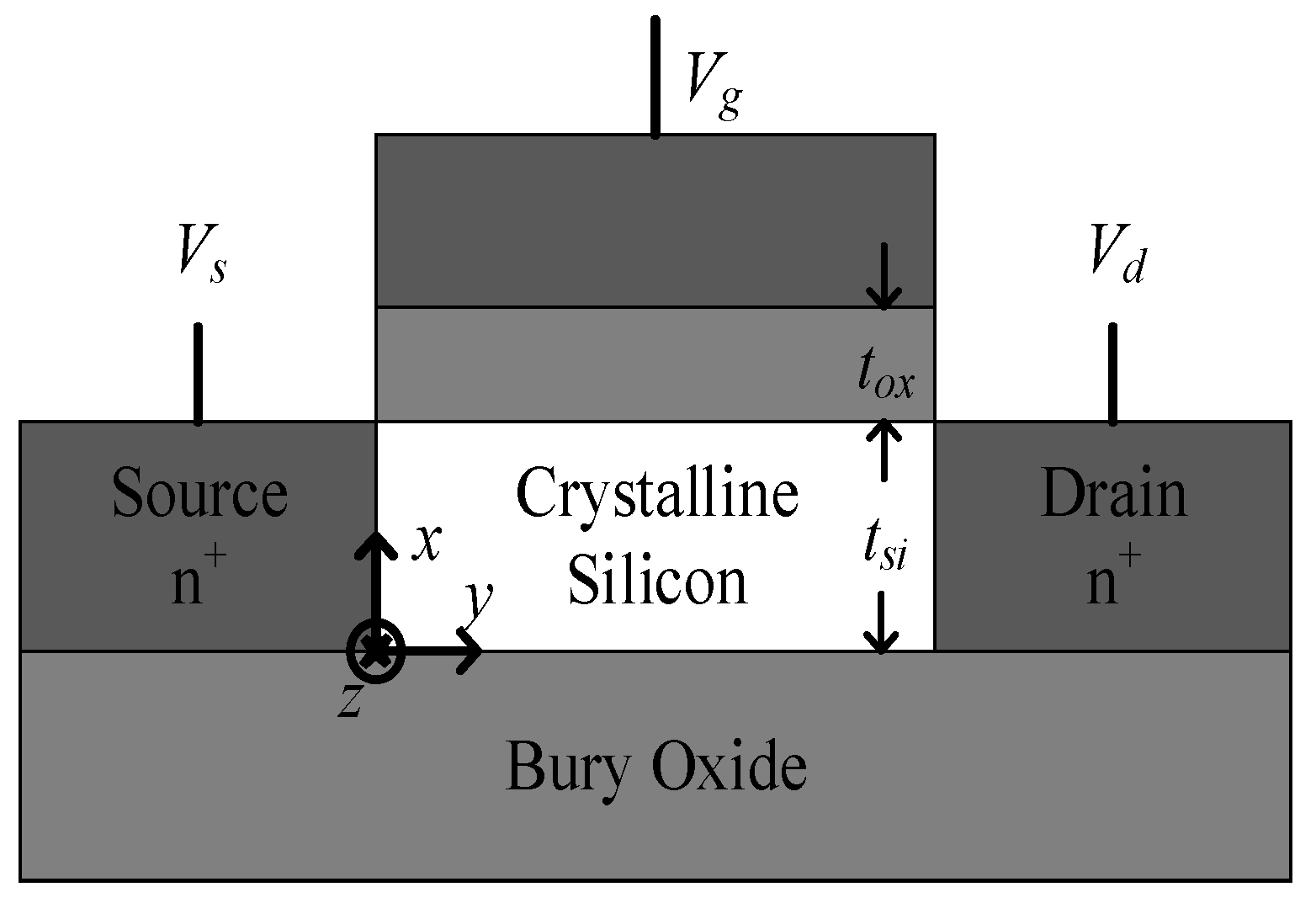
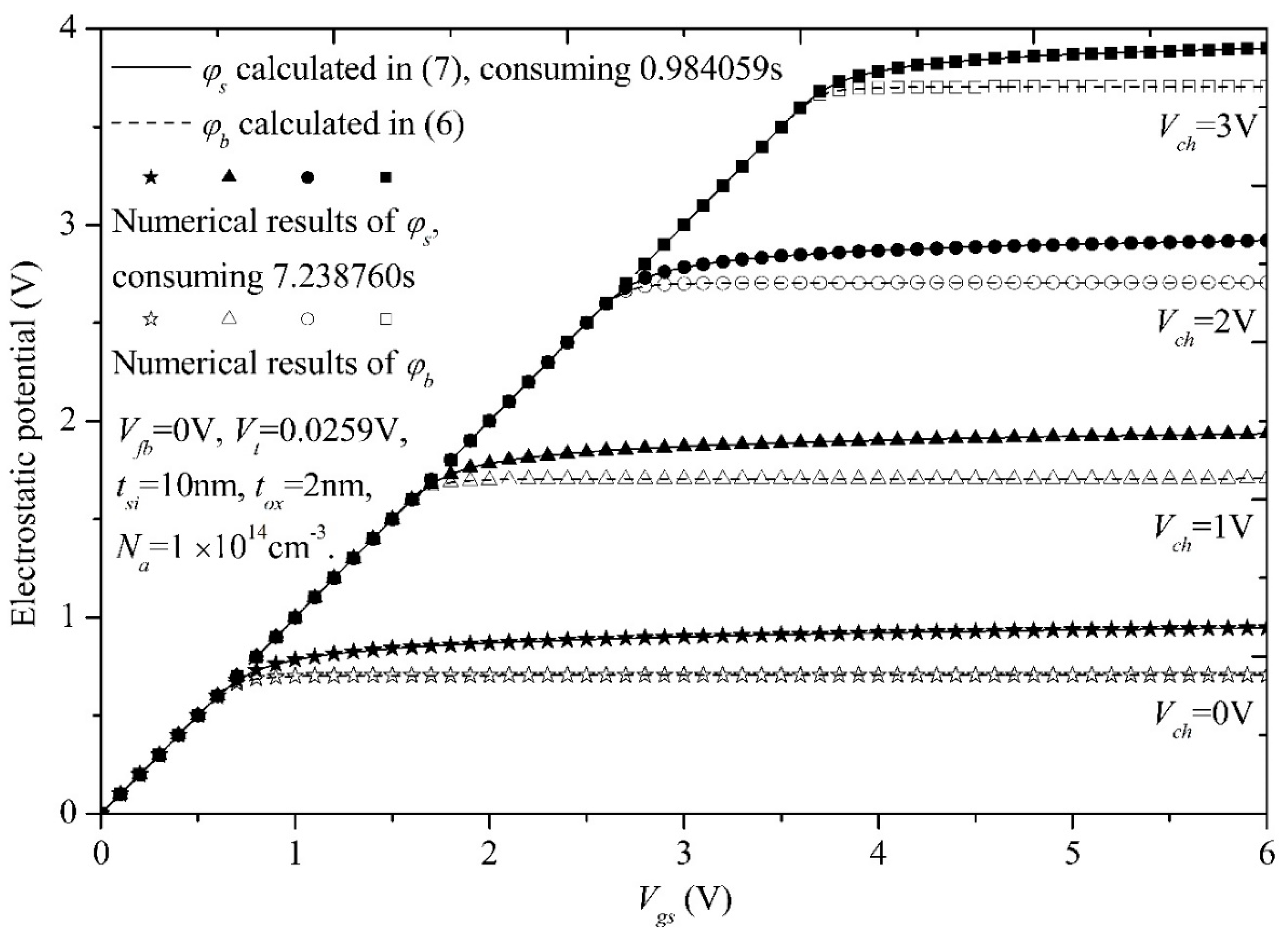
2. Surface Potential Explicit Calculation Scheme
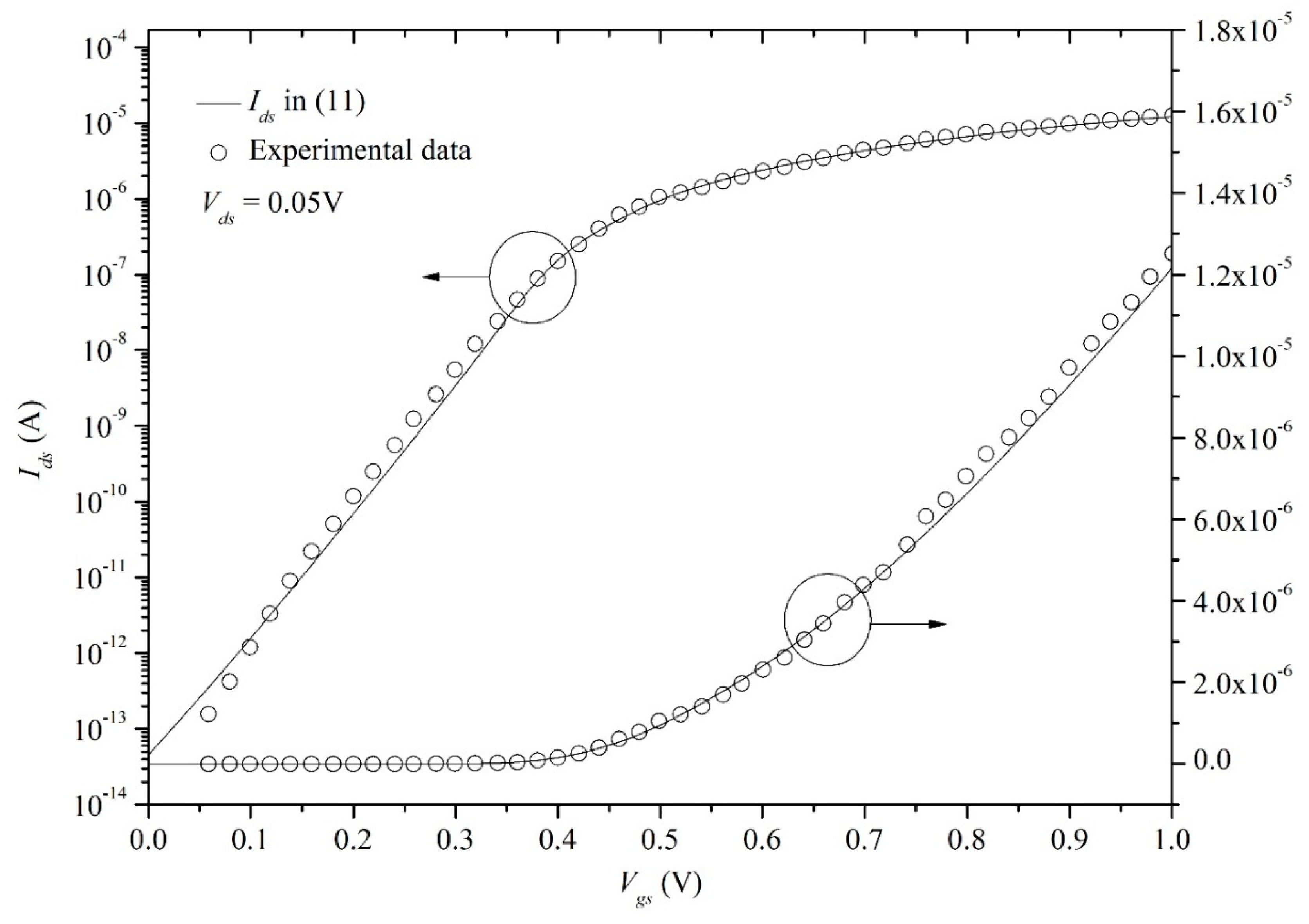
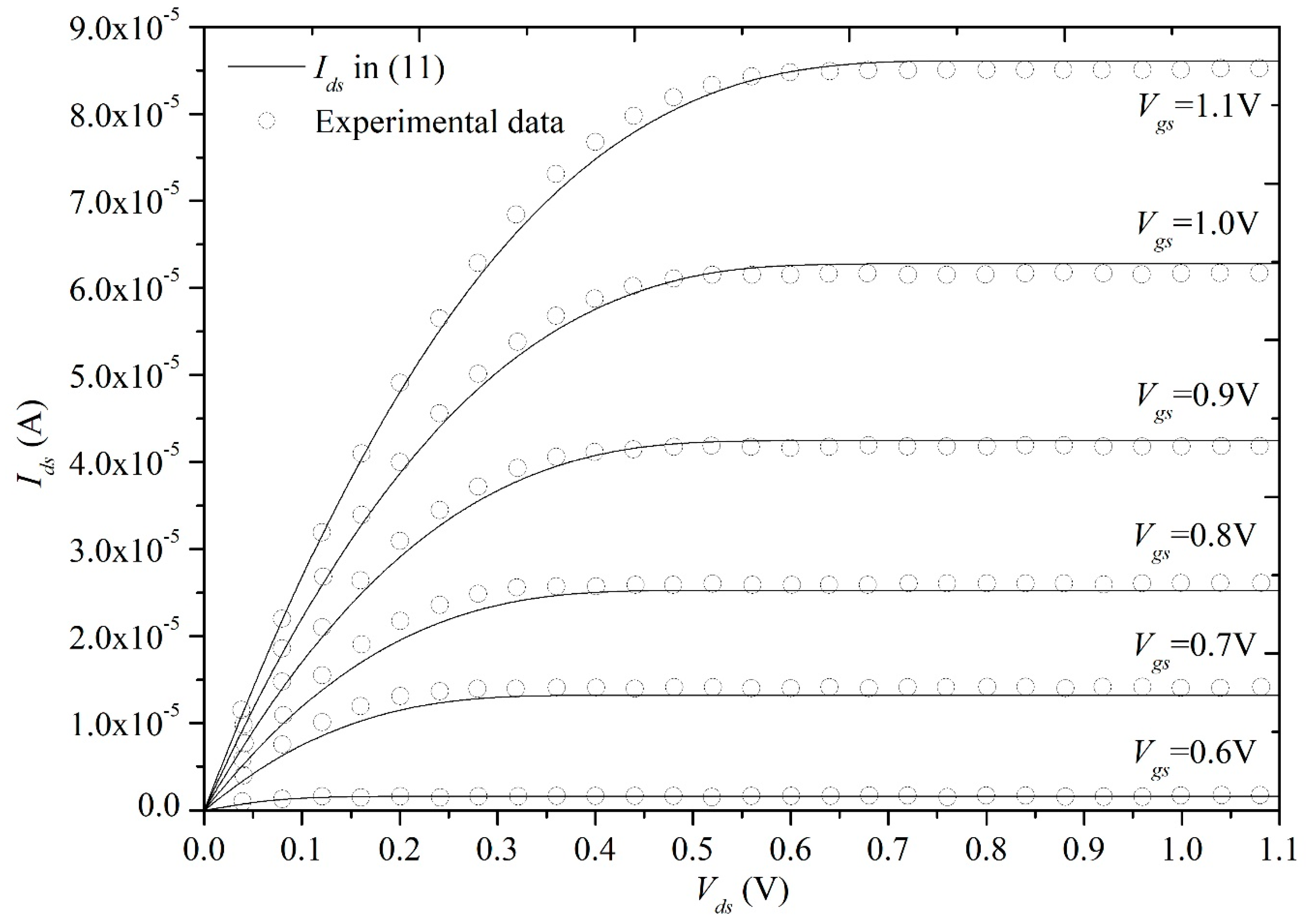
3. Analytical I-V Model
4. Discussion
- The thickness tox of dielectric between gate and channel rightly determines the ability of inducing charges, particularly for the strong inversion region, as shown in Figure 8. We can observe that φs increases as tox decreases. Thin tox leads to larger Cox, and then, according to the Gauss’s law, many more free charges are introduced in the strong inversion region. It means that larger φs and Ids can be obtained in the channel.
- The thickness tsi of the channel film can influence φb but not φs. According to Figure 9, tsi is larger and φb becomes larger. It is implied by the simplified Poisson’s equation (1) only including the doping concentration. Simultaneously, Ids is affected by tsi lightly, because the free charges in the inversion layers are confined to a very thin layer with the order of 10–100Å [30]. That is also shown in Figure 9, graphed by our model.
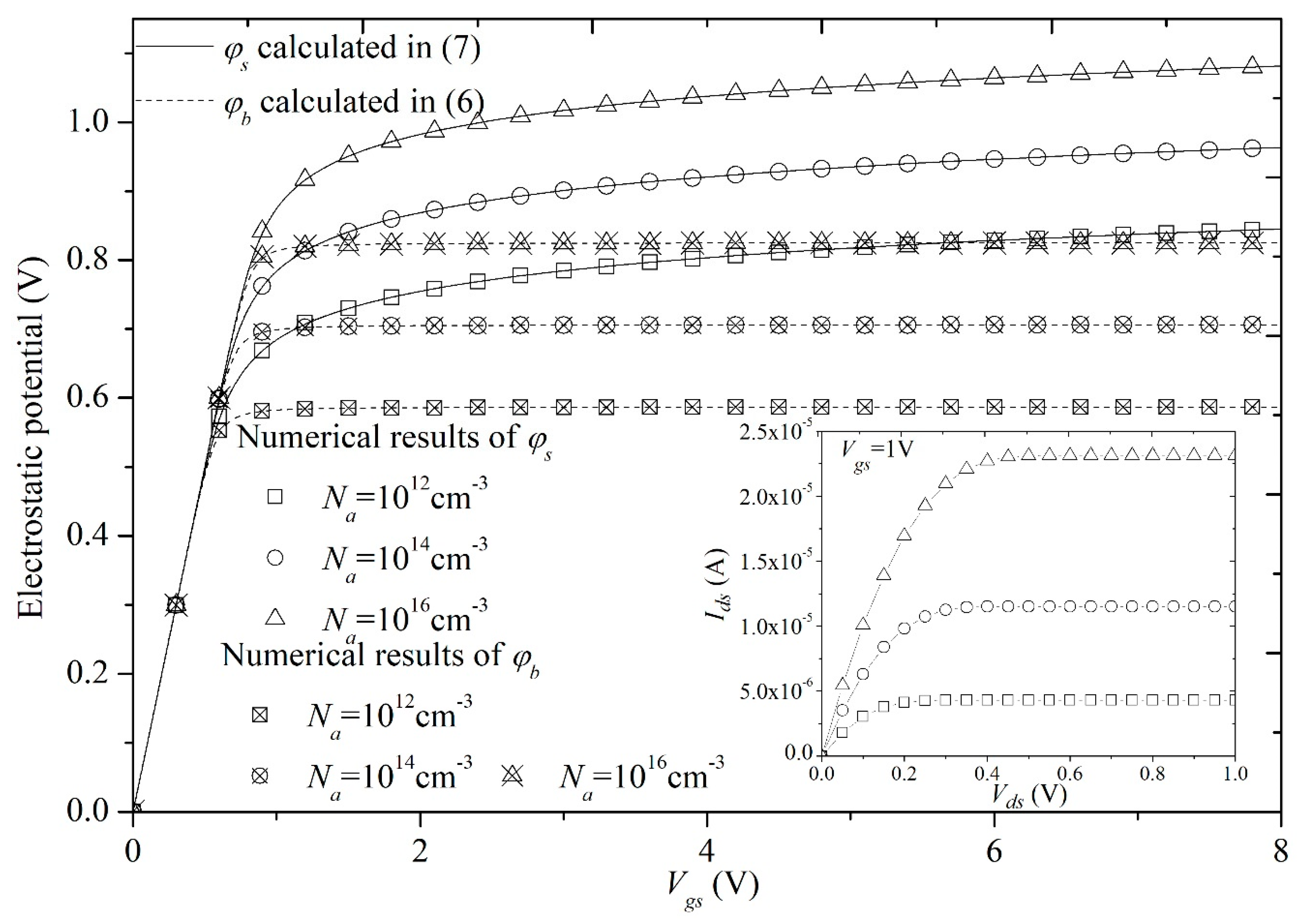
- Finally, we can observe from Figure 10 that φs, φb, and Ids are in positive correlation with the doping concentration Na, because Na directly decides the value of the free charge density.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Karatsori, T.A.; Theodorou, C.G.; Josse, E.; Dimitriadis, C.A.; GHibaudo, G. All Operation Region Characterization and Modeling of Drain and Gate Current Mismatch in 14-nm Fully Depleted SOI MOSFETs. IEEE Trans. Electron Dev. 2017, 64, 2080–2085. [Google Scholar] [CrossRef]
- Pereira, A.S.N.; Steel, G.D.; Planes, N.; Haond, M.; Giacomini, R.; Flandre, D.; Kilchytska, V. An in-depth analysis of temperature effect on DIBL in UTBB FD SOI MOSFETs based on experimental data, numerical simulations and analytical models. Solid State Electron. 2017, 128, 67–71. [Google Scholar] [CrossRef]
- Bong, J.H.; Kim, S.Y.; Jeong, C.B.; Chang, K.S.; Hwang, W.S.; Cho, B.J. Reliability improvement of a flexible FDSOI MOSFET via heat management. Appl. Phys. Lett. 2017, 110, 252101. [Google Scholar] [CrossRef]
- Amor, S.; Andre, N.; Gerard, P.; Ali, S.Z.; Udrea, F.; Tounsi, F.; Mezghani, B.; Francis, L.A.; Flandre, D. Reliable characteristics and stabilization of on-membrane SOI MOSFET-based components heated up to 335 degrees C. Semicond. Sci. Technol. 2017, 32, 014001. [Google Scholar] [CrossRef]
- Agrawal, N.; Kimura, Y.; Arghavani, R.; Datta, S. Impact of Transistor Architecture (Bulk Planar, Trigate on Bulk, Ultrathin-Body Planar SOI) and Material (Silicon or III-V Semiconductor) on Variation for Logic and SRAM Applications. IEEE Trans. Electron Dev. 2013, 60, 3298–3304. [Google Scholar] [CrossRef]
- Balteanu, A.; Sarkas, I.; Dacquay, E.; Tomkins, A.; Rebeiz, G.M.; Asbeck, P.M.; Voinigescu, S.P. A 2-Bit, 24 dBm, Millimeter-Wave SOI CMOS Power-DAC Cell for Watt-Level High-Efficiency, Fully Digital m-ary QAM Transmitters. IEEE J. Solid State Circ. 2013, 48, 1126–1137. [Google Scholar] [CrossRef]
- BSIM6 Technical Manual. Available online: http://www-device.eecs.berkeley.edu/bsim/.
- Enz, C.C.; Krummenacher, F.; Vittoz, E.A. An analytical MOS transistor model valid in all regions of operation and dedicated to lowvoltage and low-current applications. Anal. Integr. Circ. Signal Process 1995, 8, 83–114. [Google Scholar] [CrossRef]
- Scholten, A.; Smit, G.D.J.; Vries, B.D.; Tiemeijer, L.; Croon, J.; Klaassen, D.B.M.; Langevelde, R.V.; Li, X.; Wu, W.; Gildenblat, G. The new CMC standard compact MOS model PSP: Advantages for RF applications. IEEE J. Solid State Circ. 2009, 44, 1415–1424. [Google Scholar] [CrossRef]
- Miura-Mattausch, M.; Sadachika, N.; Navarro, D.; Suzuki, G.; Takeda, Y.; Miyake, M.; Warabino, T.; Mizukane, Y.; Inagaki, R.; Ezaki, T.; et al. HiSIM2: Advanced MOSFET model valid for RF circuit simulation. IEEE Trans. Electron Dev. 2006, 9, 1994–2007. [Google Scholar] [CrossRef]
- He, J.; Chan, M.; Zhang, X.; Wang, Y. A Physics-Based Analytic Solution to the MOSFET Surface Potential from Accumulation to Strong-Inversion Region. IEEE Trans. Electron Dev. 2006, 9, 2008–2016. [Google Scholar] [CrossRef]
- Ortiz-Conde, A.; García-Sánchez, F.J.; Muci, J.; Malobabic, S.; Liou, J.J. A Review of Core Compact Models for Undoped Double-Gate SOI MOSFETs. IEEE Trans. Electron Dev. 2007, 54, 131–140. [Google Scholar] [CrossRef]
- Soon, J.; Yu, B.; Yu, Y.; Taur, Y. A Review on Compact Modeling of Multiple-Gate MOSFETs. IEEE Trans. Circ. Syst. I Reg. Pap. 2009, 56, 1858–1869. [Google Scholar]
- Iniguez, B.; Jimenez, D.; Roig, J.; Hamid, H.A.; Marsal, L.F.; Pallares, J. Explicit continuous model for long-channel undoped surrounding gate MOSFETs. IEEE Trans. Electron Dev. 2005, 52, 1868–1873. [Google Scholar] [CrossRef]
- Duarte, J.; Choi, S.; Moon, D.; Ahn, J.; Kim, J.; Kim, S.; Choi, Y. A Universal Core Model for Multiple-Gate Field-Effect Transistors. Part II: Drain Current Model. IEEE Trans. Electron Dev. 2013, 60, 848–855. [Google Scholar] [CrossRef]
- Ravariu, C.; Rusu, A.; Ravariu, F.; Dobrescu, D.; Dobrescu, L. The threshold voltage model of a SOI-MOSFET on films with Gaussian profile. In Proceedings of the 3rd IEEE International Caracas Conference on Devices, Circuits and Systems, Cancun, Mexico, 15–17 March 2000; pp. D64/1–D64/5. [Google Scholar]
- Pandey, P.; Pal, B.B.; Jit, S. A new 2-D model for the potential distribution and threshold voltage of fully depleted short-channel Si-SOI MESFETs. IEEE Trans. Electron Dev. 2004, 51, 246–254. [Google Scholar] [CrossRef]
- Miura-Mattausch, M.; Feldmann, U.; Fukunaga, Y.; Miyake, M.; Kikuchihara, H.; Ueno, F.; Mattausch, H.J.; Nakagawa, T.; Sugii, N. Compact Modeling of SOI MOSFETs With Ultrathin Silicon and BOX Layers. IEEE Trans. Electron Dev. 2014, 61, 255–265. [Google Scholar] [CrossRef]
- Wu, W.; Yao, W.; Gildenblat, G. Surface-potential-based compact modeling of dynamically depleted SOI MOSFETs. Solid State Electron. 2010, 54, 595–604. [Google Scholar] [CrossRef]
- Yu, Y.S.; Kim, S.H.; Hwang, S.W.; Ahn, D. All-analytic surface potential model for SOI MOSFETs. IEE Proc. Circ. Dev. Syst. 2005, 152, 183–188. [Google Scholar] [CrossRef]
- Huang, J.; Deng, W.; Ma, X.; Ning, T. Surface Potential Calculation for Dynamic-Depletion Polysilicon TFTs with Both Gaussian and Exponential DOS Distribution. IEEE Electron Dev. Lett. 2013, 34, 774–776. [Google Scholar] [CrossRef]
- Khandelwal, S.; Chauhan, Y.S.; Lu, D.D.; Venugopalan, S.; Karim, M.A.U.; Sachid, A.B.; Nguyen, B.Y.; Rozeau, O.; Faynot, O.; Niknejad, A.M.; et al. BSIM-IMG: A Compact Model for Ultrathin-Body SOI MOSFETs With Back-Gate Control. IEEE Trans. Electron Dev. 2012, 59, 2019–2026. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On Lambert’s W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Yu, F.; Deng, W.; Huang, J.; Ma, X.; Chen, S. An Explicit Physics-Based I-V Model for Surrounding-Gate Polysilicon Transistors. IEEE Trans. Electron Dev. 2016, 63, 1059–1065. [Google Scholar] [CrossRef]
- Brews, J.R. A charge sheet model of the MOSFET. Solid State Electron. 1978, 21, 345–355. [Google Scholar] [CrossRef]
- Takagi, S.; Iwase, M.; Toriumi, A. On universality of inversion-layer mobility in n- and p-channel MOSFETs. In Proceedings of the Technical Digest., International Electron Devices Meeting, San Francisco, CA, USA, USA, 11–14 December 1988. [Google Scholar]
- Huang, C.L.; Gildenblat, G.S. Measurements and modeling of the n-channel MOSFET inversion layer mobility and device characteristics in the temperature range 60–300K. IEEE Trans. Electron Dev. 1990, 37, 1289–1300. [Google Scholar] [CrossRef]
- Yeric, G.M.; Tasch, A.F. A universal MOSFET mobility degradation model for circuit simulation. IEEE Trans. Comput. Aided Des. 1990, CAD-9, 1123–1126. [Google Scholar]
- Park, H.J.; Ko, P.K.; Hu, C. A charge sheet capacitance model of short channel MOSFETs for SPICE. IEEE Trans. Comput. Aided Des. Integr. Circ. Syst. 1991, 10, 376–389. [Google Scholar] [CrossRef]
- Arora, N. MOSFET Models for VLSI Circuit Simulation: Theory and Practice, in Shrewsbury, 1st ed.; Springer: New York, NY, USA, 1993. [Google Scholar]

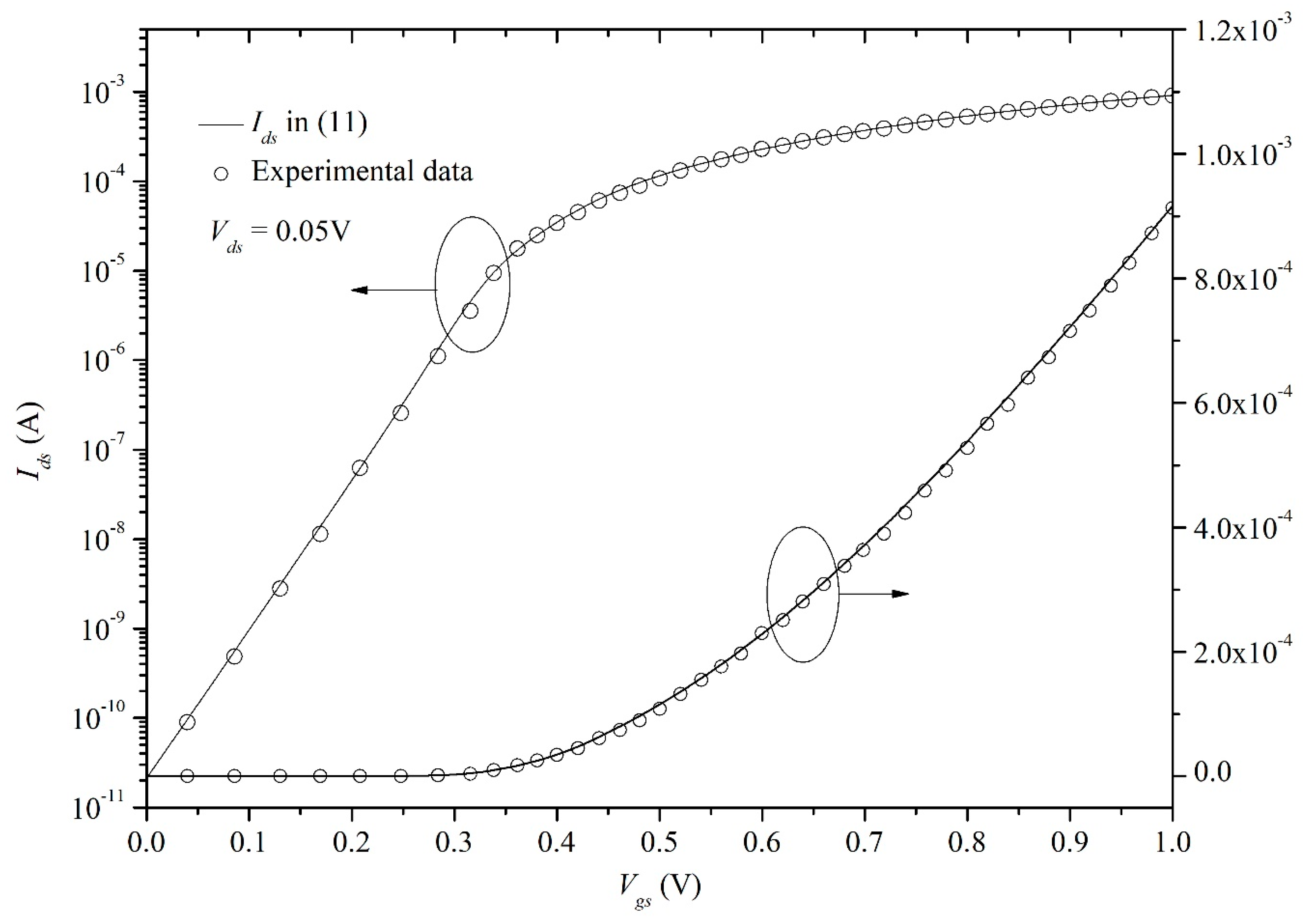
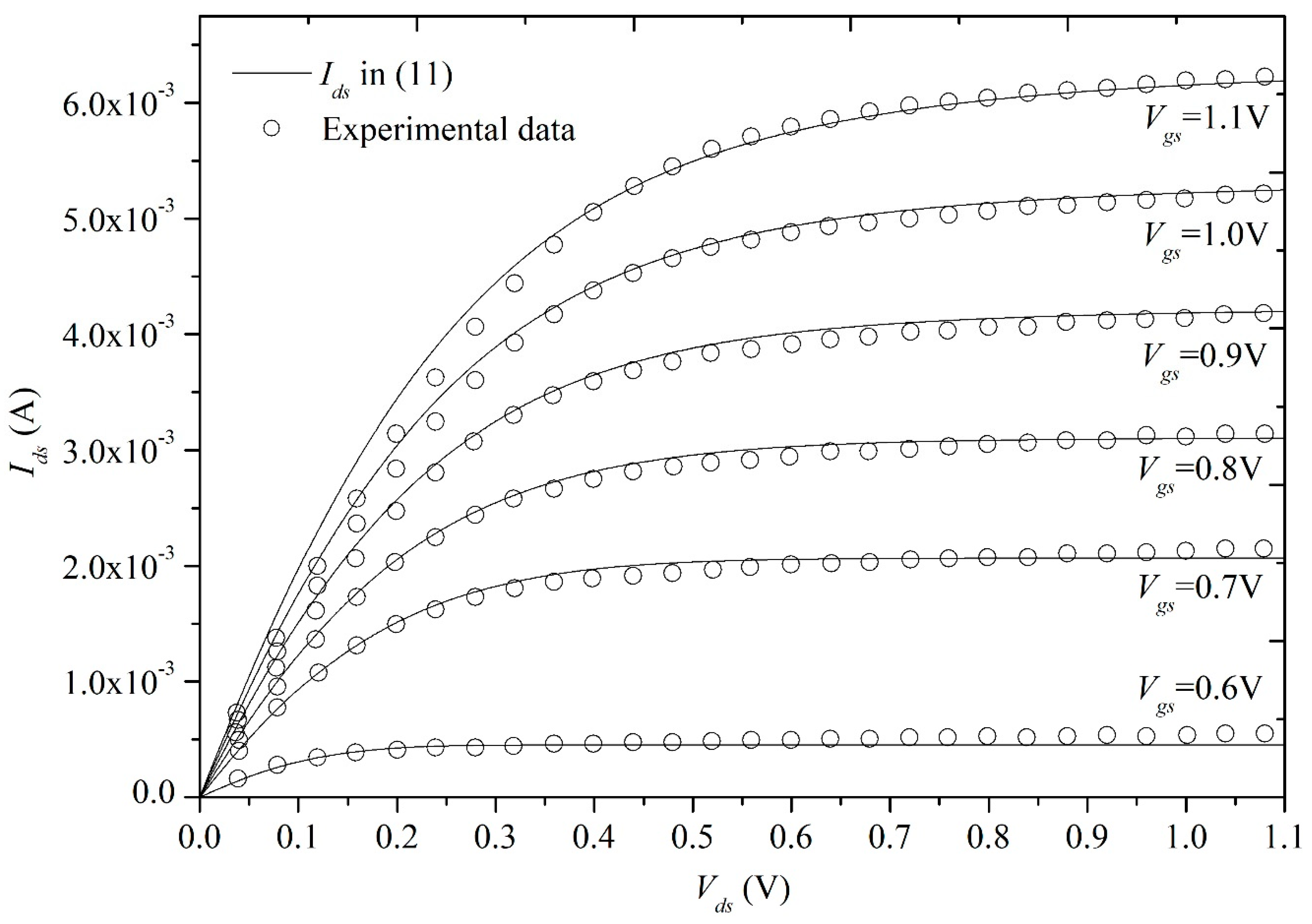
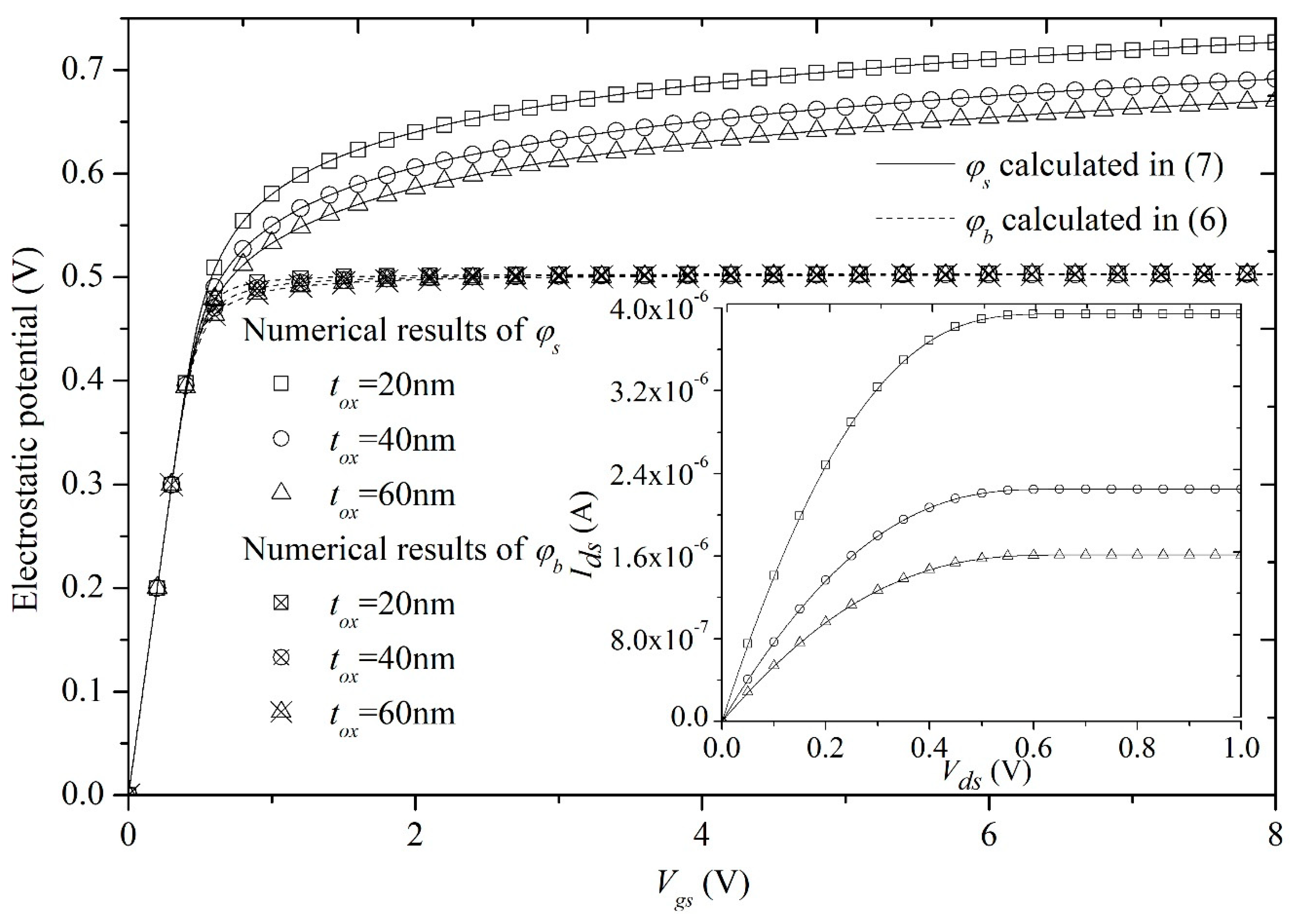
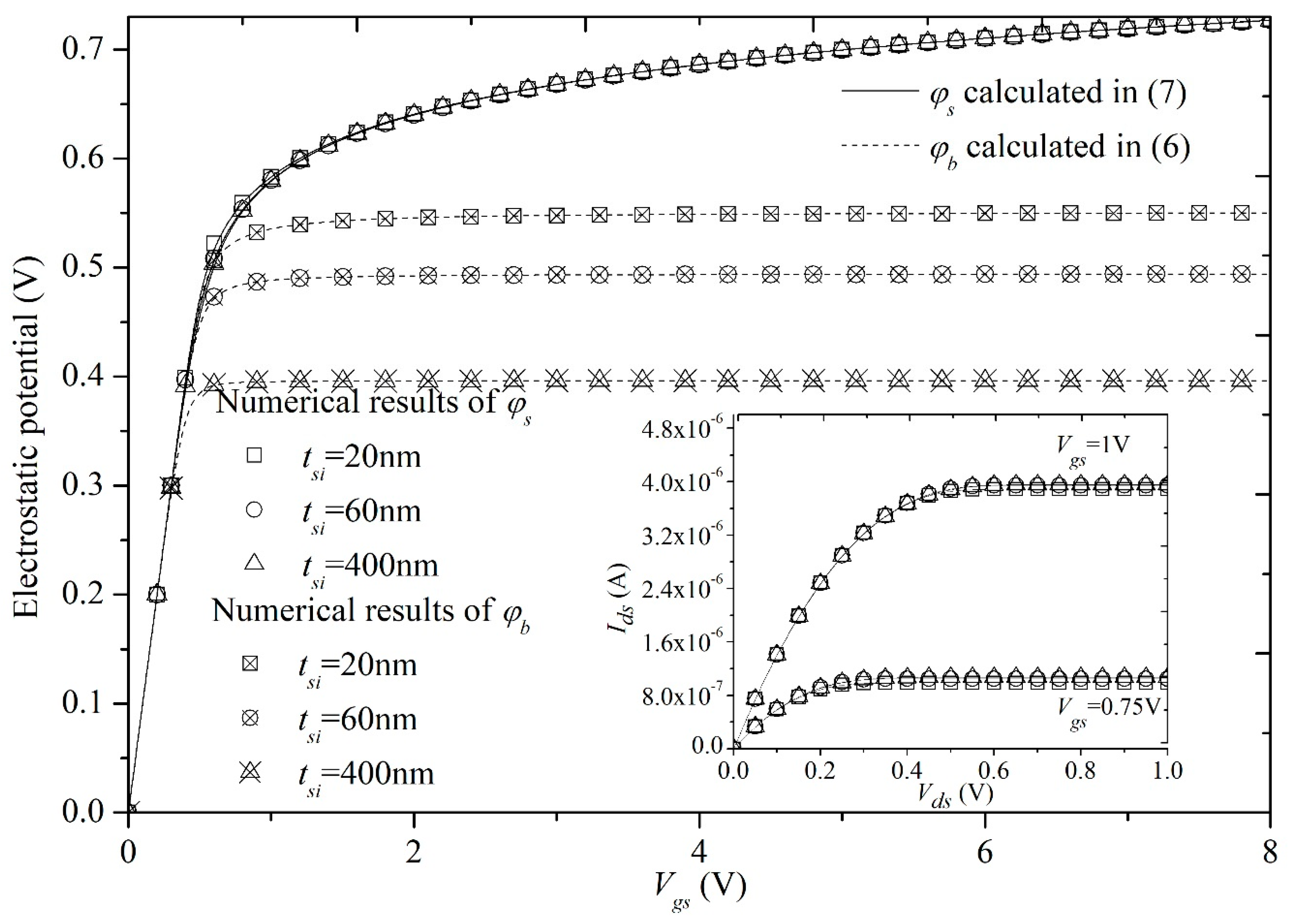
| Symbol (Units) | Value in Figure 4 and Figure 5 | Value in Figure 6 and Figure 7 | Value in Figure 8 | Value in Figure 9 | Value in Figure 10 |
|---|---|---|---|---|---|
| Na (cm−3) | 1 × 1012 | 1.08 × 1011 | 1 × 1013 | 1 × 1013 | 1 × 1012, 1 × 1014, 1 × 1016 |
| tox (nm) | 1.2 | 1.2 | 20, 40, 60 | 20 | 2 |
| tsi (nm) | 8 | 8 | 50 | 20, 60, 400 | 10 |
| Vfb (V) | 0 | 0 | 0 | 0 | 0 |
| Vch (V) | - | - | 0 | 0 | 0 |
| W (μm) | 10 | 10 | 10 | 10 | 10 |
| L (μm) | 11 | 0.03 | 10 | 10 | 10 |
| μ0 (cm2V−1) | 250 | 250 | 250 | 250 | 250 |
| θ1 (-) | 0.001 | 0.001 | - | - | - |
| θ2 (-) | 0.001 | 0.001 | - | - | - |
| Vdsat (V) | - | 0.6 | - | - | - |
| a (-) | - | 2 | - | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Yu, F.; Huang, G.; Deng, W.; Ma, X.; Huang, J. A Surface-Potential-Based Analytical I-V Model of Full-Depletion Single-Gate SOI MOSFETs. Electronics 2019, 8, 785. https://doi.org/10.3390/electronics8070785
Xu C, Yu F, Huang G, Deng W, Ma X, Huang J. A Surface-Potential-Based Analytical I-V Model of Full-Depletion Single-Gate SOI MOSFETs. Electronics. 2019; 8(7):785. https://doi.org/10.3390/electronics8070785
Chicago/Turabian StyleXu, Chuanzhong, Fei Yu, Gongyi Huang, Wanling Deng, Xiaoyu Ma, and Junkai Huang. 2019. "A Surface-Potential-Based Analytical I-V Model of Full-Depletion Single-Gate SOI MOSFETs" Electronics 8, no. 7: 785. https://doi.org/10.3390/electronics8070785
APA StyleXu, C., Yu, F., Huang, G., Deng, W., Ma, X., & Huang, J. (2019). A Surface-Potential-Based Analytical I-V Model of Full-Depletion Single-Gate SOI MOSFETs. Electronics, 8(7), 785. https://doi.org/10.3390/electronics8070785





