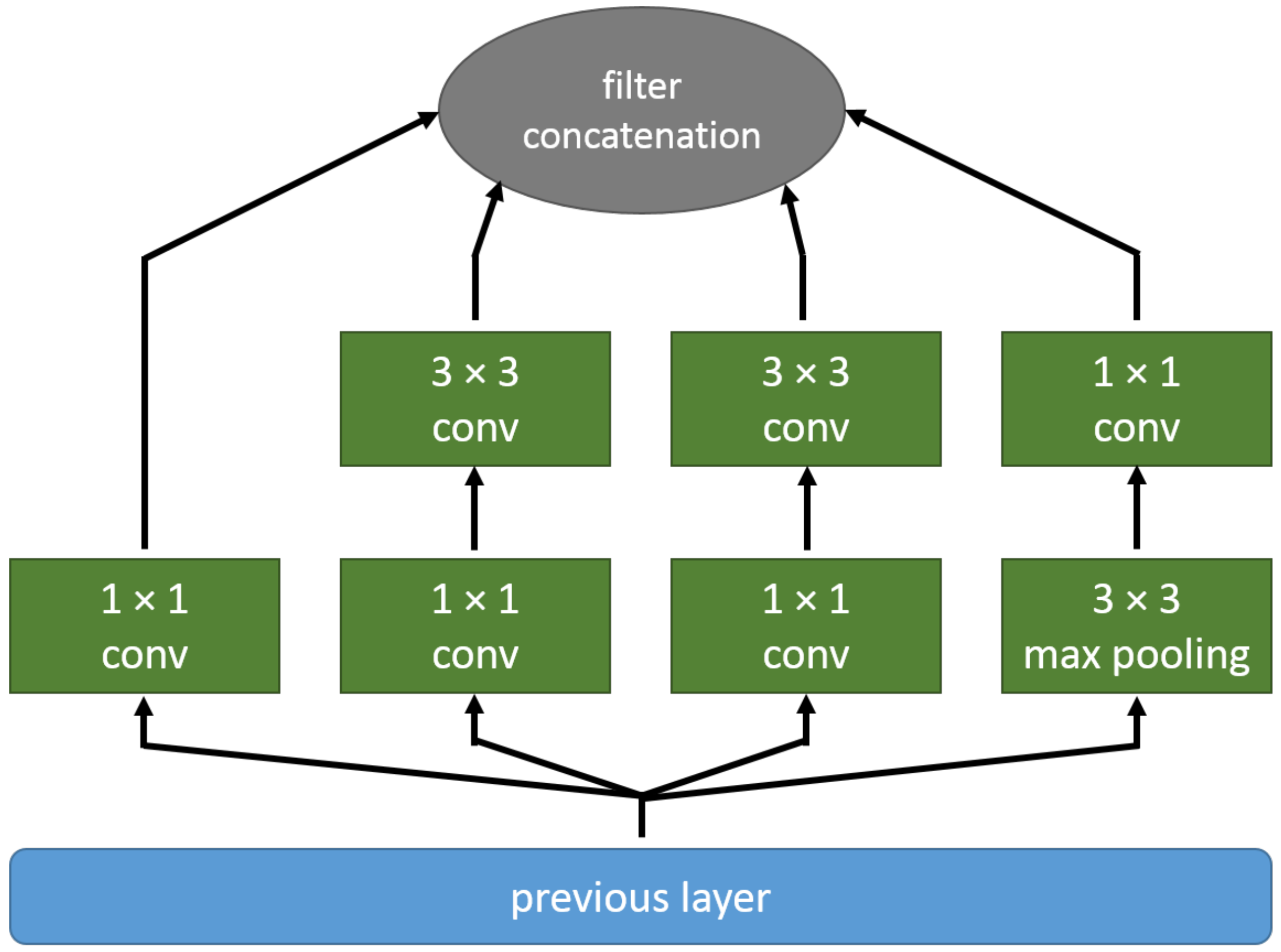
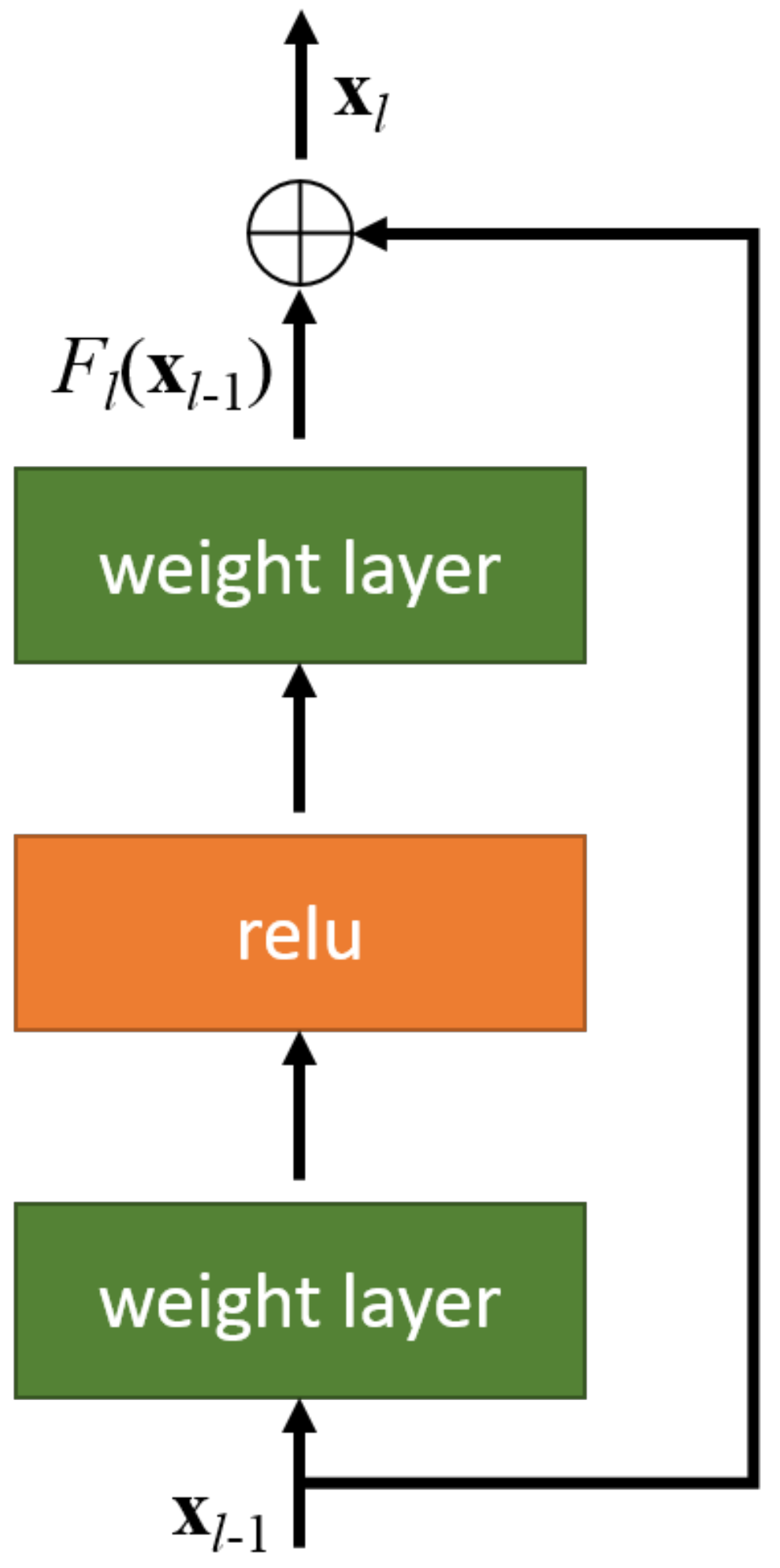
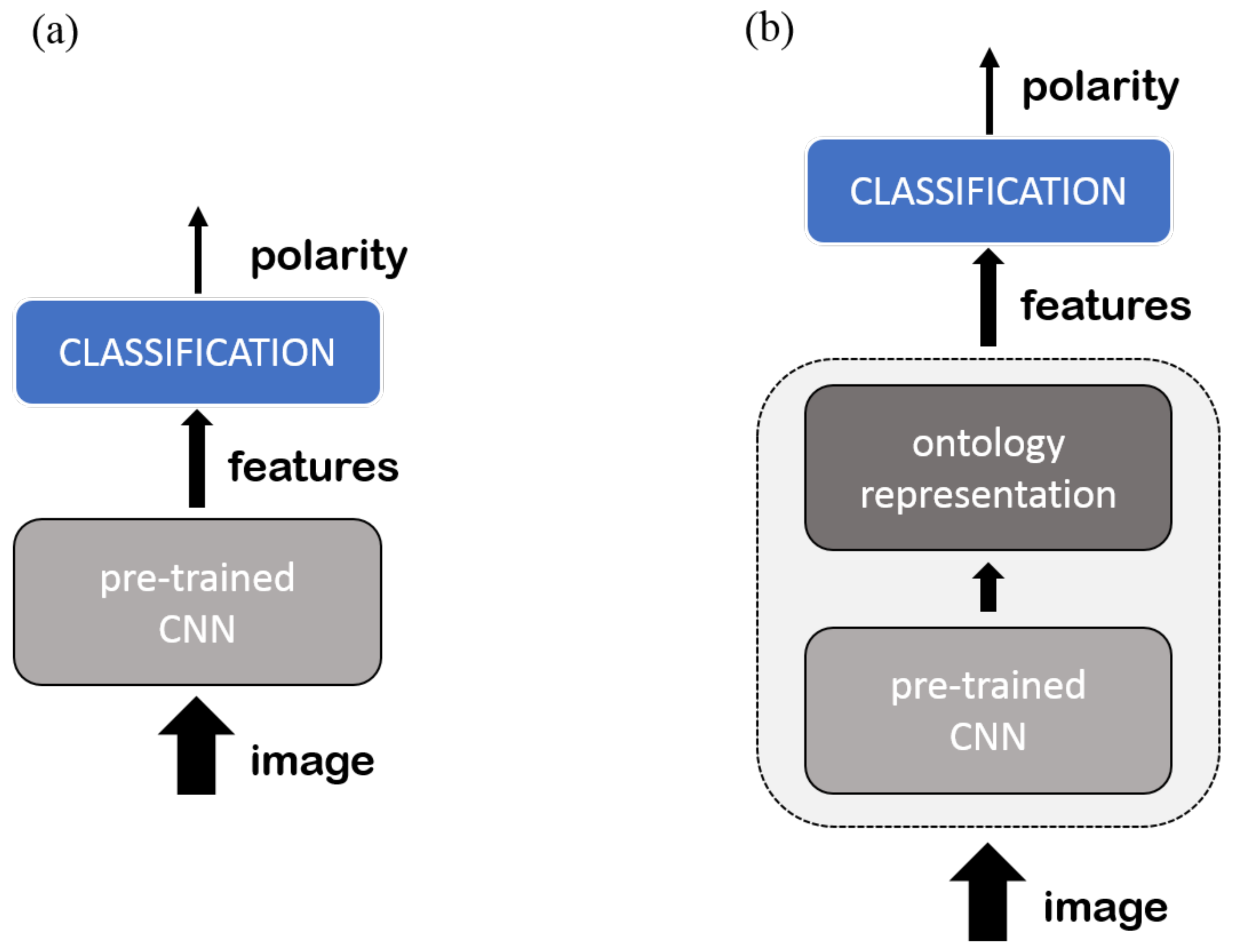
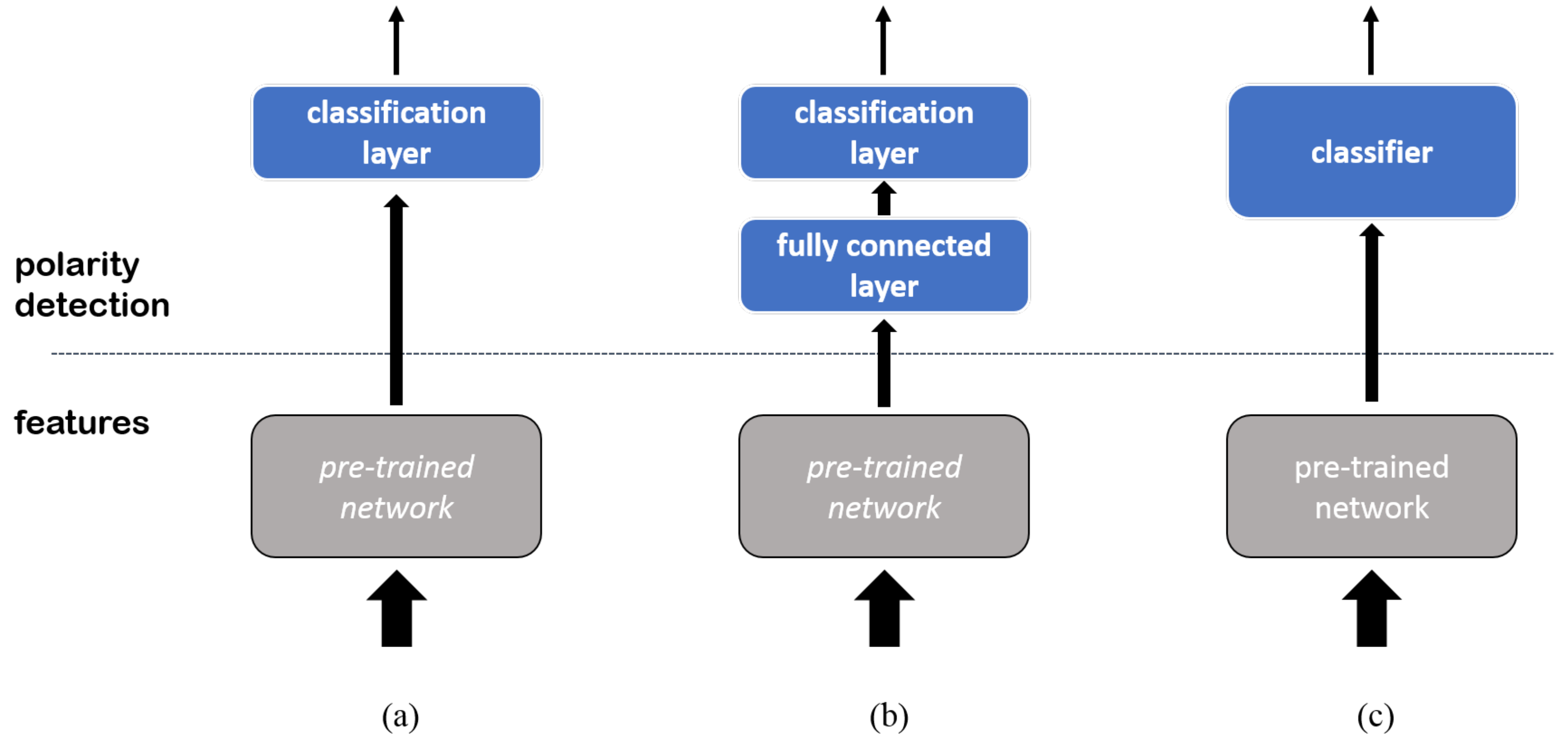
6.1. Datasets
The datasets containing labels for the polarity problem were only considered. The experiments involved the most common benchmarks for polarity detection: Twitter (Tw) [
12], Phototweet (PT) [
22], Multi-view (Mv_a and Mv_b) [
74], and ANP40 [
22].
Table 4 provides, for each dataset, the total number of patterns, the number of patterns belonging to the class “positive polarity”, and the number of patterns belonging to the class “negative polarity”. The first four benchmarks were used to test the three configurations presented in
Section 4 in the presence of small training sets. Instead, ANP40 covered the situation in which a larger dataset is available.
Twitter is the most common benchmark for image polarity recognition. In its original version, the dataset collected 1269 images obtained from image tweets, i.e., Twitter messages that also contain an image. All images were labeled via an Amazon Mechanical Turk (AMT) experiment. This paper actually utilized the “5 agree” version of the dataset. Such a version includes only the images for which all the five human assessors agreed on the same label. Thus, the eventual dataset included a total of 882 images (581 labeled as “positive” and 301 labeled as “negative”).
Phototweet [
22] is another dataset that collects image tweets; it includes a total of 603 images. Labeling was completed via an AMT experiment. Eventually, 470 images were labeled as “positive” and 133 images were labeled as “negative”. This dataset represents a challenging benchmark because (1) it is small and (2) it is quite unbalanced.
Multi-view also provides a collection of image tweets [
74]. Tweets were filtered according to a predetermined vocabulary of 406 emotional words. The vocabulary spanned ten distinct categories covering most of the feelings of human beings (e.g., happiness and depression). The eventual dataset only included those samples whose textual contents (hashtags included) included at least one emotional word. Three annotators labeled the pairs {text, image} by using a three-value scale: positive, negative, and neutral; text and image were annotated separately. This paper utilized a pruned version of the dataset: only images for which all the annotators agreed on the same label were employed, thus obtaining a total of 4109 images. As only 351 images out of 4109 were labeled as negative, such a pruned version of Multi-view resulted in being very unbalanced. Thus, two different balanced datasets (Mv_a and Mv_b) were generated by adding to the 351 “negative” images two different subsets of 351 images randomly extracted from the total amount of “positive” images.
The ANP dataset implements an ontology and is composed of a set of Flickr images [
22]. It includes 3316 adjective-noun pairs; each pair is associated with at most 1000 images, thus leading to a total of about one million pictures. The ANP tags assigned from Flickr users provided the labels for the images; hence, noise severely affects this dataset. To mitigate this issue, the presented research used a pruned version of the dataset, and the 20 ANPs with the highest polarity values and the 20 ANPs with the lowest polarity values were selected (the website of the dataset’ authors (
http://visual-sentiment-ontology.appspot.com/) was exploited as a reference). Eventually, the dataset used for the experiments included 11,857 “positive” images and 5257 “negative” images.
6.2. Experimental Setup
The experimental campaign was organized into two sessions. In the first session, Tw, Mv_a, Mv_b, and ANP40 were used as benchmarks. The first three benchmarks covered the most common scenario in which a small training set was available. This supported the assessment of the convolutional architectures for the three configurations discussed in
Section 4. ANP40 covered the dual case in which a larger dataset is available. The second session only involved the PT benchmark, which was treated separately due to its peculiar properties, namely small size and class unbalance.
In all sessions, the layer replacement configuration was set up as follows. The optimization of the layer in the pre-trained CNN followed stochastic gradient descent with momentum, with momentum = and learning rate = . In the upper classification layer, the learning rate was and the regularization parameter was . The validation patience for early stopping was two. Training involved a maximum of 10 epochs.
The same setup was adopted for the layer addition configuration. In this case, the learning rate was , and the regularization parameter was 0.5 for both the fully-connected and the classification layer. Cross-validation drove the setting of the hyper-parameter, , which could take on a discrete set of values: .
The classifier configuration did not require fine-tuning. The SVM with Gaussian kernel was trained with a standard algorithm. The two hyper-parameters, regularization term C and kernel standard deviation , were set via model selection.
6.3. Experimental Session #1
According to the proposed experimental design, eight different pre-trained architectures were used to generate as many implementations of each configuration. The experimental session aimed at comparing the generalization performances of such implementations.
For each configuration, the performances of the eight predictors were evaluated according to a five-fold strategy. Hence, for each dataset, the classification accuracy of a predictor was measured in five different experiments, corresponding to as many different splittings of the dataset into training/test pairs. Five separate runs of each single experiment were completed; each run involved a different composition of the mini-batch. As a result, for each predictor and each benchmark, 25 measurements of the classification accuracy on the test set were eventually available.
Table 5 reports on the performances measured by applying the layer replacement configuration to Tw, Mv_a, Mv_b, and ANP40. The first column marks the pre-trained architecture used for implementing the predictor; the second column gives, for the Tw dataset, the average accuracy obtained by the predictor over the 25 experiments, together with its standard uncertainty (between brackets); the third, fourth, and fifth columns report the same quantities for the experiments on the Mv_a, Mv_b, and ANP40 datasets, respectively. Best results are marked in bold. The experimental outcomes proved that
DenseNet slightly outperformed the other architectures on Tw and Mv_a.
Vgg_19 scored the best average accuracy on Mv_b; the gap between such a predictor and
Vgg_16,
Inc_v3, and
DenseNet though, was very small, especially if one considered the corresponding standard uncertainties. Furthermore,
Res_101 always proved competitive with the best solution. At the same time, one can conclude that
Inc_v3 and
Res_101 proved the best predictors on ANP40. It is worth noting that seven predictors out of eight achieved an average accuracy in the percentage range [79.7, 78.7]; only the predictor based on
AlexNet was slightly less effective on ANP40.
The results reported in
Table 5 are consistent with those presented in the literature. Layer replacement was adopted in several frameworks for image polarity detection; most of the related works used the Tw dataset as a benchmark; hence, a direct comparison was feasible. In [
44], an accuracy of
was achieved with
AlexNet, while in [
13],
Inc_v3 and
Vgg_19 attained percentage accuracy scores of
and
, respectively. These results indirectly confirm the reliability of the experimental setup adopted in this research.
The experiments involving the layer replacement configurations could point out which architecture proved most consistent on the various dataset and the different training/set pairs. Thus, for each benchmark and for each training/set pair, the eight architectures were ranked according to the classification accuracy scored by the associated predictors. In this case, the accuracy score associated with a predictor was the best accuracy over the five runs completed for a given training/set pair. In each rank, one point was assigned to the best predictor, two points to the second best predictor, and so on, until the worst predictor, which took eight points.
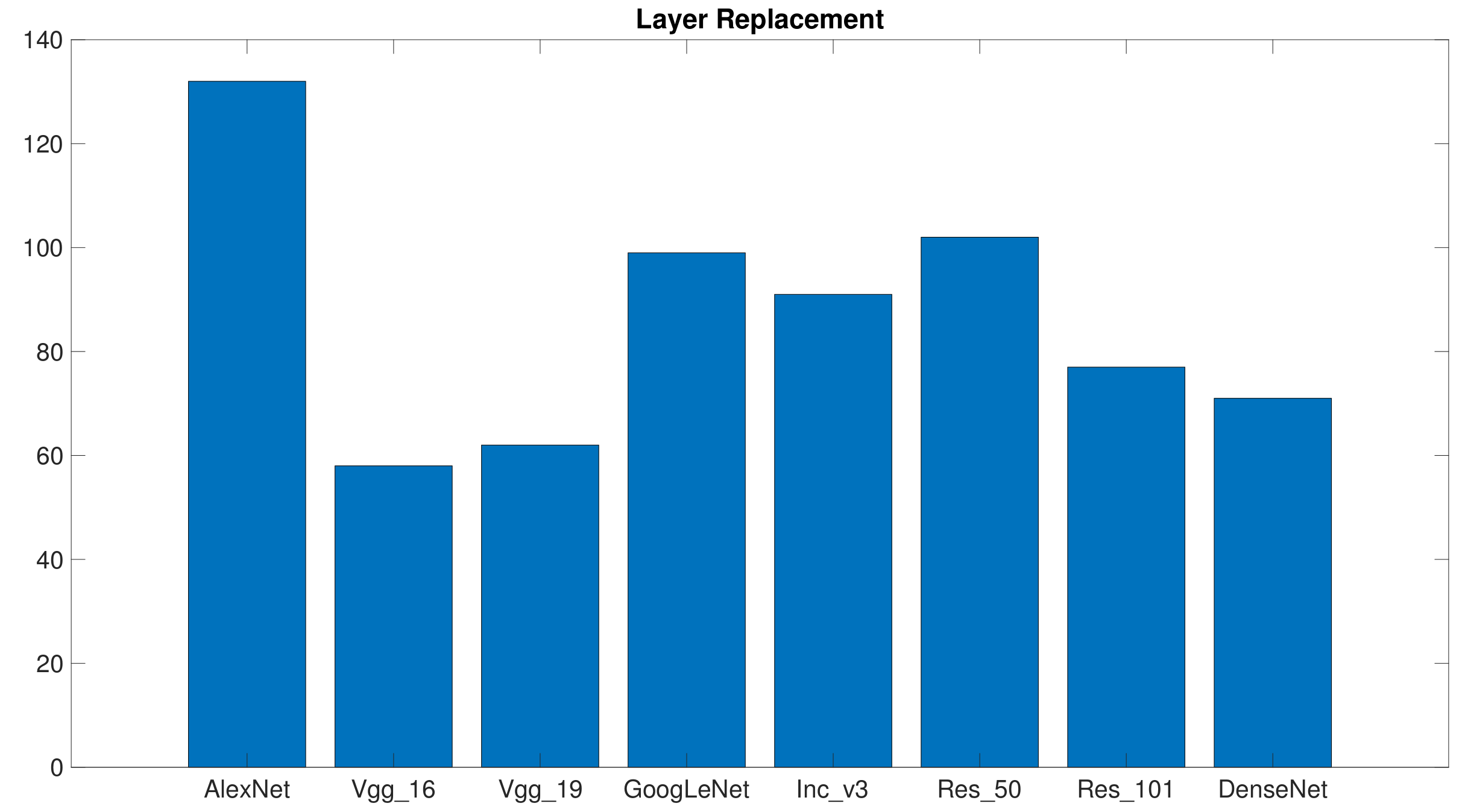
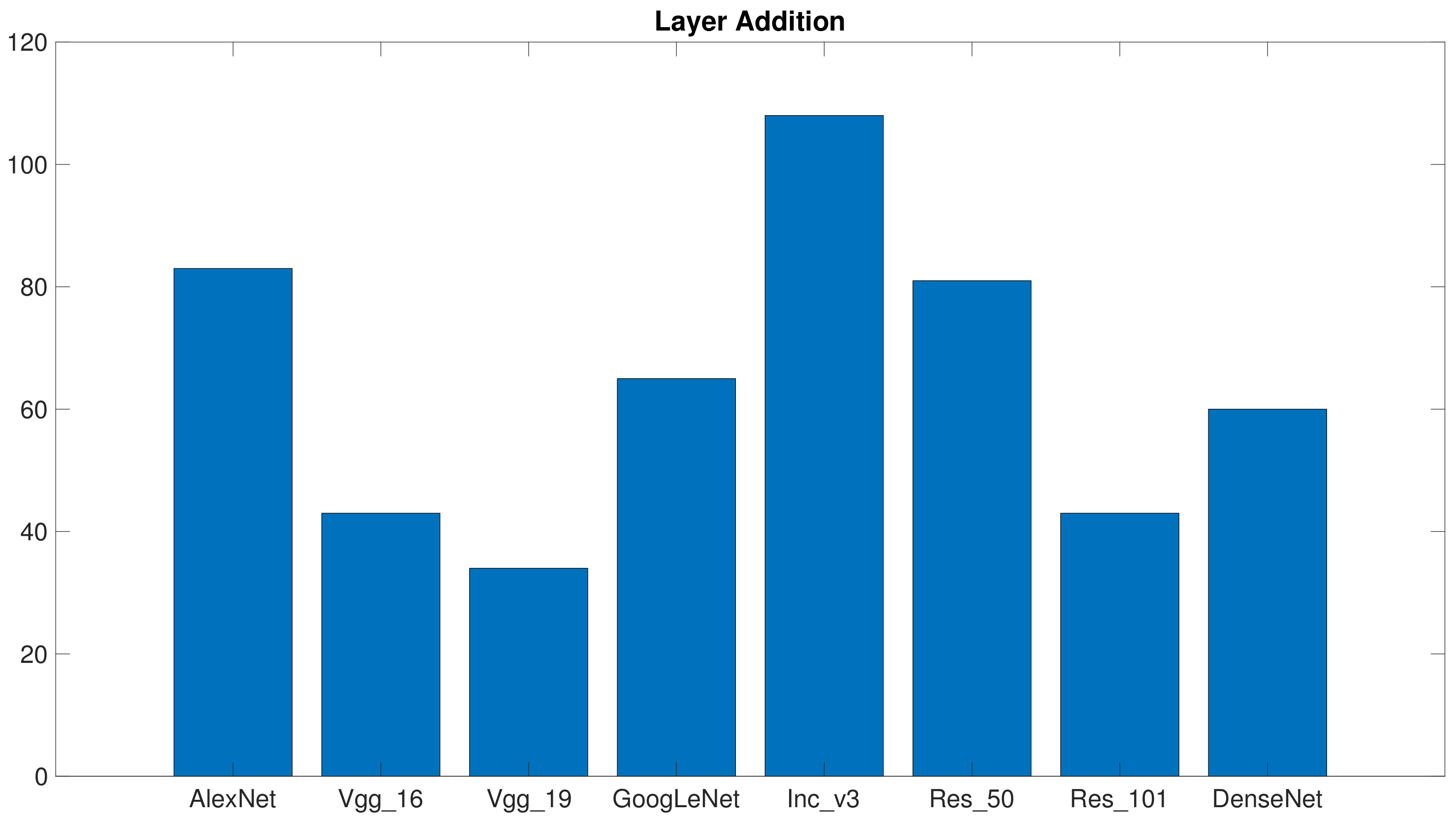
Figure 6 presents, for each architecture, the total points scored over the 20 ranks (5 training/test pairs × 4 benchmarks). In principle, a predictor could not mark less than 20 points, which would mean scoring first position (i.e., best predictor) for every rank. The graph shows that the predictors based on
Vgg_16 and
Vgg_19 resulted in being the most consistent. This outcome indeed reflected the results reported in
Table 5, which showed that
Vgg_16 and
Vgg_19 always performed effectively on the different benchmarks. One should consider, however, that a classifier obtaining a good average accuracy might get a high score if the distribution of its accuracy is non-unimodal or its variance is high.
Table 6 reports on the performance obtained when applying the layer addition configuration on Tw, Mv_a, Mv_b, and ANP40. The Table follows the same format of
Table 5. In each experiment, the training set was split into an actual training set and a validation set to support the model-selection procedure and set the hyperparameter
in the eventual predictor. Experimental outcomes pointed out that
Res_101 yielded the best average accuracy on Mv_a and Mv_b, whereas
DenseNet achieved the best performance for Tw and ANP40. Overall, the gap with respect to the runner-up was always small, especially in the case of the experiments on Mv_b. On ANP40, seven predictors out of eight again achieved almost the same average accuracy. This confirmed that the availability of a large dataset somewhat counterbalanced the possible differences between the various comparisons. Noticeably, the predictors attained better average accuracy with the layer addition configuration than with the layer replacement setup. That improvement came at the cost of a more complex training procedure, as the layer addition configuration also required completing a model selection for setting
.
The layer replacement configuration did not allow a direct comparison with the frameworks published in the literature. The related frameworks typically adopted ad-hoc solutions for the design of the classification layer, whereas the present analysis required a standard solution for fair comparisons. Nevertheless, the literature seems to confirm that the best performances were obtained when using either
VggNets or
ResNets as feature extractors.
Figure 7 provides the outcomes of the consistency assessment for the layer replacement configuration. The plot again gives, for each architecture, the total points marked over the 20 ranks (5 training/test pairs × 4 benchmarks). In this case, too,
Vgg_19 proved to be the most consistent architecture, whereas
Vgg_16 collected as much points as
Res_101. These results are not in contrast to the results of
Table 6; the practical hint is that classifiers based on
Vgg_19 most likely lead to reliable predictors. Conversely, the chances reach a bad local minimum increase when
Res_101 and
DenseNet are involved in the training process.
Table 7 reports on the performance obtained with the classification configuration on Tw, Mv_a, and Mv_b. The table follows the same format of
Table 5. In this case, ANP40 was not included in the experiments, as (
6) suggested that such a configuration should be avoided for computational reasons when large training sets are involved. The classification configuration required a model-selection procedure, as was the case for the layer addition configuration. Therefore, in each experiment, the training set was split into a training and a validation set to support the model-selection procedure to set up the hyperparameters
C and
in the eventual predictors. Predictors based on the classification configuration could benefit from a convex optimization problem in the training phase; hence, the classification accuracy obtained with a given training/test pair could be estimated without resorting to multiple runs of the experiment. The table gives the average classification accuracy values over the five training/test pairs, together with the corresponding standard uncertainty. Experimental outcomes point out a few peculiarities of the classifier configuration, without fine-tuning. First, the predictor based on
Res_101 never scored the best average accuracy; as a matter of fact, each benchmark witnessed a different winner. Secondly, the standard uncertainty associated with the average accuracy always was quite large. For each benchmark and each architecture, the variance of the accuracy over the five experiments always turned out to be quite wide; the composition of the training set played a major role. In practice, this meant that by adopting the classification configuration, one increases the risk of incurring a weak predictor, independently of the specific CNN architecture.
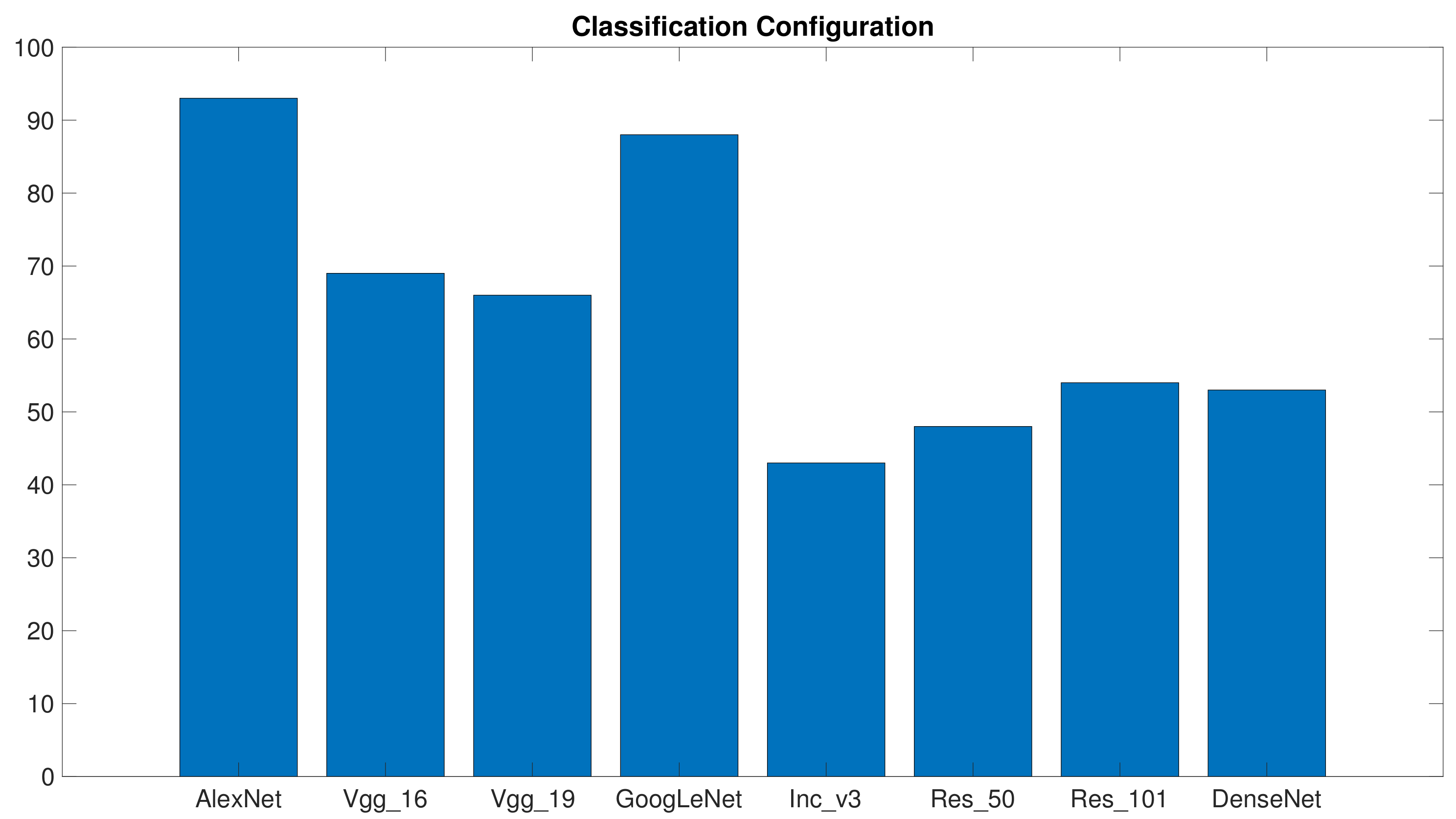
Figure 8 gives the consistency assessments for the classification configuration and follows the same format adopted in the previous graphs. The plot gives, for each architecture, the overall points scored in the 15 ranks (5 training/test pairs × 3 benchmarks). As expected, results differed significantly from those presented above:
Res_50 and
Inc_v3 proved to be the most consistent architectures, while
Vgg_16 and
Vgg_19 did not perform satisfactorily.
Interestingly, the
Inc_v3 architecture did not attain good results when involved in the configurations requiring fine-tuning.
Table 7 and
Figure 8, though, suggest that
Inc_v3 anyway represents a good starting point for image polarity detection. Making fine-tuning effective would require a more fine-grained selection of the optimizer hyper-parameters, but this would be paid at the cost of higher computational loads. As a result, the
Inc_v3 architecture may not be compliant with the premises of this analysis.
6.4. Experimental Session #2
The dataset PT poses major challenges to polarity predictors, since a naive classifier that always predicts “positive” would achieve a 78% accuracy on this dataset. On the other hand, the literature proved that it is very difficult to attain a predictor that can discriminate effectively both classes in this benchmark.
The experimental session showed that neither the layer replacement configuration, nor the classification one could yield acceptable result on PT; the classifiers always featured accuracy values lower than
for at least one of the two classes. Hence, this analysis will only consider the outcomes of the experiments with the layer addition configuration. The performances of the related eight predictors were evaluated by adopting a five-fold strategy. Accordingly, the classification accuracy of a predictor was detected in five different experiments. In each experiment, the original (imbalanced) training set was processed to obtain a more balanced set. For this purpose, oversampling [
109] was applied to the negative (minority) class.
For each predictor, five separate runs of each five-fold experiment were carried out; this routine was repeated over the four admissible values of
. This procedure led to a total of 100 estimates of the test classification accuracy for each predictor.
Table 8 reports on the related outcomes and gives, for each predictor (first column), two quantities: the number of successful trials, i.e., the trials that led to a classification accuracy greater than 50% on both classes; the average accuracy over the number of successful trials. The empirical results suggest two remarks:
Inc_v3 and
Res_50 only achieved an acceptable share of successful trials. Secondly,
Vgg_16,
Vgg_19, and
Res_101 outperformed the other comparisons in terms of average accuracy, in those few cases where successful trials were attained. In summary, the latter architectures were confirmed to be effective at polarity detection, but at the same time proved to be more prone to the problem of local minima.
The number of unsuccessful trials was in general quite high because the proposed dataset was very small and noisy. The purpose of this experiment was to evaluate the ability of the different configurations to learn complex rules with small training sets. Unsurprisingly, layer addition was the only configuration that obtained reasonable performance, possibly because it could train two layers from scratch. Layer replacement possibly failed because training just one layer from scratch would not render complex relationships adequately. The classification configurations relied on SVM, which embedded an inference function and the notion of the similarity between patterns. This might be a disadvantage when the number of training patterns is very small. In the case of layer addition, one should also take into account that the learning process strongly depends on the initial setup. In summary,
Table 8 shows that the probability of reaching a good local minimum over 100 trails significantly varies with the CNN.
6.5. Computational Complexity: An Insight on the Role of CNNs
The experimental campaign showed that, overall,
Vgg_16,
Vgg_19,
Res_101, and
DenseNet proved to be the most reliable architectures in terms of generalization abilities. Computational aspects may be a discriminant factor, as the specific CNN determines the values assumed by
and
in (
3) and (
6) when targeting an implementation on GPUs.
The computational cost of the forward phase
is taken into consideration first. In terms of storage, i.e., number of parameters, the requirements by the pair of
VggNet approaches were almost three- or four-times bigger than
Res_101 and six- or eight-times bigger than
DenseNet. Furthermore, the forward phase of
VggNets involved two- or three-times the number of floating point operations as compared with
Res_101. Notably,
DenseNet used only 4 Gflops operations in the forward phase and would therefore appear as the best choice. On the other hand, in
VggNets, most of the parameters and operations were introduced in the topmost fully-connected layers. As a result, these layers may take advantage of parallel computing, which can boost the overall efficiency when a sufficient amount of memory and computing units is available [
110,
111]. By contrast, both
Res_101 and
DenseNet exhibited a larger number of layers that needed to be computed sequentially; hence, the impact of parallel computing in improving their execution time is expected to be low. In conclusion, predictors based on
Vgg_16 and
Vgg_19 may represent the best option when the forward phase is allocated on a GPU with a considerable amount of memory. On the other hand,
DenseNet seems preferable when one has to cope with memory constraints.
Res_101 represents an intermediate solution.
Evaluating the cost of the back propagation phase
calls for a more detailed analysis. The classifier configuration does not require this phase; at the same time, the experimental campaign proved that better results can be obtained when fine-tuning is applied. For a qualitative analysis, the expression
provided a valid approximation. The actual proportion, though, can substantially differ when considering that deep CNNs are complex models involving different types of blocks. Approximations of computational costs often disregard the contributions of components such as ReLU, pooling, and batch normalization (BN) layers [
108]. However, such a simplification gets less reliable in the presence of more and more complex, non-convolutional, or fully-connected layers. This issue shows up in the analysis proposed in [
108], which is summarizes in
Table 9. The table compares the three architectures involved in the present evaluation,
VggNet,
ResNet, and
DenseNet. For each architecture, the first row gives the percentages of time spent in convolutions and fully-connected layers; the second row gives the computing time percentage of time spent in the remaining layers. Even if the experiments in [
108] did not address exactly
Res_101 and
Dense_201, one can reasonably assume that the same trend applies to those networks, as well. In conclusion, the approximation
becomes less reliable as long as newer models are proposed. For instance, batch normalization units play a crucial role in the training phase of the
ResNet and
DenseNet architectures (as per
Table 9), but these logical blocks are not included in the eventual predictors. This in turn means that
is definitely lighter than
.
The memory consumption during the training phase is an additional significant factor. Storage is nonlinear with respect to the number of parameters and is strongly influenced by the number of connections within the network. It is well known that deeper and thinner networks are less efficient in terms of parallelism and memory consumption as compared with structures with less, but wider, layers. An intuitive explanation is that, during back propagation, the output of each layer needs to be stored; hence, the memory requirement grows as the number of layers grow. Most existing implementations of
DenseNet require indeed an amount of memory that grows quadratically with the number of layers, even if
DenseNet involves a small number of parameters as compared with the other comparisons. Nonetheless, ad-hoc implementations of
DenseNet exist that make the growth linear [
112].
Overall, the plain implementation of the VggNets might result in being simpler than the plain implementation of Res_101 and DenseNet. On the other hand, an optimized implementation of DenseNet and Res_101 could attain valuable improvement in terms of performances. Anyway, one should always take into account that layers must be executed in sequential order; hence, the depth of the network impacts latency.