An Improved Model Predictive Torque Control for a Two-Level Inverter Fed Interior Permanent Magnet Synchronous Motor
Abstract
:1. Introduction
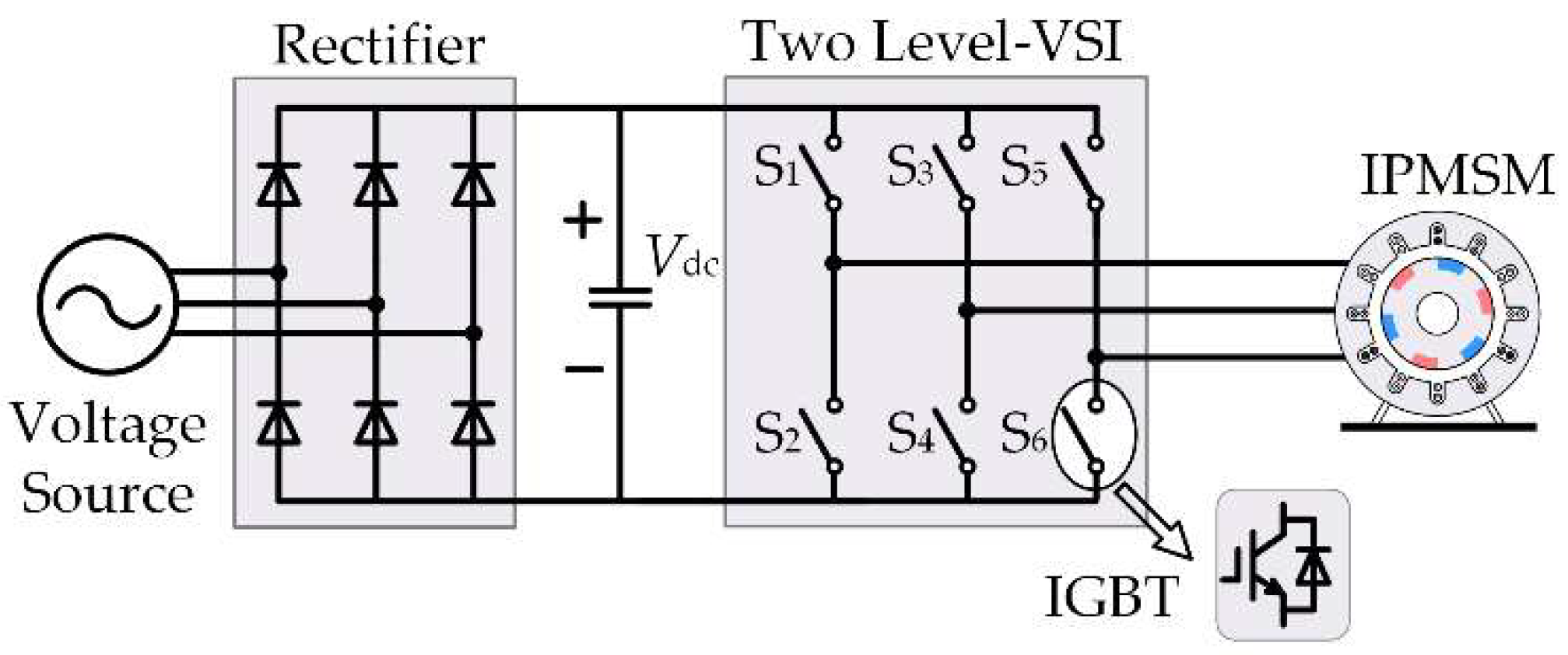
2. The Two-Level Voltage Source Inverters
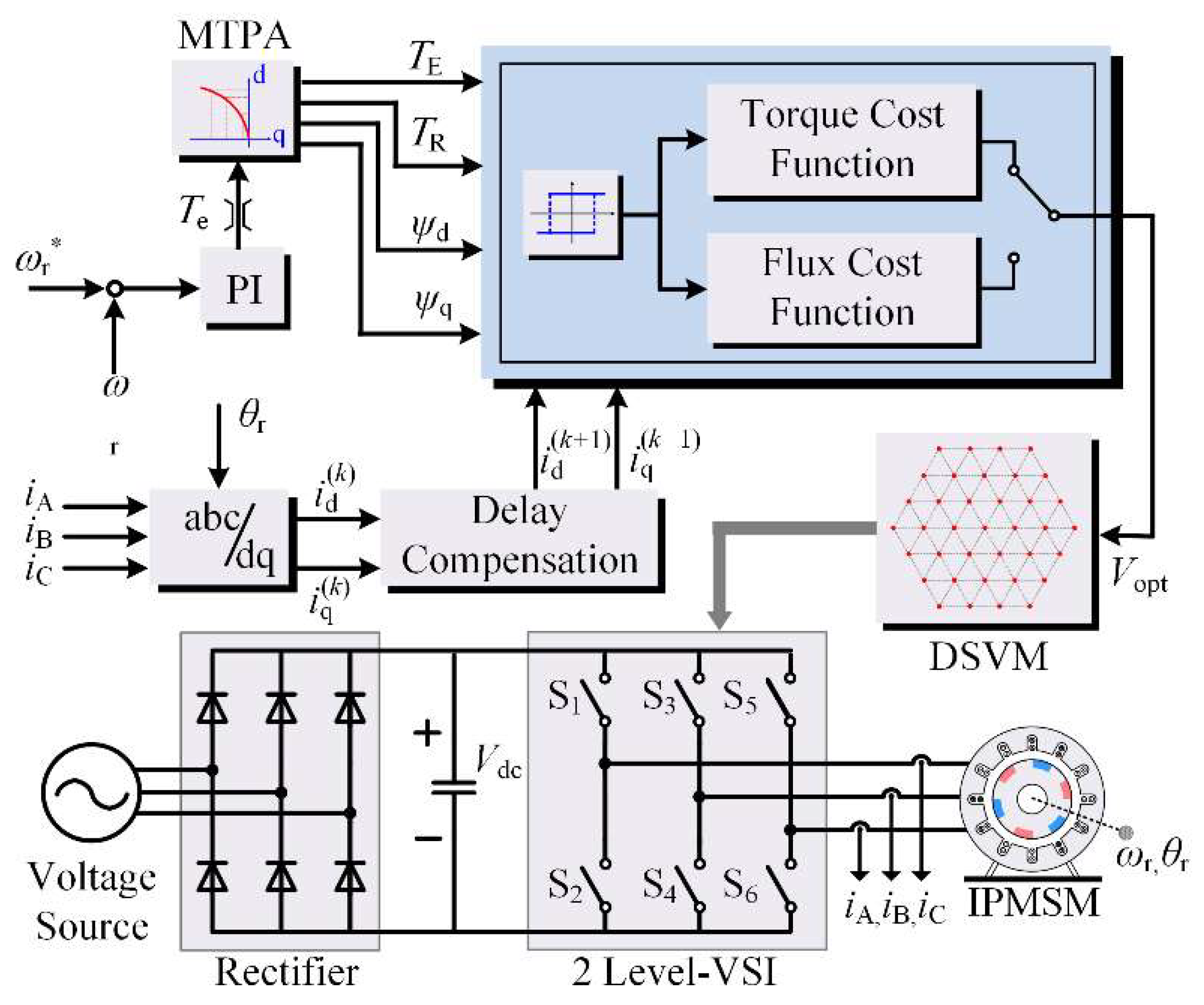
3. Model Predictive Torque Control for IPMSM
3.1. IPMSM Model
3.2. Model Predictive Torque Control
3.3. Model Predictive Flux Control
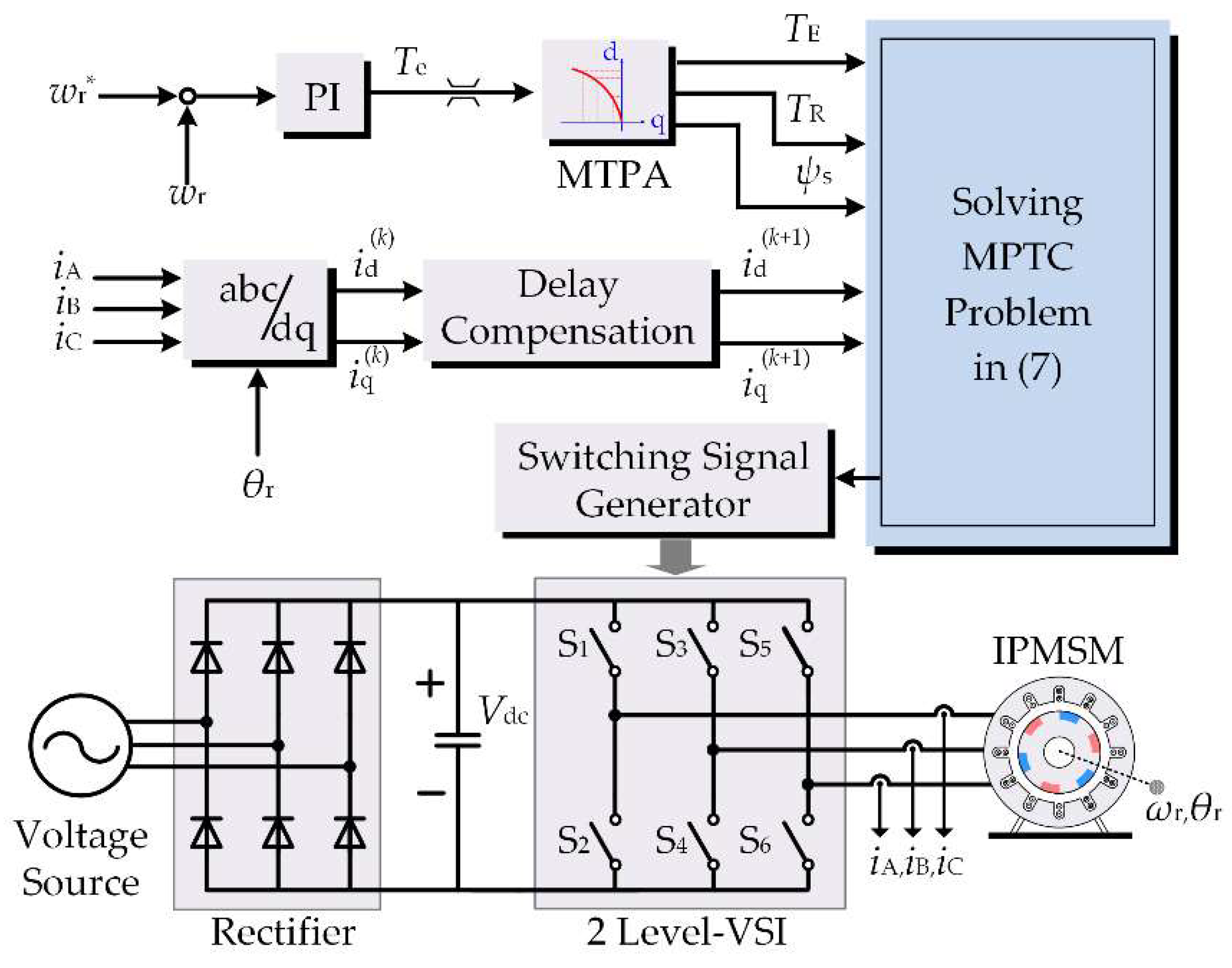
4. Improved Model Predictive Torque Control
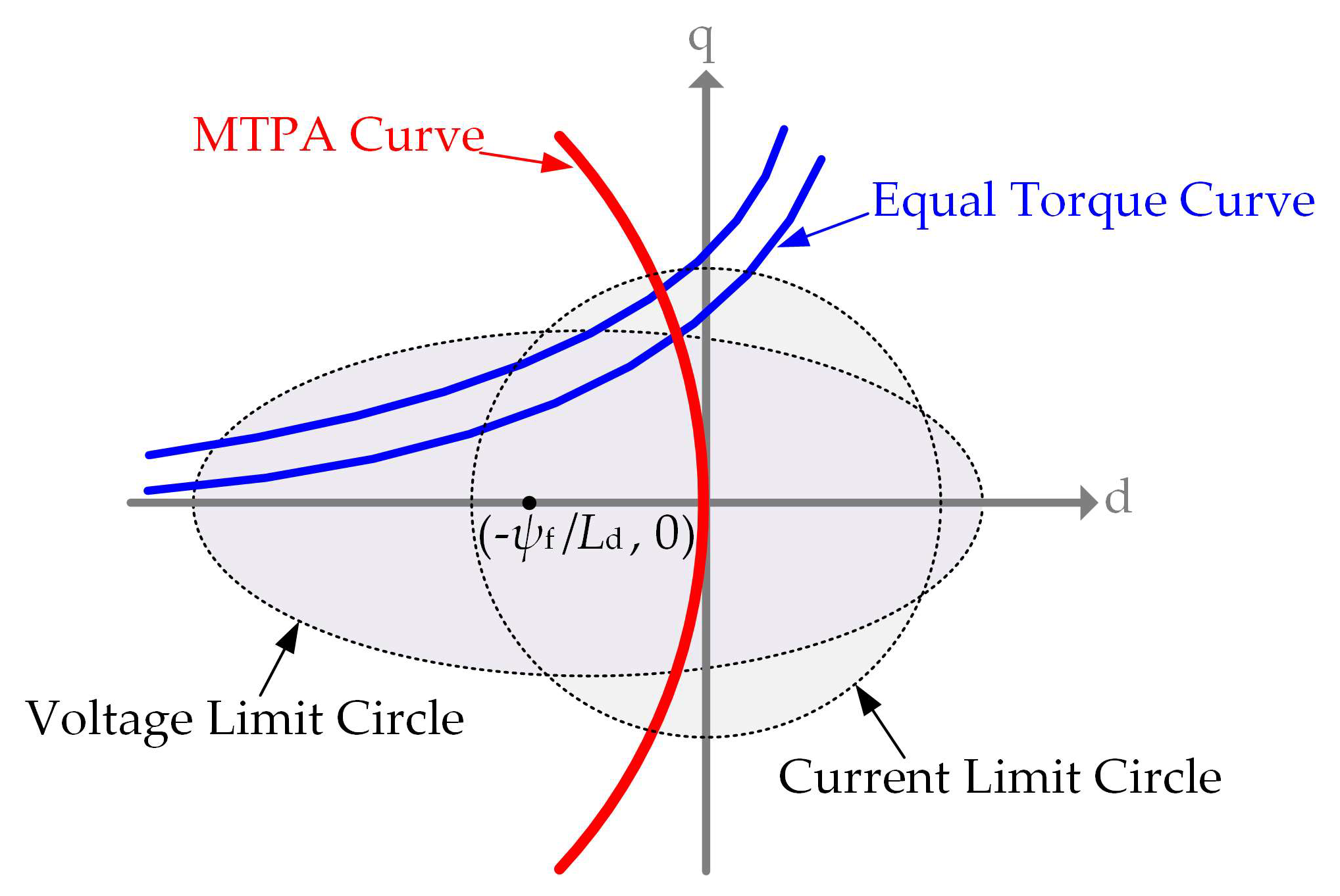
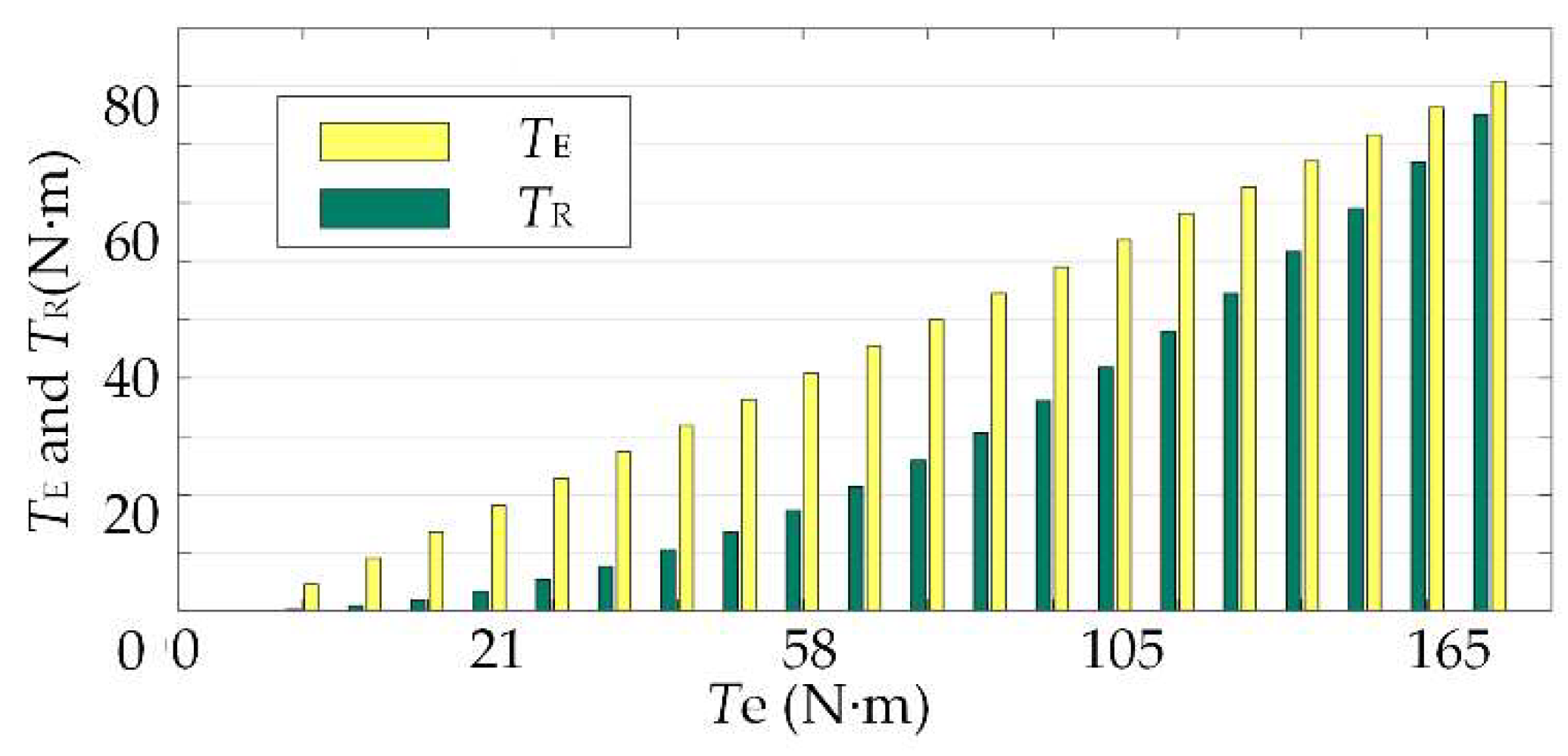
4.1. Improved Cost Function
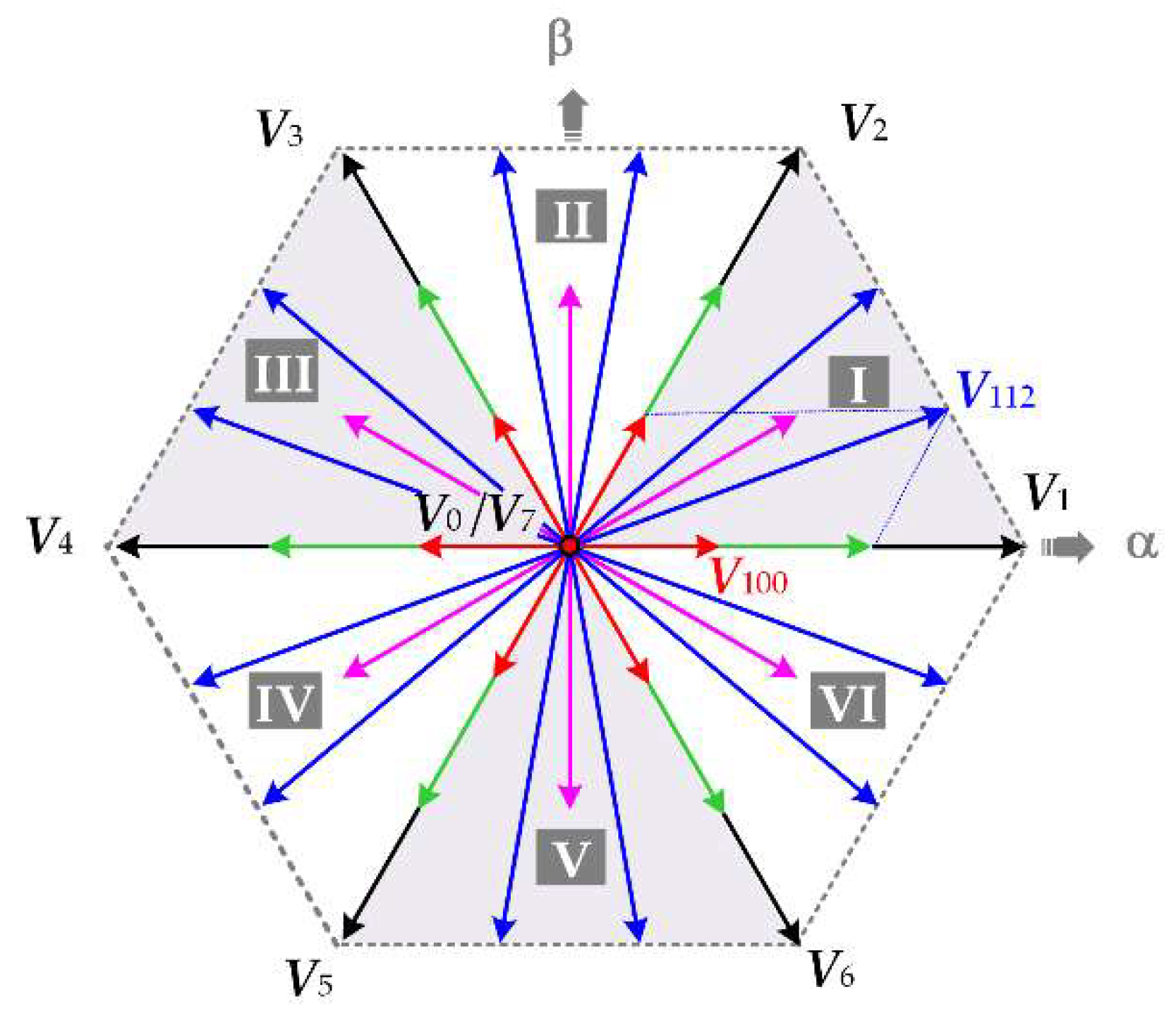
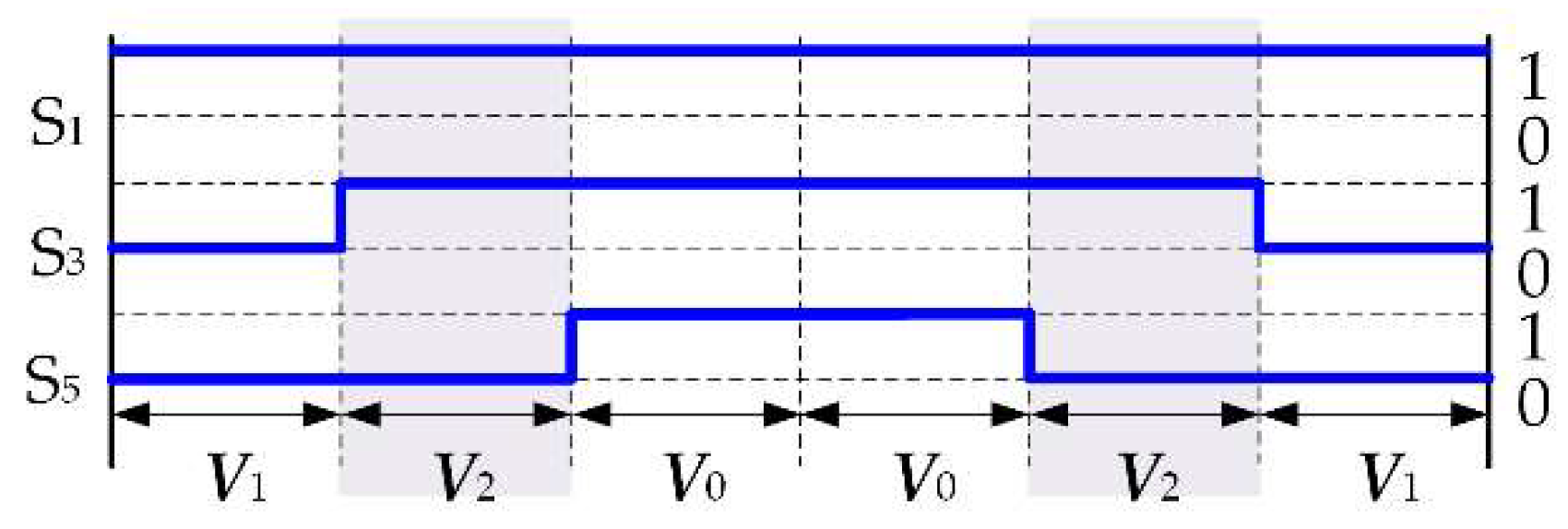
4.2. Finite Control Set
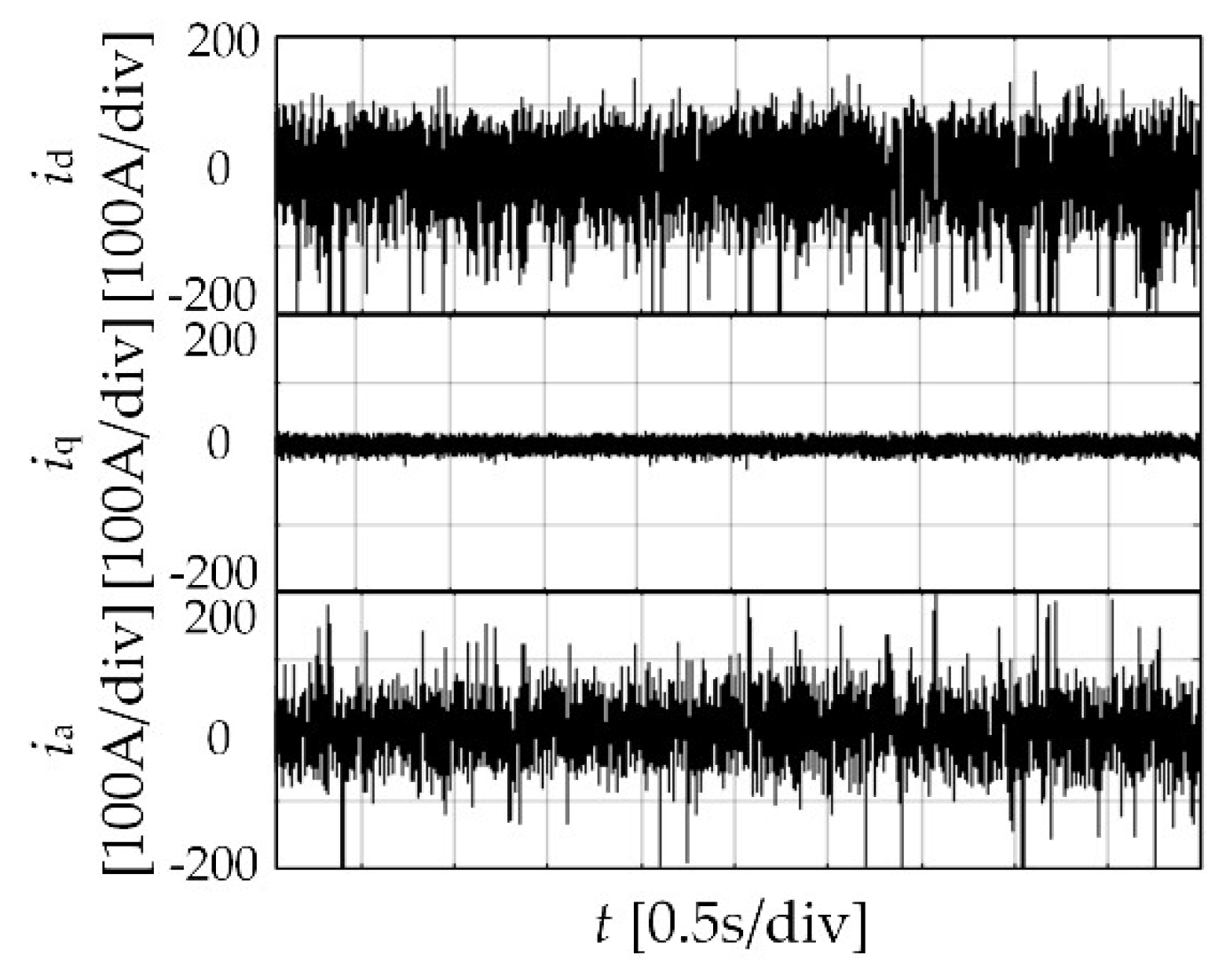
5. Simulation and Experimental Results
5.1. Simulation Analysis
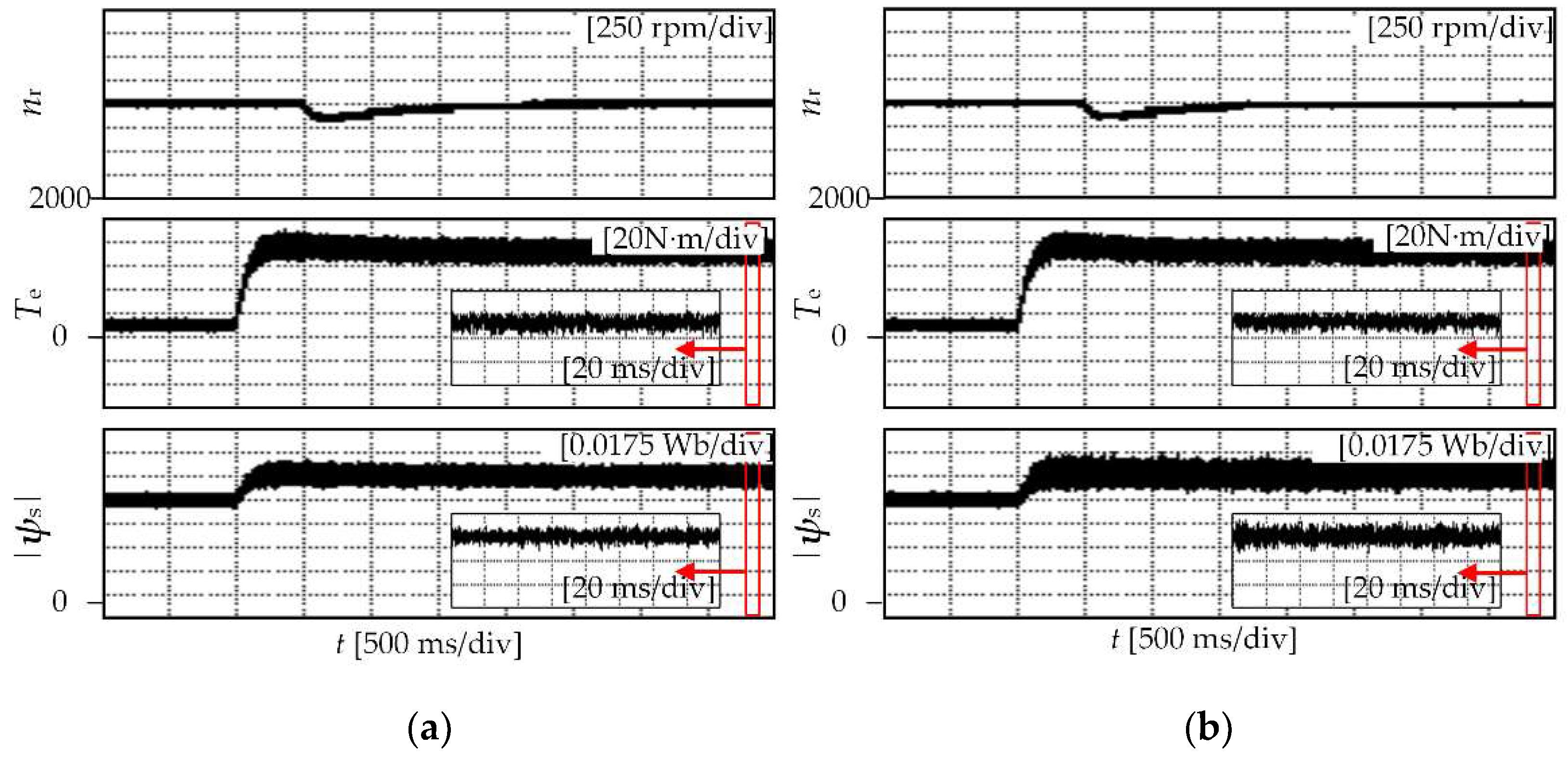
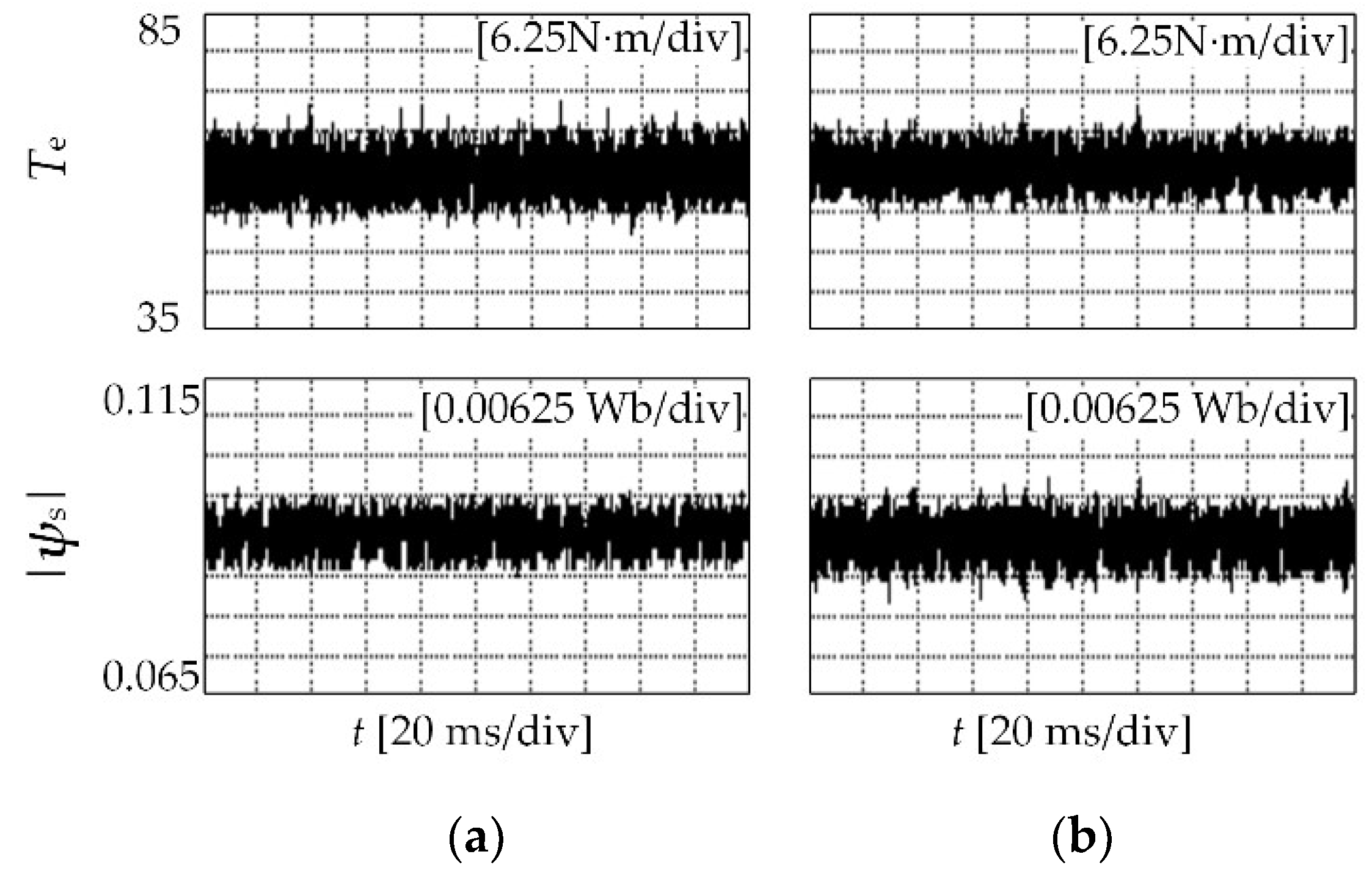
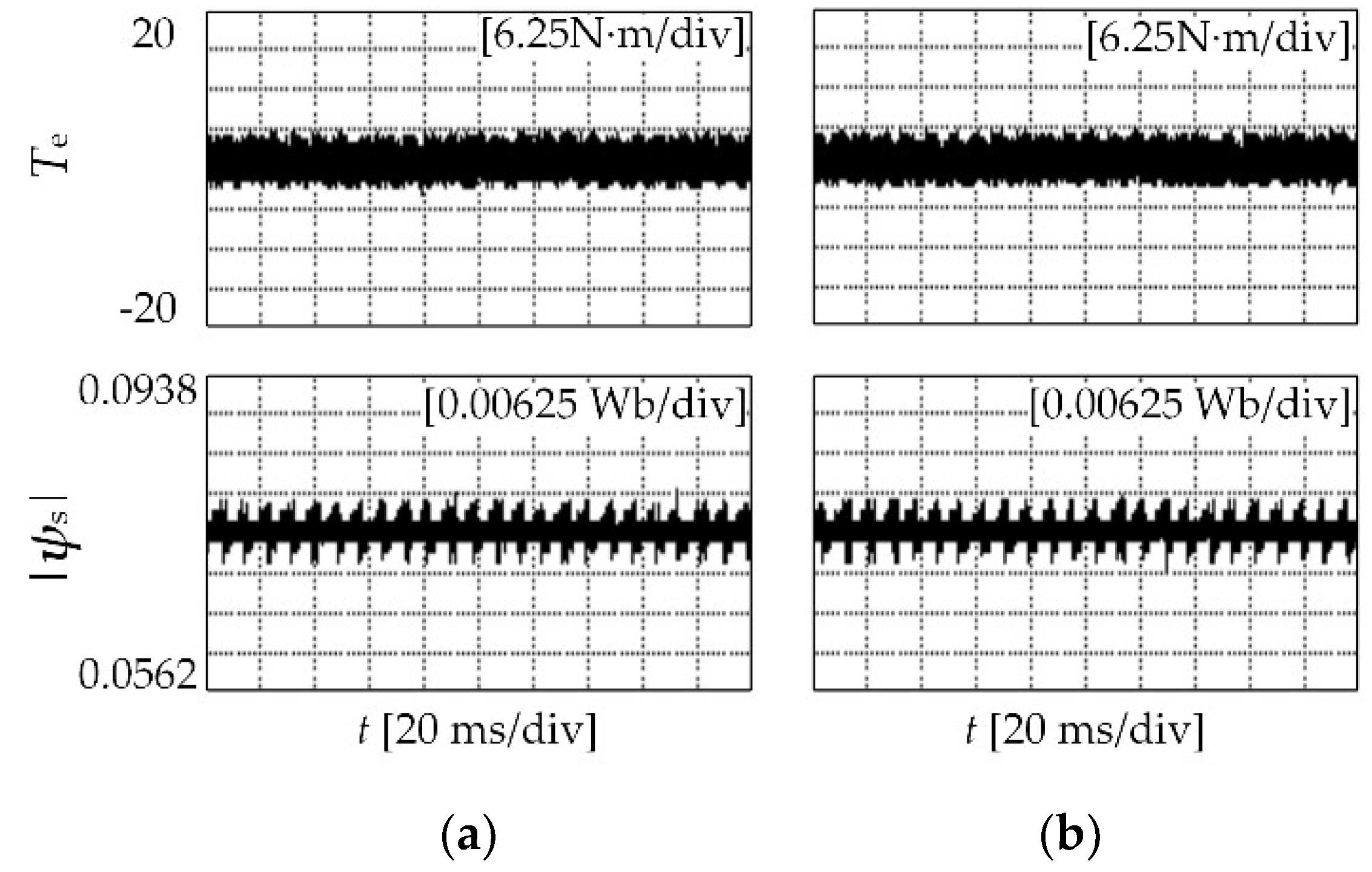
5.2. Experimental Results
6. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Yuan, T.; Wang, D. Performance Improvement for PMSM DTC System through Composite Active Vectors Modulation. Electronics 2018, 10, 263. [Google Scholar] [CrossRef]
- Kamel, T.; Abdelkader, D.; Said, B.; Padmanaban, S.; Iqbal, A. Extended Kalman Filter Based Sliding Mode Control of Parallel-Connected Two Five-Phase PMSM Drive System. Electronics 2018, 2, 14. [Google Scholar] [CrossRef]
- Wang, M.; Hsieh, M.; Lin, H. Operational Improvement of Interior Permanent Magnet Synchronous Motor Using Fuzzy Field-Weakening Control. Electronics 2018, 12, 452. [Google Scholar] [CrossRef]
- Bolognani, S.; Peretti, L.; Zigliotto, M. Online MTPA Control Strategy for DTC Synchronous-Reluctance-Motor Drives. IEEE Trans. Power Electron. 2011, 26, 20–28. [Google Scholar] [CrossRef]
- Du, M.; Tian, Y.; Wang, W.; Ouyang, Z.; Wei, K. A Novel Finite-Control-Set Model Predictive Directive Torque Control Strategy of Permanent Magnet Synchronous Motor with Extended Output. Electronics 2019, 4, 388. [Google Scholar] [CrossRef]
- Kirankumar, B.; Reddy, Y.V.S.; Vijayakumar, M. Multilevel inverter with space vector modulation: Intelligence direct torque control of induction motor. IET Power Electron. 2017, 10, 1129–1137. [Google Scholar] [CrossRef]
- Pratibha, N.; Srinivas, S.; Ittamveettil, H. Five-level torque controller-based DTC method for a cascaded three-level inverter fed induction motor drive. IET Power Electron. 2017, 10, 1223–1230. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Ren, Y.; Liu, J. Improved torque regulator to reduce steady-state error of torque response for direct torque control of permanent magnet synchronous machine drives. IET Electr. Power Appl. 2014, 8, 108–116. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, Z.Q.; Liu, J. Direct Torque Control of Permanent-Magnet Synchronous Machine Drives With a Simple Duty Ratio Regulator. IEEE Trans. Ind. Electron. 2014, 61, 5249–5258. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, J. A Novel Duty Cycle Control Strategy to Reduce Both Torque and Flux Ripples for DTC of Permanent Magnet Synchronous Motor Drives with Switching Frequency Reduction. IEEE Trans. Power Electron. 2011, 26, 3055–3067. [Google Scholar] [CrossRef]
- Masoud, A.; Farasat, M.; Jafarishiadeh, S. Model predictive current control of surface-mounted permanent magnet synchronous motor with low torque and current ripple. IET Power Electron. 2017, 10, 1120–1128. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, X. Torque ripple RMS minimization in model predictive torque control of PMSM drives. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, Korea, 26–29 October 2013; pp. 2183–2188. [Google Scholar] [CrossRef]
- Cortes, P.; Rodriguez, J.; Vargas, R.; Ammann, U. Cost Function-Based Predictive Control for Power Converters. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 2268–2273. [Google Scholar] [CrossRef]
- Rojas, C.A.; Rodriguez, J.; Villarroel, F.; Espinoza, J.R.; Silva, C.A.; Trincado, M. Predictive Torque and Flux Control Without Weighting Factors. IEEE Trans. Ind. Electron. 2013, 60, 681–690. [Google Scholar] [CrossRef]
- Muddineni, V.P.; Bonala, A.K.; Sandepudi, S.R. Enhanced weighting factors selection for predictive torque control of induction motor drive based on VIKOR method. IET Electr. Power Appl. 2016, 10, 877–888. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H.; Xia, B. Model-Predictive Control of Induction Motor Drives: Torque Control Versus Flux Control. IEEE Trans. Ind. Appl. 2016, 52, 4050–4060. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, C.; Qiao, W.; Qu, L. Adaptive Saturation Controller-Based Direct Torque Control for Permanent-Magnet Synchronous Machines. IEEE Trans. Power Electron. 2016, 31, 7112–7122. [Google Scholar] [CrossRef]
- Xia, C.; Wang, S.; Gu, X.; Yan, Y.; Shi, T. Direct Torque Control for VSI-PMSM Using Vector Evaluation Factors Table. IEEE Trans. Ind. Electron. 2016, 63, 4571–4583. [Google Scholar] [CrossRef]
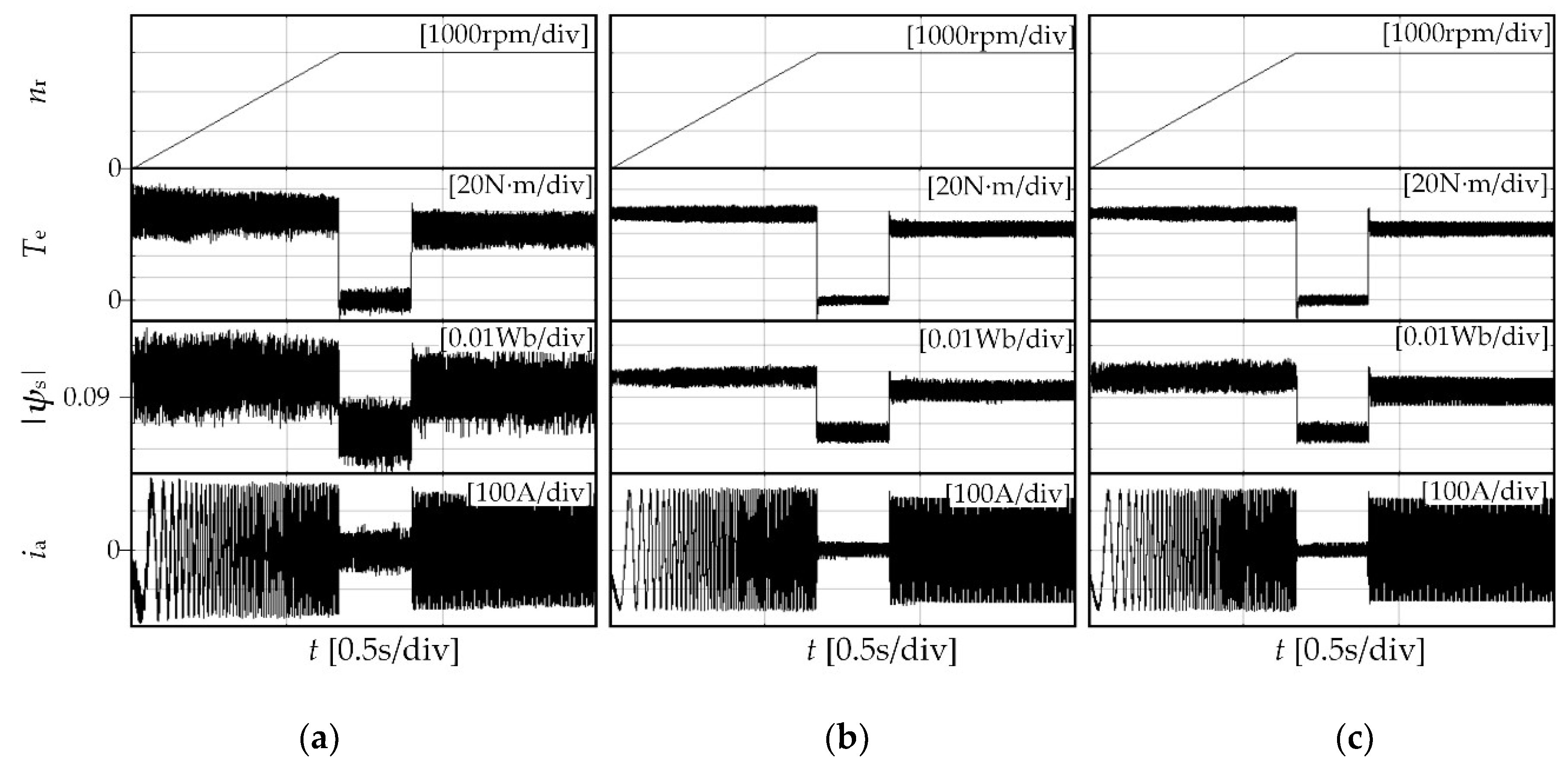
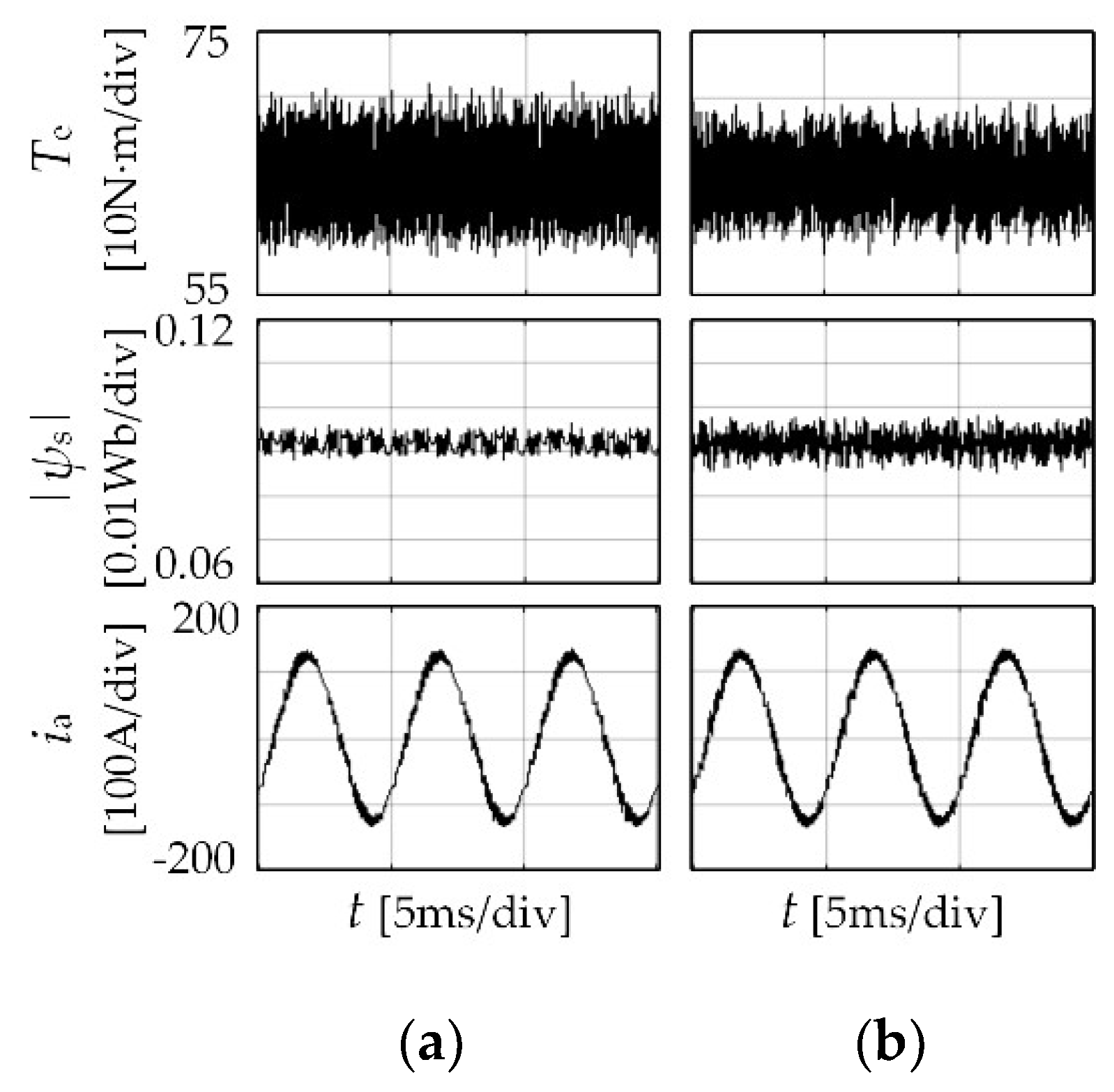
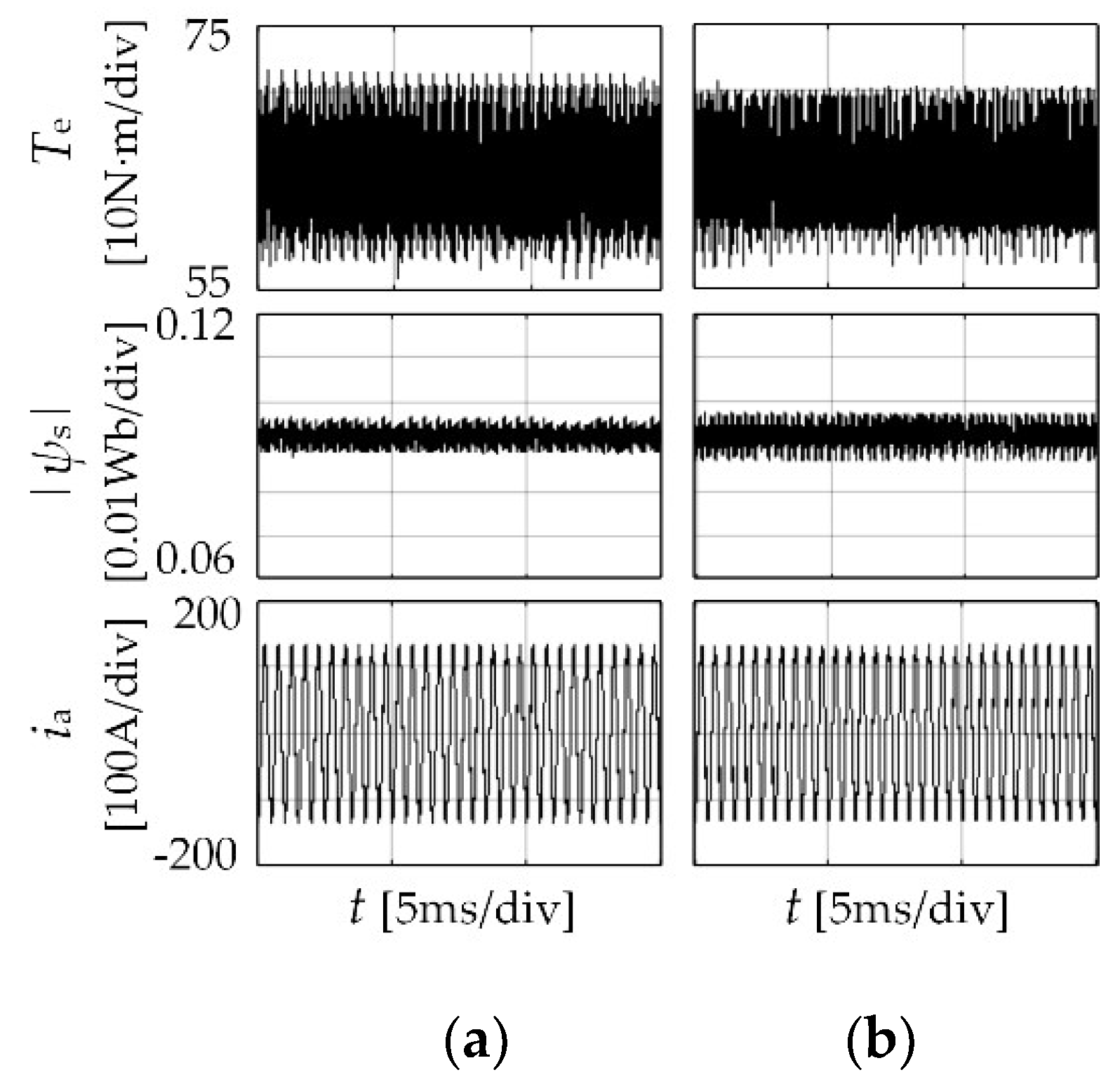

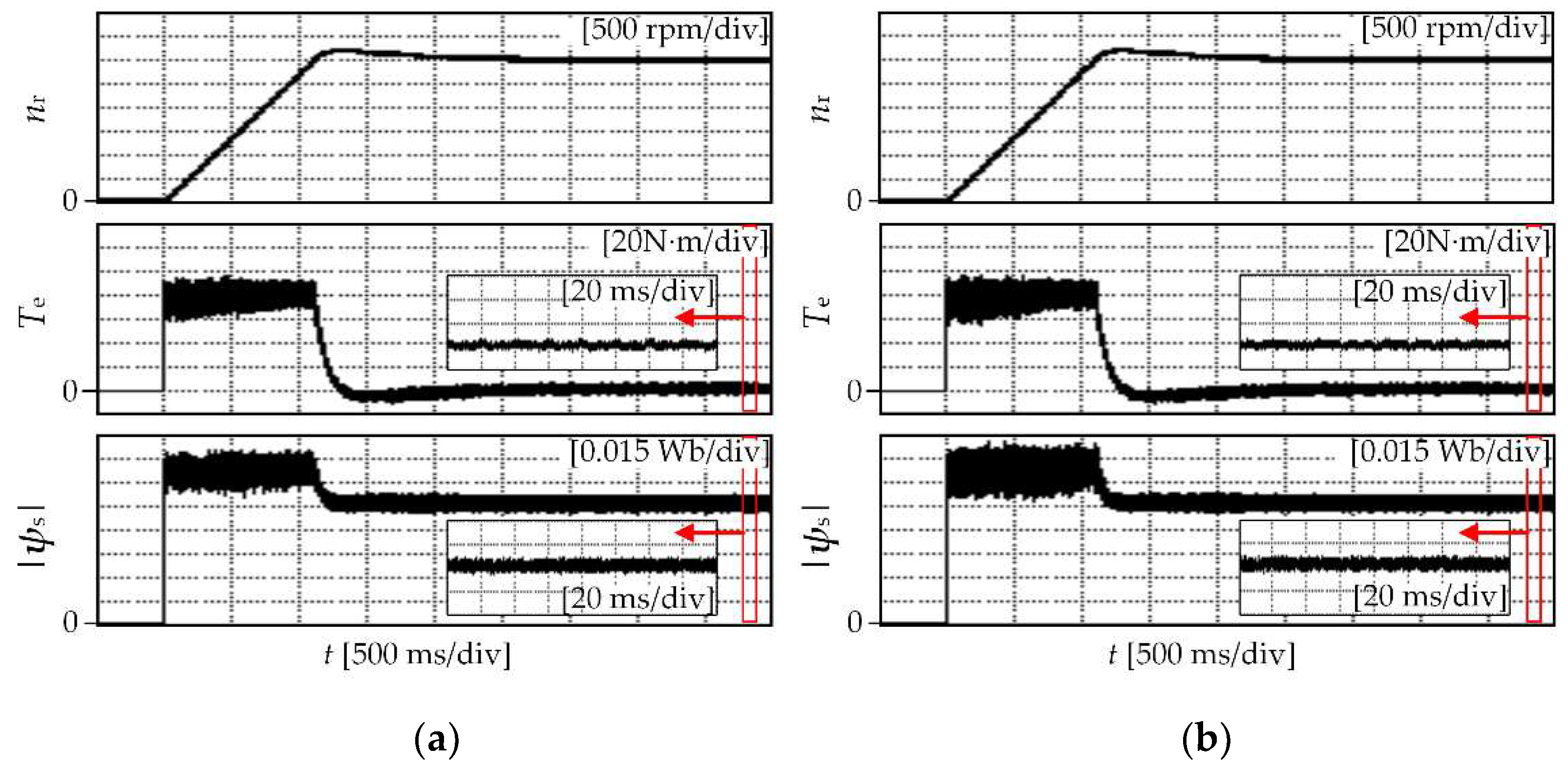
| Parameter | Value | |
|---|---|---|
| Rated voltage (Udc) | V | 320 |
| Number of pole-pairs (p) | - | 4 |
| Stator resistance (Rs) | Ω | 0.0114 |
| d-axis inductance (Ld) | mH | 0.200 |
| q-axis inductance (Lq) | mH | 0.555 |
| Permanent magnet flux linkage (ψf) | Wb | 0.07574 |
| Rated speed (nN) | r/min | 3000 |
| Rated torque (TN) | N·m | 64 |
| Maximum torque (Tmax) | N·m | 180 |
| Speed | STDEV | Load | MPFC | Improved Method |
|---|---|---|---|---|
| 10% Rated speed | σT (Nm) | Light | 1.508 | 1.502 |
| Rated | 3.358 | 3.016 | ||
| σψ (Wb) | Light | 0.00148 | 0.00154 | |
| Rated | 0.00218 | 0.00284 | ||
| Rated speed | σT (Nm) | Light | 1.604 | 1.582 |
| Rated | 3.624 | 3.094 | ||
| σψ (Wb) | Light | 0.00172 | 0.00178 | |
| Rated | 0.00267 | 0.00353 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Chen, C.; Gu, X.; Wang, Z.; Li, X. An Improved Model Predictive Torque Control for a Two-Level Inverter Fed Interior Permanent Magnet Synchronous Motor. Electronics 2019, 8, 769. https://doi.org/10.3390/electronics8070769
Zhang G, Chen C, Gu X, Wang Z, Li X. An Improved Model Predictive Torque Control for a Two-Level Inverter Fed Interior Permanent Magnet Synchronous Motor. Electronics. 2019; 8(7):769. https://doi.org/10.3390/electronics8070769
Chicago/Turabian StyleZhang, Guozheng, Chen Chen, Xin Gu, Zhiqiang Wang, and Xinmin Li. 2019. "An Improved Model Predictive Torque Control for a Two-Level Inverter Fed Interior Permanent Magnet Synchronous Motor" Electronics 8, no. 7: 769. https://doi.org/10.3390/electronics8070769
APA StyleZhang, G., Chen, C., Gu, X., Wang, Z., & Li, X. (2019). An Improved Model Predictive Torque Control for a Two-Level Inverter Fed Interior Permanent Magnet Synchronous Motor. Electronics, 8(7), 769. https://doi.org/10.3390/electronics8070769






