Robust Dynamic Sliding Mode Control-Based PID–Super Twisting Algorithm and Disturbance Observer for Second-Order Nonlinear Systems: Application to UAVs
Abstract
1. Introduction
1.1. Related Works
1.2. Main Contributions
1.3. Organizations
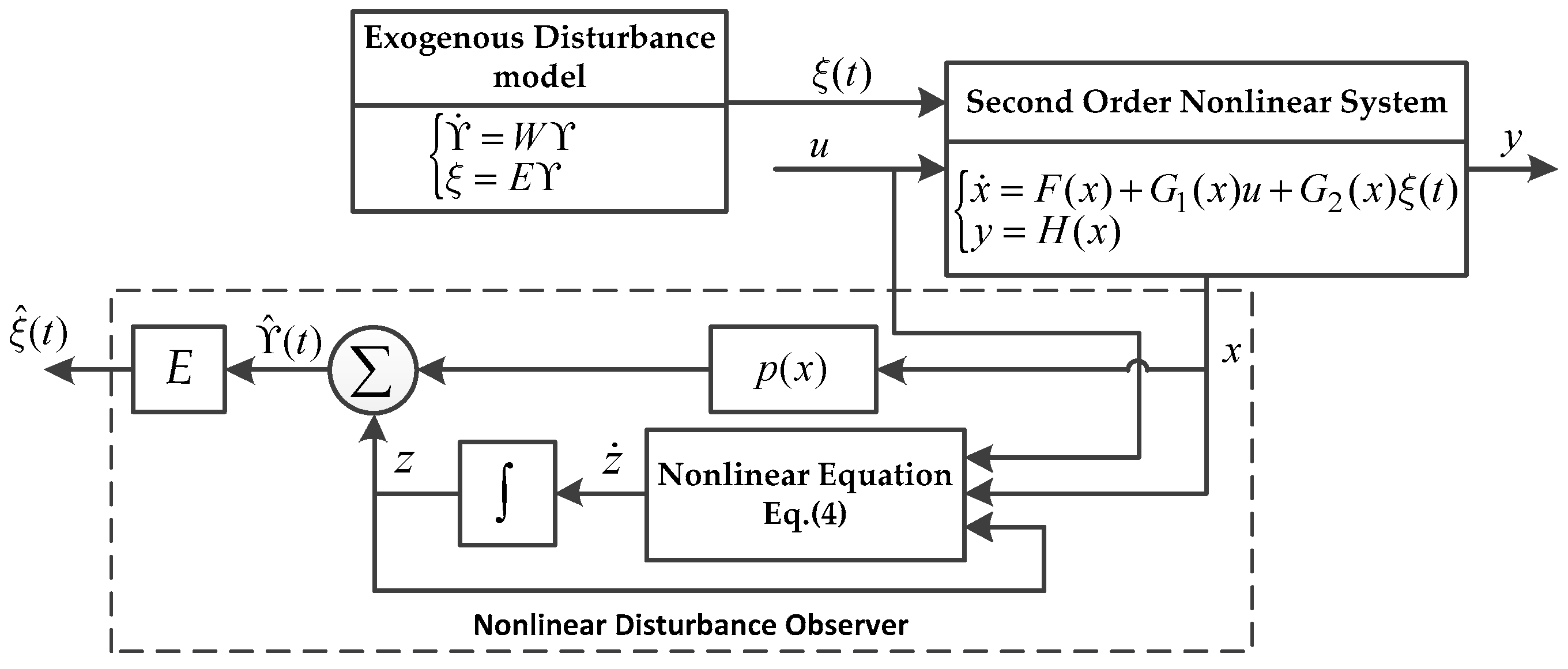
2. Robust Dynamic Sliding Mode Controller Based on Nonlinear Disturbance Observer (RDSMC-NDO)
- Step 1:
- An adaptive disturbance observer is applied to estimate the external disturbance .
- Step 2:
- The disturbance observer is integrated with a robust dynamic sliding mode control by replacing the external disturbance, , with its estimation .
2.1. Nonlinear Disturbance Observer
2.2. Robust Dynamic Sliding Mode Controllers Design Based on Nonlinear Disturbance Observer
2.2.1. Method 1: Robust Dynamic Sliding Mode Controller Based on PID Sliding Surface and Nonlinear Disturbance Observer (RDSMC-PID-NDO)
2.2.2. Method 2: Robust Dynamic Sliding Mode Controller based on PID–Super Twisting Algorithm and Nonlinear Disturbance Observer (RDSMC-PIDSTA-NDO)
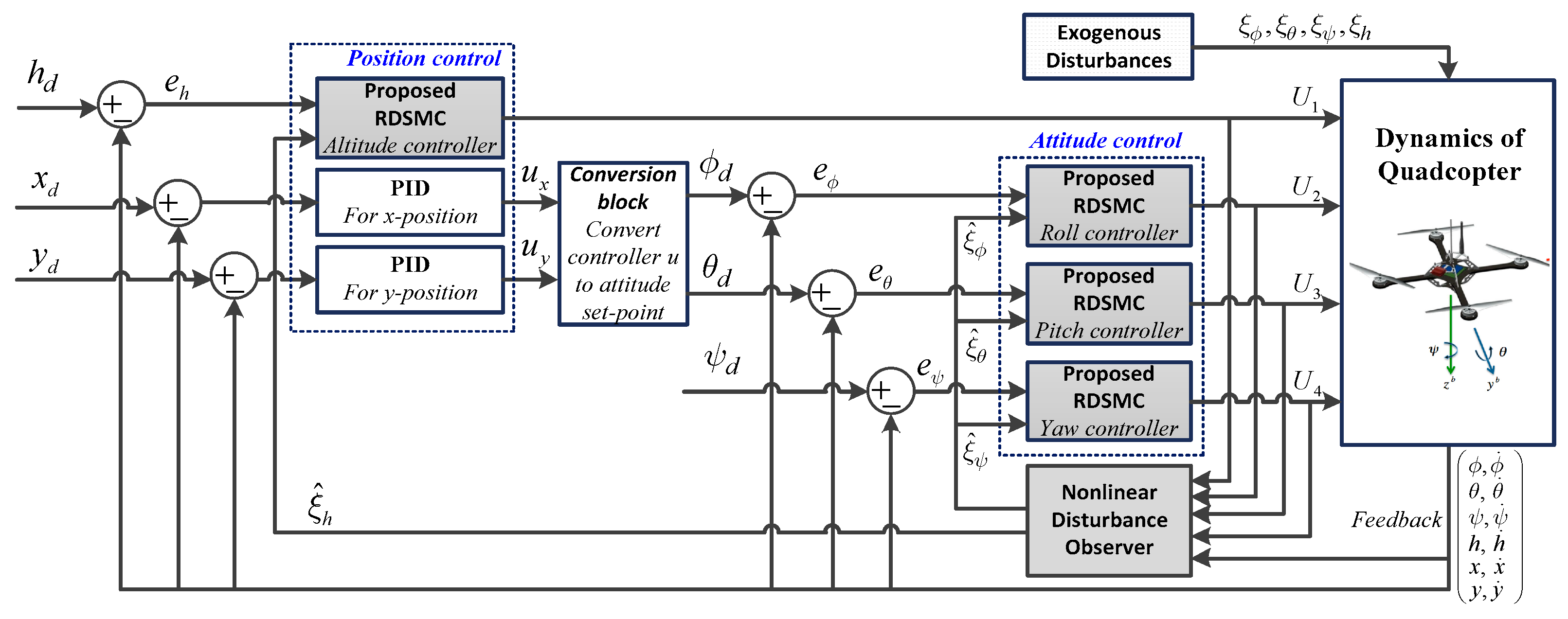
3. Apply the RDSMC-NDO to UAVs
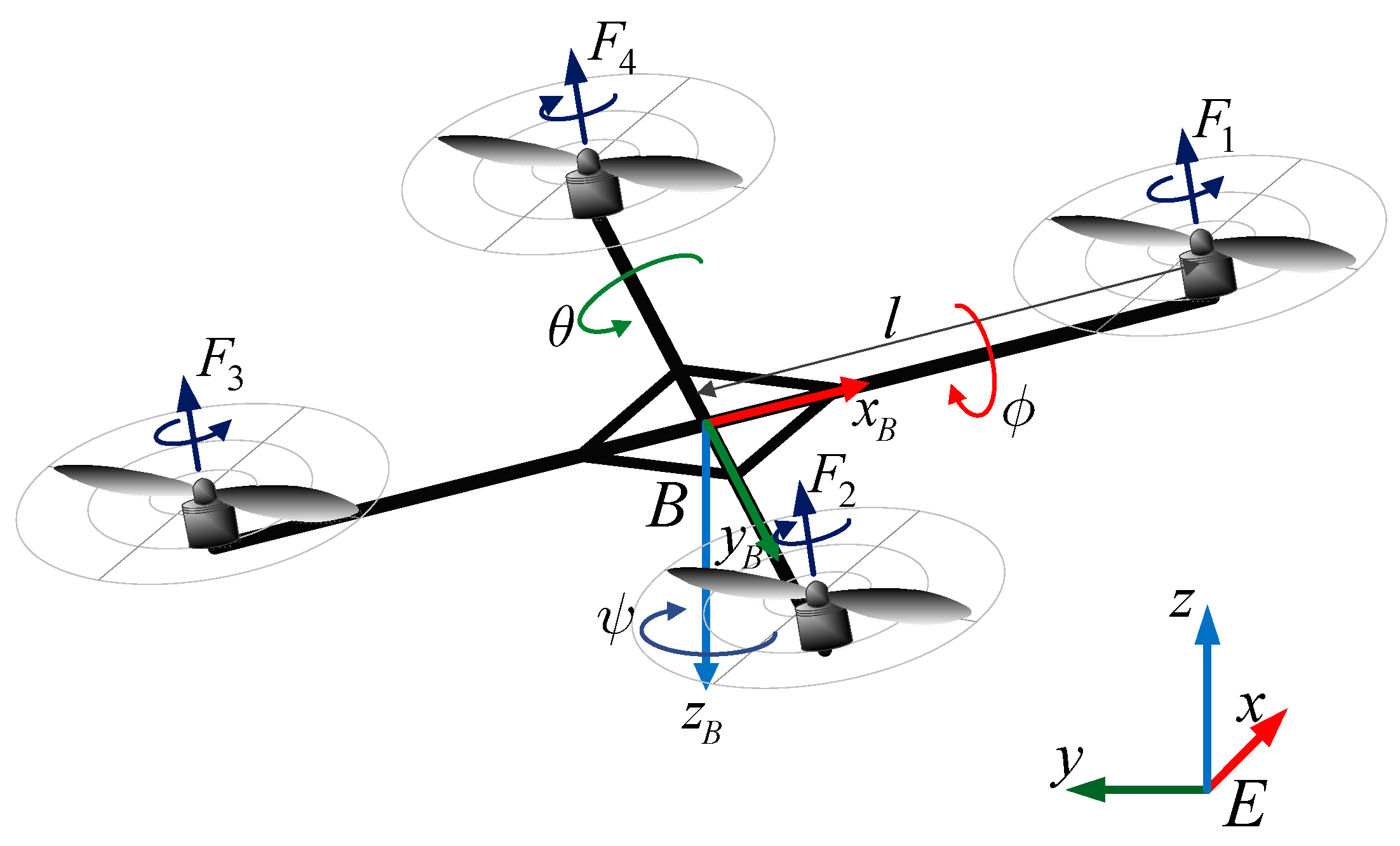
3.1. Dynamics Model of Quadcopter UAVs
3.2. Attitude Controller
3.3. Altitude Controller
4. Simulation Results and Discussions
4.1. Simulation Assumptions
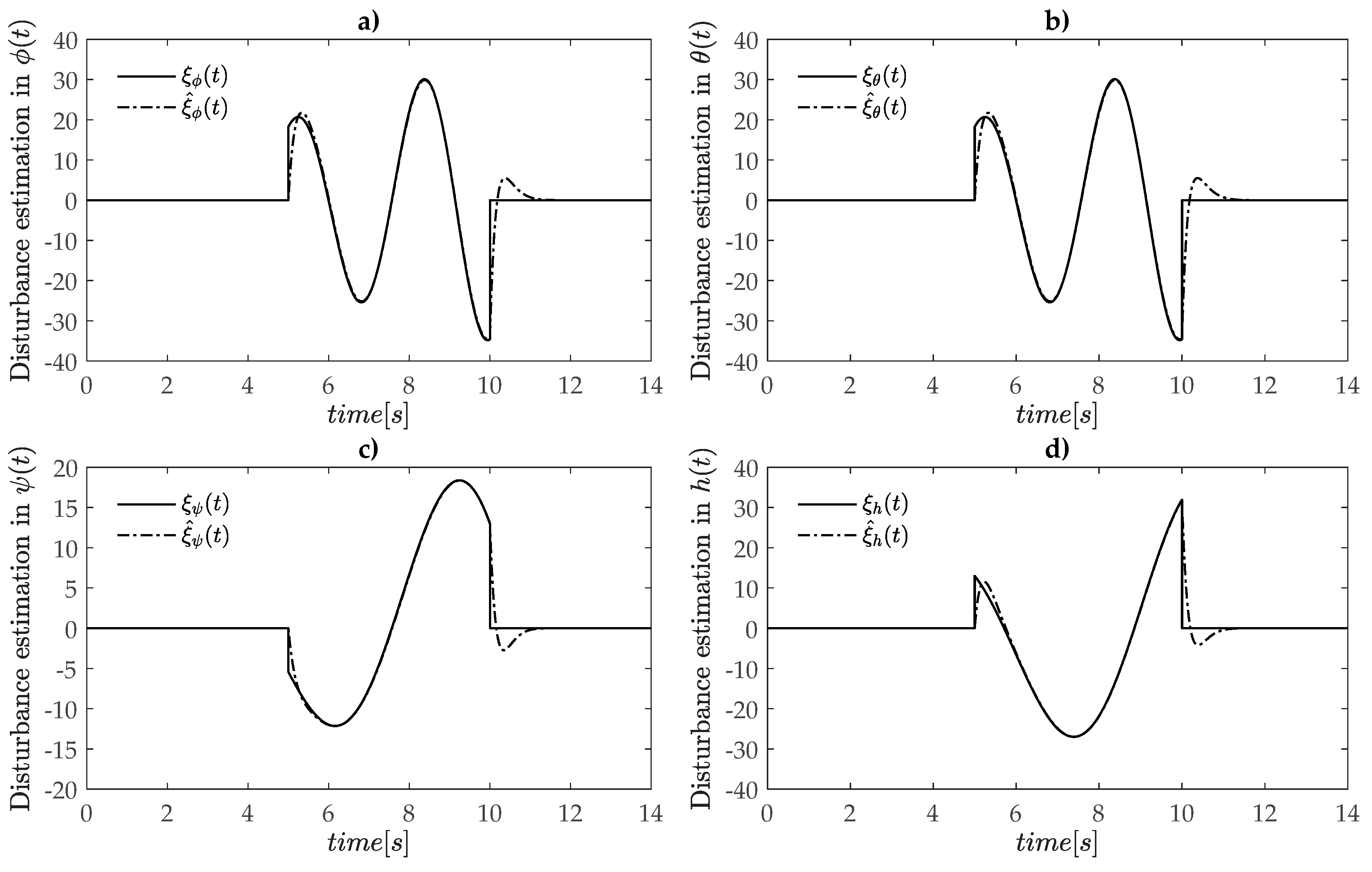
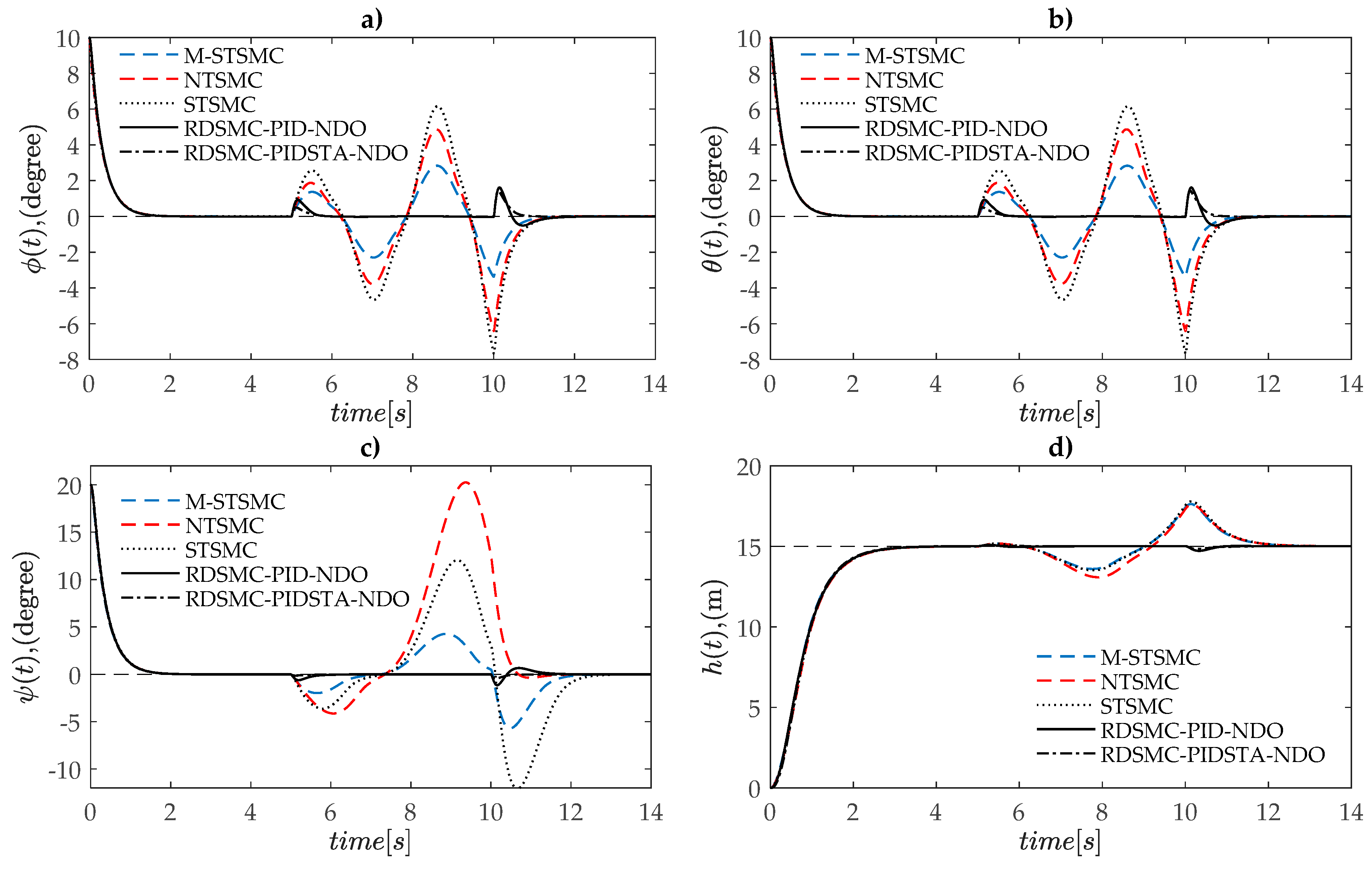
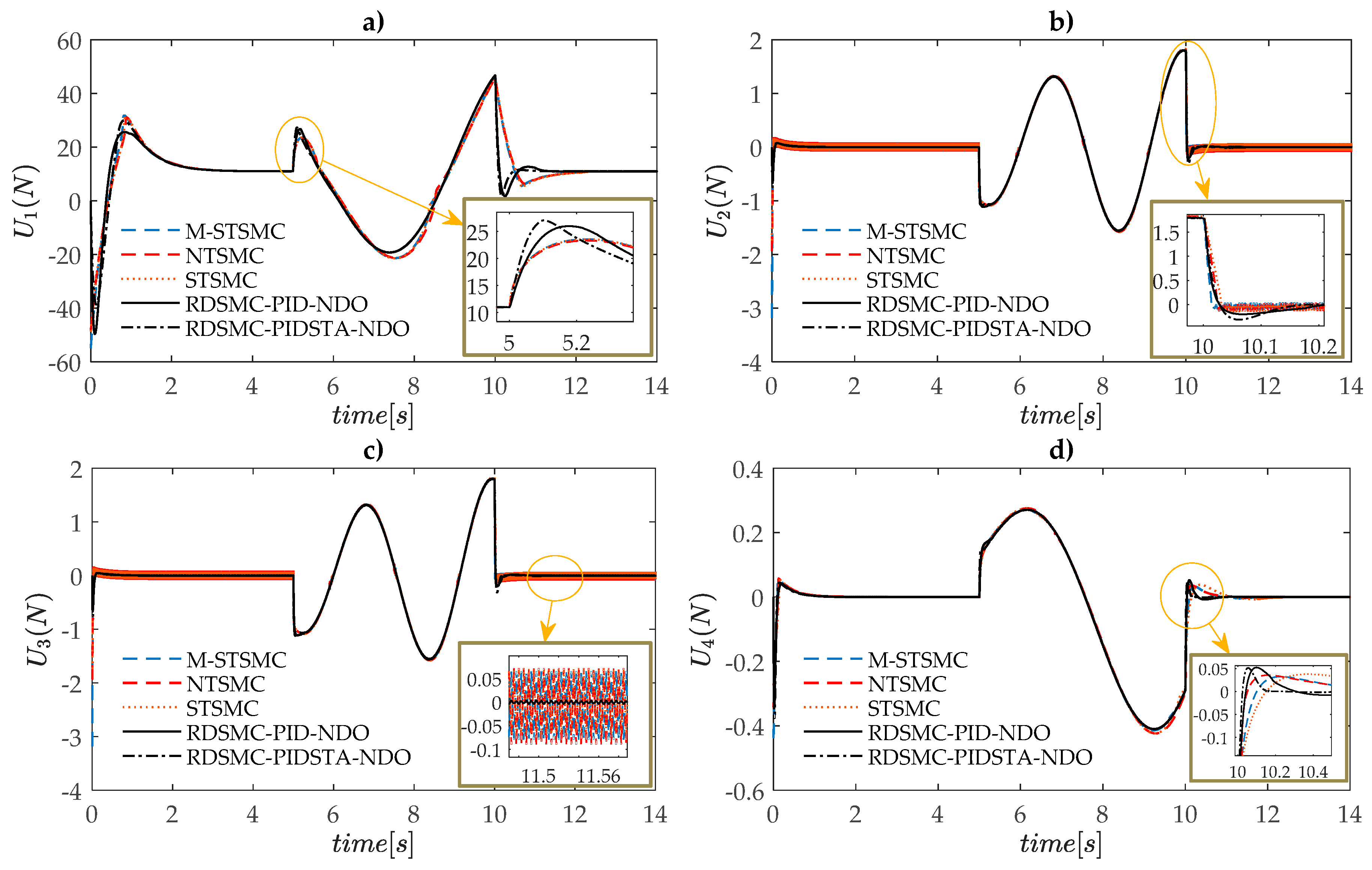
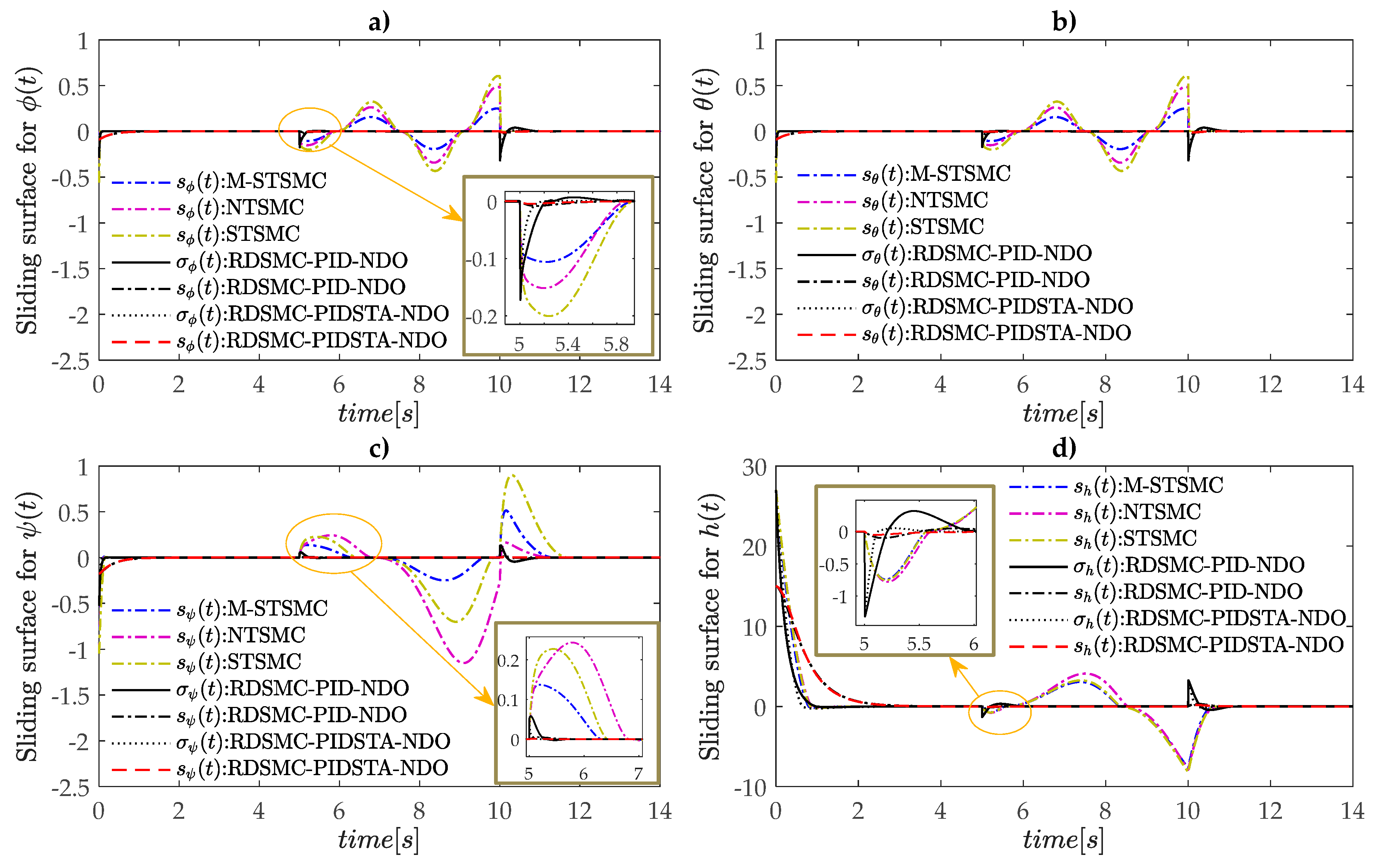
4.2. Simulation Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zheng, E.H.; Xiong, J.J.; Luo, J.L. Second order sliding mode control for a quadrotor UAV. ISA Trans. 2014, 53, 1350–1356. [Google Scholar] [CrossRef] [PubMed]
- Xiong, J.J.; Zhang, G.B. Global fast dynamic terminal sliding mode control for a quadrotor UAV. ISA Trans. 2017, 66, 233–240. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Yang, J.; Li, S. Continuous finite-time anti-disturbance control for a class of uncertain nonlinear systems. Trans. Inst. Meas. Control 2014, 36, 300–311. [Google Scholar] [CrossRef]
- Yang, J.; Su, J.; Li, S.; Yu, X. High-order mismatched disturbance compensation for motion control systems via a continuous dynamic sliding-mode approach. IEEE Trans. Ind. Inform. 2014, 10, 604–614. [Google Scholar] [CrossRef]
- Barghandan, S.; Badamchizadeh, M.A.; Motlagh, M.R.J. Improved adaptive fuzzy sliding mode controller for robust fault tolerant of a quadrotor. Int. J. Control Autom. Syst. 2017, 15, 427–441. [Google Scholar] [CrossRef]
- Van, M. An enhanced robust fault tolerant control based on an adaptive fuzzy PID-nonsingular fast terminal sliding mode control for uncertain nonlinear systems. IEEE/ASME Trans. Mechatron. 2018, 23, 1362–1371. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, P.; Xia, Y. Robust adaptive sliding–mode control for fuzzy systems with mismatched uncertainties. IEEE Trans. Fuzzy Syst. 2010, 18, 700–711. [Google Scholar] [CrossRef]
- Gong, X.; Hou, Z.C.; Zhao, C.J.; Bai, Y.; Tian, Y.T. Adaptive backstepping sliding mode trajectory tracking control for a quadrotor. Int. J. Autom. Comput. 2012, 9, 555–560. [Google Scholar] [CrossRef]
- Rodriguez, H.R.; Vega, V.P.; Orta, A.S.; Salazar, O.G. Robust backstepping control based on integral sliding mode for tracking of quadrotors. J. Intell. Robot. Syst. 2014, 73, 51–66. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, R.; Zhang, K.; Jiang, B.; Tao, G. Robust backstepping sliding-mode control and observer-based fault estimation for a quadrotor UAV. IEEE Trans. Ind. Electron. 2016, 63, 5044–5056. [Google Scholar] [CrossRef]
- Lee, T. Robust adaptive attitude tracking on SO3 with an application to a quadrotor UAV. IEEE Trans. Control Syst. Technol. 2013, 21, 1924–1930. [Google Scholar]
- Mofid, O.; Mobayen, S. Adaptive sliding mode control for finite-time stability of quad-rotor UAVs with parametric uncertainties. ISA Trans. 2018, 72, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Xian, B.; Zhang, Y.; Zhang, X. Nonlinear robust adaptive tracking control of a quadrotor UAV via immersion and invariance methodology. IEEE Trans. Ind. Electron. 2015, 62, 2891–2902. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Tan, J. Adaptive and robust control of quadrotor aircrafts with input saturation. Nonlinear Dyn. 2017, 89, 255–265. [Google Scholar] [CrossRef]
- Liu, H.; Xi, J.; Zhong, Y. Robust attitude stabilization for nonlinear quadrotor systems with uncertainties and delays. IEEE Trans. Ind. Electron. 2017, 64, 5585–5594. [Google Scholar] [CrossRef]
- Nadda, S.; Swarup, A. On adaptive sliding mode control for improved quadrotor tracking. J. Vib. Control 2017, 24, 3219–3230. [Google Scholar] [CrossRef]
- Thanh, H.L.; Hong, S.K. Quadcopter robust adaptive second order sliding mode control based on PID sliding surface. IEEE Access 2018, 6, 66850–66860. [Google Scholar] [CrossRef]
- Rios, H.; Sierra, J.G.; Dzul, A. Robust tracking output-control for a quad-rotor: A continuous sliding-mode approach. J. Frankl. Inst. 2017, 354, 6672–6691. [Google Scholar] [CrossRef]
- Dydek, Z.T.; Annaswamy, A.M.; Lavretsky, E. Adaptive control of quadcopter UAVs: A design trade study with flight evaluations. IEEE Trans. Control Syst. Technol. 2013, 21, 1400–1406. [Google Scholar] [CrossRef]
- MacKunis, W.; Wilcox, Z.D.; Kaiser, M.K.; Dixon, W.E. Global adaptive output feedback tracking control of an unmanned aerial vehicle. IEEE Trans. Control Syst. Technol. 2010, 18, 1390–1397. [Google Scholar] [CrossRef]
- Le, M.; Cheng, Y. Robust adaptive sliding mode control for switched networked control systems with disturbance and faults. IEEE Trans. Ind. Inform. 2019, 15, 193–204. [Google Scholar]
- Mystkowski, A. Implementation and investigation of a robust control algorithm for an unmanned micro-aerial vehicle. Robot. Auton. Syst. 2014, 62, 1187–1196. [Google Scholar] [CrossRef]
- Mystkowski, A. An application of mu-synthesis for control of a small air vehicle and simulation results. J. Vibroengineering 2012, 14, 79–86. [Google Scholar]
- Li, S.; Wang, Y.; Tan, J.; Zheng, Y. Adaptive RBFNNs/integral sliding mode control for a quadrotor aircraft. Neurocomputing 2016, 216, 126–134. [Google Scholar] [CrossRef]
- Yin, Y.; Niu, H.; Liu, X. Adaptive neural network sliding mode control for quad tilt rotor aircraft. Complexity 2017, 2017, 7104708. [Google Scholar] [CrossRef]
- Peng, C.; Bai, Y.; Gong, X.; Gao, Q.; Zhao, C.; Tian, Y. Modeling and robust backstepping sliding mode control with adaptive RBFNN for a novel coaxial eight-rotor UAV. IEEE/CAA J. Autom. Sin. 2015, 2, 56–64. [Google Scholar]
- Razmi, H.; Afshinfar, S. Neural network-based adaptive sliding mode control design for position and attitude control of a quadrotor UAV. Aerosp. Sci. Technol. 2019, 91, 12–27. [Google Scholar] [CrossRef]
- Ejaz, F.; Hamayun, M.T.; Hussian, S.; Ljaz, S.; Yang, S.; Shehzad, N.; Rashid, A. An adaptive sliding mode actuator fault tolerant control scheme for octorotor system. Int. J. Adv. Robot. Syst. 2019, 16. [Google Scholar] [CrossRef]
- Lei, X.; Guo, K.; Ge, S.S. Disturbance observer based control of small unmanned aerial rotorcraft. Math. Probl. Eng. 2013, 2013, 464938. [Google Scholar] [CrossRef]
- Smith, J.; Su, J.; Liu, C.; Chen, W.H. Disturbance observer based control with anti-windup applied to a small fixed wing UAV for disturbance. J. Intell. Robot. Syst. 2017, 88, 329–346. [Google Scholar] [CrossRef]
- Besnard, L.; Shtessel, Y.B.; Landrum, B. Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer. J. Frankl. Inst. 2012, 349, 658–684. [Google Scholar] [CrossRef]
- Ahmed, N.; Chen, M. Sliding mode control for quadrotor with disturbance observer. Adv. Mech. Eng. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, B.; Mao, D. Robust sliding mode control of PMSM based on rapid nonlinear tracking differentiator and disturbance observer. Sensor 2018, 18, 1031. [Google Scholar] [CrossRef] [PubMed]
- Munoz, F.; Hernandez, I.G.; Salazar, S.; Espinoza, E.S.; Lozano, R. Second order sliding mode controllers for altitude control of a quadrotor UAS: Real-time implementation in outdoor environments. Neurocomputing 2017, 233, 61–71. [Google Scholar] [CrossRef]
- Akbar, R.; Uchiyama, N. Adaptive modified super-twisting control for a quadrotor helicopter with a nonlinear sliding surface. In Proceedings of the SICE International Symposium on Control System (SICE ISCS), Okayama, Japan, 6–9 March 2017; pp. 1–6. [Google Scholar]
- Tran, M.D.; Kang, H.J. Nonsingular terminal sliding mode control of uncertain second-order nonlinear systems. Math. Probl. Eng. 2015, 2015, 181737. [Google Scholar] [CrossRef]
- Derafa, L.; Benallegue, A.; Fridman, L. Super twisting control algorithm for the attitude tracking of a four rotors UAV. J. Frankl. Inst. 2012, 349, 685–699. [Google Scholar] [CrossRef]
- Wang, J.Y.; Luo, B.; Zeng, M.; Meng, Q.H. A wind estimation method with an unmanned rotorcraft for environmental monitoring tasks. Sensors 2018, 18, 4504. [Google Scholar] [CrossRef] [PubMed]
- Langelaan, J.W.; Alley, N.; Neidhoefer, J. Wind field estimation for small unmanned aerial vehicles. J. Guid. ControlDyn. 2011, 34, 1016–1030. [Google Scholar] [CrossRef]
- Song, Y.; Luo, B.; Meng, Q.H. A rotor-aerodynamics-based wind estimation method using a quadrotor. Meas. Sci. Technol. 2018, 29, 025801. [Google Scholar] [CrossRef]
- Chen, W.H. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 47th IEEE conference on Decision and Control, Cancun, Mexico, 9–11 December 2008. [Google Scholar]
- Moreno, J.A.; Osorio, M. Strict Lyapunov functions for the super-twisting algorithm. IEEE Trans. Autom. Control 2012, 57, 1035–1040. [Google Scholar] [CrossRef]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A. Model predictive quadrotor control: Attitude, altitude and position experimental studies. IET Control Theory Appl. 2012, 6, 1812–1827. [Google Scholar] [CrossRef]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. An integral predictive/nonlinear H∞ control structure for a quadrotor helicopter. Automatica 2010, 46, 29–39. [Google Scholar] [CrossRef]
- Jia, Z.; Yu, J.; Mei, Y.; Chen, Y.; Shen, Y.; Ai, X. Integral backstepping sliding mode control for quadrotor helicopter under external uncertain disturbances. Aerosp. Sci. Technol. 2017, 68, 299–307. [Google Scholar] [CrossRef]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A. Switching model predictive attitude control for a quadrotor helicopter subject to atmospheric disturbances. Control Eng. Pract. 2011, 19, 1195–1207. [Google Scholar] [CrossRef]
- Ha, L.N.; Bui, D.H.; Hong, S.K. Nonlinear control for autonomous trajectory tracking while considering collision avoidance of UAVs based on geometric relations. Energies 2019, 12, 1551. [Google Scholar] [CrossRef]
- Thanh, H.L.; Hong, S.K. Completion of collision avoidance control algorithm for multicopters based on geometrical constrains. IEEE Access 2018, 6, 27111–27125. [Google Scholar] [CrossRef]
- Thanh, H.L.; Phi, N.N.; Hong, S.K. Simple nonlinear control of quadcopter for collision avoidance based on geometric approach in static environment. Int. J. Adv. Robot. Syst. 2018, 15, 1–17. [Google Scholar] [CrossRef]
- Wang, H.; Ye, X.; Tian, Y.; Zheng, G.; Christov, N. Model-free-based terminal SMC of quadrotor attitude and position. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2519–2528. [Google Scholar] [CrossRef]
| System Parameters | Descriptions |
|---|---|
| Ixx, Iyy, Izz (kgm2) | Moments of inertia along three axes x,y and z in the Earth frame |
| m (kg) | Total mass of a quadcopter |
| l (m) | Arm length of the quadcopter frame |
| b (Ns2) | Thrust coefficient |
| d (Nms2) | Drag coefficient |
| Jr (kgm2) | Moment of inertial of a rotor |
| Symbol | Descriptions | Value and Unit |
|---|---|---|
| m | Total mass of quadcopter | 1.12 kg |
| Ixx | Moment of inertia along x-axis | 0.0119 kg.m2 |
| Iyy | Moment of inertia along y-axis | 0.0119 kg.m2 |
| Izz | Moment of inertia along z-axis | 0.0223 kg.m2 |
| b | Thrust coefficient | 7.73213 (10−6) Ns2 |
| d | Drag coefficient | 1.27513 (10−7) Nms2 |
| Jr | Moment of inertial of a rotor | 8.5(10−4) kgm2 |
| l | Arm length | 0.23 m |
| Initial and desired states of roll controller | 10; 0 degree | |
| Initial and desired states of pitch controller | 10; 0 degree | |
| Initial and desired states of yaw controller | 20; 0 degree | |
| Initial and desired states of altitude controller | 0; 15 m |
| Symbol | Roll (φ) | Pitch (θ) | Yaw (ψ) | Altitude (h) |
|---|---|---|---|---|
| 0.5 | 0.5 | 0.5 | 1.0 | |
| 0.001 | 0.001 | 0.001 | 0.001 | |
| 0.008 | 0.008 | 0.008 | 0.1 | |
| λ | 3.3 | 3.3 | 3.0 | 1.8 |
| β | 60 | 60 | 30 | 4.5 |
| 0.5 | 0.5 | 0.1 | 1.0 | |
| 30 | 30 | 20 | 15 | |
| 0.1 | 0.1 | 0.1 | 1.0 | |
| 10 | 10 | 10 | 10 | |
| 12 | 12 | 30 | 30 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ha, L.N.N.T.; Hong, S.K. Robust Dynamic Sliding Mode Control-Based PID–Super Twisting Algorithm and Disturbance Observer for Second-Order Nonlinear Systems: Application to UAVs. Electronics 2019, 8, 760. https://doi.org/10.3390/electronics8070760
Ha LNNT, Hong SK. Robust Dynamic Sliding Mode Control-Based PID–Super Twisting Algorithm and Disturbance Observer for Second-Order Nonlinear Systems: Application to UAVs. Electronics. 2019; 8(7):760. https://doi.org/10.3390/electronics8070760
Chicago/Turabian StyleHa, Le Nhu Ngoc Thanh, and Sung Kyung Hong. 2019. "Robust Dynamic Sliding Mode Control-Based PID–Super Twisting Algorithm and Disturbance Observer for Second-Order Nonlinear Systems: Application to UAVs" Electronics 8, no. 7: 760. https://doi.org/10.3390/electronics8070760
APA StyleHa, L. N. N. T., & Hong, S. K. (2019). Robust Dynamic Sliding Mode Control-Based PID–Super Twisting Algorithm and Disturbance Observer for Second-Order Nonlinear Systems: Application to UAVs. Electronics, 8(7), 760. https://doi.org/10.3390/electronics8070760






