Limitations of Harmonics Control in Power Converters
Abstract
:1. Introduction
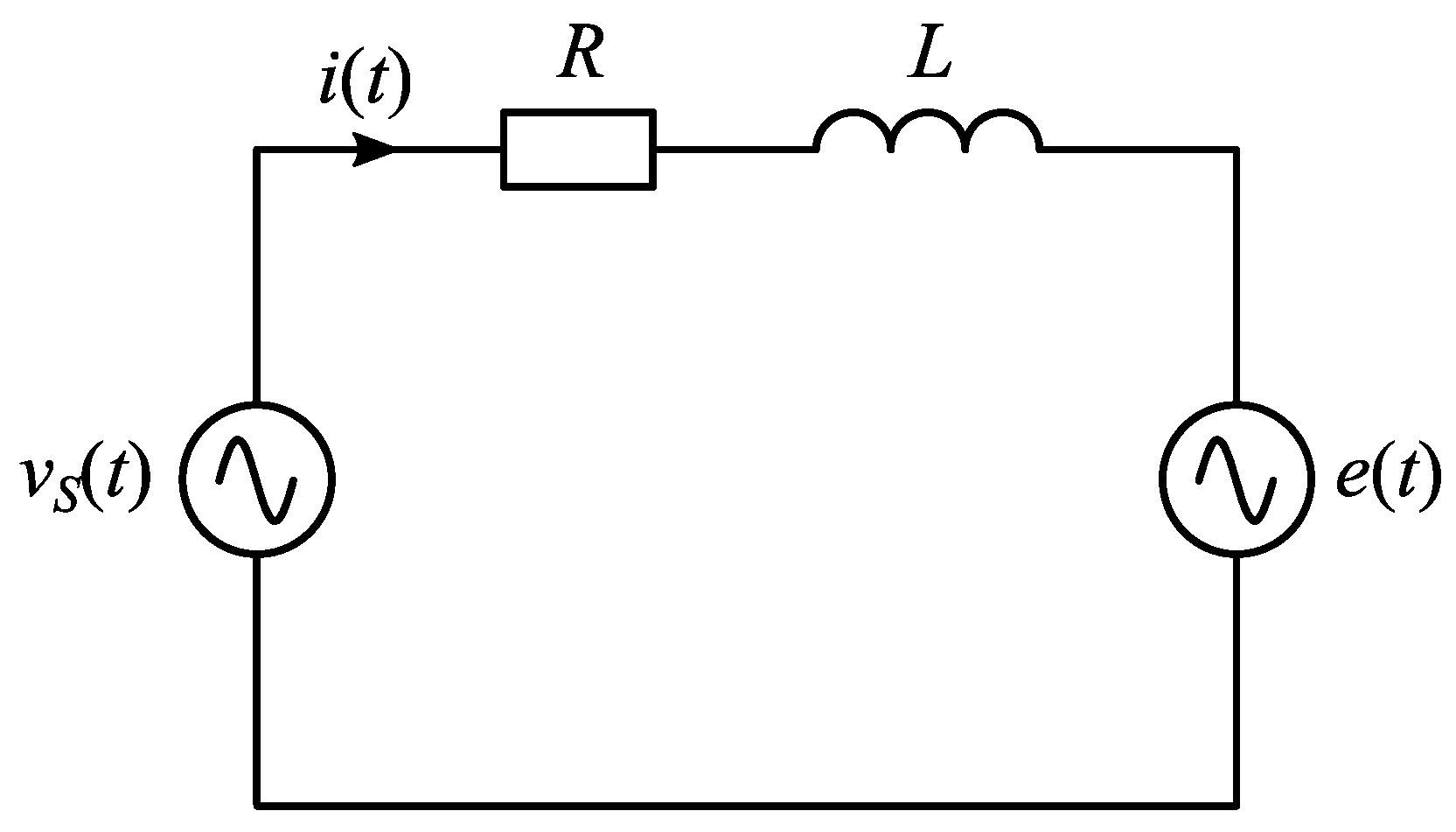
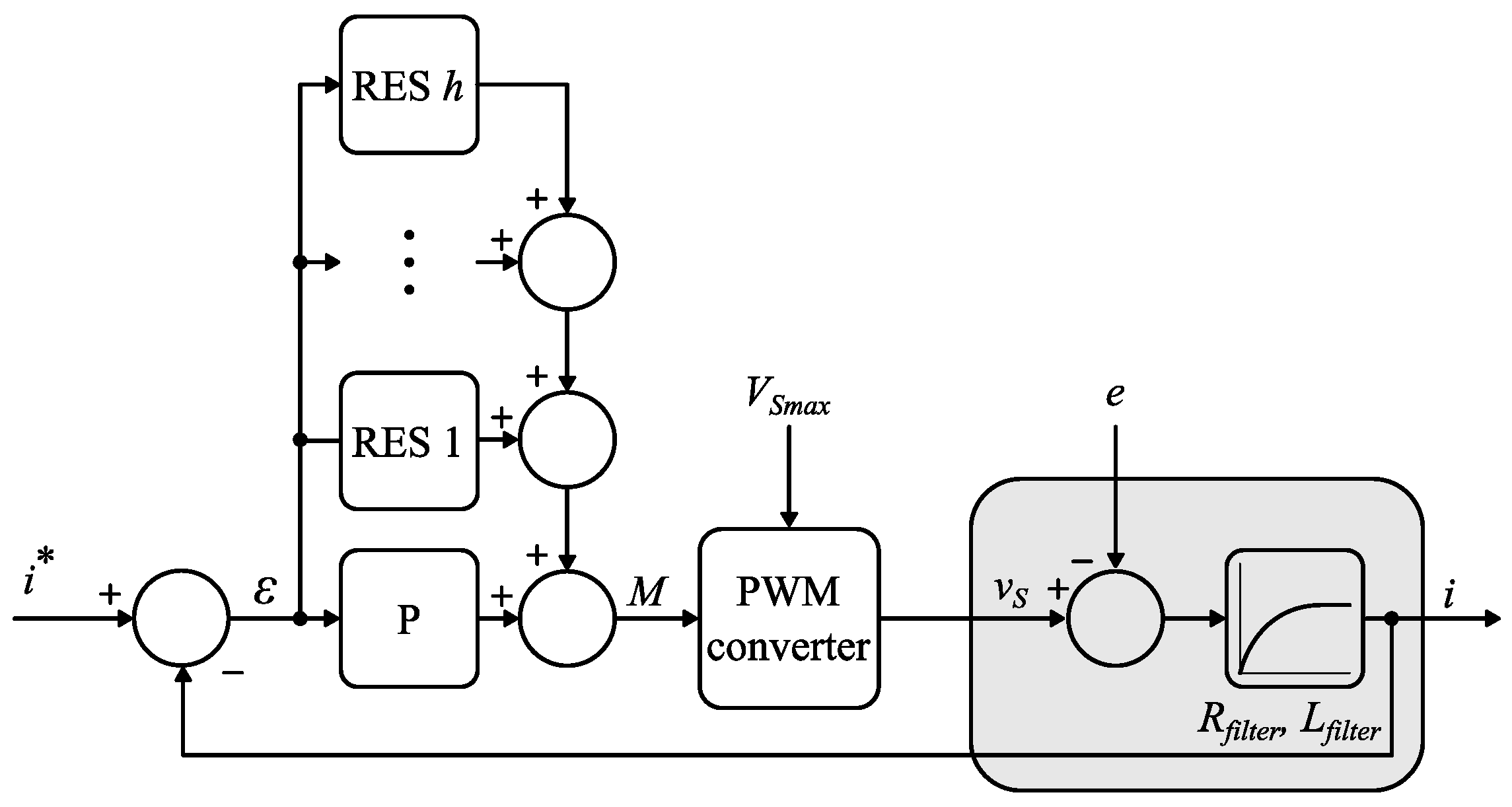
2. Methodology
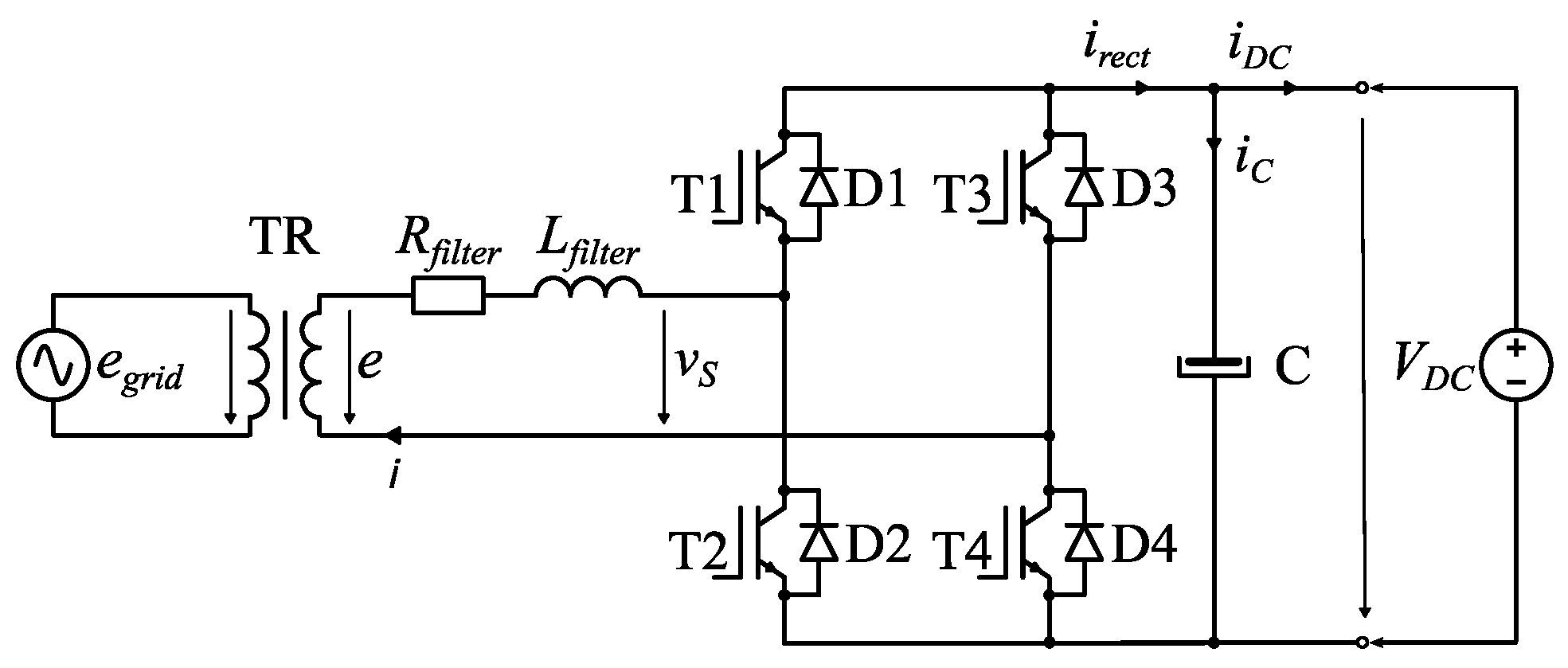
3. Experimental Setup
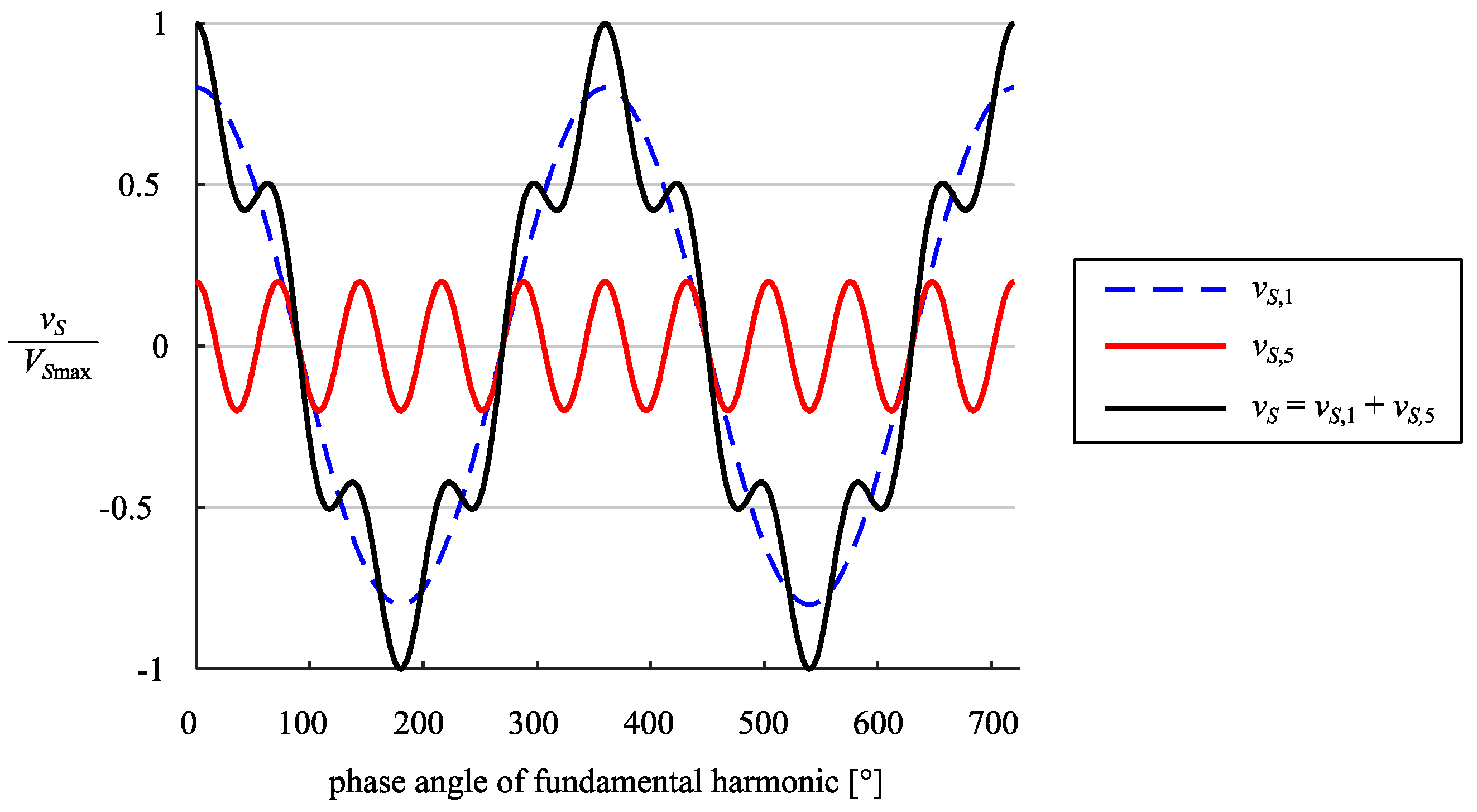
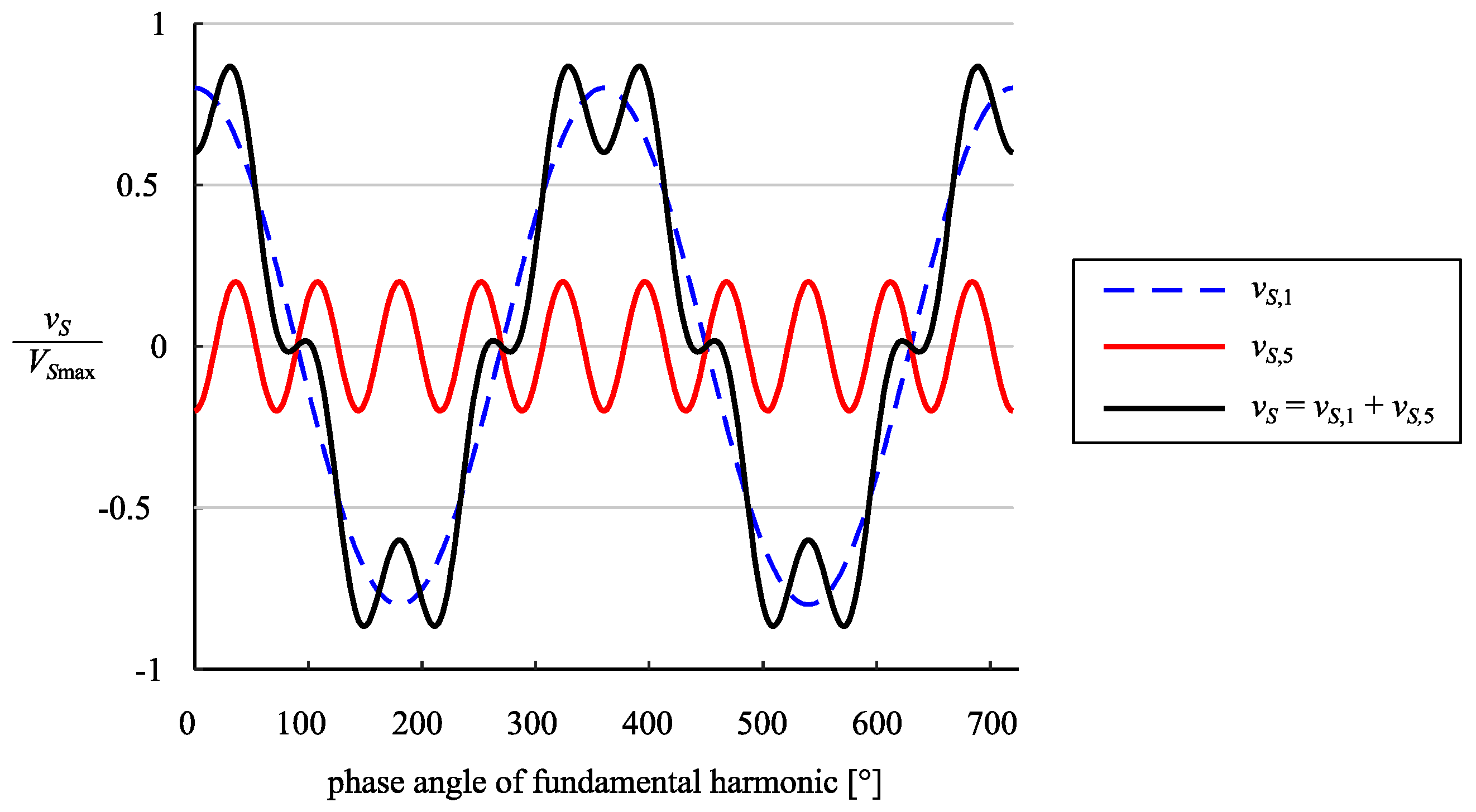
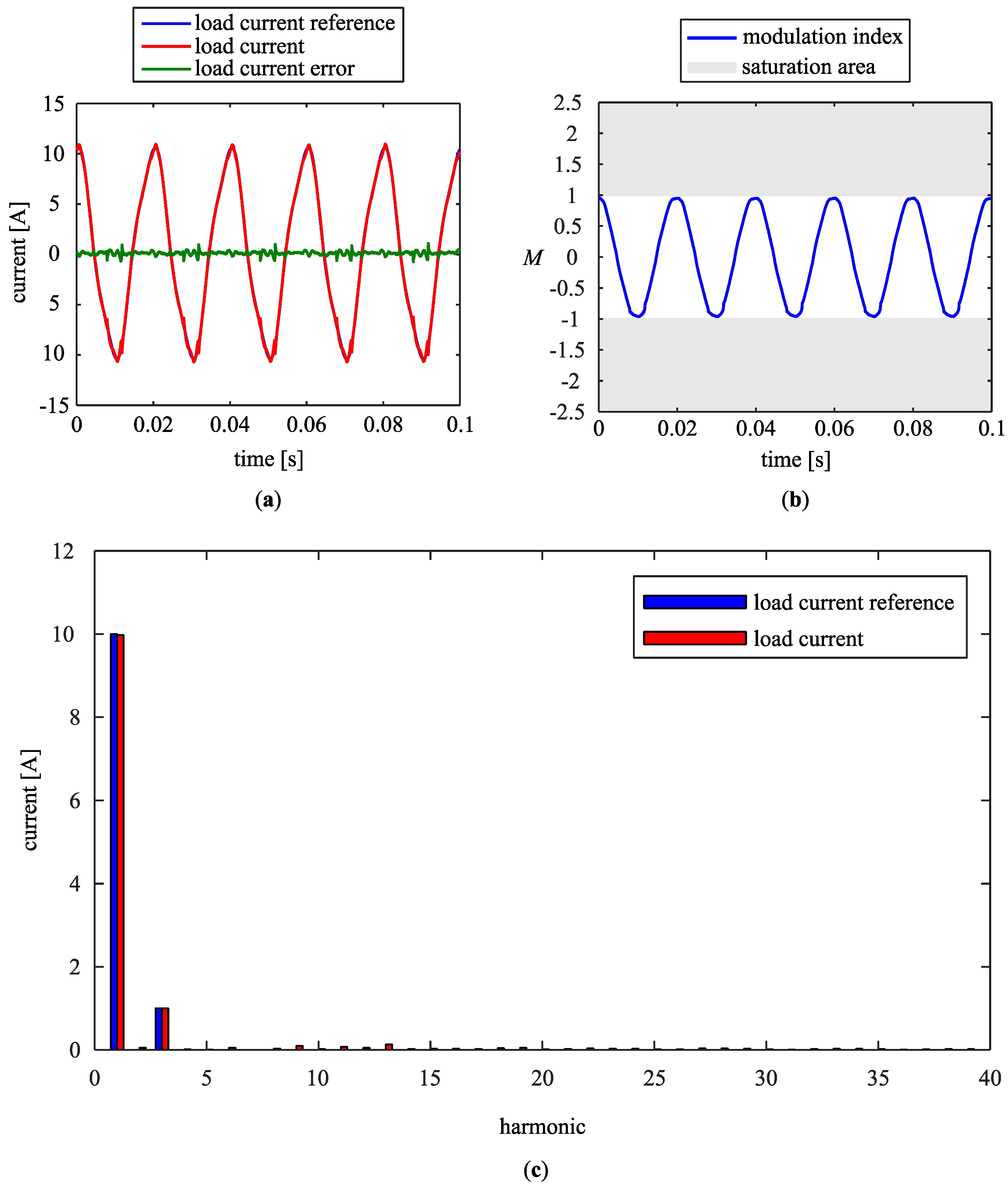
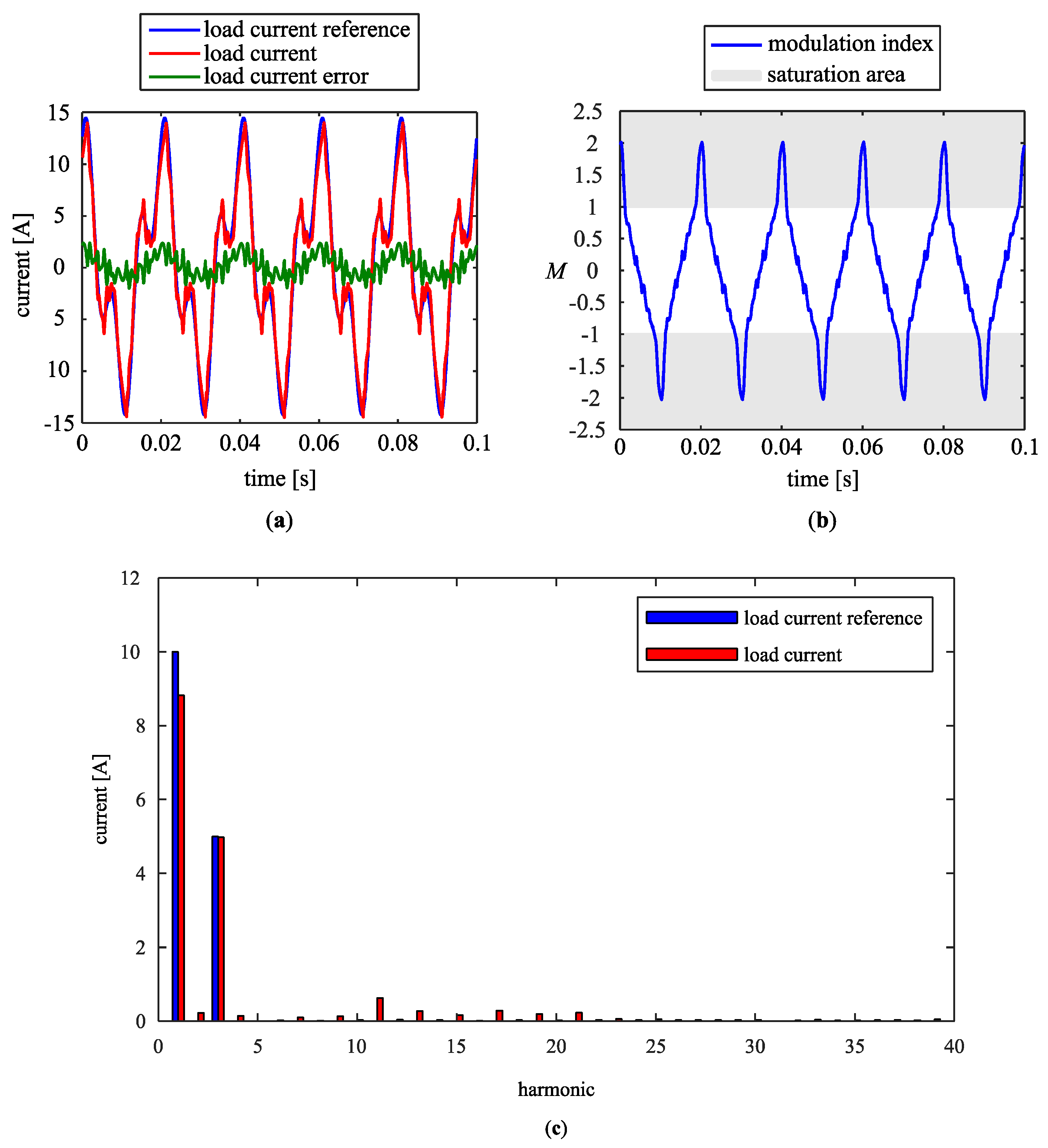
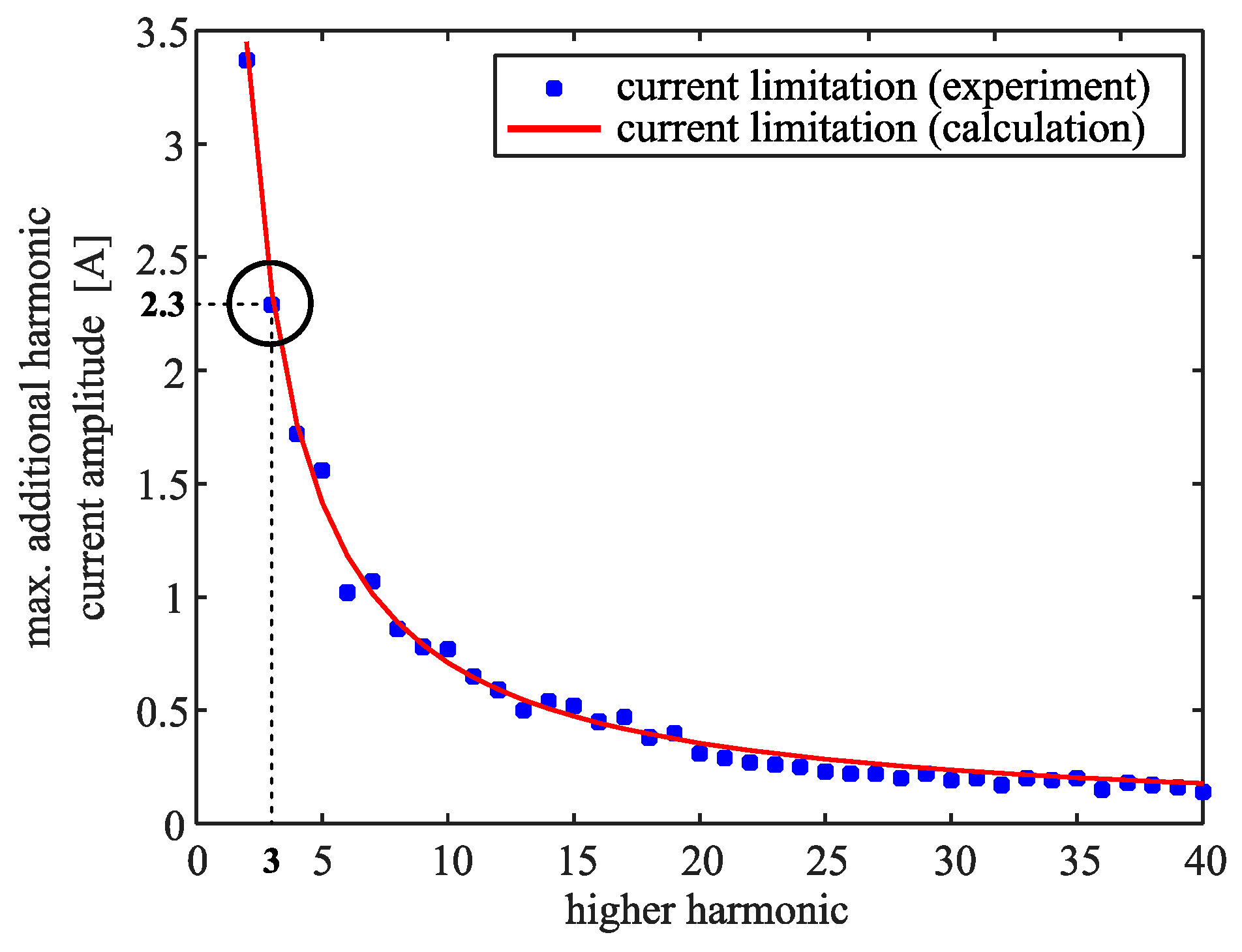
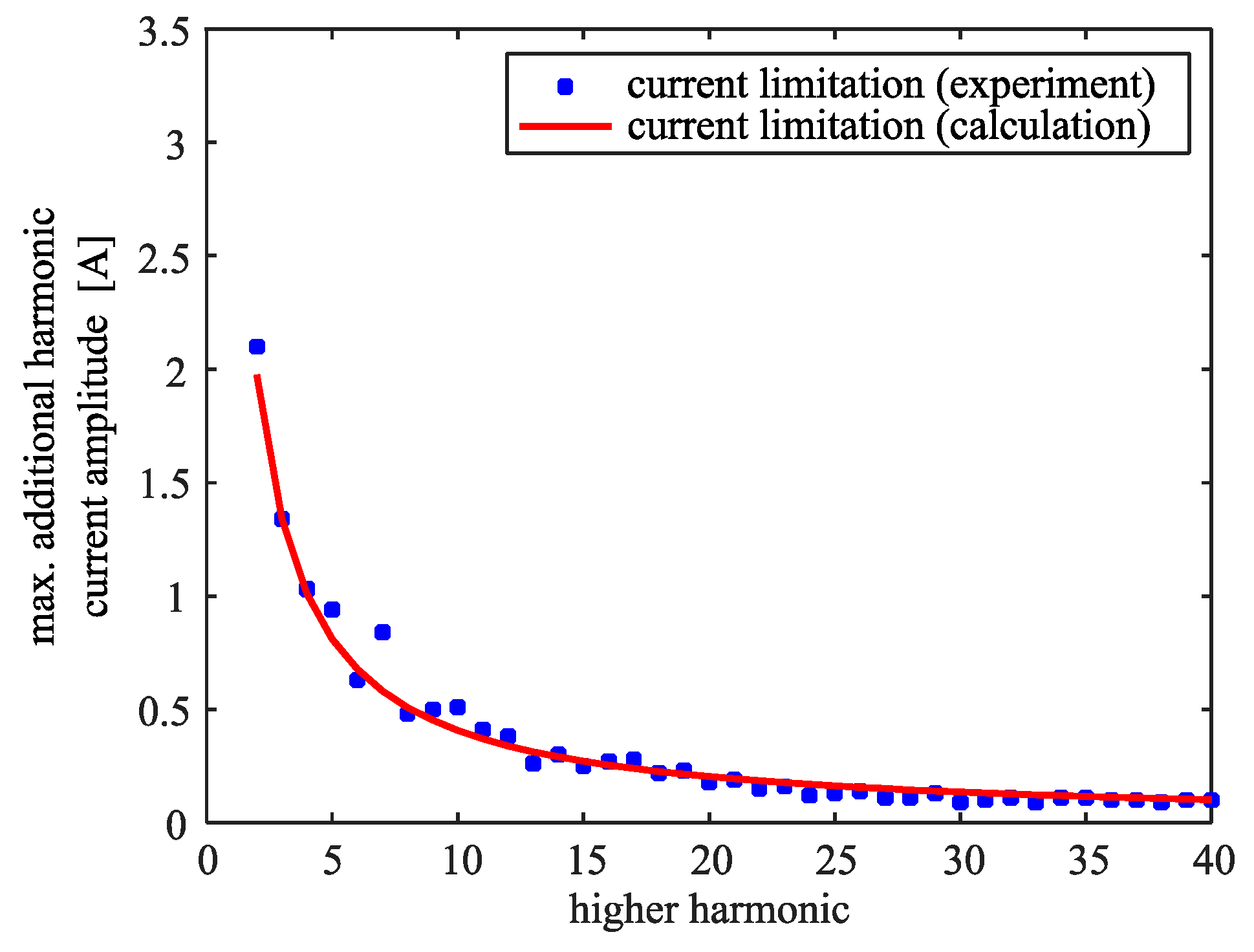
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IEC Standard for Harmonic Current Emissions; IEC 61000-3-2; IEC: Centurion, South Africa, 2001.
- IEEE Standard for Interconnecting Distributed Resources with Electric Power Systems; IEEE: Piscataway, NJ, USA, 2009; pp. 1547–2003.
- Catuogno, G.R.; Forchetti, D.G.; Leidhold, R.; Garcia, G.O. Power Flow Maximization in Permanent-Magnet Generators. IEEE Trans. Ind. Electron. 2014, 61, 6566–6573. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, K.; Wang, H.; Blaabjerg, F. Analysis and Mitigation of Dead-Time Harmonics in the Single-Phase Full-Bridge PWM Converter with Repetitive Controllers. IEEE Trans. Ind. Appl. 2018, 54, 5343–5354. [Google Scholar] [CrossRef]
- Schuelting, P.; van der Broeck, C.H.; Doncker, R. Analysis and Design of Repetitive Controllers for Applications in Distorted Distribution Grids. IEEE Trans. Power Electron. 2018, 34, 996–1004. [Google Scholar] [CrossRef]
- Lidozzi, A.; Ji, C.; Solero, L.; Zanchetta, P.; Crescimbini, F. Digital dead-beat and repetitive combined control for stand-alone four-leg VSI. IEEE Trans. Ind. Appl. 2017, 53, 5624–5633. [Google Scholar] [CrossRef]
- Lee, S.-H.; Cha, W.-J.; Kwon, B.-H.; Kim, M. Discrete-Time Repetitive Control of Flyback CCM Inverter for PV Power Applications. IEEE Trans. Ind. Electron. 2016, 63, 976–984. [Google Scholar] [CrossRef]
- Julian, A.L.; Oriti, G.; Ji, C.; Zanchetta, P. Single Phase Energy Management System Operating in Islanding Mode with Repetitive Control and Active Damping. IEEE Trans. Ind. Appl. 2018, 54, 5163–5172. [Google Scholar] [CrossRef]
- Lorenzini, C.; Flores, J.V.; Pereira, L.F.A.; Pereira, L.A. Resonant—Repetitive controller with phase correction applied to uninterruptible power supplies. Control Eng. Pract. 2018, 77, 118–126. [Google Scholar] [CrossRef]
- Herman, L.; Blazic, B.; Papic, I. A control strategy of a hybrid active filter for operation with harmonically unbalanced voltages and currents. In Proceedings of the 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 386–394. [Google Scholar]
- Mattavelli, P.; Marafao, F.P. Repetitive-Based Control for Selective Harmonic Compensation in Active Power Filters. IEEE Trans. Ind. Electron. 2004, 51, 1018–1024. [Google Scholar] [CrossRef]
- Sun, B. An Improved Repetitive Control Scheme for Active Power Filter with Frequency-Adaptive Capability. In Proceedings of the 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 25–28 October 2015. [Google Scholar]
- Hornik, T.; Zhong, Q. A Current-Control Strategy for Voltage-Source Inverters in Microgrids Based on H∞ and Repetitive Control. IEEE Trans. Power Electron. 2011, 26, 943–952. [Google Scholar] [CrossRef]
- Tang, Z.; Akin, B. Suppression of Dead-Time Distortion Through Revised Repetitive Controller in PMSM Drives. IEEE Trans. Energy Convers. 2017, 32, 918–930. [Google Scholar] [CrossRef]
- Mattavelli, P.; Tubiana, L.; Zigliotto, M. Torque-Ripple Reduction in PM Synchronous Motor Drives Using Repetitive Current Control. IEEE Trans. Power Electron. 2005, 20, 1423–1431. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, K.; Blaabjerg, F. Enhancing the Frequency Adaptability of Periodic Current Controllers with a Fixed Sampling Rate for Grid-Connected Power Converters. IEEE Trans. Power Electron. 2016, 31, 7273–7285. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Xing, Y.; Hu, H. Enhanced DFT-Based Controller for Selective Harmonic Compensation in Active Power Filters. IEEE Trans. Power Electron. 2019, 34, 8017–8030. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, K.; Blaabjerg, F. Current Harmonics from Single-Phase Grid-Connected Inverters—Examination and Suppression. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 221–233. [Google Scholar] [CrossRef]
- Dannehl, J.; Wessels, C.; Fuchs, F.W. Limitations of Voltage-Oriented PI Current Control of Grid-Connected PWM Rectifiers with LCL Filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar] [CrossRef]
- Lee, G.; Kim, S.; Hong, J.; Bahn, J. Torque Ripple Reduction of Interior Permanent Magnet Synchronous Motor Using Harmonic Injected Current. IEEE Trans. Magn. 2008, 44, 1582–1585. [Google Scholar]
- Liu, J.; Li, H.; Deng, Y. Torque Ripple Minimization of PMSM Based on Robust ILC Via Adaptive Sliding Mode Control. IEEE Trans. Power Electron. 2018, 33, 3655–3671. [Google Scholar] [CrossRef]
- Lai, C.; Feng, G.; Iyer, K.L.V.; Mukherjee, K.; Kar, N.C. Genetic Algorithm-Based Current Optimization for Torque Ripple Reduction of Interior PMSMs. IEEE Trans. Ind. Appl. 2017, 53, 4493–4503. [Google Scholar] [CrossRef]
- Xia, C.; Ji, B.; Yan, Y. Smooth Speed Control for Low-Speed High-Torque Permanent-Magnet Synchronous Motor Using Proportional–Integral–Resonant Controller. IEEE Trans. Ind. Electron. 2015, 62, 2123–2134. [Google Scholar] [CrossRef]
- Das, J.C. Passive Filters—Potentialities and Limitations. IEEE Trans. Ind. Appl. 2004, 40, 232–241. [Google Scholar] [CrossRef]
- Zhang, C. A Stationary-Frame Current Vector Control Strategy for Single-Phase PWM Rectifier. IEEE Trans. Veh. Technol. 2019, 68, 2640–2651. [Google Scholar] [CrossRef]
- Mattavelli, P.; Buso, S. Digital Control in Power Electronics, 2nd ed.; Morgan & Claypool: San Rafael, CA, USA, 2012. [Google Scholar]


| Symbol | Description |
|---|---|
| VSmax | power converter maximal output voltage |
| h | order of harmonic |
| ω1 | fundamental angular frequency of the load voltage and current |
| R | load resistance |
| L | load inductance |
| h | amplitude of load voltage h-th harmonic |
| h | amplitude of load current h-th harmonic |
| φEh | phase angle of load voltage h-th harmonic |
| φIh | phase angle of load current h-th harmonic |
| fS | sampling frequency |
| td | dead time during transistor switching |
| RT | transistor’s ON resistance |
| Symbol | Description | Test Case Values |
|---|---|---|
| Rfilter | filter AC resistance | 47 mΩ |
| Lfilter | filter inductance | 580 µH |
| RTR2 | transformer AC resistance (secondary winding) | 32 mΩ |
| LTR2 | transformer leakage inductance (secondary winding) | 8 µH |
| RT | transistor’s ON resistance | 7.2 mΩ |
| VDC | DC link voltage | 38 V |
| C | DC link capacitance | 41 mF |
| P | converter’s nominal power | 500 W |
| 1 | amplitude of load voltage 1st harmonic | 35.4 V |
| 1 | amplitude of load current 1st harmonic | 10 A |
| 3 | amplitude of load current 3rd harmonic | 1 A |
| f1 | fundamental frequency of load voltage and current | 50 Hz |
| fS | sampling frequency | 20 kHz |
| td | dead time during transistor switching | 200 ns |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sušin, D.; Nemec, M.; Ambrožič, V.; Nedeljković, D. Limitations of Harmonics Control in Power Converters. Electronics 2019, 8, 739. https://doi.org/10.3390/electronics8070739
Sušin D, Nemec M, Ambrožič V, Nedeljković D. Limitations of Harmonics Control in Power Converters. Electronics. 2019; 8(7):739. https://doi.org/10.3390/electronics8070739
Chicago/Turabian StyleSušin, Denis, Mitja Nemec, Vanja Ambrožič, and David Nedeljković. 2019. "Limitations of Harmonics Control in Power Converters" Electronics 8, no. 7: 739. https://doi.org/10.3390/electronics8070739
APA StyleSušin, D., Nemec, M., Ambrožič, V., & Nedeljković, D. (2019). Limitations of Harmonics Control in Power Converters. Electronics, 8(7), 739. https://doi.org/10.3390/electronics8070739





