This section introduces a new type of Distributed Branch-Trimming Robot Network (DBTRN) model and proposes a new Dynamic Network Topology Control Strategy (DNTCS). To make this network model work efficiently, this study introduces the BTR, analyzes the movement of each part of the BTR when the BTR walks along the ground wire or works in the area below the transmission lines. In addition, the mathematic model of the DBTRN is proposed in accordance with graph theory and features of the DBTRN model. To make the calculation more accurate, the mathematical model of the RSS of each wireless node is proposed based on the characteristics of directional antennas and the mobility of each node. Finally, the DNTCS is proposed for application of the BTR.
3.1. Preliminary
Over the past decades, many types of devices have been employed to trim trees around overhead transmission lines. Vehicles, Unmanned Aerial Vehicles (UAVs), and helicopters have been used to carry apparatuses to trim branches, which may negatively affect energized transmission lines. Numerous studies have discussed the applications of branch trimming for transmission lines [
1,
2,
28,
29]. They can be separated as ground-based robots and airborne robots supported by helicopters or UAVs. However, these applications have many drawbacks:
Ground-based robots cannot reach remote areas (e.g., ravines and mountains).
The development of airborne robots is limited by high costs, low battery life, and stability.
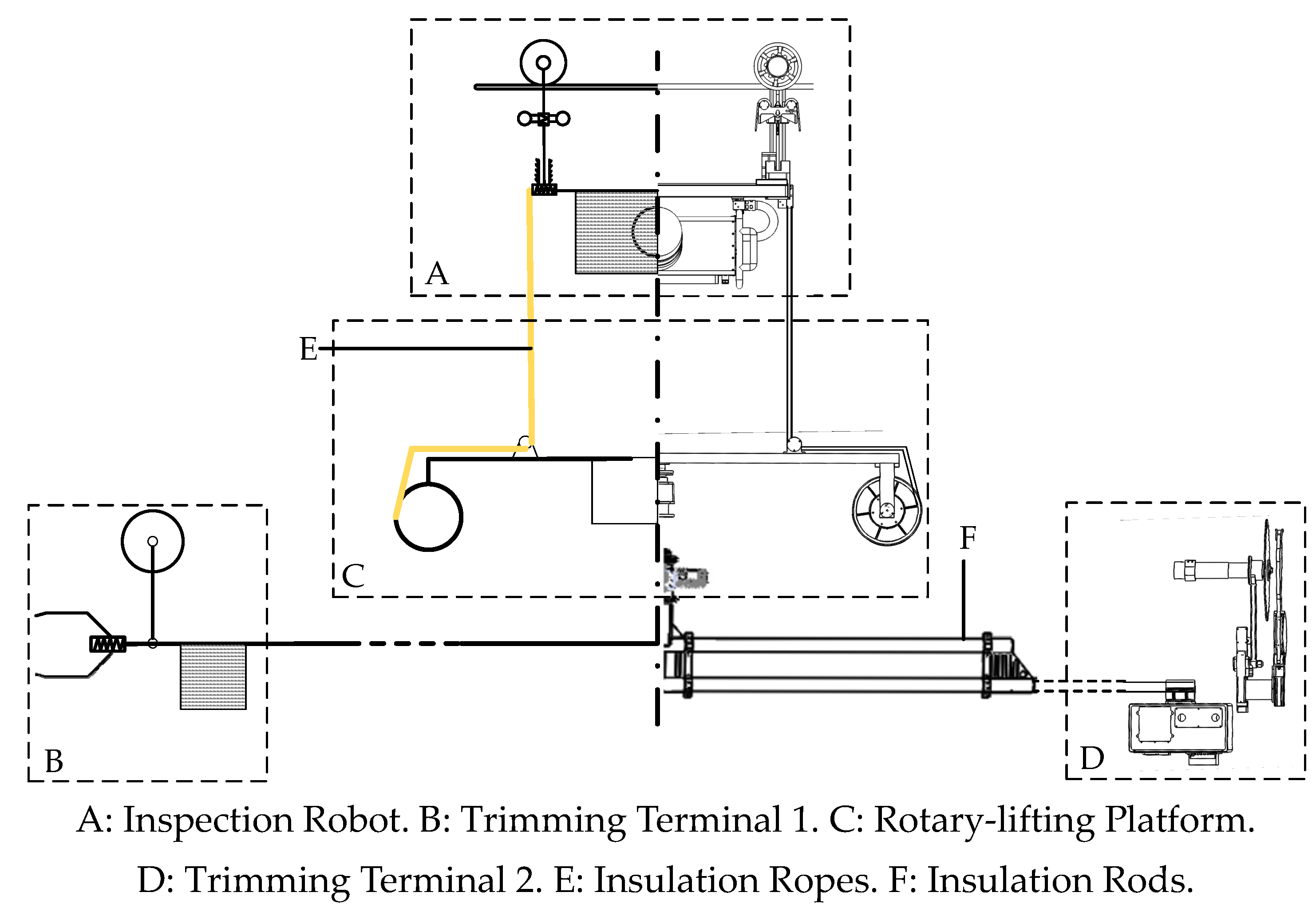
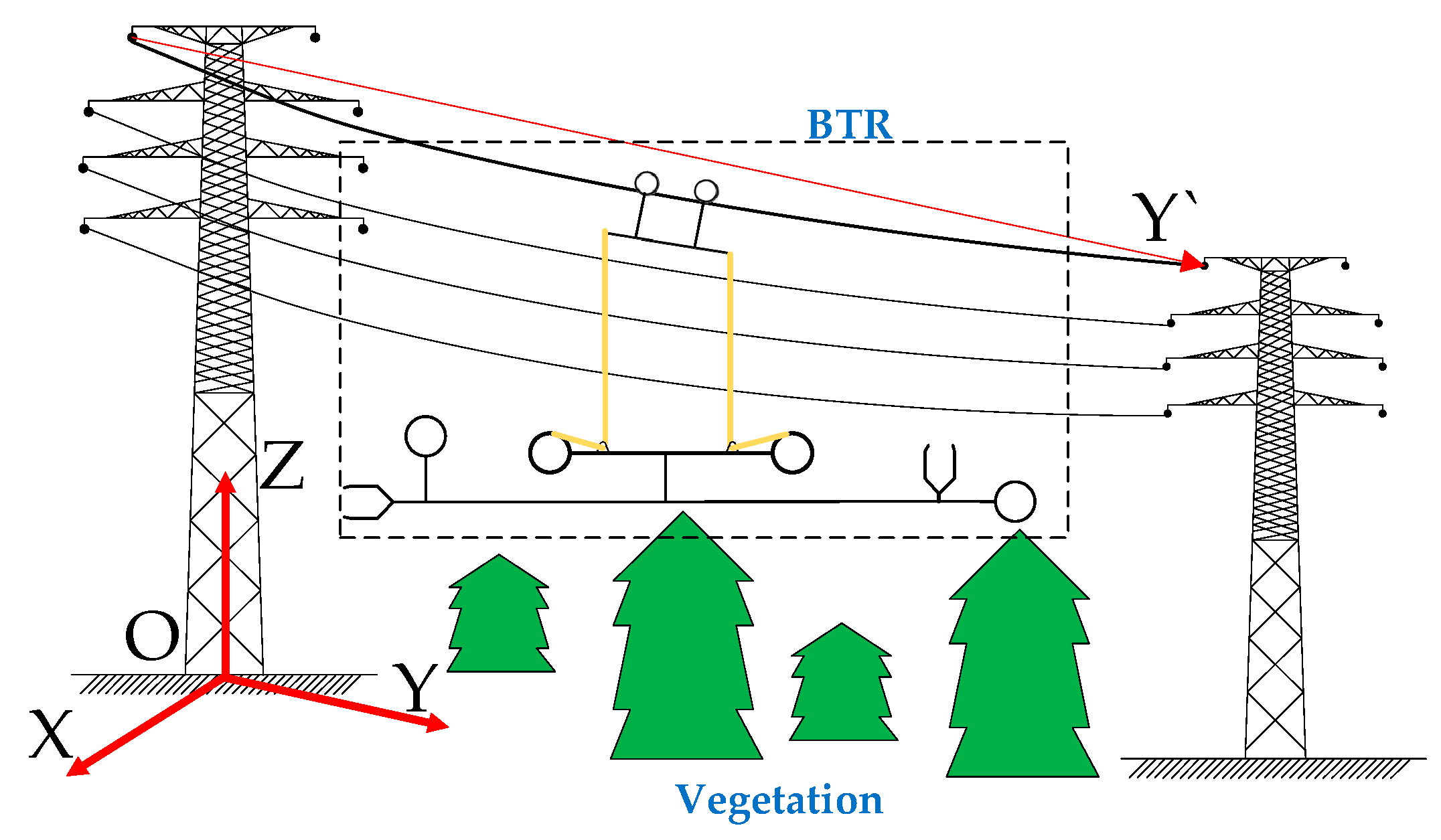
In this section, a BTR for trimming the trees around transmission lines is introduced. An abbreviated drawing of the BTR is given in
Figure 2. The BTR consists of four components, including an Inspection Robot (IR), a rotary-lifting platform, and two trimming terminals. The role of the IR in the BTR is the same as that of the vehicle in a ground-based robot and that of the helicopter in an airborne robot. The IR carries the rotary-lifting platform and two trimming terminals (together known as executing mechanisms). The IR collaborates with executing mechanisms to detect and trim hazard tree branches, and the IR moves along the ground wire as a carrier of BTR. Its combined mechanism, non-collision overcoming mechanism, and inspection method were presented in [
7,
30]. Additionally, the IR is capable of detecting hazard branches using two Pan–Tilt–Zoom (PTZ) cameras [
31].
The capabilities of the rotary-lifting platform allow the two trimming terminals to rotate around a fixed point and move in the vertical direction. The two trimming terminals were designed to detect and trim the hazard branches, and cameras also enable the detection of hazard branches. As the BTR detects and trims the hazard branches between two power towers, the IR moves along the ground wire, while the executing mechanisms work without penetrating the safety area of the energized transmission lines. Besides, it is vital to isolate the BTR from the high-voltage energized lines. Since the BTR was designed to trim branches around energized lines, insulating materials must be used in the BTR to prevent accidents (e.g., blackouts and apparatus damage) [
32]. Accordingly, insulation ropes and insulation rods are introduced in the BTR; insulation ropes are used to connect the IR and executing mechanism, and insulation rods are used to connect the rotary-lifting platform and two trimming terminals. Thus, the BTR can be considered a set of sub-robots that disperse spatially in an area around transmission lines.
The detection of hazard branches is achieved by cameras installed on the IR and two trimming terminals, and the trimming of branches is performed by trimming terminals. Therefore, the reasons why the BTR can be considered a multi-robot system are as follows.
Each component of the BTR is an independent robot that performs a certain task in the group. Moreover, the components of BTR are outfitted with sophisticated sensors and actuators to collect information around the transmission lines and perform different types of motions, respectively.
The branch-trimming task is overly complex for a single robot. The trimming task is inherently distributed, and it can be separated into a set of tasks, which can be performed by the components of the BTR.
Branching trimming tasks can be implemented intelligently and easily based on the cooperation between the sub-robots of the BTR.
However, how the sub-robots of the BTR interact with each other is hard to explain. Among the sub-robots of the multi-robot system, the IR walks along the ground wire, and the executing mechanisms operate under the phase lines. Energized high-voltage transmission lines are parallelly distributed between the IR and the other sub-robots of the multi-robot system. Due to the voltage and current of the running transmission lines, a strong electromagnetic field and an electric field would be produced in its nearby environment. Wired communication is limited in the multi-robot system for the following reasons.
The phase lines that traverse the IR and the other sub-robots of the multi-robot system significantly limit the system’s use of wired communication. When the cable approaches the energized transmission line, the electromagnetic field generated by the energized transmission lines would interfere with the data running on the cable [
33,
34,
35]. Otherwise, according to the standards for overhead transmission lines in China, no conductors will be allowed into the safety area of high-voltage energized transmission lines.
Using wired communication may increase the difficulty of cable management. Distances between the IR and other sub-robots vary due to the mobility of each sub-robot. Although the distances between the rotary-lifting platform and trimming terminal are fixed, the rotation of the Rotary-Lifting Platform (RP) may cause the cables to wind.
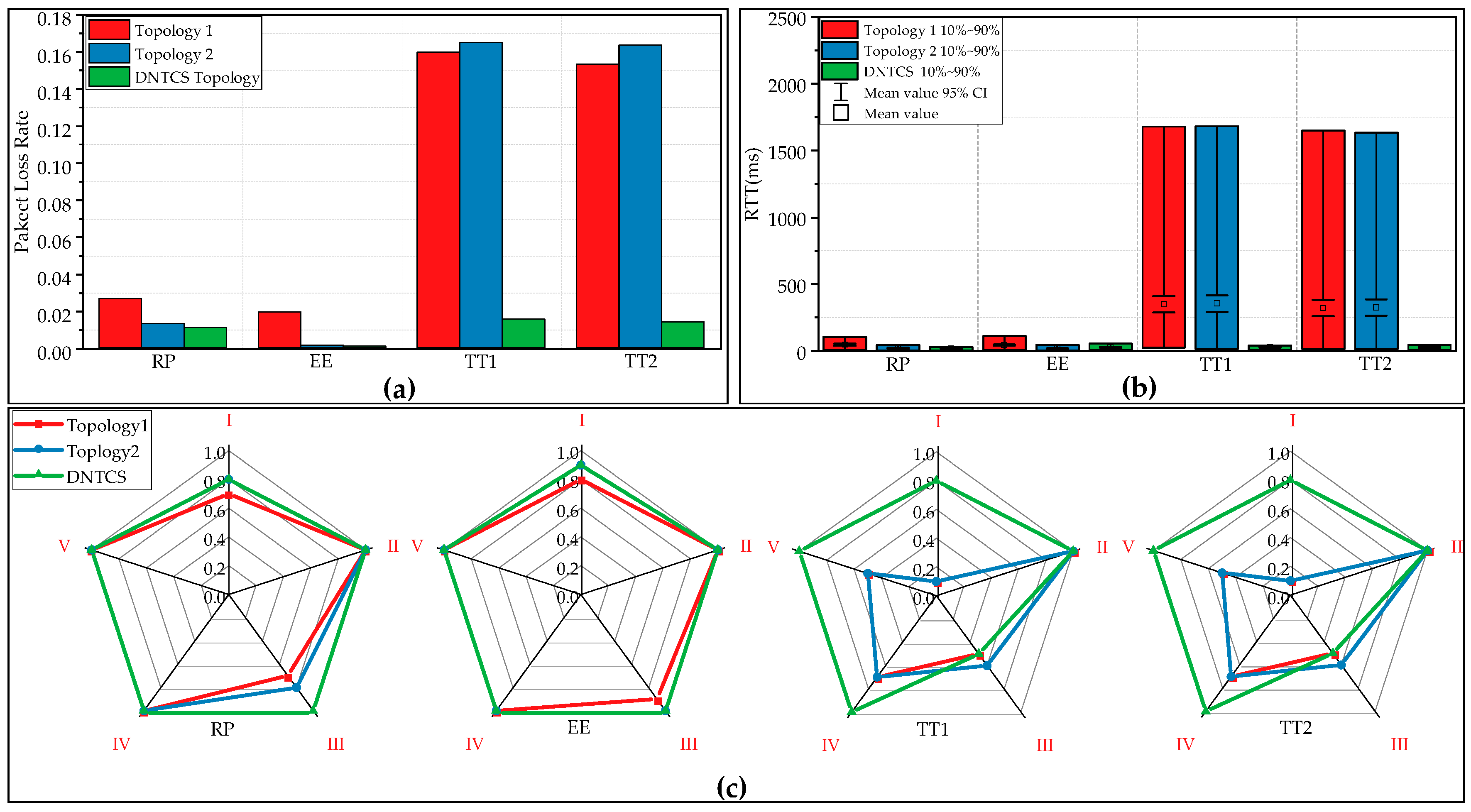
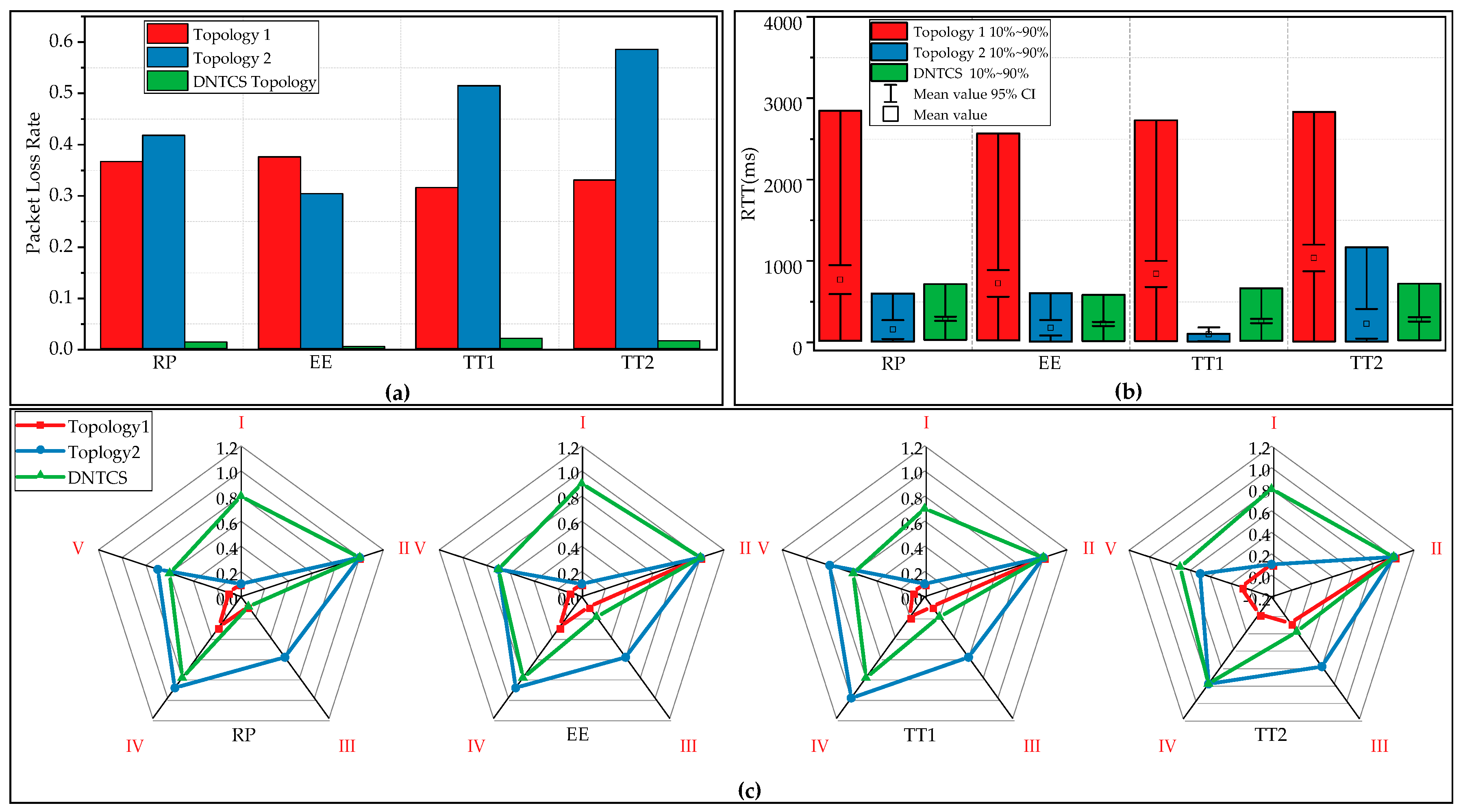
Accordingly, the capabilities of the sub-robots of the multi-robot system are limited; trimming branches around transmission lines requires the cooperation of each sub-robot. Additionally, wireless communication is used in the multi-robot system, which leads to a high packet loss rate and network delay if the network topology is not suitable. Packet loss and network delay cause errors in information collecting and motion controlling, which may decrease the efficiency of the BTR when detecting and trimming hazard tree branches. Therefore, a dynamic network topology control method is proposed to solve the network optimization problem of the BTR, which is based on a distributed network model.
3.2. Distributed Branch Trimming Robot Networks (DBTRN) Model
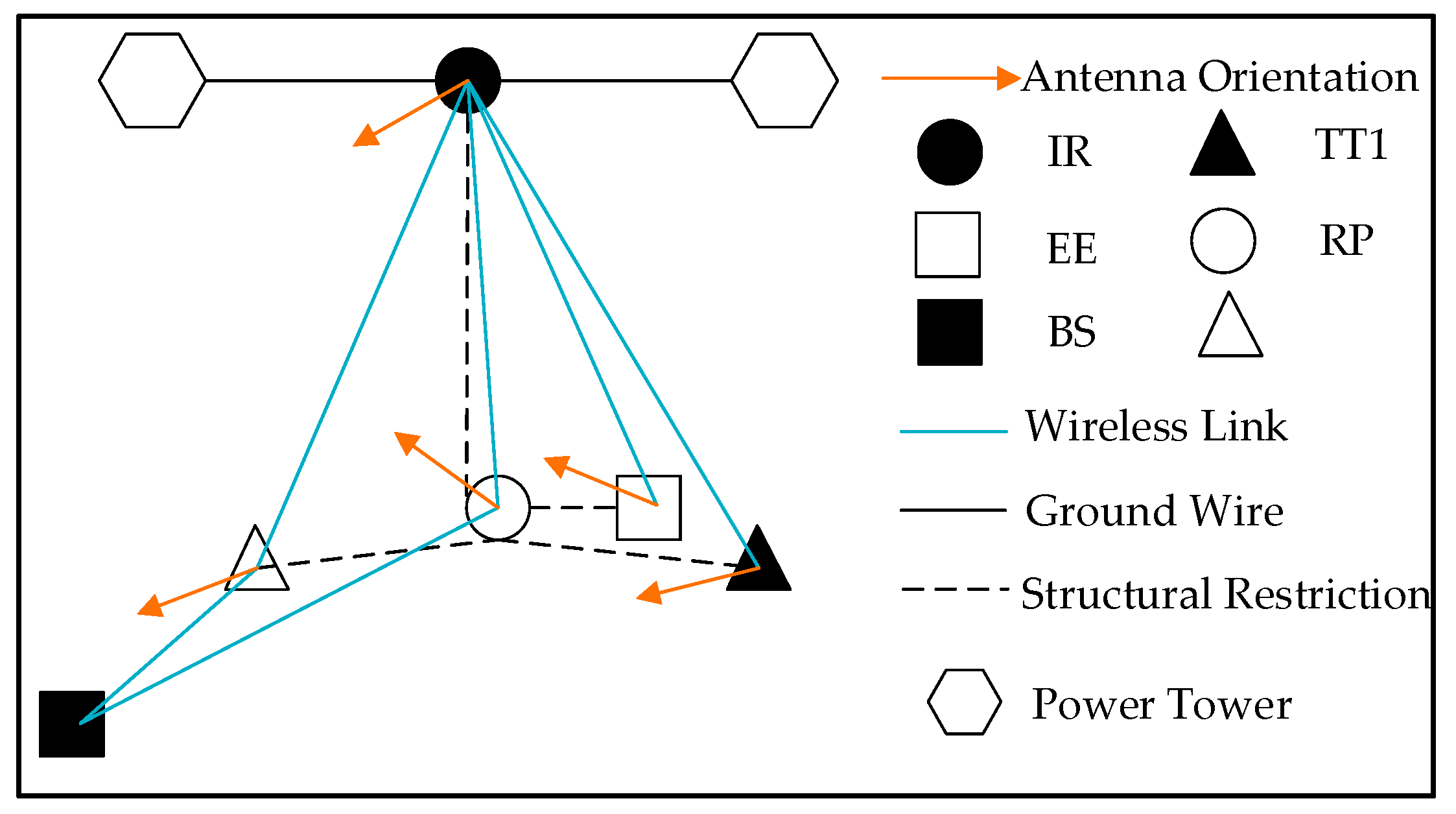
The DBTRN model is established in this section, which is shown in
Figure 3. The BTR and its components are deployed along a ground wire of a single span between two power towers. The IR is deployed along the ground wire; the other components are deployed in the three-dimensional area in the transmission line corridor of a single span. The communication nodes in the DBTRN include the IR, BS, Rotary-Lifting Platform (RP), Trimming Terminal 1 (TT1), Trimming Terminal 2 (TT2), and Emergency Equipment (EE). Among these nodes, the IR, RP, TT1, and TT2 correspond to the sub-robots of the BTR; the EE is deployed inside the RP to restart the RP in case of emergency; lastly, the IR, RP, TT1, TT2, and EE are mobile nodes, while the BS is static. All the nodes above are equipped with directional antennas. In
Figure 3, structural restriction represents the structure of the BTR that limits the distance and angle of some pairs of nodes. For instance, the distance between TT1 and TT2 is a fixed value owing to structural restriction, and the RP is directly below the IR, even though the distance is adjustable between the IR and the RP. These nodes form a wireless sensor network with dynamic network topology. The DBTRN has the following properties.
The nodes of the DBTRN have heterogeneous communication capabilities due to the movement of each node; directional antennas make the communication capabilities of mobile nodes change over time and space.
Each node regulates velocity (speed and direction) according to the location of target branches, surroundings, maximum motion range, etc.
The data delivered by these nodes have heterogenous capacity, packet delivery ratios, and network delay requirements.
3.2.1. Variable Distances between Nodes
In the DBTRN, the RSS of each node is one of the metrics of network performance. The major parameters affecting the signal strength include the distance between pairs of nodes and the orientation of the directional antenna equipped on each node. When the BTR is operating in a span, the distances between the BS and other nodes of the multi-robot system, and the distances of pairs of mobile nodes in the multi-robot system, are variable. In this section, taking the BTR working in a span as an example, the distances between the BS and mobile nodes in the multi-robot system, and the distances between pairs of nodes are discussed.
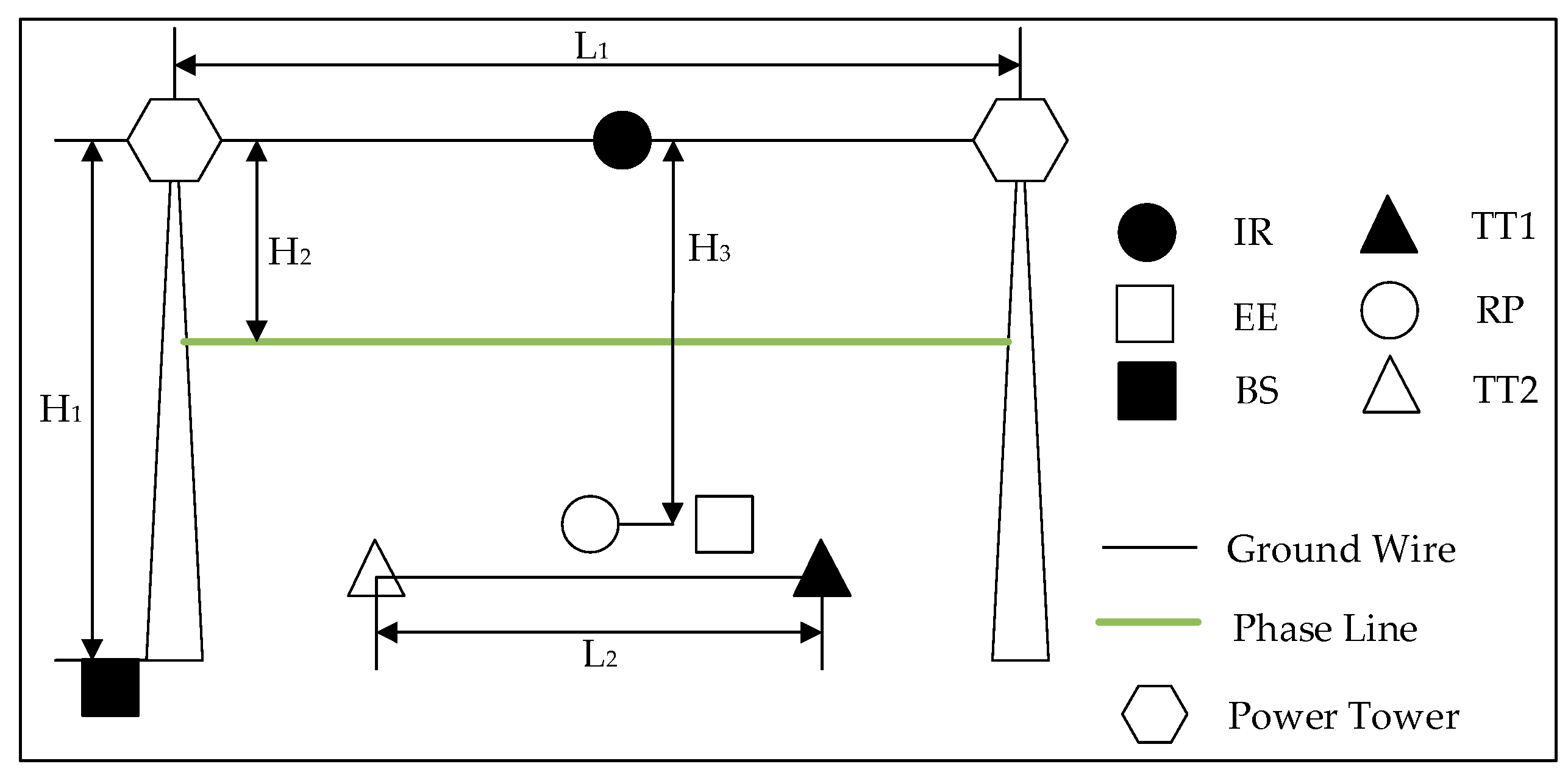
By querying the line parameters table provided by the local electric department, the distance between two towers, the maximum height of the tower, the height of the ground wire, and the height of the phase line can be obtained. The BS is placed at a point on the ground within the span, the coordinates of which are determined by the terrain between towers. The distance between the IR and other mobile nodes can be determined by the workspace and structural design of the BTR. The distribution of the DBTRN in a span is shown in
Figure 4. Here,
L1 denotes the horizontal distance between the two towers;
L2 is the distance between the two trimming terminals;
H1 is the height of the tower;
H2 is the height difference between the ground wire and the phase line; and
H3 is the height difference between the node IR and other sub-robots in the multi-robot system. Among these parameters,
L1,
L2,
H1, and
H2 are determined by the fixed parameters of the transmission lines, towers, terrains in the span, and the structure parameters of the BTR. In addition,
H3 is determined by the locations of the trees and branches around the phase line and the length of the insulation ropes.
Table 1 gives the range of each distance. The table also describes the range of distances between pairs of mobile nodes derived from the parameters presented above.
3.2.2. Mobility Model of DBTRN
The distances between the nodes affect the network performance of the DBTRN network. When the BTR detects and trims the branches in a span between two power towers, the distances between the BS and the other nodes will change. Also, distance is a vital parameter affecting network performance. To quantify the distances between nodes, this section relies on the mobility model of the DBTRN to calculate the position coordinates of each node.
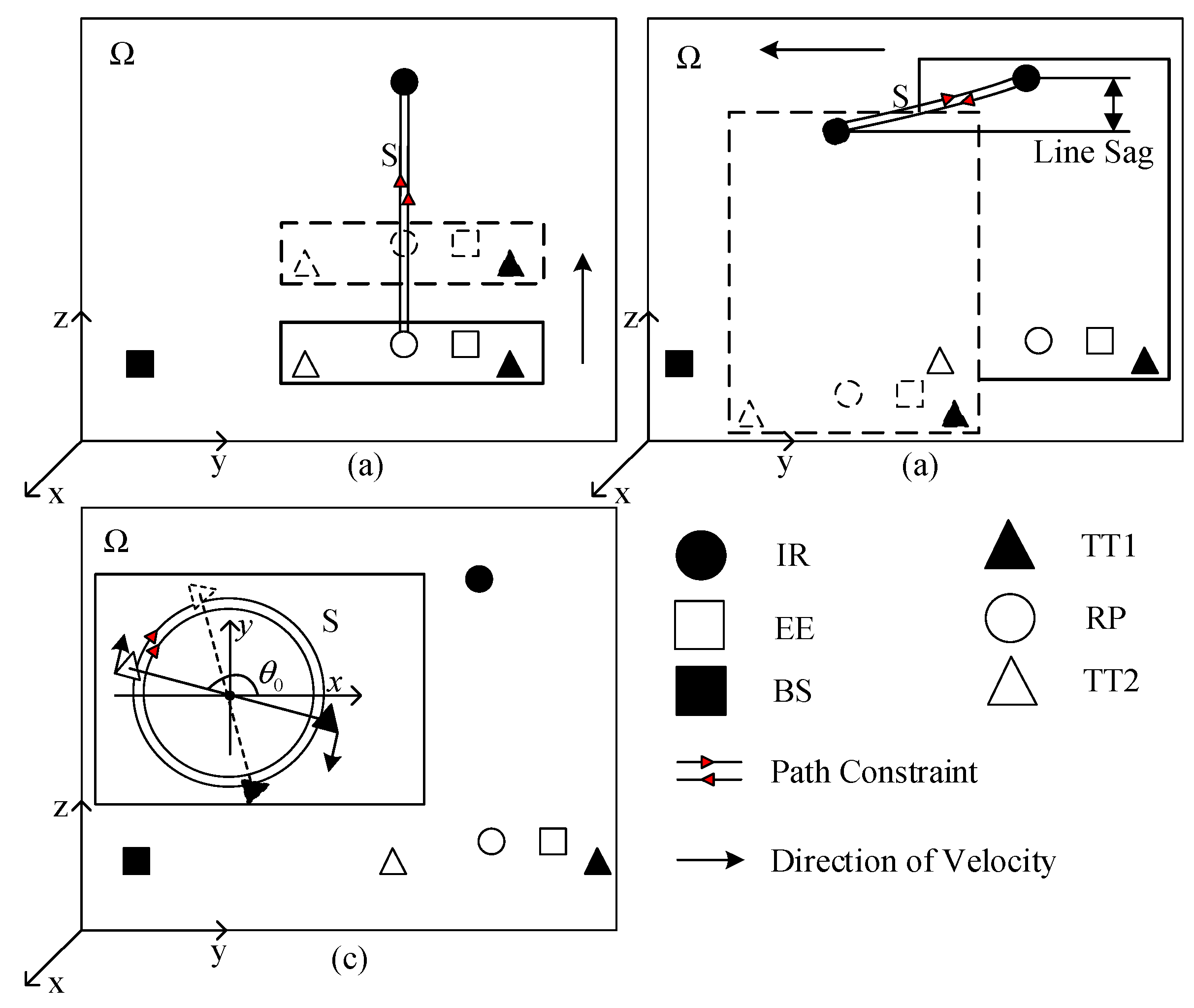
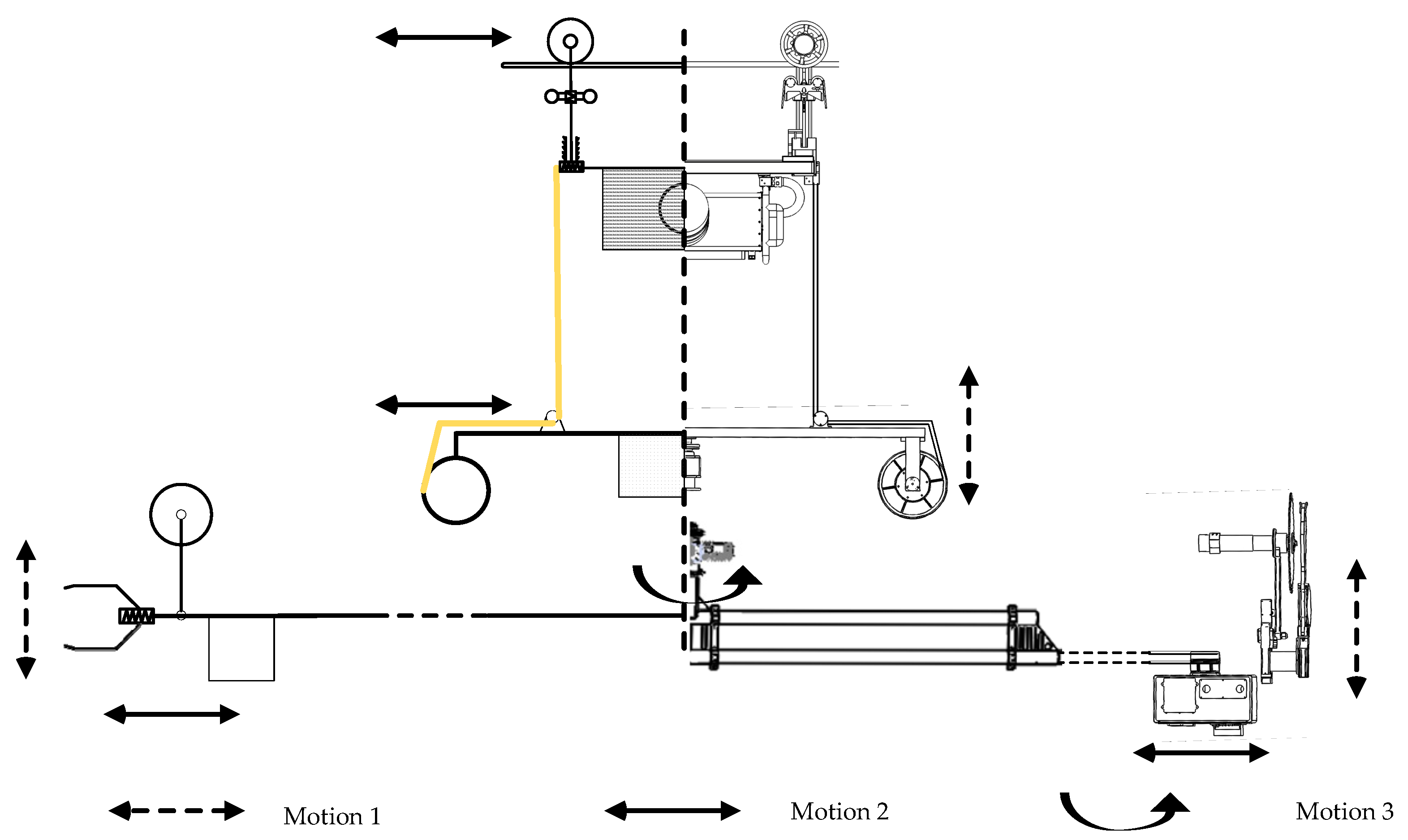
In the network model, all the nodes are deployed in a three-dimensional space in the transmission line corridor. Generally, the purpose of the BTR after it is deployed in the transmission line corridor is to find hazardous tree branches and carry out the trimming task. The mobility model of the BTR is designed and analyzed from its practical application. Motions of mobile nodes when the BTR is approaching target branches and performing trimming tasks can be classified as simple motions. The simplified BTR and mobile nodes’ movement rules are presented in this section. The movement of nodes in different motions is given in
Figure 5.
Motion 1. The RP, EE, TT1, and TT2 move in the vertical direction, which corresponds to the lifting or the declining of the executing mechanisms. The path constraints of these nodes are vertical lines, as shown in
Figure 5a. In this motion, these above nodes get a velocity vector
, where
.
Motion 2. The IR walks along the ground wire, and all mobile nodes move in the horizontal direction with the IR; these nodes get a velocity vector , where . The path constraint is the ground wire. In addition, each node decline is caused by the line sag of the ground wire when the IR moves along the ground wire.
Motion 3. TT1 and TT2 rotate around the center of the RP, and the coordinate of the center is changeable. The velocity vectors of TT1 and TT2 are
and
, respectively, where
denotes the initial angle of the line segment of TT1 and TT2, which is positive on the
X-axis;
is the rotational angular velocity of the two nodes, and
;
is time, as the two terminals have been rotating. During Motion 3 of the performing BTR, the path constraint of TT1 and TT2 is a circle, which is shown in
Figure 5c.
Motion 4. All the mobile nodes stay stationary while the BTR is trimming tree branches. When the BTR is performing a trimming task, only one joint of one trimming terminal is moving. Furthermore, mobile nodes determined by the locations of nodes are dynamic until the trimming terminal finishes the trimming task or the BTR finds it unlikely to trim hazard tree branches. In this motion, the trimming task is performed by TT1.
Motion 5. All the mobile nodes stay stationary to trim tree branches. In this motion, the trimming task is performed by TT2.
In
Figure 5,
denotes the maximum range of mobile nodes, which is a three-dimensional area that is determined by the safety distance of the energized conductors on the transmission line, the length of span, and the height of the power tower. The path constraint is determined by the ground wire and the structural restriction of the BTR.
The initial positions of each node are known, which are determined by fixed parameters such as the height of the power tower, the terrain around the power tower, the weight of the BTR, the length of the span of the BTR, and the structural size of the BTR. At the beginning of the trimming task, all of the noted parameters and angle of the directional antennas are set.
Equation (1) shows a simplified calculation of the positions of nodes in the DBTRN, in which
are the coordinates of node
, the coordinate system is shown in
Figure 6, and
denotes a set of variables that determine the initial positions of nodes in the DBTRN.
is a set of motions and durations of motions of mobile nodes before time
.
3.2.3. RSS Mathematical Model
The packet delivery ratio and network delay are major concerns of the WSNs. A high RSS generally corresponds to high packet delivery ratio and low network delay [
36,
37]. At low signal strength, the packet delivery performance is easily affected by the significant variability caused by the receiver performance and noise in the environment. Accordingly, the estimation and prediction of the RSS is vital to estimate and improve the network performance. A method is proposed in this section to improve the network performance of the DBTRN, which is achieved by assessing the RSS value of each mobile node from other nodes before the BTR performs a certain motion.
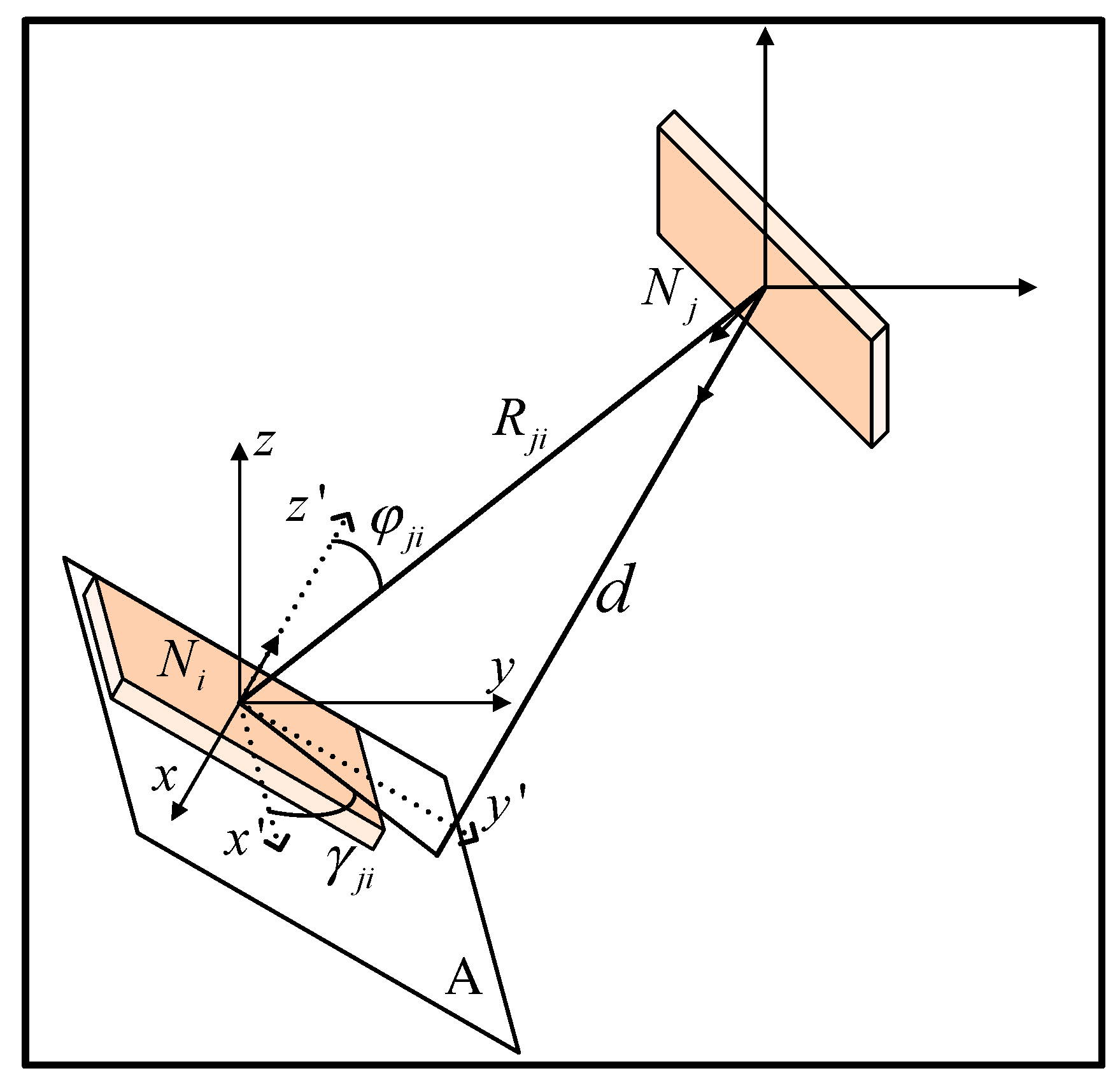
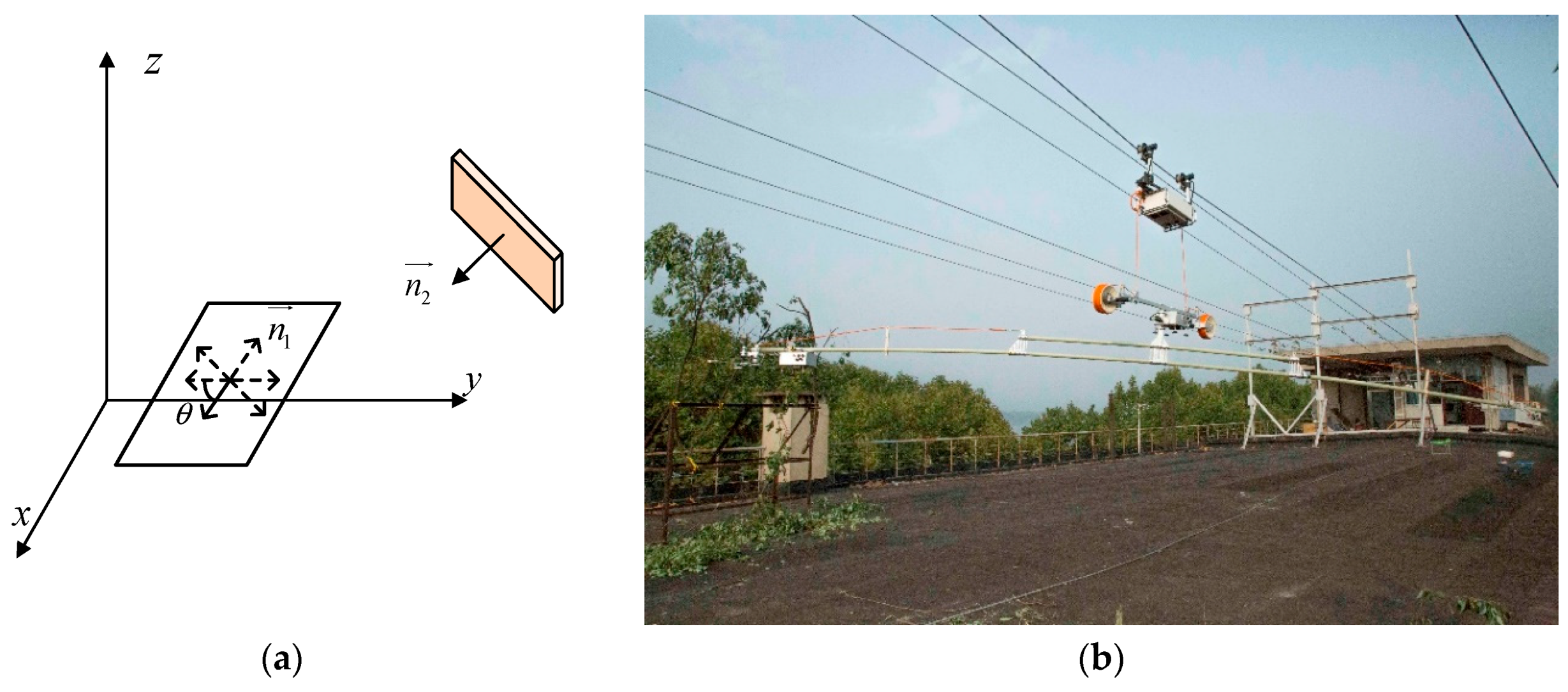
Each node in the BTR is outfitted with a directional antenna to enhance the signal strength. It makes the quantification of the RSS more complex. The RSS value is an estimate of the signal energy at the receive node [
23], which is related to the antenna gains of the receiver node and the transmitter node. As mobile nodes in the DBTRN perform a motion, changes to the antennas’ angles of arrival and the distance between nodes cause changes of antenna gains, which change with a resulting change in the signal energy level at the receiver. Thus, to ensure a good packet delivery performance, wireless nodes should predict the RSS value of each mobile node before the BTR starts to perform a motion. Assume that
denotes the coordinate of the node
, and
is the unit normal vector of the antenna plane. The RSS between any pair of nodes
and
can be calculated by the equations below.
Two directional antennas of nodes with different antenna orientations are shown in
Figure 7.
denotes the distance between node
and node
;
is the distance from node
to the antenna plane
;
is the angle measured off the Z-axis; and
is the angle measured counterclockwise off the X-axis.
and
are correlated with the positions of node
and node
, as well as the initial angles between directional antennas in a geodetic coordinate system. The variables above can be determined by the coordinates of nodes and the unit normal vectors of antenna planes, as calculated by Equation (2) to Equation (5).
The gain of an antenna is related to the directivity and radiation efficiency, and the directivity is determined merely by the radiation pattern of an antenna [
38]. In this study, the radiation efficiency is considered a constant, and the antenna gain is expressed in Equation (6), where
denotes the angle measured off the
Z-axis, and
is the angle measured counterclockwise off the
X-axis.
and
are related to the positions of node
and node
, and the initial angles between directional antennas in a geodetic coordinate system.
The RSS value can be calculated by Equation (7), which is the derivation of frees transmission [
39], where
denotes the RSS value of node
received from node
,
is the polarization loss factor (PLF) which describes power loss due to the inconsistency in polarization between a pair of antennas,
is the antenna gain of node
in the direction of the antenna of node
,
is the antenna gain of node
in the direction of the antenna installed at node
,
is the propagation speed of electromagnetic waves in vacuum,
is the distance between node
and node
, and
is the frequency of the electromagnetic waves.
Combining Equations (1) to (7), the RSS of node
received from node
at time
can be calculated. Equation (1) shows the calculation of coordinates of a node at time
; Equations (2) to (7) calculate the RSS value by the coordinates of nodes and the unit normal vectors of the current direction of the antenna plane. Based on the above equations, the expression is then simplified. The RSS of node
received from node
can be calculated by Equation (8), where
denotes the RSS of
received from
,
is a set of variables that determine the initial position of nodes in DBTRN,
is a set of motions and durations of motions before time
, and
is the unit normal vector of the antenna plane.
3.2.4. Discrete Time Mathematical Model
An optimal solution of how to determine the best network topology is proposed in this section for points at which the BTR is approaching target branches or trimming hazard tree branches. The solution is performed based on the statistical methods of RSS and motions of the BTR.
For the DBTRN, as the nodes move to perform trimming tasks, the network topology is unreliable and varying constantly. The movement of nodes not only changes the distances between pairs of nodes, it also changes the angle of arrival of directional antennas. Both variables above change the RSS of each node, which may significantly affect the packet delivery performance between nodes [
36,
37]. In order to meet the requirements of the mobile wireless nodes (RP, IR, TT1, TT2, and EE) to transmit information to the BS, this section draws on references [
25,
26,
27], and introduces graph theory to describe the network model. Additionally, the mathematical model is designed for a mobile node in the DBTRN to find an optimal path to the BS.
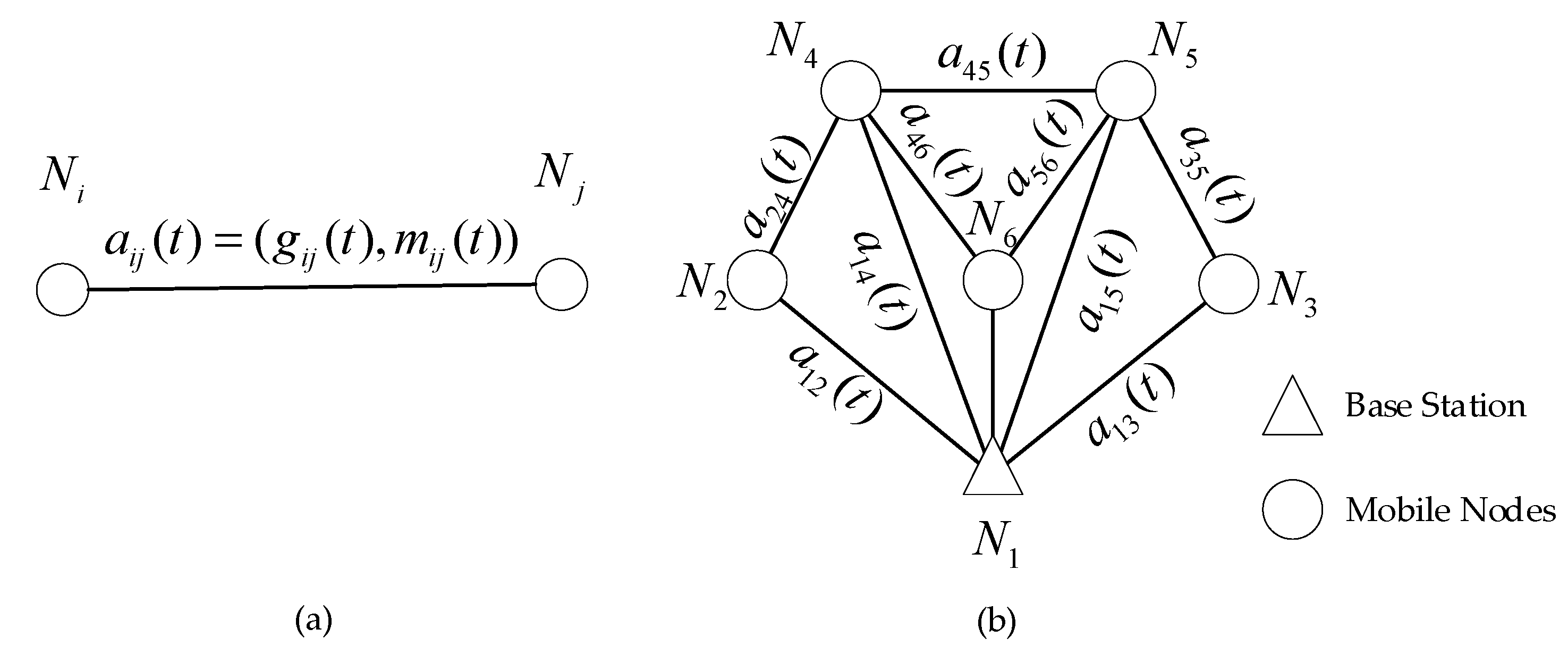
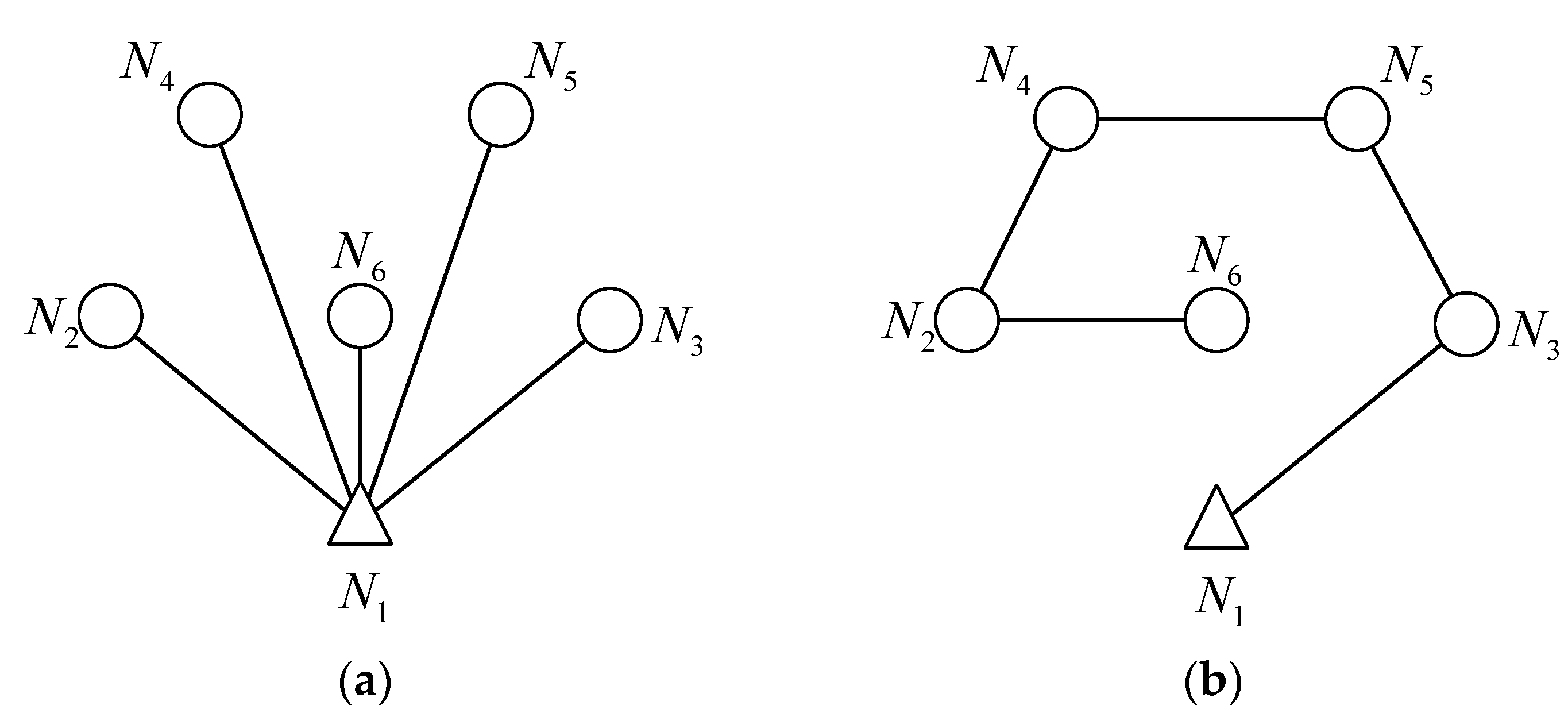
In the network mathematical model, the nodes and the information of the network can be represented by graph
at time
, where each vertex represents the corresponding node in the DBTRN with a unique ID. The graph
is illustrated in
Figure 8. An edge represents a wireless link between vertices if the corresponding nodes are within the transmission range of each other. At time
, graph
changes, which may be represented by graph
, and
represents an extension of
. All the information of the network is contained in Graph
. Besides, the weight function
of each edge in graph
is calculated by Equation (9). Equation (9) expresses the law of weight variation over time. The network changes the network topology based on the weight calculation of each wireless link. Node
decides to be connected to
or disconnected with
based on
.
The equation above illustrates the calculation of the weight of the wireless link between node and node at time , where denotes the weight of the wireless link between pairs of nodes, is the parameter related to RSS, which corresponds to the RSS between node and node . is the correlation coefficient between node and node when the BTR is performing a motion at time . In Equation (10), the objective function of the network mathematical model is proposed. As shown in the description of Equation (10), the weights of all the possible paths from node to node are compared. This comparison ensures that node connects to node with the maximum weight of the wireless links, which leads to a high packet delivery ratio and low network delay. denotes the weight of the wireless link between node and node , where node can be a relay node or does not exist; if node does not exist, that means that node connects to node directly. The constraints of the wireless links between nodes are shown in Equations (11) and (12). Equation (11) demonstrates that the number of relay nodes of the path cannot exceed the number of nodes in the network except for those in node and node . n denotes the number of relay nodes, while is the number of nodes in the DBTRN. Equation (12) shows that the relay nodes are different in the process of a packet delivering from and node .
3.3. Dynamic Network Topology Control Strategy (DNTCS)
This section introduces the DNTCS. The DNTCS primarily aims to provide the DBTRN with the most suitable network topology. The DNTCS is a network topology control strategy that is designed for the DBTRN, which is unique regarding its mobility model, QoS requirement, and operational style. The BTR mainly aims to achieve the specific goal of detecting and trimming the branches that threaten the transmission line security. Accordingly, the goal of the DNTCS is to allow the DBTRN to have the best network performance in the process of approaching and trimming branches. In
Section 3.2.2, the process of the BTR approaching and trimming branches is simplified to a few simple motions, and as shown in the description in
Section 3.2.3, every motion of the BTR may result in the poor network performance of the DBTRN. Thus, the DNTCS in this study is based on the DBTRN model and the motion model of the BTR to make the BTR more efficient in the task of detecting and trimming branches.
To achieve the above objectives, the DNTCS follows the ideas below:
Estimate the weight value of each wireless link accurately in the DBTRN before each motion of the BTR is performed, which will ensure the continuity of the BTR during the execution of the motion. It is stipulated that the DBTRN is not allowed to switch the network topology when the BTR performs a motion, because the initialization time of the switching network topology is uncertain. This indefinite time will cause unpredictable errors in the BTR’s execution. Accordingly, switching the topology of the DBTRN before each motion of the BTR is important. However, this will definitely result in taking BTR motions into consideration when the weight of wireless links is calculated. In this section, the BTR motions are quantified and modeled to make the calculation simpler.
The principle for switching the topology is decided by the weight value of each wireless link in the DBTRN. Since the network topology consists of a set of wireless links, the network topology of the DBTRN is determined by selecting a suitable wireless link between a mobile node and the BS.
The DNTCS primarily seeks to confirm a proper network topology before the BTR start a motion, which is based on the prediction of the weight of each wireless link,
. In the DNTCS, before the BTR starts a motion, the weight
of each wireless link is calculated precisely. The weight
is determined by the RSS-related parameter
and the correlation coefficient
, as expressed in Equation (9). The
is determined by the RSS value of the corresponding vertex of the wireless link.
is determined by the RSS of the nodes in the wireless networks [
25]. When the RSS of node
received from node
reaches a certain threshold,
,
is equal to 1, as expressed in Equation (13). If the RSS is smaller than the threshold
,
is calculated by Equation (14). This value stresses the distance between node
and node
and the angle of arrivals of the directional antennas installed on node
and node
. For instance, if the distance between node
and node
is too high, or the antenna gains of node
and node
are relatively low, the RSS-related parameter
will be small.
can be calculated by Equation (8):
Another important parameter when calculating the weight of the wireless link is
, which denotes the correlation coefficient between node
and node
as the BTR is performing a certain motion at time
. To improve the calculation of the equations, each node needs to be numbered. The sequential representation of nodes is shown in
Table 2.
is valued based on the necessity of being monitored when the BTR is performing motion
, as expressed in Equation (15).
In Equation (15),
(elements of Matrix
) denotes the necessity of node
being monitored when the BTR is performing motion
. For instance, when the BTR is performing motion 3, the IR should not be monitored for being static, so the necessity of it equals 0.
(elements of matrix
) is a derivative of
, representing the connectivity of a node in the network topology.
represents the connectivity of
when the BTR is performing motion
.
can be calculated by Equation (16), representing the correlation coefficient between
and node
.
Before the BTR starts to perform a motion, the motion range of mobile nodes can be calculated by the following equations. In Equation (17),
denotes the duration of the BTR performing motion
;
is the velocity of node
when the BTR is performing motion
;
is the location before the BTR performs motion
;
is the location of node
when the BTR has been performing motion
for a period of
. In Equation (18),
denotes the motion range of node
when the BTR is performing motion
; and
is the maximum motion range of the mobile nodes.
In addition, this section combines the DNTCS with the mathematical model introduced in
Section 3.2.4. Based on the mathematical model and the calculation methods presented in this study, a mobile node in the DBTRN can find an optimal path to the BS through the calculations. The weight value of each wireless link is determined by the historical information of the DBTRN, the motion to be performed by the BTR, and the location information of each node and the orientation information of the antenna. After the weight values are settled, the appropriate path from the mobile node to the BS is selected according to the objective function and constraints in
Section 3.2.4. After the appropriate path from each mobile node to the BS is determined, the network topology of the DBTRN is then confirmed. The process of the optimal path solution is presented below.
First, check whether the necessity of the node being monitored equals 1 or not. If the necessity equals 1, the following steps need to be executed. If the necessity equals 0, the following steps will not be executed.
Second, calculate weight of the wireless links between node and the other wireless nodes depended on the motion range , , and . The interval of can be obtained, ; let .
Finally, find the best path from node
to the BS based on the objective function and constraints presented in
Section 3.2.4.
After the optimal path from a mobile node to the BS is determined, the process of the proper network topology deployment is presented as follows.
First, set a motion that the BTR will perform in the subsequent time.
Second, select the optimal path from the mobile nodes to the BS if the necessity of the node being monitored in this motion equals 1.
Finally, the best deployment of network topology is obtained by combining the optimal paths from the mobile nodes to the BS.
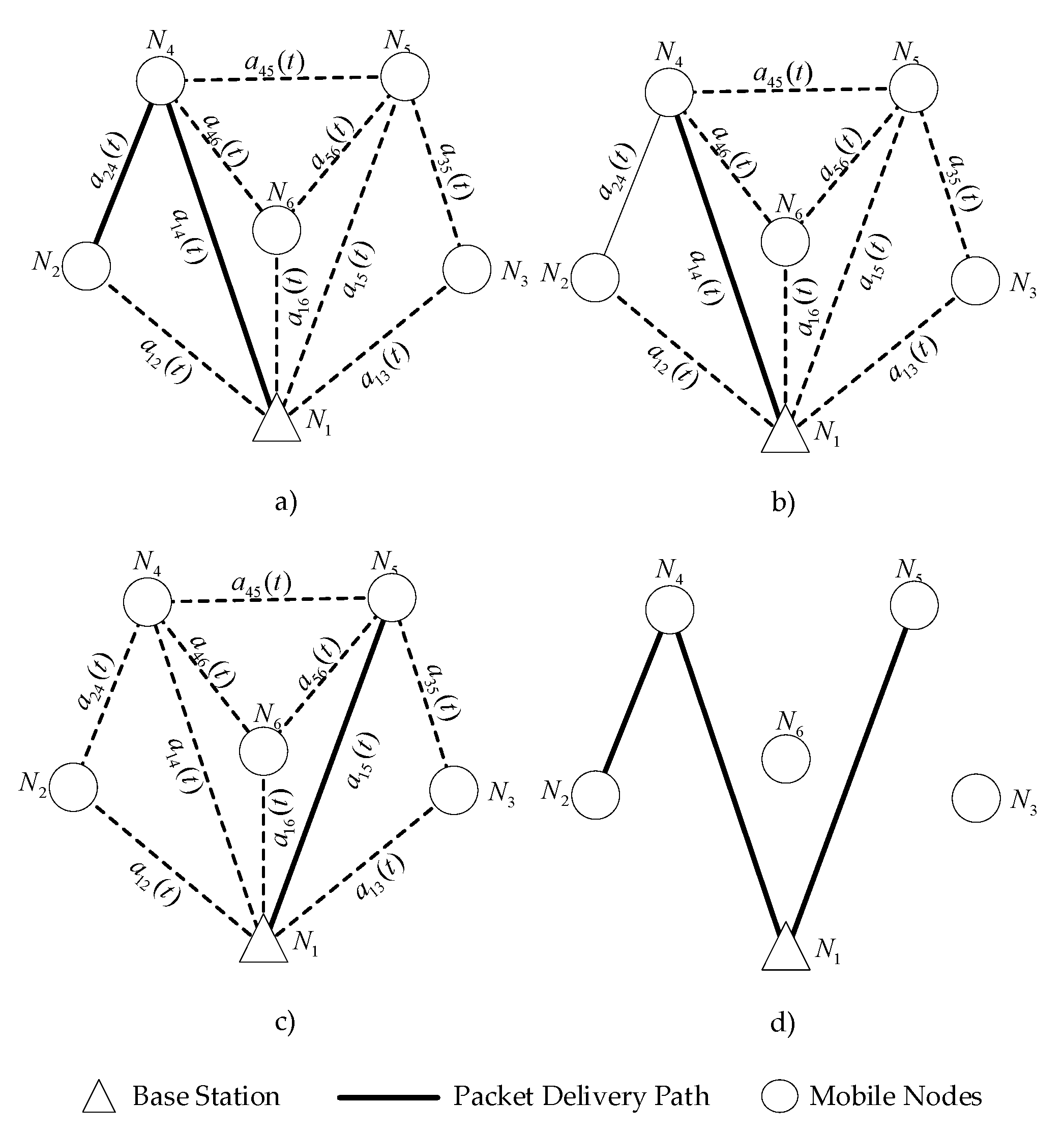
Figure 9 gives an example of the DNTCS at work. The BTR will perform motion 2 at time
. The information of nodes
,
, and
must be transmitted to
. The dynamic network topology is determined by the path selection from
to
and
to
. The network topology before the BTR performs motion 2 can be verified by the following steps.
The DNTCS solves the problem of deploying the best network topology of the DBTRN before the BTR performs a certain motion, which is performed by the optimal path selection from the mobile nodes to the BS with the objective function and constraints. The DNTCS enables calculating methods of variables in the mathematical model and a method to choose a proper network topology. The Dynamic Network Topology Control Strategy (DNTCS) is represented as pseudo-code, as shown in Algorithm 1.
| Algorithm 1. DNTCS |
| 1: | {path} = main (M, v) %M: motion type, v: velocity of nodes | |
| 2: | load locations %locations of nodes before performing a motion | |
| 3: | set matrix L, α, β, η | |
| 4: | for(i = 2: N) %N: number of nodes in the DBTRN | |
| 5: | {predict locations | (a) |
| 6: | connectivity update | (b) |
| 7: | for (0 < j < i) | |
| 8: | {update | (c) |
| 9: | update | (d) |
| 10: | update | (e) |
| 11: | update} | (f) |
| 12: | path-BS ()} | |
| 13: | path | |
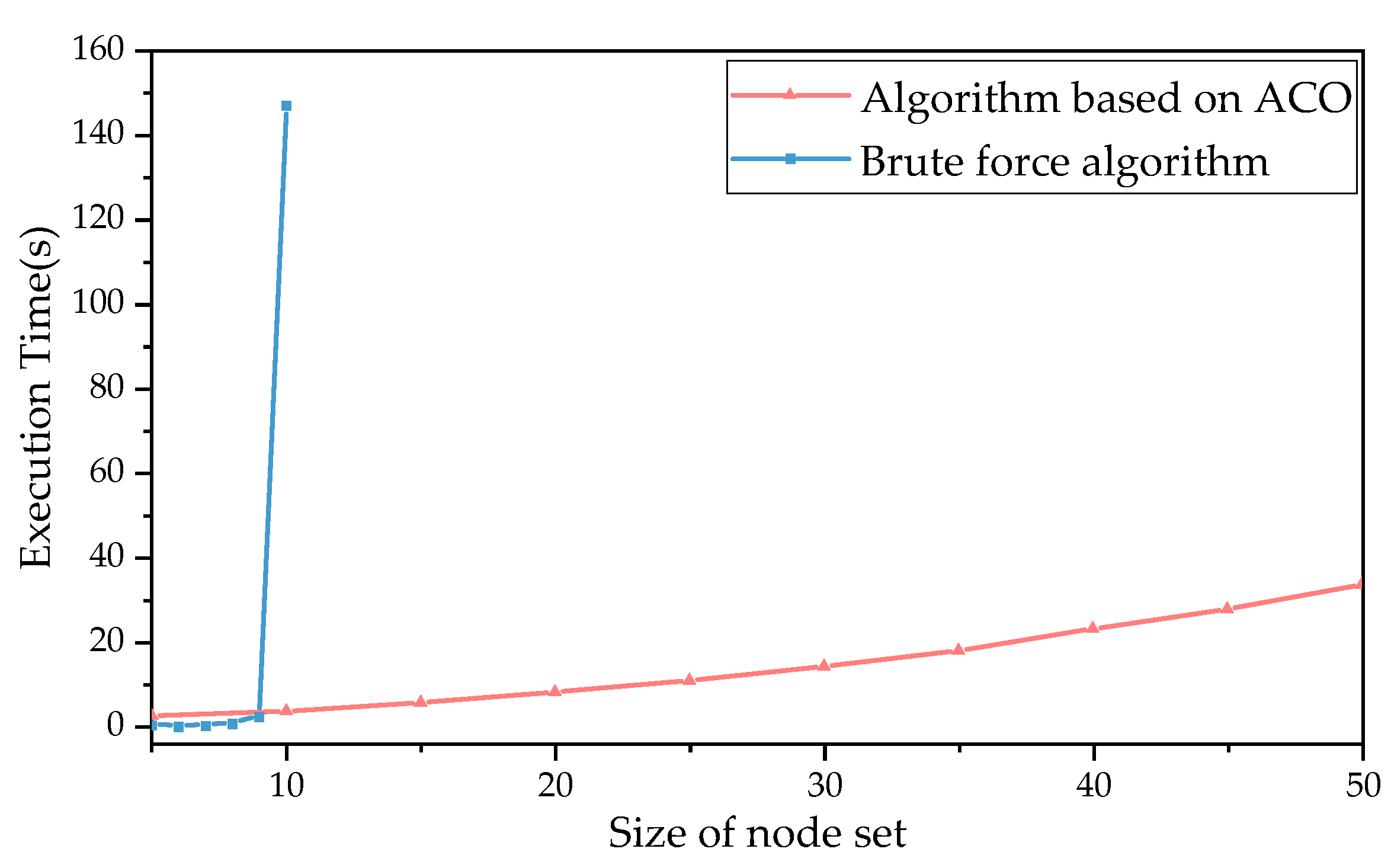
Algorithm 1 runs iteratively for increasing N values, where N is the size of a node set in the DBTRN.
Table 3 shows the time complexity of the main steps of Algorithm 1.
The function path
–BS is designed to compare the weights of all the possible paths from node
to BS; the time complexity of this function using the brute force algorithm is shown in Equation (19). The brute force algorithm is a general technique that consists of enumerating all the possible candidates for the objective function and selecting the best solution to satisfy the problem statement [
40]. Obviously, due to the time complexity of the function path
–BS, the application of the DNTCS to the DBTRN will be extensively affected as the value of
N increases.
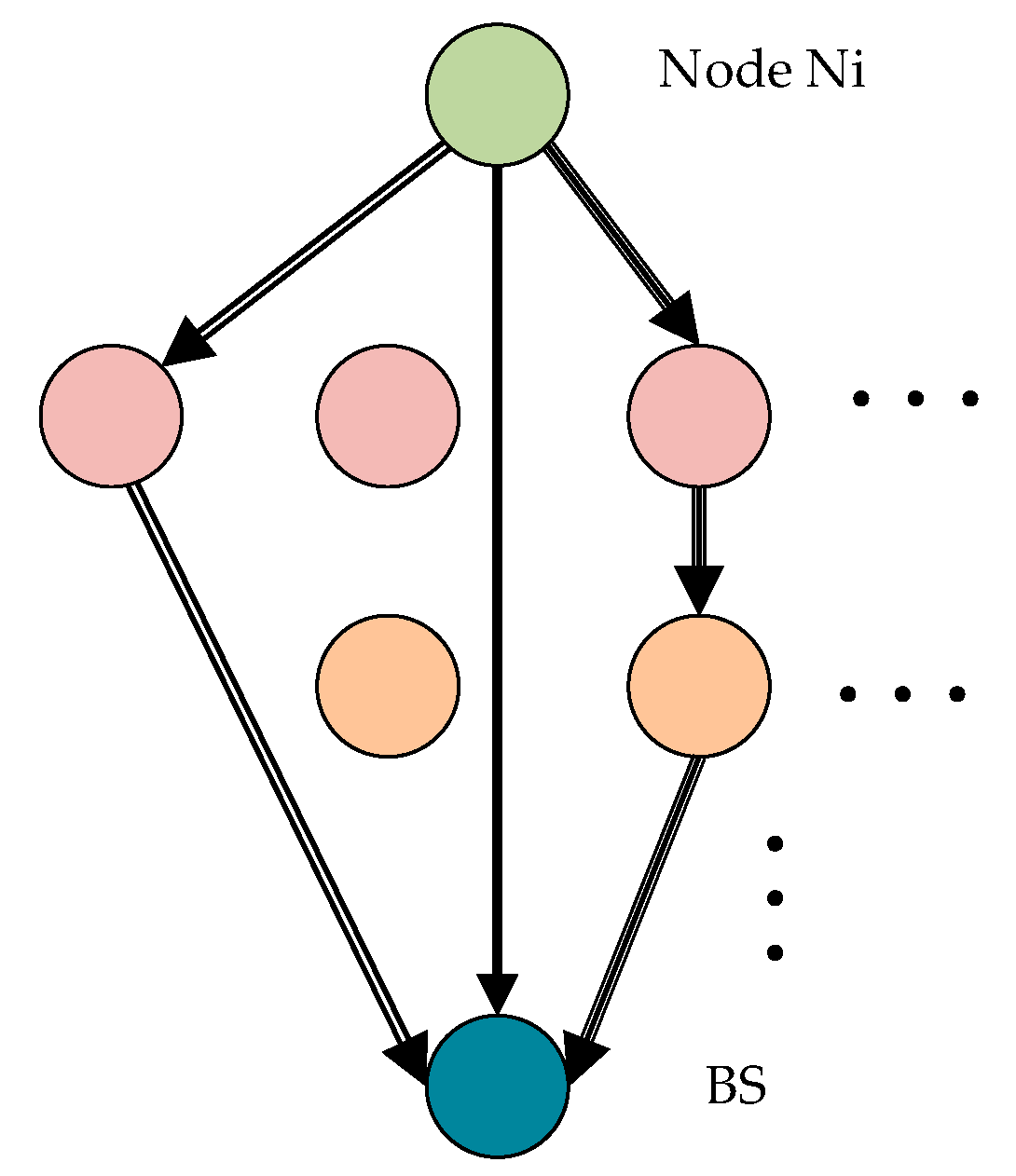
We use the ant colony optimization (ACO) algorithm to optimize the objective function in a short execution time. The paths of the objective function are shown in
Figure 10; each ant tries to find a path from node
to the BS. The other ants follow one of the paths at random, laying pheromone trails, which denotes the average weights of the paths.
ACO is a biologically inspired technique simulating the foraging process of social insects [
41,
42]. ACO uses a graph
.
denotes the nodes in the DBTRN, and
denotes the undirected edges, respectively. Two nodes
,
are neighbors, and
,
. Each edge is annotated with weights. A path is a sequence of nodes and edges between a source and destination. The objective of ACO is to find a path between the source and destination with minimal weights.
To solve the objective function in Equation (10), a path-selecting algorithm for the DBTRN based on ACO is proposed by selecting the edge with the maximum weight when an ant arrives at a node. A complete iteration of the optimized path-selecting algorithm based on ACO consists of the following steps:
Step 1: Initialization
During initialization, each edge of graph
,
in graph
is associated with the initial pheromone weight
, as shown in Equation (20):
Step 2: Construct a probabilistic solution
Constructing a path is based on stepwise estimation for each edge
,
according to Equation (21), where
denotes the neighbors of the
k-th ant at node
, and
is a parameter that controls the influence of
.
Step 3: Pheromone update
After the ant arrives at the destination node, a path is found. On this path, loops are eliminated by checking whether a path includes the same node. Additionally, the ant updates the pheromone level for all the edges on the path. The new pheromone is updated according to Equation (22), where
is the amount of pheromone deposited by the
k-th ant.
Step 4: Pheromone evaporation
In order to make the algorithm robust in dynamic networks, the pheromone needs to be evaporated over time for all the edges. The pheromone is decremented over time, as shown in Equation (23), where
is the pheromone evaporation coefficient.
The algorithm converges if a solution reaches a certain quality level or if no more changes are performed. The pseudo-code of the optimized method based on ACO is shown in Algorithm 2.
| Algorithm 2. Optimized Method |
| 1: | path Ni-BS () |
| 2: | graph_edges = |
| 3: | construct objective functions |
| 4: | initialize pheromone trails and parameters |
| 5: | set iteration number M |
| 6: | for (i = 1: M) |
| 7: | {construct a solution |
| 8: | update local pheromone |
| 9: | compute solution quality} |
| 10 | M = M + 1 |
| 11 | Path = candidate to be optimal solution |
Since the size of the node set in the DBTRN is not specified, the algorithm runs iteratively for increasing N values and has a run time of , where N is the size of the node set of the DBTRN. In comparison, a brute force algorithm would take . Compared with a traditional algorithm, the path-selecting algorithm based on ACO can reduce execution.